Канторово множество (канторов дисконтинуум, пыль Кантора)

1. Канторово множество (канторов дисконтинуум, пыль Кантора,…) - проективно универсальный объект в классе метрических компактов.

П. В. Семенов,
Дубна, 20 июля 2015
.

2. Канторово множество -1

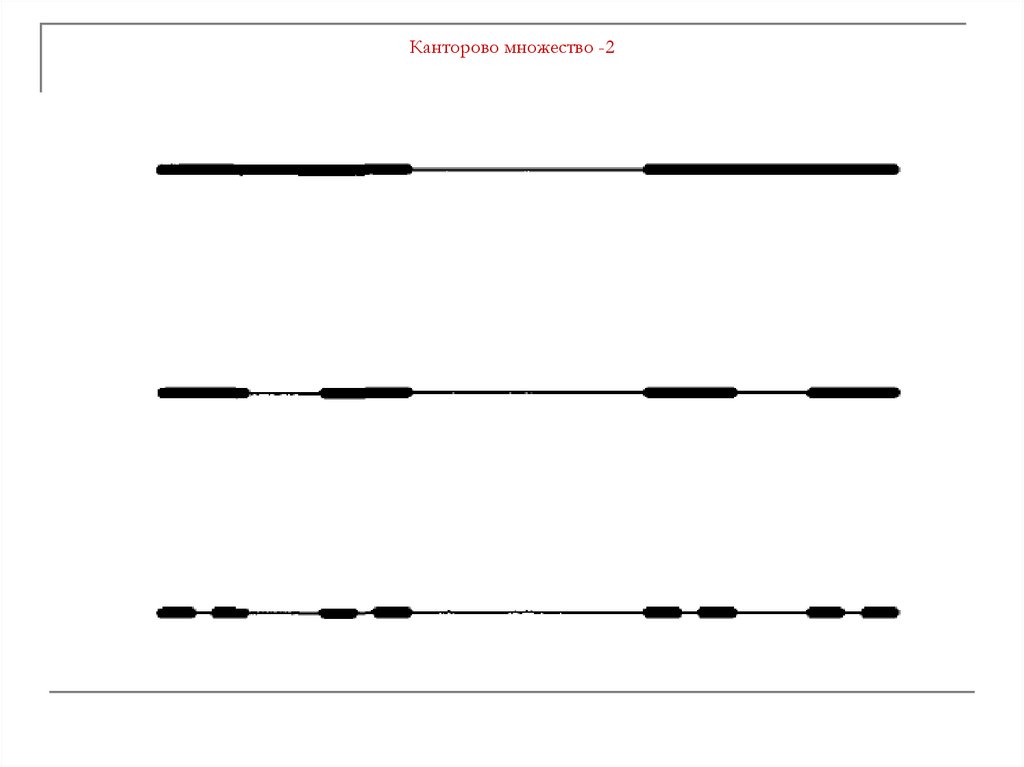
0) Отрезок I = [0; 1].
1) Делим I на три равных отрезка: I 0 , I1 , I 2
Средний интервал удаляем. Остаются I 0 , I 2
2) С каждым из двух оставшихся отрезков делаем то же.
А именно, получаем 6 отрезков длиной 1/9 I 00 , I 01 , I 02 и
I 20 , I 21 , I 22 из которых удаляем средние интервалы.
Остаются I 00 , I 02 , I 20 , I 22 .
3) С каждым из четырех оставшихся отрезков делаем то
же.
И Т. Д.

3. Канторово множество -2

4. Канторово множество -3

Сумма длин удаленных интервалов:
2
1
1
1
1
1
2 2
1 1
1
... 1 ... 1
3
3 3 3
9 9
27 27 27 27
Получается, что из отрезка длиной 1 удалили интервалы,
сумма длин которых также равна 1. А что-нибудь осталось?
Да, и осталось «столько же» точек, сколько было на [0;1].
Кодировка точек канторовского множества.
Пусть a (a1 , a2 , a3 ,....) любая послед-ть символов 0 и 2. Тогда
I a1 I a1a2 I a1a2a3 ... I a1a2a3 ...an ....
послед-ть стягивающихся отрезков, у которых есть ровно
одна общая точка ka .
{ka I a1 I a1a2 I a1a2 a3 ... I a1a2 a3 ...an ... : i
ai 0 или ai 2}

5. Канторово множество -4

Точка: 0
Точка: 1
Точка: 1/3
Точка: 7/9
Код: (2202000….)
Код: (20202020(20))
Канторово множество -4
Примеры.
Код: (000…..)
Код: (222…..)
Код: (0222…..)
Код: (20222…..)
Точка: 2 2 0 2 38
3
9 27 81 81
Точка:
2 1
3
2 0 1 2 0 1 2 0
... 1
3 1
4
3 9 9 3 9 81 3 9
9
ai
Код: a (a1 , a2 , a3 ,....) . Точка: ka i 1 3i
Точки 1-го рода - в коде есть «хвост» из 0 или «хвост» из 2, т.е.
концы удаляемых интервалов. Точки 2-го рода – остальные.

6. Канторово множество -5

Ф 1.К континуально(=существует биекция между К
и [0;1] ).
До-во.
К биективно множеству всех последовательностей
из двух символов 0 и 2,
которое биективно множеству всех подмножеств
множества натуральных чисел,
0
которое континуально ( 2 c ).

7.

8.

Ф 2. Существует сюръекция s из К
на [0;1]
Док-во.
Возьмем точку из К. Выпишем ее код из
0 и 2. Все 2 заменим на 1. Получим
последовательность из 0 и 1.
Рассмотрим ее как разложение
действительного числа из [0;1] в
бесконечную двоичную дробь. Всё.

9. Канторово множество -6

Ф 3 = Ф 1. К континуально
Док-во.
"на"
[0; 1]
[0;1]
Значит, К и [0;1] биективны подмножествам друг друга.
Остается сослаться на теорему Кантора-БернштейнаШрёдера.
"на"
[0;1] - не иньекция.
Ф 4. Сюръекция s :
Док-во.
Всегда s ci s di для любого удаляемого интервала (ci ; di )
1
1
s 0, 011111.....
0,100...
2
3
2
s
3

10. Канторово множество - 7

"на"
[0;1] непрерывна.
Ф 5. Сюръекция s :
0
1
......
Док-во. Формальный ответ:
1
log 1
3
Неформально. Если коды двух точек
1
x и y совпали на первых n местах, то x y n и тогда
3
двоичные дроби s(x),s(y) совпали на первых n местах, т.е.
2
1
s ( x) s ( y ) n
2
Остается формализовать переход
1
x y n
3
1
s( x) s( y ) n
2

11. Канторово множество - 8

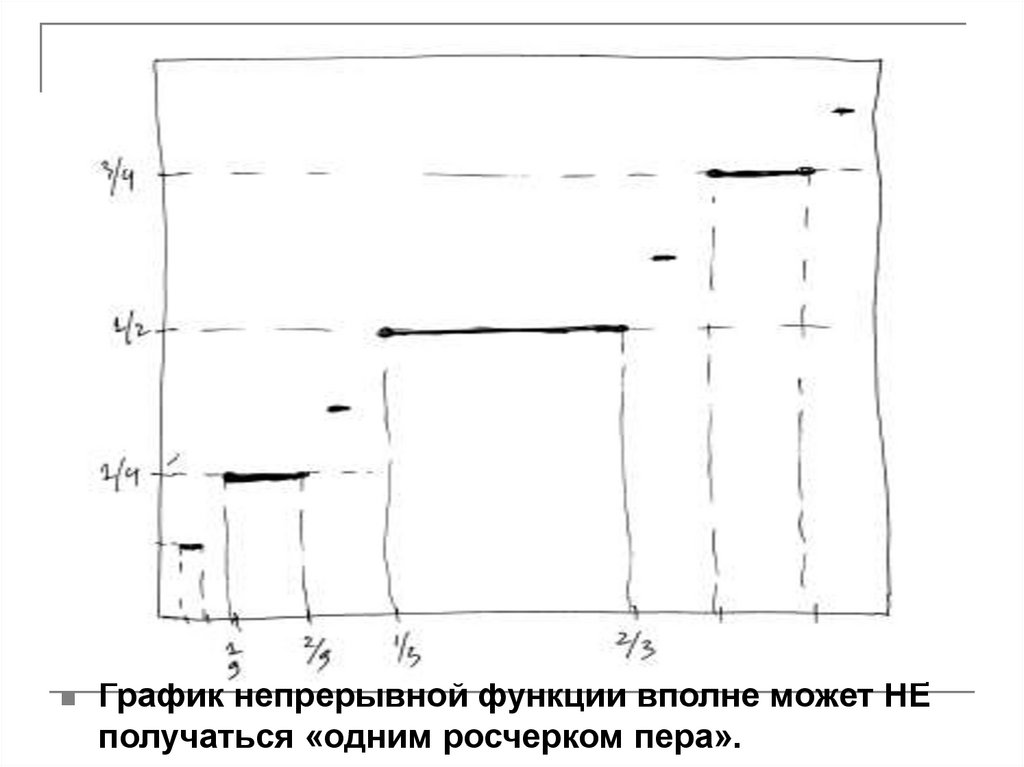
Ф 6 (Канторова лестница, «чортова» лестница).
Существует непрерывная неубывающая сюръекция
отрезка на себя, которая почти всюду постоянна.
Док-во.
"на"
[0;1] на интервалы,
Продолжим сюръекцию s :
удаляемые в процессе построения множества К самым
простым образом.
А именно, так как всегда s ci s di для любого удаляемого
интервала (ci ; di ) , то на этом интервале наша функция будет
соответствующей константой.

12.

График непрерывной функции вполне может НЕ
получаться «одним росчерком пера».

13.

14. Канторово множество - 9

Ф 7. К - компакт без изолированных точек.
Ф 8. К нигде не плотно (= в любом интервале есть
подинтервал, в котором нет точек из К).
Док-во.
1
b a
Для интервала (a;b) выберем n так, чтобы 3n 2 .
Разделим [0;1] на 3n одинаковых отрезков. Один из них,
скажем J , целиком лежит в (a;b) .
Если на n-ом шаге построения К внутренность J удаляют,
то J- нужный подинтервал.
Если нет, то на следующем шаге удаляют среднюю треть J
и эта треть - нужный подинтервал.

15. Канторово множество - 10

Ф 9. Если F - замкнутое подмножество К , то
"на"
существует непрерывная сюръекция r : K
F
такая, что r ( x) x, x F . (F – ретракт К).
Док-во.
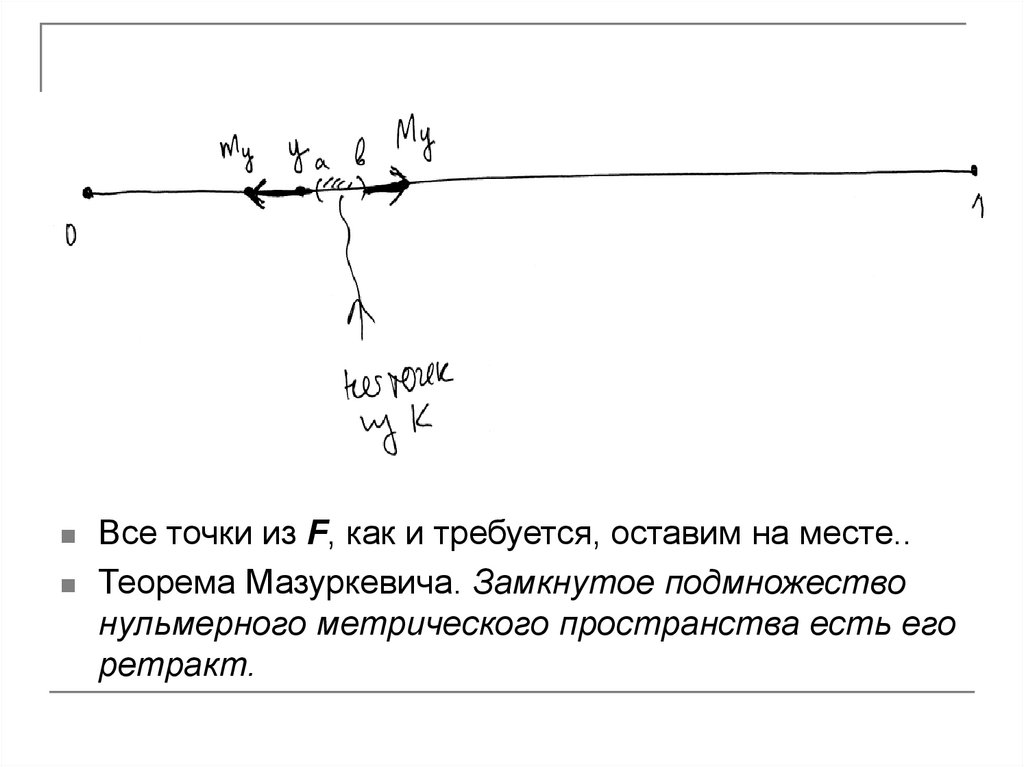
Возьмем y K \ F , my max{x F : x y}, M y min{x F : x y}
По Ф8 найдем (a; b) (m y ; M y ), (a; b) K .
Вырежем (a; b) из прямой и разрез максимально раздвинем:
K (m y ;a] отобразим в m y , а K [b; M y ) отобразим в M y

16.

Все точки из F, как и требуется, оставим на месте..
Теорема Мазуркевича. Замкнутое подмножество
нульмерного метрического пространства есть его
ретракт.

17. Канторово множество - 11

Ф 10. Для любого метрического компакта X
"на"
существует непрерывная сюръекция f : K
X.
Док-во 1 (обходное).
1) Сначала Ф10 устанавливается для специального X, для
"на"
гильбертова куба Q : fQ : K Q .
2) Затем используется (иньективная) универсальность Q :
"гомеоморфизм"
X ' Q, h : X
X'
3) Пусть F ( fQ ) 1 (X') K . Применяем Ф9 о ретракции:
"на"
r : K
F
4) Тогда f h
то, что нужно:
1
fQ r -
K
Q
f , "на"
Q
r
F
fQ , "на"
h 1
X
X '
h

18. Канторово множество - 12

Док-во 2 (почти прямое).
1) Для любого 0 в метрическом компакте X есть конечная сеть,
т.е. конечное множество {x1 , x 2 ,..., x n ( ) } такое, что x X xi x
2) Строим конечные сети для 1, 1/ 2, 1/ 3,....
3) Выписываем поочередно все сети друг за другом. Получаем
последовательность{s1 ,s2 ,...} плотную в X.
4) К каждой точке si «привязан» открытый шарик U ( si ; ri ) ri 0, i
5) Пусть a (a1 , a2 ,....) код точки k ka K .Определим X i X i (k ) X
по правилу X i [Ui ], a i 0; X i X \ Ui , a i 2
6) Пересечение X (k ) X 1 X 2 X 3 ... или пусто, или одноточечно.
7) Пусть F - множество тех точек из K, для которых X ( k ) непусто.
X (k ), k F
Оказывается, что F – замкнуто, а отображение g : k
"на"
есть непрерывная сюръекция g : F X .
"на"
8) Остается использовать Ф9 о ретракции: r : K
F
"на"
и определить f g r : K
X

19.

Mix
Ф11. К – нульмерен
(=в любой окрестности любой точки есть открытозамкнутое подмножество )
Ф12. (уникальность К)
Всякий нульмерный метрический компакт без
изолированных точек гомеоморфен К.
Ф13. Существует непрерывная сюрьекция отрезка на
любой выпуклый компакт Х.
"на"
: сюръекцию f : K
продолжить на смежные
X
интервалы по линейности.

20.

Mix
Ф14. К – однороден (=любую точку можно перевести в
любую автогомеоморфизмом) и
строго однороден (=все clopen гомеоморфны).
Ф15. (частичное решение СН)
Несчетное замкнутое числовое множество содержит
копию К и поэтому континуально.
Y непрерывно отображает полное
Ф15’ Если f : X
метрическое пространство X на несчетное
пространство Y , то X содержит копию К и поэтому
неравенство 0 X c невозможно.
Ф16. Существует измеримое, не борелевское множество.
2 K 2c c

21. Спасибо за внимание.