Похожие презентации:
Механические и электромагнитные волны. Лекция 25
1.
Лекция 25.Механические и электромагнитные
волны
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 281-293.
к.ф.-м.н.
Курочкин А.Р.
2.
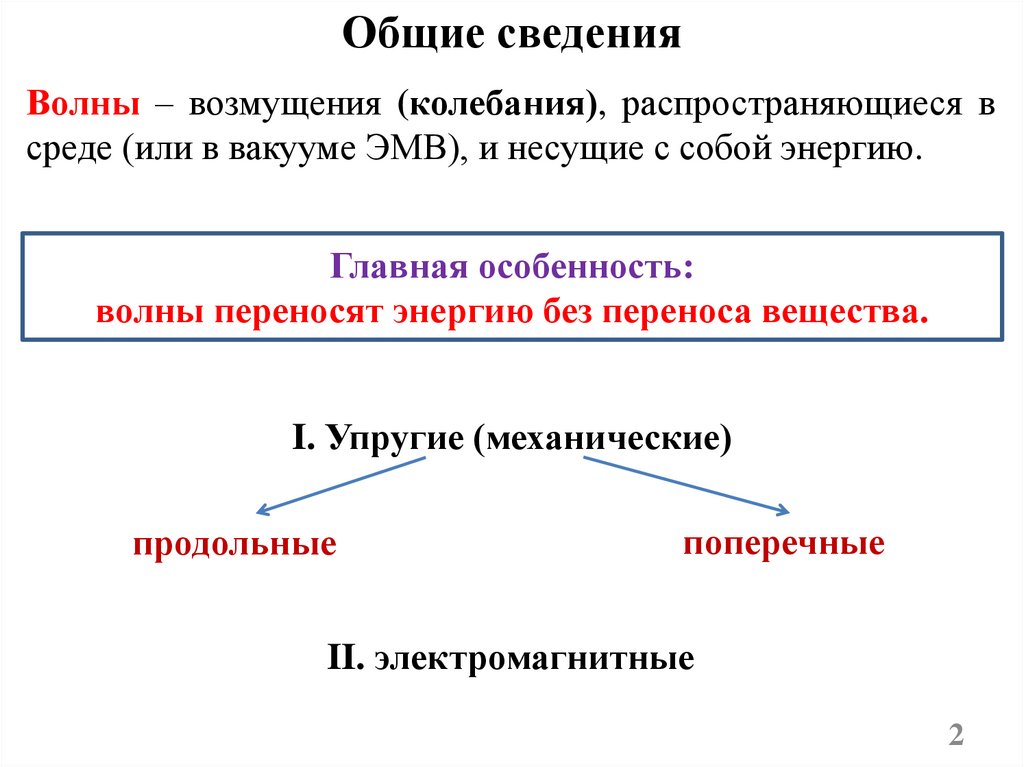
Общие сведенияВолны – возмущения (колебания), распространяющиеся в
среде (или в вакууме ЭМВ), и несущие с собой энергию.
Главная особенность:
волны переносят энергию без переноса вещества.
I. Упругие (механические)
продольные
поперечные
II. электромагнитные
2
3.
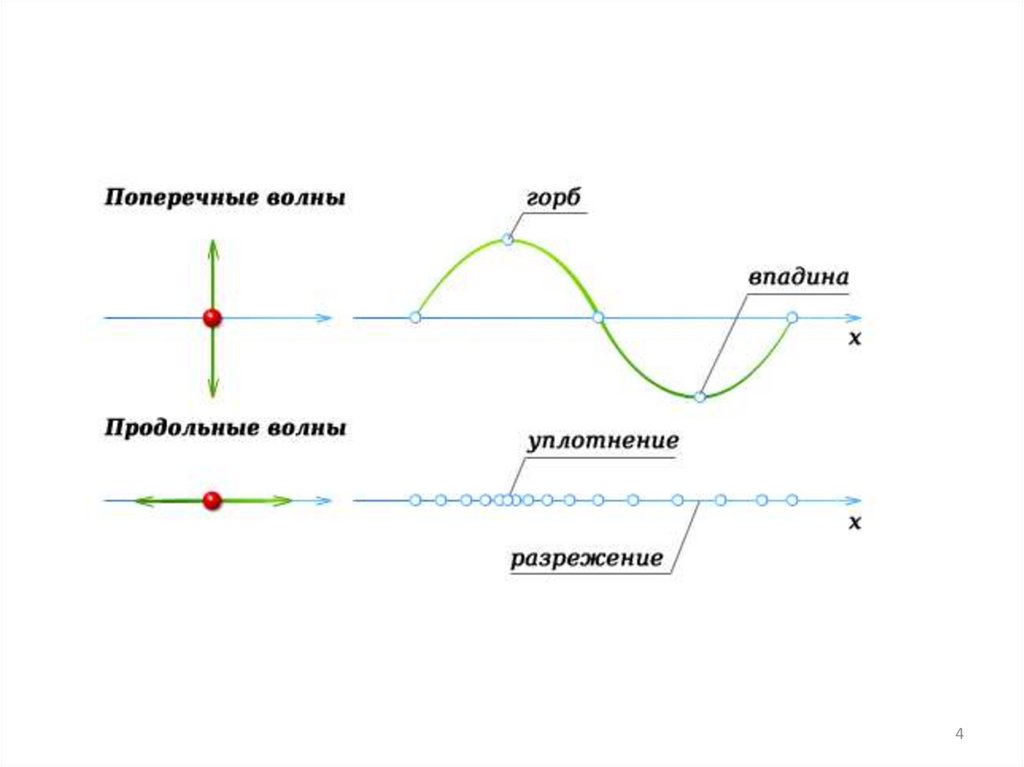
Поперечные и продольные волныПоперечная волна – волна,
в которой частицы среды
колеблются
в
направлениях,
перпендикулярных
к
направлению распространения волны.
Поперечные волны могут возбуждаться в средах, в которых
возникают упругие силы при деформации сдвига, т.е. в
твёрдых телах.
Продольная волна – волна,
в которой частицы среды
колеблются вдоль направления распространения волны.
Продольные волны могут возбуждаться в средах, в которых
возникают упругие силы при деформации сжатия и
растяжения, т.е. в твёрдых, жидких и газообразных телах.
3
4.
45.
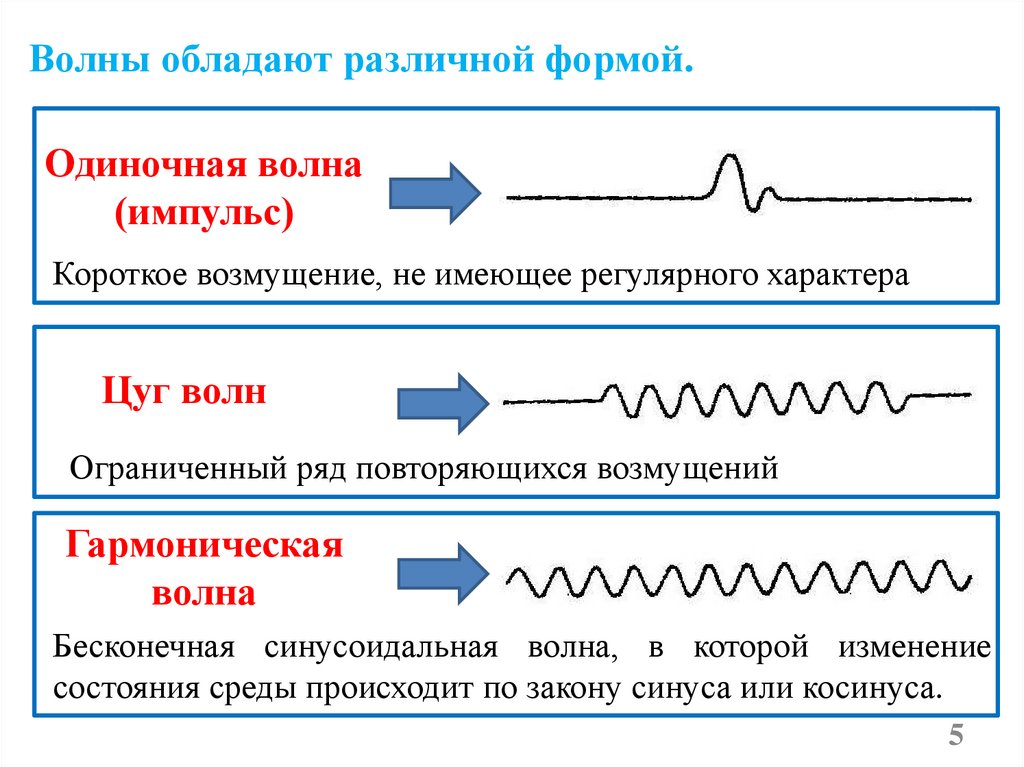
Волны обладают различной формой.Одиночная волна
(импульс)
Короткое возмущение, не имеющее регулярного характера
Цуг волн
Ограниченный ряд повторяющихся возмущений
Гармоническая
волна
Бесконечная синусоидальная волна, в которой изменение
состояния среды происходит по закону синуса или косинуса.
5
6.
Вопрос. Как инициировать возникновение упругойгармонической волны?
Ответ. Необходимо возбудить в каком-либо месте
упругой (твердой, жидкой или газообразной) среды
колебания её частиц. В результате, вследствие
взаимодействия между частицами, это колебание будет
распространяться в среде от частицы к частице со
скоростью υ.
Важно: частицы среды, в которой распространяется
волна, не вовлекаются волной в поступательное
движение, они лишь совершают колебания около
своих положений равновесия.
6
7.
Гармоническая поперечная волна,распространяющаяся со скоростью υ вдоль оси x;
Приведена зависимость между смещением ξ(x,t) частиц
среды, участвующих в волновом процессе, и расстоянием x
этих частиц от источника колебаний O для какого-то
фиксированного момента времени t.
7
8.
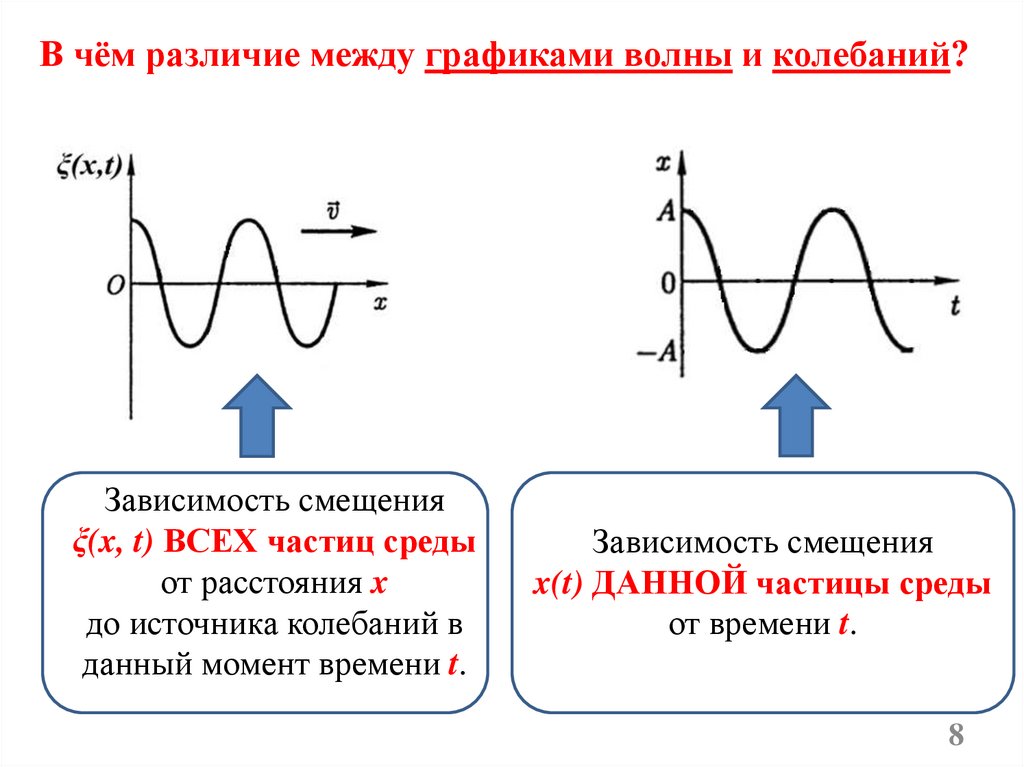
В чём различие между графиками волны и колебаний?Зависимость смещения
ξ(x, t) ВСЕХ частиц среды
от расстояния x
до источника колебаний в
данный момент времени t.
Зависимость смещения
x(t) ДАННОЙ частицы среды
от времени t.
8
9.
Длина волны λ –• расстояние
между
ближайшими
частицами,
колеблющимися
в
одинаковой фазе.
• расстояние на которое распространяется
волна за один период.
T
м
υ – скорость волны;
T – период волны;
ν – частота волны.
При распространении упругой гармонической волны
колеблются не только частицы, расположенные на оси x, а
совокупность частиц, заключённых в некотором объёме.
Распространяясь от источника колебаний, волновой процесс
охватывает всё новые и новые части пространства.
9
10.
Волновой фронт – геометрическое место точек, до которыхдоходят колебания к моменту времени t.
Волновой фронт волны представляет собой ту
поверхность, которая отделяет часть пространства, уже
вовлечённую в волновой процесс, от области, в которой
колебания ещё не возникли.
Волновая поверхность – геометрическое место точек,
колеблющихся в одинаковой фазе.
Волновую поверхность можно провести через любую
точку пространства, охваченного волновым процессом.
10
11.
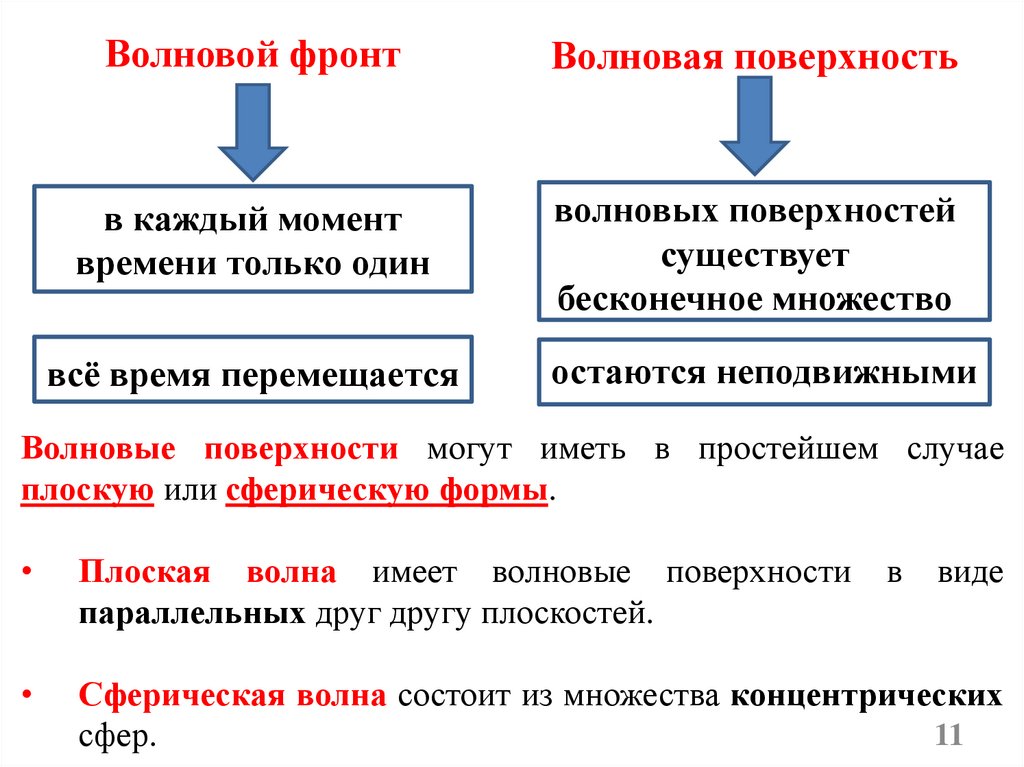
Волновой фронтВолновая поверхность
в каждый момент
времени только один
волновых поверхностей
существует
бесконечное множество
всё время перемещается
остаются неподвижными
Волновые поверхности могут иметь в простейшем случае
плоскую или сферическую формы.
Плоская волна имеет волновые поверхности
параллельных друг другу плоскостей.
Сферическая волна состоит из множества концентрических
11
сфер.
в
виде
12.
Бегущие волныБегущие волны – волны, которые переносят в пространстве
энергию.
Рассмотрим плоскую волну, колебания которой носят
гармонический характер, а ось x совпадает с направлением
распространения волны.
Колебания
частиц в
плоскости x=0
Колебания
частиц в
плоскости x
( x 0, t ) A cos t
x
( x, t ) A cos t
Колебания частиц будут отставать по времени от колебания
x
источника на ;
υ – скорость распространения волны.
12
13.
Уравнение плоской волныx
( x, t ) A cos t 0
A=const – амплитуда волны;
ω – циклическая частота;
φ0 – начальная фаза волны;
. t x – фаза плоской волны.
0
Волновое число k – показывает, сколько длин волн
укладывается на отрезке 2π.
2
2 1
k
.
м
13
14.
( x, t ) A cos t kx 0Применим формулу Эйлера
i
e cos i sin ,
i 1
2
получим
( x, t ) Ae
i t kx 0
где физический смысл имеет лишь действительная часть.
14
15.
Допустим, что при волновом процессе фаза постоянна, т.е.x
t 0 const.
Возьмём производную от выражения
d x
t 0.
dt
1 dx
1
0
dt
dx
.
dt
где υ (фазовая скорость) – скорость перемещения фазы
волны.
15
16.
В общем случае распространение волн в однороднойизотропной среде описывается волновым уравнением –
дифференциальным уравнением в частных производных
1
2 2 2 2
2
x
y
z
t
2
2
2
2
или
1
2 2 ,
t
2
где υ - фазовая скорость;
2
2
2
2 2 2 – оператор Лапласа.
x y z
16
17.
Волновое уравнениеУравнение
любой
волны
есть
решение
некоторого
дифференциального уравнения, называемого волновым.
Чтобы установить вид волнового уравнения, сопоставим вторые
частные производные по координатам и времени от функции
( x, y, z , t ) A cos t kr ,
описывающей плоскую волну.
где
kr k x x k y y k z z
Продифференцировав данное уравнение дважды по каждой из
переменных, получим:
17
18.
( x, y, z , t )A cos t k x x k y y k z z k x A sin t kr ,
x
x
2 ( x, y, z , t )
2
2
k
A
sin
t
k
x
k
y
k
z
k
A
cos
t
kr
k
x
x
y
z
x
x ( x, y , z , t )
2
x
x
Получим аналогично
2 ( x, y, z , t )
2
k
y ( x, y , z , t );
2
y
2 ( x, y, z , t )
2
k
z ( x, y , z , t )
2
z
( x, y, z , t )
A cos t k x x k y y k z z A sin t kr ,
t
t
2 ( x, y, z , t )
A sin t k x x k y y k z z 2 A cos t kr 2 ( x, y, z , t )
2
t
t
Сложим первые три уравнения
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z, t )
2
2
2
k
(
x
,
y
,
z
,
t
)
k
(
x
,
y
,
z
,
t
)
k
x
y
z ( x, y , z , t )
2
2
2
x
y
z
18
19.
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z , t )2
2
2
k
k
k
( x, y , z , t )
x
y
z
2
2
2
x
y
z
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z , t )
2
k
( x, y , z , t )
x 2
y 2
z 2
2 ( x, y, z , t )
2
( x, y , z , t )
2
t
Приравнивая правые части уравнений, получим
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z, t ) 1
2 ( x, y, z , t );
2
2
2
x
y
z
k
2 ( x, y, z , t ) 1
( x, y, z , t );
2
2
t
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z , t ) k 2 2 ( x, y, z , t )
2
x 2
y 2
z 2
t 2
2 1
2 2 2 2 2 2
k2
2
2 ( x, y, z , t ) 2 ( x, y, z , t ) 2 ( x, y, z , t ) 1 2 ( x, y, z, t ) - волновое уравнение.
2
2
2
2
x
y
z
t 2
19
20.
Электромагнитные волныЭлектромагнитная волна - переменное электромагнитное
поле, распространяющееся в пространстве с конечной
скоростью.
Источником электромагнитных волн может быть:
1. Любой электрический колебательный контур;
2. Проводник,
по
которому
течёт
переменный
электрический ток;
3. Заряженная частица, движущаяся с ускорением.
Для возбуждения электромагнитных волн необходимо
создать в пространстве переменное электрическое поле или
переменное магнитное поле изменяющееся с большой
частотой.
20
21.
Для полученияэлектромагнитных волн
непригодны
закрытые колебательные контуры,
т.к. в них электрическое поле сосредоточено
между обкладками конденсатора, а
магнитное – внутри катушки индуктивности.
Необходимо, чтобы объём пространства,
в котором создаётся ЭМП,
был достаточно велик.
21
22.
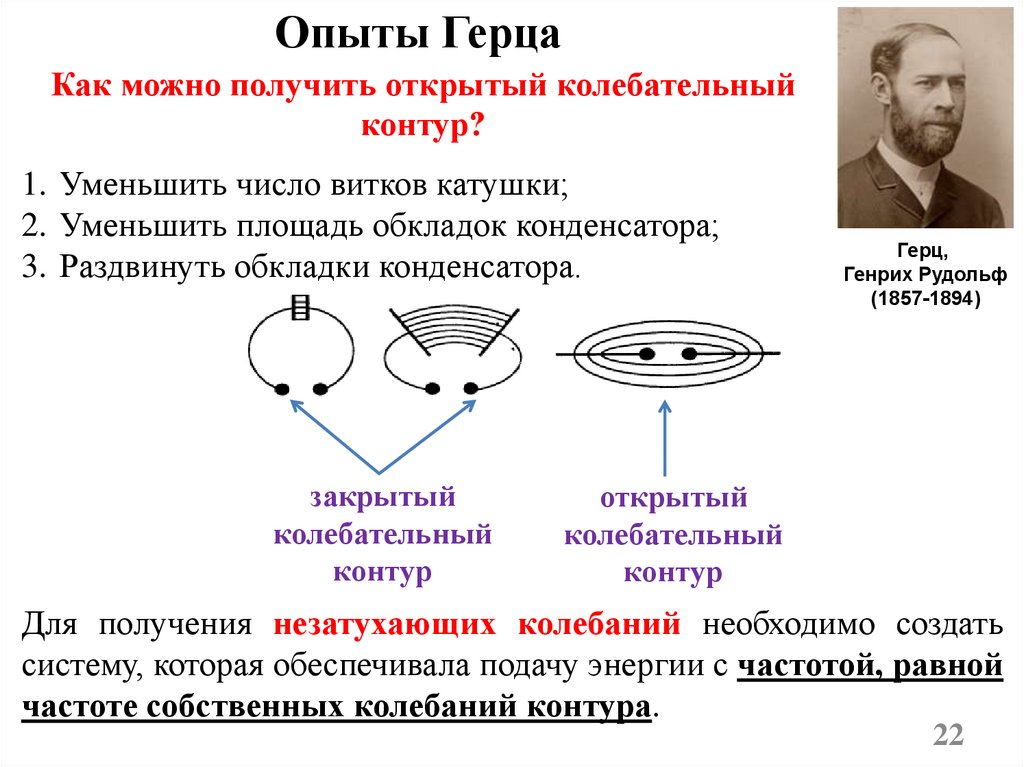
Опыты ГерцаКак можно получить открытый колебательный
контур?
1. Уменьшить число витков катушки;
2. Уменьшить площадь обкладок конденсатора;
3. Раздвинуть обкладки конденсатора.
закрытый
колебательный
контур
Герц,
Генрих Рудольф
(1857-1894)
открытый
колебательный
контур
Для получения незатухающих колебаний необходимо создать
систему, которая обеспечивала подачу энергии с частотой, равной
частоте собственных колебаний контура.
22
23.
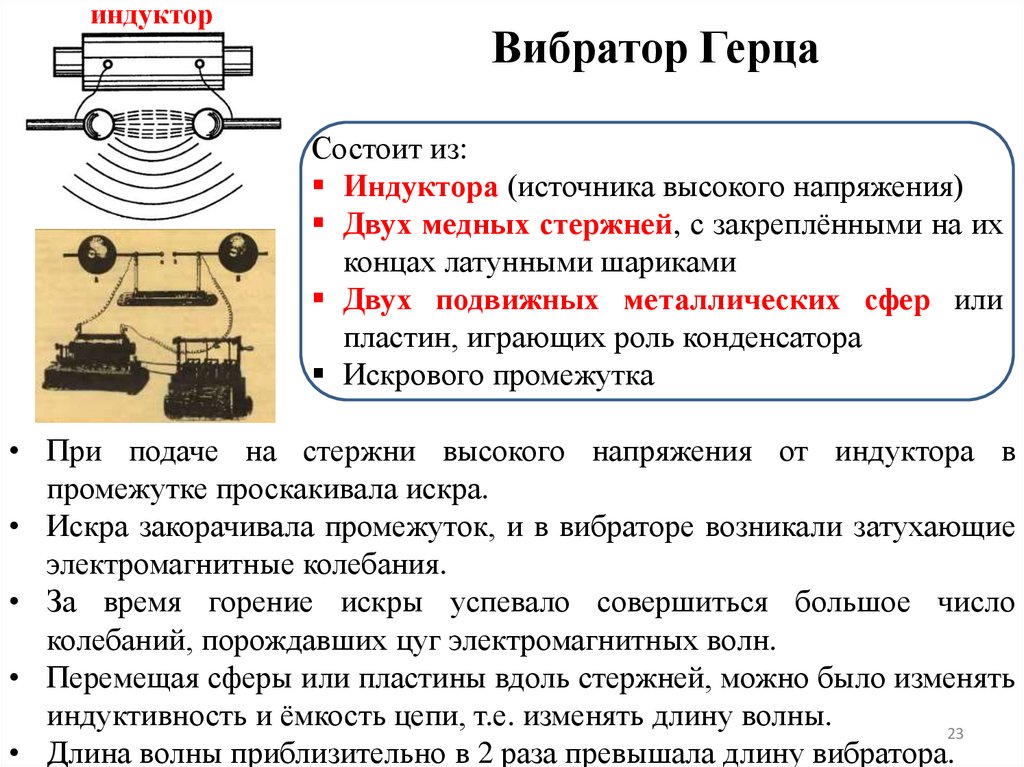
индукторВибратор Герца
Состоит из:
Индуктора (источника высокого напряжения)
Двух медных стержней, с закреплёнными на их
концах латунными шариками
Двух подвижных металлических сфер или
пластин, играющих роль конденсатора
Искрового промежутка
• При подаче на стержни высокого напряжения от индуктора в
промежутке проскакивала искра.
• Искра закорачивала промежуток, и в вибраторе возникали затухающие
электромагнитные колебания.
• За время горение искры успевало совершиться большое число
колебаний, порождавших цуг электромагнитных волн.
• Перемещая сферы или пластины вдоль стержней, можно было изменять
индуктивность и ёмкость цепи, т.е. изменять длину волны.
23
• Длина волны приблизительно в 2 раза превышала длину вибратора.
24.
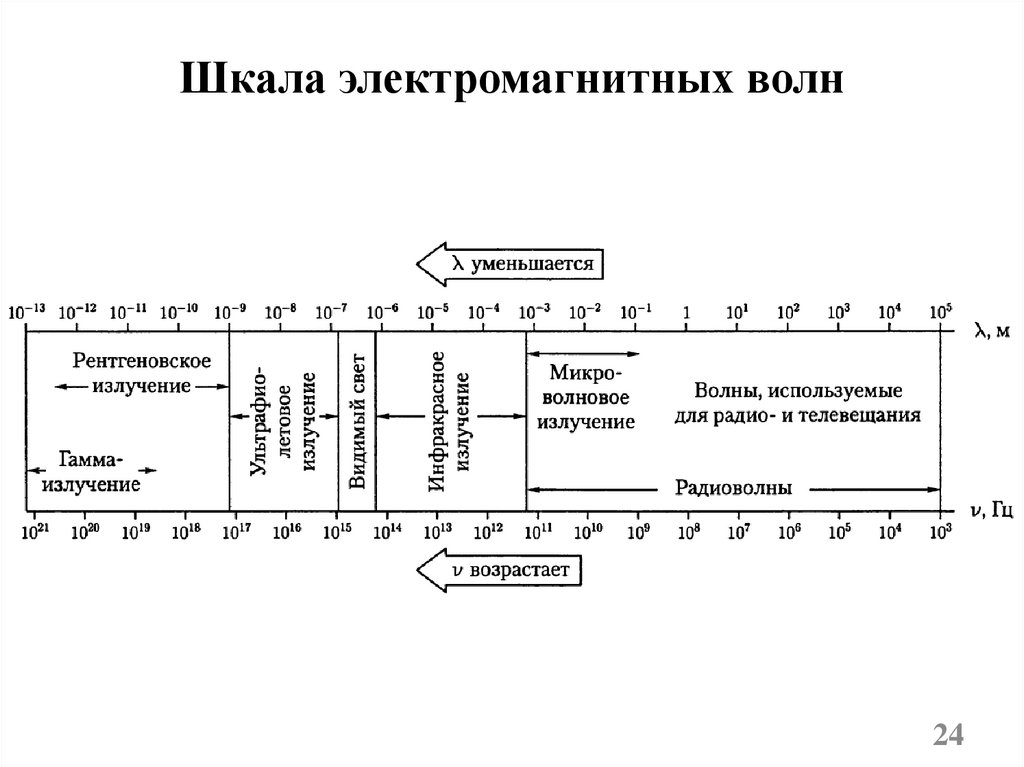
Шкала электромагнитных волн24
25.
Диапазон электромагнитных волнЭлектромагнитные волны
отличаются друг от друга
по способам их генерации и регистрации.
25
26.
Дифференциальное уравнение ЭМВИз уравнений Максвелла следует, что для однородной и
изотропной среды вдали от зарядов и токов, создающих
ЭМП, векторы напряжённостей E и H переменного ЭМП
удовлетворяют волновому уравнения типа:
1 2 E
E 2 2 ;
t
1 2 H
H 2
,
2
t
B 0 H
2
2
2
где 2 2 2 – оператор Лапласа;
x y z
υ – фазовая скорость.
26
27.
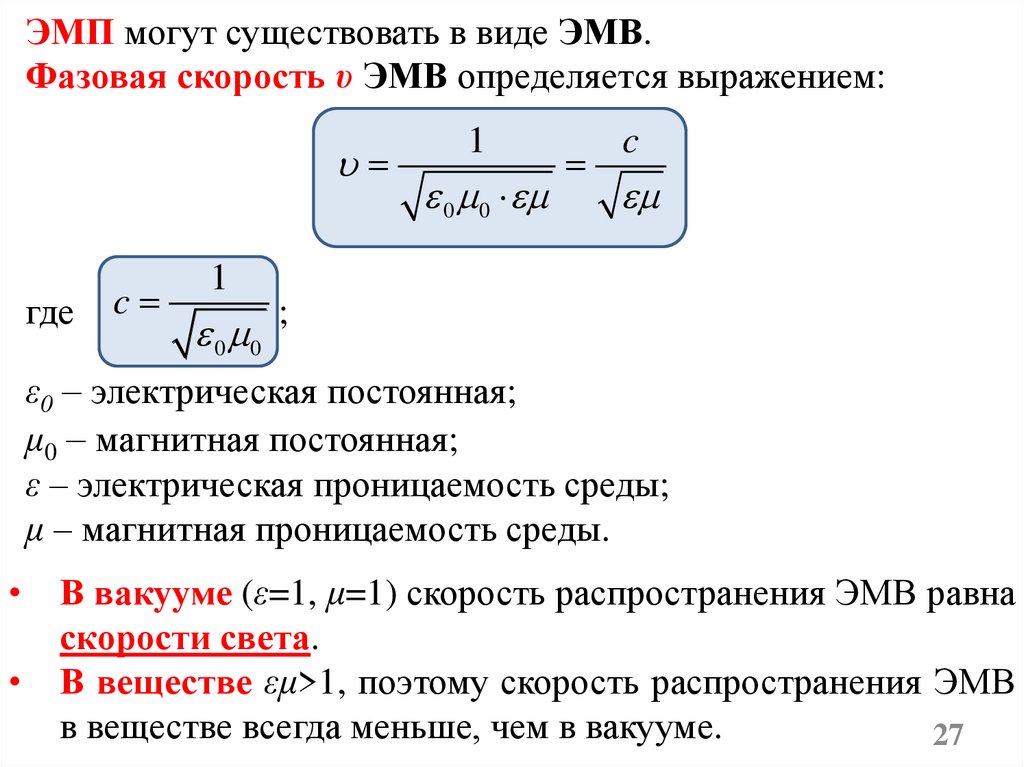
ЭМП могут существовать в виде ЭМВ.Фазовая скорость υ ЭМВ определяется выражением:
где
c
1
0 0
c
1
0 0
;
ε0 – электрическая постоянная;
μ0 – магнитная постоянная;
ε – электрическая проницаемость среды;
μ – магнитная проницаемость среды.
В вакууме (ε=1, μ=1) скорость распространения ЭМВ равна
скорости света.
В веществе εμ>1, поэтому скорость распространения ЭМВ
в веществе всегда меньше, чем в вакууме.
27
28.
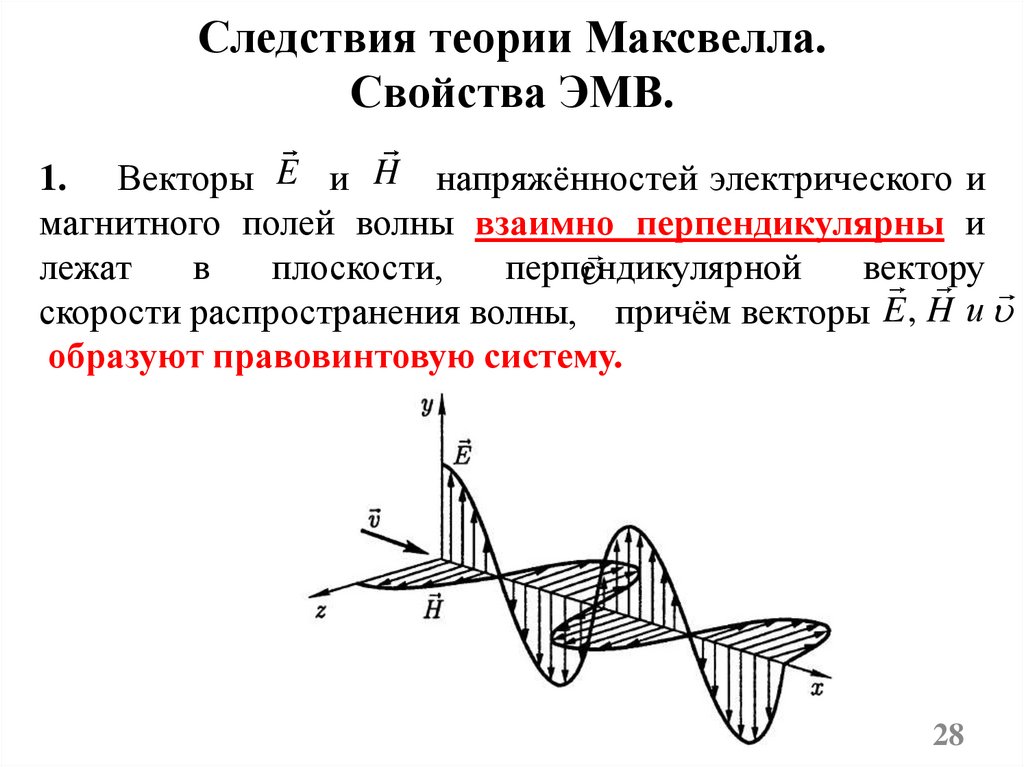
Следствия теории Максвелла.Свойства ЭМВ.
1. Векторы E и H напряжённостей электрического и
магнитного полей волны взаимно перпендикулярны и
лежат
в
плоскости,
перпендикулярной
вектору
скорости распространения волны, причём векторы E , H и
образуют правовинтовую систему.
28
29.
2. Векторы E и H всегдаколеблются в одинаковых фазах (синфазно),
[E и H одновременно достигают максимума,
одновременно обращаются в ноль]
причём мгновенные значения E и H
в любой точке связаны соотношением
0 E 0 H .
3. Из уравнений получим
1 2 E
E 2 2 ;
t
2
1
H
H
,
2
2
t
2
2 Ey
1 Ey
;
2 2
2
x
t
2
2
H
Hz
1
z
2
.
2
x 2
t
29
30.
Решением уравнений будут являться уравненияE y E0 cos t kx ;
H z H 0 cos t kx ,
E0 и H0 – амплитуды напряжённостей электрического и
магнитного полей волны;
ω – циклическая частота волны;
k – волновое число;
φ – начальные фазы колебаний в точках с координатой
x=0.
30
31.
Энергия и импульс ЭМВОбъёмная плотность w энергии ЭМВ равна
w wE wH
Подставим
0 E 2
2
0 H 2
2
.
0 E 0 H .
Получим, что объёмные плотности энергии электрического и
магнитного полей в каждый момент времени одинаковы
wE wH
w 2 wE 0 E 2 0 0 EH .
Домножив на υ, получим
S w EH .
31
32.
S w E HE H
- вектор Умова-Пойнтинга
(вектор плотности потока
электромагнитной энергии)
S EH sin 90 EH
1. Вектор S
направлен в сторону распространения
электромагнитной волны,
2. Модуль вектора
равен энергии, переносимой
S
электромагнитной волной за единицу времени через
единичную
площадку,
перпендикулярную
направлению распространения волны.
32
33.
Частота ЭМВ при переходе из одной среды в другую остаётсяпостоянной.
1 2 const
Интенсивность I ЭМВ в данной точке пространства есть модуль
среднего по времени значения плотности потока энергии,
переносимой световой волной.
I S
t
w
EH
t
Интенсивность I – величина, определяемая средней по времени
энергией, переносимой ЭМВ в единицу времени сквозь
единичную
площадку,
перпендикулярную
направлению
распространения волны.
W
P
I
S t S
33
34.
Можно показать, чтоI S
t
1 0 2
2
Emax const Emax
2 0
I
A
2
Интенсивность распространения света в однородной среде
пропорциональна квадрату амплитуды ЭМВ.
34
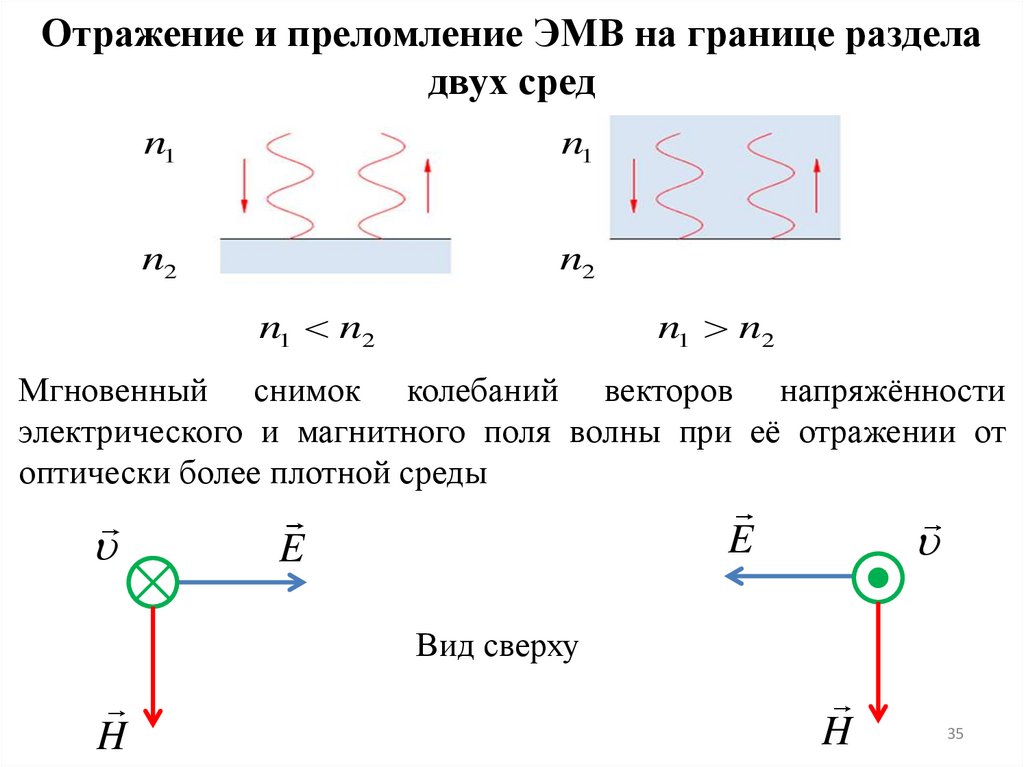
35.
Отражение и преломление ЭМВ на границе разделадвух сред
n1
n1
n2
n2
n1 n2
n1 n2
Мгновенный снимок колебаний векторов напряжённости
электрического и магнитного поля волны при её отражении от
оптически более плотной среды
E
E
Вид сверху
H
H
35
36.
n1Падающая ЭМВ
Отражённая ЭМВ
n2
Преломлённая ЭМВ
n1 n2
Колебания в падающей и в прошедшей во вторую среду волнах
происходят на границе раздела в одинаковой фазе – при
прохождении волны через эту границу фаза не претерпевает
скачка.
Eпрелом
2n1
Eпад
n1 n2
36
37.
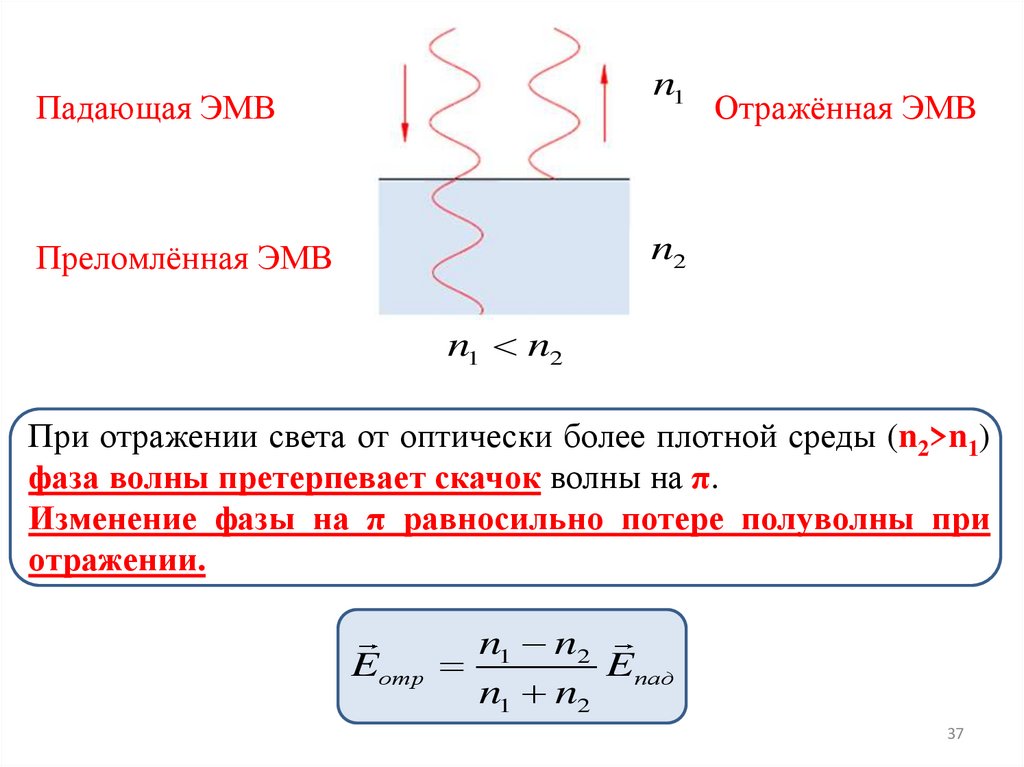
n1Падающая ЭМВ
Отражённая ЭМВ
n2
Преломлённая ЭМВ
n1 n2
При отражении света от оптически более плотной среды (n2>n1)
фаза волны претерпевает скачок волны на π.
Изменение фазы на π равносильно потере полуволны при
отражении.
Eотр
n1 n2
Eпад
n1 n2
37
38.
3. ЭМВ переносят не только энергию, но и импульс.W
pим
c
Если тело полностью поглощает падающую на него энергию, то
давление, оказываемое ЭМВ на тело, равно среднему значению
объёмной плотности энергии в падающей ЭМВ.
pдав w
Давление ЭМВ объясняется тем, что
1. под действием электрического поля волны заряженные
частицы вещества начинают упорядоченно двигаться и
2. подвергаются со стороны магнитного поля волны действию
сил Лоренца.
38
39.
Эффект ДоплераИзменение частоты (длины волны) излучения,
воспринимаемой наблюдателем (приёмником),
вследствие движения источника излучения и/или
движения наблюдателя (приёмника).
1. Источник
и
приёмник
покоятся
относительно среды (υист= υпр=0).
Доплер, Кристиан
(1803-1853)
Длина волны в рассматриваемой среде
T .
0
Волна достигнет приёмника и вызовет
чувствительного элемента с частотой
0.
T
колебания
его
Частота ν регистрации приёмника равна
частоте ν0 излучающего источника.
39
40.
2. Приёмник приближается к источнику, а источникпокоится, т.е. υпр>0, υист=0.
Скорость распространения волны относительно приёмника
станет равной υ+υпр.
Частота в этом случае будет равна
пр пр пр 0
,
T
т.е. частота колебаний, воспринимаемых приёмником, в
пр
раз больше частоты колебаний источника.
40
41.
3. Источник приближается к приёмнику, а приёмникпокоится, т.е. υист>0, υпр=0.
Скорость распространения
колебаний зависит лишь от свойств среды.
Звуковая волна, излучённая источником
пройдёт путь к приёмнику λ=υT, независимо
от того, движется ли источник или покоится.
За это же время источник пройдёт в
направлении волны расстояние υистT. т.е.
длина волны λ′ в направлении движения
сократится и станет равной
' истT ист T
41
42.
Тогда0
.
' ист T ист
частота ν колебаний, воспринимаемых приёмником,
увеличится в
ист
раз.
42
43.
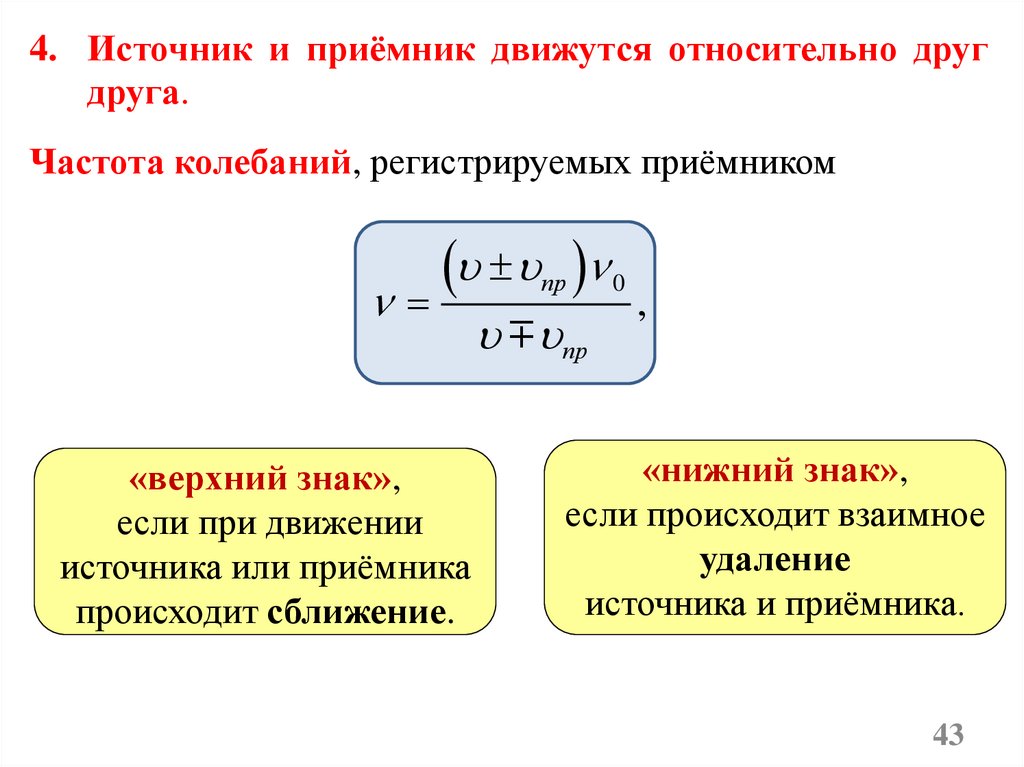
4. Источник и приёмник движутся относительно другдруга.
Частота колебаний, регистрируемых приёмником
пр
пр
«верхний знак»,
если при движении
источника или приёмника
происходит сближение.
0
,
«нижний знак»,
если происходит взаимное
удаление
источника и приёмника.
43






























 Физика
Физика