Постоянный электрический ток

1.

Постоянный электрический ток
Тема лекции
Сегодня 2 ноября 2021 г.

2.

План:
• Электрический ток и его характеристики.
• Законы постоянного электрического тока.
• Разветвлённые цепи. Правила Кирхгофа.

3.

Электрический ток и его характеристики
Электрический ток - упорядоченное движение электрических зарядов
Условия существования электрического тока:
1. наличие в теле свободных заряженных частиц (носителей тока),
2. наличие электрического поля.
Сила тока – скалярная физическая величина равная отношению заряда,
прошедшего через поперечное сечение проводника, ко времени, за которое этот
заряд прошёл:
q
I
t
В СИ измеряется в Амперах (А).
Сила тока численно равна заряду, прошедшему через поперечное сечение за
одну секунду.
За направление тока принимается направление, в котором перемещаются
положительные носители.
Постоянный электрический ток – это ток, который не меняется ни по величине и
ни по направлению.

4.

Если сила тока меняется во времени, то выражение записывается в
дифференциальном виде:
I
dq
dt
Сила тока характеризует течение тока во всем сечении. Но в разных участках
сечения может проходить разное количество заряда. Более детальную
информацию от течении заряда в проводнике дает вектор плотности тока.
Плотность тока – векторная физическая величина равная отношению силы тока,
протекающего через перпендикулярное направлению тока сечение проводника,
к величине площади этого сечения:
I
j
S
I – сила тока, протекающее через сечение S
S↓ - сечение, перпендикулярное течению зарядов
↓
Плотность тока измеряется в амперах на метр в квадрате (А/м2).
Если плотность тока в разных точках сечения разная, то применяется выражение:
dI
j
dS
dI – сила тока, протекающее через сечение dS
dS↓ - бесконечно малое сечение
↓

5.

Зная плотность тока во всех точках проводника можно найти силу тока.
Если плотность тока в сечении одинаковая:
I jS
Если плотность тока в сечении неодинаковая:
I jdS
S
↓

6.

Сторонние силы. Эдс. Напряжение
В замкнутой цепи должны иметься участки, на которых перенос положительных
зарядов происходит в направлении возрастания φ, т. е. против сил
электростатического поля. Перемещение носителей на этих участках возможно
лишь с помощью сторонних сил.
Сторонние силы – это неэлектростатического происхождения, способные
перемещать положительный заряд из точки с меньшим потенциалом в точку с
большим потенциалом.
Эти силы могут иметь химическую, электромагнитную, механическую или
иную природу, кроме электростатической.
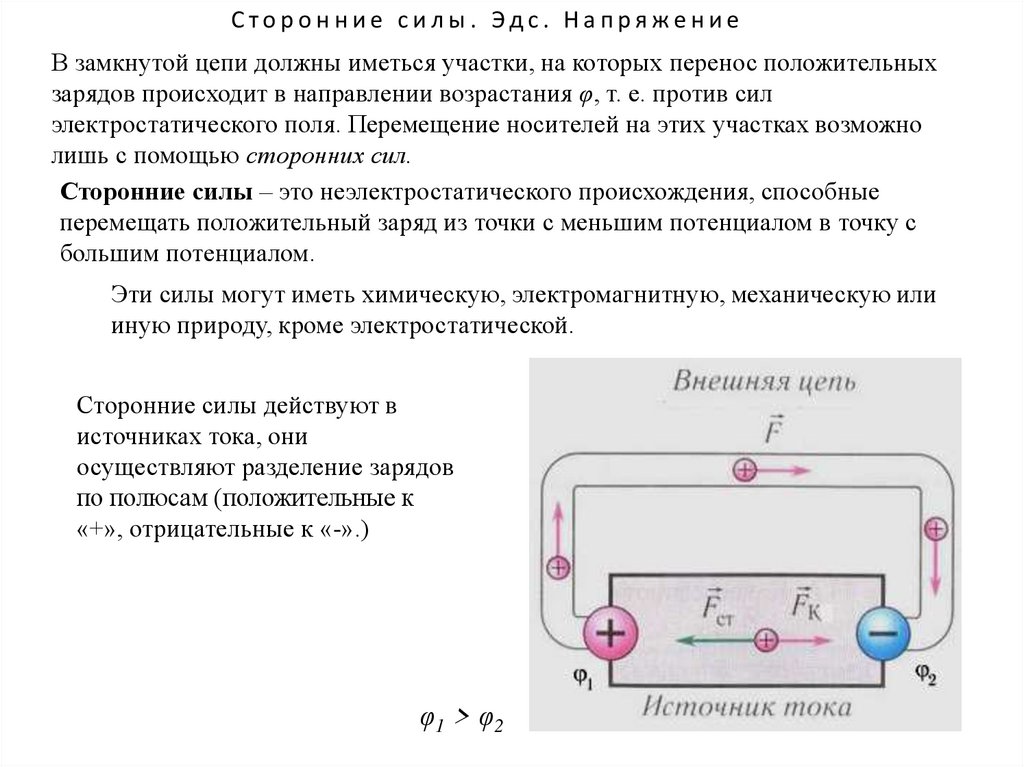
Сторонние силы действуют в
источниках тока, они
осуществляют разделение зарядов
по полюсам (положительные к
«+», отрицательные к «-».)
φ1 > φ2

7.

При перемещении заряда сторонние и электрические силы совершают работу.
Электродвижущая сила (эдс) – физическая величина равная отношению работы
сторонних сил по перемещению заряда к величине этого заряда:
Aст
q
Аст – работа сторонних сил по перемещению заряда q
Эдс измеряется в вольтах (В).
Эдс численно равна работе сторонних сил по перемещению 1 кулона заряда.
Эдс = 1,5 В.

8.

Напряжение – физическая величина, равная отношению работы
электростатических и сторонних сил по перемещению заряда к величине этого
заряда:
U
A Aст
q
Проведем преобразования.
U
A Aст
A
A
ст 1 2
q
q
q
1 2
Таким образом, получаем:
U ( 1 2 )
Участок цепи, в котором отсутствуют сторонние силы, называют однородным. В
противном случае он будет называться неоднородным.
Для однородного участка напряжение равно разности потенциалов:
U ( 1 2 ) ( 1 2 )

9.

Закон Ома. Сопротивление
Закон Ома: сила тока, текущего по металлическому проводнику,
пропорциональна напряжению на проводнике.
I
U
R
R - электрическое сопротивление проводника.
Сопротивление измеряется в Омах (Ом).
Ом это сопротивление такого проводника, в котором при напряжении 1 вольт
течет ток силой 1 ампер.
Величина сопротивления зависит от формы и размеров проводника, а также
от свойств материала, из которого он сделан.
Для однородного цилиндрического проводника:
l — длина проводника,
S — площадь его поперечного сечения,
ρ —удельное электрическое сопротивление.
l
R
S
l
S

10.

Выведем закон Ома в дифференциальной форме.
U
I
R
SEl
jS
l
j
E
El
jS
l
S
делим обе части уравнения на
Sиl
введем обозначение:
1
Закон Ома в дифференциальной форме:
j E
j – плотность тока,
γ – удельная проводимость,
Е – напряженность электрического поля
Формула связывает плотность тока в любой точке внутри проводника с
напряженностью электрического поля в этой же точке.

11.

Закон Ома для неоднородного участка цепи
Неоднородным называется участок цепи, в котором действуют сторонние силы, и,
следовательно, содержит эдс.
( 1 2 ) 12
I
R r
- закон Ома для неоднородного участка цепи.
φ1, φ2 - потенциалы,
ε12 – эдс на участке 1-2,
R – сопротивление проводника
Если источник включен как на рис. (а)
(повышает потенциал участка по
выбранному направлению тока), то ЭДС
в формуле берется со знаком «плюс»,
Если источник включен как на рис. (б)
(понижает потенциал участка по
выбранному направлению тока), то ЭДС
в формуле берется со знаком «минус»,

12.

Если соединить между собой проводником точки 1 и 2, то получим замкнутую
цепь.
В таком случае 1 2 , и закон Ома примет вид:
I
R r
- закон Ома для замкнутой цепи
ε - эдс,
R – сопротивление проводника,
r – внутренне сопротивление проводника.

13.

Работа и мощность тока. Закон Джоуля-Ленца
Работа тока электрического тока на участке цепи:
А IUt
I – сила тока,
U – напряжение на участке,
t – время.
Разделив работу на время, за которое она совершается, получим выражение для
мощности, развиваемую током на рассматриваемом участке цепи.
P IU
I – сила тока,
U – напряжение на участке.
Часто используют внесистемную единицу измерения работы – 1 киловатт*час.
1 кВт*ч = 1000 Вт * 3600 с = 3.600.000 Дж.

14.

В случае, когда проводник неподвижен и химических превращений в нем не
совершается, работа тока затрачивается на увеличение внутренней энергии
проводника, в результате чего проводник нагревается.
Q A
Q
I
R
При протекании тока в проводнике выделяется количество теплоты Q,
которое можно определить из закона Джоуля-Ленца:
Q I Rt
2
I – сила тока,
R – сопротивление,
t – время.

15.

Разветвленные цепи. Правила Кирхгофа
Обобщенный закон Ома позволяет рассчитать практически любую сложную цепь.
Однако непосредственный расчет разветвленных цепей, содержащих несколько
замкнутых контуров, довольно сложен. Эта задача решается более просто с
помощью правил Кирхгофа.
Первое правило формулируется для узла.
Узлом называется точка, в которой сходятся
три и более проводника.
Первое правило Кирхгофа: алгебраическая
сумма токов, сходящихся в узле, равна нулю.
I1 I 2 I 3 ... I N 0
Токи, входящие в узел, считаются положительными, а выходящие –
отрицательными.

16.

Второе правило Кирхгофа: в любом замкнутом контуре разветвленной
электрической цепи алгебраическая сумма ЭДС, действующих в этом контуре,
равна сумме произведений токов в каждой его ветви на их сопротивления
I R
i
k
n
Контур – это любой замкнутый участок цепи.
Для примера запишем 2 правило для
контура, состоящего из 4 участков:
Выберем направлением обхода (например, по часовой
стрелке).
Все токи, совпадающие по направлению с направлением
обхода контура, считаются положительными, не
совпадающие - отрицательными.
Те эдс, которые повышают потенциал в направлении обхода, считаем
положительными, а которые понижают – отрицательными.
I1R1 I 2 R2 I 3 R3 I 4 R4 1 2 n

17.

Схема применения правил Кирхгофа:
1. На всех без исключения участках цепи стрелками показываем направление
тока, которое выбираем произвольно;
2. Записываем уравнение согласно первому правилу для всех узлов,
имеющихся в рассматриваемой цепи, кроме одного. Токи, которые входят в
узел, считаем положительными, а которые выходят – отрицательными;
3. Произвольно выбираем направление обхода контуров.
4. Для всех независимых контуров записываем 2 правило (независимыми
считаются контуры, которые не могут быть получены наложением других контуров);
5. Решаем получившуюся систему уравнений;
6. Если после проведения расчетов значение силы тока окажется
отрицательным, то это означает, что на самом деле ток течет в сторону
противоположную, указанной на схеме.

18.

Природа носителей тока в металлах
Опыт Рикке, 1901 г.
Рикке взял три цилиндра — два медных и один алюминиевый — с тщательно
отшлифованными торцами. После взвешивания цилиндры были сложены
вместе в последовательности: медь—алюминий—медь. Через такой составной
проводник пропускался непрерывно ток одного и того же направления в
течение года.
Cu
Al
Cu
I
За все время через цилиндры прошел заряд, равный 3,5*106 Кл.
Взвешивание показало, что пропускание тока не оказало на вес цилиндров
никакого влияния. При исследовании соприкасавшихся торцов под
микроскопом не было обнаружено проникновения одного металла в другой.
Результаты опыта свидетельствовали о том, что перенос заряда в металлах
осуществляется не атомами, а какими-то частицами, входящими в состав всех
металлов. Такими частицами могли быть открытые в 1897 г. Томсоном
электроны.