Задача линейного программирования. Табличный симплекс-метод

1. Задача линейного программирования. Табличный симплекс-метод

2. Рассмотрим ЗЛП

max 2 x1 x2
3
x
x
3
1
2
2 x1 2 x2 5
x 0
1
x2 0

3. Приведем к канонической форме

max 2 x1 x2
3
x
x
3
1
2
2 x1 2 x2 5
x 0
1
x2 0
max 2 x1 x2
3
x
x
x
3
1
2
3
2 x1 2 x2 x4 5
x1 0
x 0
2
x3 0
x4 0

4. Матричный вид ЗЛП

max CX
max 2 x1 x2
x1
AX b
x2
3
x
x
x
3
1
2
3
X
x3
2 x1 2 x2 x4 5 X 0
b 0
x4
x1 0
3 1 1 0
3
x 0
A
b
2
2 2 0 1
5
x3 0
C 2 1 0 0
x4 0

5. Начальный базис

• 0. Начальный базис
P=E
x1 x2 x3 x4
1 2 1
A
2 1 0
0
1
• Базис: x3, x4
3x1 x2 x3 3
2 x1 2 x2 x4 5
x3 3 3x1 x2
x4 5 2 x1 2 x2

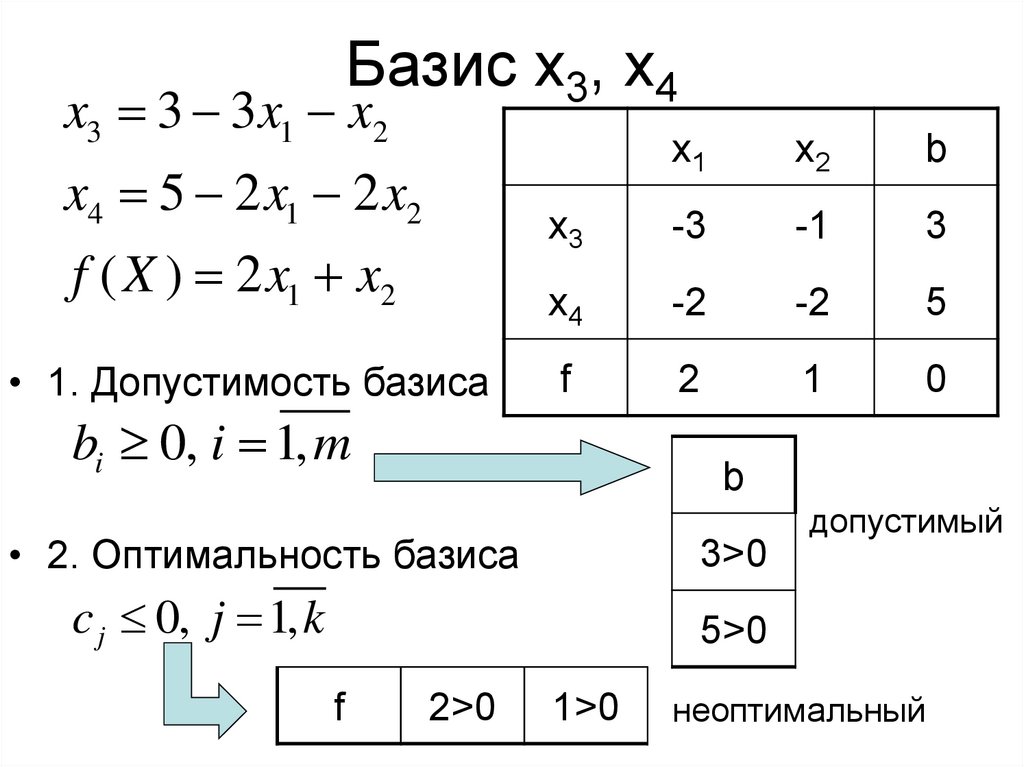
6. Базис x3, x4

x3 3 3 x1 x2
x4 5 2 x1 2 x2
f ( X ) 2 x1 x2
• 1. Допустимость базиса
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
bi 0, i 1, m
b
• 2. Оптимальность базиса
3>0
c j 0, j 1, k
допустимый
5>0
f
2>0
1>0
неоптимальный

7. Базис x3, x4

• 3. Проверка наличия
решения
cl 0 ail 0
x1
x2
b
x3
-3<0
-1<0
3
x4
-2<0
-2<0
5
f
2>0
1>0
0
ОДР замкнута, решение есть
• 4. Ввод в базис
cr max c j
1 j k
f
x1
x2
2
1
Разрешающий столбец: x1

8. Базис x3, x4

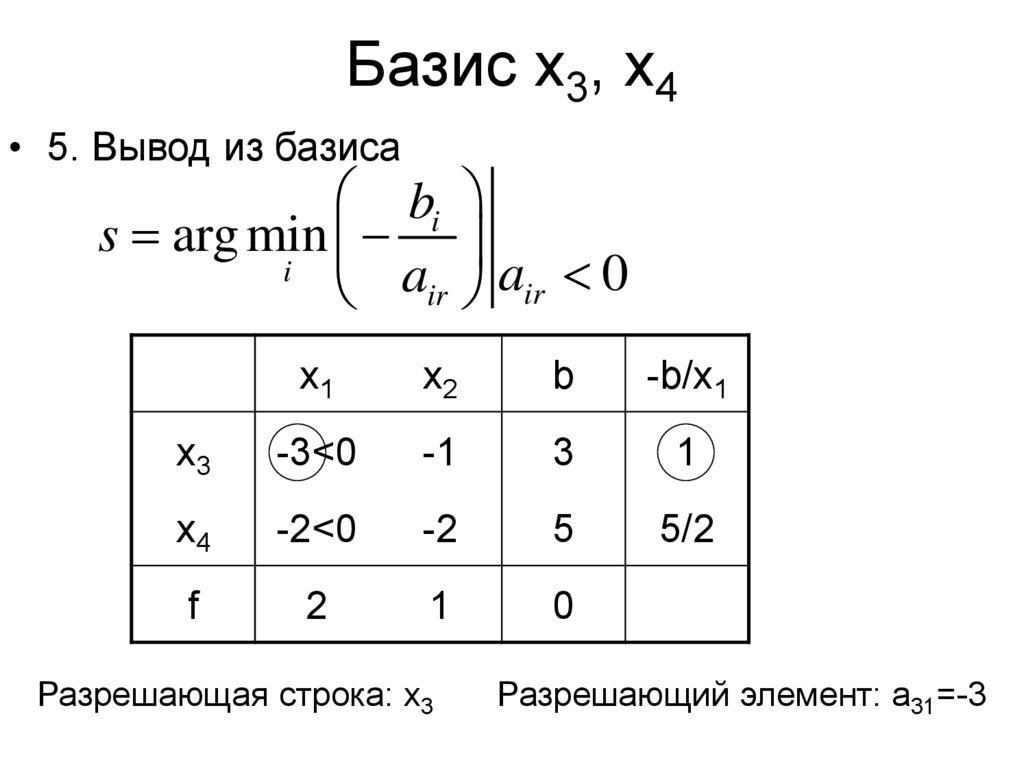
• 5. Вывод из базиса
bi
s arg min
i
air
air 0
x1
x2
b
-b/x1
x3
-3<0
-1
3
1
x4
-2<0
-2
5
5/2
f
2
1
0
Разрешающая строка: x3
Разрешающий элемент: a31=-3

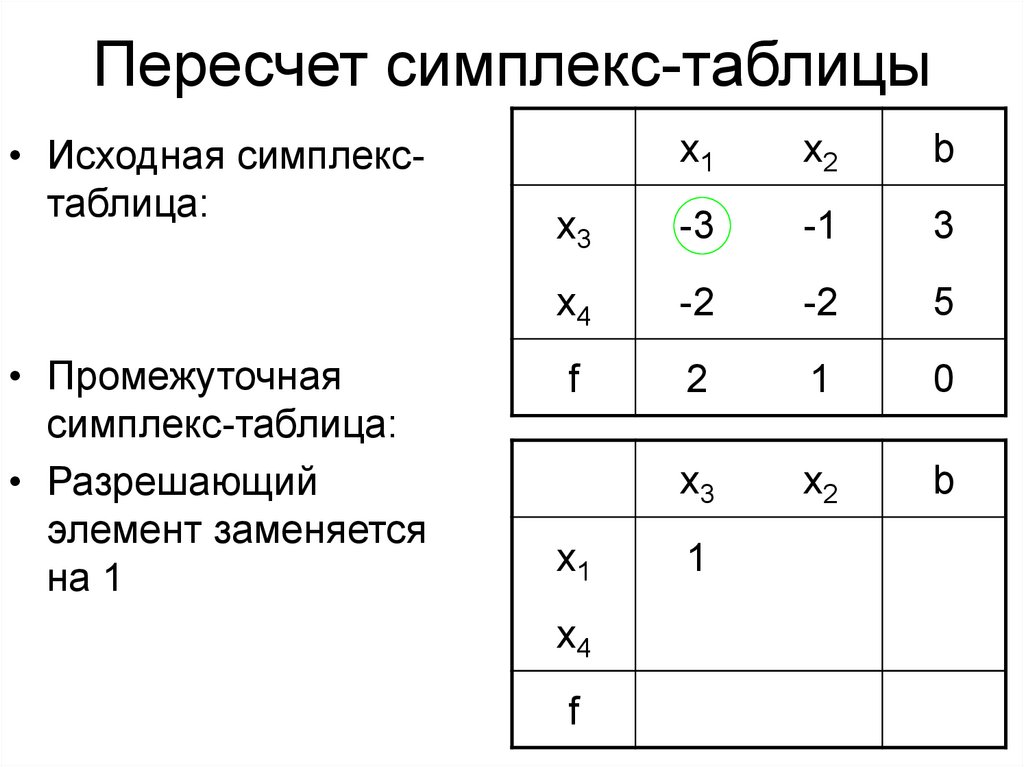
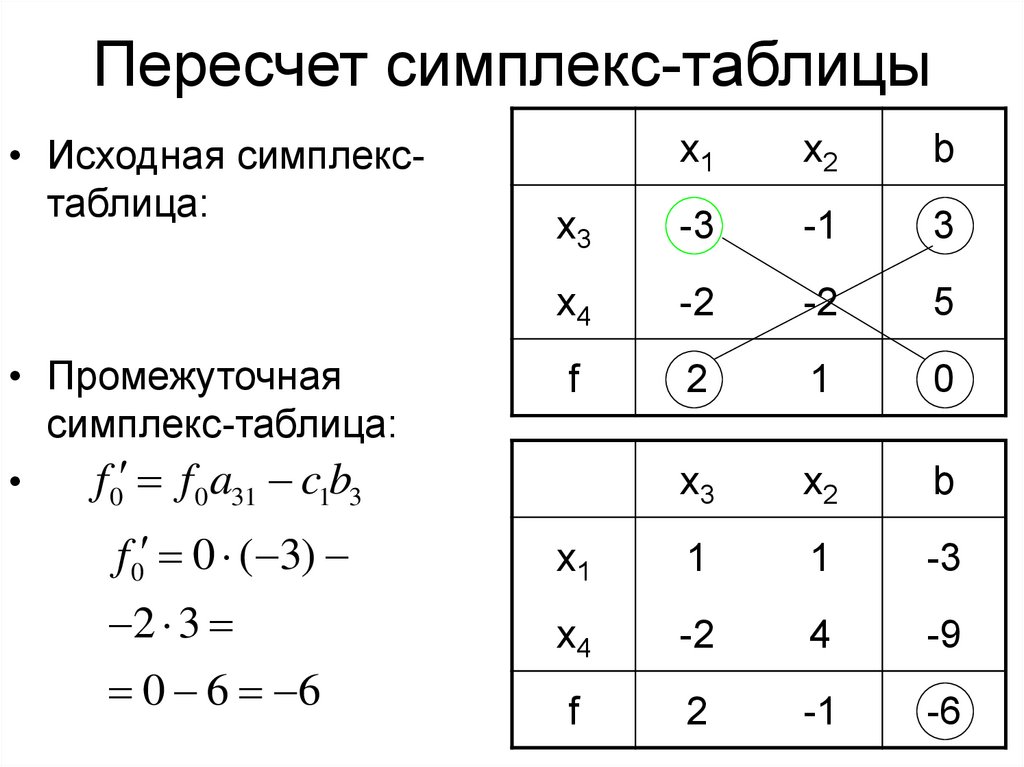
9. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• Разрешающий
элемент заменяется
на 1
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
x1
x4
f
1

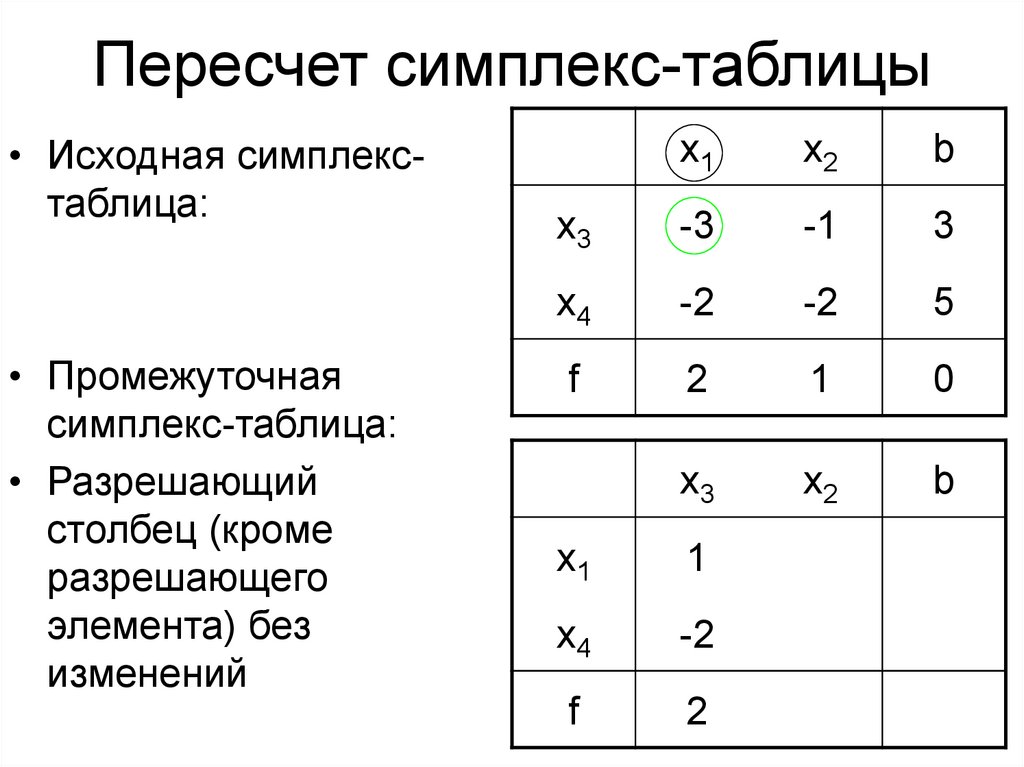
10. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• Разрешающий
столбец (кроме
разрешающего
элемента) без
изменений
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
x1
1
x4
-2
f
2

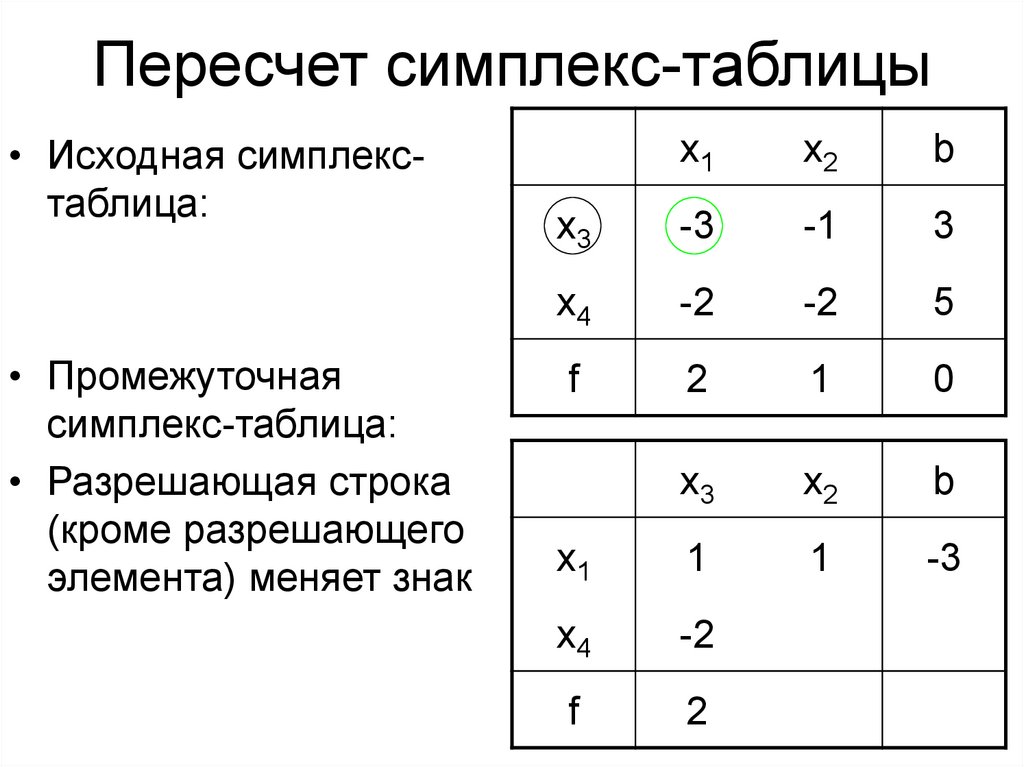
11. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• Разрешающая строка
(кроме разрешающего
элемента) меняет знак
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
x1
1
1
-3
x4
-2
f
2

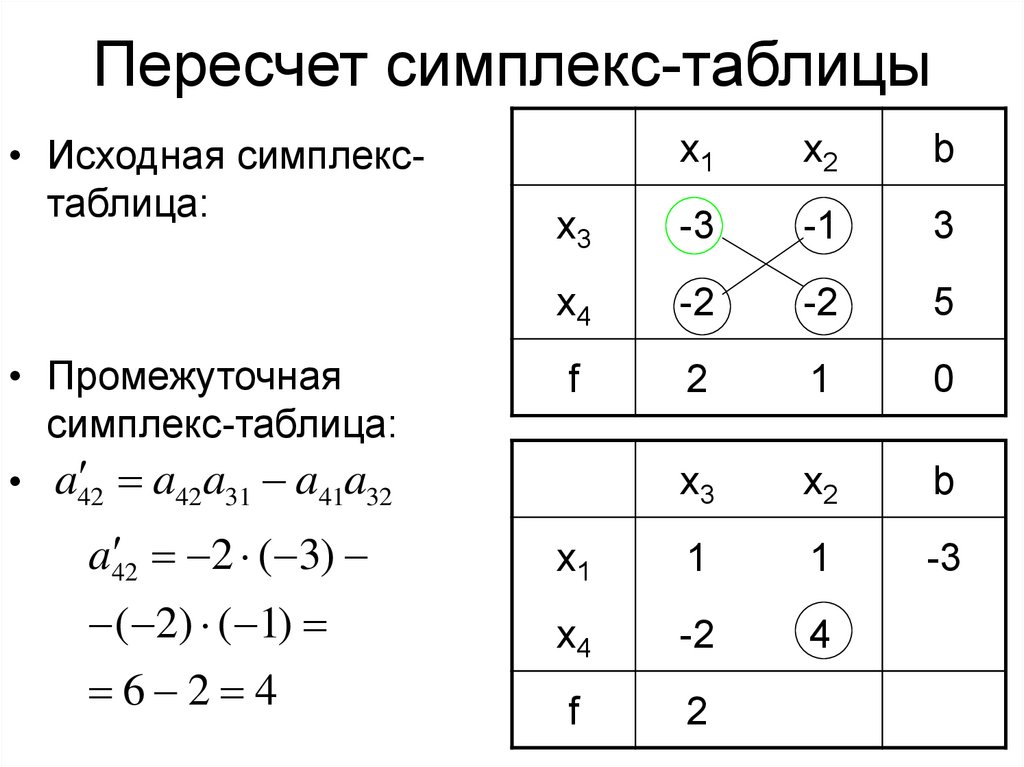
12. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
a42 a31 a41a32
• a42
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
-3
2 ( 3)
a42
x1
1
1
( 2) ( 1)
x4
-2
4
f
2
6 2 4

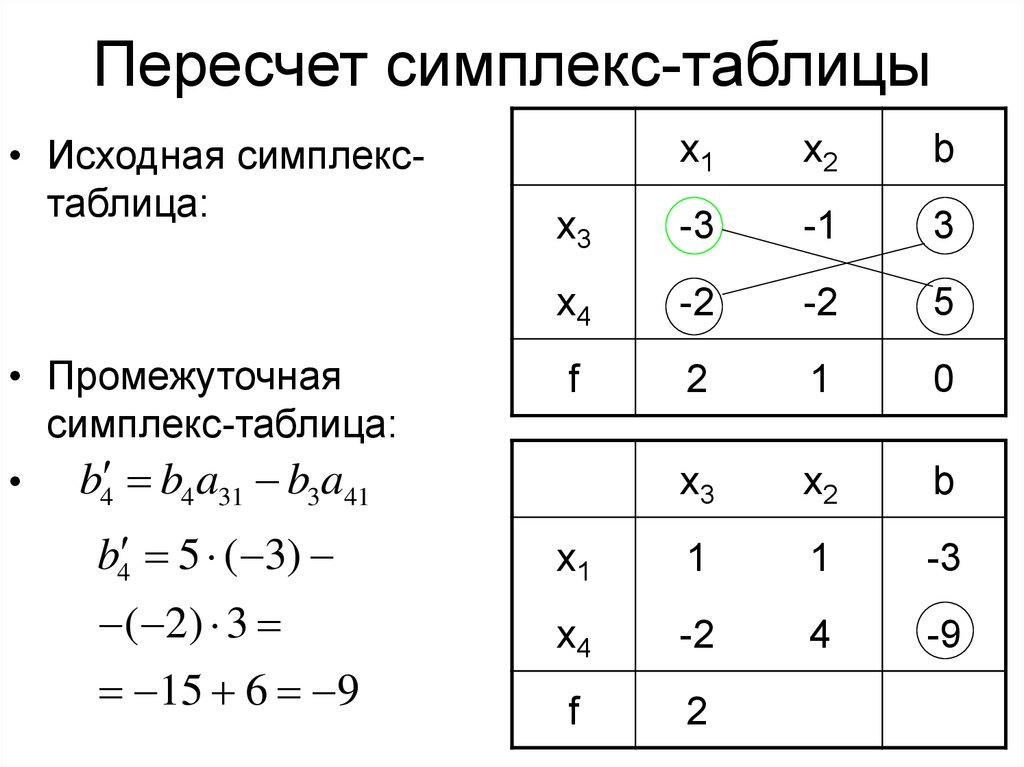
13. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• b4 b4 a31 b3a41
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
b4 5 ( 3)
x1
1
1
-3
( 2) 3
x4
-2
4
-9
f
2
15 6 9

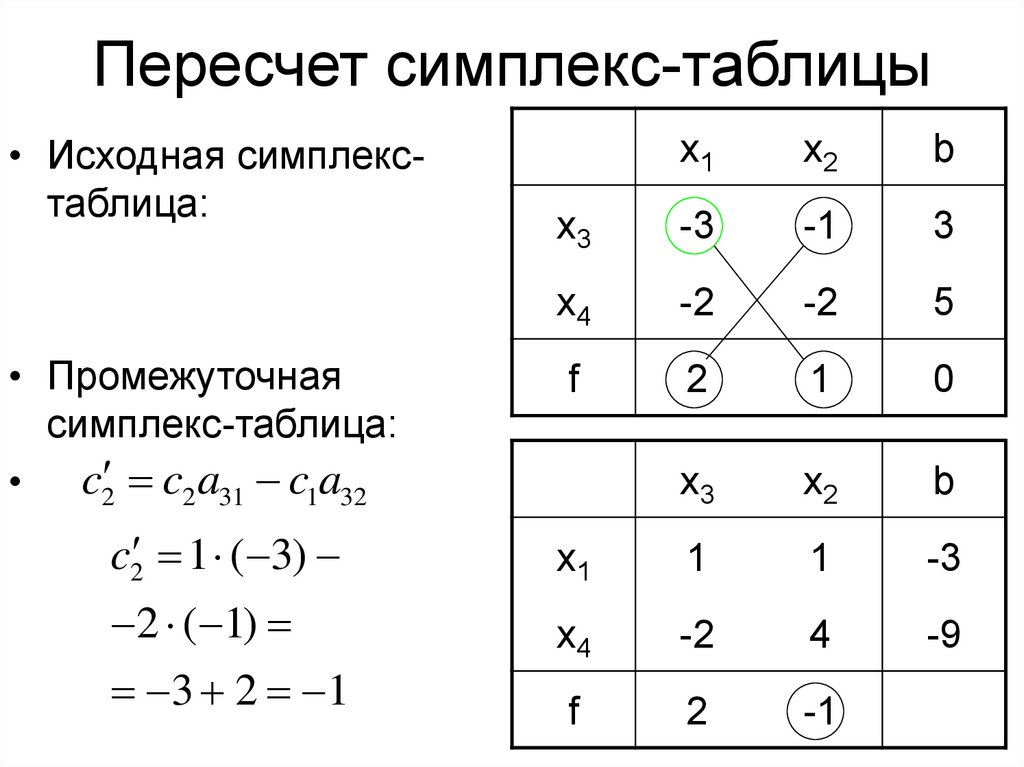
14. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• c2 c2 a31 c1a32
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
c2 1 ( 3)
x1
1
1
-3
2 ( 1)
x4
-2
4
-9
f
2
-1
3 2 1

15. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
f 0 f 0 a31 c1b3
x1
x2
b
x3
-3
-1
3
x4
-2
-2
5
f
2
1
0
x3
x2
b
f 0 0 ( 3)
x1
1
1
-3
2 3
x4
-2
4
-9
f
2
-1
-6
0 6 6

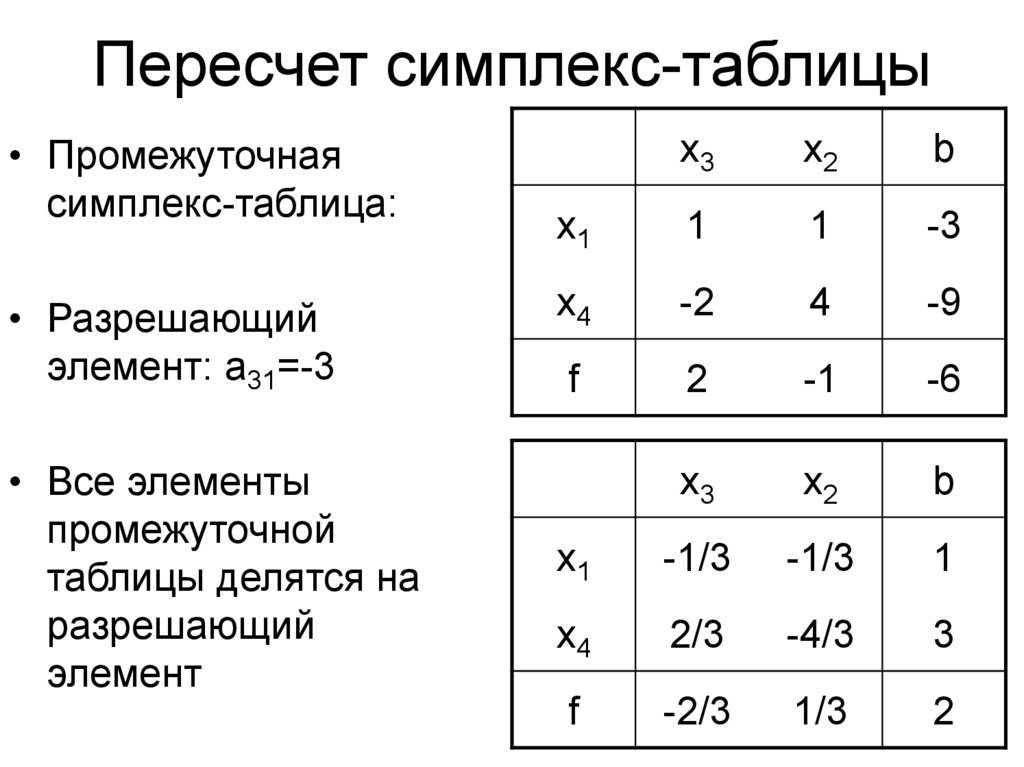
16. Пересчет симплекс-таблицы

• Промежуточная
симплекс-таблица:
• Разрешающий
элемент: a31=-3
• Все элементы
промежуточной
таблицы делятся на
разрешающий
элемент
x3
x2
b
x1
1
1
-3
x4
-2
4
-9
f
2
-1
-6
x3
x2
b
x1
-1/3
-1/3
1
x4
2/3
-4/3
3
f
-2/3
1/3
2

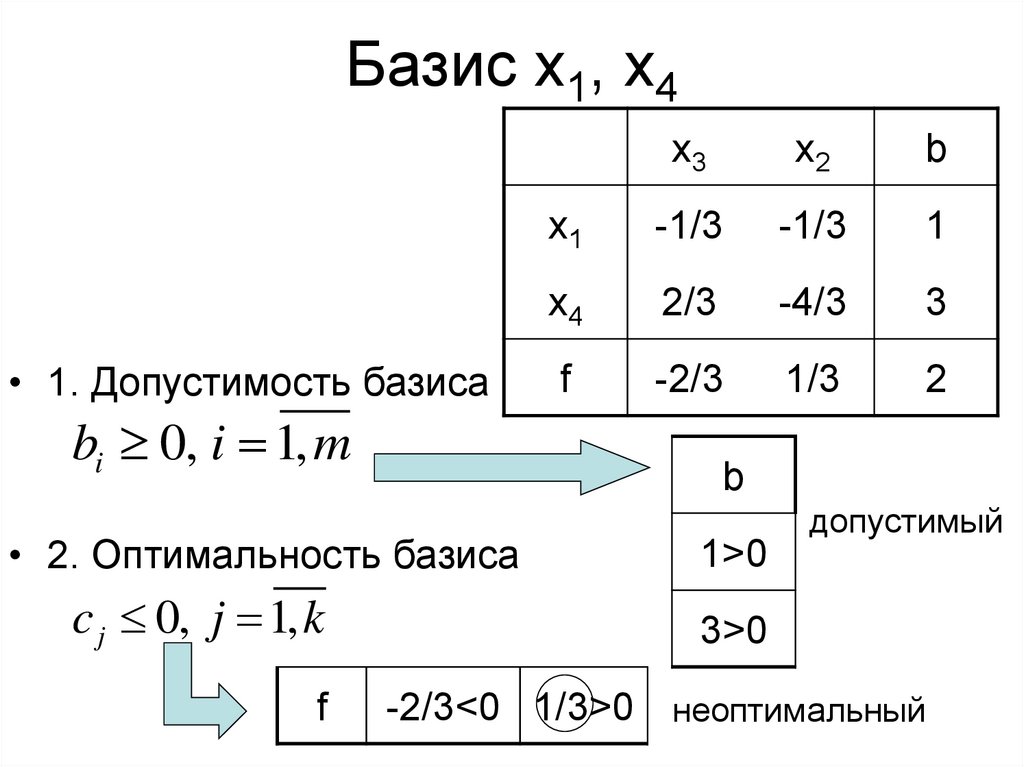
17. Базис x1, x4

• 1. Допустимость базиса
bi 0, i 1, m
f
x2
b
x1
-1/3
-1/3
1
x4
2/3
-4/3
3
f
-2/3
1/3
2
b
• 2. Оптимальность базиса
c j 0, j 1, k
x3
1>0
допустимый
3>0
-2/3<0 1/3>0 неоптимальный

18. Базис x1, x4

• 3. Проверка наличия
решения
cl 0 ail 0
x3
x2
b
x1
-1/3 -1/3<0
1
x4
2/3 -4/3<0
3
f
-2/3 1/3>0
2
ОДР замкнута, решение есть
• 4. Ввод в базис
cr max c j
1 j k
f
x3
x2
-2/3
1/3
Разрешающий столбец: x2

19. Базис x1, x4

• 5. Вывод из базиса
bi
s arg min
i
air
air 0
x3
x2
b
-b/x2
x1
-1/3
-1/3
1
3
x4
2/3
-4/3
3
9/4
f
-2/3
1/3
2
Разрешающая строка: x1
Разрешающий элемент: a12=-4/3

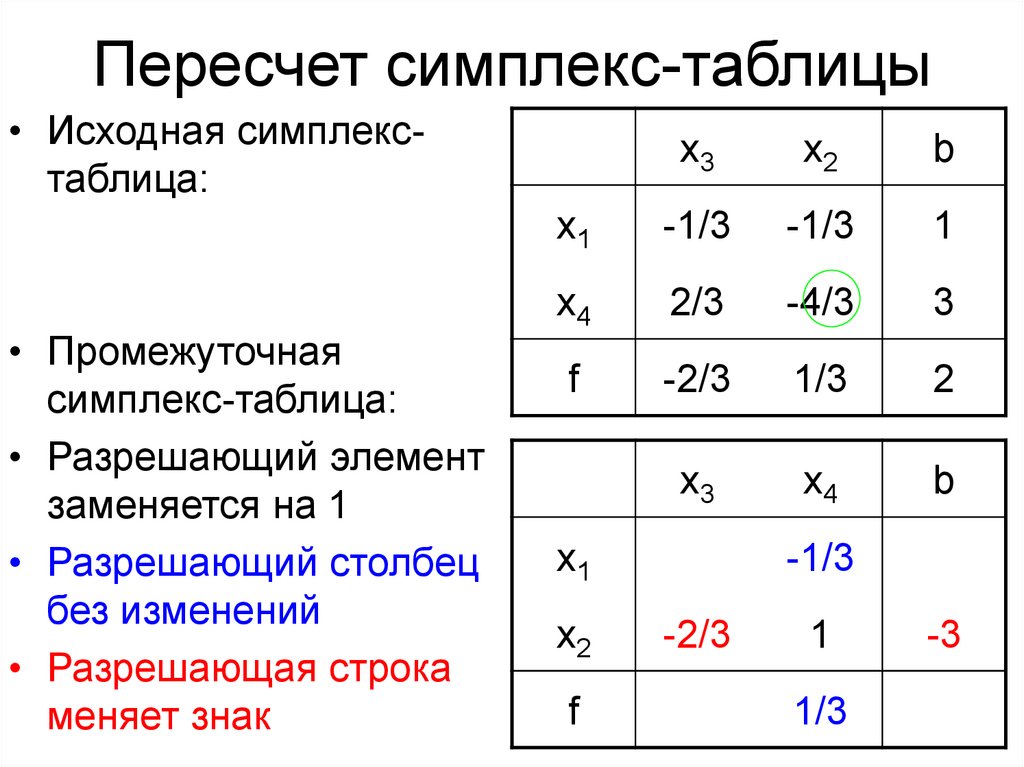
20. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
• Разрешающий элемент
заменяется на 1
• Разрешающий столбец
без изменений
• Разрешающая строка
меняет знак
x3
x2
b
x1
-1/3
-1/3
1
x4
2/3
-4/3
3
f
-2/3
1/3
2
x3
x4
b
x1
x2
f
-1/3
-2/3
1
1/3
-3

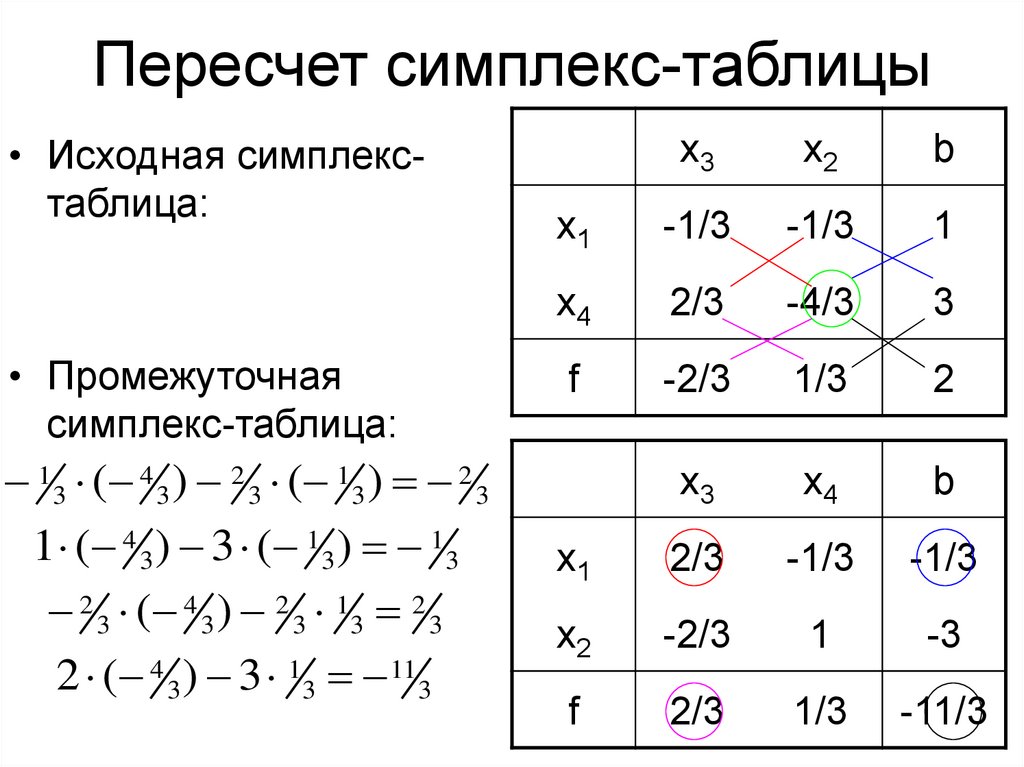
21. Пересчет симплекс-таблицы

• Исходная симплекстаблица:
• Промежуточная
симплекс-таблица:
1 3 ( 4 3 ) 2 3 ( 1 3 ) 2 3
1 ( 4 3 ) 3 ( 1 3 ) 1 3
2 3 ( 4 3 ) 2 3 1 3 2 3
2 ( 4 3 ) 3 13 113
x3
x2
b
x1
-1/3
-1/3
1
x4
2/3
-4/3
3
f
-2/3
1/3
2
x3
x4
b
x1
2/3
-1/3
-1/3
x2
-2/3
1
-3
f
2/3
1/3
-11/3

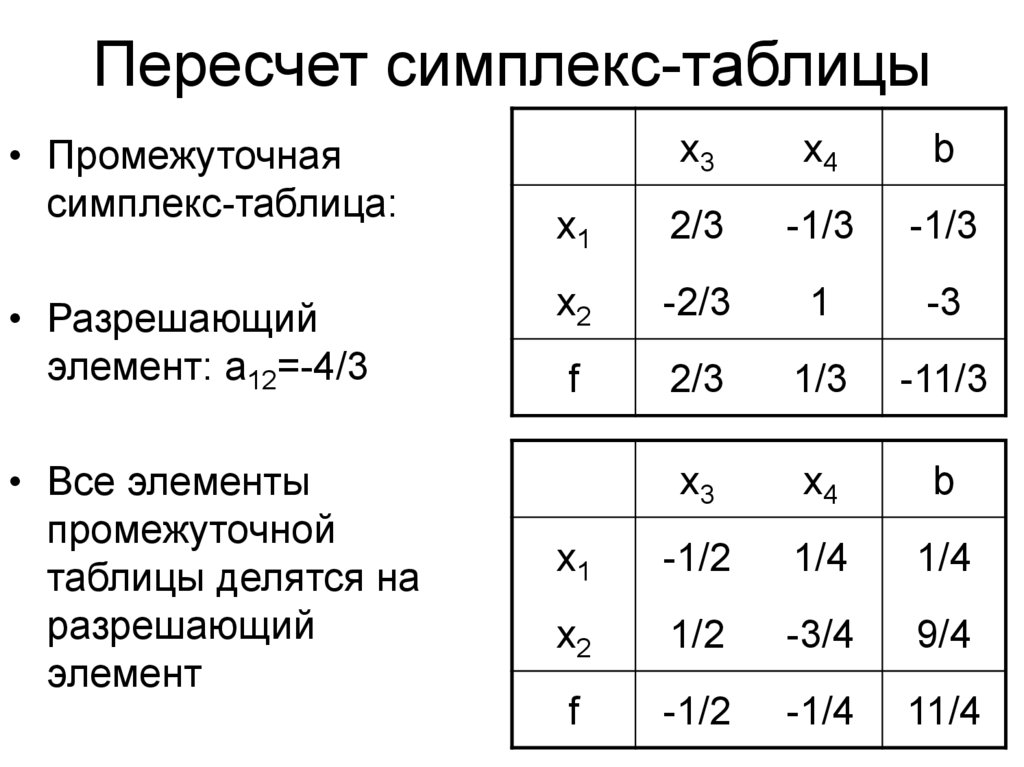
22. Пересчет симплекс-таблицы

• Промежуточная
симплекс-таблица:
• Разрешающий
элемент: a12=-4/3
• Все элементы
промежуточной
таблицы делятся на
разрешающий
элемент
x3
x4
b
x1
2/3
-1/3
-1/3
x2
-2/3
1
-3
f
2/3
1/3
-11/3
x3
x4
b
x1
-1/2
1/4
1/4
x2
1/2
-3/4
9/4
f
-1/2
-1/4
11/4

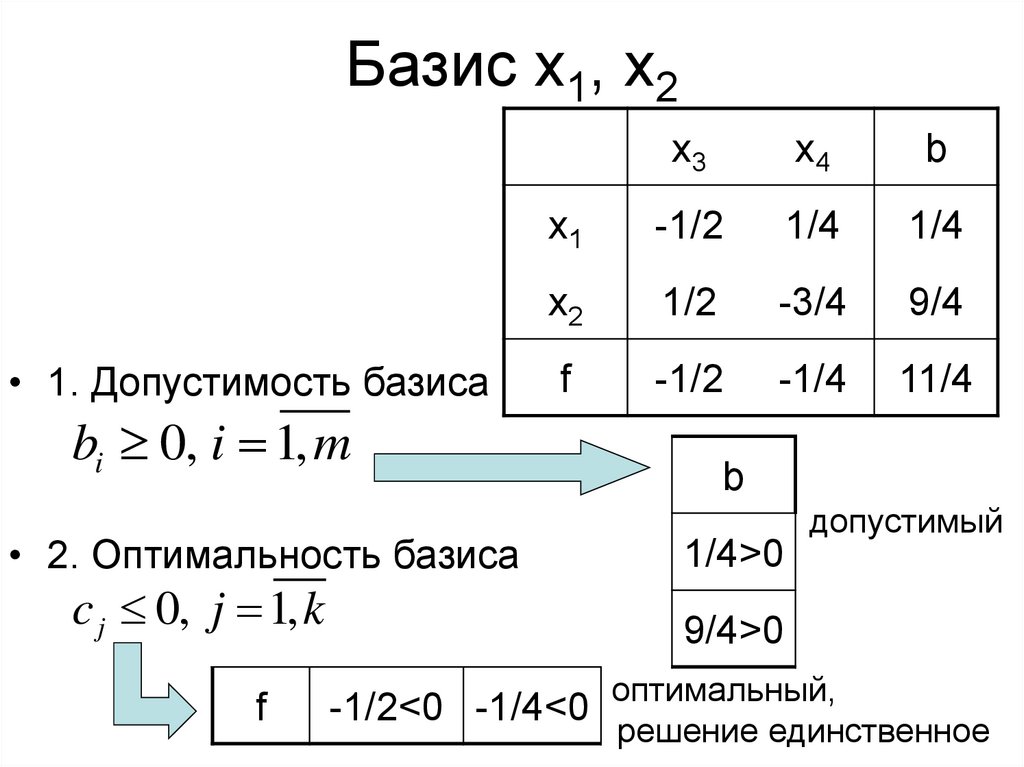
23. Базис x1, x2

• 1. Допустимость базиса
bi 0, i 1, m
• 2. Оптимальность базиса
c j 0, j 1, k
f
x3
x4
b
x1
-1/2
1/4
1/4
x2
1/2
-3/4
9/4
f
-1/2
-1/4
11/4
b
1/4>0
допустимый
9/4>0
-1/2<0 -1/4<0 оптимальный,
решение единственное

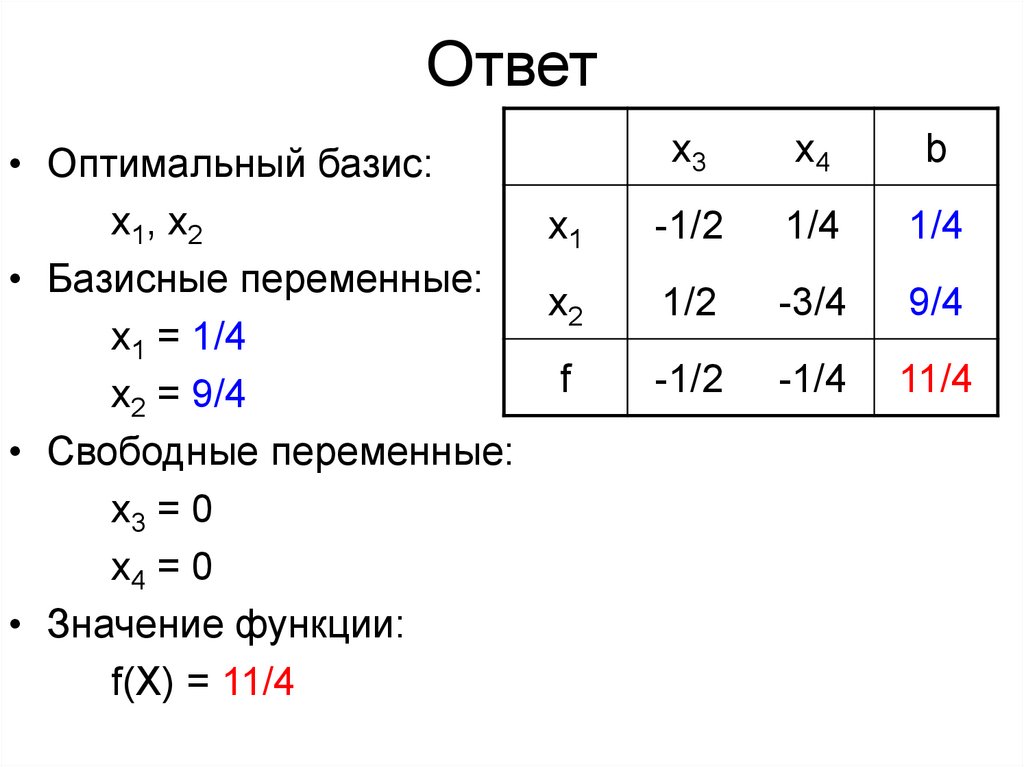
24. Ответ

• Оптимальный базис:
x 1, x 2
x1
• Базисные переменные:
x2
x1 = 1/4
f
x2 = 9/4
• Свободные переменные:
x3 = 0
x4 = 0
• Значение функции:
f(X) = 11/4
x3
x4
b
-1/2
1/4
1/4
1/2
-3/4
9/4
-1/2
-1/4
11/4