Похожие презентации:
Температура как мера средней кинетической энергии
1.
Температура – мера среднейкинетической энергии.
2.
Центральное место в учении о тепловыхявлениях занимает понятие температура.
Температура – это физическая величина,
характеризующая степень нагретости тела.
В состоянии теплового равновесия все тела
системы имеют одинаковую температуру, хотя
другие макроскопические параметры могут
отличаться. (пример с мячом внесенным с
холода в теплое помещение).
Тепловое равновесие – это такое состояние
системы, при котором макроскопические
параметры (p, V, t) сколь угодно долго остаются
неизменными.
3.
Для измерения температуры служаттермометры – это устройства, в которых
используется зависимость какого-либо
параметра от температуры.
В жидкостных термометрах
используется зависимость
объема жидкости от
температуры.
4.
В металлических термометрах используютсябиметаллические пластинки: две пластинки из
разных металлов, соединенные между собой.
Коэффициент линейного расширения металлов
разный, поэтому при нагревании и охлаждении
пластинки изгибаются, через передаточный
механизм это передается стрелке прибора.
5.
Электрические термометрыиспользуют зависимость
сопротивления проводников
или полупроводников от
температуры.
Недостатком все этих термометров является то,
что шкала прибора зависит от конкретного
вещества, используемого в приборе.
Например, если разбился любимый комнатный
стеклянный термометр, то мы не сможем в него
переставить стеклянную трубочку с жидкостью от
другого термометра – шкала не подойдет.
6.
Какое же вещество можно использовать втермометрах, чтобы избавиться от этой
зависимости?
Оказалось, что все разреженные газы (водород,
кислород, гелий …) расширяются при нагревании
одинаково и одинаково меняют свое давление при
изменении температуры.
На основе этого в физике появилась
универсальная газовая шкала температур или
как ее еще называют абсолютная шкала
температур.
7.
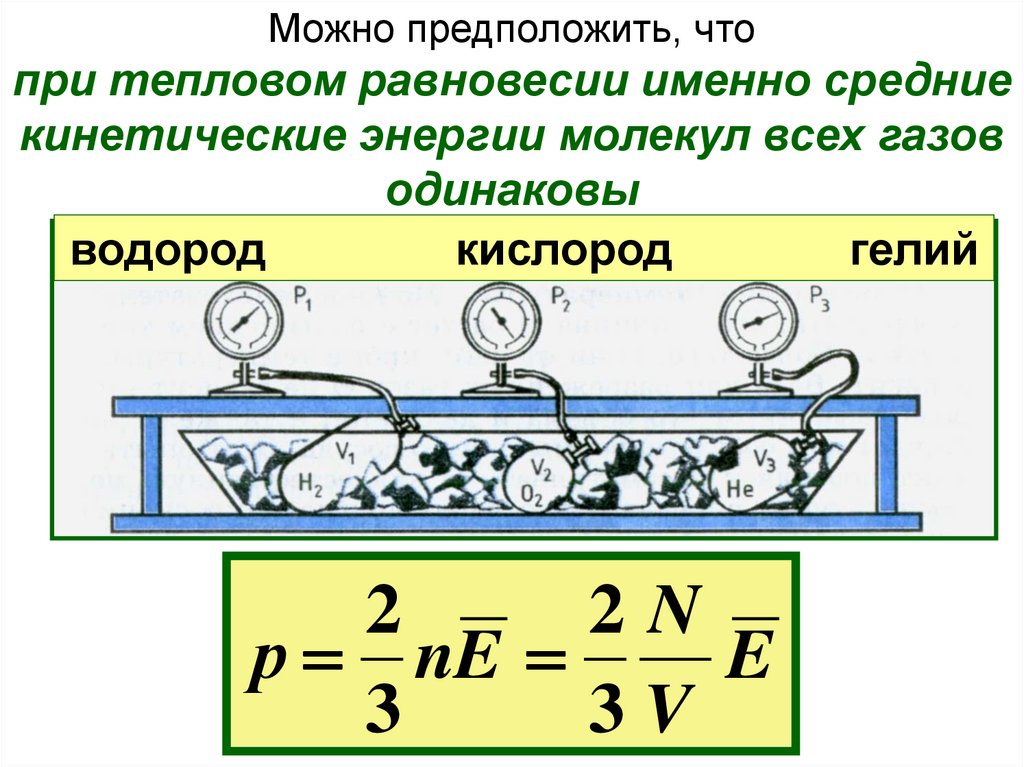
Можно предположить, чтопри тепловом равновесии именно средние
кинетические энергии молекул всех газов
одинаковы
водород
кислород
гелий
2
2N
р nE
E
3
3V
8.
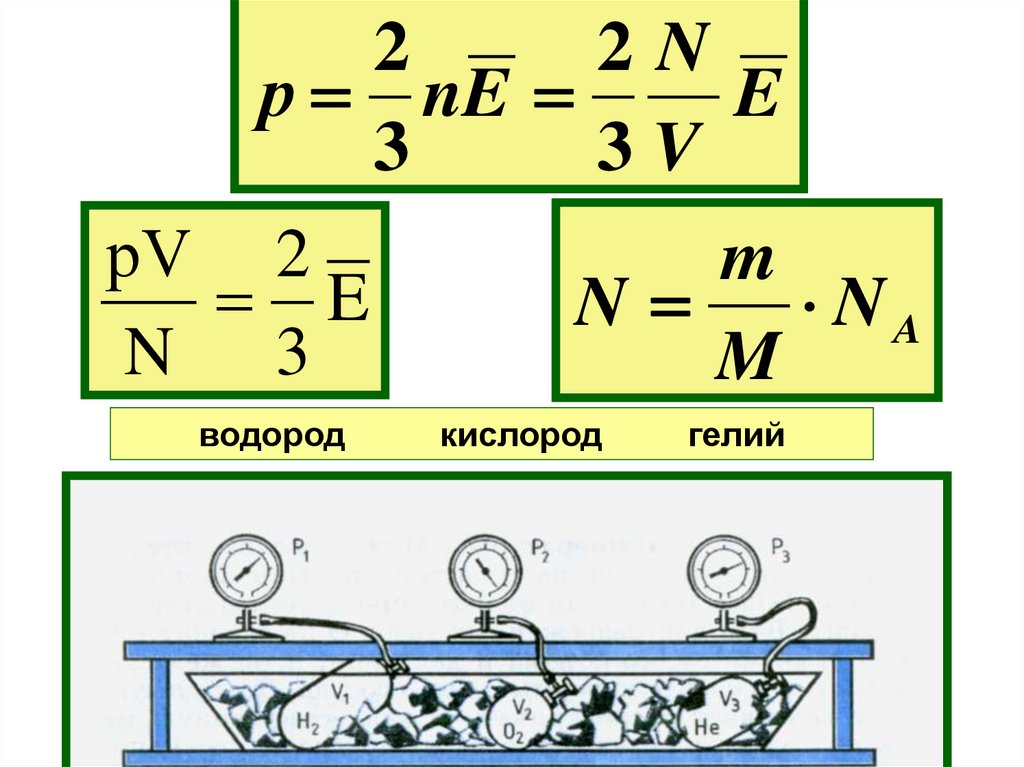
22N
р nE
E
3
3V
рV 2
E
N 3
водород
m
N
NA
M
кислород
гелий
9.
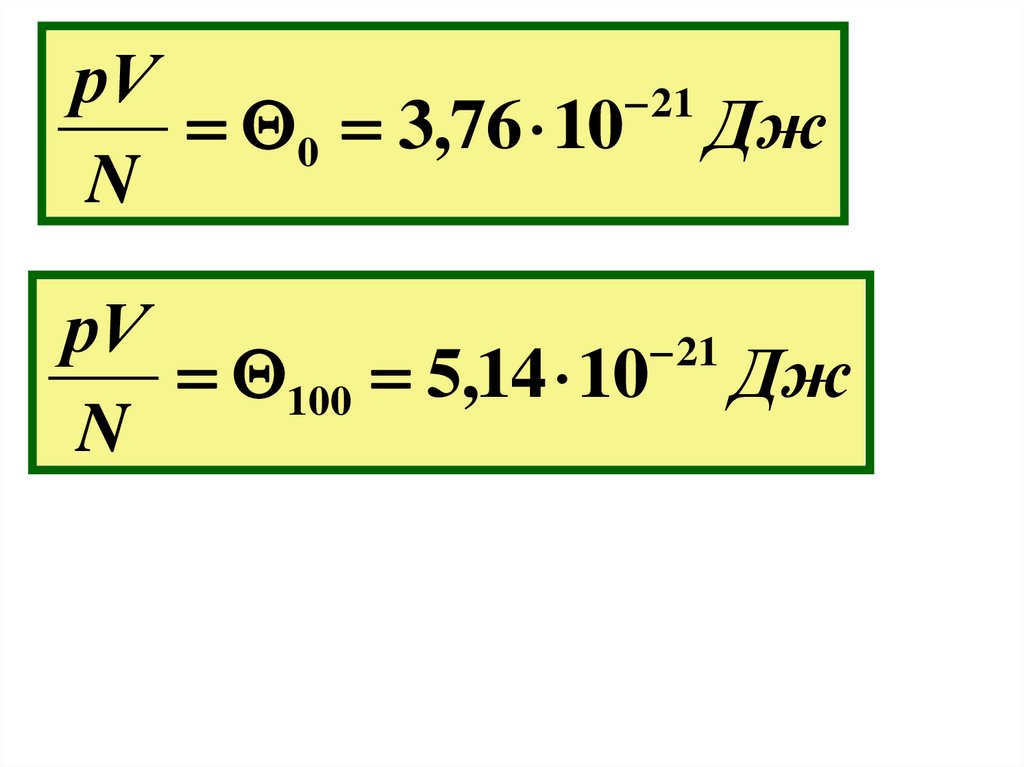
рV21
0 3,76 10 Дж
N
рV
21
100 5,14 10 Дж
N
10.
На основе этого в физикепоявилась универсальная газовая
шкала температур или как ее еще
называют абсолютная шкала
температур.
11.
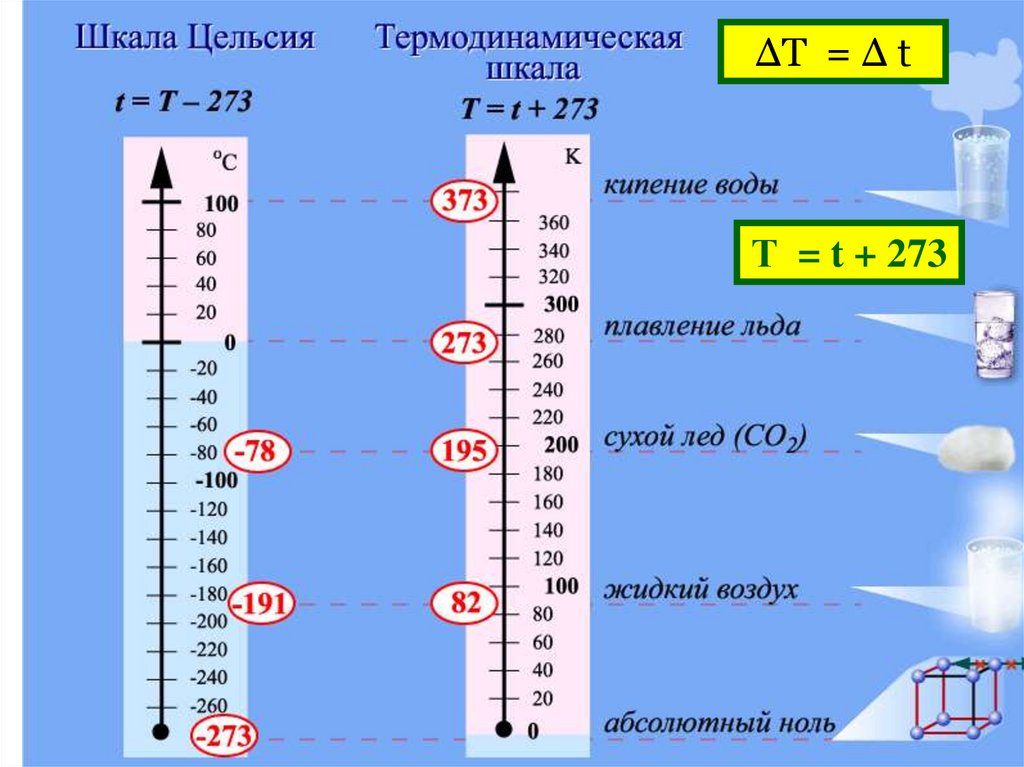
ΔТ = Δ tТ = t + 273
12.
- температура в энергетическихединицах
kT
Т- температура в градусах Кельвина
(абсолютная температура)
k- коэффициент пропорциональности,
постоянная Больцмана.
100 0 kT2 kT1 k (T2 T1 )
13.
100 0 kT2 kT1 k (T2 T1 )100 0
k
T2 T1
(5,14 3,76) 10
100 К
23 Дж
1,38 10
K
21
Дж
Постоянная Больцмана связывает температуру в
энергетических единицах с температурой в Кельвинах.
14.
Итак, наряду с традиционной температурнойшкалой Цельсия и температурой по шкале
Цельсия – t (измеряется в ºС)
Появилась абсолютная шкала температур –
шкала Кельвина и абсолютная температура – Т,
измеряемая в кельвинах (К).
- связь абсолютной
температуры с температурой
по шкале Цельсия.
В отличие от температуры Цельсия абсолютная
температура не бывает отрицательной, ее
минимальная температура – это абсолютный
нуль температур.
T = t + 273
15.
Единица измерения абсолютной температурыподобрана так, что
1K 1 C
Это значит, что если Δt = 10ºC, то и ΔТ = 10К
Проверим:
пусть начальная температура воды t1= 0ºC,
конечная температура t2 = 10ºC, тогда Δt =10ºC
По абсолютной шкале температур:
Т1 = t1 +273 = 273K
T2= t2 + 273 = 283K,
тогда ΔТ = 10К
но температура на улице 1ºC = 274К !!! (а не 1К)
16.
Опыты с различными газами показали, что длялюбых разреженных газов:
величина
pV
N
пропорциональна температуре, т.е.
pV
N
kT , но
n концентрация, тогда
N
V
p
kT
(1) p nkT зависимость давления газа
n
от температуры
k – коэффициент пропорциональности,
называется постоянная Больцмана:
k = 1,38∙10-23 Дж/К
17.
Согласно основному уравнению МКТидеального газа:
2
p nE (2)
3
Из уравнений (1) и (2) следует:
(3)
2
nkT nE
3
- связь средней кинетической энергии
3
E kT молекулы с температурой:
температура – мера средней
2
кинетической энергии
молекул.
18.
Мы знаем также, что средняя кинетическаяэнергия молекулы равна
(4)
m0
E
2
2
Из формул (3) и (4) следует:
m0
3
2
kT m0 3kT
2
2
3kT - Средняя квадратичная (или
средняя) скорость молекулы
m0
(m0 – масса молекулы)
2
(5)














 Физика
Физика








