Аксиомы стереометрии и их следствия. Планиметрия и стереометрия

1.

Аксиомы стереометрии и
их следствия.
1

2.

Планиметрия
Стереометрия
Изучает свойства
геометрических фигур на
плоскости
Изучает свойства фигур в
пространстве
В переводе с греческого
слово «геометрия»
означает «землемерие»
«гео» – по-гречески земля,
«метрео» – мерить
Слово «стереометрия»
происходит от греческих слов
«стереос» объемный,
пространственный, «метрео»
– мерить
2

3.

Планиметрия
Стереометрия
Основные фигуры: точка,
Основные фигуры: точка,
прямая, плоскость
прямая
Наряду с этими фигурами мы
будем рассматривать
Другие фигуры: отрезок, луч,
геометрические тела и их
треугольник, квадрат, ромб,
поверхности.
параллелограмм, трапеция,
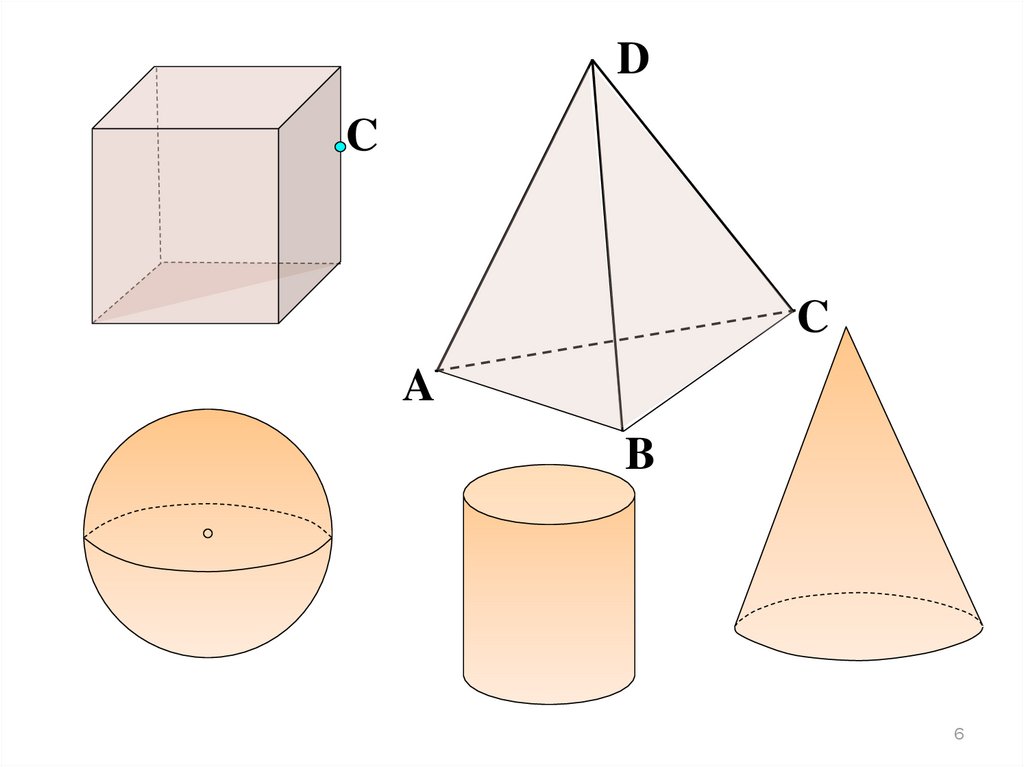
Например, многогранники.
прямоугольник, выпуклые и
Куб, параллелепипед, призма,
невыпуклые n-угольники,
пирамида.
круг, окружность, дуга и др.
Тела вращения.
Шар, сфера, цилиндр, конус.
3

4.

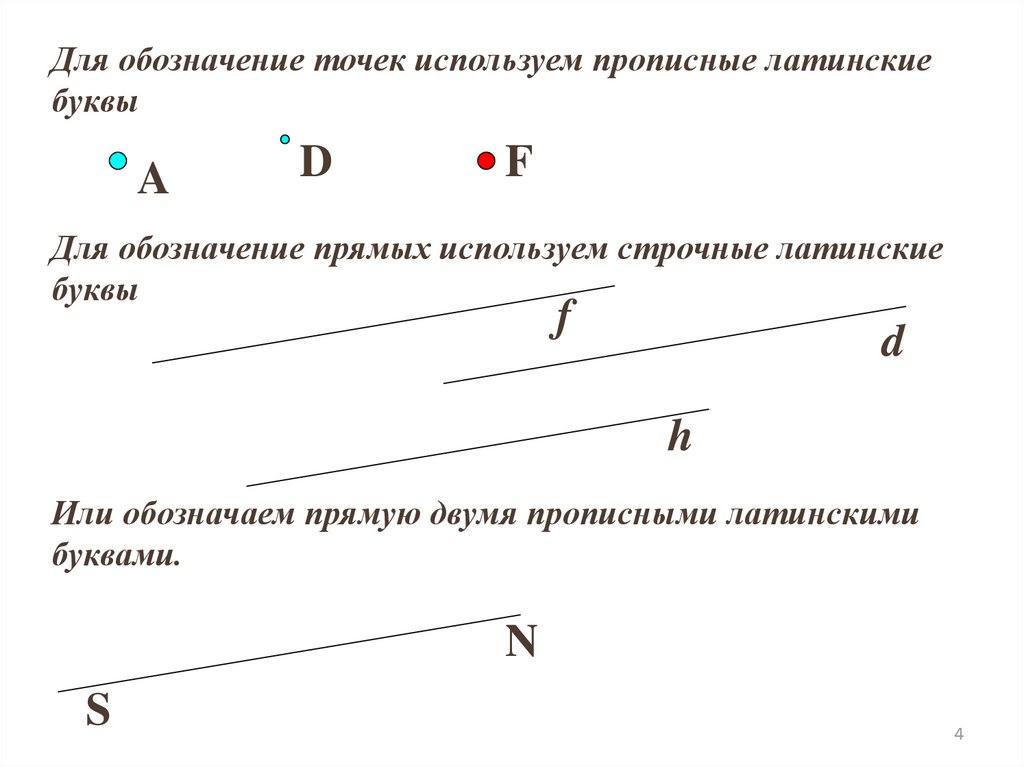
Для обозначение точек используем прописные латинские
буквы
A
D
F
Для обозначение прямых используем строчные латинские
буквы
f
d
h
Или обозначаем прямую двумя прописными латинскими
буквами.
N
S
4

5.

Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде
параллелограммов. Плоскость как геометрическую фигуру
следует представлять себе простирающейся неограниченно
во03.11.2021
все стороны.
www.konspekturoka.ru
5

6.

D
C
C
A
B
6

7.

Основные свойства точек, прямых и плоскостей выражены
в аксиомах. Из множества аксиом мы сформулируем только
три.
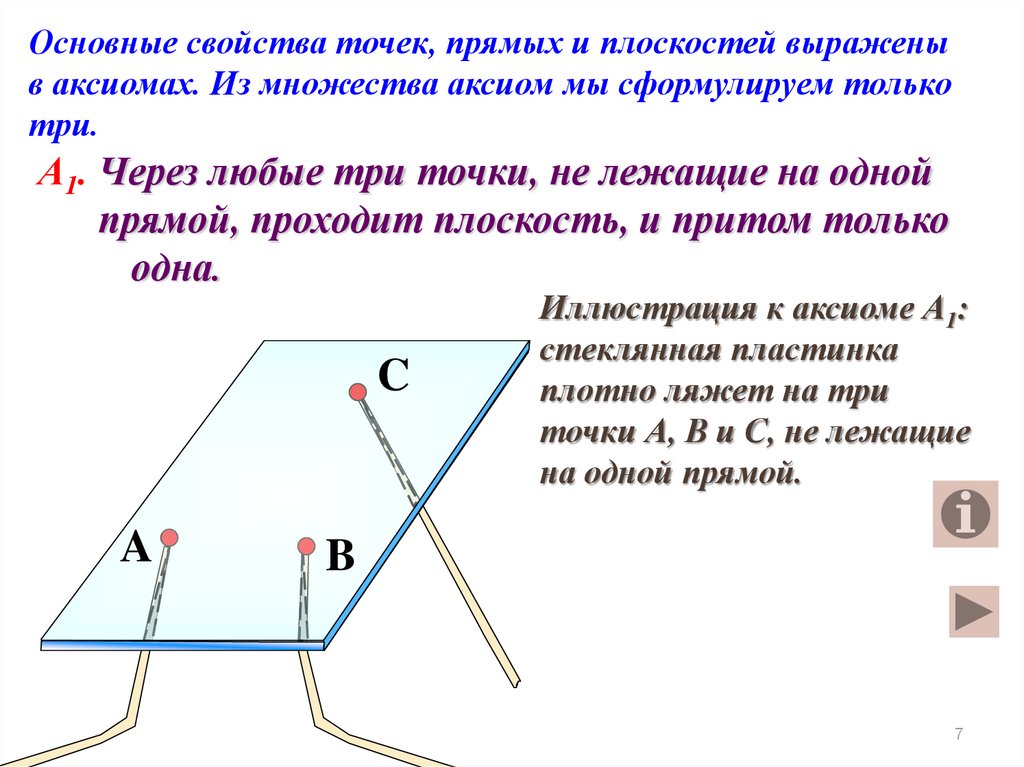
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только
одна.
C
A
Иллюстрация к аксиоме А1:
стеклянная пластинка
плотно ляжет на три
точки А, В и С, не лежащие
на одной прямой.
B
7

8.

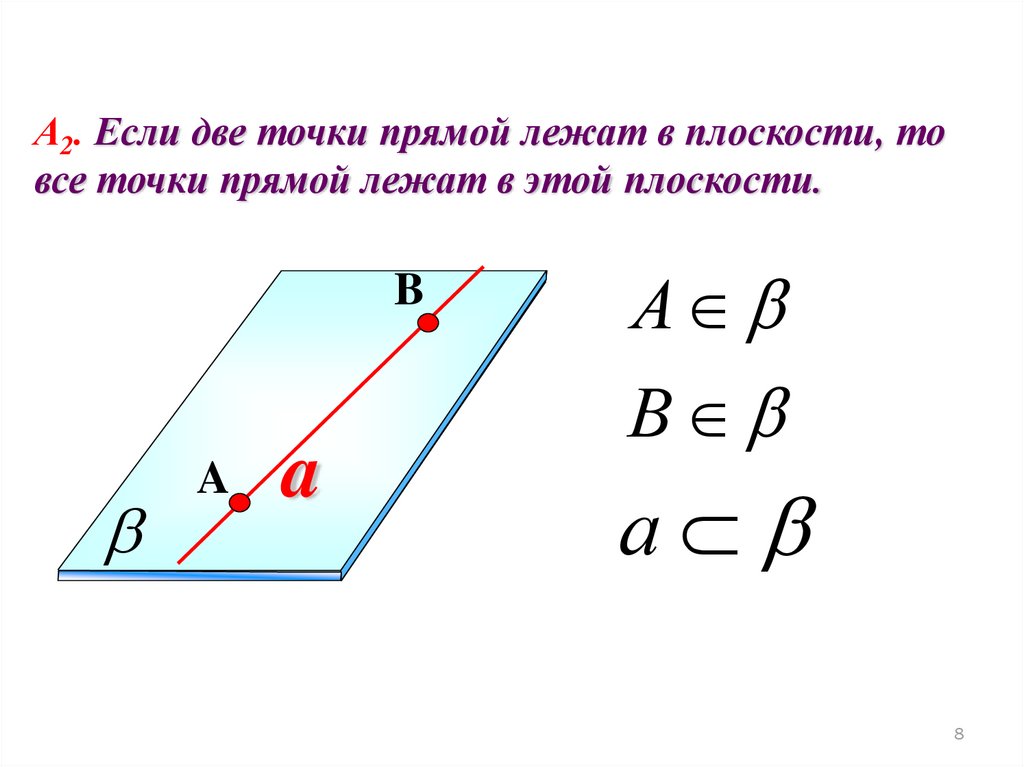
А2. Если две точки прямой лежат в плоскости, то
все точки прямой лежат в этой плоскости.
B
A
a
А
В
а
8

9.

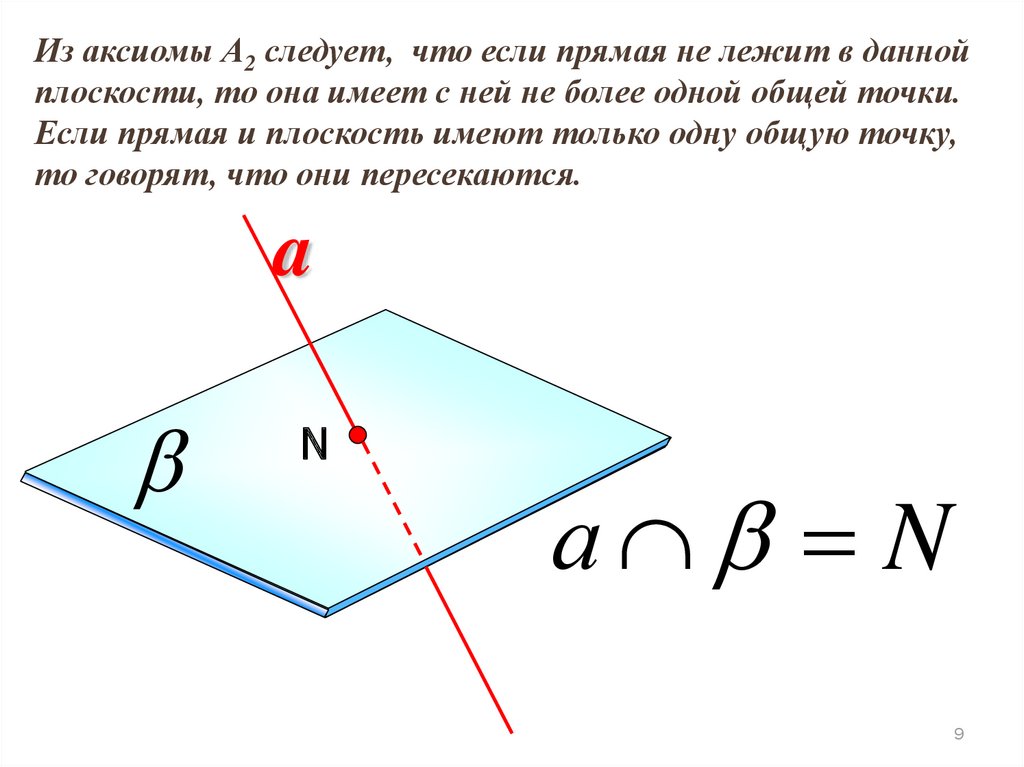
Из аксиомы А2 следует, что если прямая не лежит в данной
плоскости, то она имеет с ней не более одной общей точки.
Если прямая и плоскость имеют только одну общую точку,
то говорят, что они пересекаются.
a
N
а N
9

10.

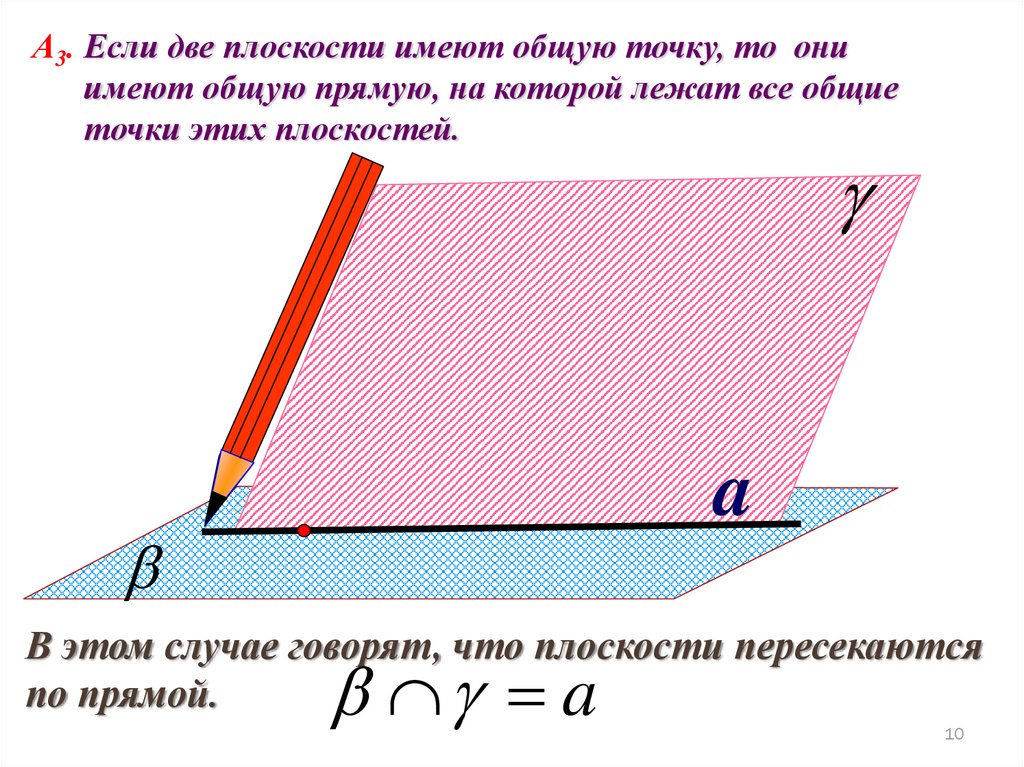
А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
В этом случае говорят, что плоскости пересекаются
по прямой.
a
10

11.

C
B
A
B a
A
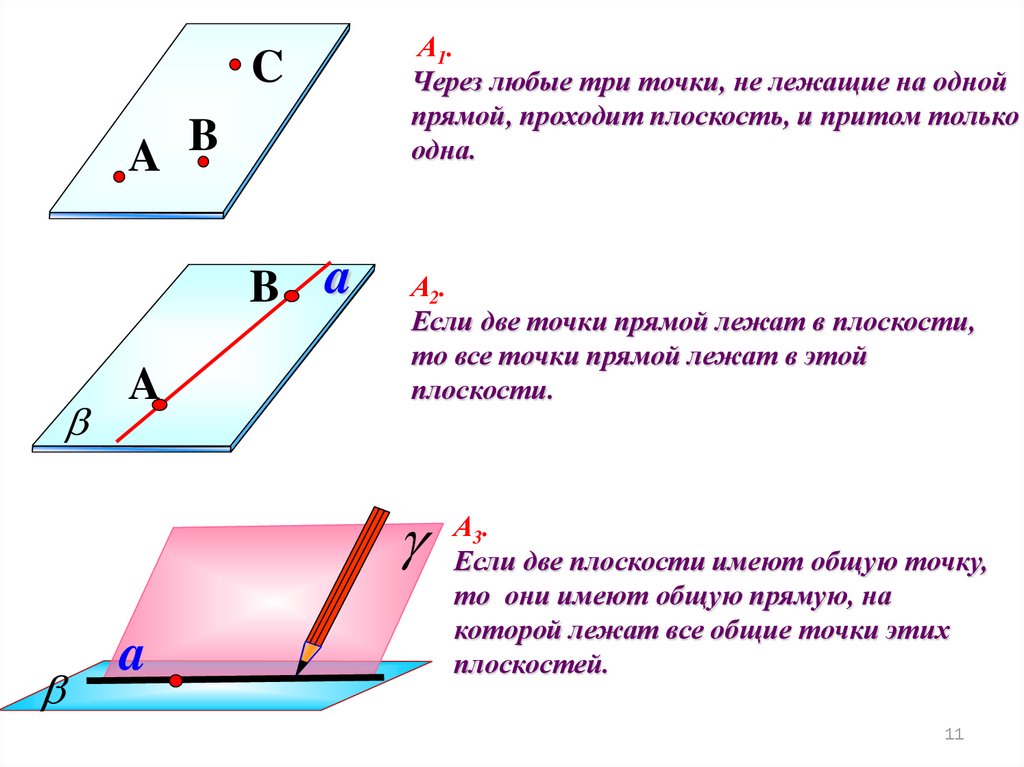
А1.
Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только
одна.
А2.
Если две точки прямой лежат в плоскости,
то все точки прямой лежат в этой
плоскости.
a
А3.
Если две плоскости имеют общую точку,
то они имеют общую прямую, на
которой лежат все общие точки этих
плоскостей.
11

12.

Способы задания плоскости
1) Через три точки не лежащие на
одной прямой.
2) Через прямую и не лежащую на
ней точку
3) Через две пересекающиеся
прямые

13.

Расположение двух
плоскостей
1) Плоскости параллельны
2) Плоскости пересекаются по
прямой

14.

Расположение прямой и
плоскости
1) Прямая лежит в плоскости
2) Прямая пересекает плоскость
3) Прямая параллельна плоскости

15.

Расположение двух прямых
1) Параллельны
2) Пересекаются
3) Скрещивающиеся

16.

D
K
P
M
A
E
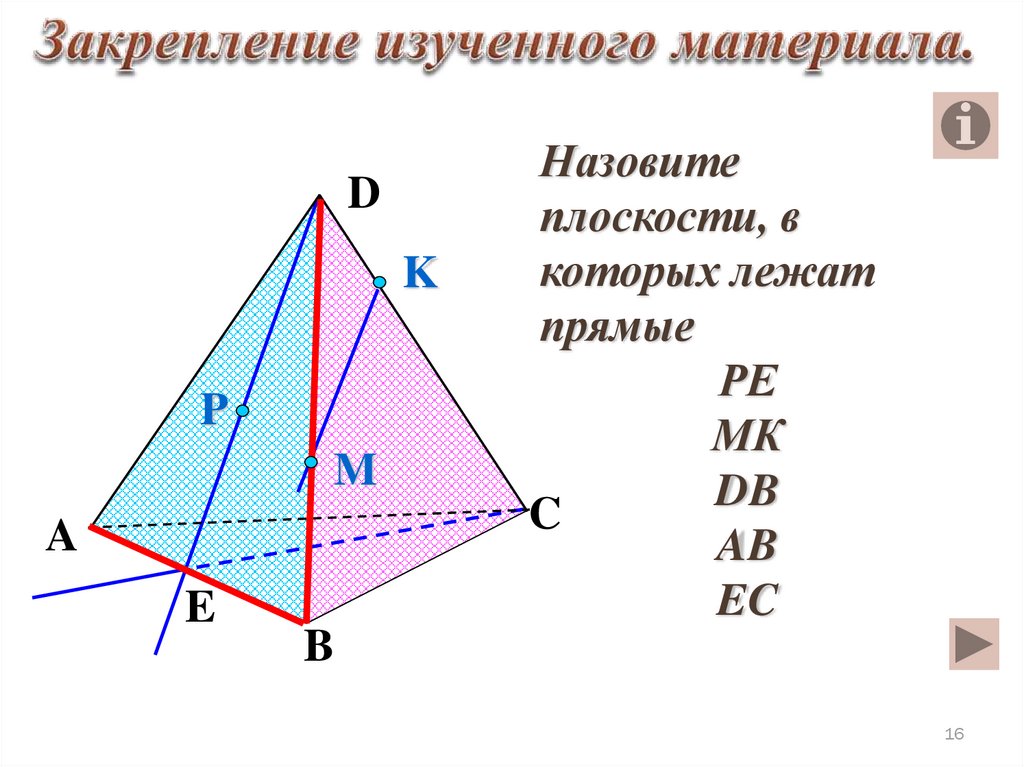
Назовите
плоскости, в
которых лежат
прямые
РЕ
МК
DB
C
AB
EC
B
16

17.

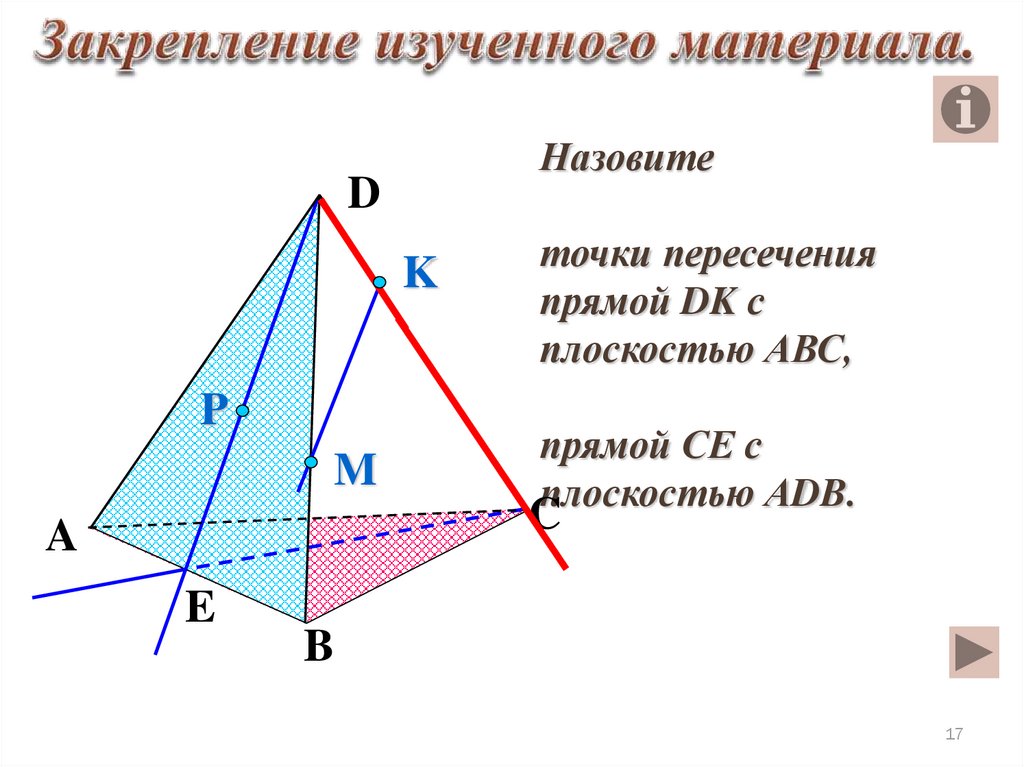
Назовите
D
K
P
M
точки пересечения
прямой DK с
плоскостью АВС,
прямой СЕ с
плоскостью АDB.
C
A
E
B
17

18.

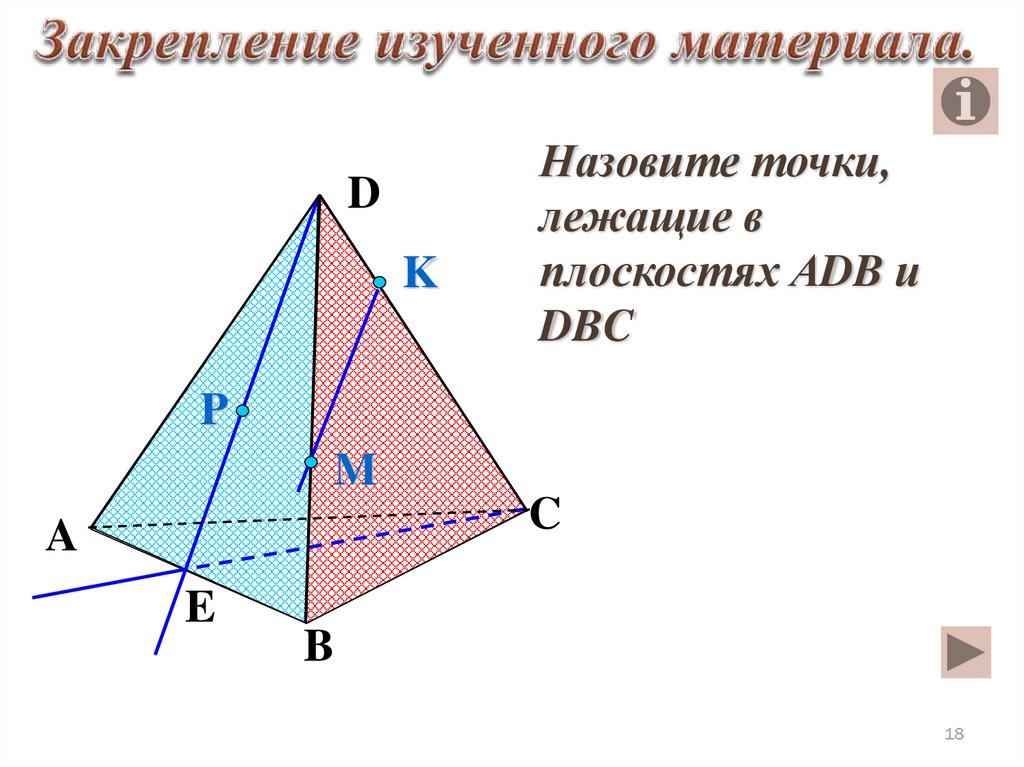
D
K
Назовите точки,
лежащие в
плоскостях АDB и
DBC
P
M
C
A
E
B
18

19.

D
K
P
M
A
E
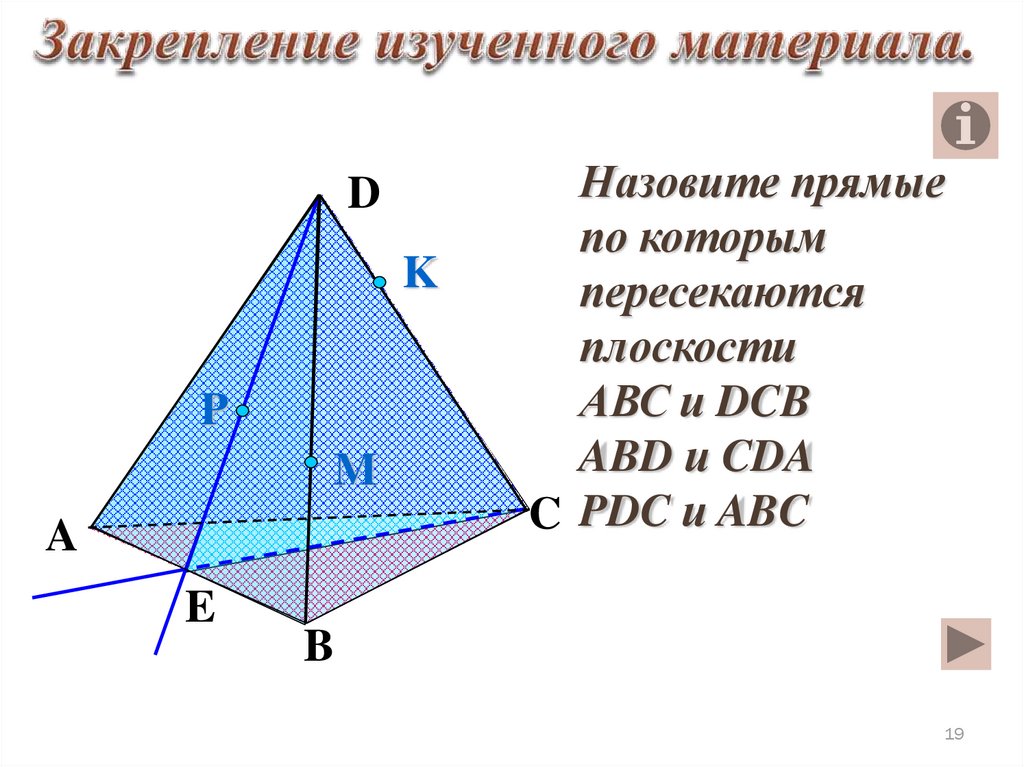
Назовите прямые
по которым
пересекаются
плоскости
АВС и DCB
ABD и CDA
C PDC и ABC
B
19