Параллельные прямые в пространстве

1.

Параллельные прямые в
пространстве

2.

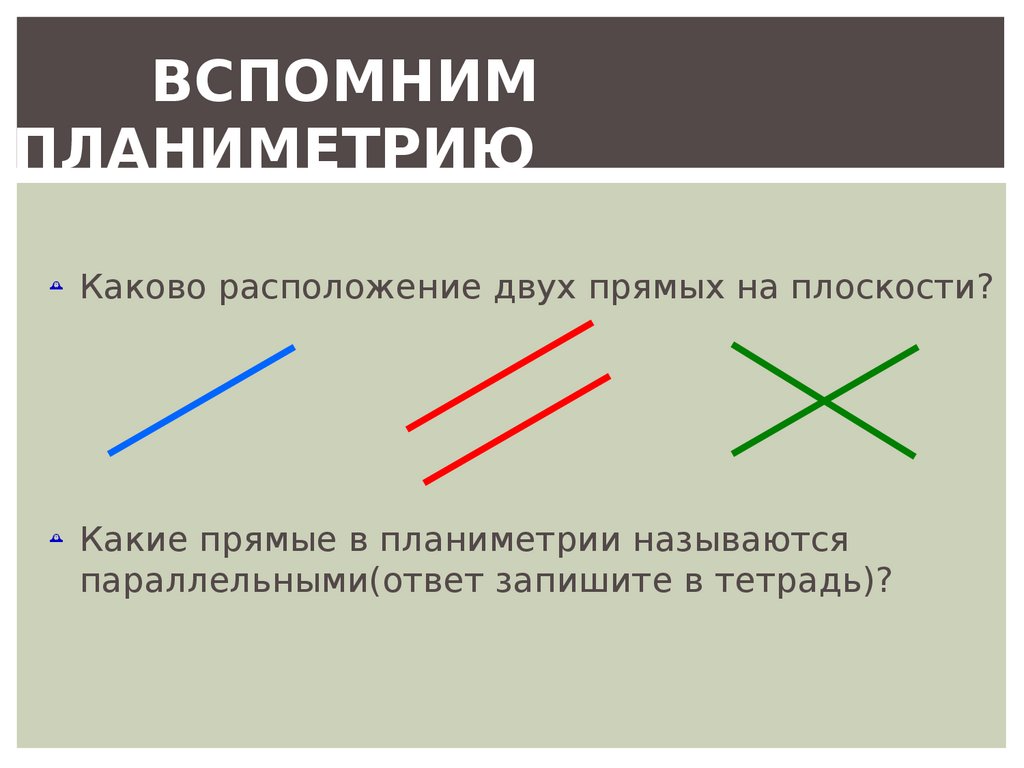
ВСПОМНИМ
ПЛАНИМЕТРИЮ
Каково расположение двух прямых на плоскости?
Какие прямые в планиметрии называются
параллельными(ответ запишите в тетрадь)?

3.

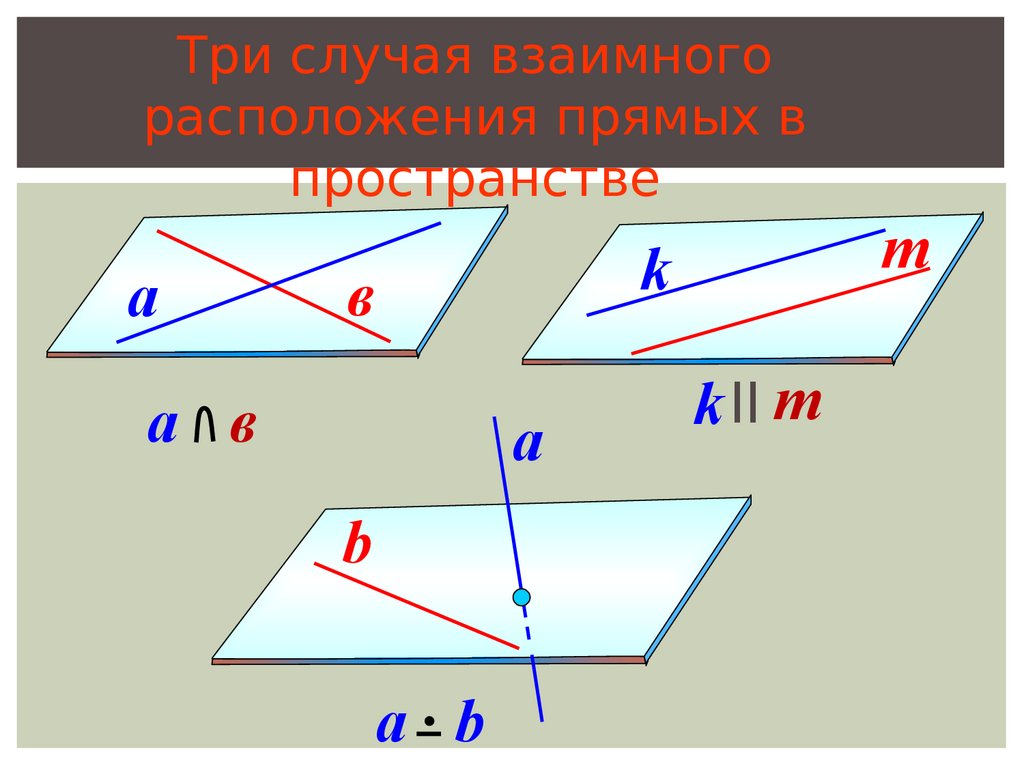
Три случая взаимного
расположения прямых в
пространстве
а
m
k
в
а в
a
b
a b
k II m

4.

Расположение прямых в
пространстве (три случая)
Две прямые в пространстве параллельны друг
другу, пересекаются или скрещиваются.

5.

КАКИЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
НАЗЫВАЮТСЯ ПАРАЛЛЕЛЬНЫМИ?
Определение
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются
a b
если
a b
,a b

6.

Теорема. Через любую точку
пространства, не лежащую на данной
прямой, проходит прямая, параллельная
данной, и притом только одна.
Прямая и не лежащая
на ней точка определяют плоскость
М
b
a

7.

Лемма. Если
одна из двух параллельных
прямых пересекает данную плоскость, то и
другая прямая пересекает данную плоскость.
a
Плоскости
и имеют
общую точку М, значит они
пересекаются по прямой
(А3)
р
b
М
Прямая р лежит в плоскости
и пересекает прямую а в т. М.
Поэтому она пересекает
и
параллельную ей
b
Прямая р лежит также впрямую
плоскости
, поэтому N – точка
точке N.
плоскости . Значит, Nв–некоторой
общая точка прямой b и
плоскости .
N

8.

Теорема
с
Если две прямые параллельны
третьей прямой, то они
параллельны.
aIIс, bIIс
Докажем, что
a
b
К
aIIb
Докажем, что а и b
1) Лежат в одной
плоскости
2) не пересекаются
1) Точка К и прямая а определяют плоскость.
Докажем,
что прямая b лежит в этой плоскости
.
Допустим, что прямая b пересекает плоскость . Тогда по
лемме с также пересекает . По лемме и а также
пересекает
. Это невозможно, т.к. а лежит в плоскости

9.

РЕШЕНИЕ ЗАДАЧ(запишите в
тетрадь )
1
Дан куб. Являются ли параллельными
прямые:
1) АА1 и DD1, АА1 и СС1? Ответ
обоснуйте.
2) АА1 и DС? Они пересекаются?
Две прямые
называются
скрещивающимися,
если они не лежат в
одной плоскости.

10.

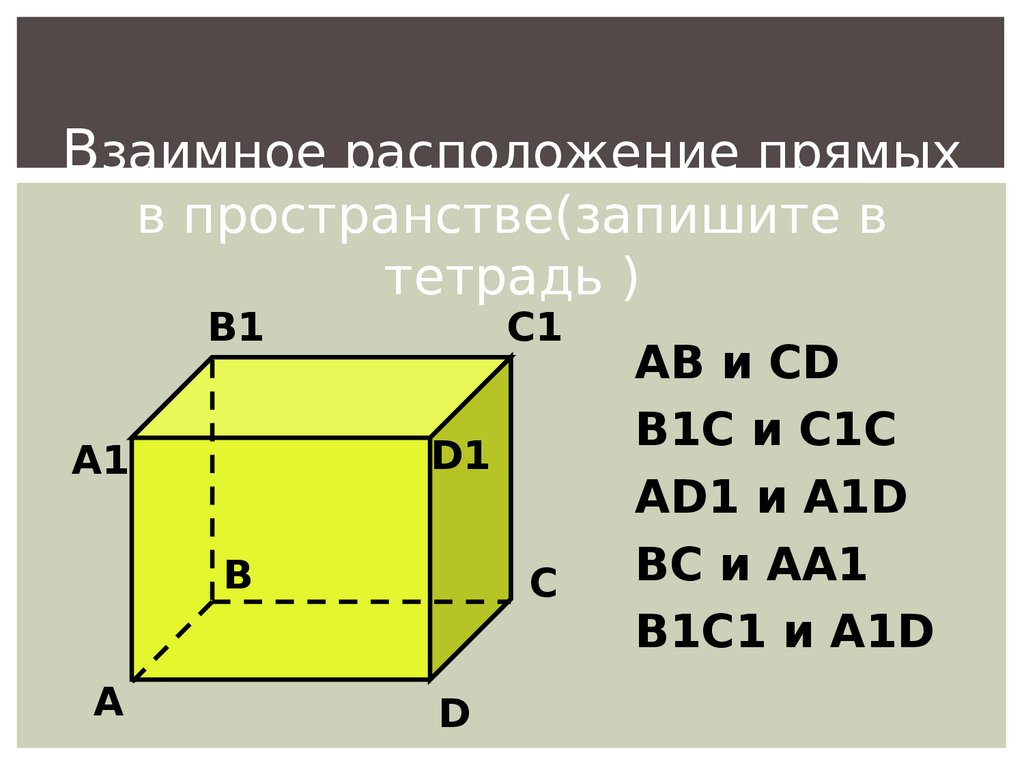
Взаимное расположение прямых
в пространстве(запишите в
тетрадь )
B1
C1
D1
А1
B
А
C
D
AB и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C1 и A1D

11.

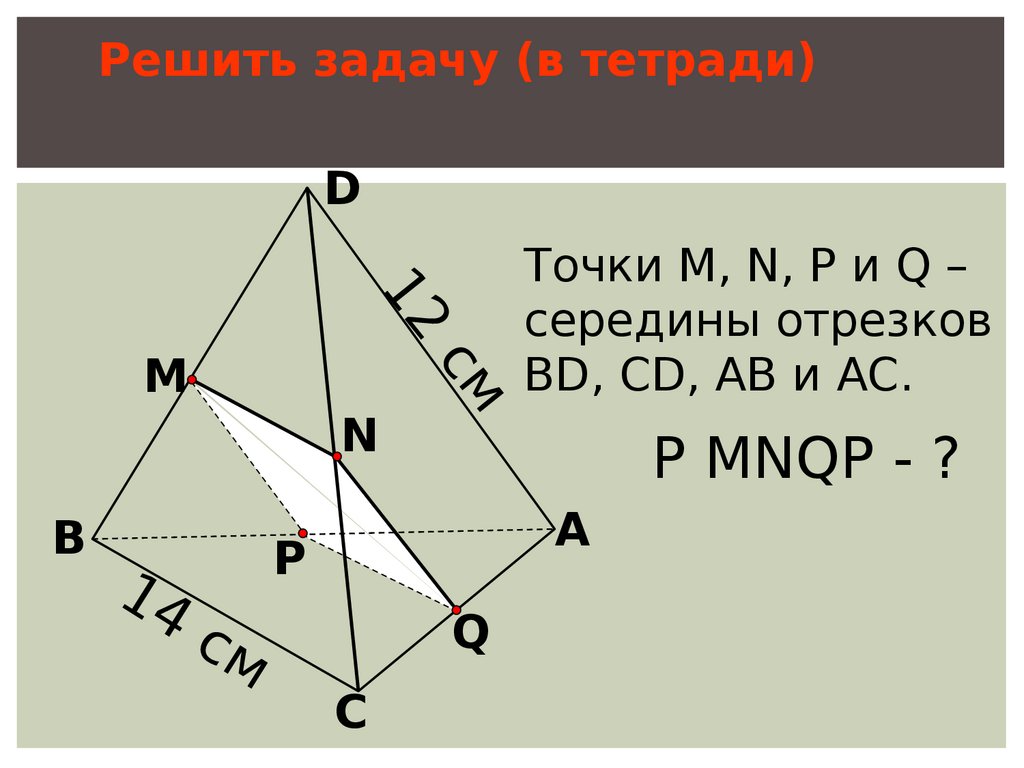
Решить задачу (в тетради)
D
12
N
В
14
см
M
Точки М, N, P и Q –
середины отрезков
BD, CD, AB и АС.
Р MNQP - ?
А
P
см
Q
С

12.

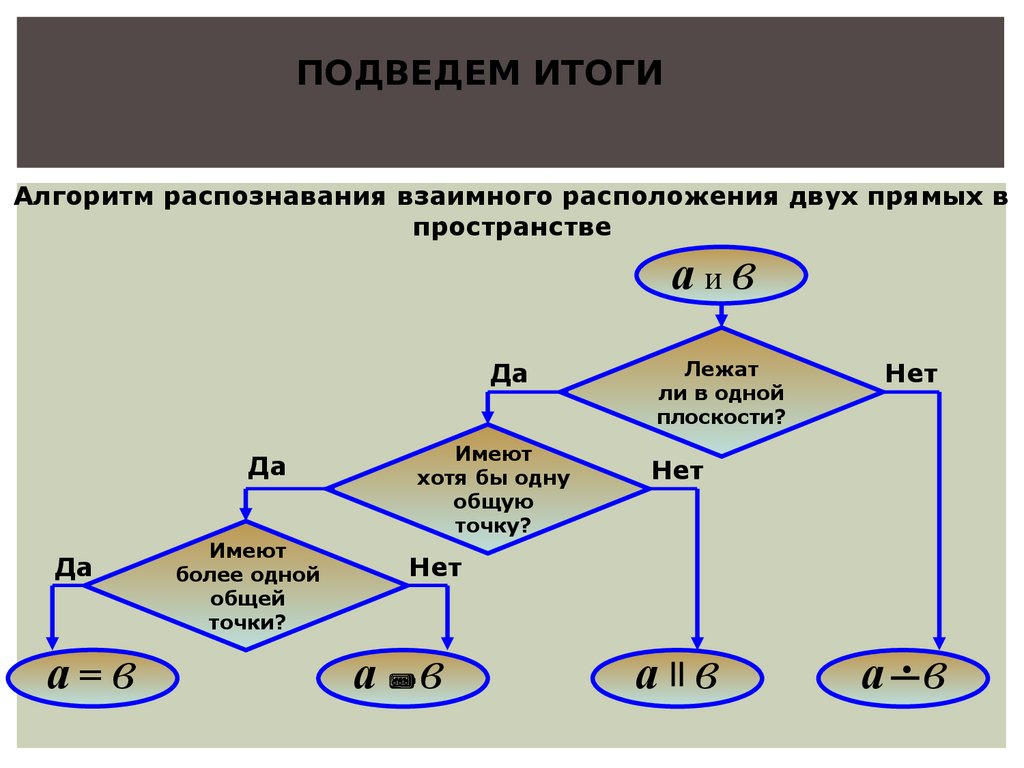
ПОДВЕДЕМ ИТОГИ
Алгоритм распознавания взаимного расположения двух прямых в
пространстве
аив
Да
Да
Да
а=в
Имеют
более одной
общей
точки?
Имеют
хотя бы одну
общую
точку?
Лежат
ли в одной
плоскости?
Нет
Нет
Нет
а в
а
в
а .в