Похожие презентации:
Физика. Механика. Термодинамика и молекулярная физика
1.
ФИЗИКАМеханика.
Термодинамика и молекулярная физика
(или статистическая физика).
Электричество и магнетизм.
Оптика (или теория волн).
Атомная физика (или квантовая физика).
Ядерная физика.
2.
Модуль 1Электростатика и
постоянный ток
2
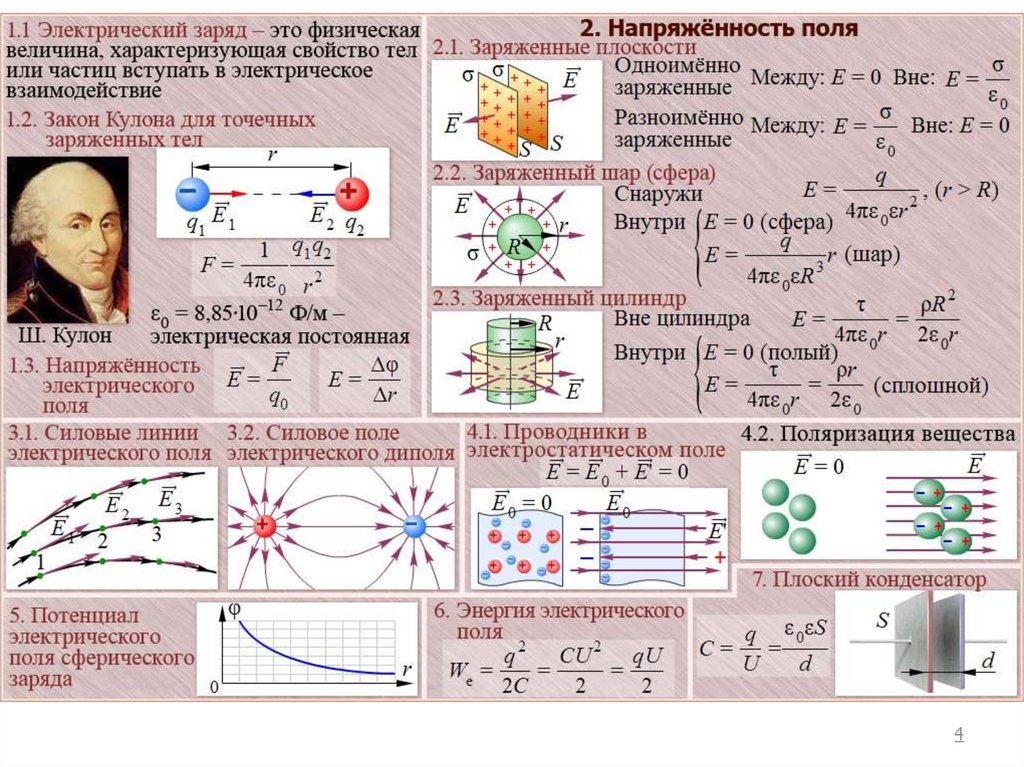
3. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
34.
45.
• Электрические заряды не существуютсами по себе, а являются внутренними
свойствами элементарных частиц –
электронов, протонов и др.
• Опытным путем в 1914 г. американский
физик Р. Милликен показал что
электрический заряд дискретен.
Заряд q любого тела составляет целое
кратное от элементарного электрического
заряда : q = n×e.
19
e 1,6 10
Кл
6.
Закон сохранения заряда – один изфундаментальных
законов
природы,
сформулированный в 1747 г. Б. Франклином
и подтвержденный в 1843 г. М. Фарадеем:
алгебраическая
сумма
зарядов,
возникающих при любом электрическом
процессе на всех телах, участвующих в
процессе равна нулю.
Суммарный электрический заряд
замкнутой системы не изменяется.
7.
Электростатика – раздел,изучающий статические
(неподвижные) заряды и
связанные с ними электрические
поля.
Перемещение зарядов либо отсутствует,
либо происходит так медленно, что возникающие
при движении зарядов магнитные поля ничтожны.
7
8.
Сила взаимодействия междузарядами определяется только
их взаимным расположением.
Следовательно,
энергия
электростатического
взаимодействия – потенциальная
энергия.
8
9.
• Несмотря на обилие различных веществв природе, существуют только
два вида электрических зарядов:
заряды подобные тем, которые возникают
на стекле, потертом о шелк –
положительные
заряды, подобные тем, которые появляются на
янтаре, потертом о мех отрицательные
• Назвал их так
Бенджамин Франклин в 1746 г.
9
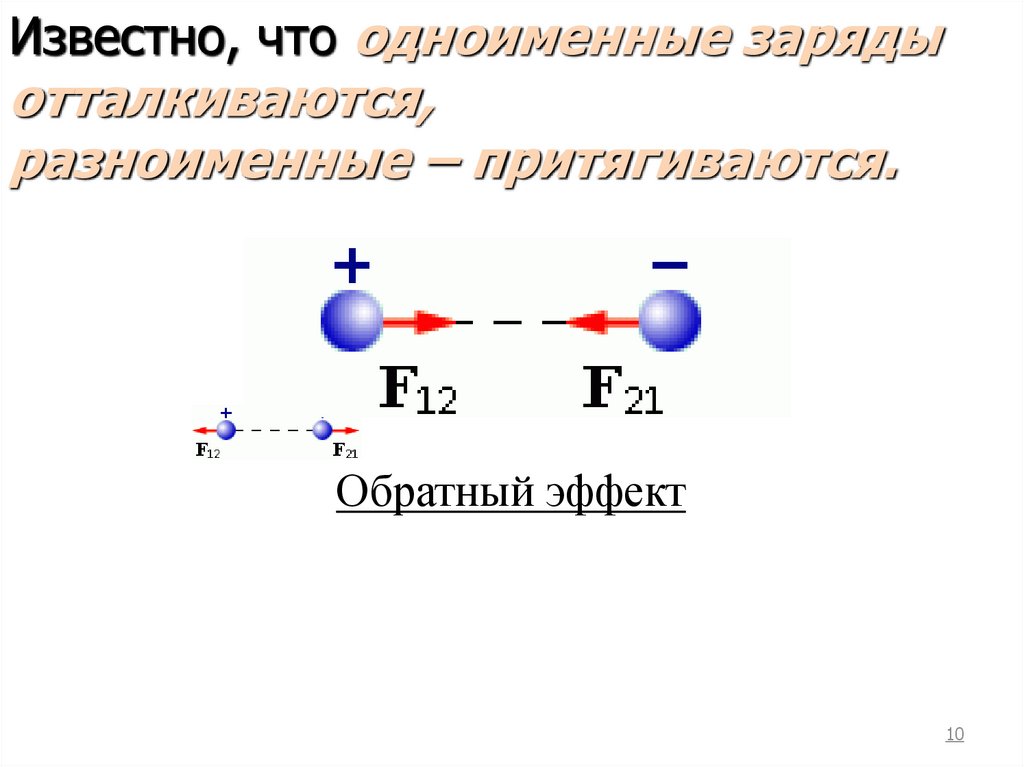
10.
Известно, что одноименные зарядыотталкиваются,
разноименные – притягиваются.
Обратный эффект
10
11.
• Если поднести заряженное тело (с любымзарядом) к легкому – незаряженному, то
между ними будет притяжение – явление
электризации легкого тела через влияние.
• На ближайшем к заряженному телу конце
появляются заряды противоположного
знака (индуцированные заряды) это
явление называется
• электростатической индукцией.
11
12.
• Таким образом, всякий процессзаряжения есть процесс
разделения зарядов.
• Сумма зарядов не изменяется,
заряды только
перераспределяются.
12
13.
Закон Кулона• сила взаимодействия точечных зарядов в
вакууме пропорциональна величине зарядов и
обратно пропорциональна квадрату
расстояния между ними.
q1q2
F k0 2
r
13
14.
q1q2F ko 2
r
• здесь k – коэффициент
пропорциональности, зависящий от
системы единиц.
0
14
15.
• В системе СИ единица заряда1 Кл = 1А * 1с
Н м
k0
9 10
2
4 0
Кл
1
2
9
• где ε0 – электрическая постоянная;
• 4π здесь выражают сферическую симметрию
закона Кулона.
15
16.
• Электрическая постоянная относится к числуфундаментальных физических констант и
равна
2
0 8,85 10
12
Кл
12 Ф
8,85 10
2
Н м
м
• Элементарный заряд в СИ:
• Отсюда следует, что
e 1,6 10
19
Кл.
1 Кл 6,25 10 e.
18
• Поскольку элементарный заряд мал, мы как бы
не замечаем его дискретности (заряду 1 мкКл
соответствует ~ 1013 электронов).
16
17.
• В векторной форме закон Кулона выглядит так:q1q2 r12
F2 k 0 2
F1
r12 r12
• где F1 – сила, действующая на заряд q1
• F2 – сила, действующая на заряд q2
• r - единичный вектор, направленный от
положительного заряда к отрицательному.
17
18.
• В электростатике взаимодействие зарядовподчиняется третьему закону Ньютона:
силы взаимодействия между зарядами
равны по величине и направлены
противоположно друг другу вдоль прямой,
связывающей эти заряды
18
19.
• Если заряды не точечные, то в такой форме законКулона не годится – нужно разбить заряженное
тело на элементарные части и проинтегрировать
по объему.
• Вся совокупность фактов говорит, что
закон Кулона справедлив при
107 – 10-15 м
• Внутри ядра действуют уже другие законы, не
кулоновские силы.
19
20. Электростатическое поле в вакууме. Напряженность электростатического поля
Почему заряды взаимодействуют?
Имеет место борьба двух теорий:
теория дальнодействия – Ньютон, Ампер
теория близкодействия – Фарадей, Максвелл и
т.д.
• Для электростатического поля справедливы обе
эти теории.
20
21.
• Вокруг заряда всегда есть электрическоеполе, основное свойство которого
заключается в том, что на всякий другой
заряд, помещенный в это поле, действует
сила.
• Электрические и магнитные поля – частный
случай более общего – электромагнитного
поля (ЭМП).
• Они могут порождать друг друга,
превращаться друг в друга.
• Если заряды не движутся, то магнитное поле
не возникает.
21
22.
• ЭМП – есть не абстракция, а объективнаяреальность – форма существования
материи, обладающая определенными
физическими свойствами, которые мы
можем измерить.
• Не существует статических электрических
полей, не связанных с зарядами, как не
существует «голых», не окруженных полем
зарядов.
22
23.
• Силовой характеристикой поля,создаваемого зарядом q является
отношение силы, действующей на
пробный заряд q’ , помещенный в
данную точку поля, к величине этого
заряда, называемое напряженностью
электростатического поля, т.е.
F
q
E
2
q' 4 0 r
23
24.
Силовая характеристикой поля –напряженность
электростатического поля:
F
q
E
2
q' 4 0 r
q’
- пробный заряд
24
25.
• Напряженность в векторной формеq r
E
2
4 0 r r
• здесь r – расстояние от заряда до точки,
где мы изучаем это поле.
Тогда
F q' E
25
26.
• Вектор напряженностиэлектростатического поля равен силе,
действующей в данной точке на
помещенный в нее пробный единичный
положительный заряд.
• Из данного определения следует, что
напряженность может быть выражена
как – ньютон на кулон (Н/Кл).
• 1 Н/Кл – напряженность такого поля,
которое на точечный заряд 1 Кл
действует с силой в 1 Н.
26
27.
• В СИq
Е
2
4 πε0 r
• размерность напряженности:
Н
В
E или
Кл
м
27
28. Сложение электростатических полей. Принцип суперпозиции
• Если поле создается несколькимиточечными зарядами, то на пробный
заряд q’ действует со стороны заряда qk
такая сила, как если бы других зарядов не
было.
28
29.
• Результирующая сила определитсявыражением:
F Fk
k
• – это принцип суперпозиции или независимости
действия сил
1 qqk rk
F
F
k
2
k 4 πε0 rk rk
k
29
30.
т.к. F q ' E то E – результирующая
напряженность поля в точке, где расположен
пробный заряд, так же подчиняется принципу
суперпозиции:
Е Е1 Е 2 ... Е k .
k
• Это соотношение выражает принцип
наложения
или суперпозиции электрических полей и
представляет важное свойство электрического
поля.
30
31.
Принцип наложения или суперпозицииэлектрических полей:
• Напряженность результирующего поля,
системы точечных зарядов равна
векторной сумме напряженностей
полей, созданных в данной точке каждым
из них в отдельности.
Е Е1 Е 2 ... Е k .
k
31
32. Пример 1
А• Е Е 1 Е 2 Е 3 ... Е k т. е.
Е Е Е
задача симметрична
k
Е Еk
Е Е
Е 2 Е сos
k
32
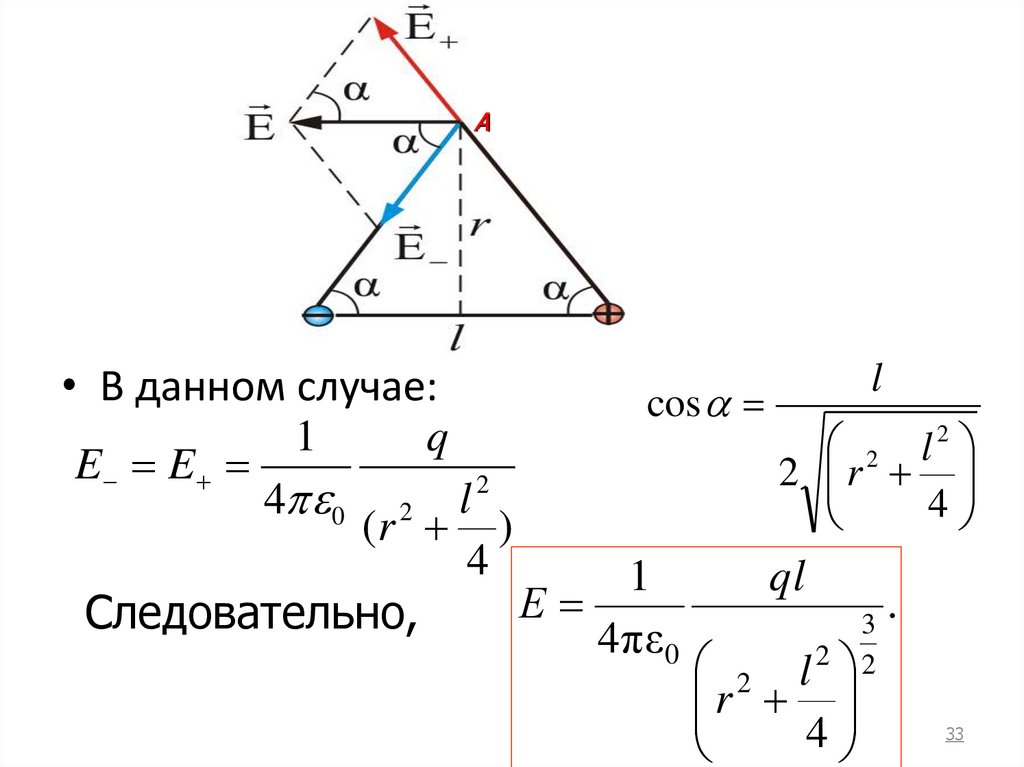
33.
Аl
• В данном случае:
cos
1
q
2 l2
E E
2 r
2
4 0 2 l
4
(r )
4
1
ql
Е
.
Следовательно,
3
4 πε0
2 l2 2
r
4
33
34.
• Рассмотрим другой пример. Найдемнапряженность электростатического поля Е,
создаваемую двумя положительными
зарядами q1 и q2 в точке А, находящейся на
расстоянии r1 от первого и r2 от второго
зарядов
34
35.
q1E1
2
4 πε0 r1
q2
E2
2
4 πε 0 r2
Воспользуемся теоремой косинусов:
E
E12
E22
1
2 E1E2 cosα
4 πε0
r
2
где cosα
r12
r2
2r1r2
2
.
2
q1
r14
2
q2
r24
2q1q2
2 2 cosα ,
r1 r2
35
36.
• Если поле создается не точечными зарядами, тоиспользуют обычный в таких случаях прием. Тело
разбивают на бесконечно малые элементы и
определяют напряженность поля, создаваемого
каждым элементом, затем интегрируют по всему
телу:
где dE
Е dE ,
– напряженность поля, обусловленная
заряженным элементом. Интеграл может быть
линейным, по площади или по объему в
зависимости от формы тела.
36
37.
• Для решения подобных задач пользуютсясоответствующими значениями плотности
заряда:
• dq / dl – линейная плотность заряда,
измеряется в Кл/м;
dq / dS
- поверхностная плотность заряда
измеряется в Кл/м2;
dq / dV
– объемная плотность заряда,
измеряется в Кл/м3.
37
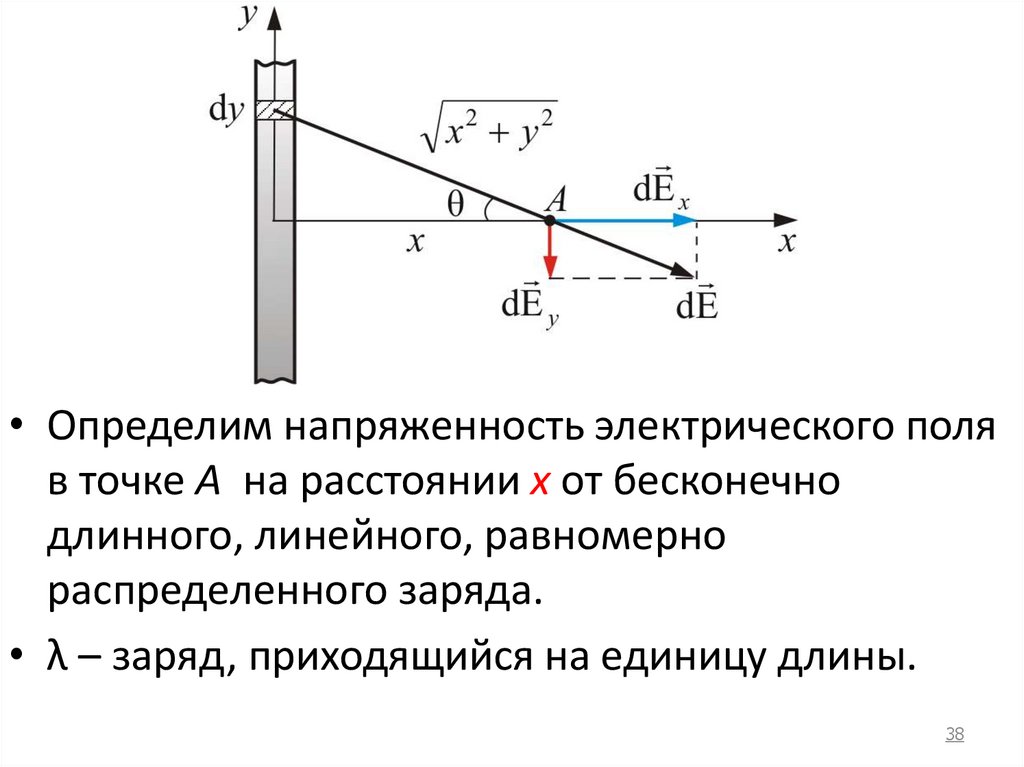
38.
• Определим напряженность электрического поляв точке А на расстоянии х от бесконечно
длинного, линейного, равномерно
распределенного заряда.
• λ – заряд, приходящийся на единицу длины.
38
39.
• Считаем, что х – мало по сравнению сдлиной проводника. Элемент длины dy,
несет заряд dq = dy λ. Создаваемая этим
элементом напряженность электрического
поля в точке А:
dy
dE
.
2
2
4 0 ( x y )
1
39
40.
• Вектор dE имеет проекции dEx и dEy причемdE y dE sin θ.
• Т.к. проводник бесконечно длинный, а задача
симметричная, то у – компонента вектора dE
dE x dE cos θ;
обратится в ноль (скомпенсируется), т.е. .
E y dE sin θ 0
40
41.
λcosθdy
• Тогда E E x dEcosθ
2
2
4 πε 0 x y
y xtg θ,
• Теперь выразим y через θ. Т.к.
• То dy xdθ / cos θ
2
( x y ) x / cos θ
2
2
2
2
2
1
E
cos d
.
4 0 x
2 0 x
2
41
42.
E.
2 0 x
• Напряженность электрического
поля линейно распределенных
зарядов изменяется обратно
пропорционально расстоянию до
заряда.
42
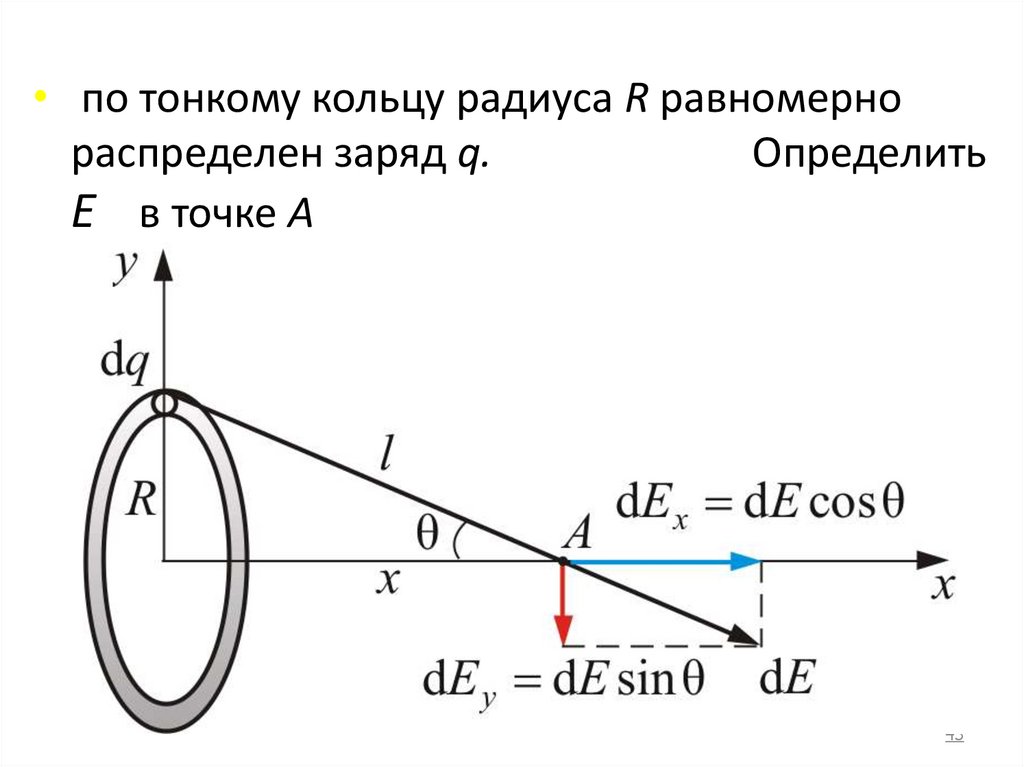
43.
• по тонкому кольцу радиуса R равномернораспределен заряд q.
Определить
Е в точке А
43
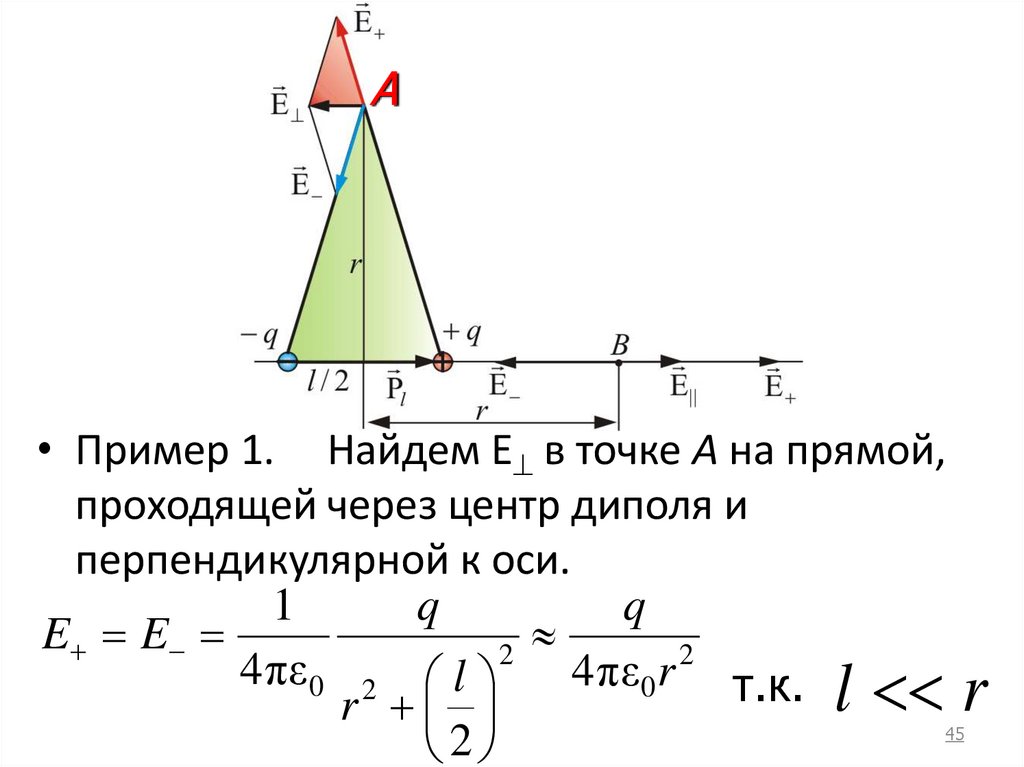
44. Электростатическое поле диполя
• Электрическим диполем называется системадвух одинаковых по величине, но разноименных
точечных зарядов, расстояние между
которыми значительно меньше расстояния до
тех точек, в которых определяется поле
системы
• Плечо диполя – вектор, направленный от
отрицательного заряда к положительному и
численно равный расстоянию между зарядами.
44
45.
А• Пример 1. Найдем Е в точке А на прямой,
проходящей через центр диполя и
перпендикулярной к оси.
1
q
q
E E
2
2
4 πε0 2 l
4 πε0 r т.к.
l
r
2
r
45
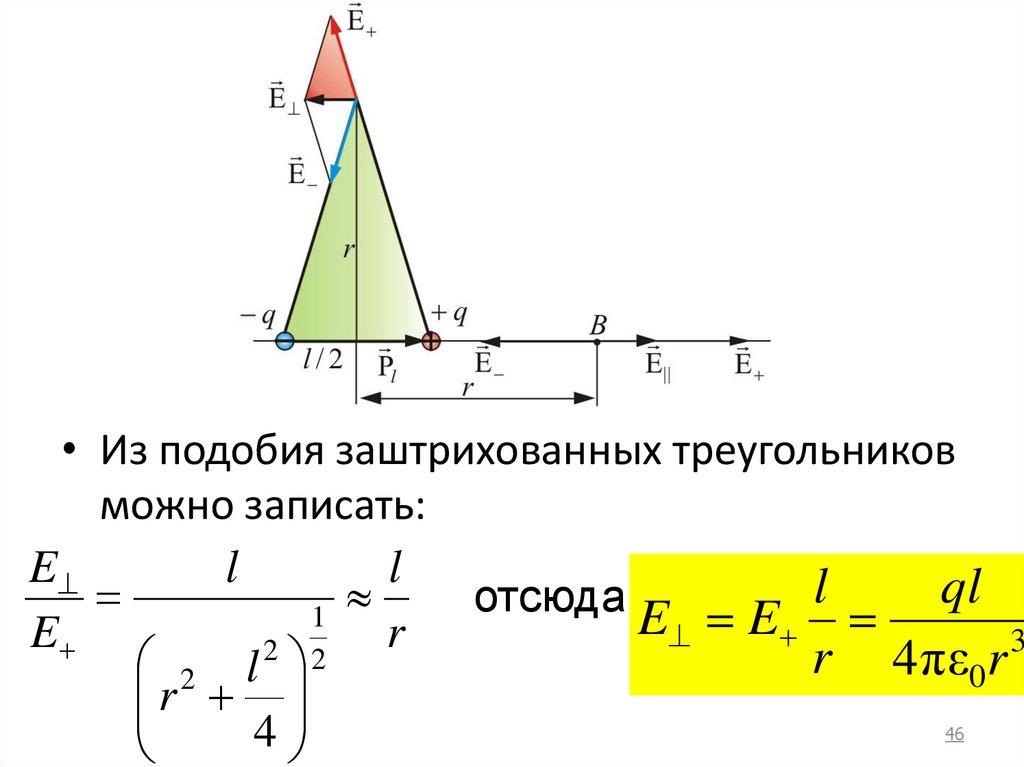
46.
• Из подобия заштрихованных треугольниковможно записать:
E
l
l
l
ql
отсюда
1
E E
E
r
3
2 2
r 4πε0r
2 l
r
4
46
47.
Обозначим вектор: Р q l
–
электрический момент диполя (или
дипольный момент) – произведение
положительного
заряда диполя на плечо .
• Направление l совпадает с
направлением P , т.е. от отрицательного
заряда к положительному.
• Тогда, учитывая что ql P , получим:
P
E
3
4 πε0 r или
P
E
3
4 0 r
47
l
48.
• Пример 2.2ql
Е||
3
4 0 r
На оси диполя, в точке В :
или
2P
E ||
.
3
4 πε 0 r
48
49.
pE
.
3
4 0 r
Поле в точках А1 и А2 отличается в два раза (по
модулю). Направлено в противоположные стороны.
Напряженность поля диполя убывает обратно
пропорционально кубу расстояния от диполя до
точки наблюдения, т.е. быстрее, чем поле точечного
заряда.
50.
• Пример 3.В произвольной точке С
P
2
E
3 cos φ 1,
3
4 πε0 r
где
φ φ1 φ 2
При :
π
P
φ1 φ 2 , E1
;
3
2
4 πε0 r
2P
φ1 φ 2 0, Е2
3
4 πε0 r
50
51.
• Электрическое поле диполя.51
52.
• Из приведенных примеров видно, чтонапряженность электрического поля
системы зарядов равна
геометрической сумме
напряженностей полей каждого из
зарядов в отдельности (принцип
суперпозиции).
52
























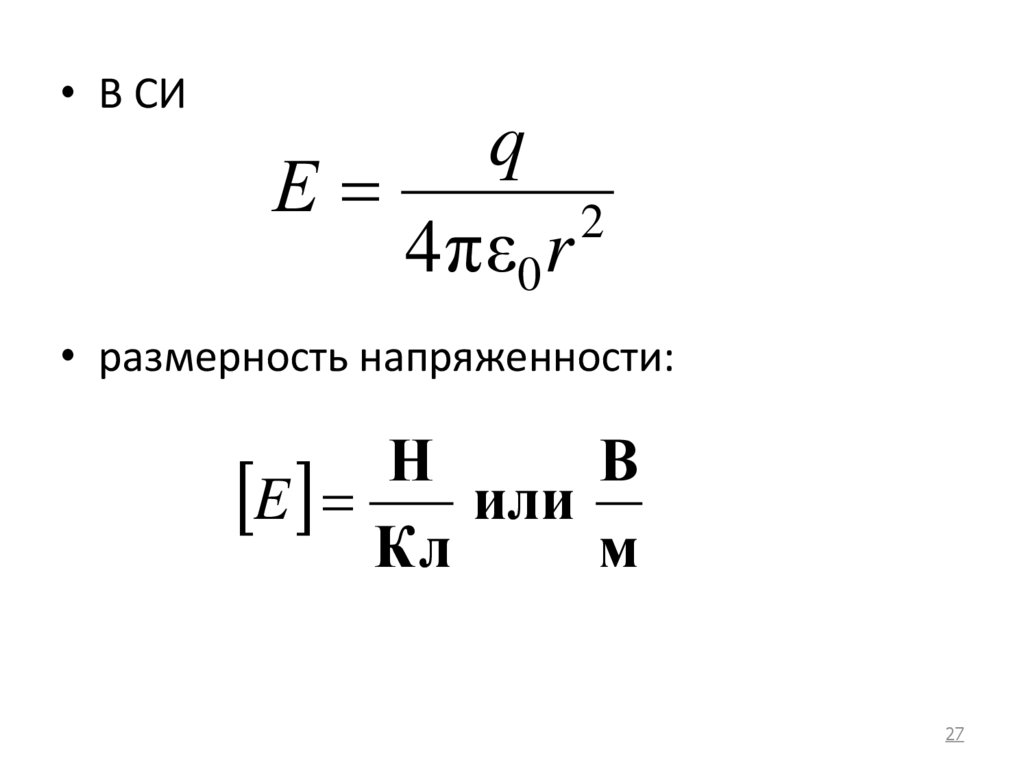




















 Физика
Физика








