Похожие презентации:
Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса. Лекция 1
1. Учебники
• 1. Мартинсон Л.К., Морозов А.Н., СмирновЕ.В. Электромагнитное поле. 2013 и др.
• 2. Иродов И.Е. Электромагнетизм.
Основные законы. 2003 идр.
• Савельев И.В. Курс общей физики.
Электричество и магнетизм. 2004 и др.
Доп. материалы на персональной страничке www.bmstu.ru/ps/~chuev
Презентации лекций: http://hoster.bmstu.ru/ Зарегистрироваться или
войти гостем Кодовое слово: не требуется. Далее Новые курсы.
Электромагнетизм и оптика – 2020-2021.
А.С. Чуев - 2020
1
2. Лекция 1. Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля
1. Электрический заряд. Закон Кулона.2. Напряженность электростатического поля.
Силовые линии.
3. Принцип суперпозиции и его применение к расчету
поля системы неподвижных зарядов.
4. Поток вектора напряженности электрического
поля.
5. Теорема Гаусса в интегральной и
дифференциальной формах в вакууме и ее
применение для расчета электрических полей.
А.С. Чуев - 2020
2
3.
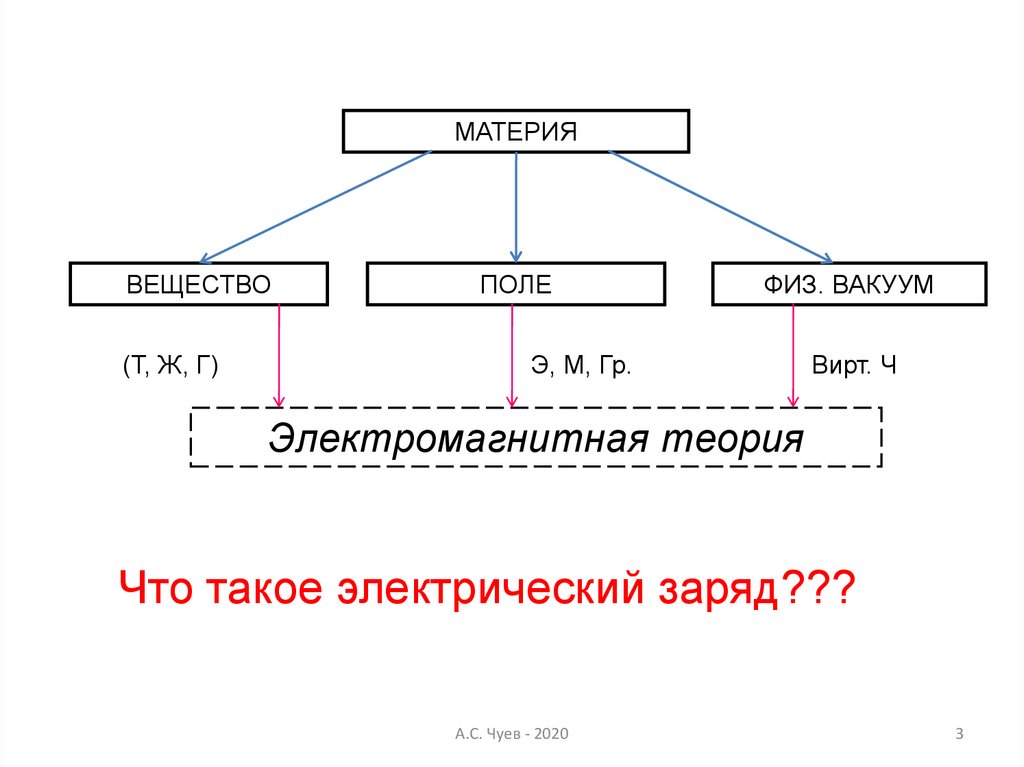
МАТЕРИЯВЕЩЕСТВО
(Т, Ж, Г)
ПОЛЕ
ФИЗ. ВАКУУМ
Э, М, Гр.
Вирт. Ч
Электромагнитная теория
Что такое электрический заряд???
А.С. Чуев - 2020
3
4.
А.С. Чуев - 20204
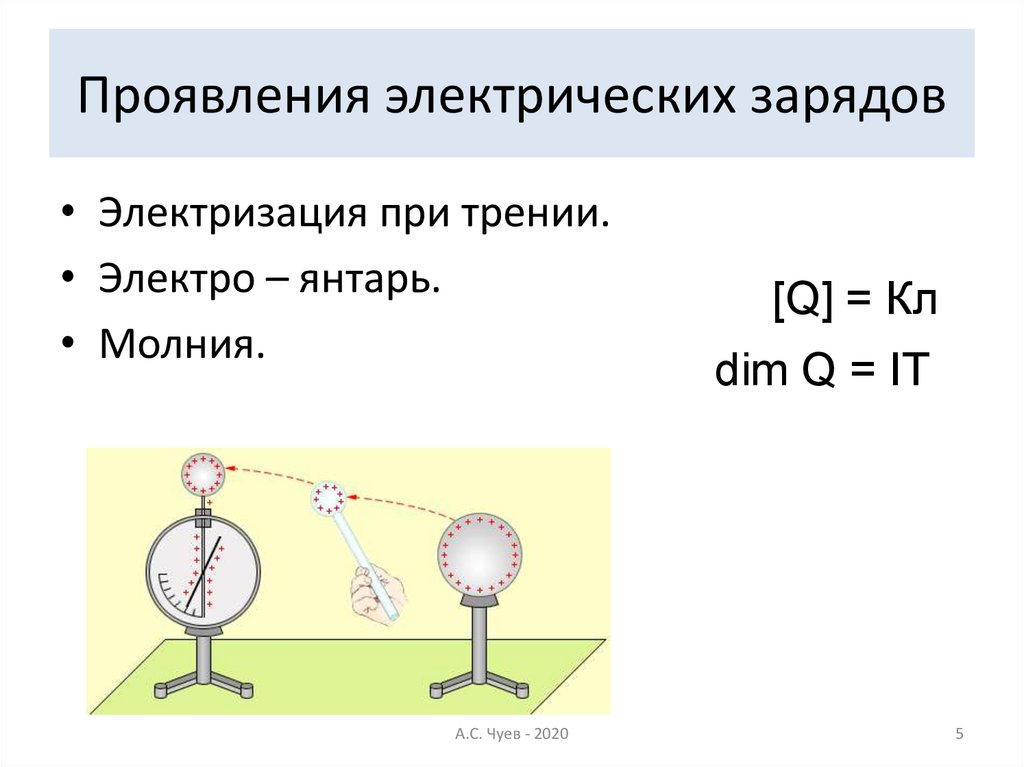
5. Проявления электрических зарядов
• Электризация при трении.• Электро – янтарь.
• Молния.
А.С. Чуев - 2020
[Q] = Кл
dim Q = IT
5
6.
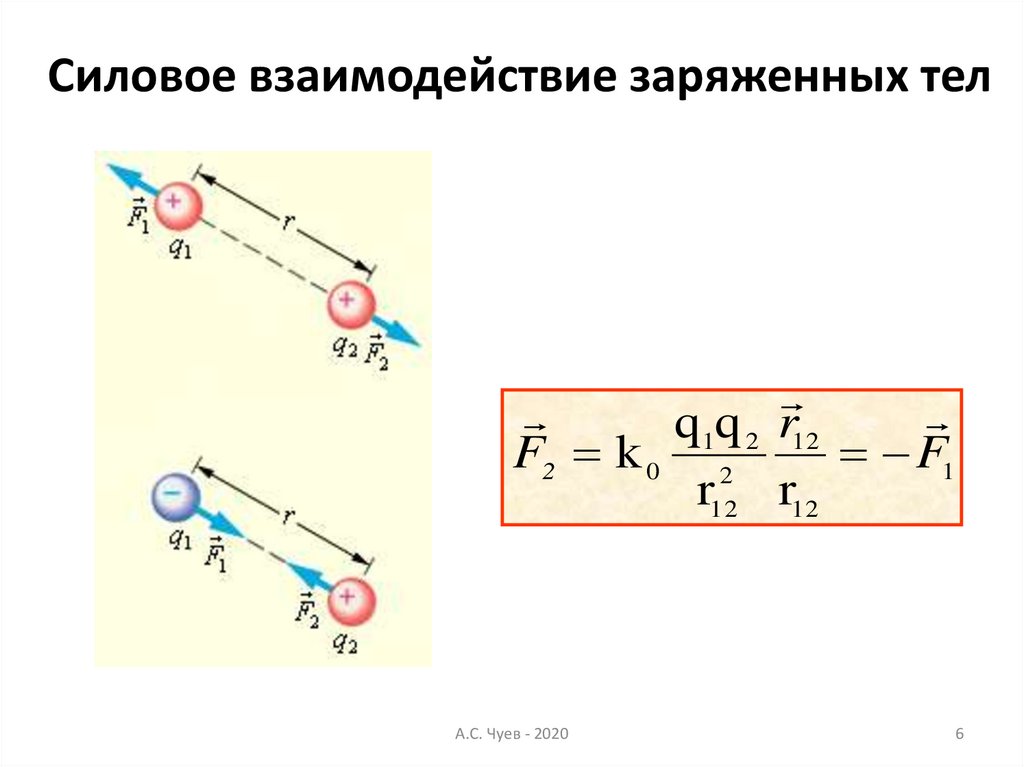
Силовое взаимодействие заряженных телq1q 2 r12
F2 k 0 2
F1
r12 r12
А.С. Чуев - 2020
6
7.
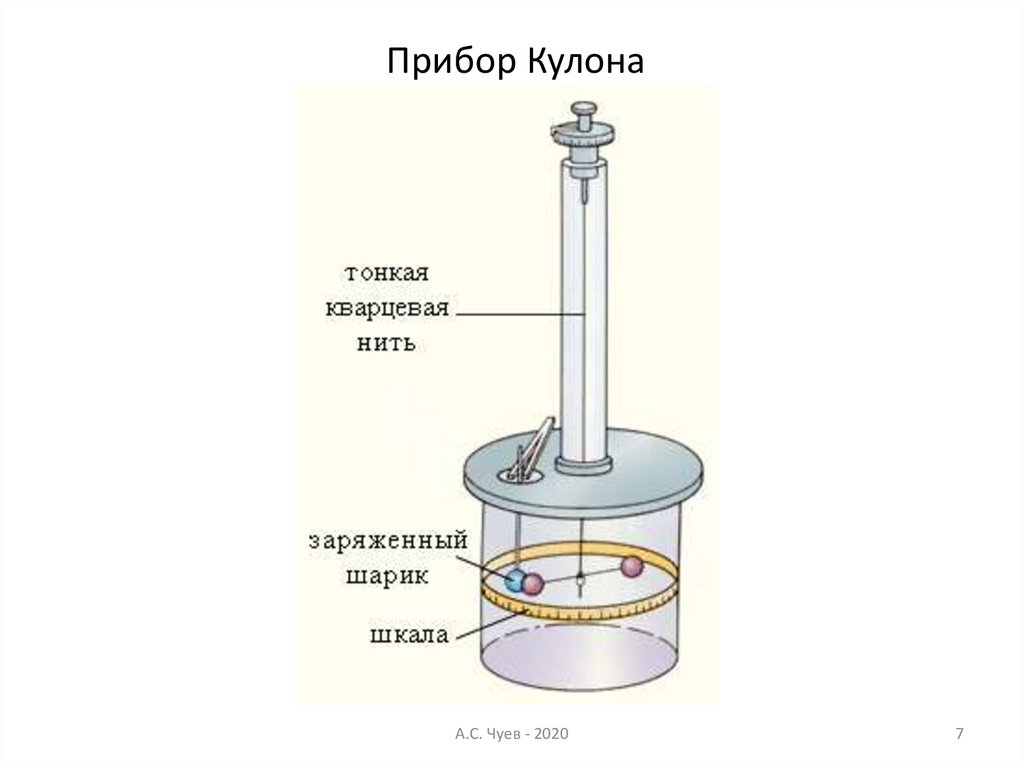
Прибор КулонаА.С. Чуев - 2020
7
8. Закон Кулона
q1q2F ko 2
r
q1q 2 r12
F2 k 0 2
F1
r12 r12
2
1
Н
м
9
9 10
В СИ: k 0
2
4 0
Кл
А.С. Чуев - 2020
с
2
8
9.
• Электрические заряды не существуютсами по себе, а являются внутренними
свойствами элементарных частиц –
электронов, протонов и др.
• Опытным путем в 1914 г. американский
физик Р. Милликен показал что
электрический заряд дискретен.
• Заряд q любого тела составляет целое кратное от
элементарного электрического заряда :
q ne
e 1,602 10
А.С. Чуев - 2020
19
Кл
9
10.
Определения плотностей заряда:dq / dl
– линейная плотность заряда,
измеряется в Кл/м;
dq / dS
- поверхностная плотность заряда
измеряется в Кл/м2;
dq / dV
– объемная плотность заряда,
измеряется в Кл/м3.
А.С. Чуев - 2020
10
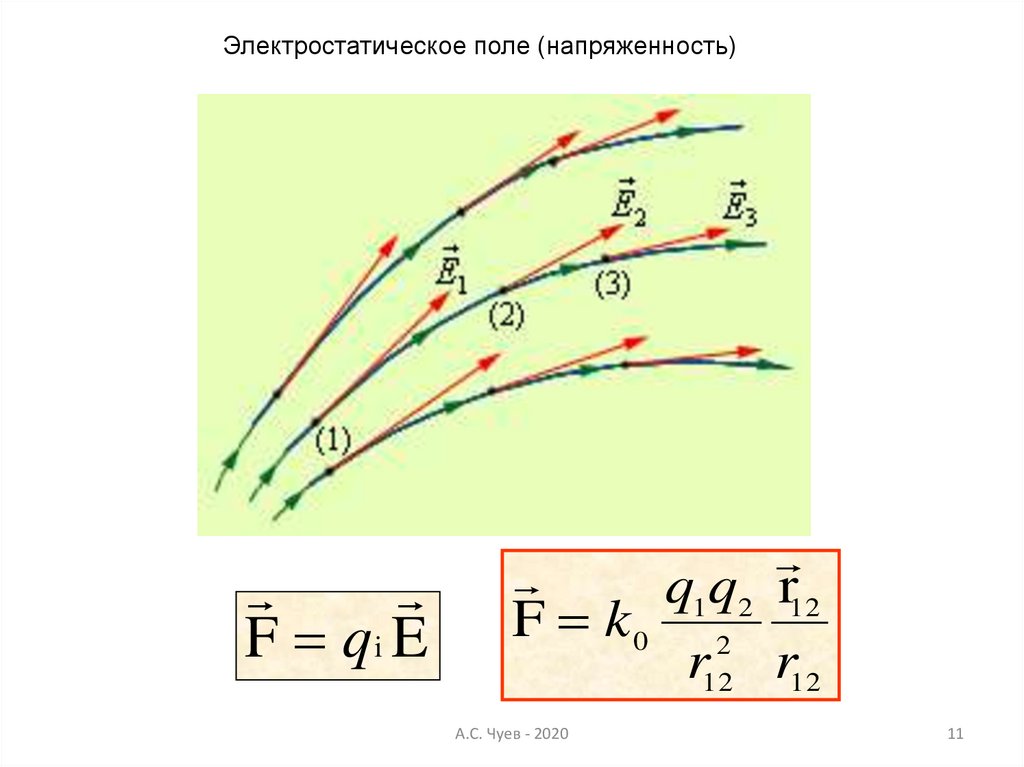
11.
Электростатическое поле (напряженность)F qi E
q1q2 r12
F k0 2
r12 r12
А.С. Чуев - 2020
11
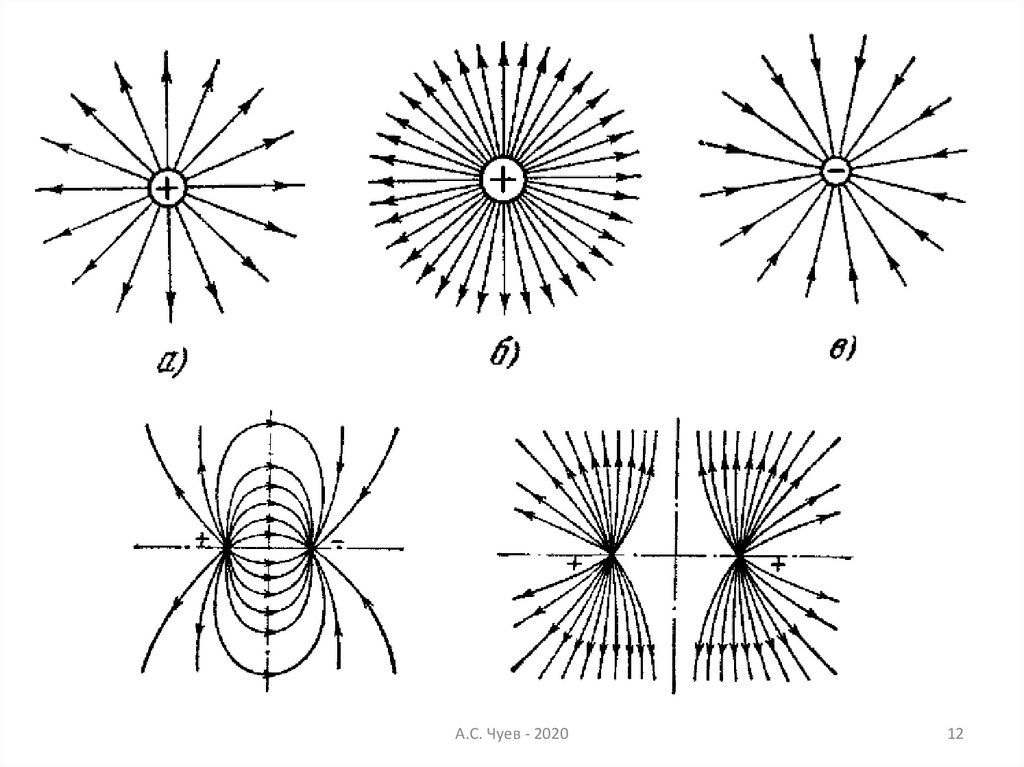
12.
А.С. Чуев - 202012
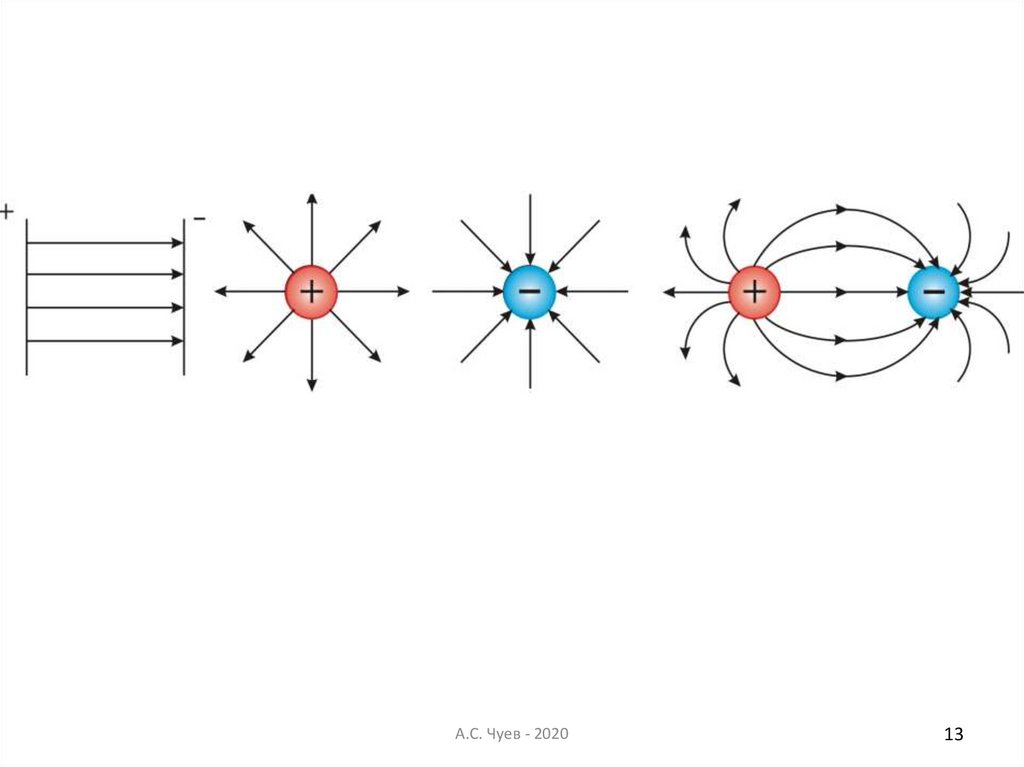
13.
А.С. Чуев - 202013
14.
Силовая характеристикаэлектростатического поля напряженность
Определение Е со стороны
пробного заряда:
это отношение силы к
величине пробного заряда
Определение Е со стороны
заряда, создающего поле
А.С. Чуев - 2020
F
E
qПр
E
q0
e
2 r
4 0 r
1
14
15.
Иная форма записи :E
q r
2
4 πε 0 r r
здесь r – расстояние от заряда q до точки, где
мы воспринимаем это поле.
q0
F
E
2
q' ε 0 4 πr
В скалярном виде:
q0 q
F 4 r
П const
0
2
А.С. Чуев - 2020
15
16.
Энергетическая характеристикаэлектростатического поля –
электрический потенциал (скалярный)
Определение потенциала со
стороны пробного заряда: это
отношение энергии к величине
пробного заряда
W
qПр
Определение потенциала со
стороны заряда, создающего
поле
1 q0
ε 0 4 r
А.С. Чуев - 2020
16
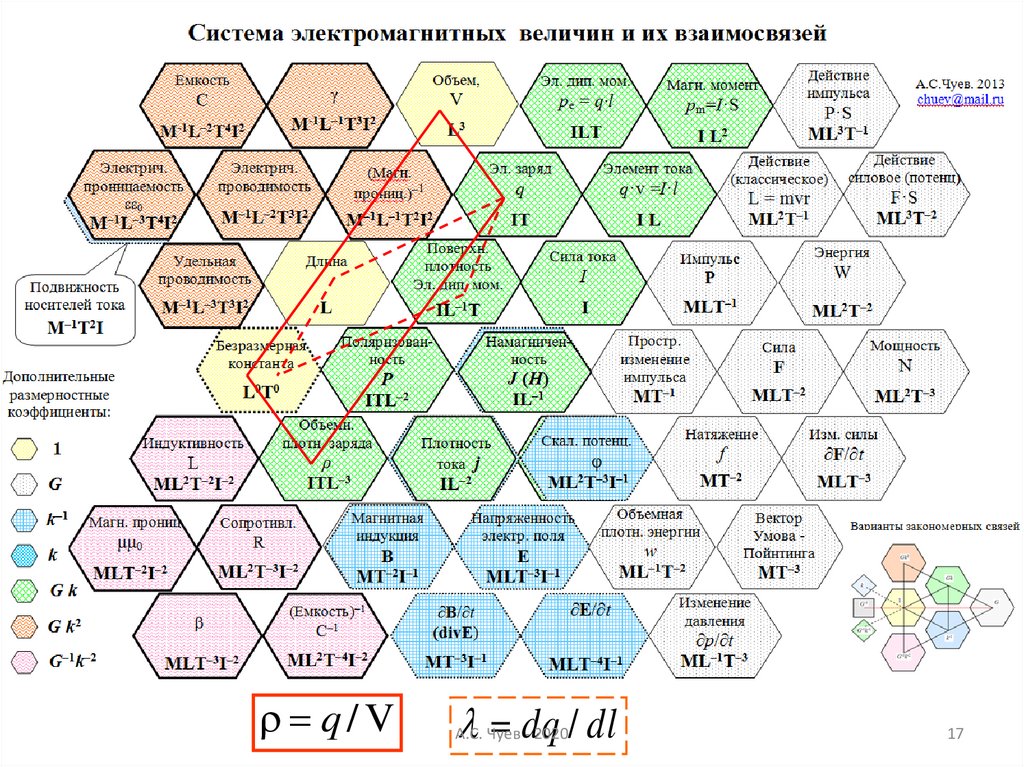
17.
q/Vdq / dl
А.С. Чуев - 2020
17
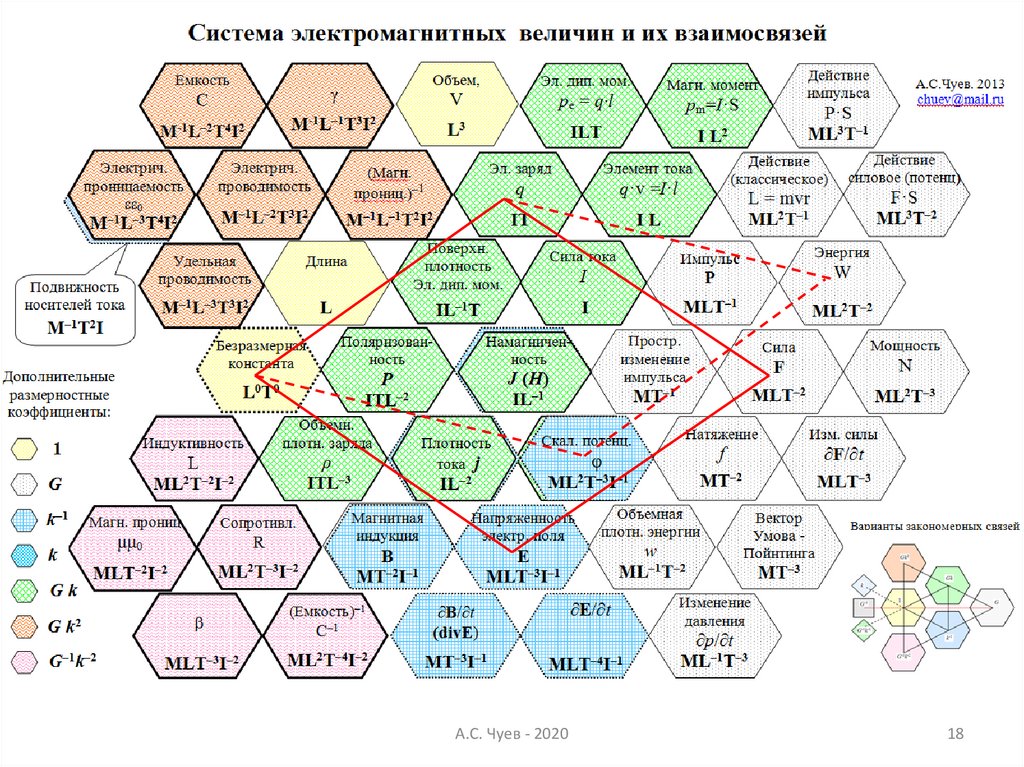
18.
А.С. Чуев - 202018
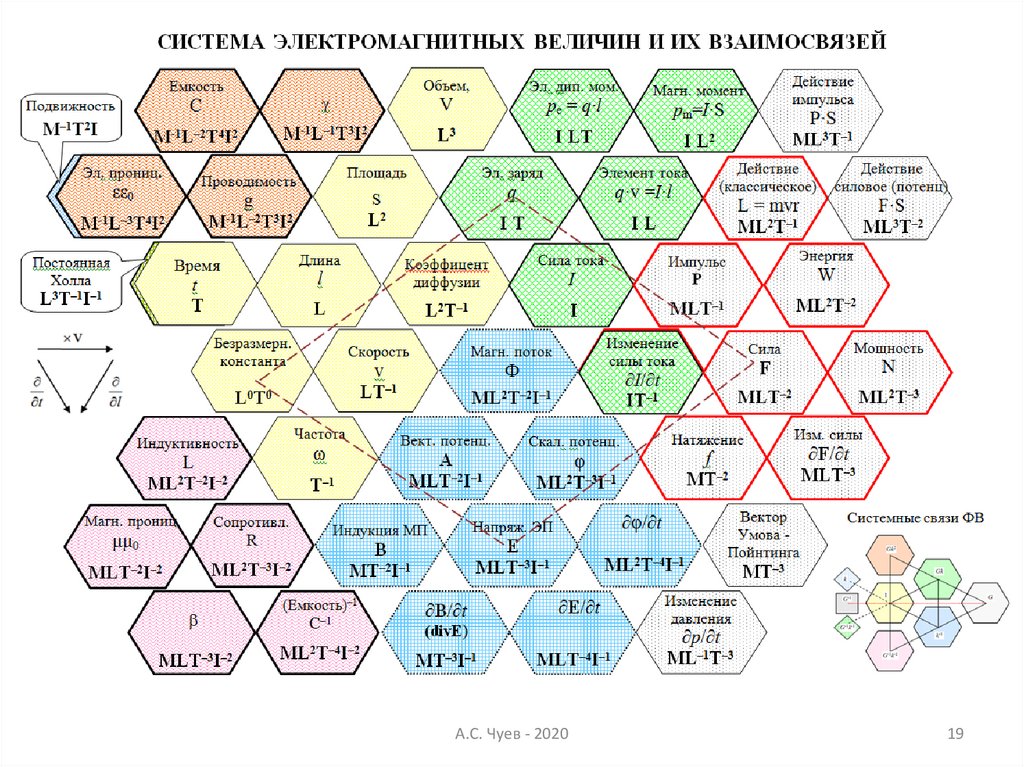
19.
А.С. Чуев - 202019
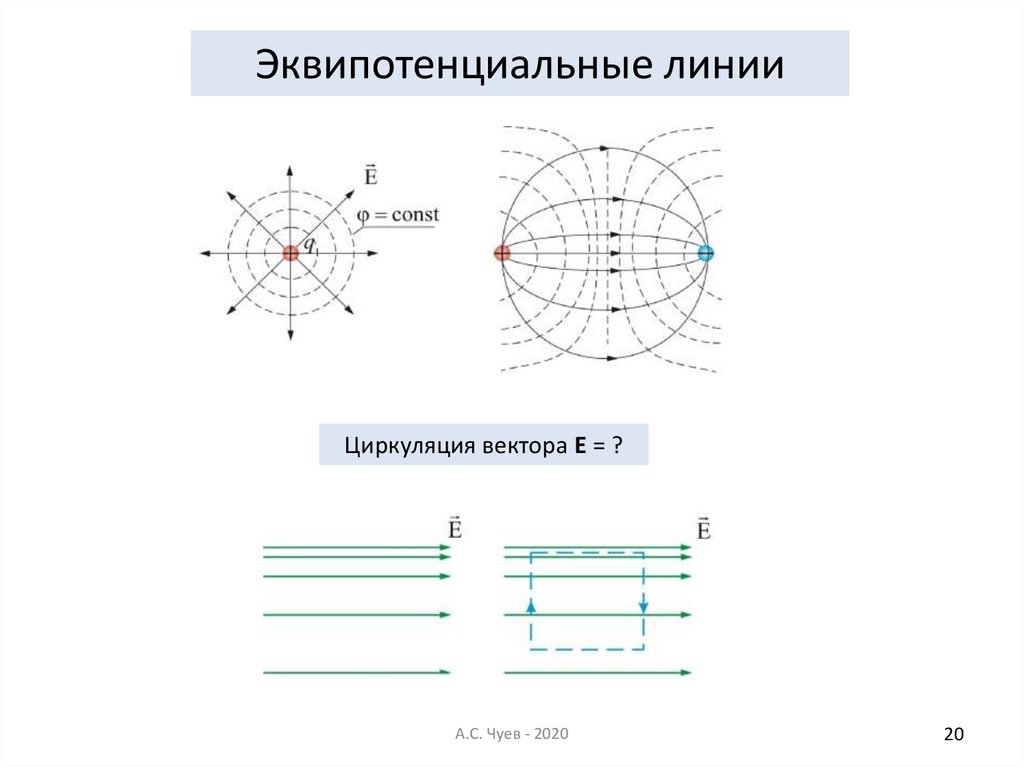
20.
Эквипотенциальные линииЦиркуляция вектора Е = ?
А.С. Чуев - 2020
20
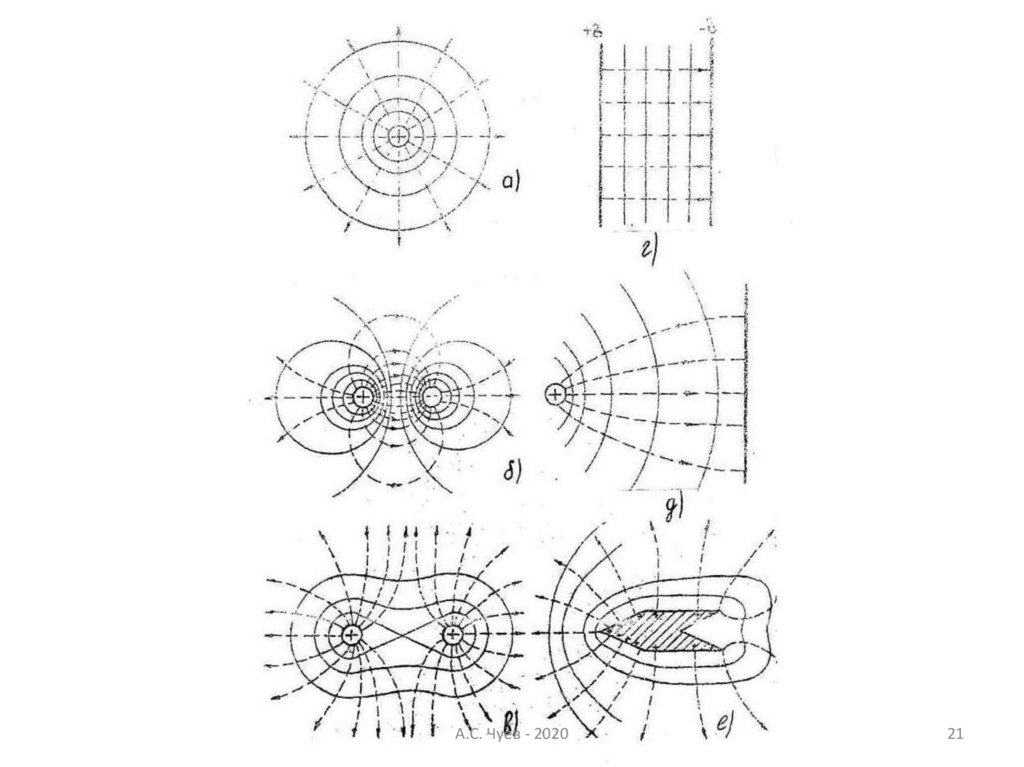
21.
А.С. Чуев - 202021
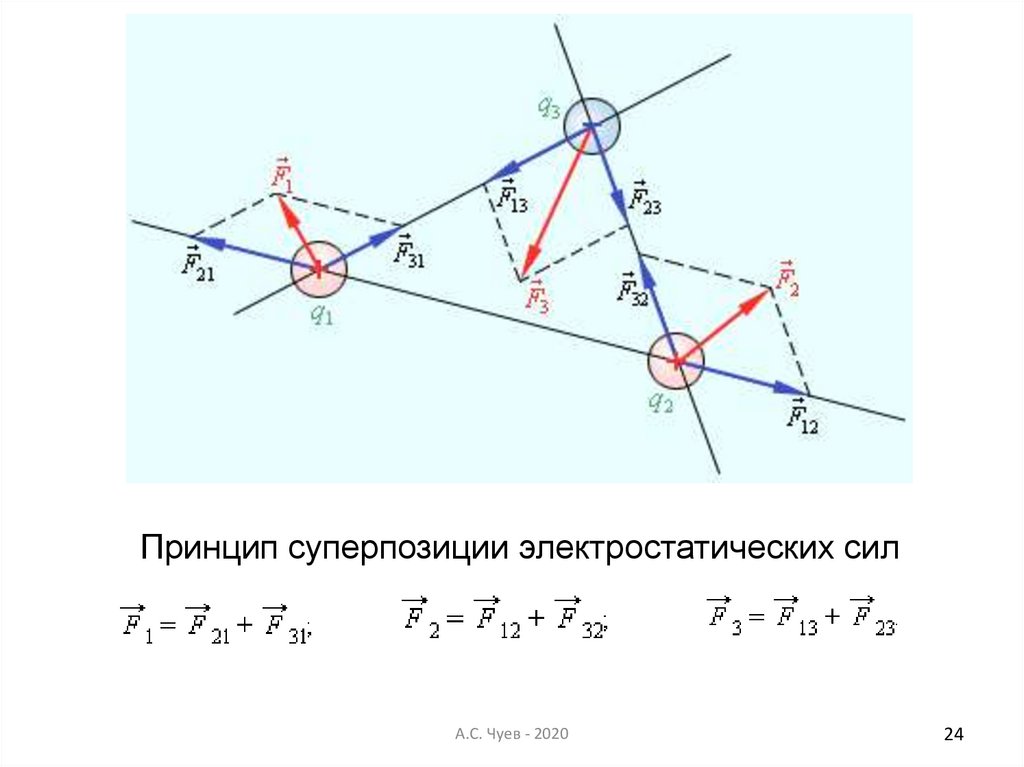
22. Сложение действия электростатических сил. Принцип суперпозиции
• Если поле создается несколькими точечнымизарядами, то на пробный заряд q’ действует
несколько сил, складываемых по принципу
суперпозиции (линейного наложения).
• То есть со стороны каждого отдельного заряда
q0 действует такая сила, как если бы других
зарядов не было.
А.С. Чуев - 2020
22
23.
Принцип наложения или суперпозицииэлектрических полей:
• Напряженность результирующего поля,
системы точечных зарядов равна
векторной сумме напряженностей
полей, созданных в данной точке каждым
из них в отдельности.
Е Е1 Е 2 ... Е k .
k
А.С. Чуев - 2020
23
24.
Принцип суперпозиции электростатических силА.С. Чуев - 2020
24
25.
Электрический дипольЭлектрический дипольный момент
А.С. Чуев - 2020
pe q l
25
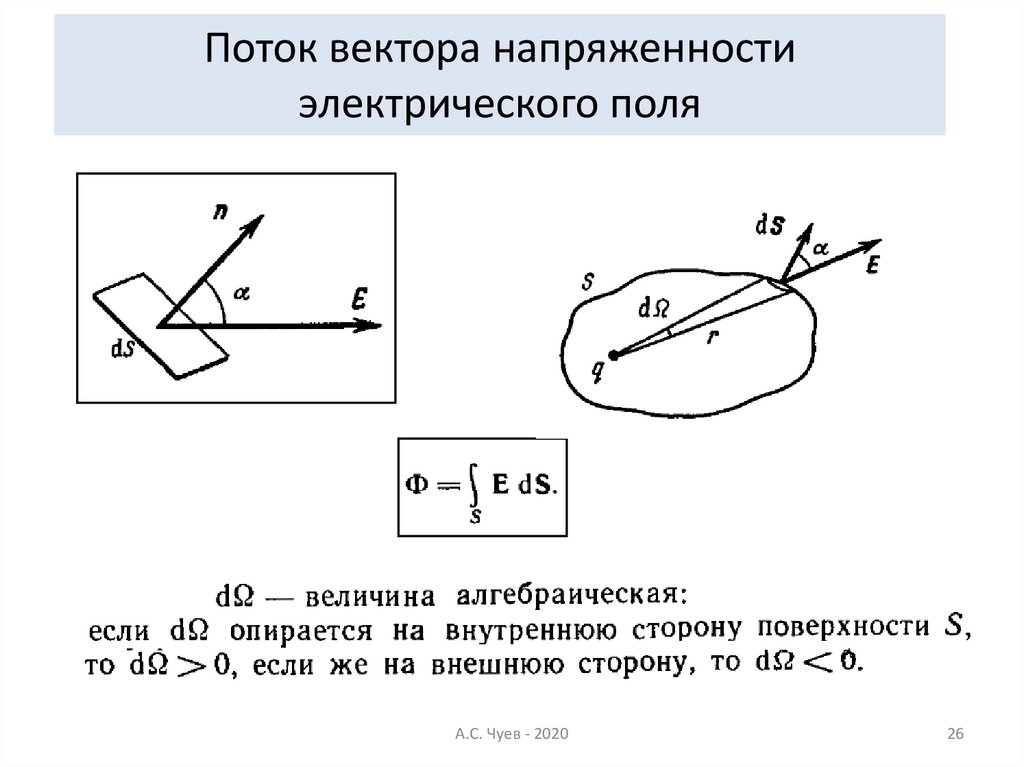
26.
Поток вектора напряженностиэлектрического поля
А.С. Чуев - 2020
26
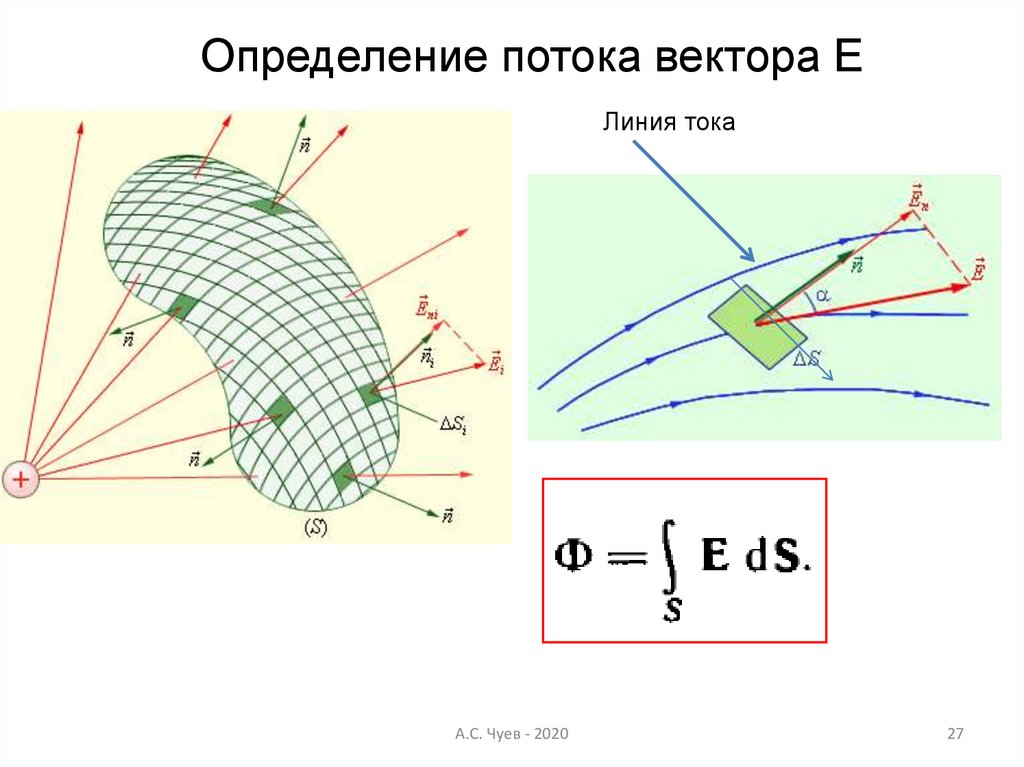
27.
Определение потока вектора ЕЛиния тока
А.С. Чуев - 2020
27
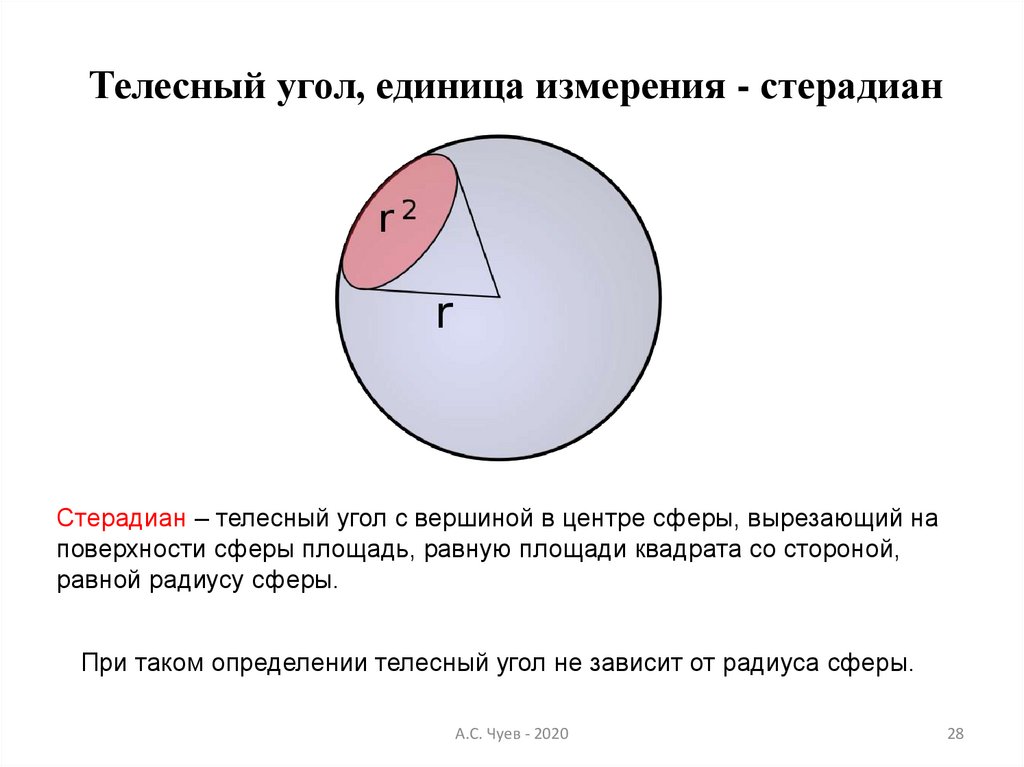
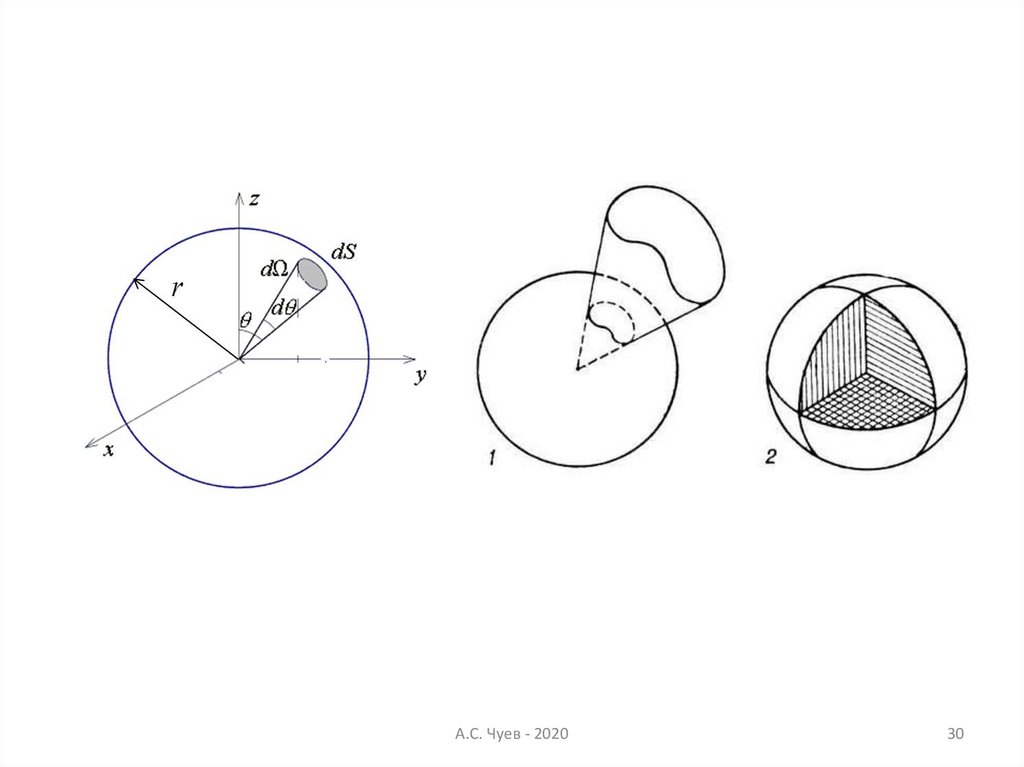
28.
Телесный угол, единица измерения - стерадианСтерадиан – телесный угол с вершиной в центре сферы, вырезающий на
поверхности сферы площадь, равную площади квадрата со стороной,
равной радиусу сферы.
При таком определении телесный угол не зависит от радиуса сферы.
А.С. Чуев - 2020
28
29.
Плоский угол, единица измерения - радиан1 радиан — центральный угол, длина дуги которого равна радиусу
окружности. При таком определении угол не зависит то радиуса.
А.С. Чуев - 2020
29
30.
А.С. Чуев - 202030
31.
А.С. Чуев - 202031
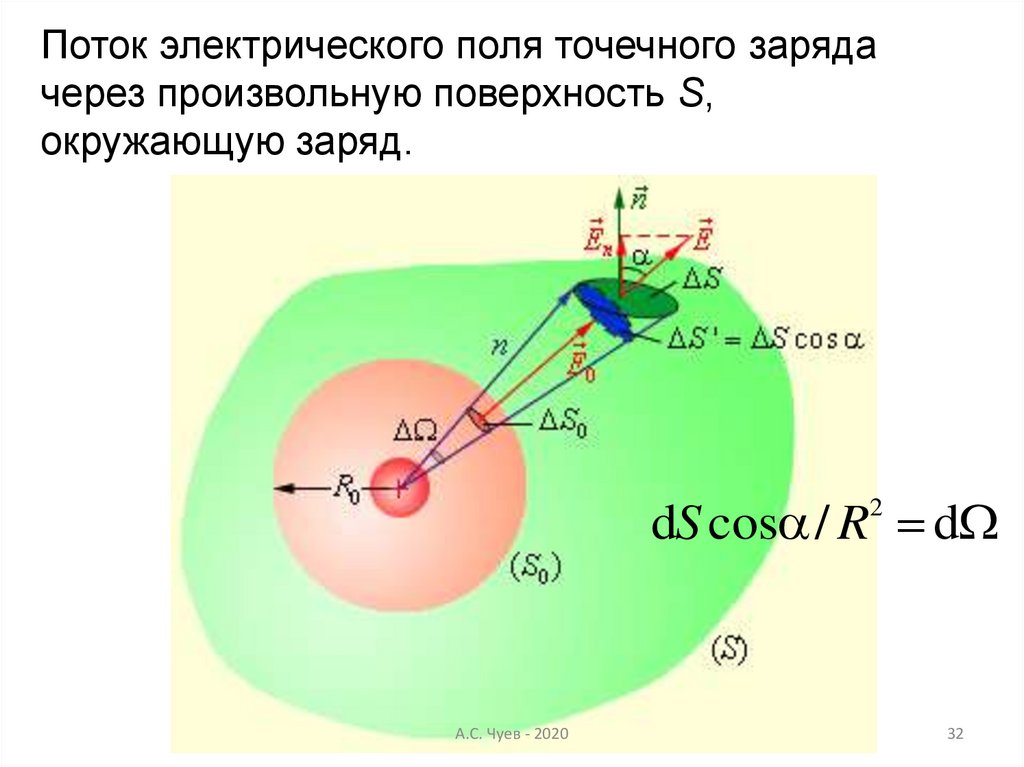
32.
Поток электрического поля точечного зарядачерез произвольную поверхность S,
окружающую заряд.
dS cos / R d
2
А.С. Чуев - 2020
32
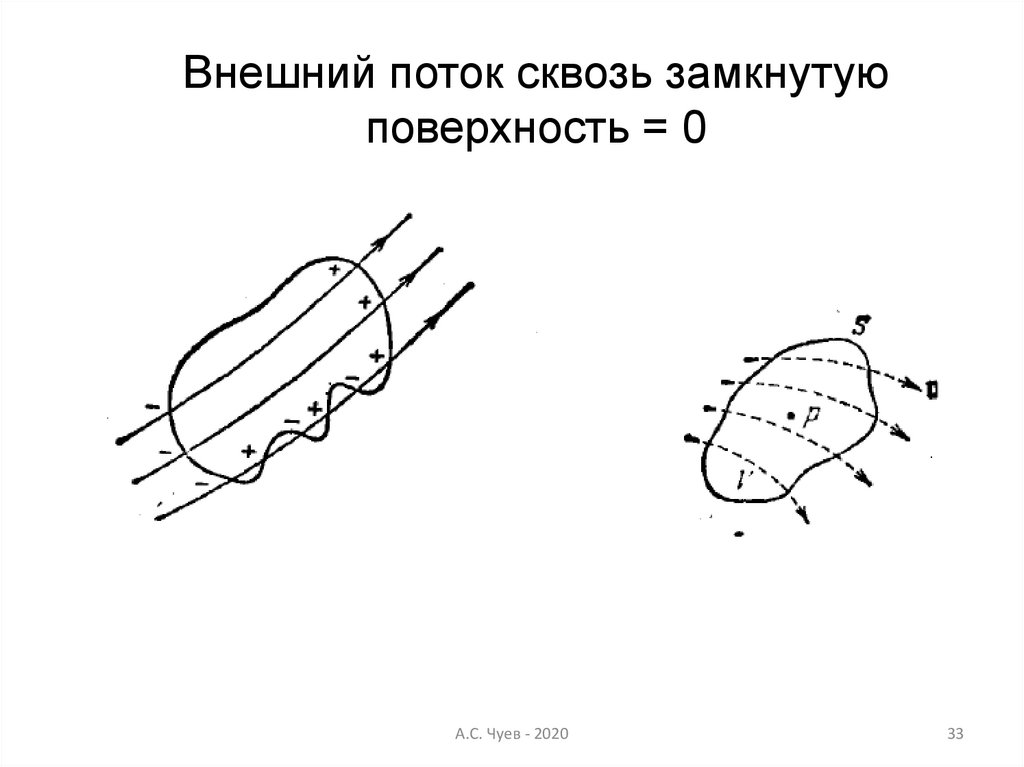
33.
Внешний поток сквозь замкнутуюповерхность = 0
А.С. Чуев - 2020
33
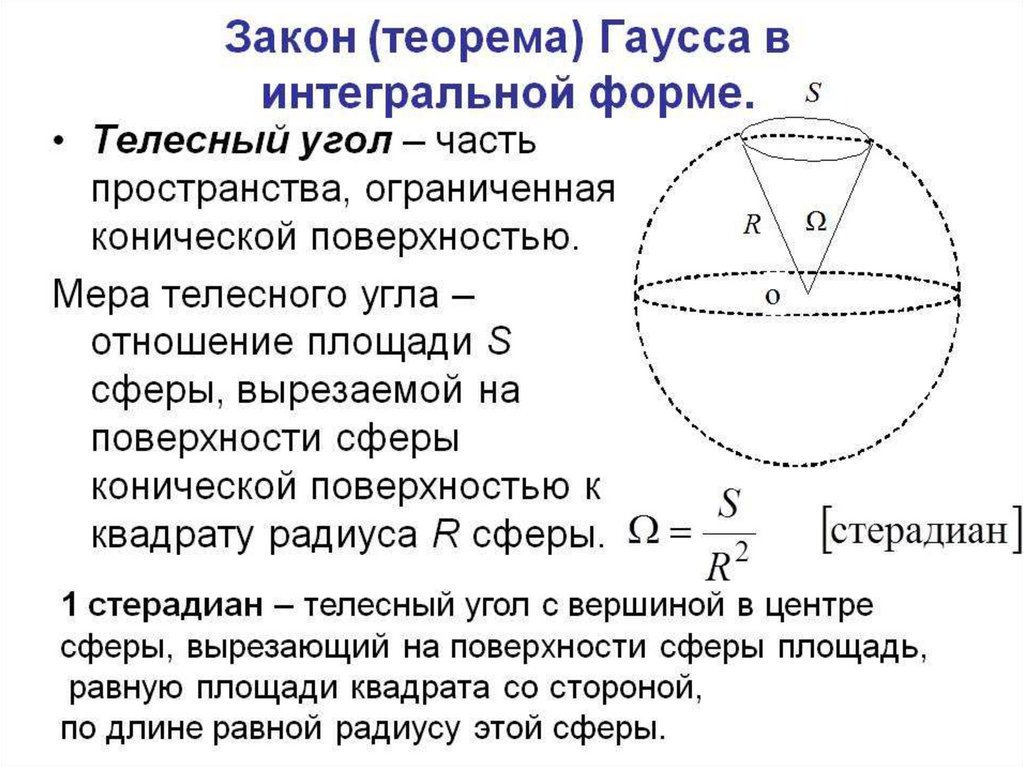
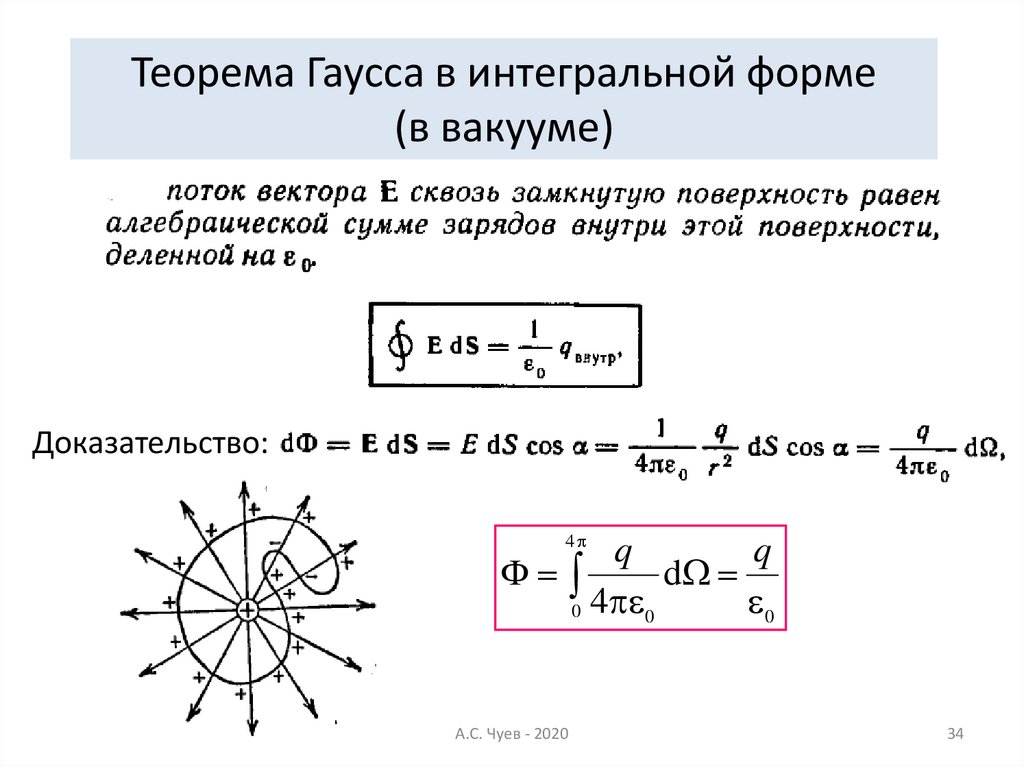
34.
Теорема Гаусса в интегральной форме(в вакууме)
Доказательство:
4
q
q
Ф
d
0
0 4 0
А.С. Чуев - 2020
34
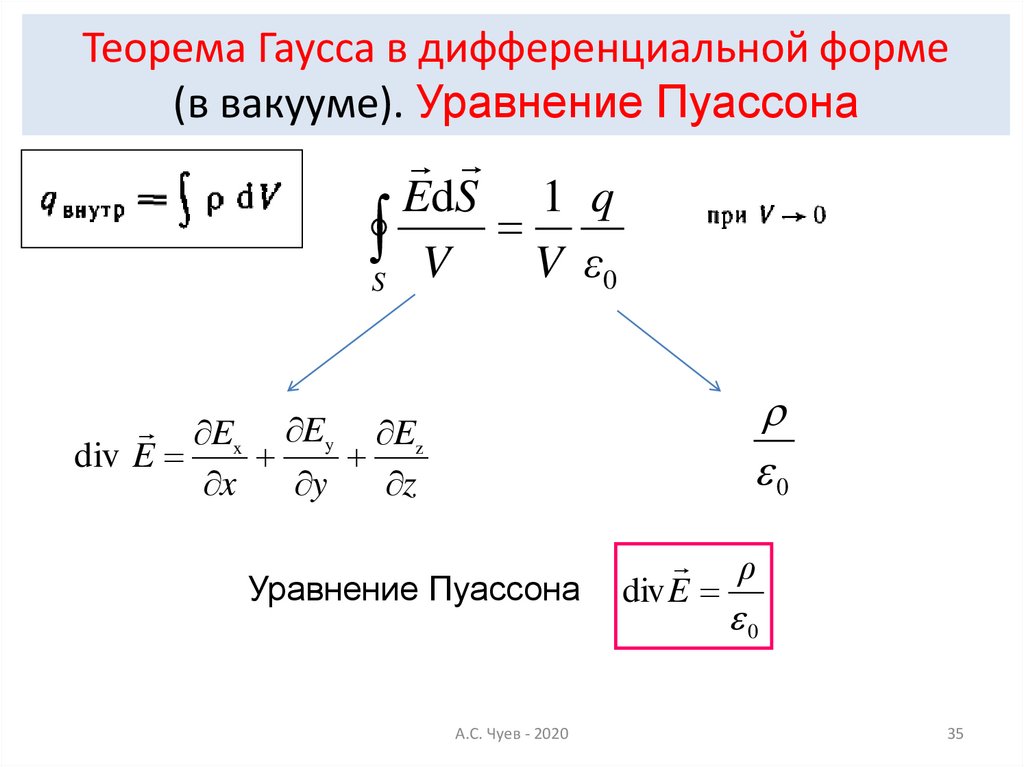
35.
Теорема Гаусса в дифференциальной форме(в вакууме). Уравнение Пуассона
EdS 1 q
S V V ε0
0
Ex Ey Ez
div E
x
y
z
Уравнение Пуассона
А.С. Чуев - 2020
ρ
div E
0
35
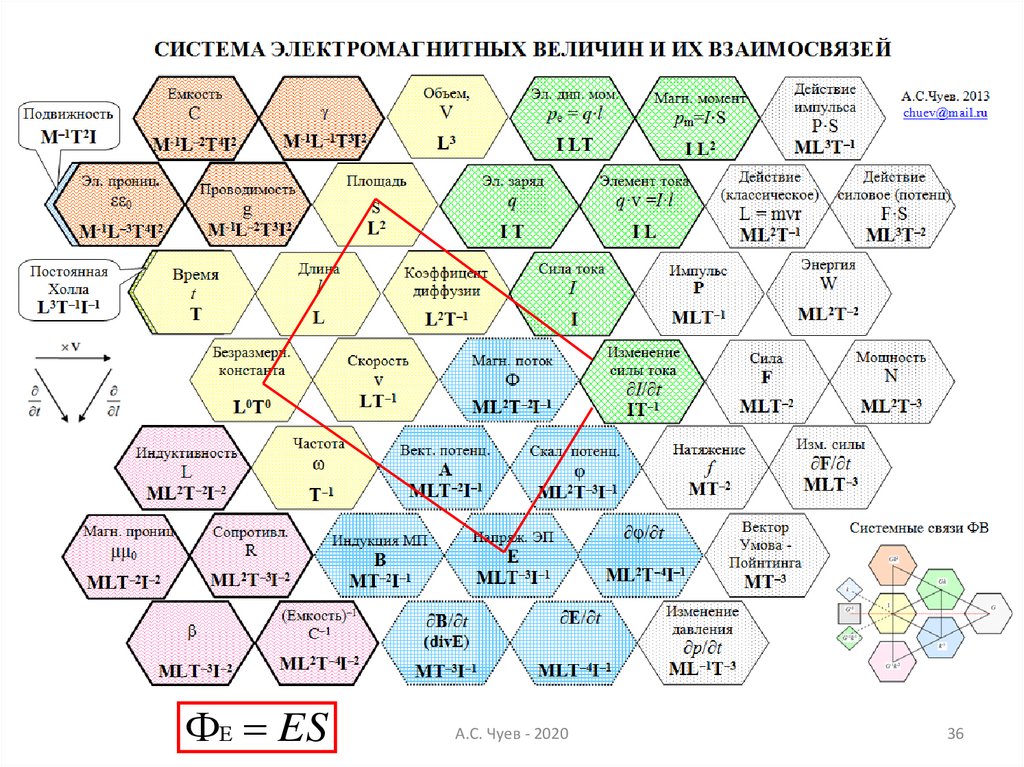
36.
ФЕ ESА.С. Чуев - 2020
36
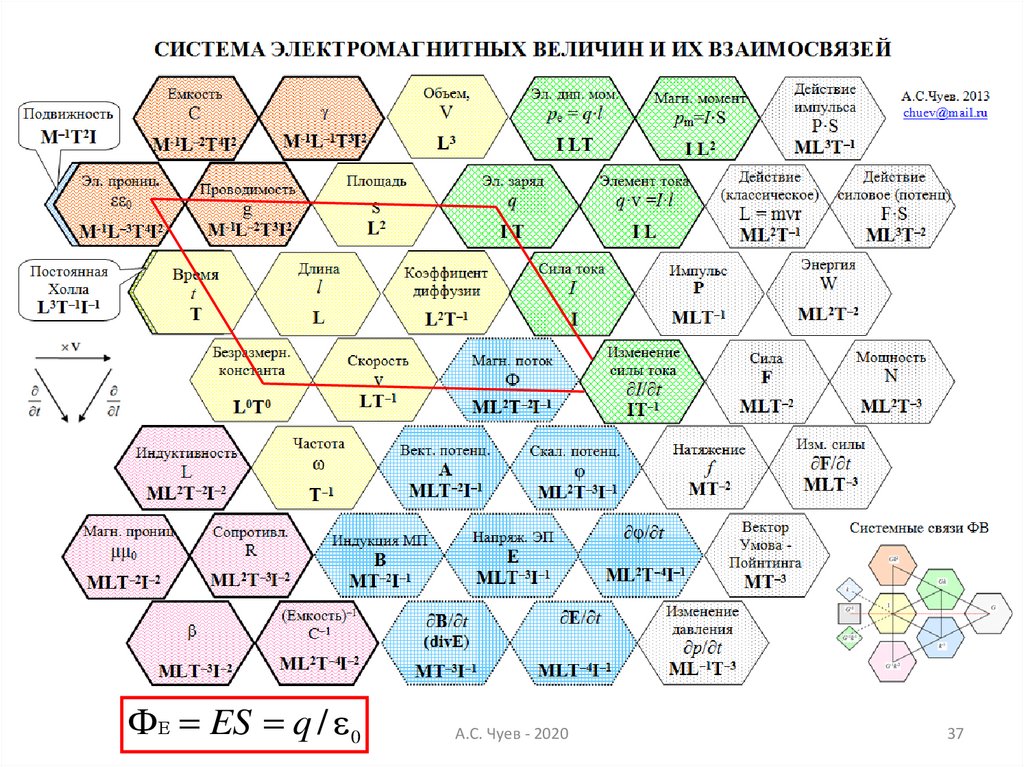
37.
ФЕ ES q / 0А.С. Чуев - 2020
37
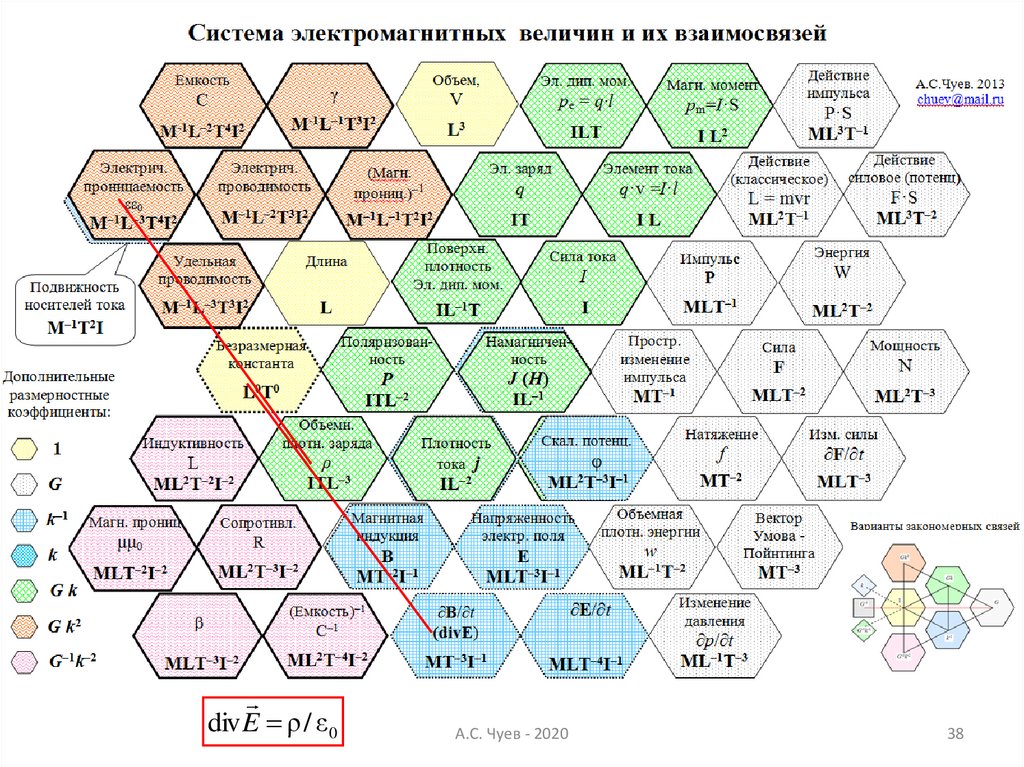
38.
div E ρ / ε 0А.С. Чуев - 2020
38
39. Приводимые далее примеры рассмотреть самостоятельно
А.С. Чуев - 202039
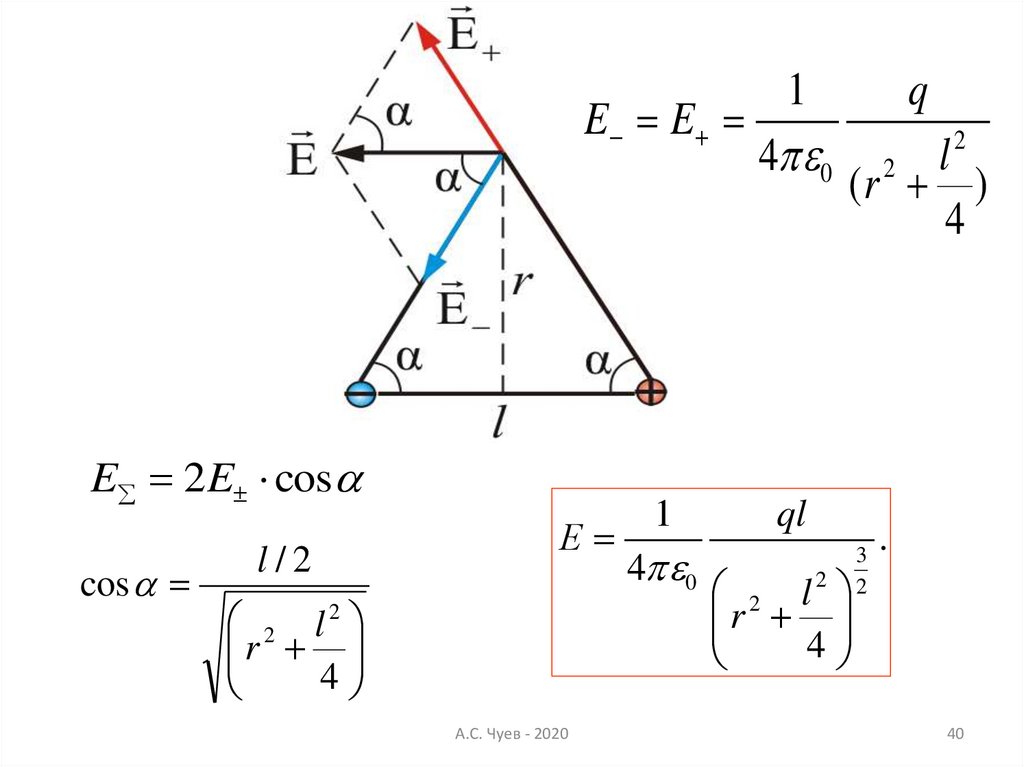
40.
1E E
4 0
E 2E cos
cos
l/2
Е
2 l2
r
4
А.С. Чуев - 2020
1
4 0
q
2
l
(r )
4
2
ql
2 l2
r
4
3
2
.
40
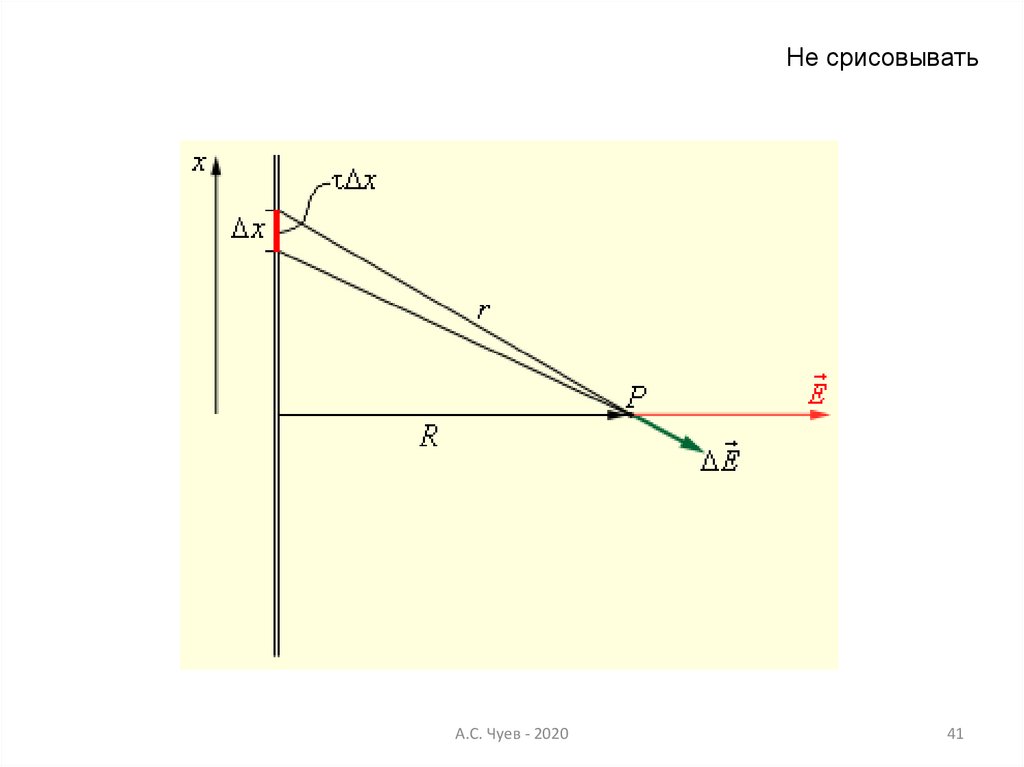
41.
Не срисовыватьА.С. Чуев - 2020
41
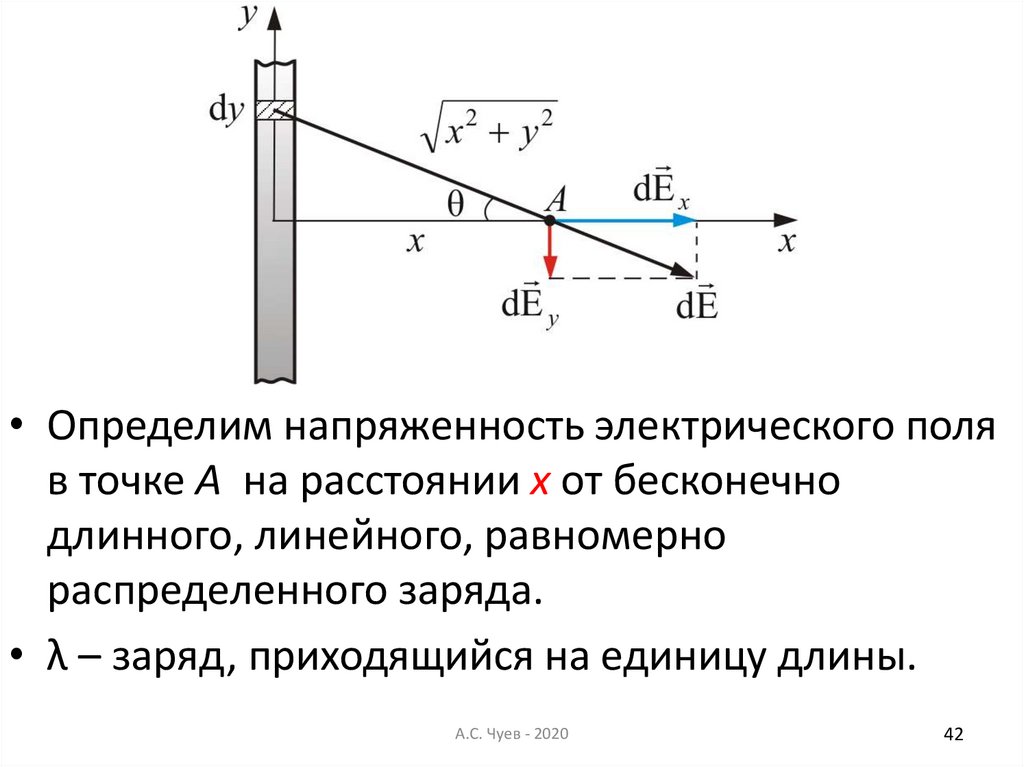
42.
• Определим напряженность электрического поляв точке А на расстоянии х от бесконечно
длинного, линейного, равномерно
распределенного заряда.
• λ – заряд, приходящийся на единицу длины.
А.С. Чуев - 2020
42
43.
• Считаем, что х – мало по сравнению сдлиной проводника. Элемент длины dy,
несет заряд dq = dy λ. Создаваемая этим
элементом напряженность электрического
поля в точке А:
1
dy
dE
.
2
2
4 0 ( x y )
А.С. Чуев - 2020
43
44.
• Вектор dE имеет проекции dEx и dEy причемd E y d E sin θ.
• Т.к. проводник бесконечно длинный, а задача
симметричная, то у – компонента вектора dE
d E x d E cos θ ;
обратится в ноль (скомпенсируется), т.е.:
E y d E sin θ 0
А.С. Чуев - 2020
44
45.
Тогдаλ
cosθdy
E E x dEcosθ
4 πε 0 x 2 y 2
Теперь выразим y через θ.
Т.к. y x tg θ ,
то
d y x d θ / cos θ
2
С учетом:
( x y ) x / cos θ
2
2
2
2
2
1
E
cos d
.
4 0 x
2 0 x
2А.С. Чуев - 2020
45
46.
E.
2 0 x
• Напряженность электрического поля от
линейно распределенных зарядов
(заряженной нити) изменяется обратно
пропорционально расстоянию до заряда.
А.С. Чуев - 2020
46
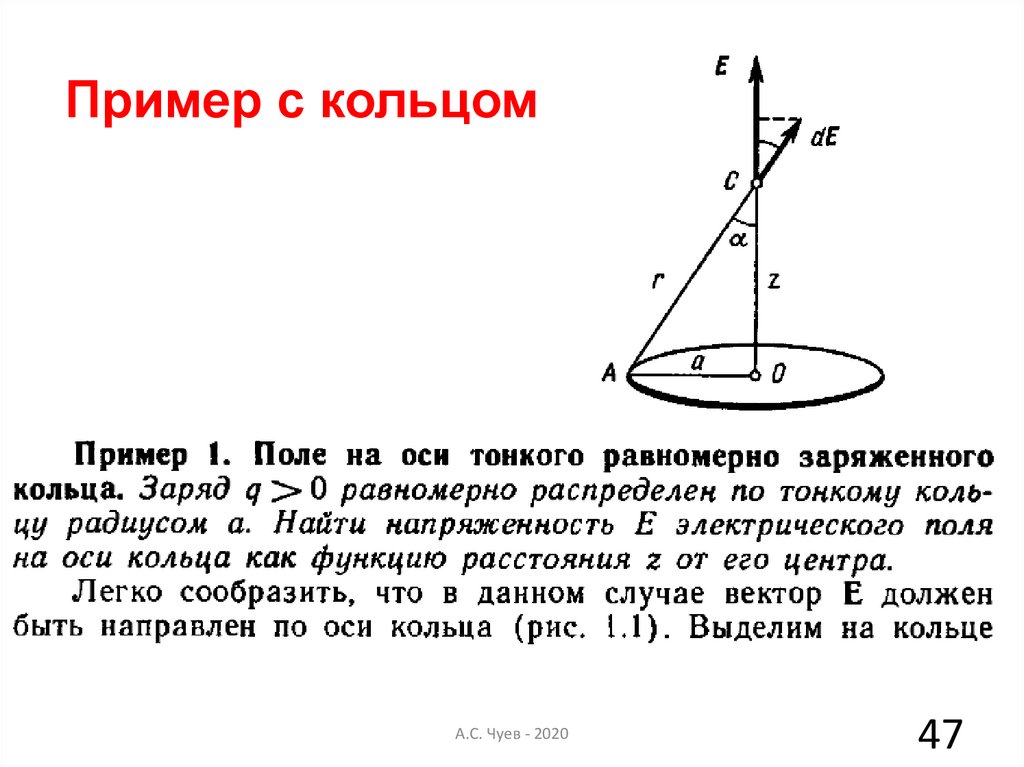
47.
Пример с кольцомА.С. Чуев - 2020
47
48.
А.С. Чуев - 202048
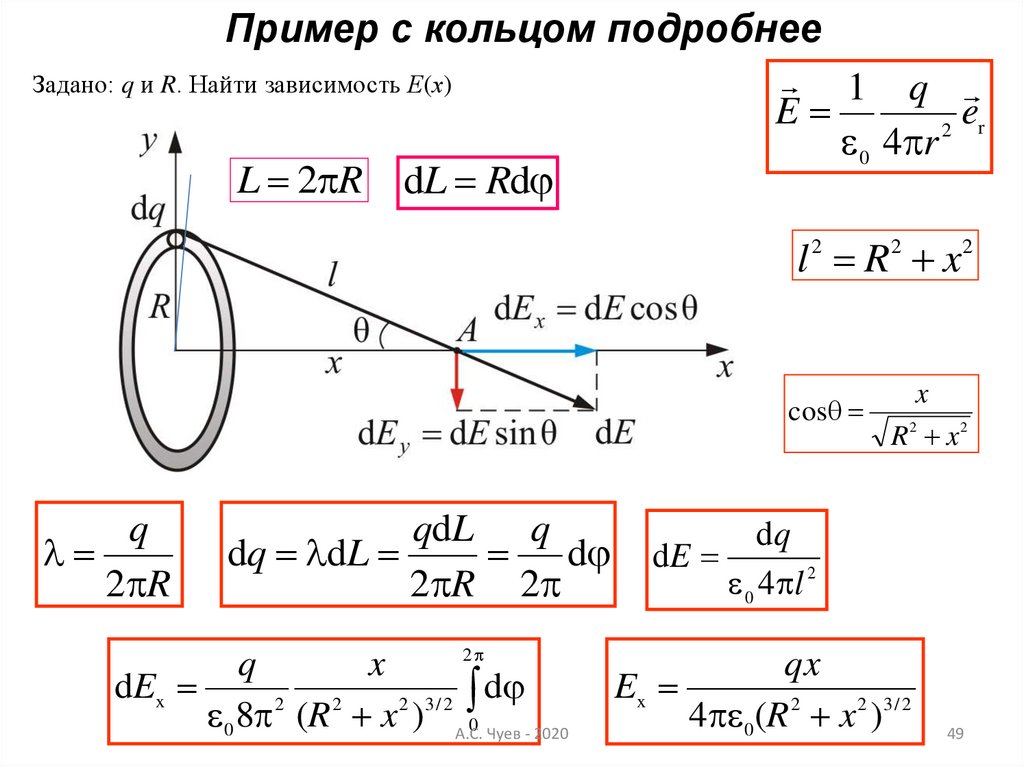
49.
Пример с кольцом подробнее1 q
Задано: q и R. Найти зависимость Е(х)
E
e
2 r
0 4 r
L 2 R dL Rd
l 2 R2 x 2
cos
q
2 R
qdL q
dq dL
d
2 R 2
2
q
x
dEx
d
2
2
2 3/ 2
0 8 (R x ) А.С.0 Чуев - 2020
x
R2 x2
dq
dE
0 4 l 2
qx
Ex
4 0(R 2 x 2 )3 / 2
49
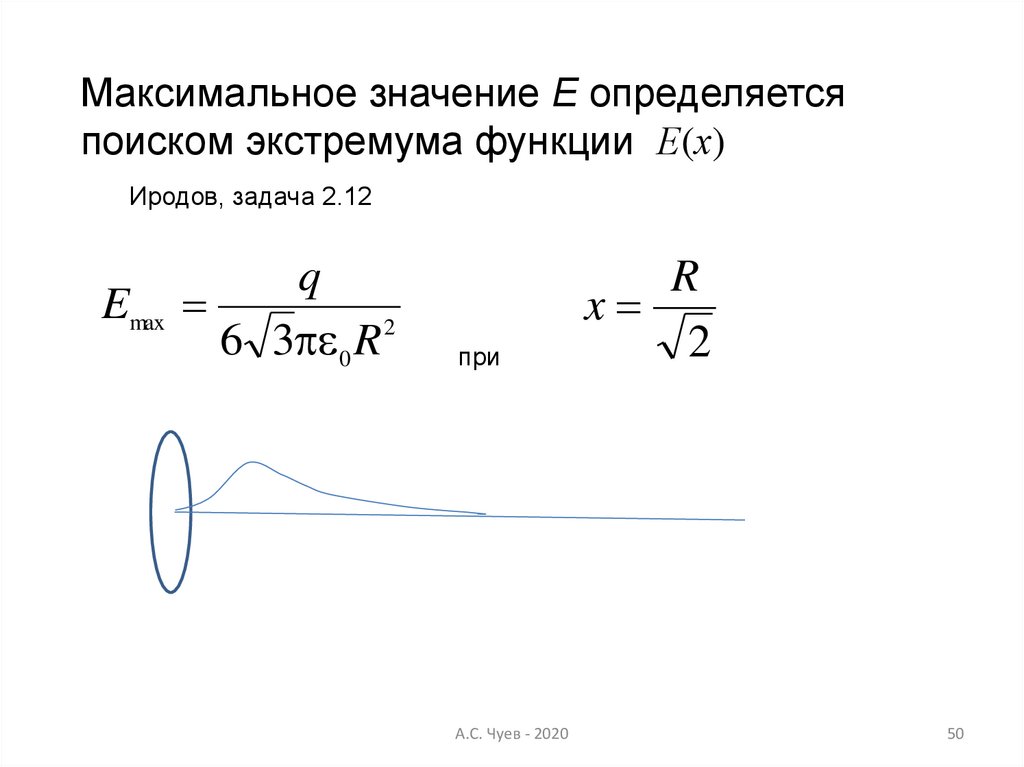
50.
Максимальное значение Е определяетсяпоиском экстремума функции Е(х)
Иродов, задача 2.12
Emax
q
2
6 3 0 R
при
А.С. Чуев - 2020
R
x
2
50
51.
МАТЕРИЯВЕЩЕСТВО
(Т, Ж, Г)
ПОЛЕ
З, П
ФИЗ. ВАКУУМ
Э, М, Гр.
Вирт. Ч
Электромагнитная теория
А.С. Чуев - 2020
51
52.
ФакультативноА.С. Чуев - 2020
52
53.
Конец лекции 1А.С. Чуев - 2020
53





















 Физика
Физика








