Простейшие представления о кинетике химических реакций

1.

ЛЕКЦИЯ 8
СОПУТСТВУЮЩИЕ ЯВЛЕНИЯ
ПРОСТЕЙШИЕ ПРЕДСТАВЛЕНИЯ О КИНЕТИКЕ ХИМИЧЕСКИХ РЕАКЦИЙ
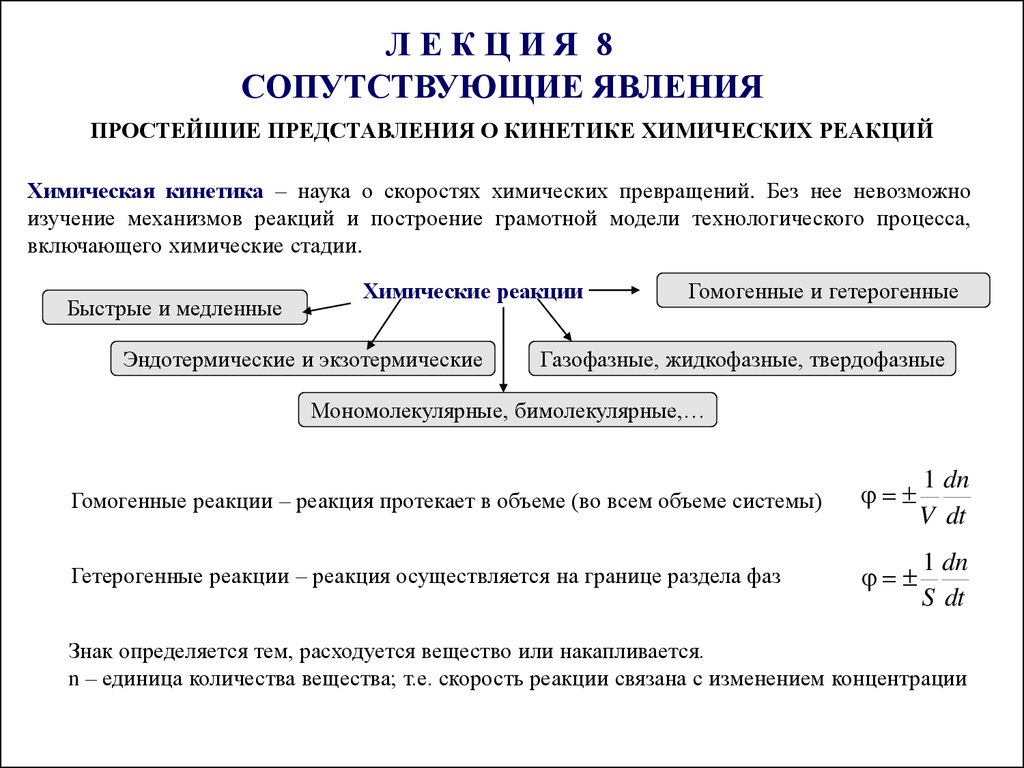
Химическая кинетика – наука о скоростях химических превращений. Без нее невозможно
изучение механизмов реакций и построение грамотной модели технологического процесса,
включающего химические стадии.
Быстрые и медленные
Химические реакции
Эндотермические и экзотермические
Гомогенные и гетерогенные
Газофазные, жидкофазные, твердофазные
Мономолекулярные, бимолекулярные,…
Гомогенные реакции – реакция протекает в объеме (во всем объеме системы)
1 dn
V dt
Гетерогенные реакции – реакция осуществляется на границе раздела фаз
1 dn
S dt
Знак определяется тем, расходуется вещество или накапливается.
n – единица количества вещества; т.е. скорость реакции связана с изменением концентрации

2.

Концентрации: мольные (объемные) – моль/м3
Относительные мольные
Массовые
yA
СA
nA
;
n A nB ...
mA
;
m A mB ...
С учетом стехиометрии:
aA bB cC dD
nA ,nB ,...
yB
CB
1 d X i
i dt
nB
;
n A nB ...
mB
;
m A mB ...
1 d A
1 d B 1 d C 1 d D
A dt
B dt
C dt
D dt
Математической основой для количественного описания реакций является закон
действующих масс:
k
ni
X
i
i
k – константа скорости реакции
ni
- порядок реакции по i-му веществу

3.

Реакции – простые и сложные
Если процесс протекает в одну стадию (не сопровождается образованием промежуточных
продуктов), то такую реакцию называют простой или элементарной
A 2B продукты
k A B 2
Для элементарных реакций порядки равны стехиометрическим коэффициентам
Сумма порядков по каждому веществу дает суммарный порядок реакции
Для сложной реакции, как правило, нет соответствия между порядками и стехиометрическими
коэффициентами.
Как правило, реакции протекают в несколько элементарных стадий.
Скорость реакции в данный момент времени дается тангенсом угла наклона концентрационных
кривых, получаемых экспериментально, в этот момент времени.
C
k A B ...
2
1
t
Элементарные реакции бывают реакциями нулевого, первого и
второго порядка. Большинство химических реакций можно
представить как те или иные комбинации элементарных стадий.
(1)

4.

Самые распространенные комбинации
параллельные
последовательные
обратимые
-Реакцию, в которой реагент подвергается превращению по двум или нескольким путям
одновременно, называют параллельной.
-В последовательной реакции продукт, образующийся в одной стадии, является реагентом в
другой.
-Если две стадии реакции противоположного направления происходят с соизмеримой
вероятностью, то такую реакцию называют обратимой.
Существуют сложные реакции, сочетающие в себе два или все три названных типа.
Уравнения (1), полученные на основе анализа экспериментальных данных или на основе
формальной кинетики, имеют физический смысл, если порядки реакции – простые
положительные числа. Дробные порядки оказываются «кажущимися» и есть следствие
сложного механизма реакции, не описываемого простой реакционной схемой.
k A B ...
(1)

5.

Прямая задача химической кинетики
1.
2.
3.
Определяют кинетическую схему реакции – или ее
механизм (определенную совокупность стадий)
На основе схему формулируют математическую модель
реакции (определяют число участников, число реакций и
взаимосвязи между ними)
Решают полученную систему дифференциальных
уравнений и получают кинетические кривые
Обратная задача химической кинетики
По экспериментальным данным рассчитывают кинетические
параметры реакций (порядки реакций по реагентам,
константы скоростей реакций. Т.е. задача состоит в том, чтобы
установить механизм реакции.

6.

Примеры гомогенных реакции
A B
k
(2)
d A dt k A
(3)
d B dt k B
(4)
Простая реакция первого порядка
Вследствие сохранения вещества в системе
A B A 0 B 0 const
нам достаточно одного уравнения (3).
Начальные
концентрации
Интегрирование этого уравнения при постоянстве давления и температуры дает
ln A
Угол наклона прямой
определяет константу
скорости реакции
(5)
A A 0 exp kt
ln A01
ln A03
d A
d ln A k T , p dt
A
ln A kt C , C ln A 0
(6)
В реакции первого порядка расходование реагента во
времени происходит экспоненциально
ln A02
t
Прямые соответствуют разным
начальным условиям
Введем период полупревращения - время достижения
концентрацией реагента половины первоначальной
ln 2
величины.
t
12
k

7.

y
A
A 0 B 0
z
B
A 0
относительные концентрации
B
A 0 B 0
(7)
y z 1
A 0
B
2
Пересечение кривых соответствует половине
начальной концентрации реагента
A
t
Простая реакция второго порядка
2 A B
k
(8)
d A dt 2k A 2
(9)
Множитель 2 появляется потому, что в каждом элементарном акте расходуются две молекулы.
1
1
2kt
A A 0
A
A 0
1 2kt A 0
(10)

8.

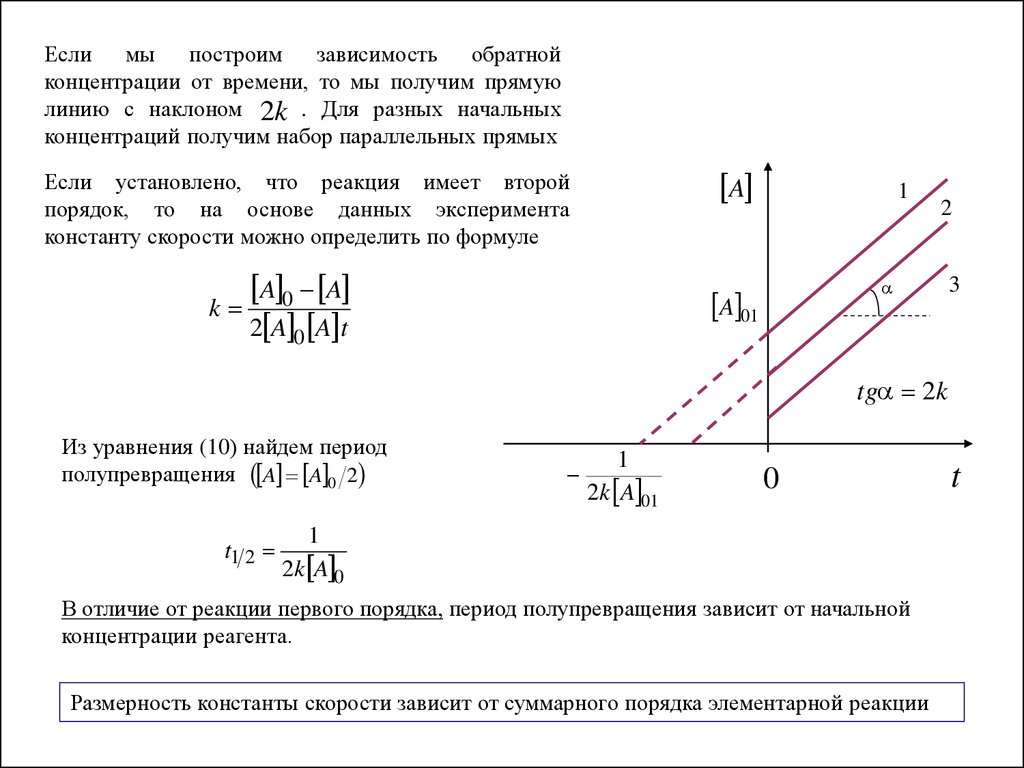
Если мы построим зависимость обратной
концентрации от времени, то мы получим прямую
линию с наклоном 2k . Для разных начальных
концентраций получим набор параллельных прямых
A
Если установлено, что реакция имеет второй
порядок, то на основе данных эксперимента
константу скорости можно определить по формуле
A 0 A
k
2 A 0 A t
1
2
A 01
3
tg 2k
Из уравнения (10) найдем период
полупревращения A A 0 2
t1 2
1
2k A 01
0
1
2k A 0
В отличие от реакции первого порядка, период полупревращения зависит от начальной
концентрации реагента.
Размерность константы скорости зависит от суммарного порядка элементарной реакции
t

9.

Другой реакцией, в которой в образовании продукта участвуют две молекулы, будет реакция вида
A 1 A 2 P
d P
k A 1 A 2 ;
dt
(11)
Это – бимолекулярная реакция с суммарным вторым порядком.
Стехиометрические начальные концентрации.
d P 1
k A 12
dt
(12)
Этот случай сводится к предыдущему, но вместо 2k в уравнении стоит k
1
1
kt
A A 0
(13)
Один из реагентов берется в избытке так, что его концентрацию в ходе реакции можно считать
практически неизменной
A 20 A 10
d A 1
keff A 1
dt
keff k A 20
(14)
Этот случай сводится к первому. Говорят, что в этом случае реакция проходит в условиях
псевдопервого порядка

10.

k1
При протекании двух параллельных реакций
первого порядка реакционную схему можем
представить в виде
P1
A
(15)
k2
d A dt k1 k 2 A
d P1 dt k1 A
P2
(16)
d P2 dt k 2 A
Независимы только два уравнения. Первое уравнение интегрируется сразу
A A 0 exp k1 k 2 t
Из двух других следует
P1 P2 k1
Уравнение материального баланса
Кинетические
уравнения для
продуктов
интегрируются
непосредственно
k2
A 0 A P1 P2
P1
k1
A 1 exp k1 k2 t
k1 k 2 0
P2 k2 A 0 1 exp k1 k2 t
k1 k 2
(17)
(18)
(19)
(20)

11.

A 0 P 1 P 2
Изменение концентраций во времени
для двух параллельных реакций
A
P 1
P 2
t
Как расходование реагента, так и образование
продуктов, подчиняются закону скорости
первого порядка: графики зависимостей
ln A , ln P 1 P 1 , ln P 2 P 2
от времени дают прямую линию, тангенс угла
наклона которой равен k1 k2
Для определения каждой из констант по данным эксперимента нужно из (20) исключить
выражение в квадратных скобках с помощью (17). Найдем
P 1 k1
A 0 A k1 k2
P 2 k2
A 0 A k1 k2
Графики зависимости концентраций продуктов от концентрации реагента
представляют собой прямые линии с разными наклонами.
(21)
A 0 A

12.

Последовательность двух реакций первого порядка отвечает схеме
k
k
1
2
A
B
P
(22)
Кинетический анализ зависит от соотношения реакционной способности реагента и
промежуточного продукта
k1 k2 Промежуточный продукт гораздо менее реакционноспособен, чем исходный реагент.
k1 k2
Первая стадия практически завершается до того, как начинается вторая стадия. В
результате каждую стадию можно рассматривать как независимую реакцию первого
порядка.
Вторая стадия быстро следует за первой, поэтому в любой момент времени
справедливо
B A
При построении кинетической модели вполне можно принять
d B dt 0
Такой подход соответствует методу стационарных состояний Боденштейна
В случае незначительного различия реакционной способности исходного реагента и
промежуточного продукта
d A dt k1 A
d B dt k1 A k 2 B
d P dt k 2 B
(23)

13.

Интегрирование системы уравнений (23) с учетом уравнения материального баланса приводит
к формулам
A A 0 exp k1t
Задача на дом:
k1
A exp k1t exp k2t
B
найти решение
k 2 k1 0
системы
P A 0 1 1 k2 exp k1t k1 exp k2t
кинетических
k2 k1
уравнений (23)
P
A 0
A
P
B
Кривая B , очевидно, проходит через
максимум. Положение максимума можно
найти из условия
d B
0,
dt
которое дает
tmax
t
ln k1 k 2
k1 k2
(25)

14.

Большую группу реакций составляют гомогенные каталитические реакции, в которых
катализатор участвует в образовании высокореакционноспособного промежуточного
продукта, не меняя стехиометрии реакции. Если катализатором реакции является
конечный
или
промежуточный
продукт,
то
такие
реакции
называют
автокаталитическими.
Существует фундаментальное различие между понятиями «схема реакции» и «механизм
реакции». Схема остается формальным описанием реакции (ее макроскопического
проявления) и не требует никаких предположений о свойствах компонентов. Установление
механизма реакции должно дать ответ на ряд вопросов: где расположены активные центры
в реагентах; какие свойства проявляют реагенты; какие связи рвутся или образуются в
каждой из стадий реакции; что представляют собой промежуточные продукты; каковы
состав и структура промежуточных комплексов? Эти вопросы определяются современными
представлениями о строении вещества и теории химической связи, т.е. при изучении
микропроцессов.
Очевидно, что скорость реакции зависит от условий ее осуществления, в частности, от
температуры и давления.
Существует несколько уравнений, пригодных для количественного описания
температурной зависимости констант скорости элементарных реакций. Самое известное из
них – уравнение Аррениуса — имеет вид
Предэкспоненциальный
множитель
k k0e Ea
RT
Энергия
активации
(26)

15.

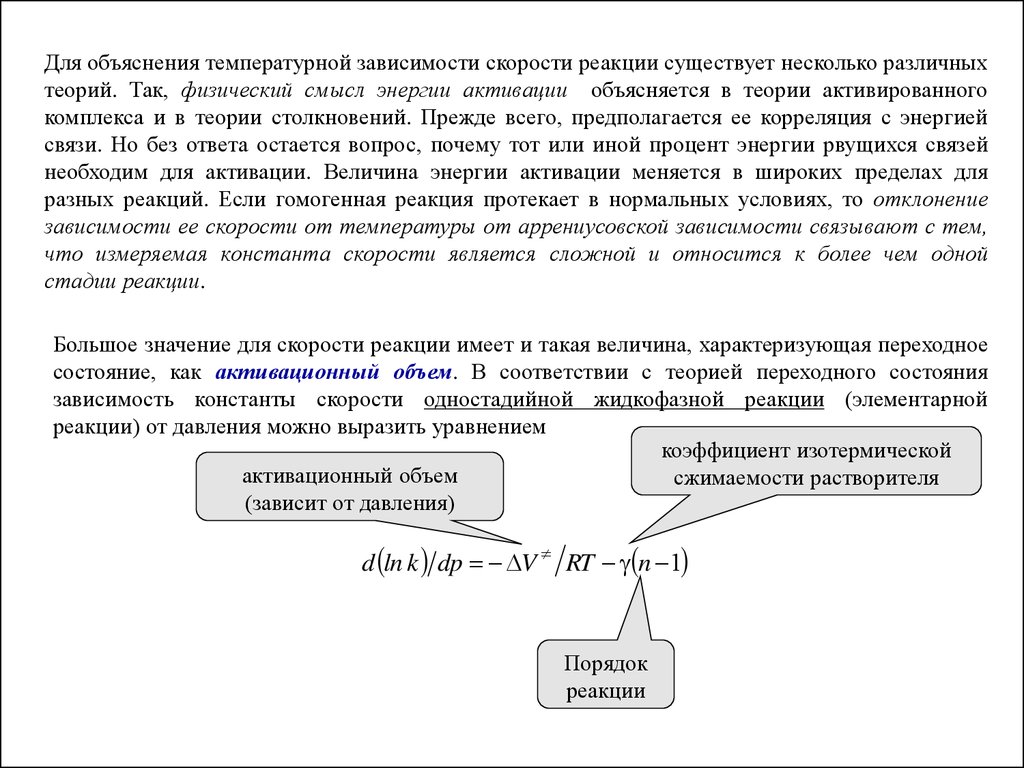
Для объяснения температурной зависимости скорости реакции существует несколько различных
теорий. Так, физический смысл энергии активации объясняется в теории активированного
комплекса и в теории столкновений. Прежде всего, предполагается ее корреляция с энергией
связи. Но без ответа остается вопрос, почему тот или иной процент энергии рвущихся связей
необходим для активации. Величина энергии активации меняется в широких пределах для
разных реакций. Если гомогенная реакция протекает в нормальных условиях, то отклонение
зависимости ее скорости от температуры от аррениусовской зависимости связывают с тем,
что измеряемая константа скорости является сложной и относится к более чем одной
стадии реакции.
Большое значение для скорости реакции имеет и такая величина, характеризующая переходное
состояние, как активационный объем. В соответствии с теорией переходного состояния
зависимость константы скорости одностадийной жидкофазной реакции (элементарной
реакции) от давления можно выразить уравнением
коэффициент изотермической
активационный объем
сжимаемости растворителя
(зависит от давления)
d ln k dp V RT n 1
Порядок
реакции

16.

Что же делать в случае сложных реакций в многофазных системах?
1. Если реакция протекает в несколько стадий, то законы справедливы для
каждой из стадий, а скорость сложного химического процесса
определяется скоростью наиболее медленной реакцией. Эту реакцию
называют лимитирующей стадией всего процесса.
2. Наиболее медленной стадией реакции может быть процесс иной природы
R1
R1
R2
R2
Ti Ni TiNi
(1)
2Ti Ni Ti2 Ni
(2)
Ti 3Ni TiNi3
(3)
4TiNi Ti2 Ni TiNi3 Ti
(4)
w1 k1 T , p Ti Ni product ,structure
w2 k2 T , P Ti 2 Ni product , structure
……
может быть следствием процессов на микроуровне

17.

Где взять параметры?
1.Справочники 2.Эксперимент 3.Независимые модели
Для химических реакций: химическая термодинамика; квантовая химия,
молекулярная динамика
Эксперимент и ТНП:
Скорость химической реакции пропорциональна химическому сродству реакции
(1)
X Y
2Z
Изменения чисел молей веществ
связаны стехиометрией
w kA
(2)
dN X dNY dN Z
d
1
1
2
(3)
- химическая переменная, или степень полноты реакции, степень
превращения
1
X Y 2 Z d 0 Химические потенциалы
d
S
(4)
i
T
зависят от температуры,
Химические сродство:
A X Y 2 Z
давления (напряжений),
структурных параметров
Теплофизические и механические свойства: эксперимент; микромеханика

18.

Литература
1. Эмануэль Н.М., Кнорре Д.Г. Курс химической кинетики
2. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической
кинетике
3.Коробов В.И., Очков В.Ф. Химическая кинетика: введение с
Mathcad/Maple/MCS, М.: Горячая линия – Телеком, 2009, 384 С.

19.

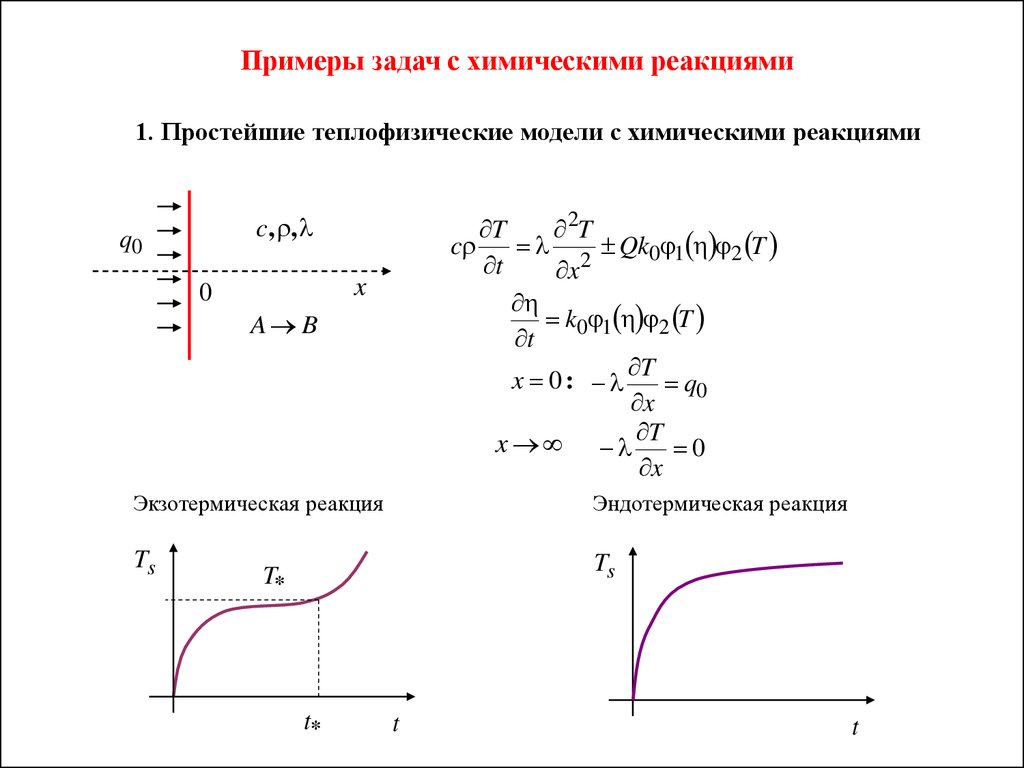
Примеры задач с химическими реакциями
1. Простейшие теплофизические модели с химическими реакциями
c, ,
q0
T
2T
c
Qk0 1 2 T
2
t
x
k0 1 2 T
t
T
x 0:
q0
x
x T 0
x
x
0
A B
Экзотермическая реакция
Эндотермическая реакция
Ts
Ts
T*
t*
t
t

20.

Примеры задач с химическими реакциями
2.Синтез композита в вакуумной камере
Нагрев образца осуществляется излучением при
регулируемом изменении температуры стенок
вакуумной печи, а образец свободен от внешних
нагрузок . kk 0
L* T t*
- толщина прогретого слоя
L* l
Следовательно, можно пренебречь распределением
температуры в образце
В условиях эксперимента температура плавления не
достигается
V0 c
dT
T T T 4 Te4 S n V0W1
dt
(1)

21.

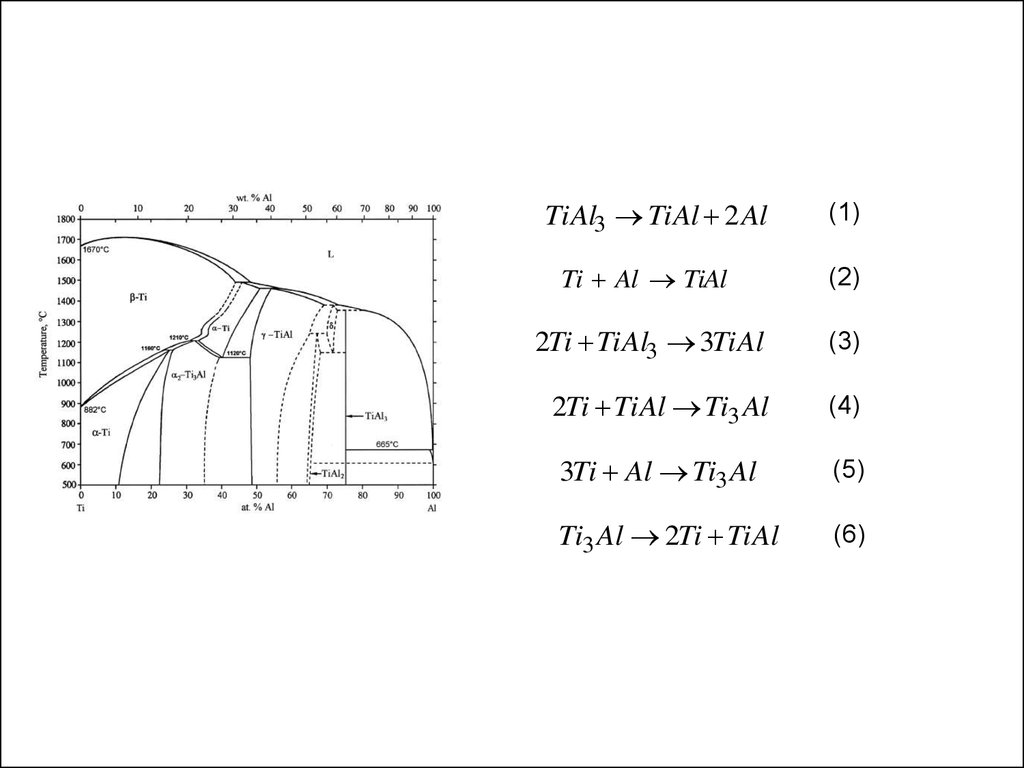
TiAl3 TiAl 2 Al
(1)
Ti Al TiAl
(2)
2Ti TiAl3 3TiAl
(3)
2Ti TiAl Ti3 Al
(4)
3Ti Al Ti3 Al
(5)
Ti3 Al 2Ti TiAl
(6)

22.

E
i ki exp ai exp mi y y ni
RT
dy1
y1 1 y22 y1 3
dt
dy2
y2 y3 2 2 y1 y22 3 2 y22 y4 4 3 y3 y23 5 2 y5 6
dt
dy3
2 y1 1 y 2 y3 2 y 22 y3 5
dt
dy4
y1 1 y2 y3 2 3 y1 y22 3 y22 y4 4 y5 6
dt
dy5
y 22 y1 4 y3 y 23 5 y5 6
dt
ceff
dT
T T T 4 Te4 Sn Weff
dt
y1 TiAl3
y2 Ti
y3 Al
y4 TiAl
y5 Ti3 Al
Жесткая система
ОДУ, специальные
методы

23.

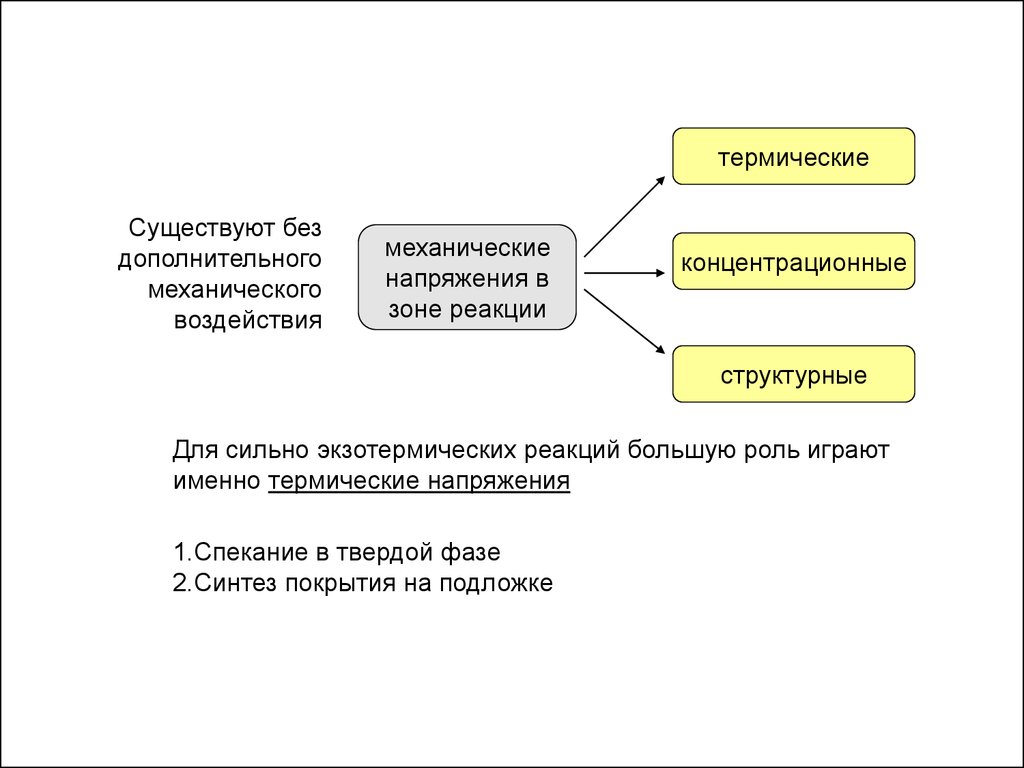
термические
Существуют без
дополнительного
механического
воздействия
механические
напряжения в
зоне реакции
концентрационные
структурные
Для сильно экзотермических реакций большую роль играют
именно термические напряжения
1.Спекание в твердой фазе
2.Синтез покрытия на подложке

24.

V/V0
3
y3,моль/см
1,2
0,6
При оценке изменения
объема прессовки
учитывается вклад в
деформации изменения
температуры и изменение
объема в ходе реакций
3
2
0,4
1,0
2
3
0,2
4
1
0,8
0,0
4
t,c
4
2,0x10
4,0x10
3
y5,моль/см
Условия спекания
1
4
0,0
y4,моль/см
1
4
4
2,0x10
4,0x10
Al
3
0,3
2
(Ta= 1200, 1300,
1350, 1400 C)
0,6
4
3
0,2
2
3
0,1
0,0
0,3
4
4
2,0x10
4
4,0x10
t,c
0,0
1
4
2,0x10
30
15
3
0
1
2
0
15
30
Содержание TiAl3
45
4
4,0x10
/ k,%
-15
t,c
Изменение хода кривых при
изменении температуры спекания
t,c

25.

Примеры задач с химическими реакциями
3. Теория твердофазного горения
В теории горения требуется определить характер распространения фронта
горения; установить возможность стационарных режимов, исследовать их
устойчивость; изучить структуру волны горения и др.
Простейшие модели основаны на следующих предположениях:
1) поле температур в волне горения одномерно; температура изменяется только
в направлении перемещения фронта горения; температурные неоднородности,
связанные с гетерогенностью системы, несущественны; 2) диффузионный
перенос продукта горения в направлении перемещения фронта горения
отсутствует и важен только для вида кинетической функции, определяющей
характер тепловыделения; 3) скорость тепловыделения в зависимости от
температуры при горении определяется обычными законами, справедливыми и
для гомогенных реакций; в зоне реакции вещества не плавятся; 4) физические
параметры не изменяются в ходе процесса [14, 15].

26.

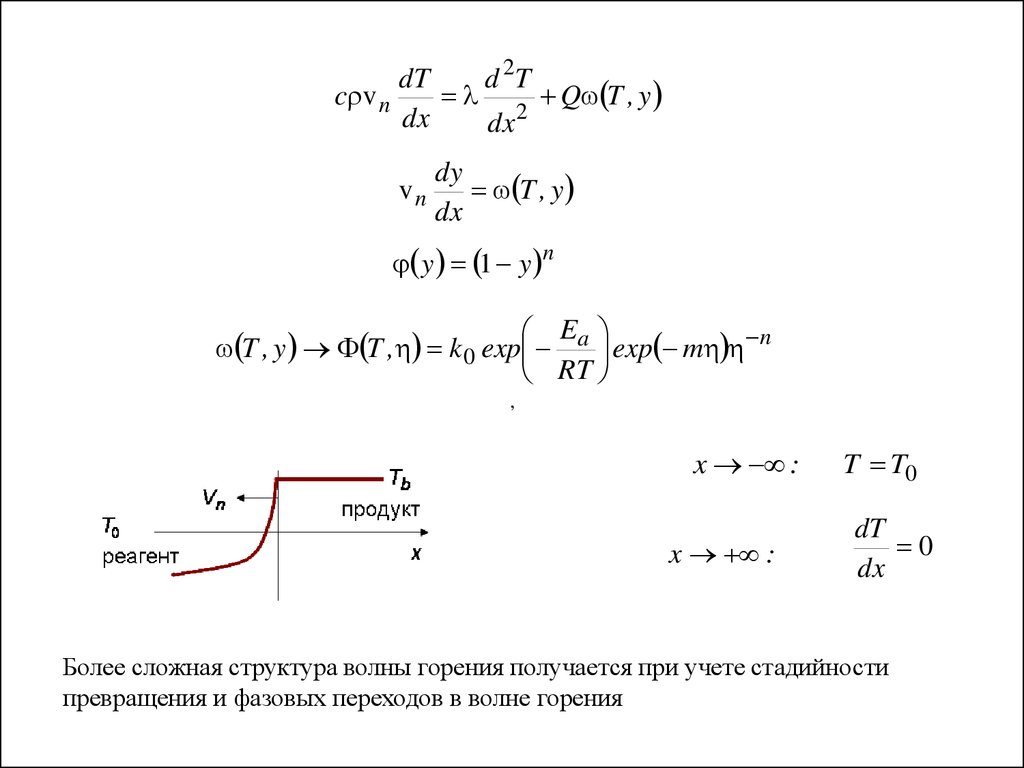
dT
d 2T
c v n
2 Q T , y
dx
dx
vn
dy
T , y
dx
y 1 y n
E
T , y T , k 0 exp a exp m n
RT
,
x :
x :
T T0
dT
0
dx
Более сложная структура волны горения получается при учете стадийности
превращения и фазовых переходов в волне горения

27.

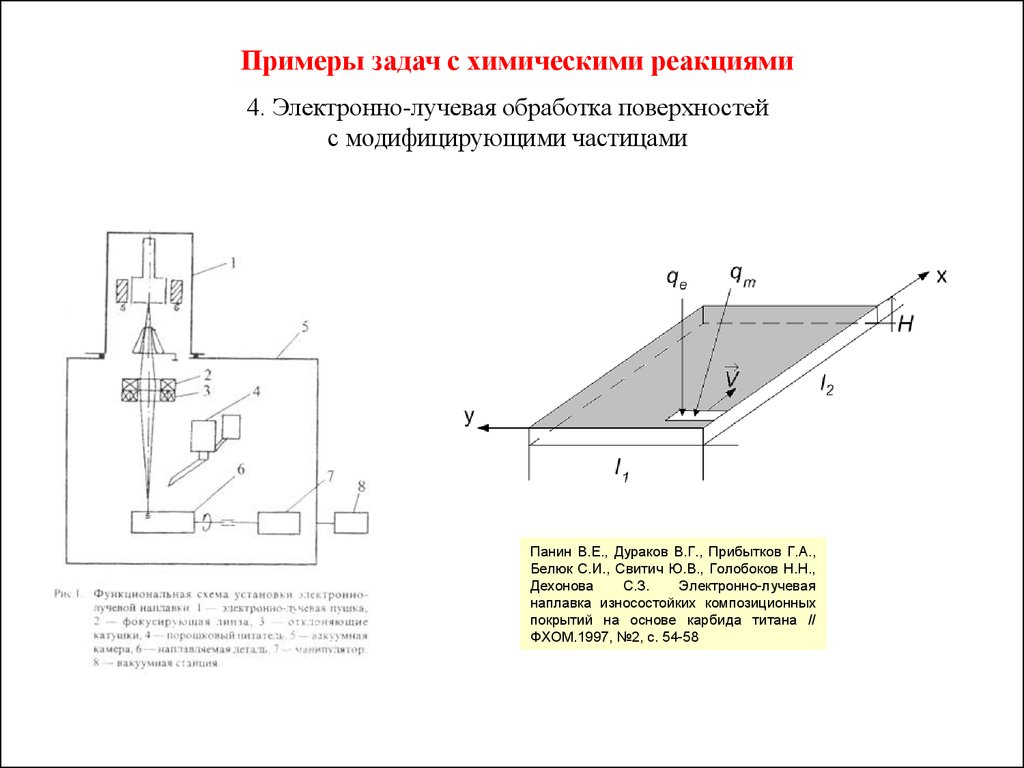
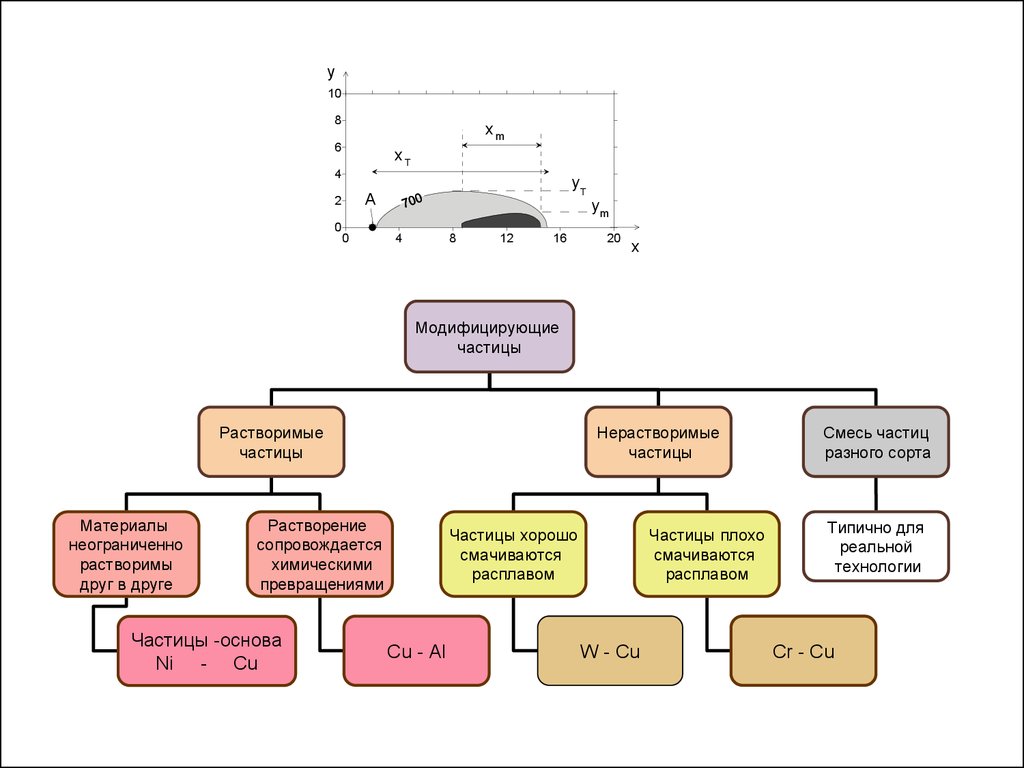
Примеры задач с химическими реакциями
4. Электронно-лучевая обработка поверхностей
с модифицирующими частицами
Панин В.Е., Дураков В.Г., Прибытков Г.А.,
Белюк С.И., Свитич Ю.В., Голобоков Н.Н.,
Дехонова
С.З.
Электронно-лучевая
наплавка износостойких композиционных
покрытий на основе карбида титана //
ФХОМ.1997, №2, с. 54-58

28.

y
10
8
xm
6
xT
4
0
yT
A
2
0
ym
4
8
12
16
20
x
Модифицирующие
частицы
Растворимые
частицы
Материалы
неограниченно
растворимы
друг в друге
Нерастворимые
частицы
Растворение
сопровождается
химическими
превращениями
Частицы -основа
Ni - Cu
Частицы хорошо
смачиваются
расплавом
Cu - Al
Частицы плохо
смачиваются
расплавом
W - Cu
Смесь частиц
разного сорта
Типично для
реальной
технологии
Cr - Cu

29.

ceff eff
( ( T 4 T04 ) qe )
T
T
T
W ( T , p ,...)
eff
eff
x y
y
H
t x
p
t
qm T , p ,...
(2)
, y y 0 / 2;
0
qe
q0 exp ( x Vt )2 at2
, y y0 / 2 ,
(3)
qm qm0 exp ( x xa Vt )2 y 2 a 2p
(4)
W Qch Q p
x :
y 0:
T
0
y
t 0:
(6)
T T0 ,
T
0
x
y :
l 0,
(5)
T
0
y
p 0,
s 1
(7)
(8)
(1)

30.

Плавление – через теплоемкость; используется теория двухфазной зоны
0-0.3 вес % меди на
диаграмме состояния Al+Cu
Cu 1
CuAl 2
CuAl2 3
Cu Al CuAl
CuAl Al CuAl2
Cu 2Al CuAl2
(9)
Al 4
Добавляются уравнения химической кинетики
1
1 3 ;
t
2
1 2 ;
t
(10)
3
2 3 ;
t
( p , T ) M Al M Cu
Cm
;
t
( M Cu (1 ) M Al ) 2
(11)
- объемная доля «материала частиц» в растворе

31.

Растворение:
(T , p ) 1 ( p ) 2 (T ) 1 ( p ) k0 exp Ea RT
W Qch Q p
Qch
m
hk ( d k
dt )
(13)
k 1
E
1 1 4 k 01 exp a1 ;
RT
E
2 2 4 k 02 exp a 2 ;
RT
E
3 1 24 k 03 exp a3 ;
RT
(14)
(12)

32.

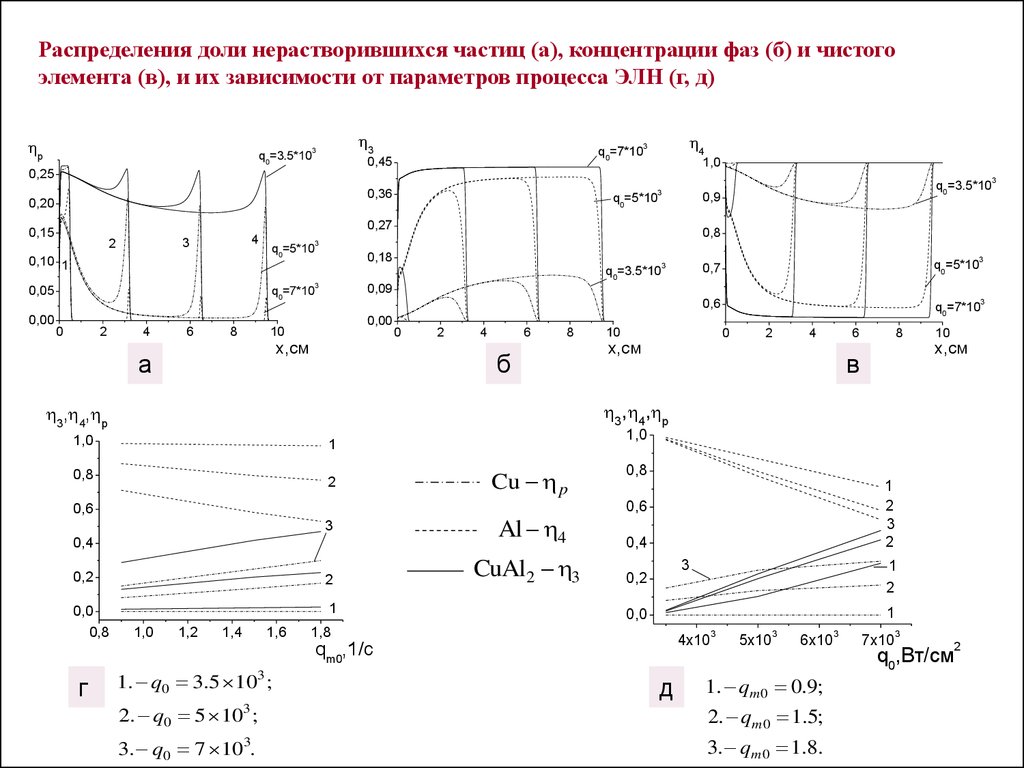
Распределения доли нерастворившихся частиц (а), концентрации фаз (б) и чистого
элемента (в), и их зависимости от параметров процесса ЭЛН (г, д)
p
3
3
q0=3.5*10
4
3
q0=7*10
0,45
1,0
0,25
3
0,36
0,20
4
3
2
0,10 1
0,8
3
q0=5*10
0,18
3
q0=3.5*10
3
0,05
2
4
6
8
0,00
10
x,см
а
0
2
4
6
8
б
1,0
0,6
q0=7*10
10
3
0
2
4
6
x,см
8
10
x,см
в
1,0
1
0,8
2
0,6
3
0,4
0,2
2
1
0,0
1,0
1,2
1,4
1,6
Cu p
Al 4
CuAl2 3
0,8
1
2
3
2
0,6
0,4
3
0,2
1. q0 3.5 103 ;
1
2
1
0,0
1,8
3
4x10
qm0,1/c
г
q0=5*10
3, 4, p
3, 4, p
0,8
3
0,7
0,09
q0=7*10
0
q0=3.5*10
0,9
0,27
0,15
0,00
3
q0=5*10
д
3
5x10
3
6x10
1. qm 0 0.9;
2. q0 5 103 ;
2. qm 0 1.5;
3. q0 7 103.
3. q m 0 1.8.
3
7x10
q0,Вт/см
2