Похожие презентации:
Предел функции по Коши
1. Предел функции по Коши
Пусть функция у = f(x) определена в окрестности точки x0. Всамой точке x0 функция может быть и не определена.
Определение. Число А называется пределом функции f(x) при
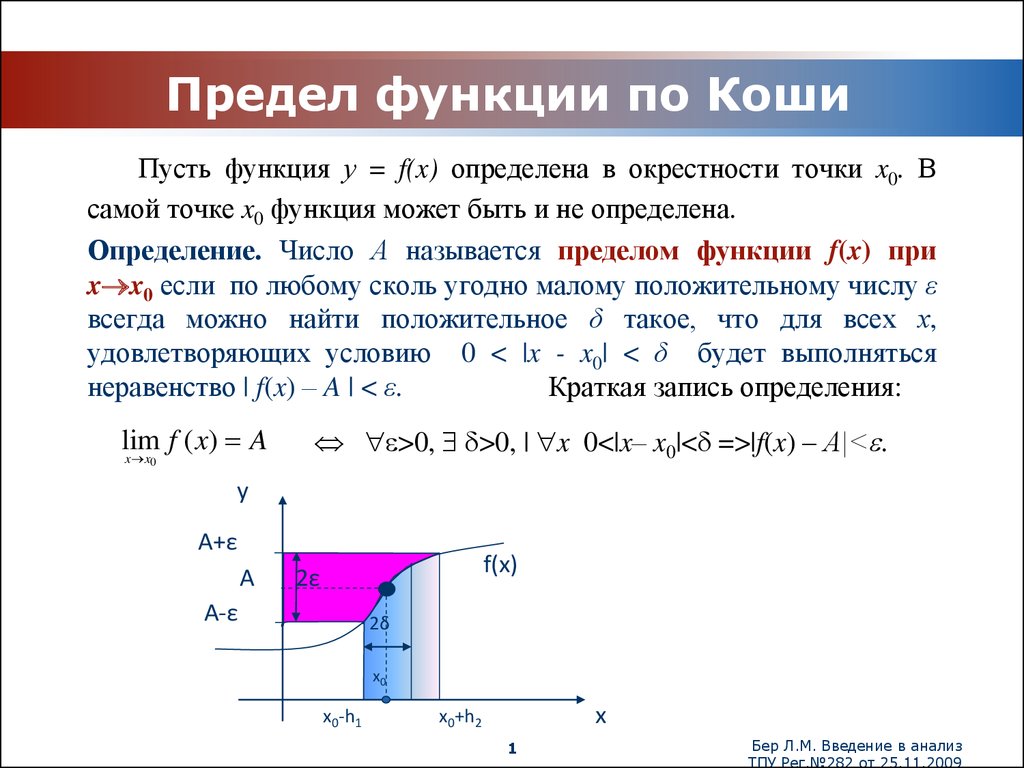
x x0 если по любому сколь угодно малому положительному числу ε
всегда можно найти положительное δ такое, что для всех х,
удовлетворяющих условию 0 < |x - x0| < δ будет выполняться
неравенство | f(x) – A | < ε.
Краткая запись определения:
lim
f ( x) A
x x
0
>0, >0, | x 0<|x– x0|< =>|f(x) – А|< .
y
A+ε
A
f(x)
2ε
A-ε
2δ
x0
x0-h1
x
x0+h2
1
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
2.
обозначениепредела
lim f ( x) A
x x 0
f(x) называется б. м.
lim f ( x) 0
краткая запись
определения
Геометрическая
иллюстрация
пример
>0, >0, |
x 0< | х – x0| < =>|f(x) – A|<
>0, >0, |
x 0< | х – x0| < =>|f(x)|<
x x0
f(x) называется б. б.
lim f ( x)
x x0
f(x) называется б. б.
lim f ( x)
x x0
lim f ( x ) A
x
f(x)
>0, >0, |
x | х| >1/ =C =>|f(x) – A|<
y
2
-C 0
2ε
C
x
2x
lim 2 2 2
x
x 1
lim
f ( x) A
x
lim
f ( x) A
x
2
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
3. Предел функции по Гейне
Пусть функция у = f(x) определена в окрестности точки x0. Всамой точке x0 функция может быть и не определена.
Определение. Вещественное число А называется пределом
функции f(x) при х x0, если для любой последовательности
xn значений аргумента, стремящейся к x0 соответствующая
последовательность значений функции f(xn) сходиться к А.
При этом предполагается, что xn такая, что xn D(f) и
xn x0 n N
Теорема 1. Определение предела функции по Гейне и по
Коши эквивалентны.
3
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
4. Свойства пределов
1. Если предел функции f(x) при х x0 существует, то онединственный.
2. Если функция f(x) при х x0 имеет конечный предел, то
она ограничена в некоторой окрестности точки x0.
3.
Функция имеет предел тогда и только тогда, когда ее
можно представить как сумму постоянной, равной этому
пределу и бесконечно малой величины.
lim
f ( x) A f ( x) A ( x), ( x) б.м.в. при x x0
x x
0
4
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
5. Свойства пределов
4. Если функции f(x) и g(x) имеют предел при х x0 , то ихсумма, разность, произведение и частное имеют предел при
х x0, причем
lim f ( x) g ( x) lim f ( x) lim g ( x)
a)
;
b) lim f ( x) g ( x) lim f ( x) lim g ( x) ;
c)
f ( x) lim f ( x)
x x0
x x0
x x0
x x0
lim
x x
0
g ( x)
lim g ( x)
x x0
x x0
, g ( x) 0, lim
g ( x) 0
x x
x x0
0
x x0
d) Если функция f(x) имеет предел при
х x0, то
произведение с*f(x) имеет предел при
х x0, с –
константа, причем
c f ( x) c lim
lim
f ( x) .
x x
x x
5. Пусть lim
f ( x) A и существует проколотая окрестность
x x
U*(x0, ) такая, что f(x) > 0 x U*(x0, ), тогда А 0.
0
0
0
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
6. Свойства пределов
6. Пустьи пусть lim g ( x) B
lim
f ( x) A
x x
и
x x0
0
f(x) < g(x)
x U*(x0, ) (или f(x) ≤ g(x)), тогда А ≤ B.
7. Пусть x U*(x0, ) выполняется f(x) ≤ g(x) ≤ (x). Если
существует lim f ( x)
и существует lim ( x)
, причем
x x0
x x0
lim f ( x) lim ( x) A
x x0
x x0
, то существует и lim g ( x) A .
x x0
8. Свойство о пределе композиции функций.
Пусть f : X Y , g : Y Z и существуют lim f ( x) y lim g ( y) z
0
x x0
y y0
тогда g(f(x))=g f имеет предел при х x0, причем
lim
g ( f ( x)) lim
g ( y) z0
x x
y y
0
.
0
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
0
7. Свойства б.м. функции
1. Сумма, разность, произведение двух б.м. при x x0 естьфункция б.м. при x x0.
2. Пусть (x) - б.м. при x x0, f(x) – ограниченна в U*( x0, ),
тогда (x) f(x) – б.м. при x x0.
3. Если (x) - б.м. при x x0, то с (x) - б.м. при x x0,
с-константа.
4. Если функция у = f(x) – б.м. при x x0 и
f(x) 0 в
некоторой окрестности точки x0, то функция y=1/f(x) – б.б.
при x x0. Если функция у = f(x) - б.б. при x x0, и f(x) 0
в некоторой окрестности точки x0, то функция y = 1/f(x) –
б.м. при x x0.
5. О роли б.м. в теории пределов.
Бер Л.М. Введение в анализ
ТПУ Рег.№282 от 25.11.2009
8. Односторонние пределы
Определение. Число А называется пределом функцииf(x) при х x0 слева, если для любого >0 существует такое
>0, что для всех х, отвечающих условию 0 < х0 – x <
выполняется неравенство |f(x) – А|< .
Число А называется пределом функции f(x) при х x0
справа, если для любого >0 существует такое >0, что для
всех х, отвечающих условию 0 < х – x0< выполняется
неравенство |f(x) – А|< .
Обозначение:
lim f ( x) или f(x – 0) предел слева при х x ,
x x 0
0
0
lim f ( x) или f(x0+0) предел справа при х x0.
x x0 0
0
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
9. Односторонние пределы
Теорема 2. (О существовании конечного предела.)Пусть x0 R. Функция f(x) имеет конечный предел при х x0
тогда и только тогда, когда существуют конечные и равные
f ( x) A .
между собой пределы lim f ( x) = lim f ( x) =A, при этом xlim
x
x x0 0
x x0 0
0
Замечание 1. Все свойства пределов остаются верными и в
случае односторонних пределов.
Замечание 2. Определение одностороннего предела на языке
последовательностей дается также как и определение предела
при х x0 с той лишь разницей, что для последовательности
{xn} должно выполняться условие xn < x0 для предела слева и
xn > x0 для предела справа.
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
10. Замечательные пределы
Теорема 3. Предел отношения sin x к своему аргументу xравен единице, когда аргумент стремится к нулю, т. е.
sin x
lim
1 – 1 замечательный предел.
x 0
x
x
1
1
lim
1 x x e ) – 2 замечательный предел.
1 e (или lim
x
x 0
x
Следствия:
1) lim
x 0
arcsin x
1 ,
x
2) lim
x 0
tgx
1
x
, 3) lim
x 0
arctgx
1 .
x
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
11. Сравнение бесконечно малых
Пусть (x), (x) – б.м. при x x0, где x0 – конечно или б.б.Определение. Если lim ( x) 0 , то говорят, что (x) б.м. более
x x
( x)
высокого порядка, чем (x) при х x0, или что (x) - б.м. низшего
0
порядка относительно (x). Обозначение: (x) =о( (x)).
Определение. Если lim
x x
0
( x)
c , где с = const 0, то (x)
( x)
и (x)
называют б.м. одного порядка.
( x)
В частности, если
, то (x) и (x) называются
lim
1
x x
( x)
эквивалентными. Обозначение: (x) ~ (x).
0
Определение. Б.м. (x) называется бесконечно малой порядка k
( x)
относительно б.м. (x), если lim
c , где с = const 0.
k
x x
( x)
0
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
12.
Теорема 2. (О замене б.м. на эквивалентную.)Если (x) ~ 1(x), (x) ~ 1(x) и
предел отношения б.м.
lim
x x
0
( x)
c , то lim 1 ( x) c , т.е.
x x
( x)
1 ( x)
0
не меняется при
замене их
эквивалентными бесконечно малыми:
1 ( x)
( x)
lim
lim
x x
( x ) x x 1 ( x )
0
0
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
13. Таблица эквивалентностей
Пусть (х) 0 при x x0. Тогда при x x0n ( x)
1 (х)
(~x) (х)
1
sin
n
ln (1 + (х)) ~ (х)
~
x
arcsin (x) ~ (х)
log a (1 + (х)) ~ ln a
tg (х) ~ (х)
e (х) - 1 ~ (х)
arctg (х) ~ (х)
a (х) – 1 ~ (х) 1n а
1 - cos (х) ~
2 x
2
n
1 ( x) 1 ~
( x)
n
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
14.
Теорема 2. (Критерий эквивалентности б.м.)Б.м. (x) и (x) при x x0 эквивалентные б.м. тогда и только
тогда, когда их разность (x) – (x) – б.м. более высокого
порядка, чем (x) и (x) при x x0.
Замечание 1. Аналогично б.м. можно сравнивать и б.б., а
именно
если f(x) и (x)-б.б. при x x0 и
,
f ( x)
lim
0, то
x x0
( x)
1
f(x) б.б. более высокого порядка, чем (x);
f(x) б.б. более низкого порядка, чем (x);
f(x) и (x) эквивалентные б.б. при x x0.
Замечание 2. Теоремы 1 и 2 для б.б. функций остаются
верными с той лишь разницей, что главной частью б.б.
функции является б.б. более высокого порядка.
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
15. Спасибо за внимание
LOGOСпасибо за внимание
Бер Л.М. Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009














 Математика
Математика








