Похожие презентации:
Цилиндр
1.
№16Цилиндр
2.
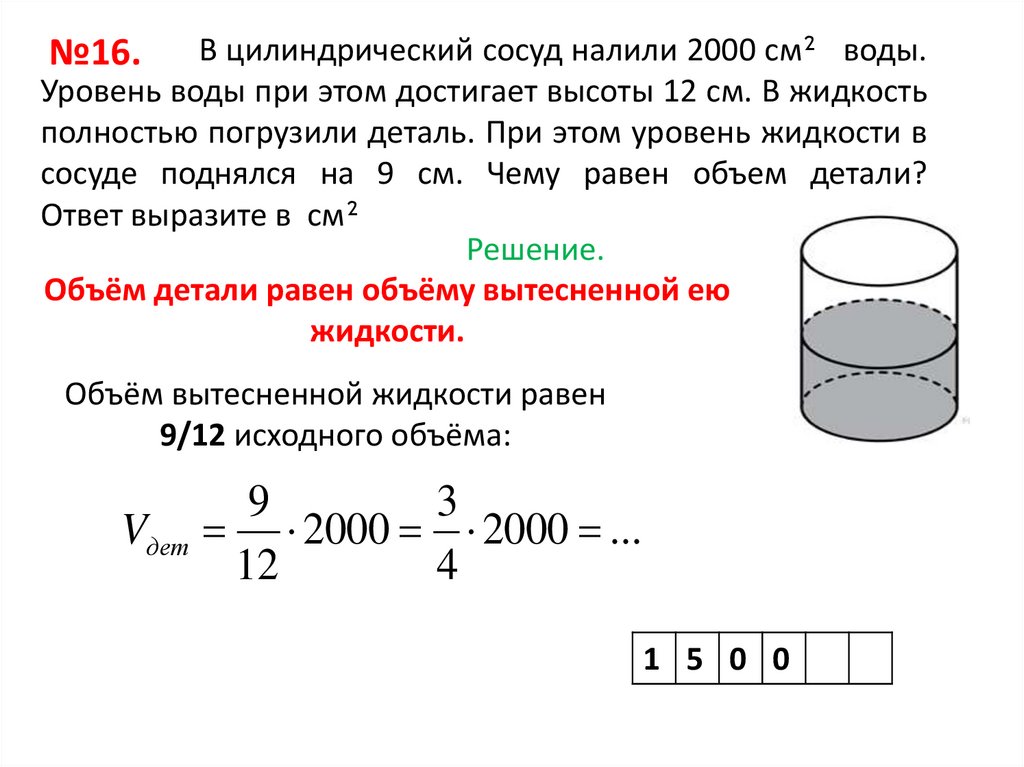
№16.В цилиндрический сосуд налили 2000 см² воды.
Уровень воды при этом достигает высоты 12 см. В жидкость
полностью погрузили деталь. При этом уровень жидкости в
сосуде поднялся на 9 см. Чему равен объем детали?
Ответ выразите в см²
Решение.
Объём детали равен объёму вытесненной ею
жидкости.
Объём вытесненной жидкости равен
9/12 исходного объёма:
Vдет
9
3
2000 2000 ...
12
4
1 5 0 0
3.
В цилиндрическом сосуде уровень жидкостидостигает 16 см. На какой высоте будет находиться уровень
жидкости, если ее перелить во второй сосуд, диаметр которого
в 2 раза больше первого?
Ответ выразите в см. Решение.
V1 V2
№16.
Vц S H
Отсюда высота
Vц R H
Vц
Vц 1
H
2
2
R
R
2
Число π — это величина постоянная, объем жидкости
V в данной задаче тоже не изменяется.
То есть, высота уровня жидкости обратно пропорциональна
радиусу основания сосуда.
Так как радиус увеличился в 2 раза, то высота
уменьшится в 4 раза. ( 2²= 4 )
4
Н1 16
H2
...(см)
4
4
4.
№16. Объем первого цилиндра равен 12 м3. У второгоцилиндра высота в три раза больше, а радиус основания —
в два раза меньше, чем у первого. Найдите объем второго
цилиндра. Ответ дайте в кубических метрах.
Решение.
Пусть объём первого цилиндра равен
объём второго
V2 R2 H 2
2
V1 R1 H1
2
где R₁ R₂ — радиусы оснований цилиндров, H₁ H₂ — их высоты.
Т.к.
Н 2 3Н1 , R2 0,5R2 ,
то выразим объём второго цилиндра через объём первого:
2
3
3
2
R1
V2 R2 H 2 3H1 R1 H1 V1
4
4
2
3
3
V2 V1 12 ...
9
4
4
2
5.
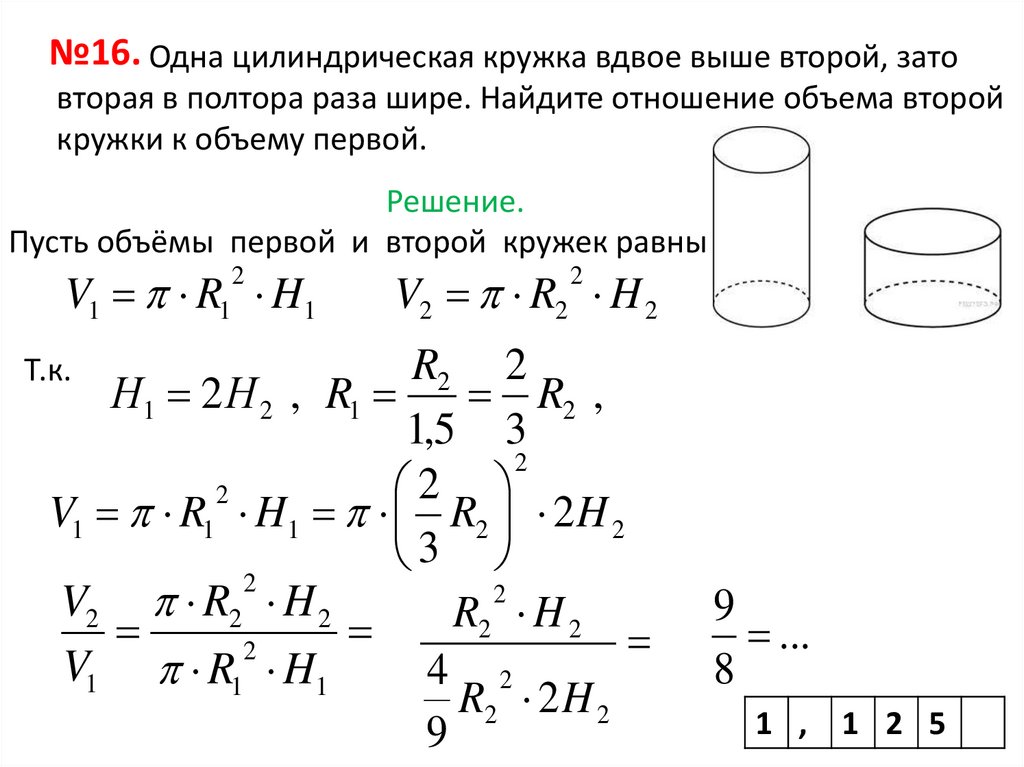
№16. Одна цилиндрическая кружка вдвое выше второй, затовторая в полтора раза шире. Найдите отношение объема второй
кружки к объему первой.
Решение.
Пусть объёмы первой и второй кружек равны
V1 R1 H1
2
V2 R2 H 2
2
R2 2
Н1 2 Н 2 , R1
R2 ,
1,5 3
2
2
2
V1 R1 H1 R2 2 H 2
3
2
2
V2 R2 H 2
R2 H 2
2
V1 R1 H1
4 2
R2 2 H 2
9
Т.к.
9
...
8
1 ,
1 2 5
6.
№16.Даны две кружки цилиндрической формы. Перваякружка вдвое выше второй, а вторая в четыре раза шире
первой. Во сколько раз объём второй кружки больше
объёма первой?
Решение.
Пусть объёмы первой и второй кружек равны
V1 R1 H1
V2 R2 H 2
1
Т.к. Н 2 Н 2 , R2 4 R1 ,
2
2
2
V2 4 R1 0,5H1
2
V2 R2 H 2 4 R1 0,5H1
...
2
2
V1 R1 H1
R1 H1
2
2
8
7.
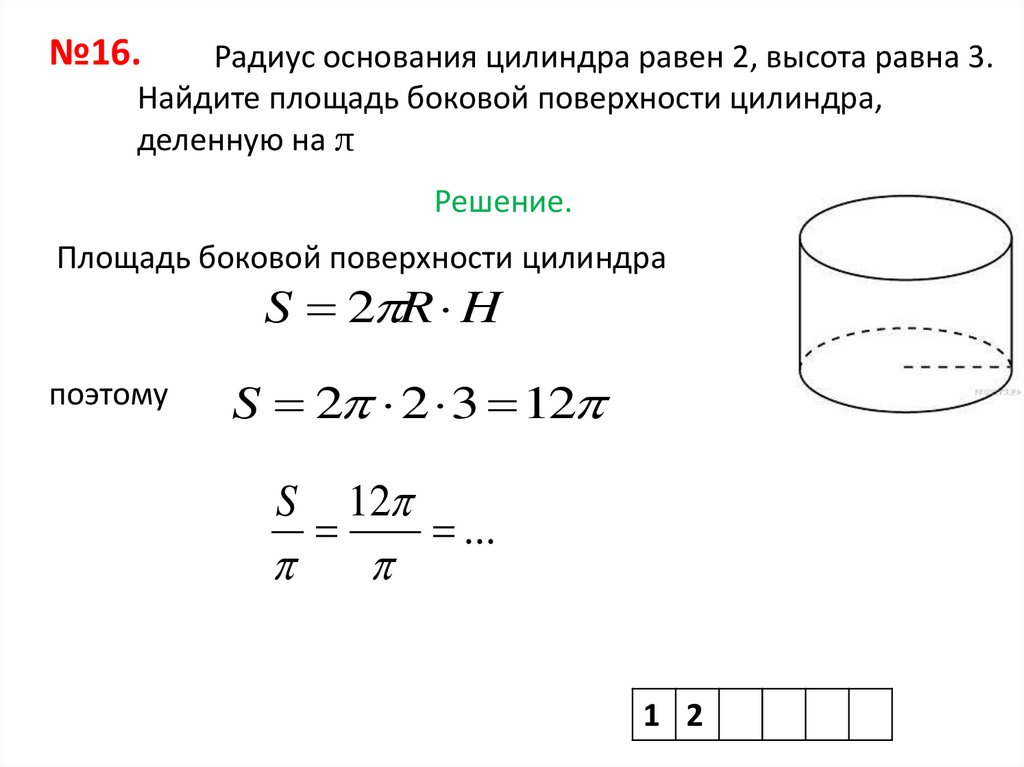
№16.Радиус основания цилиндра равен 2, высота равна 3.
Найдите площадь боковой поверхности цилиндра,
деленную на π
Решение.
Площадь боковой поверхности цилиндра
S 2 R H
поэтому
S 2 2 3 12
S 12
...
1 2
8.
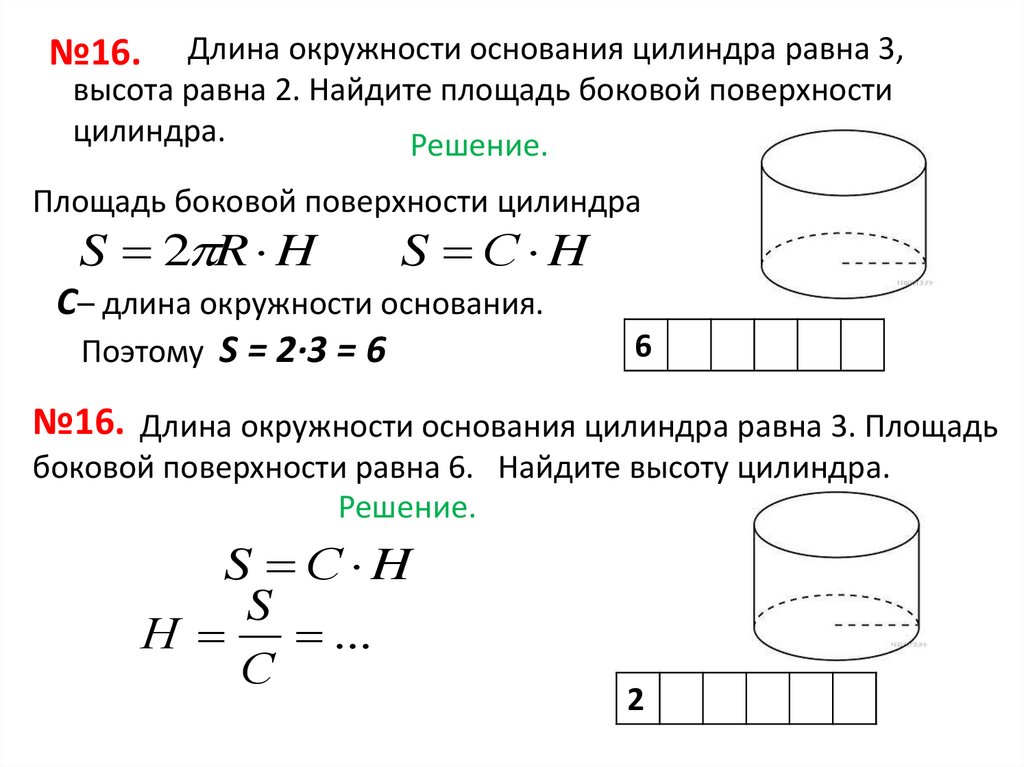
Длина окружности основания цилиндра равна 3,высота равна 2. Найдите площадь боковой поверхности
цилиндра.
Решение.
№16.
Площадь боковой поверхности цилиндра
S 2 R H
S С H
C– длина окружности основания.
Поэтому S = 2·3 = 6
6
№16. Длина окружности основания цилиндра равна 3. Площадь
боковой поверхности равна 6. Найдите высоту цилиндра.
Решение.
S С H
S
Н
...
С
2
9.
№16. В бак, имеющий форму цилиндра, налито 5 л воды.После полного погружения в воду детали, уровень воды в
баке поднялся в 1,2 раза. Найдите объём детали.
Ответ дайте в кубических сантиметрах, зная, что в одном
литре 1000 кубических сантиметров.
Решение.
Объём детали равен объёму вытесненной ею
жидкости.
После погружения детали в воду объём стал равен
5 · 1,2 = 6 литров,
поэтом объём детали равен 6 − 5 = 1 л = 1000 см3.
1 0 0 0
10.
№16.Вода в сосуде цилиндрической формы находится на
уровне h = 40cм. На каком уровне окажется вода, если её
перелить в другой цилиндрический сосуд, у которого радиус
основания вдвое больше, чем у первого? Ответ дайте в
сантиметрах.
Решение.
Объём воды, налитой в цилиндр, высотой h и радиусом R равен
V = πR²h
Следовательно, при увеличении радиуса цилиндра
в 2 раза, при неизменном объёме,
высота стола воды окажется в 2²= 4 раза меньше,
значит, вода во втором цилиндре достигнет уровня
h₂= 40 : 4= 10 см.
1 0
11.
№16. В сосуд цилиндрической формы налили воду до уровня80 см. Какого уровня достигнет вода, если её перелить в другой
цилиндрический сосуд, у которого радиус основания в 4 раза
больше, чем у первого? Ответ дайте в см.
Решение.
Объём воды, налитой в цилиндр, высотой h и радиусом R равен
V = πR²h
Следовательно, при увеличении радиуса цилиндра
в 4 раза, при неизменном объёме,
высота стола воды окажется в 4²= 16 раза меньше,
значит, вода во втором цилиндре достигнет уровня
h₂= 80 : 16 = 5 см.
5







 Математика
Математика








