Тени в ортогональных проекциях

1.

Тени в ортогональных
проекциях

2.

Тени показывают на ортогональных и
аксонометрических проекциях различных
строительных конструкций и сооружений для
придания большей наглядности и рельефности
их изображениям
1. Факельное освещение – точечный
источник света, который находится на небольшом
расстоянии от объекта.
Световые лучи образуют связку прямых.
2. Солнечное освещение – источник света
находится в бесконечности.
Световые лучи параллельны друг другу.

3.

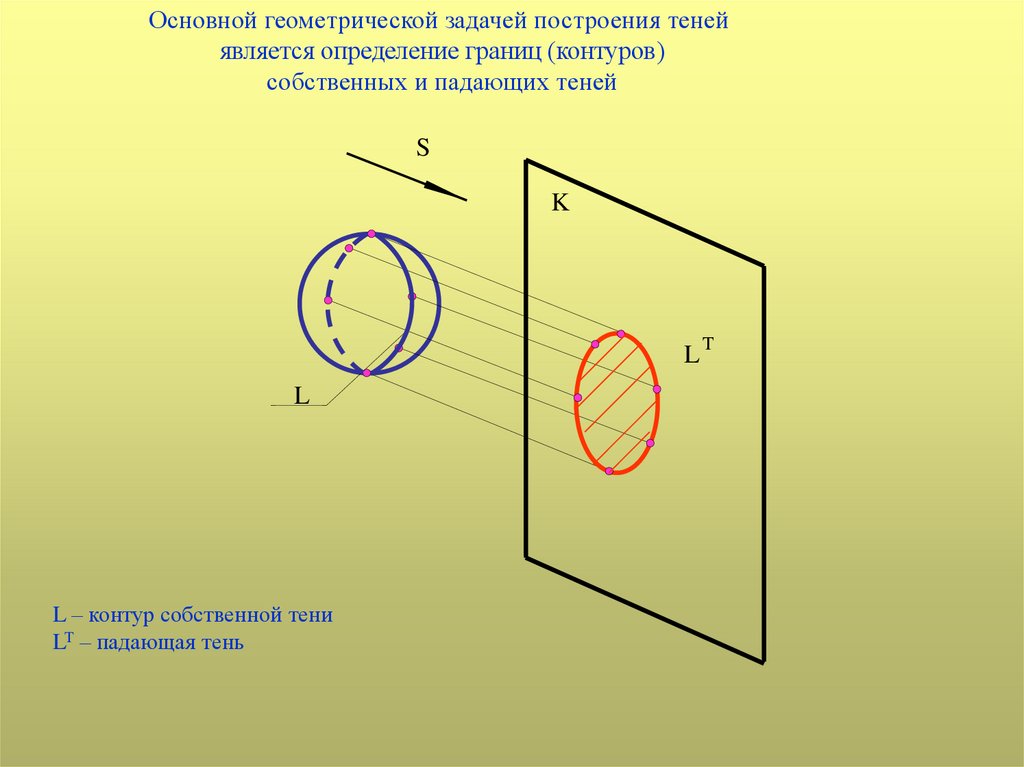
Основной геометрической задачей построения теней
является определение границ (контуров)
собственных и падающих теней
S
K
L
L
L – контур собственной тени
LT – падающая тень
T

4.

1. Собственная тень – неосвещенная
часть поверхности тела.
2. Контур собственной тени – линия,
разграничивающая освещенную часть
поверхности тела от собственной
тени.
3. Падающая тень – это тень,
отбрасываемая предметом на
плоскость.
4. Контур падающей тени есть тень от
контура собственной тени.

5.

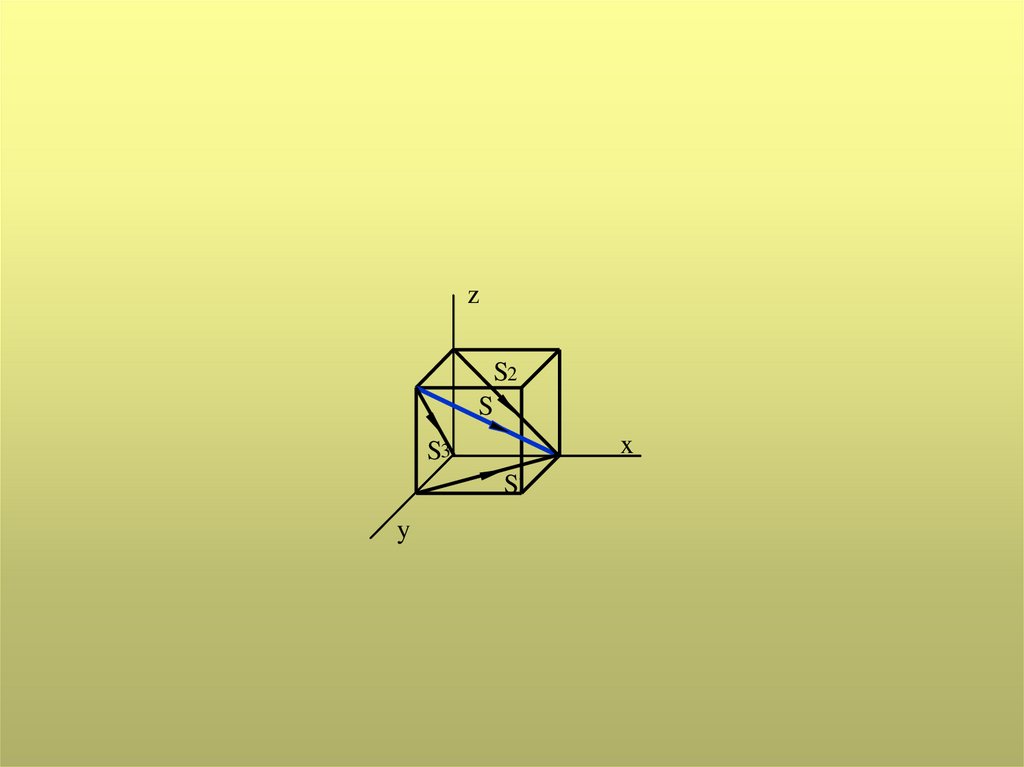
Направление светового луча на
чертежах в ортогональных
проекциях выбирается параллельно
диагонали куба, грани которого
параллельны плоскостям проекций.
Проекции светового луча на
плоскости П1, П2, П3 составляют
угол 450 с соответствующими
координатными осями х, y, z.

6.

z
S2
S
x
S3
S1
y

7.

Тень от точки
Тень, падающая от некоторой точки на
поверхность, определяется как точка
пересечения поверхности со световым лучом,
проходящим через эту точку.
Введем обозначения:
АТ – тень от точки А на плоскость проекций;
А1Т – горизонтальная проекция тени;
А2Т – фронтальная проекция тени;
(АТ) – мнимая тень точки А на плоскость

8.

z
A2
S2
T
A2
B2
x
0
T
B1
S1
A1
B1
Для построения теней этих точек через их проекции
необходимо провести проекции световых лучей
и найти их следы:
- на фронтальной плоскости проекций (АТ);
- на горизонтальной плоскости проекций (ВТ)

9.

Тень от точки на
плоскую фигуру
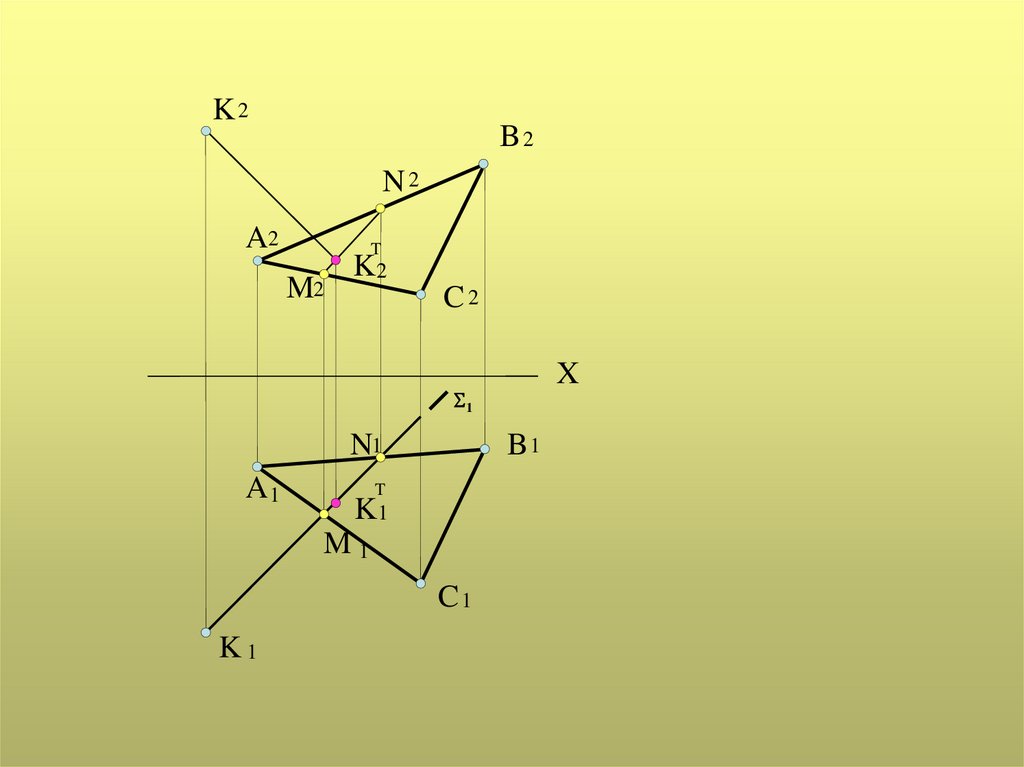
Тенью от точки К на произвольную плоскую фигуру
является точка пересечения светового луча, проходящего
через точку К, с плоской фигурой
Алгоритм решения:
через точку К проводится световой луч по углом 450
(через проекции точки К1и К2 проводятся проекции
светового луча);
световой луч заключается в проецирующую плоскость ;
определяется линия пересечения MN плоскости с
плоскостью треугольника АВС (ее проекции M1N1 и
М2N2);
определяется точка пересечения КТ (ее проекции К1 Т и
К2Т) светового луча с линией MN

10.

K2
B2
N2
A2
T
M2
K2
C2
X
1
N1
A1
B1
T
K1
M1
C1
K1

11.

Тень от точки на
поверхность многогранника
Тенью от точки на поверхность
многогранника
является точка
пересечения
светового
луча,
проходящего
через
точку,
с
поверхностью этого многогранника

12.

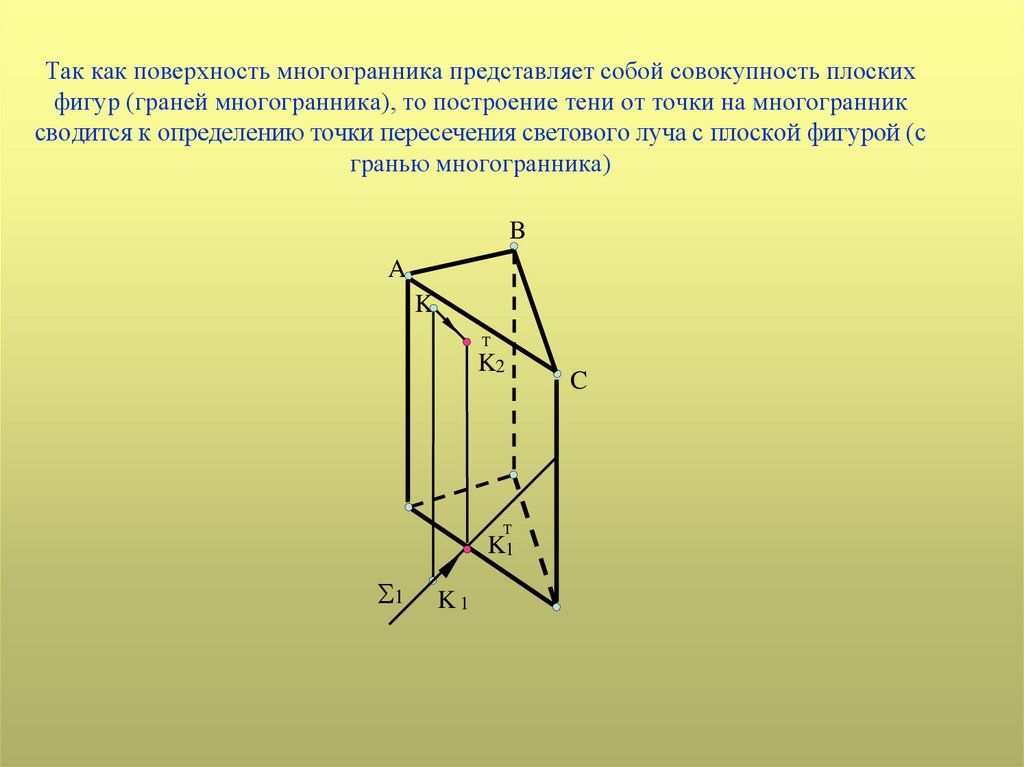
Так как поверхность многогранника представляет собой совокупность плоских
фигур (граней многогранника), то построение тени от точки на многогранник
сводится к определению точки пересечения светового луча с плоской фигурой (с
гранью многогранника)
B
A
K
T
K2
T
K1
1
K1
C

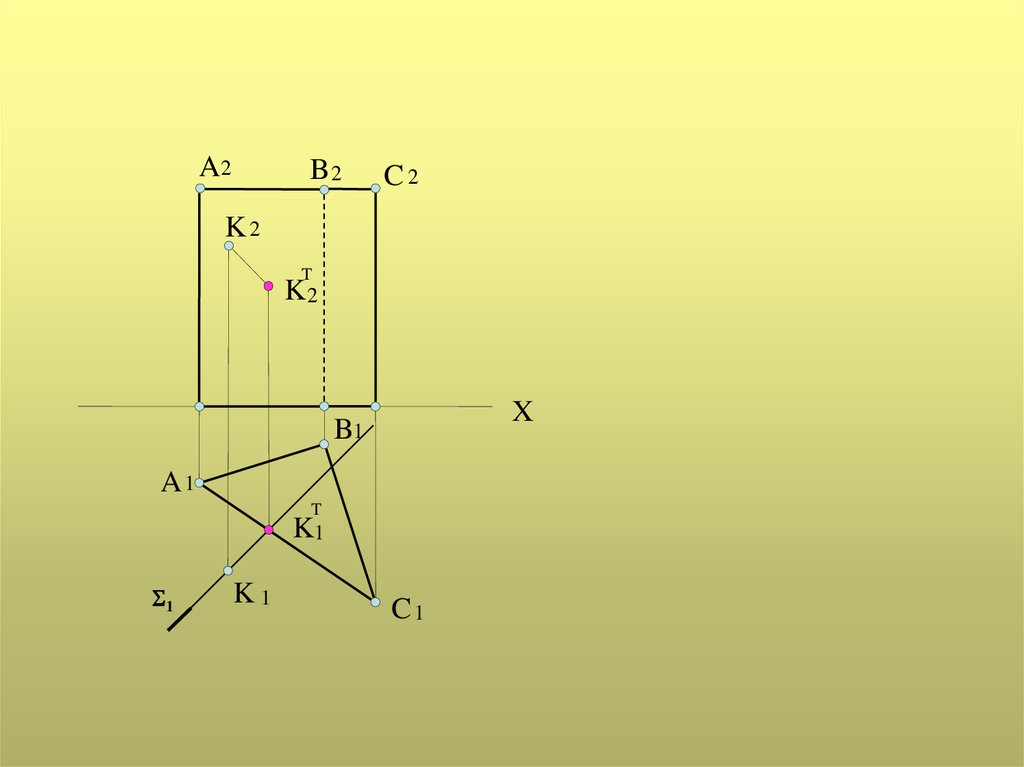
13.

A2
B2
C2
K2
T
K2
X
B1
A1
T
K1
1
K1
C1

14.

Тень от прямой на плоскости
проекций
Тень от прямой на плоскости проекций есть
линия пересечения лучевой плоскости с
плоскостью проекций.
Таким образом, тень от прямой на плоскости
проекций есть прямая линия.
Чтобы определить тень от прямой на
плоскость проекций достаточно найти тени на эту
плоскость проекций от двух точек прямой.
Если тени от точек падают на разные плоскости
проекций, то необходимо воспользоваться мнимой
тенью точки (АТ).

15.

B2
A2
X
T
A1
T
B1
A1
B1

16.

B2
A2
T
B2
K
X
T
A1
A1
T
B1
B1

17.

Тени на плоскости
проекций от прямых
частного положения

18.

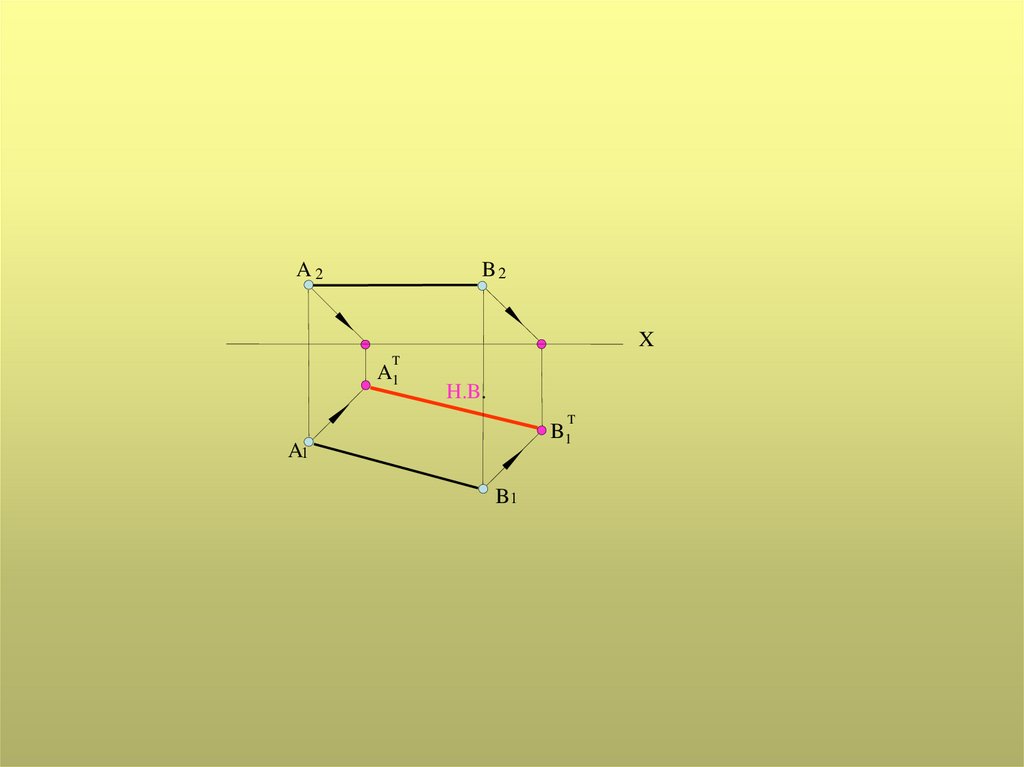
A2
B2
X
T
A1
H.B.
T
B1
A1
B1

19.

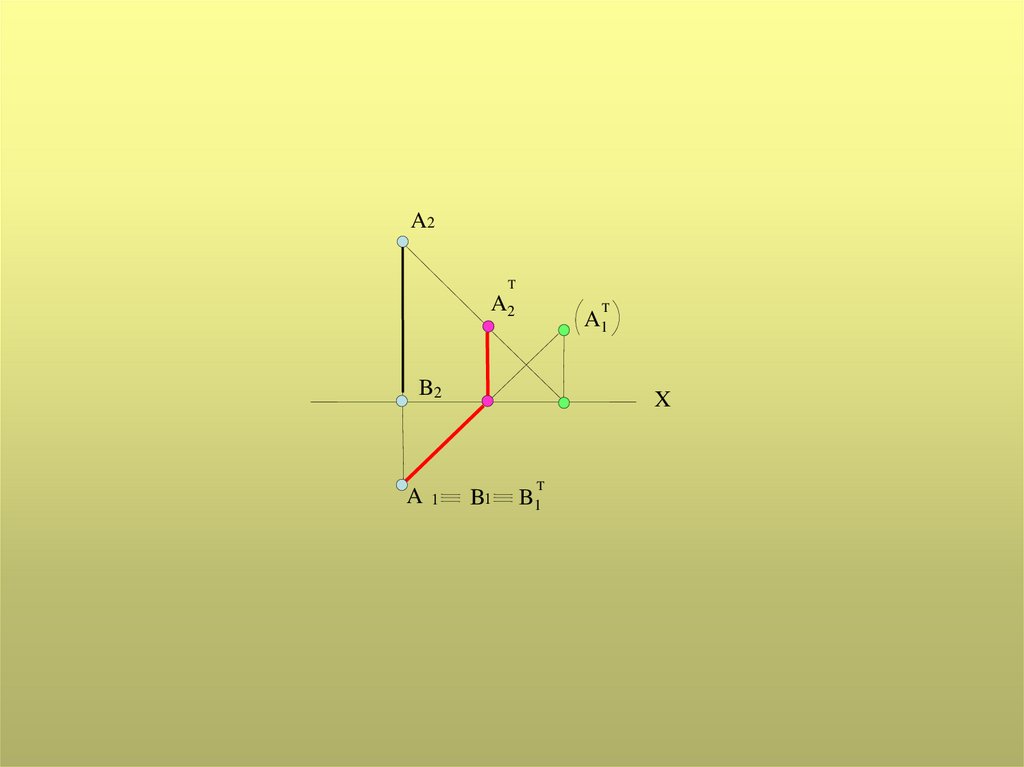
A2
T
A2
T
A1
B2
A
1
X
B1
T
B1

20.

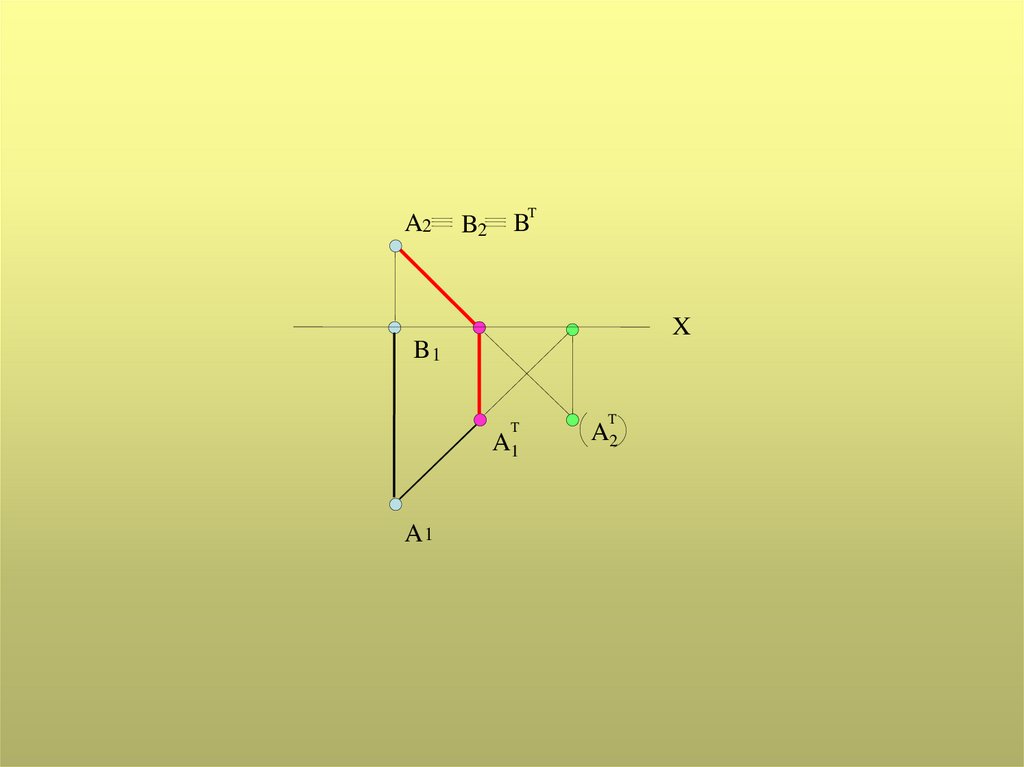
A2
B2
T
B
X
B1
T
A1
A1
T
A2

21.

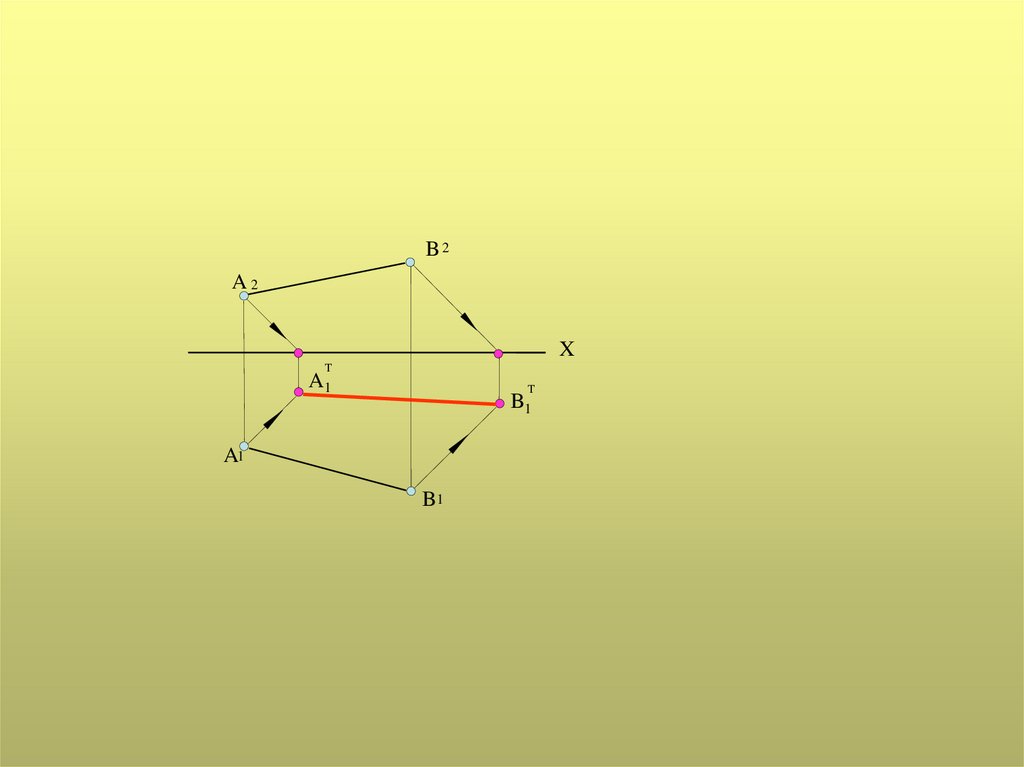
1. Тень от прямой, параллельной
плоскости проекций, параллельна и
равна самой прямой.
2. Тень от вертикального отрезка прямой
на плоскость проекций - на одной
плоскости совпадает с направлением
проекции светового луча, а на другой
плоскости
параллельна
проекции
самого
отрезка,
т.е.
является
вертикальной прямой.

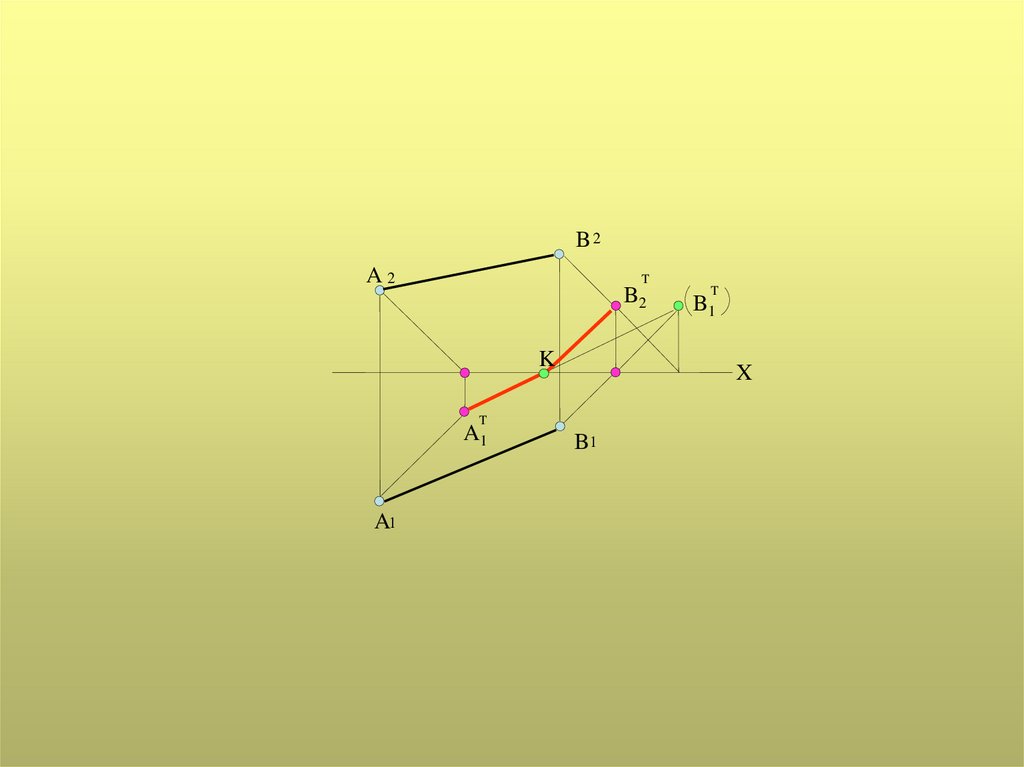
22.

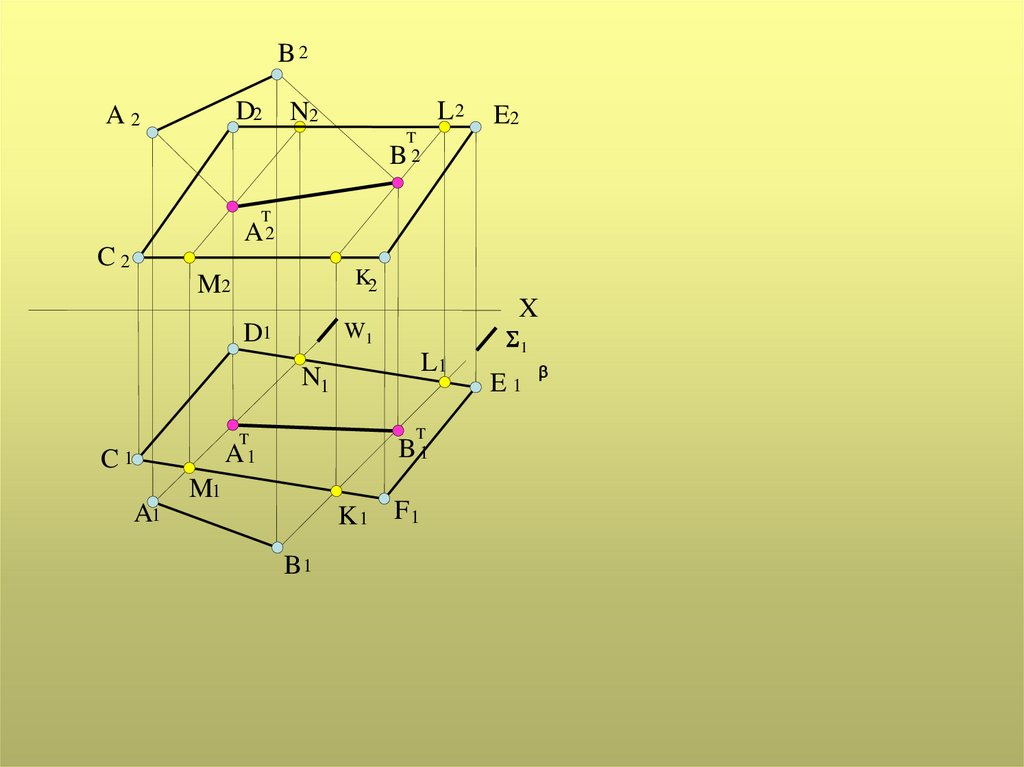
Тень от прямой на произвольную
плоскость
Тень от прямой на плоскость общего
положения есть линия пересечения лучевой
плоскости, проходящей через прямую, с этой
плоскостью.
Так как линия пересечения двух плоскостей
есть прямая, то тень от прямой на любую
плоскость есть прямая линия.
Для построения тени достаточно
определить тени от двух любых точек прямой
на плоскость.

23.

B2
D2
A2
L2
N2
E2
T
B2
T
A2
C2
K2
M2
D1
X
W1
L1
N1
T
T
B1
A1
C1
M1
K1 F1
A1
B1
1
E1

24.

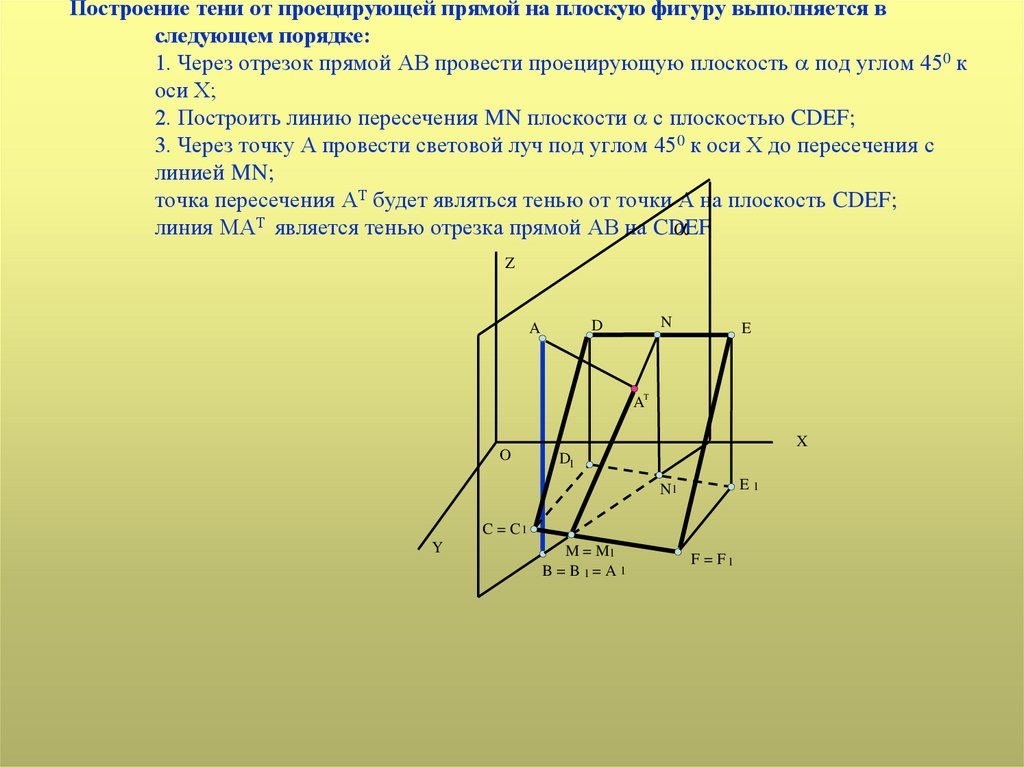
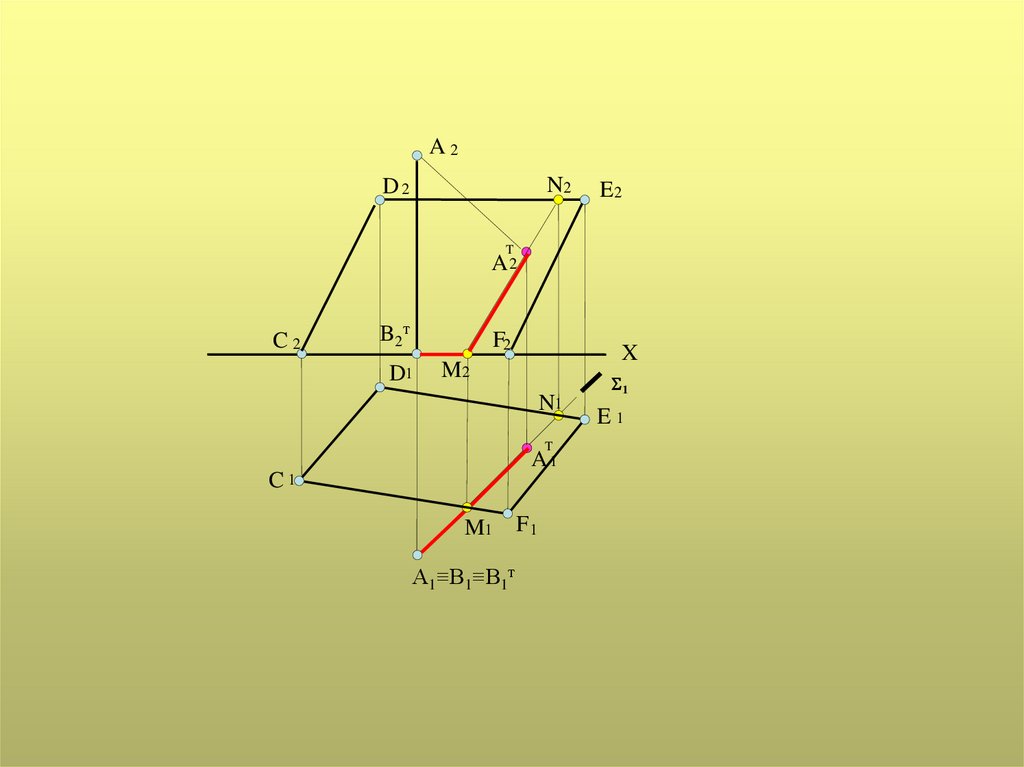
Построение тени от проецирующей прямой на плоскую фигуру выполняется в
следующем порядке:
1. Через отрезок прямой АВ провести проецирующую плоскость под углом 450 к
оси Х;
2. Построить линию пересечения MN плоскости с плоскостью CDEF;
3. Через точку А провести световой луч под углом 450 к оси Х до пересечения с
линией MN;
точка пересечения АТ будет являться тенью от точки А на плоскость CDEF;
линия МАТ является тенью отрезка прямой АВ на CDEF
Z
N
D
A
E
AT
O
X
D1
E1
N1
C = C1
Y
M = M1
B = B 1= A 1
F = F1

25.

A2
N2
D2
E2
T
A2
C2
B2 т
F2
D1
X
M2
N1
T
A1
C1
M1
А1≡B1≡В1т
F1
1
E1

26.

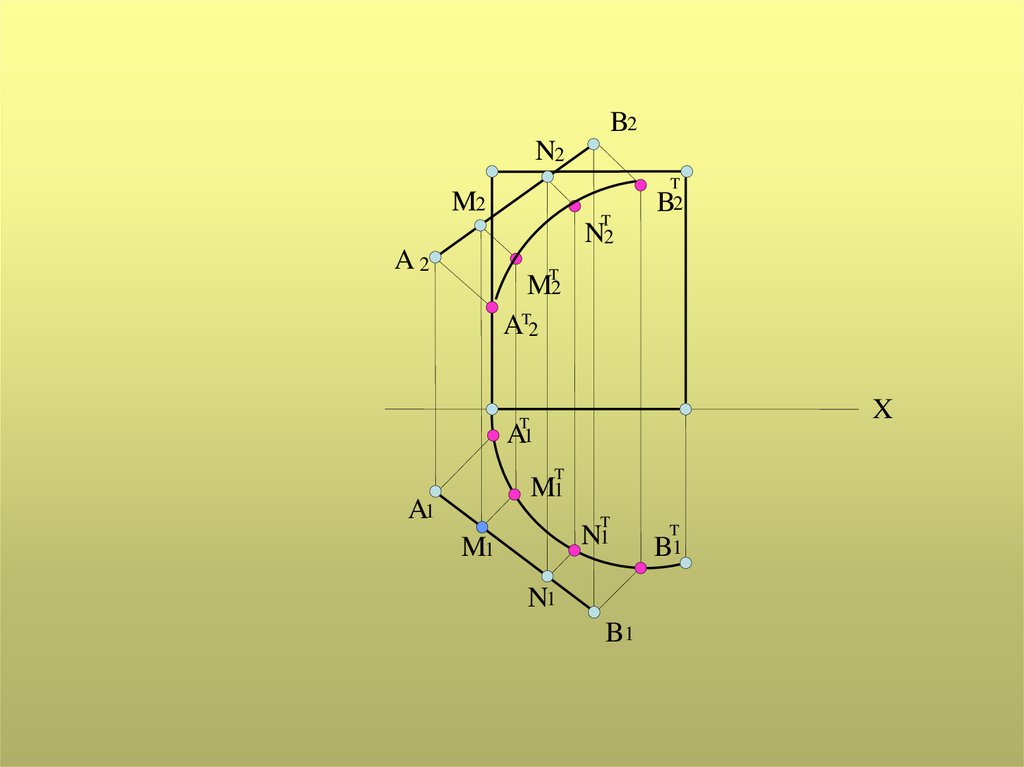
Тень от прямой на поверхность
Тень от прямой на поверхность
представляет собой линию пересечения
лучевой плоскости, проходящей через
прямую, с поверхностью
Тень от прямой на поверхность
определяется как совокупность теней на
поверхность от нескольких точек этой
прямой

27.

B2
N2
T
M2
T
B2
N2
A2
MT2
AT2
X
T
A1
T
M1
A1
T
N1
M1
N1
B1
T
B1

28.

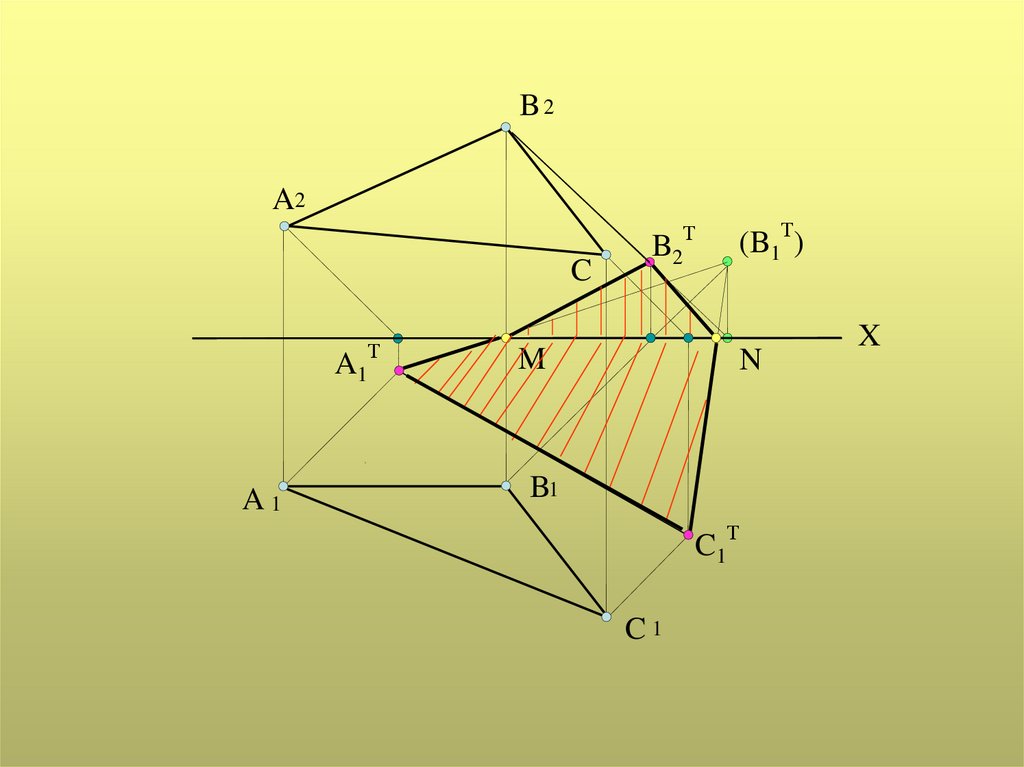
Тень от плоской фигуры на
плоскости проекций
Падающая тень от плоской фигуры на
плоскости проекций может быть построена как
совокупность теней от ее вершин и сторон
Если тени от вершин плоской фигуры падают
на разные плоскости проекций, то для
определения действительной тени плоской
фигуры необходимо воспользоваться мнимой
тенью ее вершины

29.

B2
A2
C2
X
A1Т
B 1Т
A1
C1Т
B1
C1

30.

B2
A2
C
Т
A1
A1
Т
Т
B2
(B1 )
M
N
B1
Т
C1
C1
X

31.

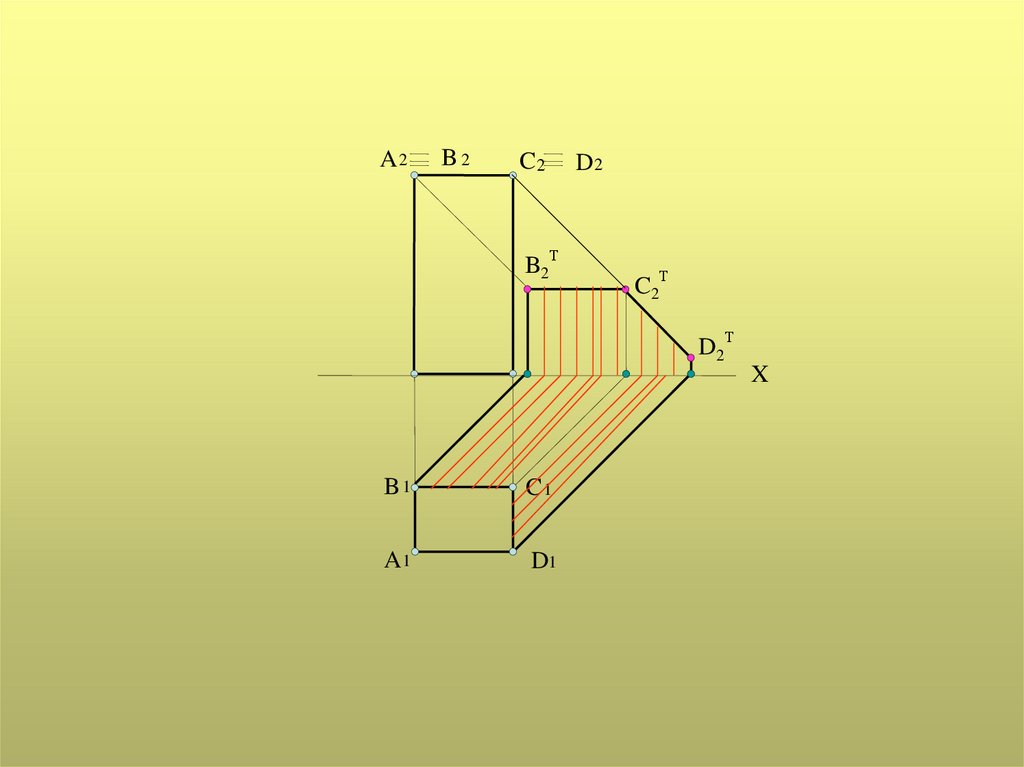
Тень от многогранника
Построение собственной и падающей теней
многогранника сводится к определению
собственных и падающих теней плоских
фигур – его граней
В собственной тени находятся две грани
многогранника, поэтому падающей тенью
многогранника будет совокупность падающих
теней этих граней

32.

A2
B2
C2
B2Т
D2
C 2Т
D2Т
X
B1
C1
A1
D1

33.

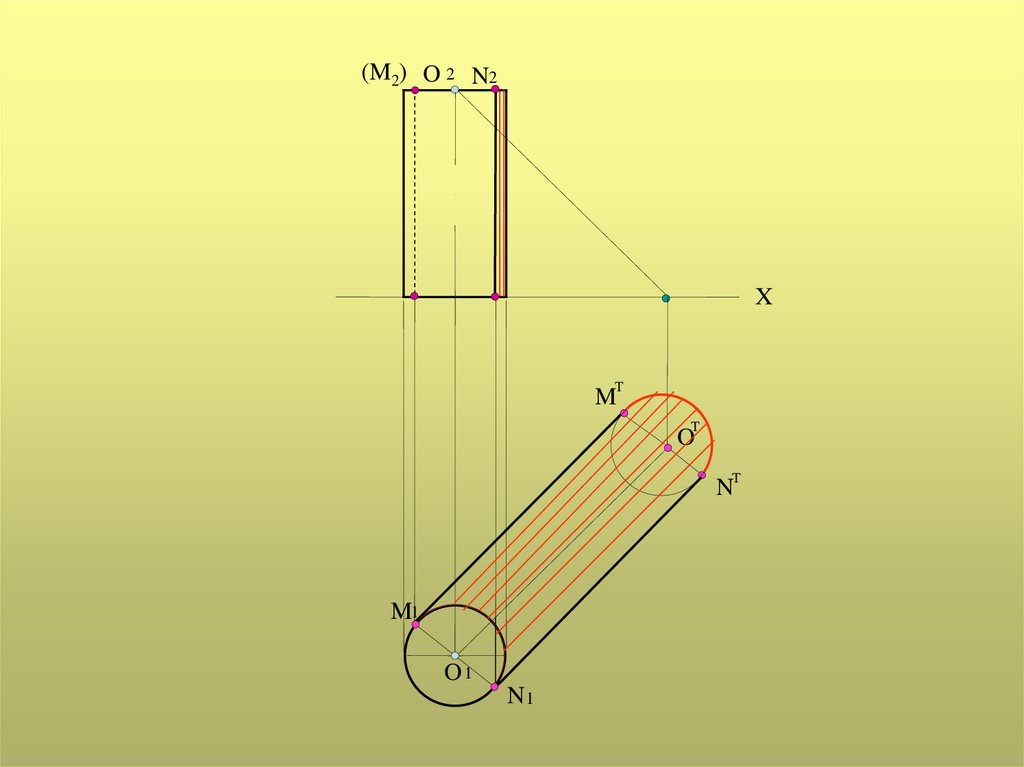
Тень от прямого кругового
цилиндра
Для определения контура собственной тени прямого кругового цилиндра
проводятся две проецирующие лучевые плоскости, касательные к поверхности
цилиндра и составляющие с плоскостью проекций угол 450
Образующие, по которым плоскости касаются цилиндра, и
полуокружности нижнего и верхнего оснований определяют контур собственной
тени
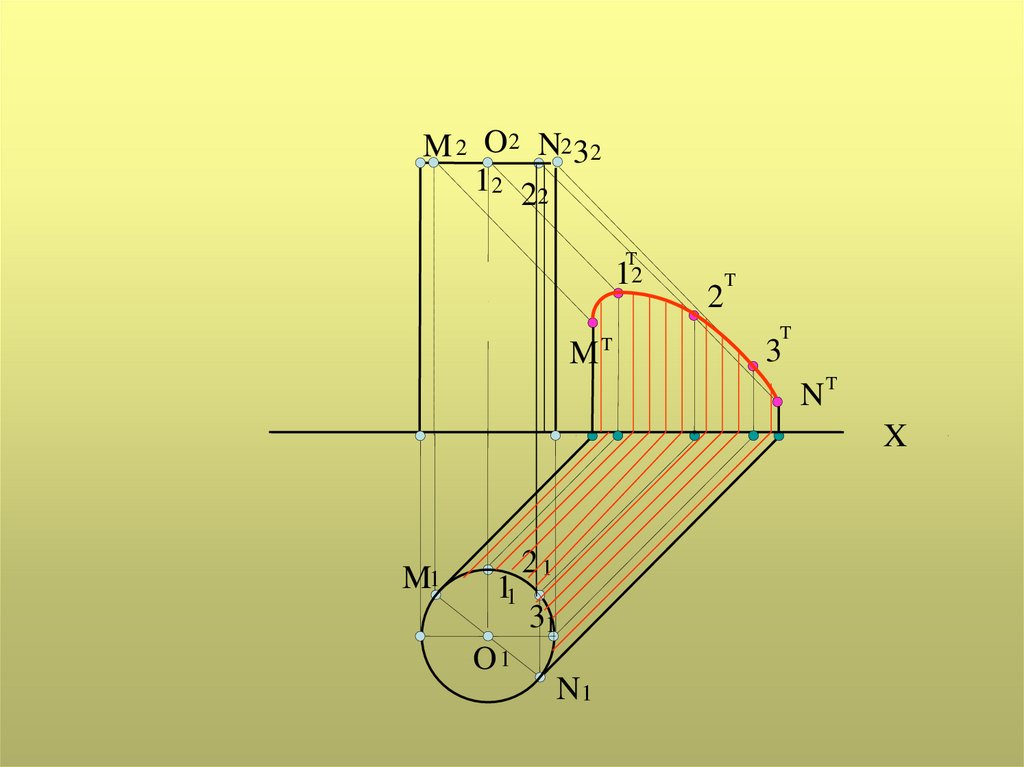
Падающая тень от цилиндра ограничена тенью от контура собственной
тени:
- тень от первой образующей;
- тень от второй образующей;
- полуокружность, совпадающая с основанием цилиндра;
- полуокружность, центром которой является тень от центра верхнего основания
цилиндра
Если цилиндр расположен в пространстве так, что тень от него
одновременно падает на обе плоскости проекций, то тень от полуокружности на
плоскость проекций строится по произвольно выбранным на этой
полуокружности точкам

34.

(M2) O 2 N2
X
T
M
T
O
T
N
M1
O1
N1

35.

M 2 O2 N2 32
12 22
T
12
M
T
2
T
T
3
NT
X
M1
11
21
31
O1
N1

36.

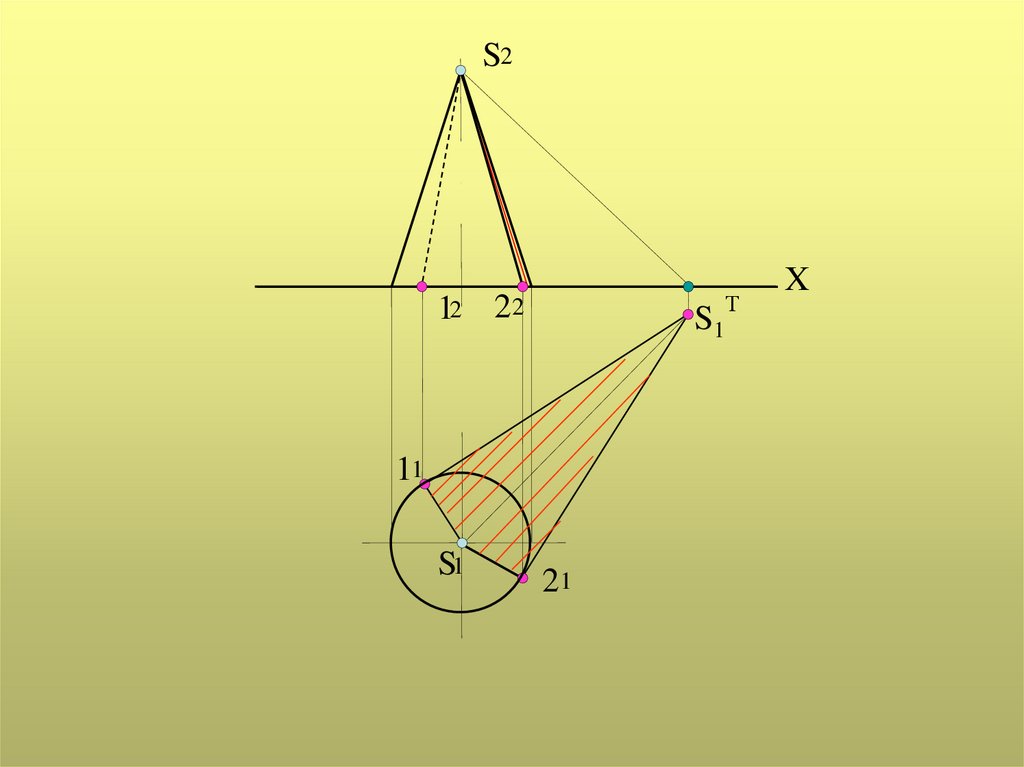
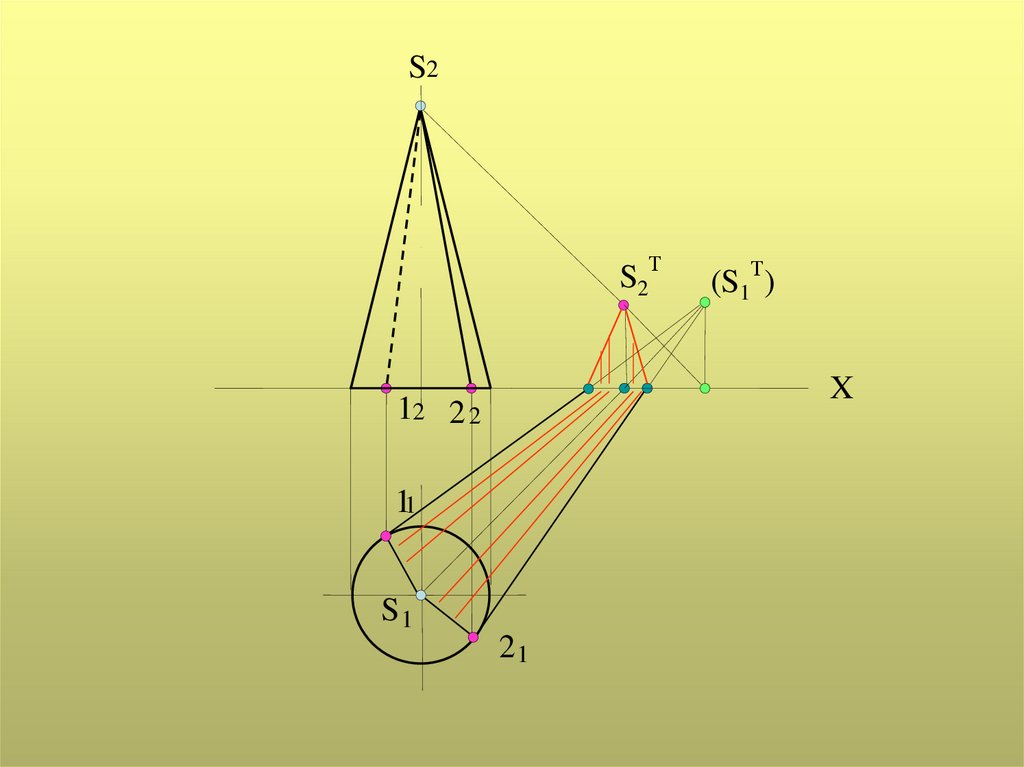
Тень от прямого кругового конуса
Алгоритм решения:
определяется тень на плоскость от вершины конуса – ST;
из точки ST проводятся две прямые, касательные к окружности основания конуса;
точки касания этих прямых определяют положение образующих конуса, которые
являются контуром собственной тени конуса;
дуга окружности основания конуса (меньшая) и тени от образующих определяют
контур падающей тени заданного конуса.
Величина части поверхности конуса, находящейся в собственной тени,
зависит от угла наклона его образующих к плоскости проекций:
- если образующие конуса составляют с плоскостью проекций угол меньше 450, то
тень от вершины конуса оказывается внутри окружности основания конуса,
следовательно вся его поверхность находится в свету;
- если образующие конуса составляют с плоскостью проекций угол 450, тень от
вершины конуса падает на окружность его основания, следовательно на его
поверхности имеется только одна теневая образующая
Если тень от конуса падает на обе плоскости проекций, то сначала
необходимо найти мнимую тень

37.

S2
12 22
S1
11
S1
21
Т
X

38.

S2
S2Т
(S1Т)
X
12 2 2
11
S1
21