Тени точки, прямой, плоскости. Лекция №1

1.

Международная образовательная корпорация
Казахская головная архитектурно-строительная академия
Шапрова Гульнара Габидуловна
к.п.н., ассоц.профессор факультета Архитектуры
[email protected]
Gulnara Tutor (YouTube)
КУРС ЛЕКЦИЙ ПО ИНЖЕНЕРНОЙ ГРАФИКЕ П/П

2.

Лекция №1
Общие сведения построения теней на комплексном чертеже.
Задание источника света. Тень точки, линии и плоской фигуры
При оформлении чертежей фасадов зданий или других архитектурных
сооружений возникает необходимость придать изображаемому предмету объемность,
рельефность форм, т.е. придать чертежу наглядность и выразительность. Это
достигается благодаря наличию светотени, полученной в результате освещения здания или
сооружения солнечными лучами.

3.

Принимается ряд условных положений, а именно:
- освещенные тела сами не являются источниками
света;
- пределом распространения светового луча является
первая, встретившаяся на его пути материальная точка;
- воздействие воздушной среды не учитывается.
При этих условиях все задачи на построение теней
решаются с помощью способов начертательной геометрии.
На архитектурно-строительных чертежах могут быть
построены тени изображаемого объекта как при искусственном
(лампа, свеча и т.п.), так и при естественном (солнце) его
освещении.

4.

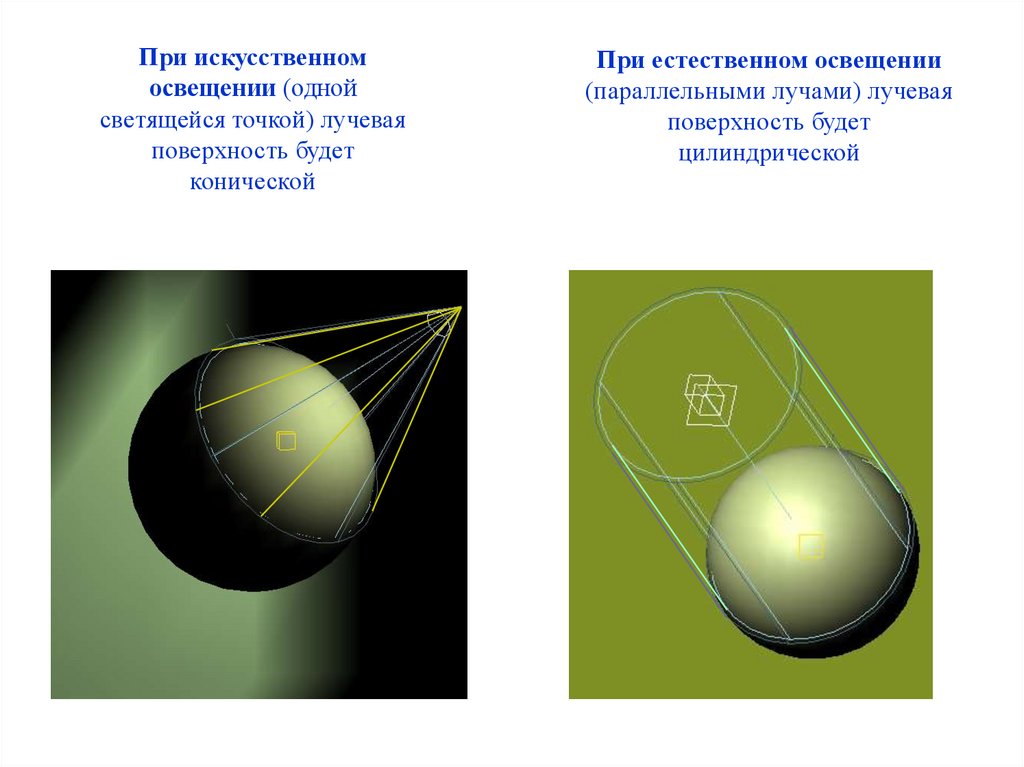
При искусственном
освещении (одной
светящейся точкой) лучевая
поверхность будет
конической
При естественном освещении
(параллельными лучами) лучевая
поверхность будет
цилиндрической

5.

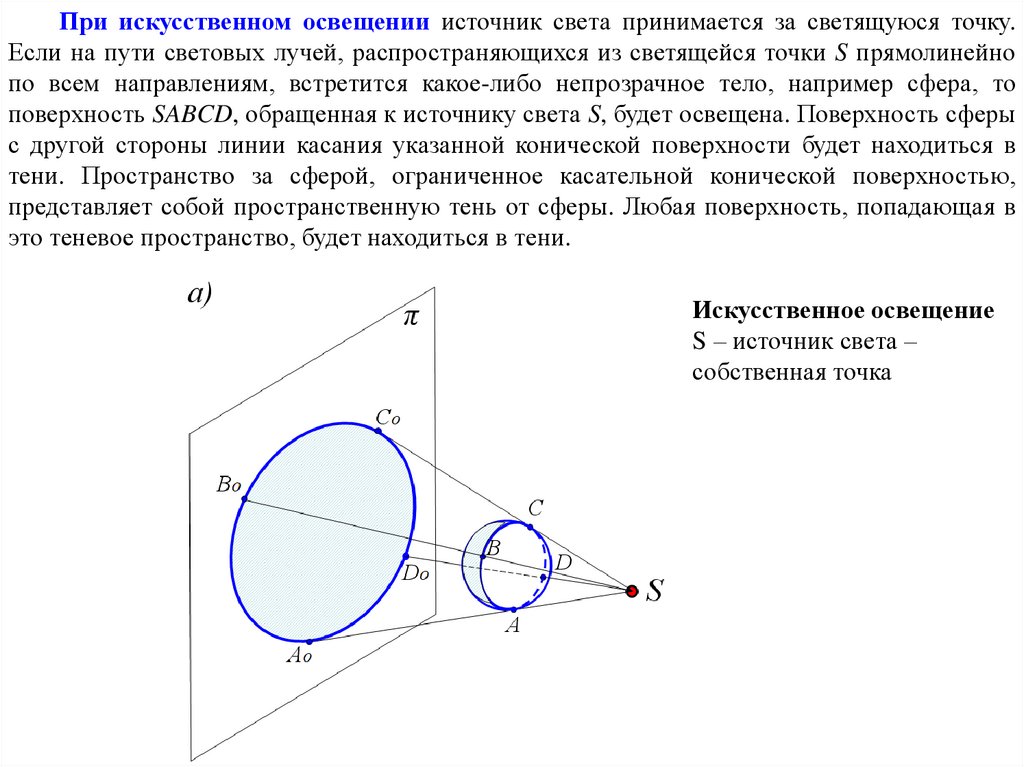
При искусственном освещении источник света принимается за светящуюся точку.
Если на пути световых лучей, распространяющихся из светящейся точки S прямолинейно
по всем направлениям, встретится какое-либо непрозрачное тело, например сфера, то
поверхность SABCD, обращенная к источнику света S, будет освещена. Поверхность сферы
с другой стороны линии касания указанной конической поверхности будет находиться в
тени. Пространство за сферой, ограниченное касательной конической поверхностью,
представляет собой пространственную тень от сферы. Любая поверхность, попадающая в
это теневое пространство, будет находиться в тени.
Искусственное освещение
S – источник света –
собственная точка

6.

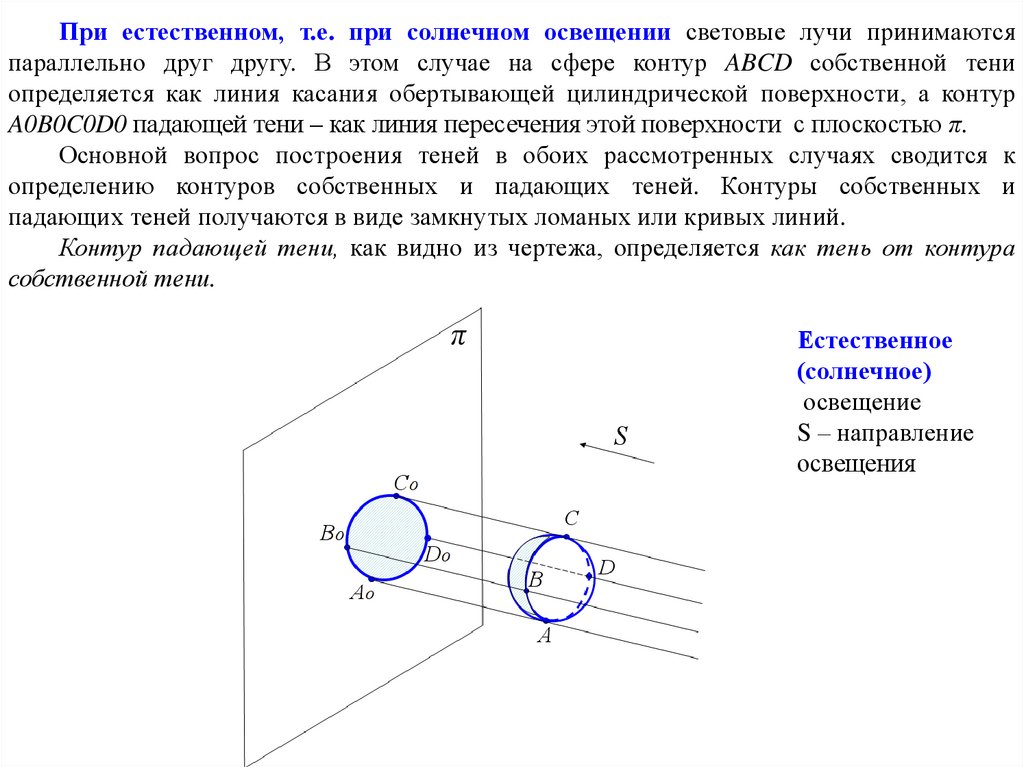
При естественном, т.е. при солнечном освещении световые лучи принимаются
параллельно друг другу. В этом случае на сфере контур ABCD собственной тени
определяется как линия касания обертывающей цилиндрической поверхности, а контур
A0B0C0D0 падающей тени – как линия пересечения этой поверхности с плоскостью π.
Основной вопрос построения теней в обоих рассмотренных случаях сводится к
определению контуров собственных и падающих теней. Контуры собственных и
падающих теней получаются в виде замкнутых ломаных или кривых линий.
Контур падающей тени, как видно из чертежа, определяется как тень от контура
собственной тени.
Естественное
(солнечное)
освещение
S – направление
освещения

7.

Собственные ии падающие
падающие тени
тени
Собственные
Неосвещенная часть поверхности называется
собственной тенью
Тень, полученная от одного предмета на другой
или от одной части поверхности на другую ее
часть , называется падающей тенью
А линия, ее ограничивающая, – границей или
контуром падающей тени
Граница падающей тени является тенью от
границы собственной тени

8.

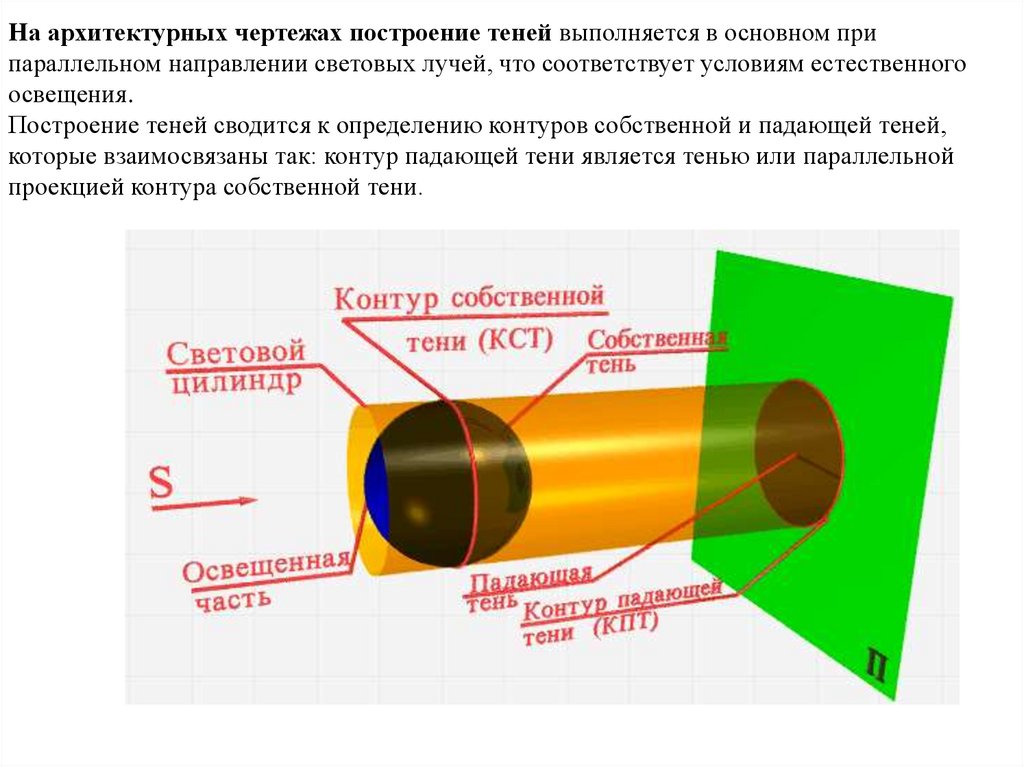
На архитектурных чертежах построение теней выполняется в основном при
параллельном направлении световых лучей, что соответствует условиям естественного
освещения.
Построение теней сводится к определению контуров собственной и падающей теней,
которые взаимосвязаны так: контур падающей тени является тенью или параллельной
проекцией контура собственной тени.

9.

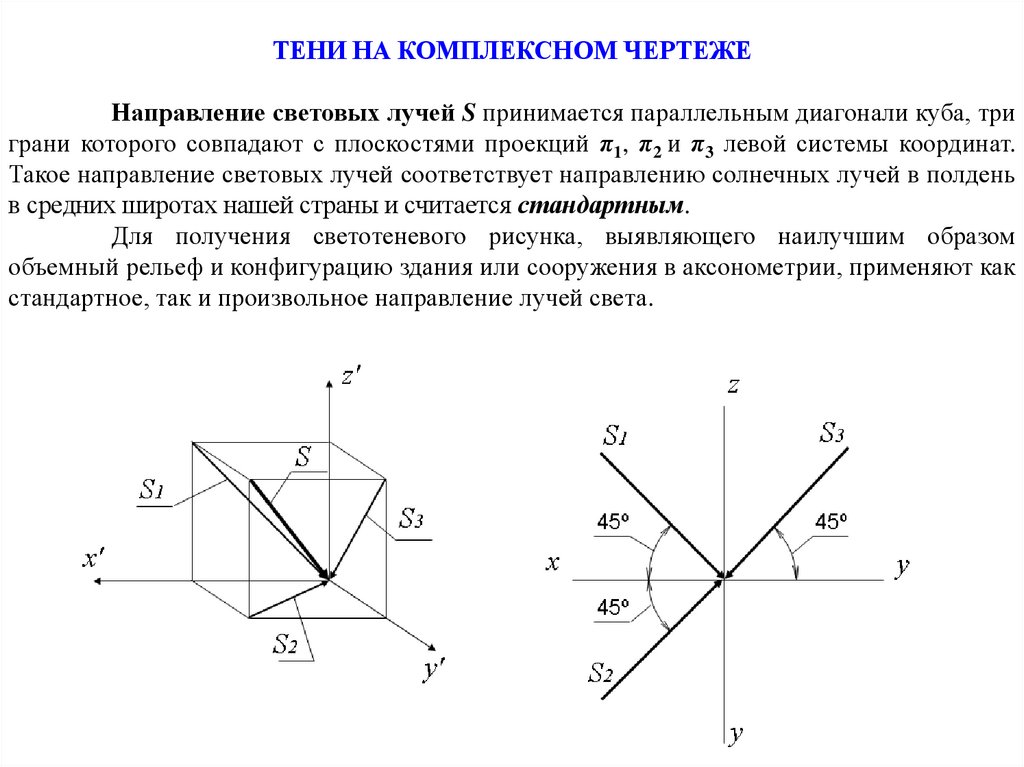
ТЕНИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Направление световых лучей S принимается параллельным диагонали куба, три
грани которого совпадают с плоскостями проекций π1, π2 и π3 левой системы координат.
Такое направление световых лучей соответствует направлению солнечных лучей в полдень
в средних широтах нашей страны и считается стандартным.
Для получения светотеневого рисунка, выявляющего наилучшим образом
объемный рельеф и конфигурацию здания или сооружения в аксонометрии, применяют как
стандартное, так и произвольное направление лучей света.

10.

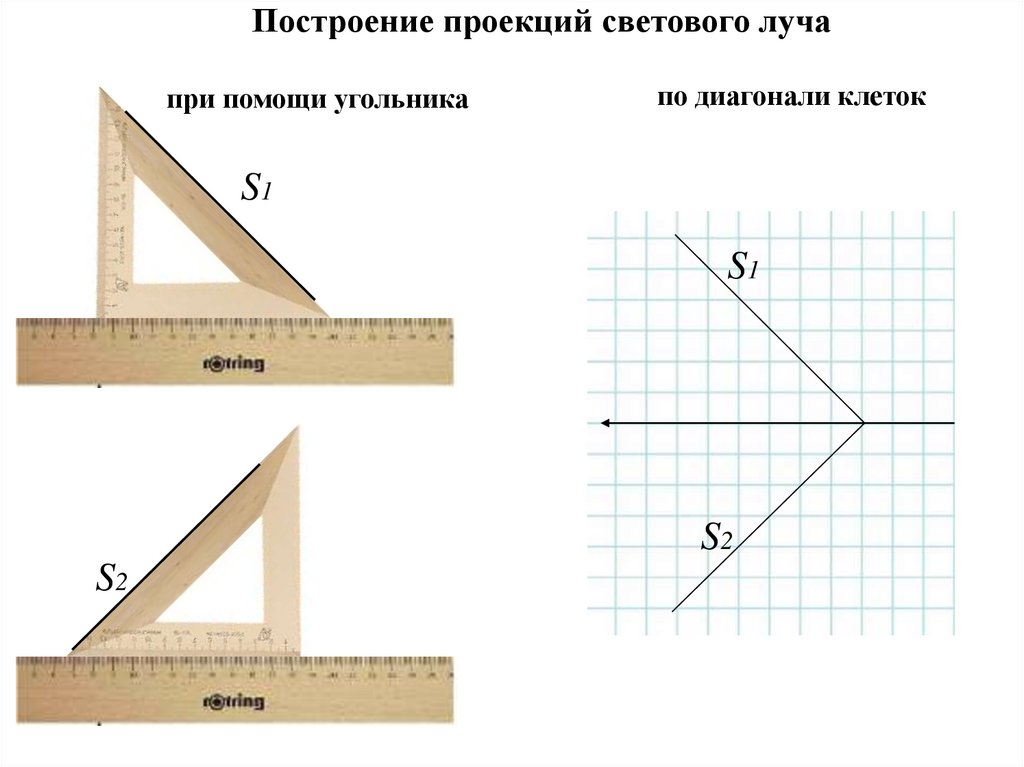
Построение проекций светового луча
при помощи угольника
по диагонали клеток
S1
S1
S2
S2

11.

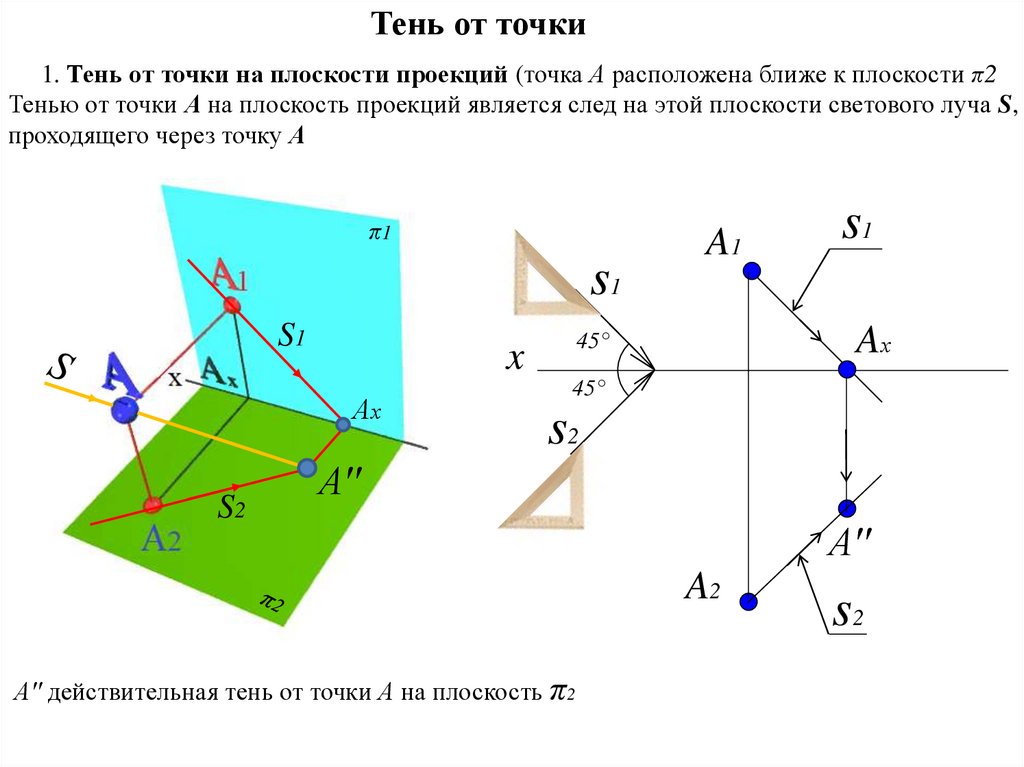
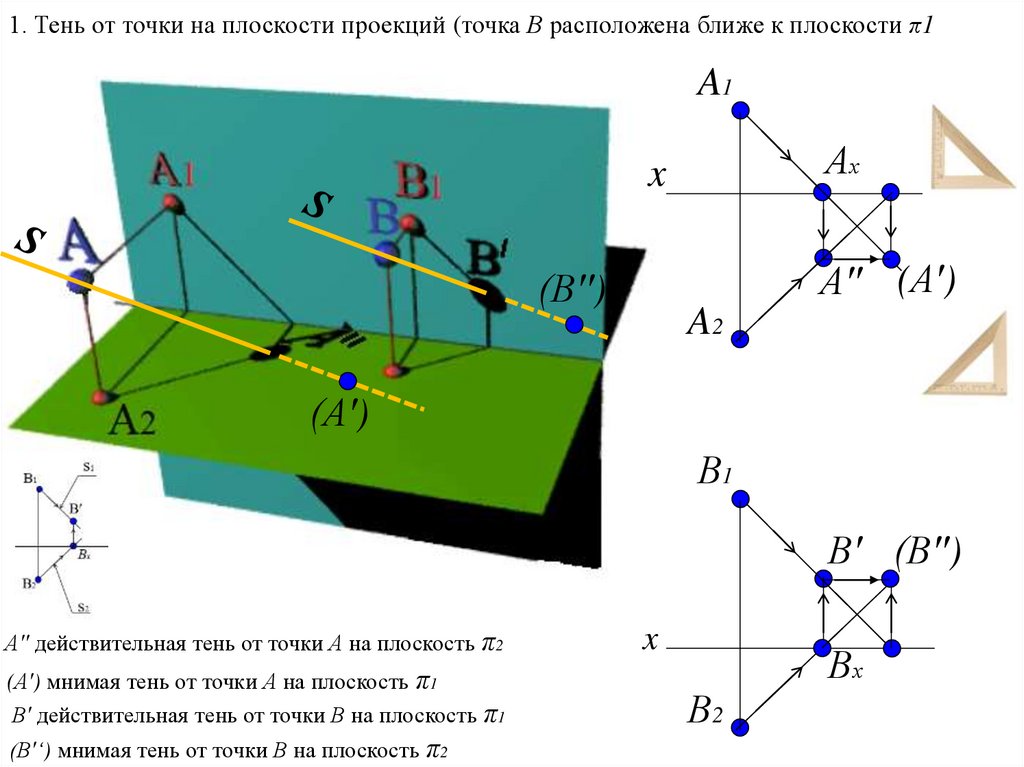
Тень от точки
1. Тень от точки на плоскости проекций (точка А расположена ближе к плоскости π2
Тенью от точки А на плоскость проекций является след на этой плоскости светового луча S,
проходящего через точку А
π1
s1
S1
S2
s1
Aх
45°
x
Ах
A1
45°
s2
А''
A′′
A2
A′′ действительная тень от точки А на плоскость π2
s2

12.

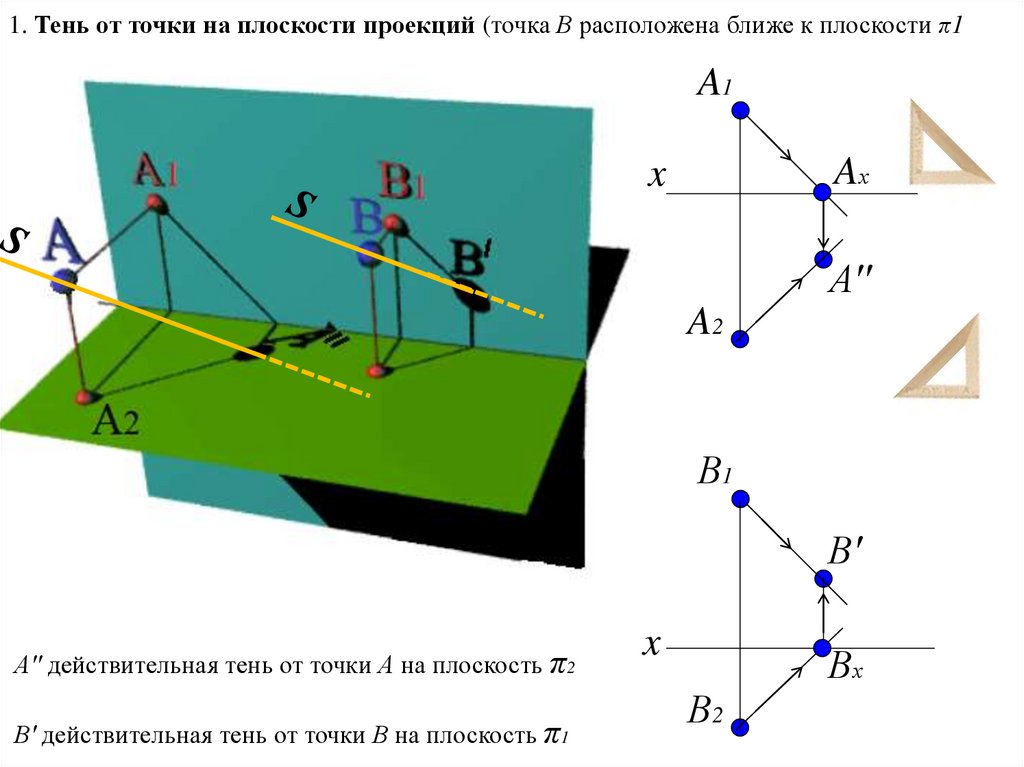
1. Тень от точки на плоскости проекций (точка В расположена ближе к плоскости π1
A1
Aх
x
A′′
A2
В1
В′
A′′ действительная тень от точки А на плоскость π2
В′ действительная тень от точки В на плоскость π1
x
Вх
В2

13.

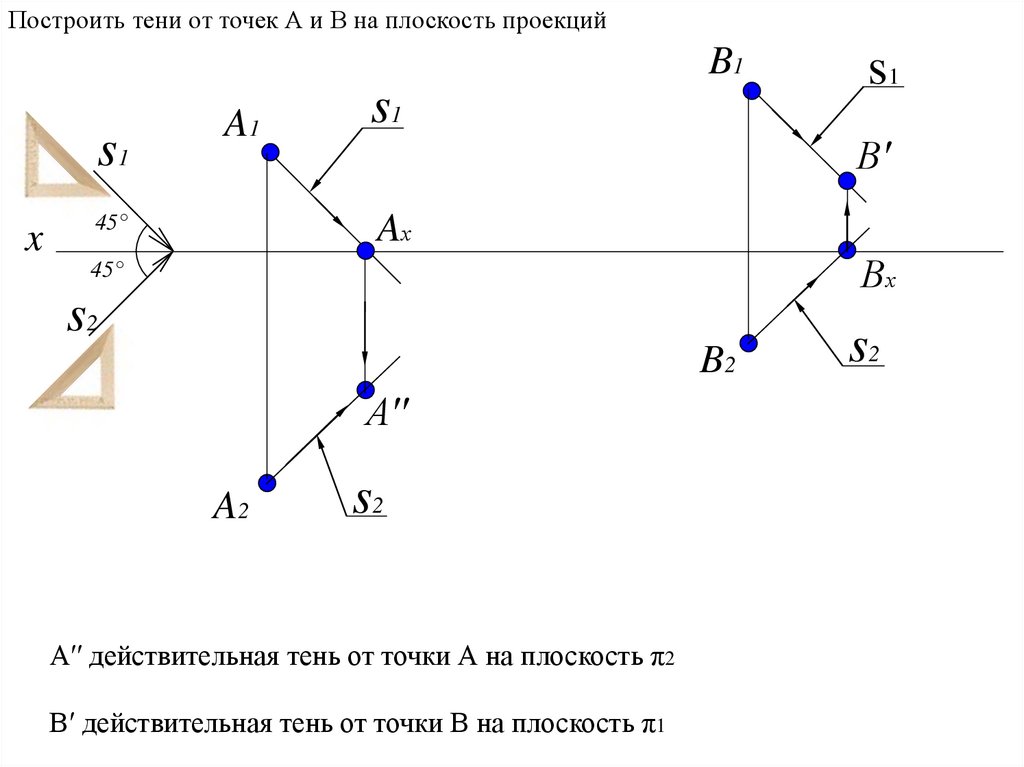
Построить тени от точек А и В на плоскость проекций
B1
s1
x
A1
s1
s1
B′
Aх
45°
Вх
45°
s2
B2
A′′
A2
s2
A′′ действительная тень от точки А на плоскость π2
B′ действительная тень от точки В на плоскость π1
s2

14.

1. Тень от точки на плоскости проекций (точка В расположена ближе к плоскости π1
A1
Ах
x
A′′ (A′)
(В′′)
A2
(А′)
В1
В′ (В′')
A′′ действительная тень от точки А на плоскость π2
(A′) мнимая тень от точки А на плоскость π1
В′ действительная тень от точки В на плоскость π1
(В′‘) мнимая тень от точки В на плоскость π2
x
Вх
В2

15.

Построить действительные и мнимые тени от точек А и В на плоскости проекций
B1
s1
x
A1
B′
Aх
45°
Вх
45°
s2
B2
A′′
(A′)
A2
A′′ действительная тень от точки А на плоскость π2
(A′) мнимая тень от точки А на плоскость π1
B′ действительная тень от точки В на плоскость π1
(B′′) мнимая тень от точки В на плоскость π2
(B′′)

16.

Построить тени точек А и С на плоскости проекций
А1 ≡А′
x
С1
45°
45°
(А′′)
А2
С2 ≡С′′
(С′)
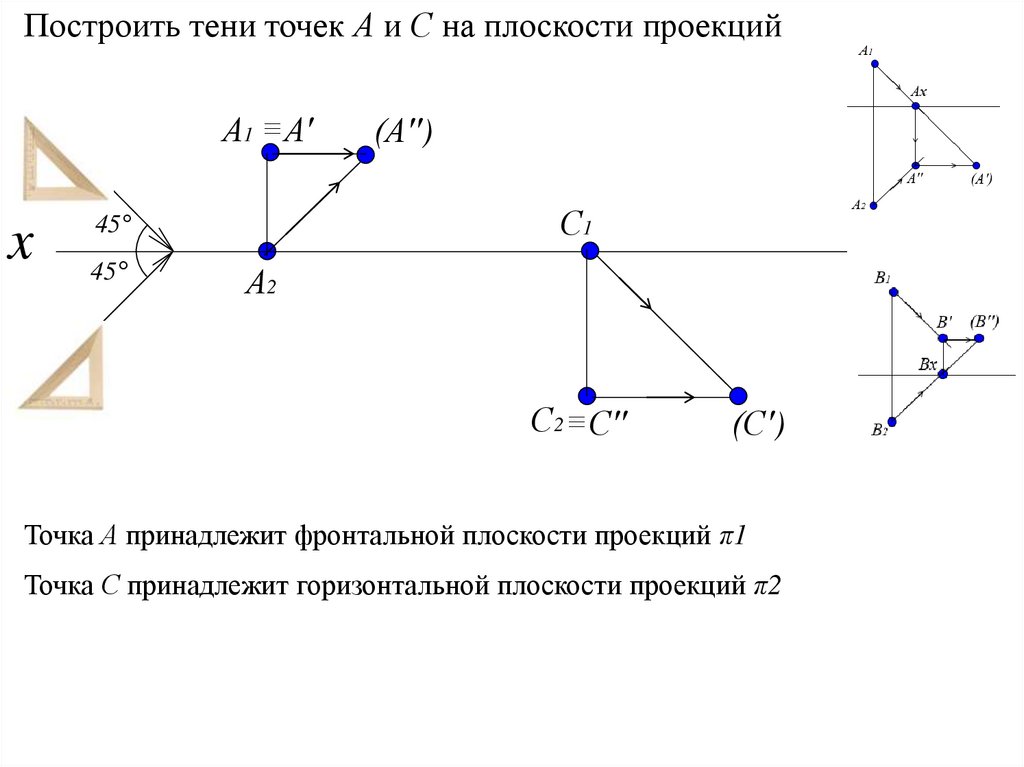
Точка А принадлежит фронтальной плоскости проекций π1
Точка С принадлежит горизонтальной плоскости проекций π2

17.

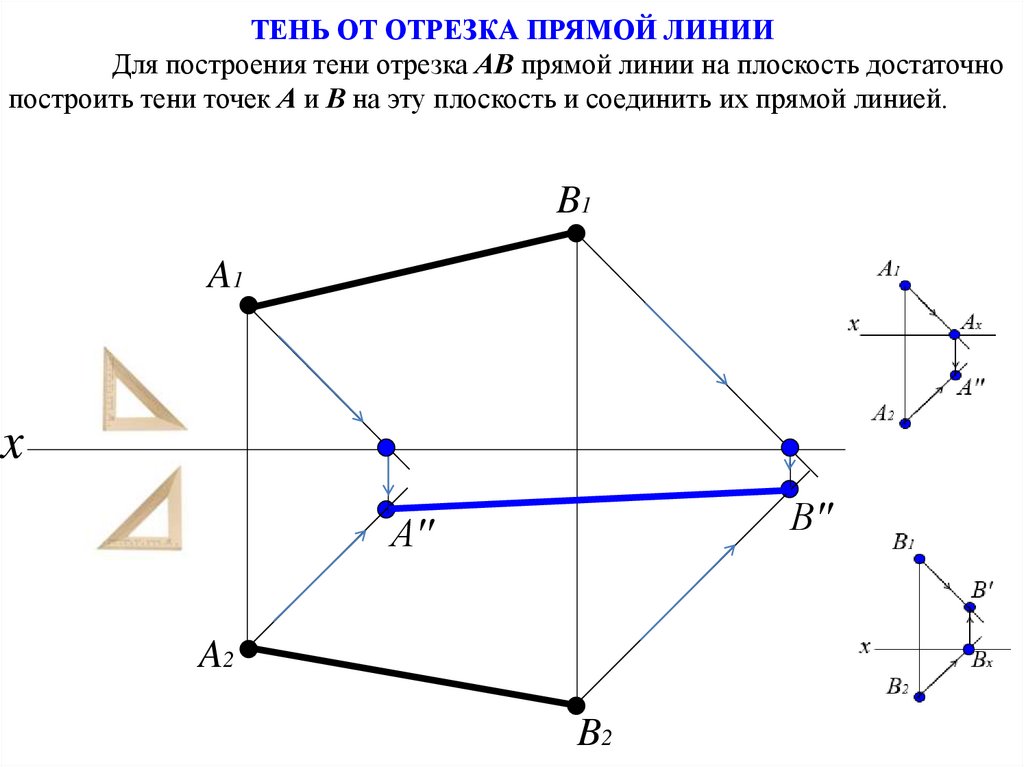
ТЕНЬ ОТ ОТРЕЗКА ПРЯМОЙ ЛИНИИ
Для построения тени отрезка АВ прямой линии на плоскость достаточно
построить тени точек А и В на эту плоскость и соединить их прямой линией.
B1
A1
x
B′′
A′′
A2
B2

18.

Построить тень отрезка прямой АВ на плоскость проекций
B1
A1
B′
A′
x
A2
B2

19.

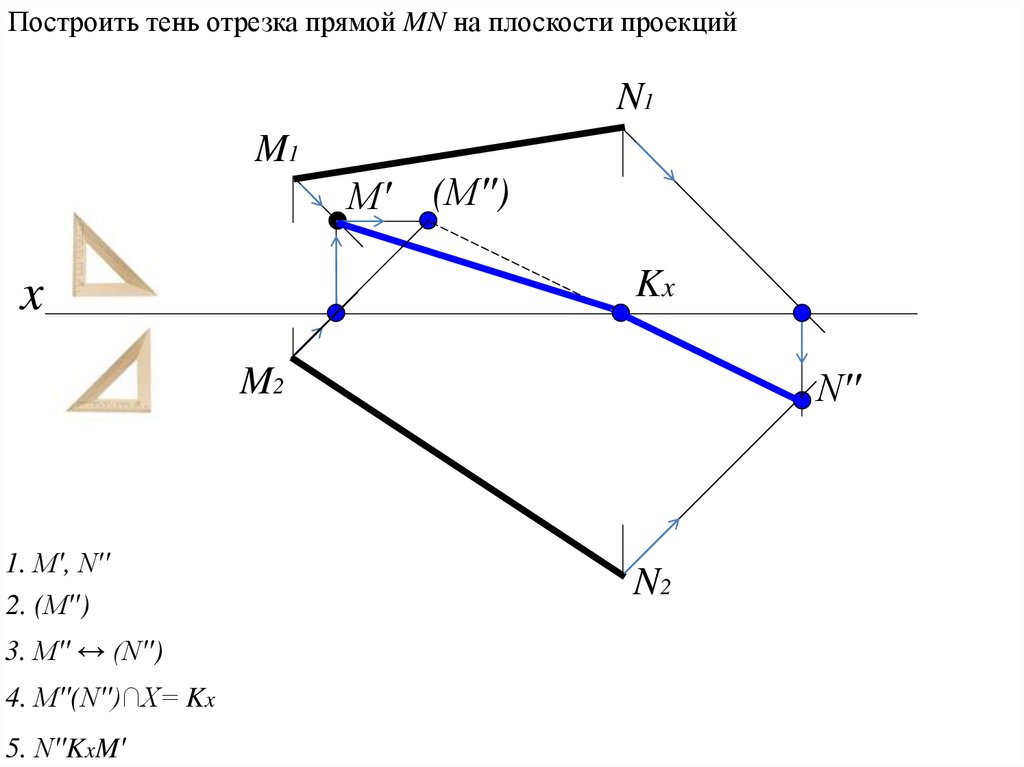
Построить тень отрезка прямой MN на плоскости проекций
N1
M1
M′
(M′′)
Kx
x
N′′
M2
1. M′, N′′
2. (M′′)
3. M′′ ↔ (N′′)
4. M′′(N′′)∩Х= Kx
5. N′′KxM′
N2

20.

Построить тень отрезка прямой АВ на плоскости проекций
A1
А′
B1
x
Kx
A2
(B′)
1.
2.
3.
4.
5.
A′, B′′
(B′)
A′↔(B′)
А′(В′)∩Х=Kx
A′KxB′′
B′′
B2

21.

Тени от геометрических объектов,
занимающих частное положение
ТЕНЬ ОТ ОТРЕЗКА ВЕРТИКАЛЬНОЙ ПРЯМОЙ

22.

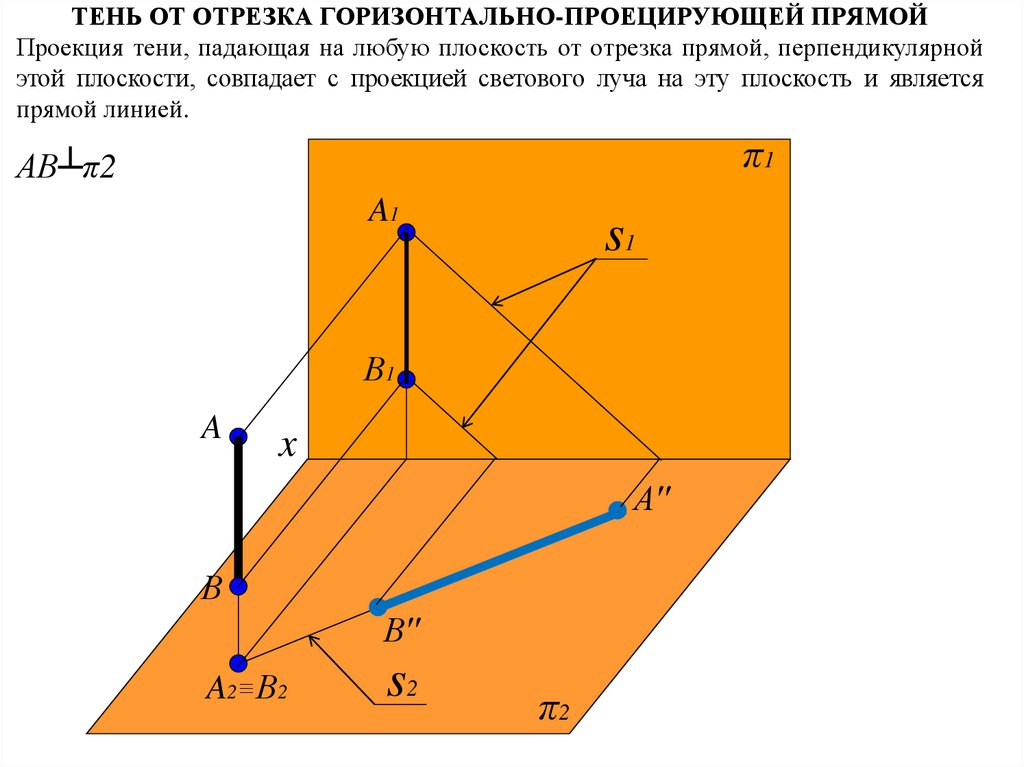
ТЕНЬ ОТ ОТРЕЗКА ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Проекция тени, падающая на любую плоскость от отрезка прямой, перпендикулярной
этой плоскости, совпадает с проекцией светового луча на эту плоскость и является
прямой линией.
π1
AB┴π2
A1
s1
В1
A
x
А''
В
В''
A2≡В2
s2
π2

23.

ТЕНЬ ОТ ОТРЕЗКА ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Проекция тени, падающая на любую плоскость от отрезка прямой, перпендикулярной
этой плоскости, совпадает с проекцией светового луча на эту плоскость и является
прямой линией.
CD┴π1
C1≡D1
D
π1
s1
D'
С
С'
x
D2
С2
s2
π2

24.

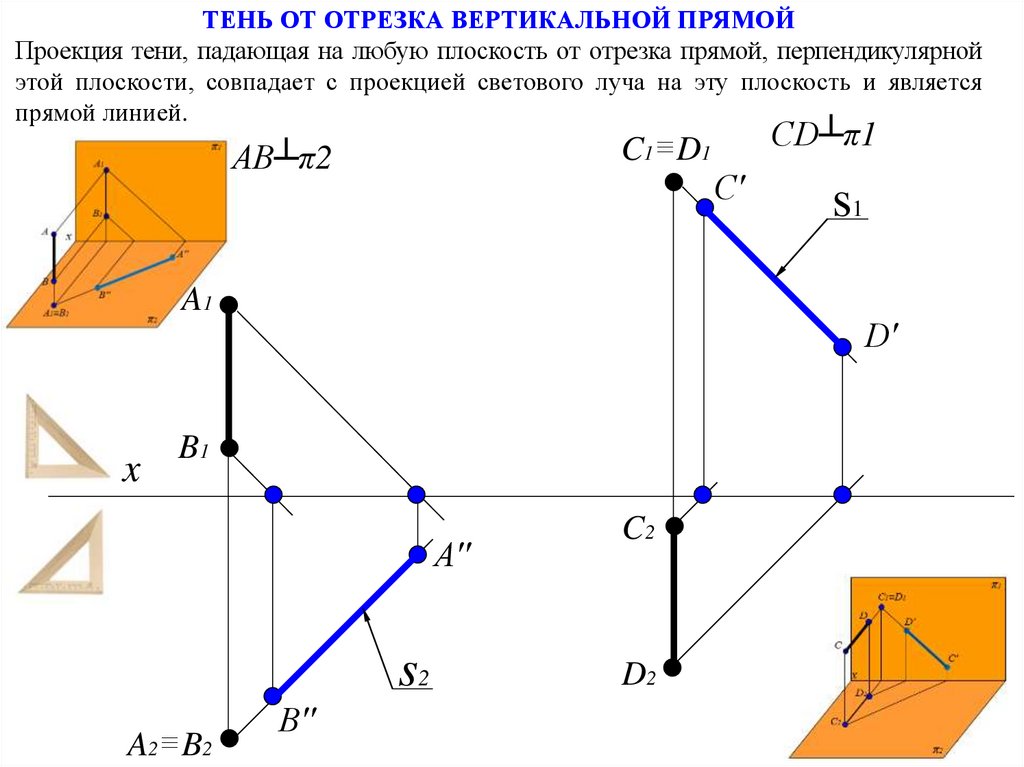
ТЕНЬ ОТ ОТРЕЗКА ВЕРТИКАЛЬНОЙ ПРЯМОЙ
Проекция тени, падающая на любую плоскость от отрезка прямой, перпендикулярной
этой плоскости, совпадает с проекцией светового луча на эту плоскость и является
прямой линией.
AB┴π2
C′
A1
x
s1
D′
B1
A′′
s2
A2≡B2
CD┴π1
C1≡D1
B′′
C2
D2

25.

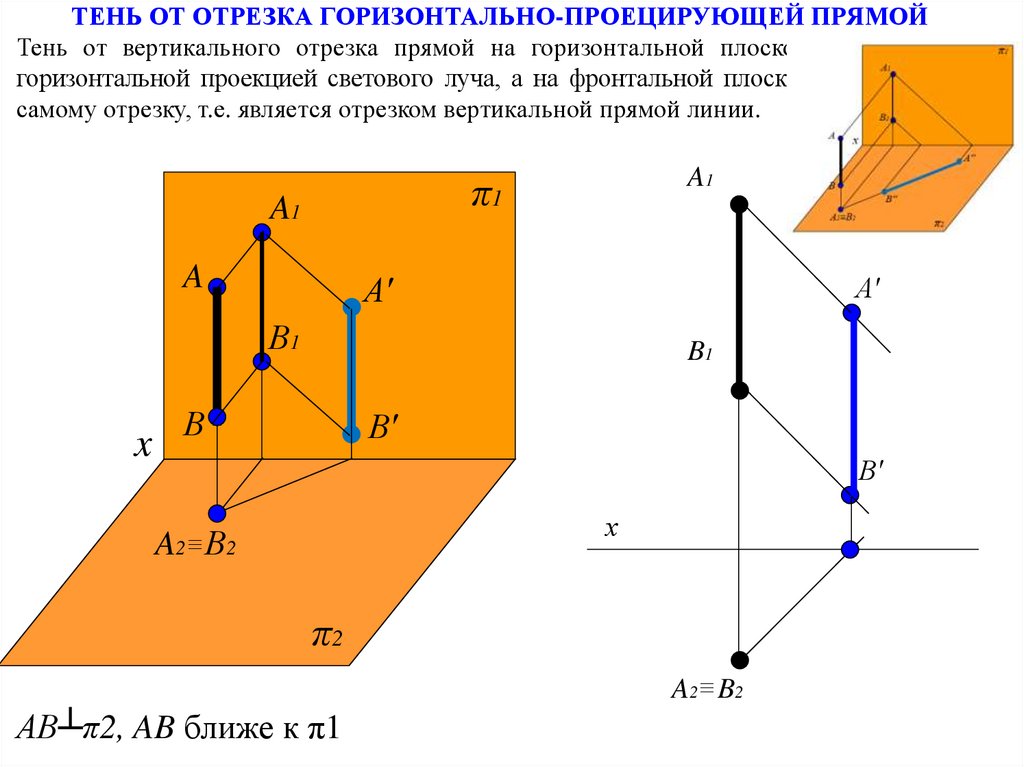
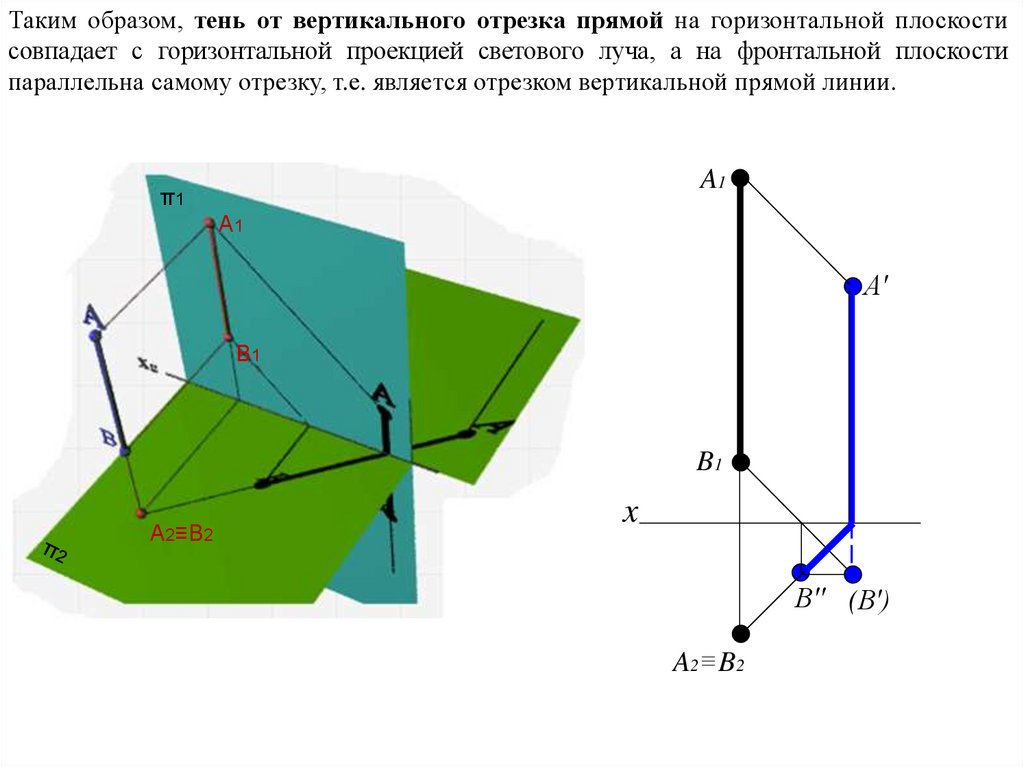
ТЕНЬ ОТ ОТРЕЗКА ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Тень от вертикального отрезка прямой на горизонтальной плоскости совпадает с
горизонтальной проекцией светового луча, а на фронтальной плоскости параллельна
самому отрезку, т.е. является отрезком вертикальной прямой линии.
A1
π1
A1
A
А'
A′
В1
x
B1
В
В'
B′
х
A2≡В2
π2
A2≡B2
AB┴π2, AB ближе к π1

26.

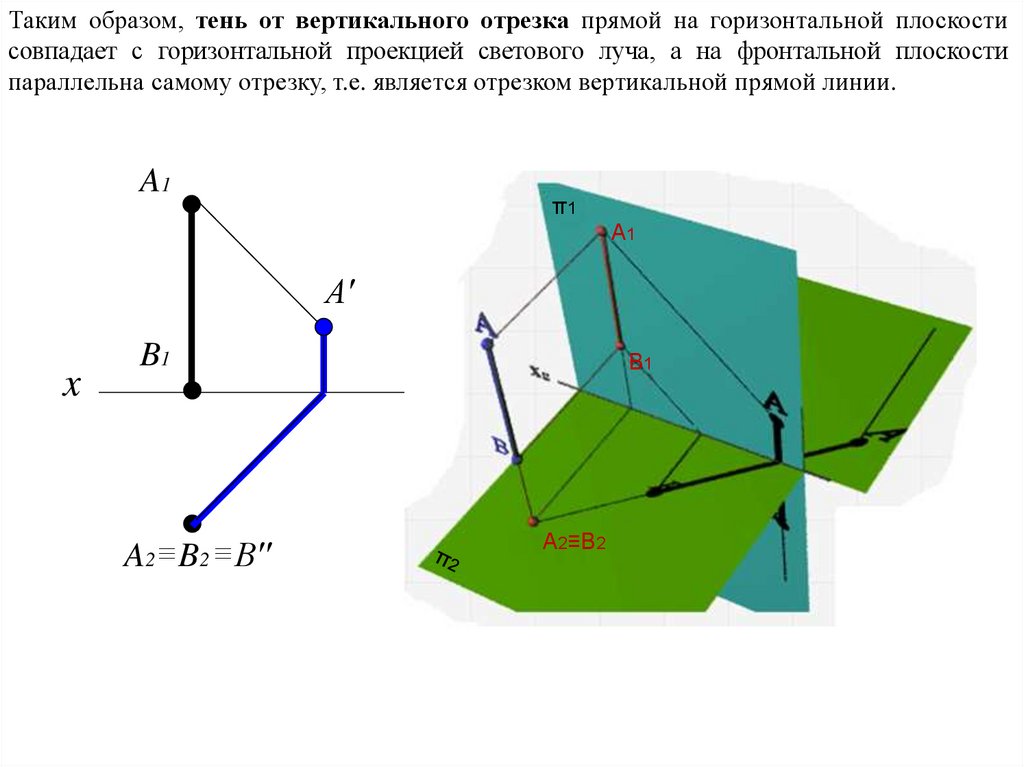
Таким образом, тень от вертикального отрезка прямой на горизонтальной плоскости
совпадает с горизонтальной проекцией светового луча, а на фронтальной плоскости
параллельна самому отрезку, т.е. является отрезком вертикальной прямой линии.
A1
π1
А1
A′
В1
B1
А2≡В2
x
B′′ (B′)
A2≡B2

27.

Таким образом, тень от вертикального отрезка прямой на горизонтальной плоскости
совпадает с горизонтальной проекцией светового луча, а на фронтальной плоскости
параллельна самому отрезку, т.е. является отрезком вертикальной прямой линии.
A1
π1
А1
A′
x
B1
A2≡B2 ≡B′′
В1
А2≡В2

28.

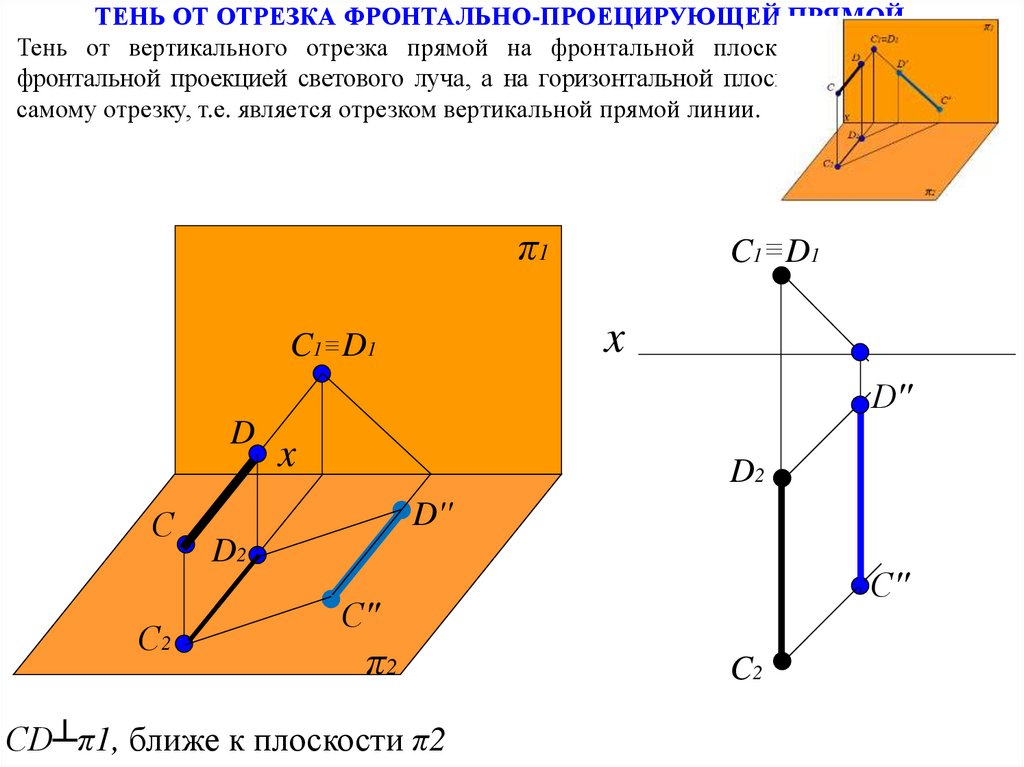
ТЕНЬ ОТ ОТРЕЗКА ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Тень от вертикального отрезка прямой на фронтальной плоскости совпадает с
фронтальной проекцией светового луча, а на горизонтальной плоскости параллельна
самому отрезку, т.е. является отрезком вертикальной прямой линии.
π1
C1≡D1
x
C1≡D1
D′′
D
С
С2
x
D2
D''
D2
C′′
С''
π2
CD┴π1, ближе к плоскости π2
C2

29.

ТЕНЬ ОТ ОТРЕЗКА, ПЕРПЕНДИКУЛЯРНОГО ФРОНТАЛЬНОЙ ПЛОСКОСТИ
ПРОЕКЦИЙ
Тень от отрезка прямой, перпендикулярной фронтальной плоскости проекций, на
фронтальной плоскости совпадает с фронтальной проекцией светового луча, а на
горизонтальной плоскости параллельна самому отрезку, т.е. перпендикулярна
фронтальной плоскости проекций.
E1≡F1
C1≡D1
C′
A1≡B1
E′
(C′′)
x
A′′
E2
C2
A2
F′′
D′′
B′′
B2
D2
F2

30.

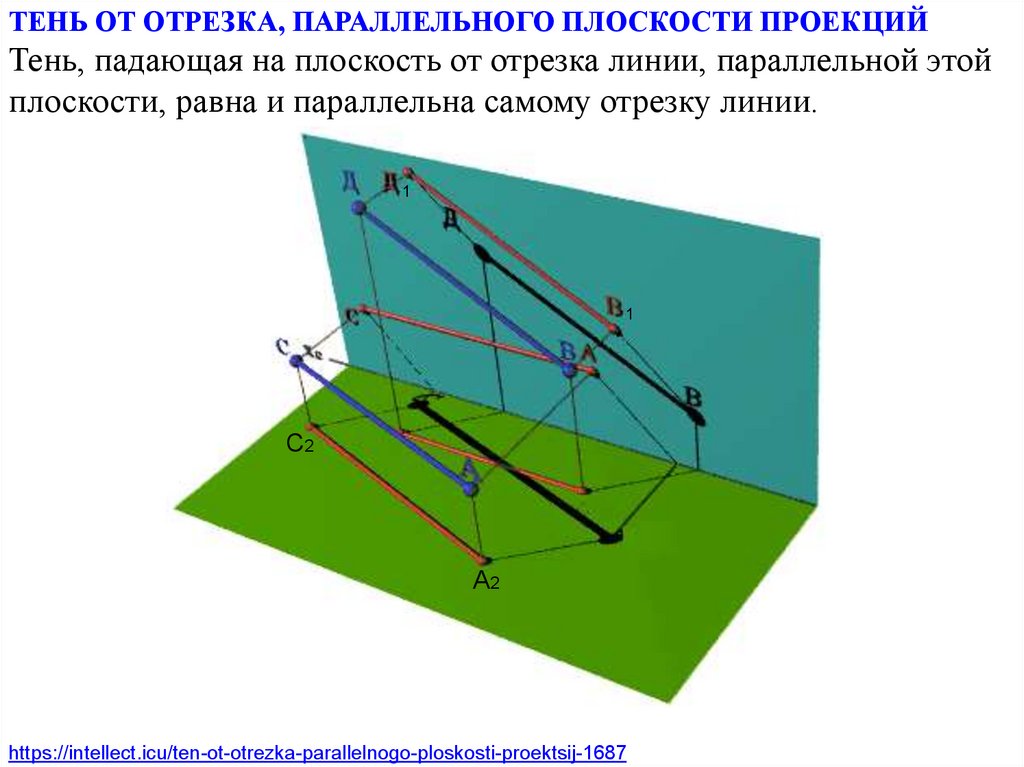
ТЕНЬ ОТ ОТРЕЗКА, ПАРАЛЛЕЛЬНОГО ПЛОСКОСТИ ПРОЕКЦИЙ
Тень, падающая на плоскость от отрезка линии, параллельной этой
плоскости, равна и параллельна самому отрезку линии.
1
1
С2
А2
https://intellect.icu/ten-ot-otrezka-parallelnogo-ploskosti-proektsij-1687

31.

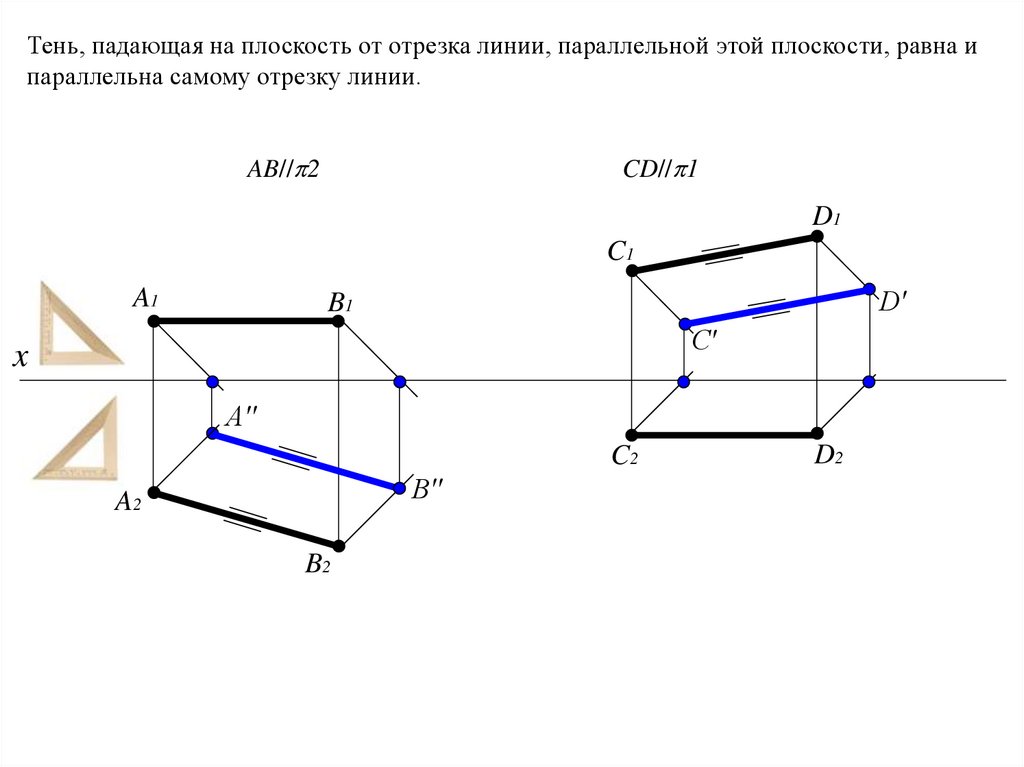
Тень, падающая на плоскость от отрезка линии, параллельной этой плоскости, равна и
параллельна самому отрезку линии.
AB// 2
CD// 1
D1
C1
A1
D′
B1
C′
x
A′′
C2
B′′
A2
B2
D2

32.

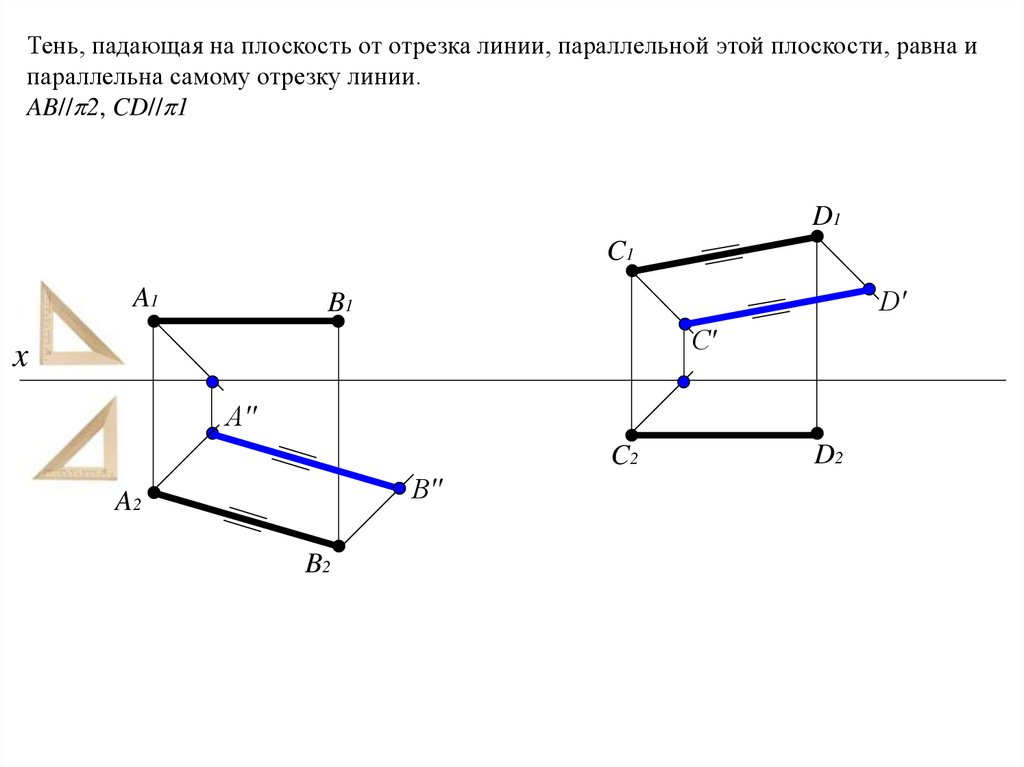
Тень, падающая на плоскость от отрезка линии, параллельной этой плоскости, равна и
параллельна самому отрезку линии.
AB// 2, CD// 1
D1
C1
A1
D′
B1
C′
x
A′′
C2
B′′
A2
B2
D2

33.

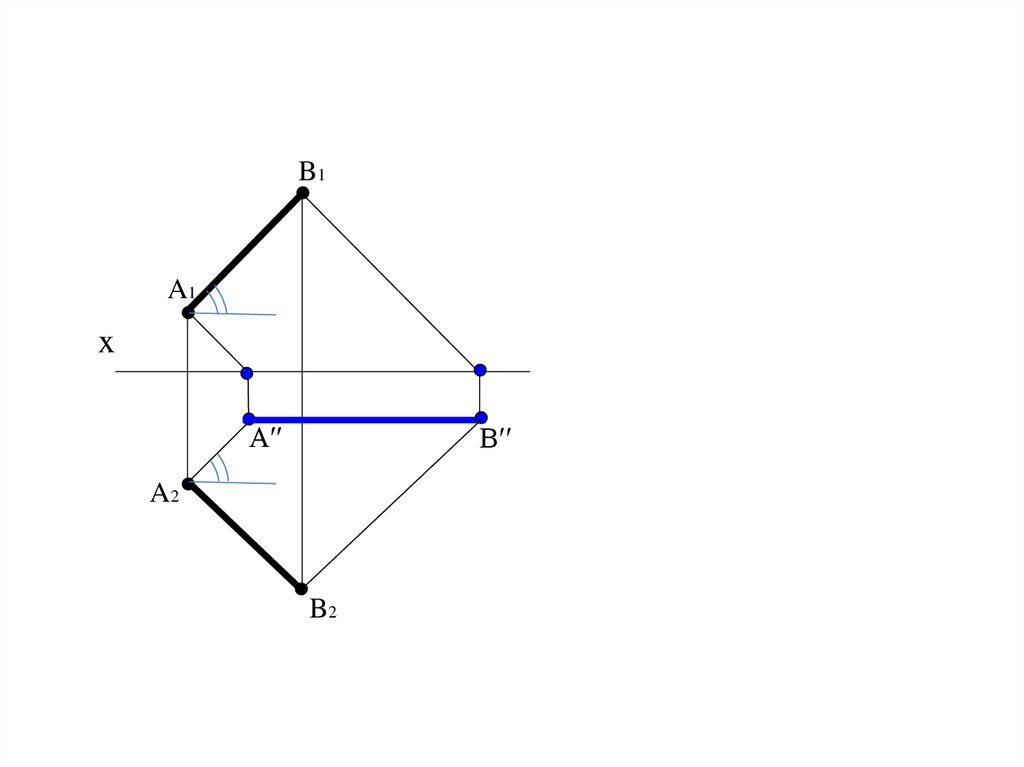
B1
A1
x
A′′
B′′
A2
B2

34.

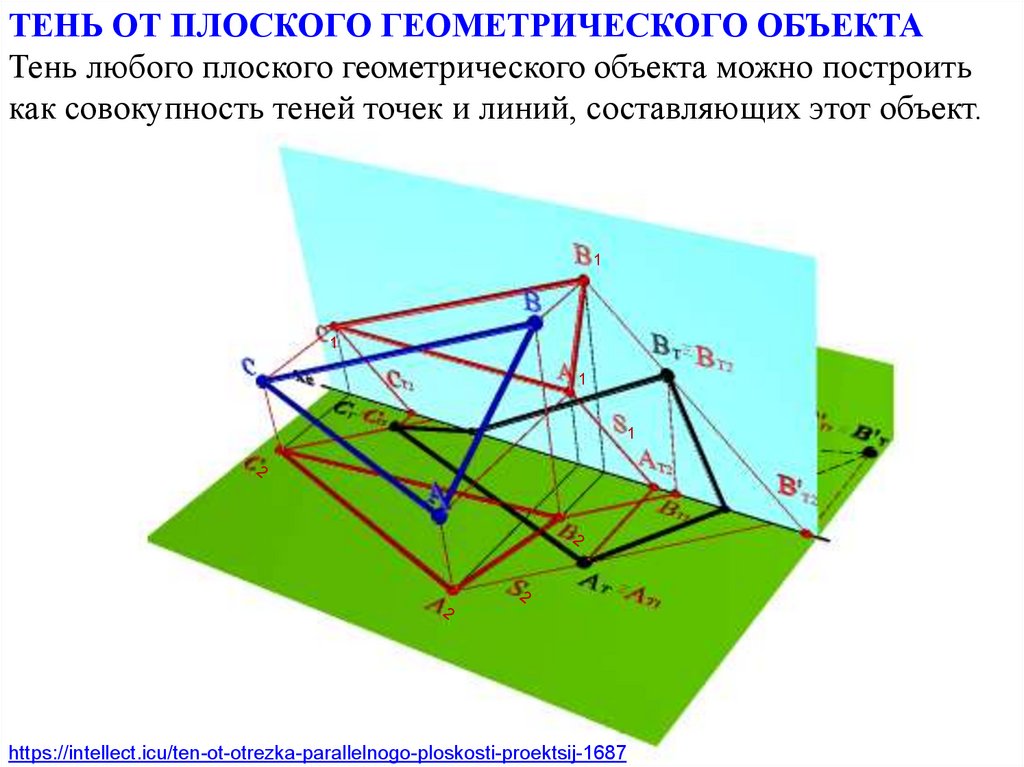
ТЕНЬ ОТ ПЛОСКОГО ГЕОМЕТРИЧЕСКОГО ОБЪЕКТА
Тень любого плоского геометрического объекта можно построить
как совокупность теней точек и линий, составляющих этот объект.
1
1
1
1
https://intellect.icu/ten-ot-otrezka-parallelnogo-ploskosti-proektsij-1687

35.

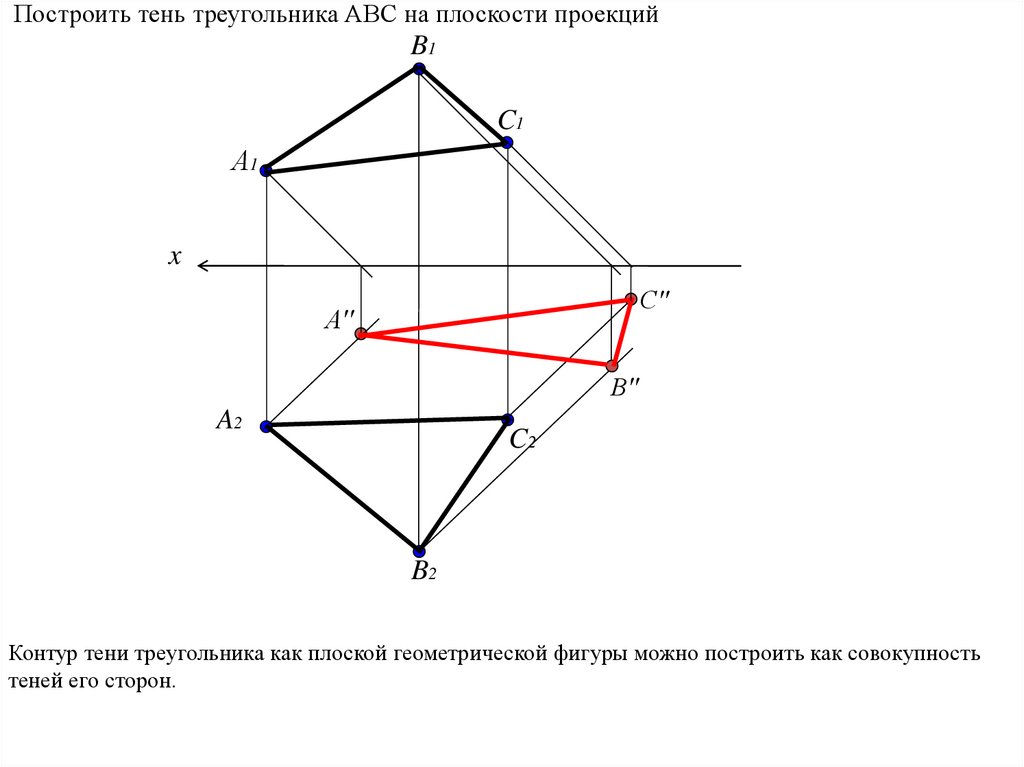
Построить тень треугольника АВС на плоскости проекций
B1
C1
А1
x
C′′
A′′
В′′
A2
C2
B2
Контур тени треугольника как плоской геометрической фигуры можно построить как совокупность
теней его сторон.

36.

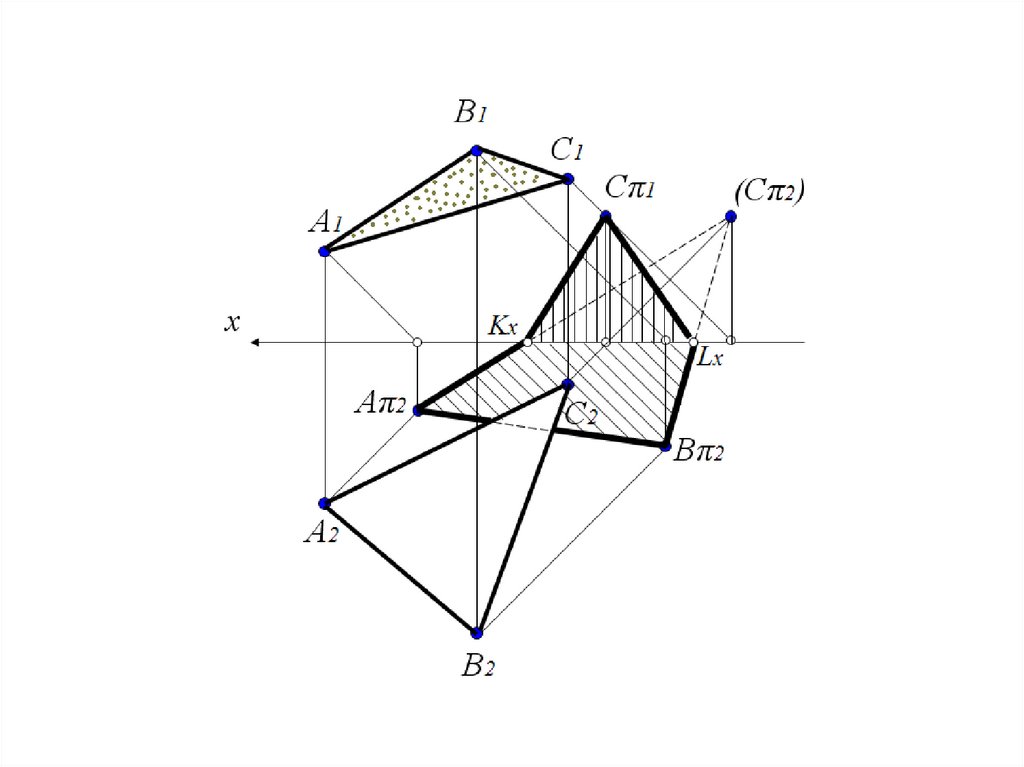
Построить тень треугольника АВС на плоскости проекций
B1
C1
C′
(C′′)
А1
Кх
x
A′′
Мх
C2
В′′
A2
B2
Контур тени треугольника как плоской геометрической фигуры можно построить как совокупность
теней его сторон.

37.

38.

ТЕНИ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ
ОБЪЕКТОВ ЧАСТНОГО ПОЛОЖЕНИЯ
При изображении архитектурных
фрагментов, строительных конструкций и
сооружений часто приходится строить
падающие тени от плоских геометрических
объектов, которые находятся в частном
положении относительно плоскостей
проекций.
В соответствии с основным свойством
параллельного проецирования падающая
тень плоского геометрического объекта,
параллельного плоскости проекций,
параллельна ортогональной проекции
объекта и конгруэнтна самому объекту.
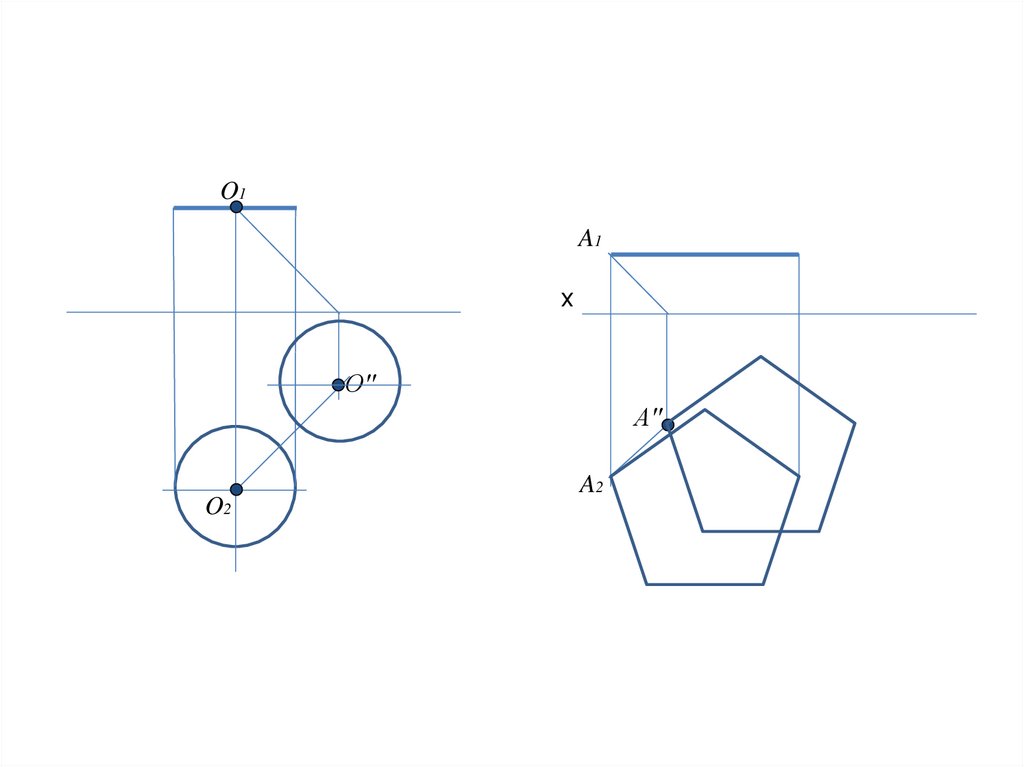
Для построения тени круга достаточно
найти тень его центра и провести
окружность радиуса данного круга.
Для построения тени многоугольника
достаточно найти тень одной вершины и
построить конгруэнтный многоугольник.
https://intellect.icu/ten-ot-otrezka-parallelnogo-ploskosti-proektsij-1687

39.

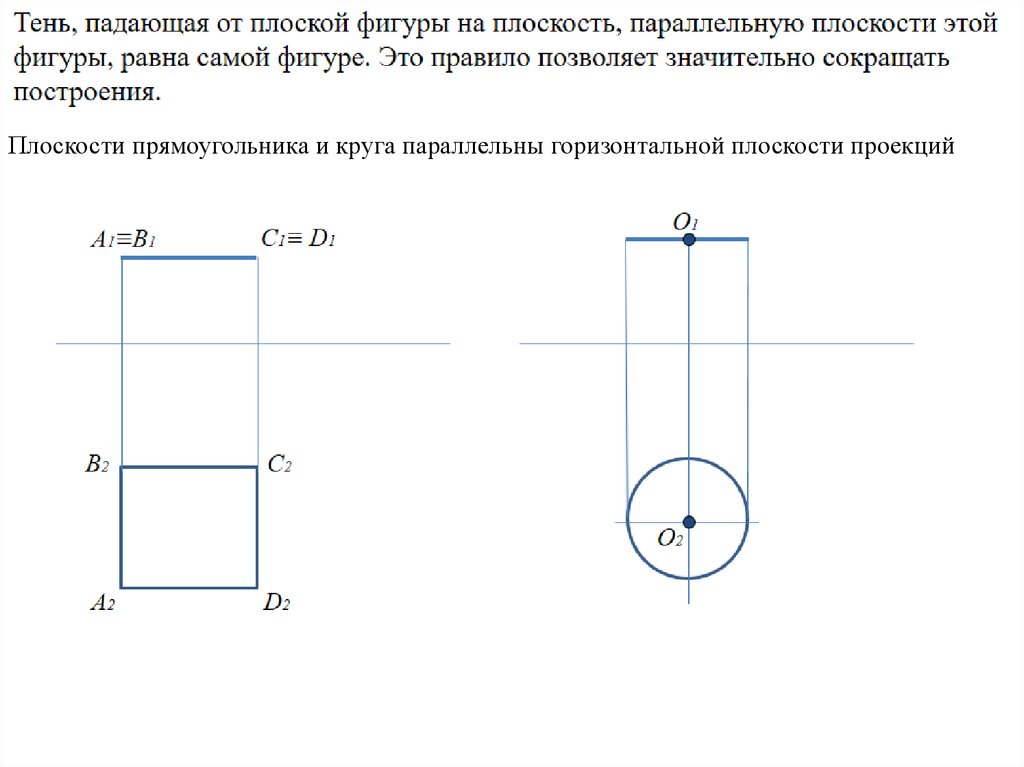
Плоскости прямоугольника и круга параллельны горизонтальной плоскости проекций

40.

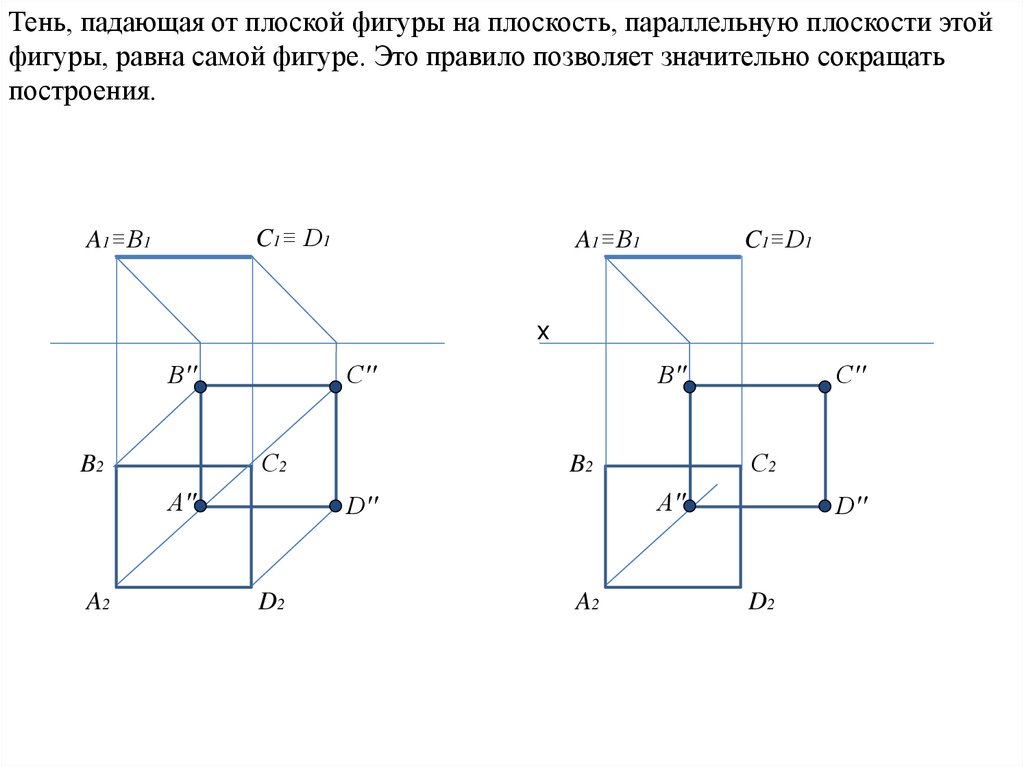
Тень, падающая от плоской фигуры на плоскость, параллельную плоскости этой
фигуры, равна самой фигуре. Это правило позволяет значительно сокращать
построения.
C1≡ D1
A1≡B1
A1≡B1
C1≡D1
х
В′′
C′′
С2
B2
A′′
A2
В′′
С2
B2
A′′
D′′
D2
C′′
A2
D′′
D2

41.

O1
A1
х
O′′
A′′
O2
A2