Электромагнитные колебания. Метод векторных диаграмм. Метод комплексных амплитуд. Переменный ток

1. Электромагнитные колебания Метод векторных диаграмм Метод комплексных амплитуд Переменный ток

ВоГУ
Лекция 33 (15)
Электромагнитные колебания
Метод векторных диаграмм
Метод комплексных амплитуд
Переменный ток
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1

2. План

3.

Метод векторных диаграмм
dq
I
dt
I I 0 cos t
Ёмкость в цепи переменного тока
q q0 sin t
dq
I
q0 cos t
I 0 q0
dt
q0
q q0
Uc
sin t
cos t
C C
C
2
U c U C 0 cos t
2
q0 I 0
UC0
C C
3

4.

Ёмкость в цепи переменного тока
I0
UC 0
I 0 RC
C
I I 0 cos t
U c U C 0 cos t
2
1
RC
C
– ёмкостное сопротивление
напряжение отстаёт по фазе от тока на
2
Векторная диаграмма:

5.

Метод векторных диаграмм Индуктивность в цепи переменного тока
I I 0 cos t
dI
L I 0 sin t
si L
dt
Второе правило Кирхгофа:
si U L 0
U L si L I 0 sin t
U L U L0 cos t напряжение опережает ток по фазе на
2
2
Векторная диаграмма:
U L 0 L I 0 RL I 0
RL L – индуктивное сопротивление
5

6.

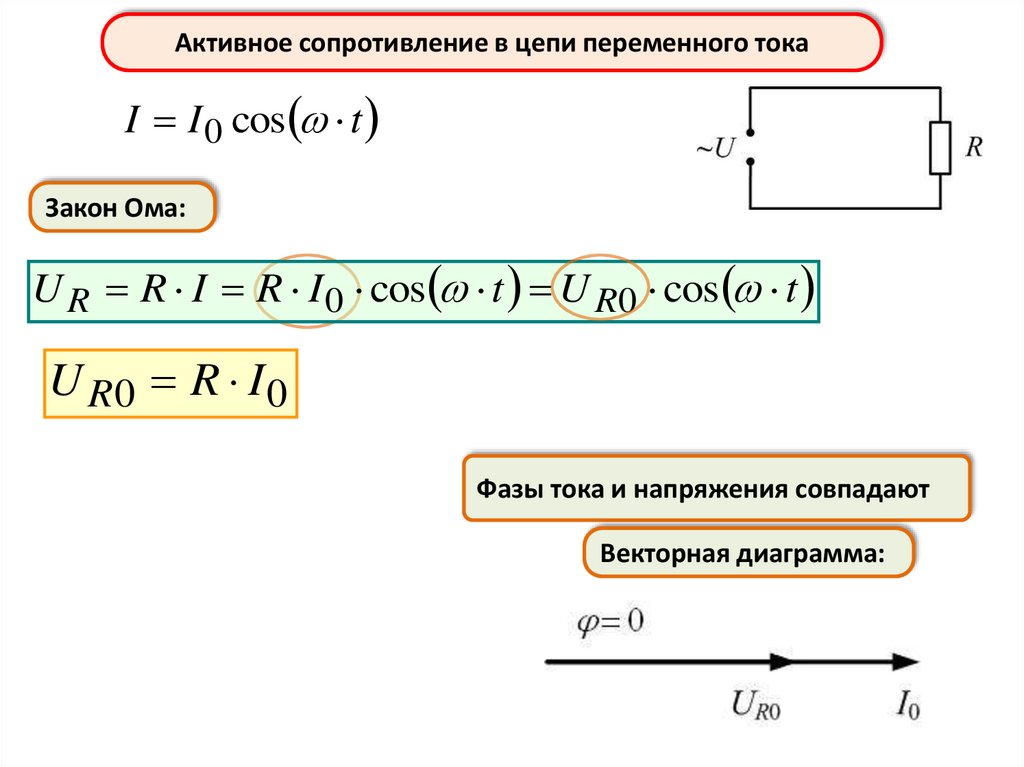
Активное сопротивление в цепи переменного тока
I I 0 cos t
Закон Ома:
U R R I R I 0 cos t U R0 cos t
U R0 R I 0
Фазы тока и напряжения совпадают
Векторная диаграмма:

7.

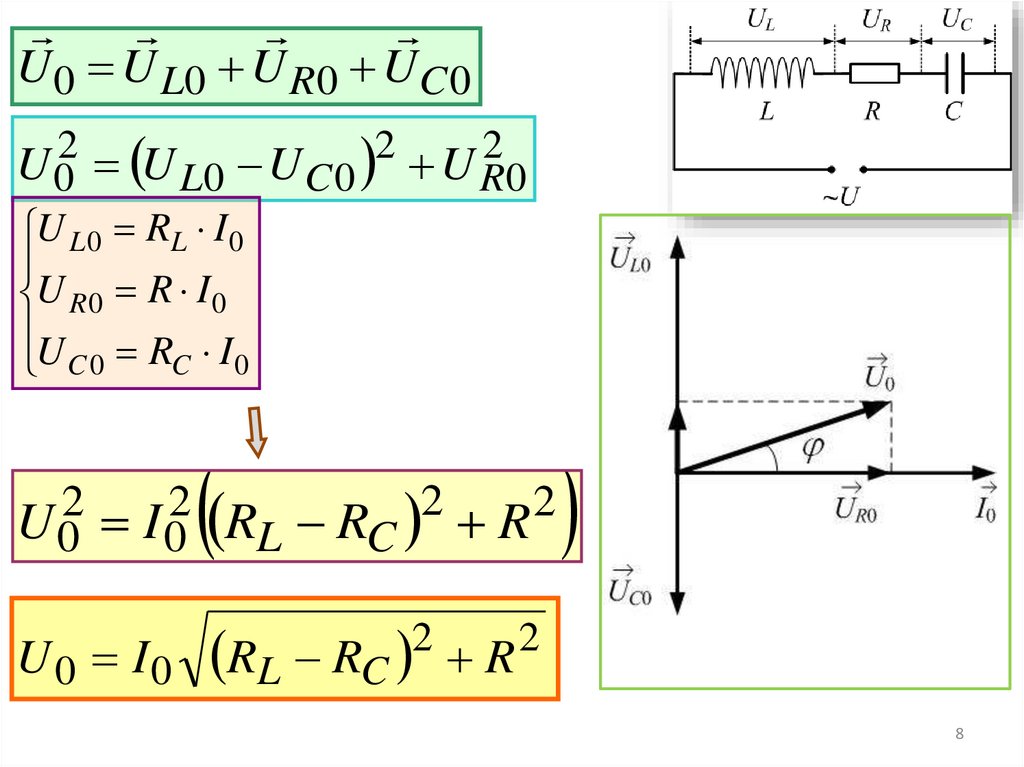
Последовательная цепь переменного тока
Напряжения складываются; ток - общий
U 0 U L0 U R 0 U C 0
~ U U 0 cos t
U L U L0 cos t 2
U R U R 0 cos t
U c U C 0 cos t
2
U L 0 L I 0 RL I 0
U R 0 R I 0
1
U C 0
I 0 RC I 0
C
7

8.

U 0 U L0 U R 0 U C 0
2
2
2
U 0 U L0 U C 0 U R0
U L 0 RL I 0
U R 0 R I 0
U R I
C
0
C0
2
2
2
2
U 0 I 0 RL RC R
U0 I0
RL RC
2
R
2
8

9.

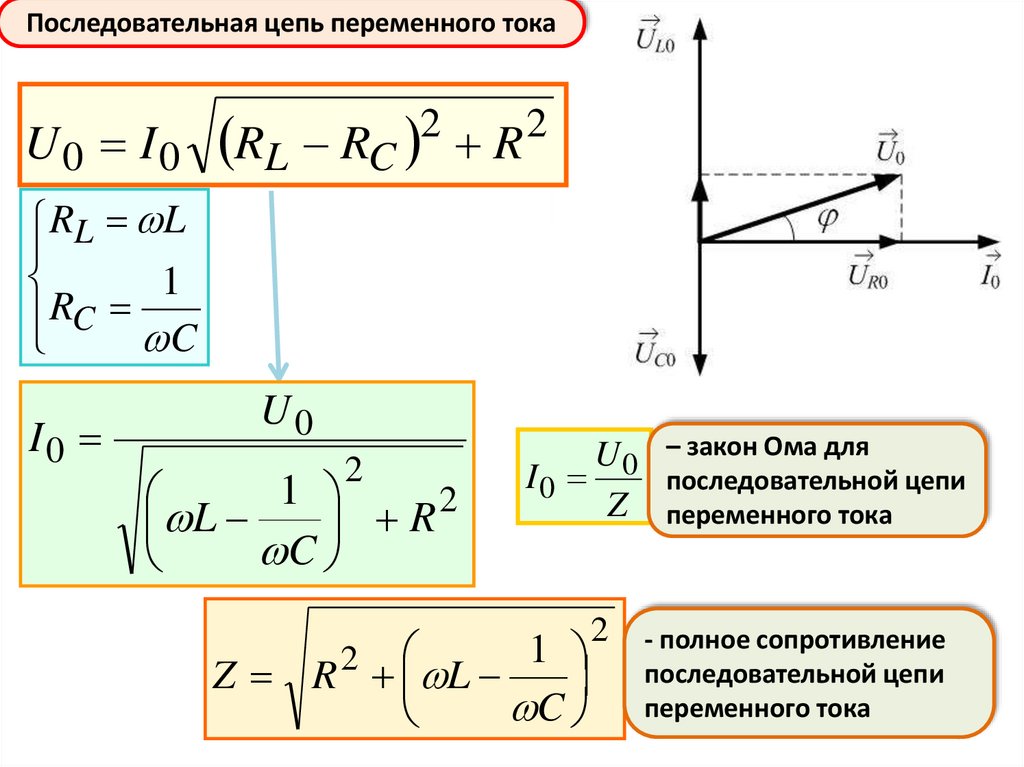
Последовательная цепь переменного тока
U0 I0
RL RC
2
R
2
RL L
1
RC C
I0
U0
2
1
2
L
R
C
U0
I0
Z
1
2
Z R L
C
2
– закон Ома для
последовательной цепи
переменного тока
- полное сопротивление
последовательной цепи
переменного тока
9

10.

Угол сдвига фаз между
током и напряжением:
U L0 U C 0 RL I 0 RC I 0
tg
U R0
RI0
RL RC
tg
R
RL L
1
RC C
1
L
C
tg
R
10

11.

Резонанс в последовательной цепи
1
L
C RL RC
Ток максимален:
2
1
Z R L
R
C
U0 U0
I0
Z
R
2
U L 0 U C 0 U L0 UC 0
U 0 U L0 U R 0 U C 0
U 0 U R0
Это – резонанс напряжений:
напряжения в противофазе и
компенсируют друг друга
Сдвиг фаз:
1
L
C 0
tg
11
R

12.

Последовательная цепь:
метод комплексных амплитуд
Колебательные процессы
удобно описывать с помощью
комплексных чисел
i 1
2
U U 0 cos t
i t
ˆ
U U0 e
Uˆ U 0 ei t U 0 cos t i U 0 sin t
Re Uˆ U 0 cos t
Im Uˆ U 0 sin t
12

13.

Дифф. уравнение:
qˆ 2 qˆ 2 qˆ f ei t
0
0
Обозначения:
U0
f0
L
R
2
L
1
2
0
LC
Решение ищем в виде:
ˆq Aˆ e i t
13

14.

qˆ Aˆ e i t
Считаем производные:
̂q Aˆ i e i t
qˆ Aˆ i 2 ei t Aˆ 2 ei t
Подставляем в дифф.ур.:
qˆ 2 qˆ 2 qˆ f ei t
0
0
Aˆ 2 ei t 2 Aˆ i ei t 02 Aˆ ei t f 0 ei t
Преобразуем:
2
2 ˆ
ˆ
ˆ
A 2 A i 0 A f 0
2
2
ˆ
A 0 2 i f 0
Aˆ
f0
02 2 2 i

15.

Модуль полученной комплексной амплитуды и есть
обычная вещественная амплитуда заряда:
q0 Aˆ
Aˆ
f0
02 2 2 i
q0 Aˆ
02
f0
i 2
2
q0
02
f0
02
4
2 2
2
f0
4
2 2
2
2
2

16.

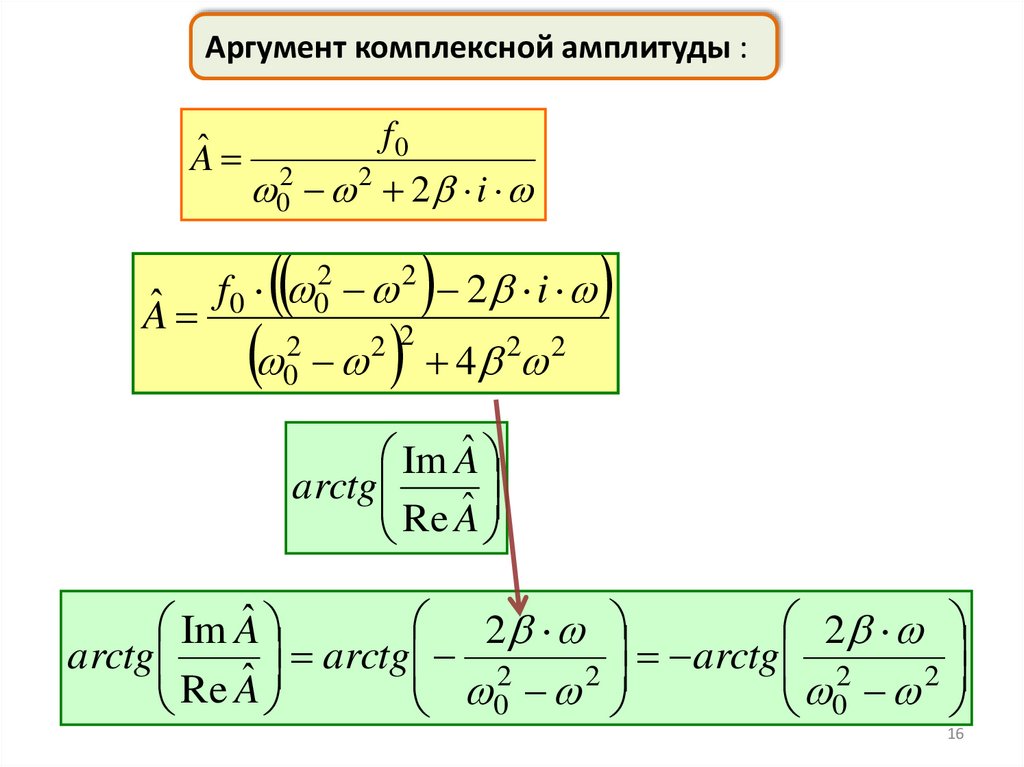
Аргумент комплексной амплитуды :
Aˆ
Aˆ
f0
02 2 2 i
f0 02 2 2 i
02
4
2 2
2
2
Im Aˆ
arctg
ˆ
Re
A
2
2
Im Aˆ
arctg
arctg
arctg
2 2
2 2
ˆ
Re
A
0
0
16

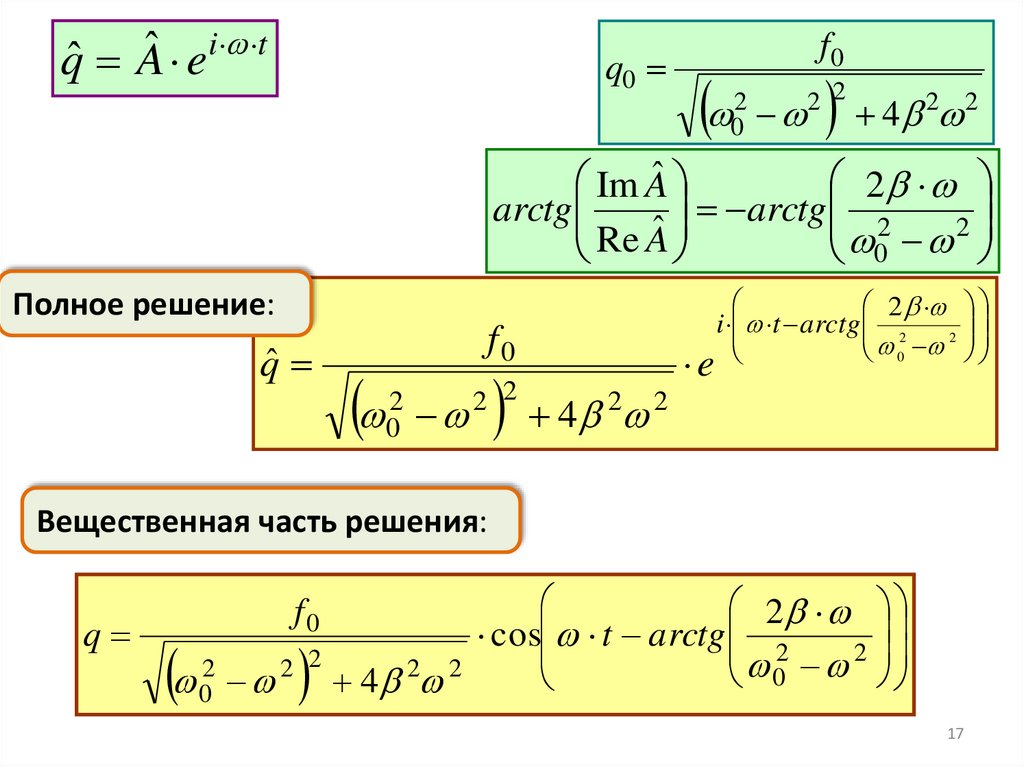
17.

i t
ˆ
qˆ A e
q0
f0
02
4
2 2
2
2
2
Im Aˆ
arctg
arctg
2
2
ˆ
Re
A
0
Полное решение:
qˆ
02
f0
2 2
e
2
i t arctg 2
2
0
4 2 2
Вещественная часть решения:
q
02
f0
2 2
2
cos t arctg 2
2
2 2
0
4
17

18.

Вещественная часть решения:
q
02
f0
2 2
2
cos t arctg 2
2
2 2
0
4
q q0 cos t 0
Амплитуда заряда:
Фаза:
q0 q0 ( )
02
f0
4
2 2
2
2
2
tg 0 2
0 2
18

19.

ˆI q ˆ Aˆ i ei t
Сила тока:
i t
ˆ
U U0 e
Напряжение:
i t
ˆ
U
U0 e
U0
ˆ
Z
i
t
Iˆ Aˆ i e
Aˆ i
Полное сопротивление:
Комплексная амплитуда:
Aˆ
f0
2
2
0 2 i
2
2
U
i 2
0
0
ˆ
Z
f0 i
19

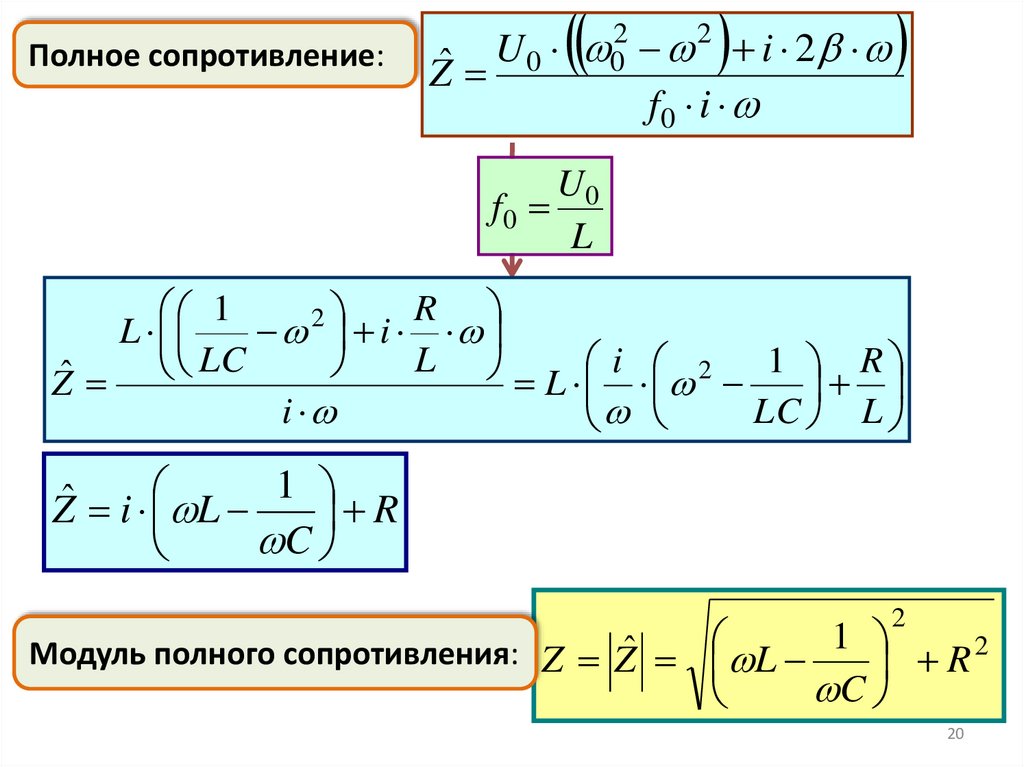
20.

Полное сопротивление:
2
2
U
i 2
0
0
ˆ
Z
f0 i
U0
f0
L
R
1
2
L
i
L
1 R
i 2
LC
ˆ
Z
L
i
LC L
1
ˆ
Z i L
R
C
2
Модуль полного сопротивления: Z Zˆ L 1 R 2
C
20

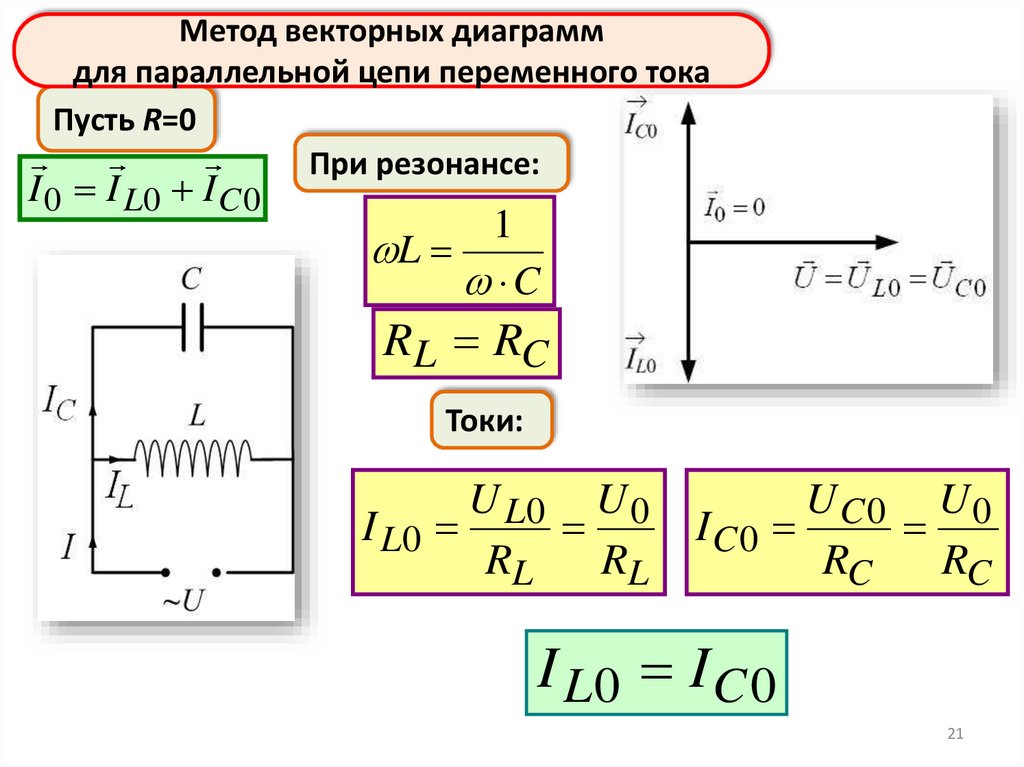
21.

Метод векторных диаграмм
для параллельной цепи переменного тока
Пусть R=0
При резонансе:
I 0 I L0 I C 0
1
L
C
RL RC
Токи:
U L0 U 0
I L0
RL
RL
UC0 U0
IC 0
RC
RC
I L0 I C 0
21

22.

Резонанс токов
I 0 I L0 I C 0
RL RC
I L0 I C 0
Токи в обеих ветвях одинаковы по величине, но колеблются
в противофазе.
Они компенсируют друг друга, и общий ток равен нулю:
I 0 I L0 I C 0 0
Это - резонанс токов
22

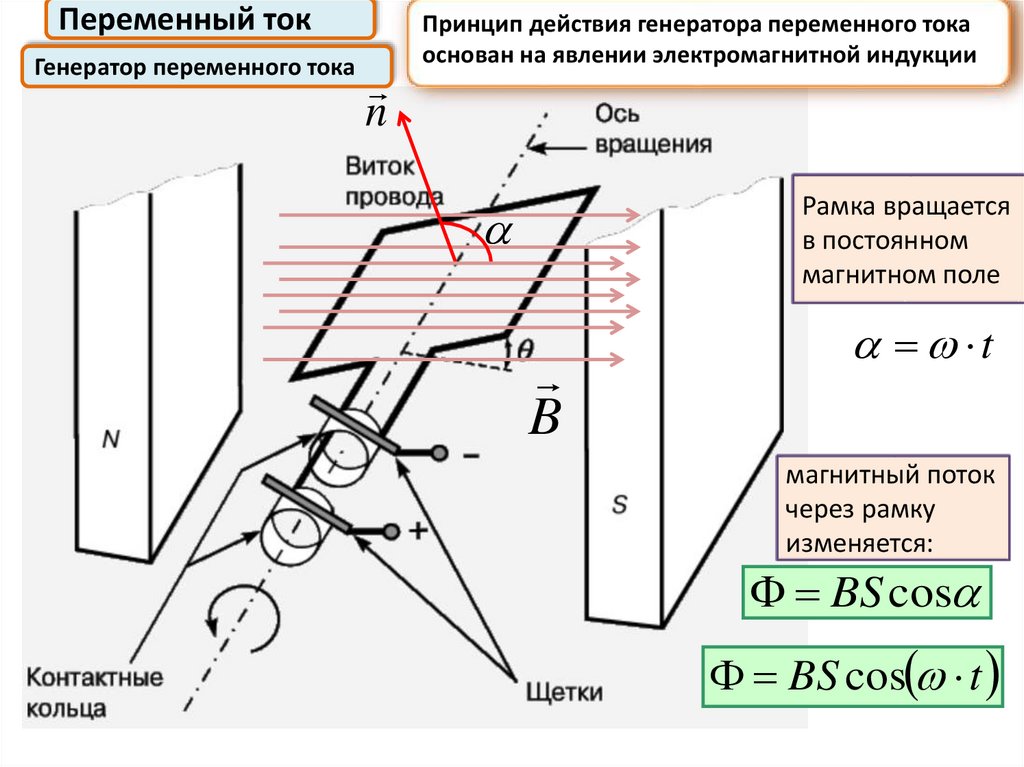
23.

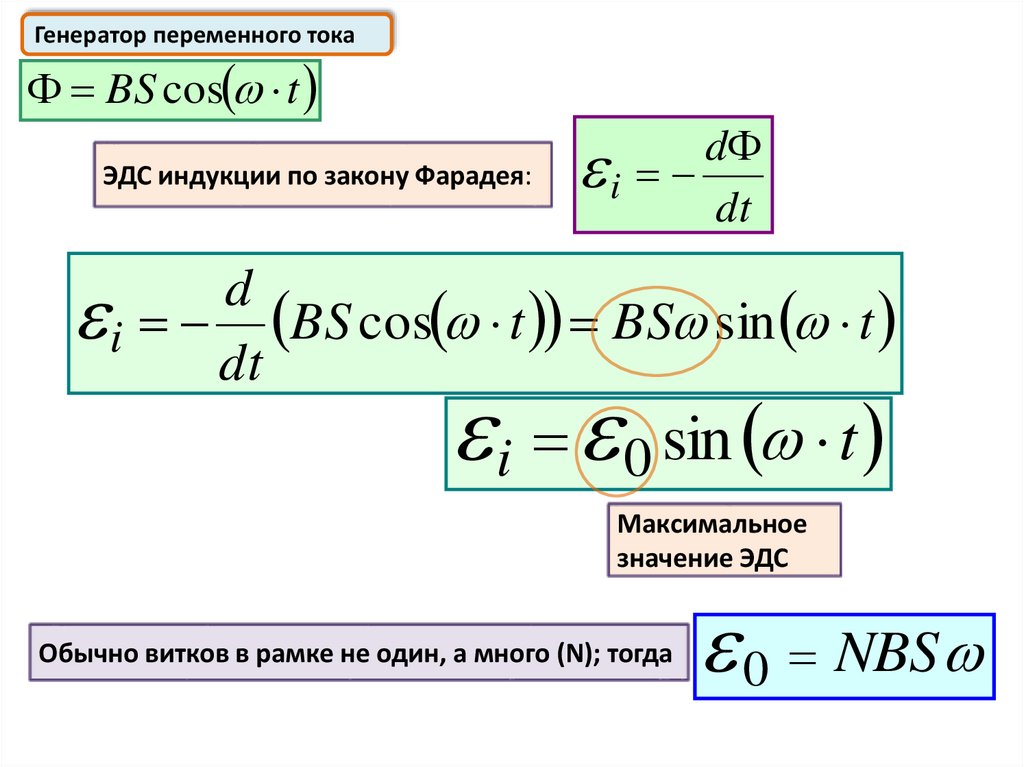
Переменный ток
Генератор переменного тока
n
Принцип действия генератора переменного тока
основан на явлении электромагнитной индукции
Рамка вращается
в постоянном
магнитном поле
B
t
магнитный поток
через рамку
изменяется:
BS cos
BS cos t

24.

Генератор переменного тока
BS cos t
ЭДС индукции по закону Фарадея:
d
i
dt
d
i BS cos t BS sin t
dt
i 0 sin t
Максимальное
значение ЭДС
Обычно витков в рамке не один, а много (N); тогда
0 NBS

25.

Генератор переменного тока
В промышленных генераторах вращается электромагнит, в то время как
обмотки, в которых наводится ЭДС, остаются неподвижными.
Если использовать, например, три симметрично расположенных обмотки, то
в каждой из них фаза ЭДС индукции будет сдвинута на 1200; это уже
трёхфазный ток

26.

Мощность переменного тока
Сдвиг фаз между током и напряжением в общем случае равен φ
Мгновенные значения тока и напряжения:
U U 0 cos t
I I 0 cos t
Мгновенная мощность:
Pм U I
Pм U 0 cos t I 0 cos t
1
cos cos cos cos
2
1
Pм U 0 I 0 cos 2 t cos
2
26

27.

Мощность переменного тока
1
Pм U 0 I 0 cos 2 t cos
2
Мгновенная мощность изменяется во времени с частотой, в два раза большей
частоты тока
Мгновенные значения мощности неважны; важно знать среднюю мощность:
1
P Pм U 0 I 0 cos 2 t cos
2
0
1
P U 0 I 0 cos
2
27

28.

Эффективные значения тока и напряжения
Определения:
1
P U 0 I 0 cos
2
U0
Uэ
2
I0
Iэ
2
Смысл таких определений:
P U э I э cos
Эффективное значение переменного тока
(или напряжения) численно равно такому
постоянному току (или напряжению),
который даёт ту же мощность, что и
данный переменный ток
При отсутствии сдвига фаз (φ=0):
P U э I э I э2 R
2
Uэ
R
28

29.

Понятие о спектральном разложении. Ряд Фурье
Теорема Фурье:
любую периодическую функцию можно
представить в виде ряда Фурье
(разложить по гармоническим составляющим)
f t f t T
T
2
0
f t a0 an cos n 0t bn sin n 0t
n 1
Для чётной функции:
f t f t
bn 0
f t a0 an cos n 0t
n 1

30.

Интеграл Фурье
Непериодическую функцию тоже можно разложить по
гармоническим составляющим, но это она будет иметь
непрерывный спектр:
Ряд Фурье переходит в интеграл Фурье

31.

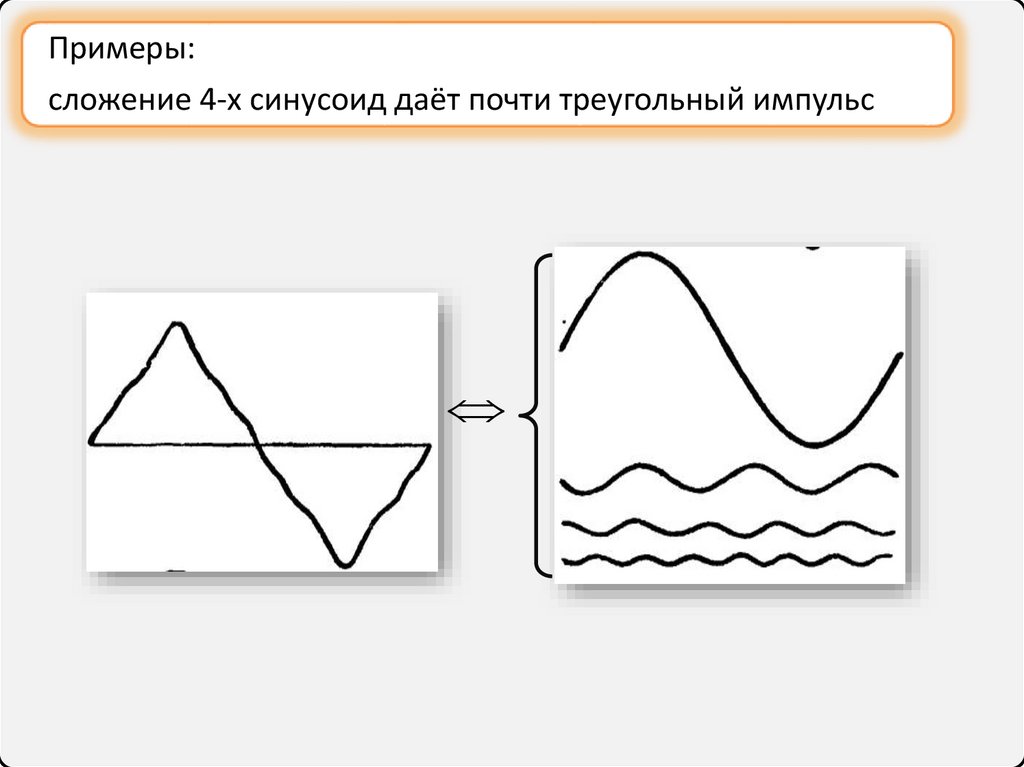
Примеры:
сложение 4-х синусоид даёт почти треугольный импульс

32.

Примеры: «пила» раскладывается на гармонические
составляющие тем точнее, чем больше членов ряда

33.

Примеры: прямоугольный импульс

34.

Сложение двух колебаний, близких по частоте, даёт биения

35.

Модуляция
Для передачи информации на большие расстояния
используют высокочастотные колебания.
В общем случае высокочастотное колебание имеет вид
где ωо– несущая частота.
Если ωо=const, φо=const, A(t)=A0=const, то колебание
является гармоническим.
Оно не содержит никакой информации.
Процесс управления одним или несколькими
параметрами высокочастотного колебания по закону
управляющего сигнала называется модуляцией.

36.

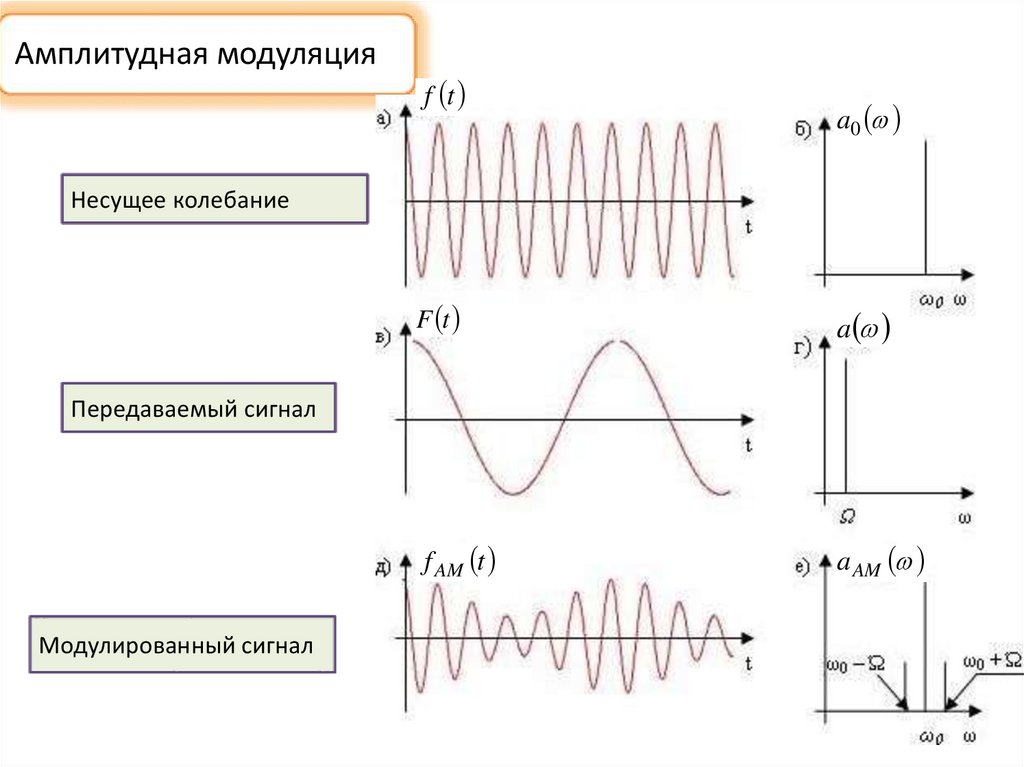
Амплитудная модуляция
f t
a0
Несущее колебание
F t
a
Передаваемый сигнал
f AM t
Модулированный сигнал
a AM

37.

Амплитудная модуляция
Передаваемый сигнал
Несущая частота
АМ - сигнал

38.

Амплитудная модуляция
Спектральный состав:
a
Передаваемый сигнал
а) до модуляции
a
б) после модуляции управляющим сигналом
Несущая частота

39.

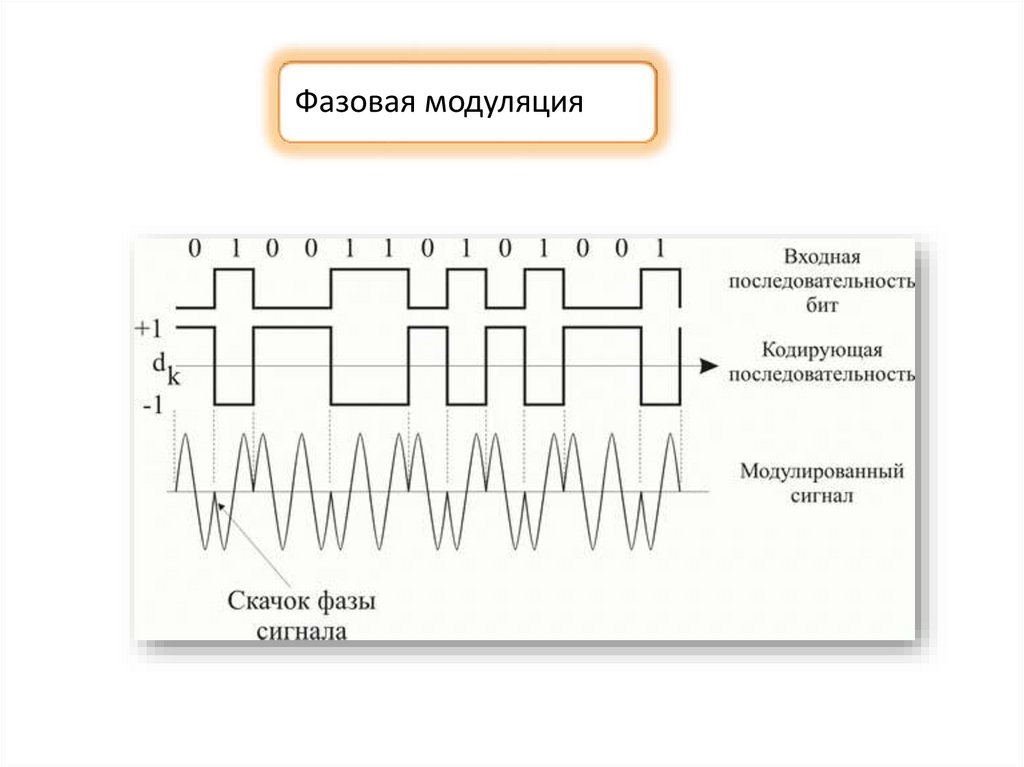
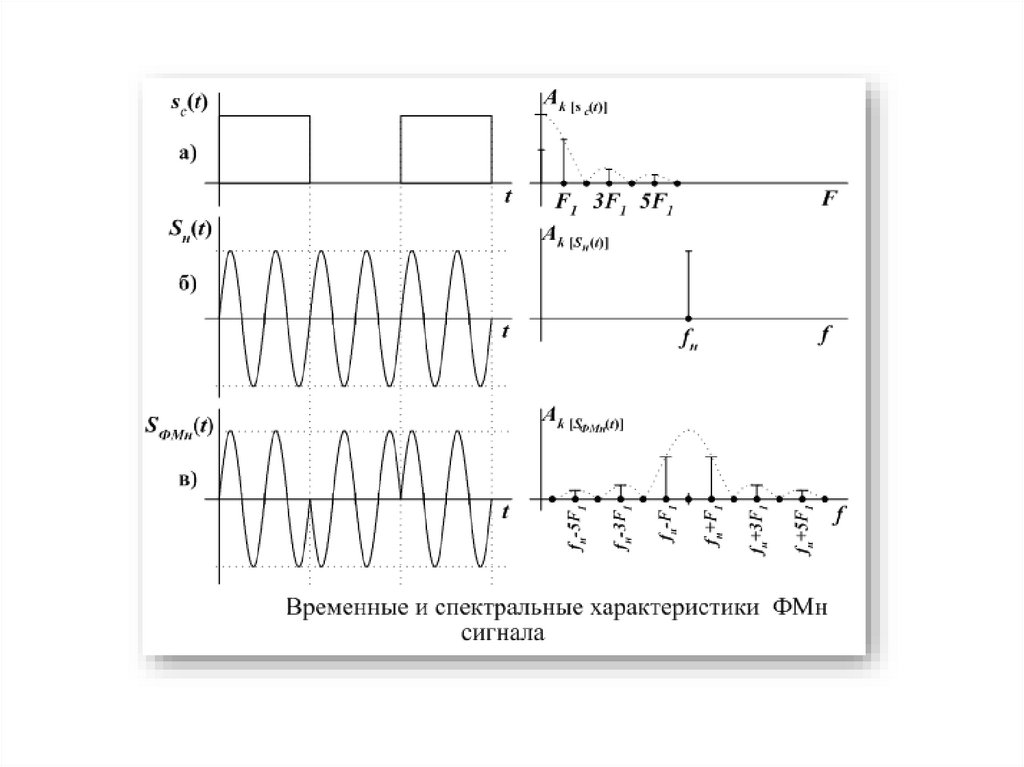
Фазовая модуляция

40.

Амплитудная модуляция
Частотная модуляция
Фазовая модуляция