Похожие презентации:
Методы анализа лис-цепей (обзор)
1. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ (ОБЗОР)
Кафедра «КРЭМС»МЕТОДЫ
АНАЛИЗА ЛИСЦЕПЕЙ (ОБЗОР)
Зырянов
Юрий Трифонович
доктор технических наук
профессор
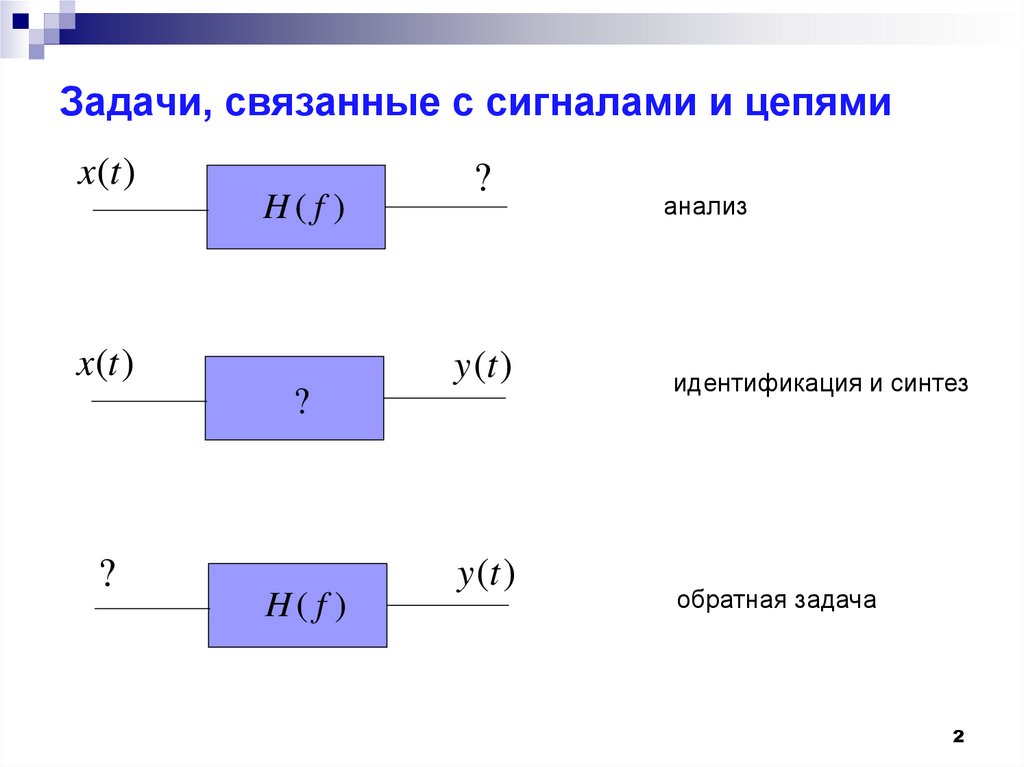
2. Задачи, связанные с сигналами и цепями
x(t )H( f )
x(t )
?
y (t )
?
?
H( f )
y (t )
анализ
идентификация и синтез
обратная задача
2
3.
X ( f ) x(t )e j 2 ft dtH( f )
Y( f ) H( f )X ( f )
F
F
1
x(t )
h(t )
y (t ) x( )h(t )d
L
L
X ( p ) x(t )e pt dt
H ( p)
1
Y ( p) H ( p) X ( p)
0
ИХ, КЧХ, ПФ функциональное описание
Принципиальная схема, дифференциальное уравнение структурные
способы описания
3
4.
Точные методы анализа ЛИС-цепей:1. Временной метод (интеграл Дюамеля)
2. Метод, основанный на решении дифференциального
уравнения цепи
3. Операторный и спектральный методы
4. Метод комплексной огибающей (будет рассмотрен позже)
Они позволяют точно решить задачу анализа для любой
ЛИС-цепи и при любом воздействии
Приближенные методы основаны на некоторых
упрощающих допущениях
Метод мгновенной частоты (будет рассмотрен позже) и др.
Разные приближенные методы приводят к разным
результатам !
5. Метод, основанный на решении ДУ
Дифференциальные уравнения вообще связывают значениянекоторых физических величин со скоростями их изменения,
скоростями изменения скоростей (ускорениями) и т.д.
ЛИС-цепи с сосредоточенными параметрами описываются
наиболее простыми ДУ– обыкновенными линейными
дифференциальными уравнениями с постоянными
коэффициентами
(ЛИС-цепи с распределенными параметрами описываются
линейными дифференциальными уравнениями в частных
производных с постоянными коэффициентами)
n
an
d y (t )
dt n
... a0 y (t ) bm
x(t ) входной сигнал
(воздействие)
m
d x(t )
dt m
... b0 x(t )
y (t ) выходной сигнал
(отклик)
6. Линейные ДУ с постоянными коэффициентами
Если входной сигнал задан, то тем самым задана вся праваячасть уравнения
an
an
d n y (t )
dt n
d n y (t )
dt n
... a0 y (t ) f (t )
неоднородное уравнение
... a0 y (t ) 0
соответствующее
однородное уравнение
Начальные условия состояние цепи в начальный момент времени
an an 1
n
n 1
... a1 a0 0
характеристическое уравнение
Если коэффициенты уравнения вещественны, то корни либо
вещественны, либо образуют комплексно-сопряженные пары. При этом
некоторые корни могут совпадать (быть кратными).
7. Решение ЛДУ с ПК (пример см. в учебнике)
Если все корни1, 2 ,..., n простые, то общее решение
однородного дифференциального уравнения описывает
собственные колебания цепи и имеет вид
y(t ) C1e 1t C2e 2t ... Cne nt
C1, C2 ,..., Cn определяются начальными условиями
При наличии кратного корня (кратности m) присутствуют
слагаемые вида
e k t , te k t , ....,
Для устойчивости
цепи свободные
колебания должны
затухать со временем
t
m 1 k t
e
все корни характеристического
уравнения должны иметь
отрицательные вещественные
части (лежать в левой половине
комплексной плоскости)
8. Связь спектрального метода с ДУ
Пусть на вход ЛИС-цепи воздействуетТогда
x(t ) e j t
y(t ) H ( )e j t
k
d
d
x(t ) j e j t , ... , k x(t ) ( j ) k e j t
dt
dt
k
d
d
j t
y (t ) j H ( )e , ... , k y (t ) ( j ) k H ( )e j t
dt
dt
an j H ( )e
n
j t
... a0 H ( )e
j t
bm j e
bm j bm 1 j
m
H ( )
m j t
an j an 1 j
n
m 1
n 1
... b0e j t
... b1 j b0
... a1 j a0
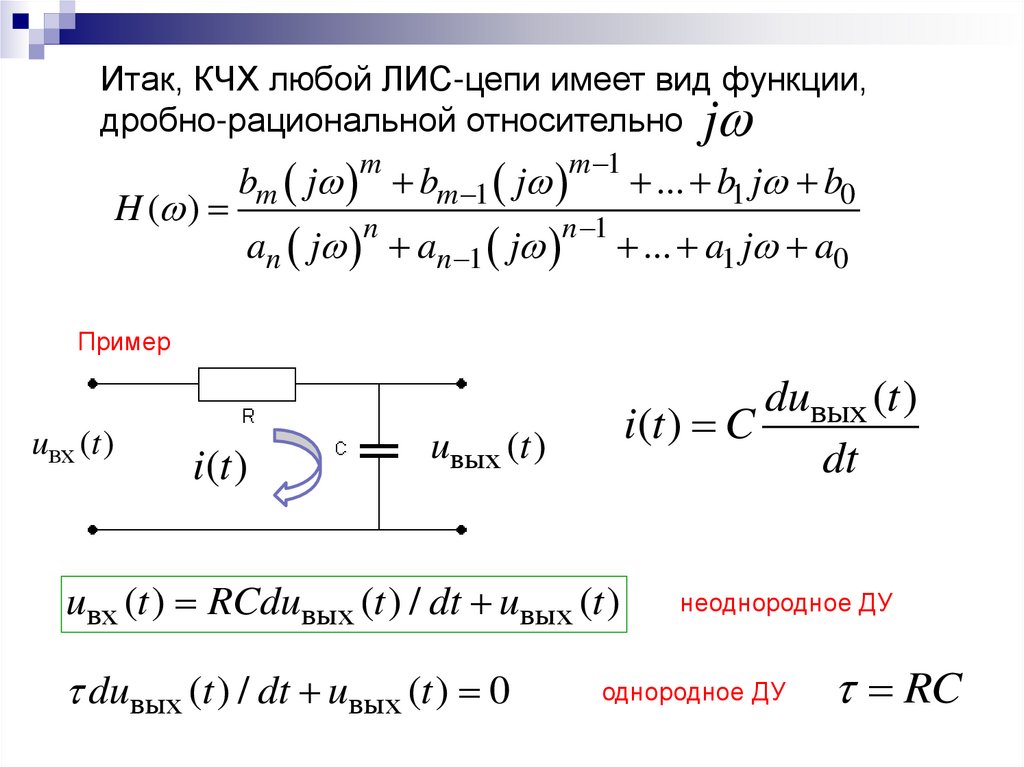
9.
Итак, КЧХ любой ЛИС-цепи имеет вид функции,дробно-рациональной относительно j
bm j bm 1 j
m
H ( )
an j an 1 j
n
m 1
n 1
... b1 j b0
... a1 j a0
Пример
uвх (t )
i(t )
duвых (t )
i(t ) C
dt
uвых (t )
uвх (t ) RCduвых (t ) / dt uвых (t )
duвых (t ) / dt uвых (t ) 0
неоднородное ДУ
однородное ДУ
RC
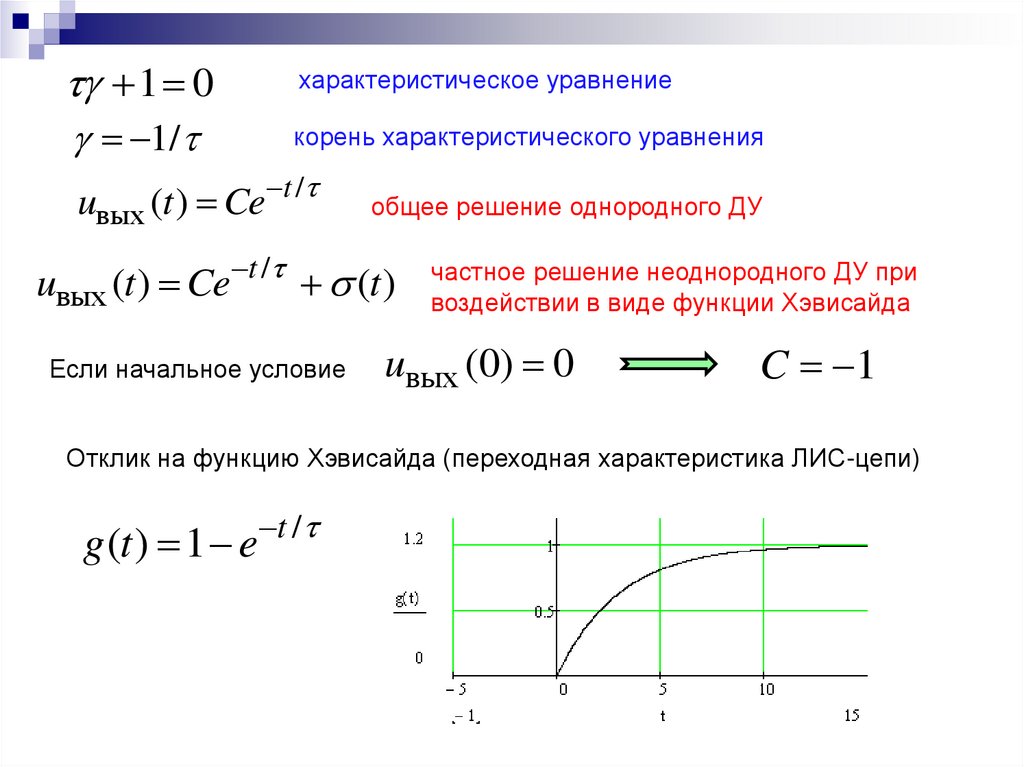
10.
1 0характеристическое уравнение
1/
корень характеристического уравнения
uвых (t ) Ce t /
uвых (t ) Ce
t /
общее решение однородного ДУ
(t )
Если начальное условие
частное решение неоднородного ДУ при
воздействии в виде функции Хэвисайда
uвых (0) 0
C 1
Отклик на функцию Хэвисайда (переходная характеристика ЛИС-цепи)
g (t ) 1 e t /
11.
bm j bm 1 jm
H ( )
an j an 1 j
n
m 1
n 1
... b1 j b0
... a1 j a0
H ( ) 1/ 1 j RC
Если на входе дельта-функция
(сп. плотность ≡1)
Y ( ) 1/ 1 j RC
Обратным преобразованием
Фурье получаем отклик ИХ
1 t /
h(t ) e
12. Операторный метод
X ( p) x(t )ept
dt
d
p
dt
y (t )
0
1
2 j
c j
Y ( p)e pt dt
c j
Дифференциальное уравнение заменяется алгебраическим
an pnY ( p) ... a1 pY ( p) a0Y ( p) bm p m X ( p) ... b1 pX ( p) b0 X ( p)
Y ( p)
K ( p)
X ( p)
K ( p)
операторная передаточная функция
bm p m bm 1 p m 1 ... b1 p b0
an p n an 1 p n 1 ... a1 p a0
Y ( p) K ( p) X ( p)
13. Метод комплексной огибающей
обычно применяется для анализа частотно-избирательныхцепей при узкополосных воздействиях
x(t ) Re (t )e
j 2 F0t
1
(t )e j 2 F0t * (t )e j 2 F0t
2
Спектральная плотность
1
X ( f ) f F0 * f F0
2
( f )
Z( f )
X(f )
F0
F0
f
14.
ИХ частотно-избирательной цепи (полосового фильтра)h(t ) Re (t )e
j 2 F0t
1
(t )e j 2 F0t * (t )e j 2 F0t
2
1
H ( f ) f F0 * f F0
2
( f )
H( f )
( f )
Z( f )
X(f )
F0
F0
f
Тогда спектральная плотность сигнала на выходе фильтра
равна
Y( f ) H f X f
15.
11
*
f F0 f F0
f F0 * f F0
2
2
1
*
*
f F0 f F0 f F0 f F0
4
1
Y ( f ) f F0 * f F0
2
где
1
f f f
2
y (t ) Re (t )e
Итак,
j 2 F0t
1
(t )e j 2 F0t * (t )e j 2 F0t ;
2
(t ) (t ) 12 (t )
Низкочастотный эквивалент ЧИЦ имеет ИХ
1 (t )
2
16. НЕСТАЦИОНАРНЫЕ ЛИНЕЙНЫЕ ЦЕПИ
17. Линейные нестационарные цепи
Линейные нестационарные цепи с сосредоточеннымипараметрами описываются обыкновенными линейными
дифференциальными уравнениями с переменными
коэффициентами
n
an (t )
d y (t )
dt
n
... a0 (t ) y (t )
bm (t )
x(t ) входной сигнал
(воздействие)
d m x (t )
dt
m
... b0 (t ) x(t )
y (t ) выходной сигнал
Общего метода решения нет
(отклик)
18.
Модуляция – это изменение одного или несколькихпараметров колебания, называемого несущим колебанием
(переносчиком), в соответствии с изменениями первичного
(информационного) сигнала.
18
19.
Модуляция – это изменение одного или несколькихпараметров колебания, называемого несущим колебанием
(переносчиком), в соответствии с изменениями первичного
(информационного) сигнала.
при модуляции (а также демодуляции) происходят такие
преобразования сигнала, которые сопровождаются
появлением новых частотных составляющих,
отсутствовавших в спектре исходного сигнала
X(f )
0
F0
Низкие частоты
Высокие частоты
f
19
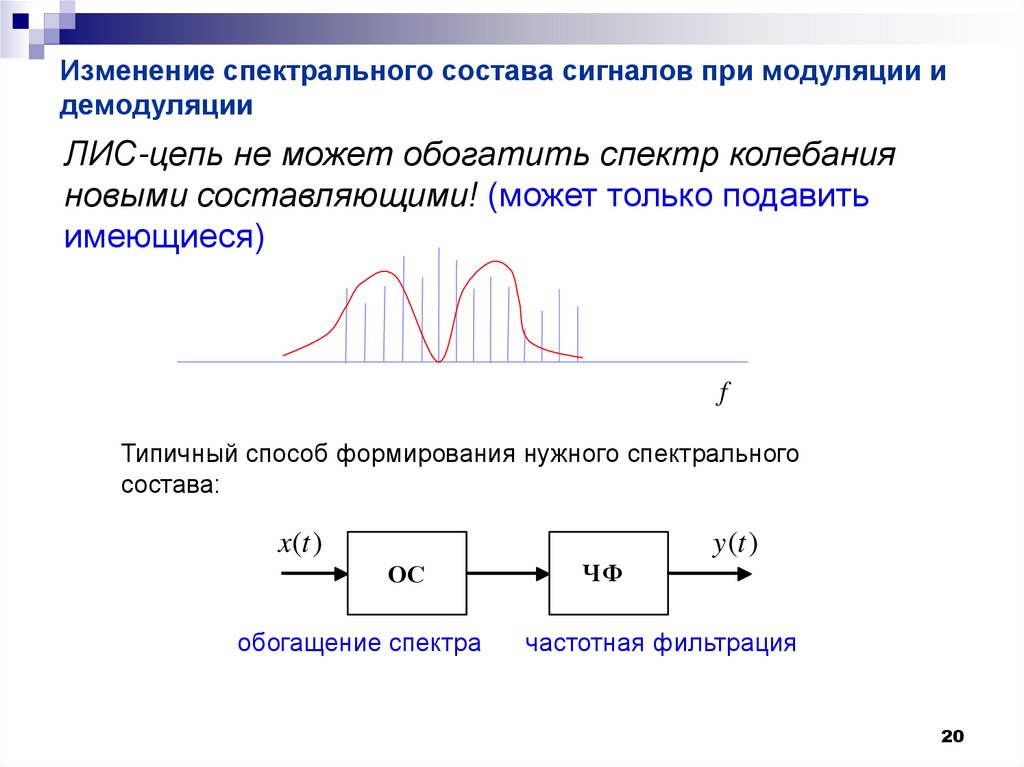
20. Изменение спектрального состава сигналов при модуляции и демодуляции
ЛИС-цепь не может обогатить спектр колебанияновыми составляющими! (может только подавить
имеющиеся)
f
Типичный способ формирования нужного спектрального
состава:
x(t )
y (t )
ОС
обогащение спектра
ЧФ
частотная фильтрация
20
21. Линейные нестационарные цепи
y (t ) L x(t ) L x( ) (t )d x( )L (t ) dx( )h(t , )d
где h(t, ) - отклик цепи в момент t на входной
сигнал в виде -функции, воздействующий на
цепь в момент . Заменим переменную
y (t ) x(t )h(t , t )d
Пусть на входе колебание
e
j 2 ft
y (t ) e j 2 f (t ) h(t , t )d e j 2 ft e j 2 f h(t , t )d
H ( f , t )e j 2 ft
21
22. Линейные нестационарные цепи
Пусть на входе колебаниеe
j 2 ft
y (t ) e j 2 f (t ) h(t , t )d e j 2 ft e j 2 f h(t , t )d
H ( f , t )e
j 2 ft
H ( f , t ) h(t , t )e
j 2 f
d
y(t ) H ( f , t )e j 2 ft
Можно представить
e
j 2 f 0 t
Однако эта функция зависит не только
от частоты, но и от времени
H ( f , t ) K ( f , t )e
у(t ) K ( f0 , t )e
j ( f , t )
j[2 f0t ( f0 , t )]
22
23.
y (t ) x(t )h(t , t )dподставим обратное ПФ для
входного сигнала
y (t )
j 2 f (t )
X
(
f
)
e
h(t , t )df d
X ( f ) h(t , t )e j 2 f d e j 2 ft df
X ( f ) H ( f , t )e j 2 ft df
X ( f )H ( f , t)
Это не спектральная плотность !!!
23
24. Воздействие гармонического колебания на линейную параметрическую цепь
ii (t )
u (t )
s (t )
s (t ) 1/ R(t )
u
проводимость
(крутизна ВАХ)
Простейший случай напряжение и крутизна
изменяются по гармоническому закону с разными
частотами
s (t ) S0 S1 cos( 1t 1)
u (t ) U cos( 2t 2 )
0
1
2
24
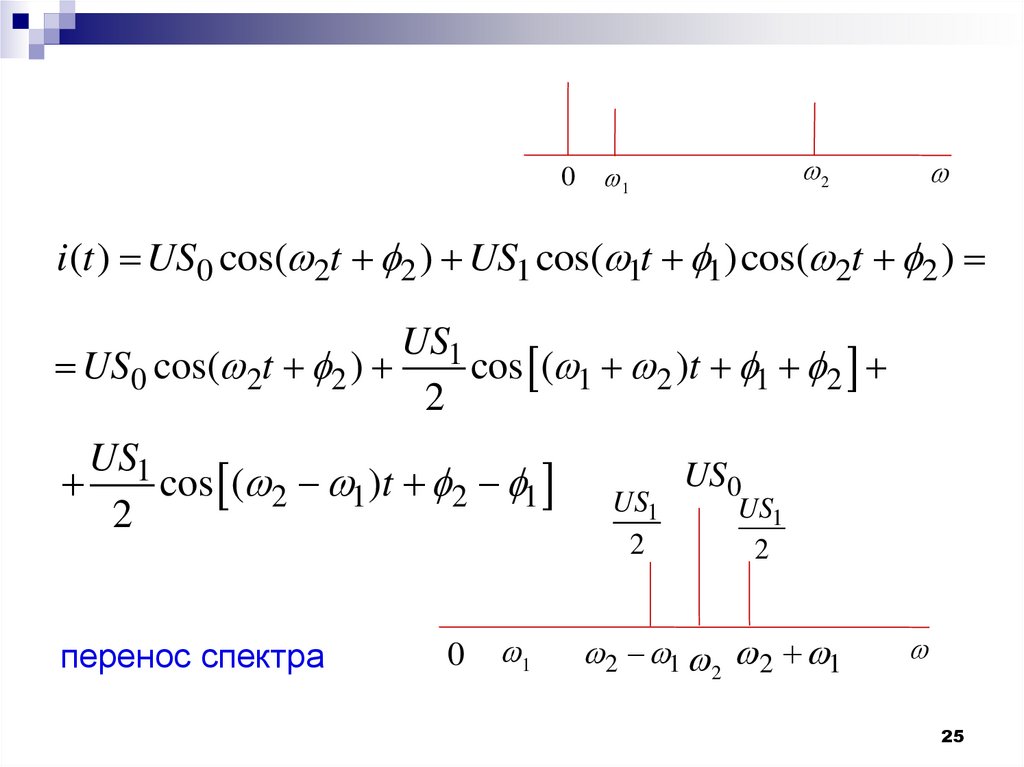
25.
02
1
i (t ) US0 cos( 2t 2 ) US1 cos( 1t 1)cos( 2t 2 )
US1
US0 cos( 2t 2 )
cos ( 1 2 )t 1 2
2
US1
cos ( 2 1 )t 2 1
2
перенос спектра
0
1
US1
2
US0
US1
2
2 1 2 2 1
25




















 Физика
Физика








