Сверхтекучесть. Классические и квантовые жидкости

1.

Сверхтекучесть. Классические и
квантовые жидкости.
Выполнила работу
студентка 4 курса
очной формы обучения
группы 23Ф181
Корнева Лидия Николаевна

2.

Содержание
●Понятие сверхтекучести
●Ранние эксперименты с жидким гелием
●Гелий II и фазовые переходы второго рода
●Открытие сверхтекучести
●Квантовые жидкости
●Двухжидкостная модель гелия-II
●Основные факты о сверхтекучести
●Применение явления сверхтекучести

3.

Понятие сверхтекучести
Сверхтекучесть – это состояние
вещества, находясь в котором оно теряет
вязкость (внутреннее трение), в результате
чего вещество способно с легкостью
проходить через капилляры и узкие щели
без какого-либо трения.
•Наиболее известное вещество такого рода –
сверхтекучий гелий

4.

Ранние эксперименты с
жидким гелием
•Впервые сверхтекучий гелий получил нидерландский
физик и химик Хейке Камерлинг-Оннес в 1908-м году.
•В 1913 году Камерлинг-Оннес был
удостоен Нобелевской премии по физике «за
исследования свойств вещества при низких
температурах, которые привели к производству
жидкого гелия».
•Камерлинг-Оннес заслужил у коллег почётное
прозвище «Господин Абсолютного Нуля».
Хейке Камерлинг-Оннес
(1853-1926)
5

5.

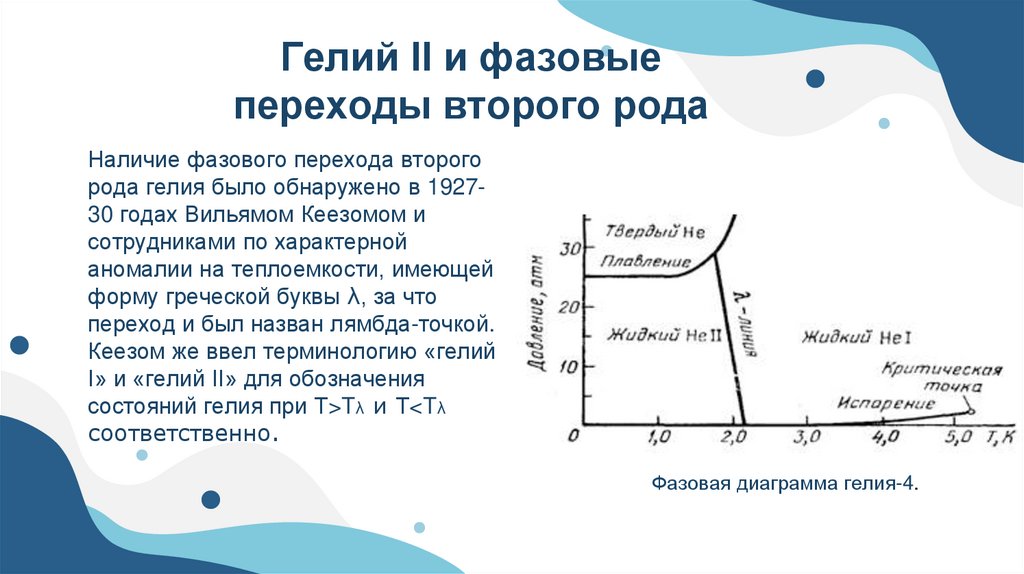
Гелий II и фазовые
переходы второго рода
Наличие фазового перехода второго
рода гелия было обнаружено в 192730 годах Вильямом Кеезомом и
сотрудниками по характерной
аномалии на теплоемкости, имеющей
форму греческой буквы λ, за что
переход и был назван лямбда-точкой.
Кеезом же ввел терминологию «гелий
I» и «гелий II» для обозначения
состояний гелия при Т>Tλ и Т<Tλ
соответственно.
Фазовая диаграмма гелия-4.

6.

Открытие сверхтекучести
В 1938-м году сверхтекучесть была открыта
советским физиком Петром Капица, и независимо от
него, канадские исследователи Джон Ален и Дон
Мисенер показали, что гелий II имеет практически
нулевую вязкость. Для этого Капица исследовал
протекание через сверхтонкие щели, а Ален и
Мисенер – через тонкие капилляры. в 1978-м году
Капица получил Нобелевскую премию «за
фундаментальные открытия в физике низких
температур».
Петр Леонидович Капица
(1894-1984)

7.

Квантовые жидкости
При температурах, близких к абсолютному нулю, когда волна де Бройля частиц,
отвечающая их тепловому движению, становится сравнимой с расстоянием между
ними и происходит квантовое вырождение жидкости, в свойствах жидкости на
первый план выдвигаются квантовые эффекты; в таких случаях говорят о
квантовых жидкостях.
Бозе-жидкость-жидкость, состоящая
из частиц с нулевым или целым
спином, бозонов (жидкий 4Не)
Ферми-жидкость- жидкость,
состоящая из частиц с полуцелым
спином, фермионов (жидкий 3Не)

8.

Двухжидкостная модель гелия-II
В 1941-м году советский физик-теоретик Лев Ландау
предложил теорию сверхтекучести:
При отличных от нуля температурах гелий II ведет
себя так, как если бы он представлял собой смесь
двух различных жидкостей. Одна из них сверхтекуча
и при движении вдоль твердой поверхности не
обнаруживает никакой вязкости. Другая же ведет
себя так, как обычная нормальная вязкая жидкость.
При этом весьма существенно, что между обеими
этими движущимися «друг через друга» частями
массы жидкости нет трения, т. е. не происходит
передачи импульса от одной из них к другой. За
новаторские теории конденсированных сред, в особ
енности жидкого гелия, Лев Ландау получил в 1962м году Нобелевскую премию.
Лев Давидович Ландау
(1908 -1968)

9.

Двухжидкостная модель гелия-II
В квантовой бозе-жидкости элементарные возбуждения с малыми
импульсами р соответствуют обычным гидродинамическим звуковым волнам,
т. е. представляют собой фононы. Это значит, что энергия таких квазичастиц
является линейной функцией их импульса:
(1)
где
- Скорость звука в жидкости, определяемая как:
Статистически равновесное распределение элементарных возбуждений
в бозе-жидкости дается формулой распределения Бозе:
(2)

10.

Двухжидкостная модель гелия-II
Выражения для термодинамических величин твердого тела при низких
температурах:
Свободная энергия:
(3)
Энтропия:
(4)
Энергия:
(5)
Теплоемкость:
(6)
- Средняя скорость
звука
- Энергия всех
атомов тела в
положении
равновесия

11.

Двухжидкостная модель гелия-II
Термодинамические величины жидкости для таких близких к
абсолютному нулю температур, при которых практически все
имеющиеся в жидкости элементальные возбуждения обладают
малыми энергиями, т.е. являются фононами:
Свободная энергия жидкости:
Энергия:
Теплоемкость:
(7)
(8)
(9)
-Свободная энергия при абсолютном нуле

12.

Двухжидкостная модель гелия-II
В тепловом равновесии большинство элементарных возбуждений в
жидкости имеет энергии в областях вблизи минимумов функции ε(р), т.е. в
области малых ε (область вблизи ε=0), и в области значения ε(р0).
Поэтому именно эти области особенно
существенны. Вблизи точки р=р0 функция
ε(р) может быть разложена по
степеням р-р0. Линейный член в
разложении отсутствует и с точностью
до членов второго порядка имеем:
(10)
Квазичастицы этого типа называют ротонами.

13.

Двухжидкостная модель гелия-II
Для вычисления ротонной части термодинамических величин жидкого гелия исходим из
формулы для свободной энергии больцмановского газа:
(11)
При этом под N в этой формуле надо понимать число ротонов в жидкости. Приравняв
к нулю, найдем для числа ротонов:
(12)
Соответствующее значение свободной энергии:
(13)
В эти формулы надо подставить в (10) с учетом:

14.

Двухжидкостная модель гелия-II
В результате получим:
(14)
Отсюда вклад ротонов в энтропию и теплоемкость:
(15)
Мы видим, что температурная зависимость ротонной части термодинамических
величин в основном экспоненциальна. Поэтому при достаточно низких
температурах ротонная часть меньше фононной, а при более высоких
температурах положение меняется, и ротонный вклад превосходит фононный.
Квантовая жидкость с энергетическим спектром описанного типа обладает
замечательным свойством так называемой сверхтекучести.

15.

Двухжидкостная модель гелия-II
Рассмотрим жидкость, текущую по капилляру с постоянной скоростью v в системе
координат, движущейся вместе с жидкостью. В этой системе гелий покоится, а стенки
капилляра движутся со скоростью –v.
Предположим, что в жидкости появляется одно элементарное возбуждение с импульсом р
и энергией ε(р). Тогда энергия Е0 жидкости сделается равной энергии этого возбуждения ε,
а ее импульс Р0 импульсу р. Перейдем теперь обратно к системе координат где капилляр
покоится. В итоге имеем для энергии Е и импульса Р жидкости в этой системе:
(16)
(17)
(18)

16.

Двухжидкостная модель гелия-II
Геометрически отношение ε /р есть тангенс угла наклона прямой, проведенной из начала
координат в некоторую точку кривой. Его минимальное значение будет в точке, где прямая
проведенная из начала координат будет касательна к кривой. Если это минимальное
значение отлично от нуля, то при не слишком больших скоростях течения в жидкости не
смогут появиться возбуждения. Это значит, что ее течение не будет замедляться, т.е.
жидкость обнаружит явление сверхтекучести.
Вывод: к сверхтекучести приведет всякий спектр, в котором достаточно малые
возбуждения являются фононами.

17.

Двухжидкостная модель гелия-II
Рассмотрим теперь ту же жидкость, но уже при температуре отличной от абсолютного
нуля (хотя и близкой к нему). В этом случае жидкость не находится в основном
состоянии- она содержит возбуждения.
(16)
(19)

18.

Двухжидкостная модель гелия-II
(20)
(21)
Вывод: При отличных от нуля температурах часть массы жидкости
будет вести себя как нормальная вязкая жидкость, «цепляющаяся» при
движении о стенки сосуда; остальная же часть массы будет вести себя
как не обладающая вязкостью сверхтекучая жидкость.

19.

Основные факты о сверхтекучести
Энтропия в веществе в сверхтекучем состоянии равна нулю
и не возрастает.
Теплопроводность при нулевой температуре – бесконечная.
В таком случае гелий проводит тепло с конечной скоростью,
хоть и довольно высокой.
Тонкие пленки. Сверхтекучий гелий имеет свойство покрывать
тонкой пленкой любую твердую поверхностью, «переползая» по
стене вверх, несмотря на силу притяжения. Пленка
сверхтекучей жидкости двигается от места с меньшей
температурой к месту с большей температурой. Скорость
движения такой пленки растет с уменьшением температуры и
может достигать несколько метров в секунду.

20.

Основные факты о сверхтекучести
Фонтанный эффект. Если погрузить колбочку с жидким гелием
и нагревателем в ней, в большую емкость гелия, то при работе
нагревателя, с колбочки начнет бить фонтан гелия, при том, что
количество гелия в колбе не будет уменьшаться.
Квантовые вихри. Если объект движется в сверхтекучей
жидкости (или жидкость быстро течет), то в ней могут
образовываться замкнутые контуры потока, которые называют
квантовыми вихрями. От обычных вихрей они отличаются тем,
что не пропадают со временем.

21.

Высокотемпературная сверхтекучесть
В 2017-м году была открыта и
экспериментально подтверждена более
экзотическая система — фотонное
сверхтекучее вещество. Исследователи с
CNR NANOTEC в Лечче, Италия, и
канадского Политехнического университета
Монреаля смогли создать фотонное
сверхтекучее вещество при комнатной
температуре.
Профессор канадского Политехнического
университета Монреаля, Стефан Кена-Кохкен

22.

Применение явления
сверхтекучести
Сверхтекучесть не имеет какого-либо
определенного и популярного
применения. На сегодня – это лишь
интересное и плохо изученное явление,
которое находит применение в очень
специфических областях. Так,
сверхтекучий гелий используется для
охлаждения нагревающихся систем. В
перспективе, такой охладитель будет
применен для охлаждения сложнейших
конструкций, в силу своих способностей
– проникать в мельчайшие щели и
самостоятельно двигаться в сторону
источника тепла.

23.

Литература
В. А. Гольдаде, Л. С. Пинчук «Физика конденсированного состояния».
Под редакцией члена-корреспондента Национальной академии наук
Беларуси Н. К Мышкина. Минск. «Белорусская наука», 2009.- 58 с.
Л. Д. Ландау, Е. М. Лифшиц «Гидродинамика. Теоретическая физика т.
6» 3-е изд. перераб. –М.: Наука. Гл. ред. Физ-мат. лит., 1986.- 736 с.
Л. П. Питаевский, Е. М. Лифшиц «Статистическая физика. В 2 ч. Ч. 2.
Теория Конденсированного состояния.» 3-е изд. стереот. –М.: Наука. Гл.
ред. Физ-мат. лит., 2002.- 496 с.
В. Н. Глазков «Сверхтекучесть гелия-4. Магнитные свойства
сверхпроводников первого рода. Термодинамика сверхпроводников»,
29.03.2017 (лекция).

24.

Спасибо
за
внимание!
CREDITS: This presentation template was
created by Slidesgo, including icons by Flaticon,
infographics & images by Freepik