Фазированные антенные решетки и их назначение. Структура курса

1. Структура курса

• Введение
– Фазированные антенные решетки и их назначение
• Теория ФАР
– Основные характеристики ФАР
– Диаграммоформирование в ФАР
• Техника ФАР
–
–
–
–
Схемы возбуждения ФАР
Широкополосные ФАР
Принципы конструирования ФАР
Калибровка и контроль ФАР
1

2. Типы диаграммоформирования

• Формирование остронаправленного
луча (лучей)
• Создание ДН сложной формы
• Формирование нуля (нулей) в
диаграмме направленности
2

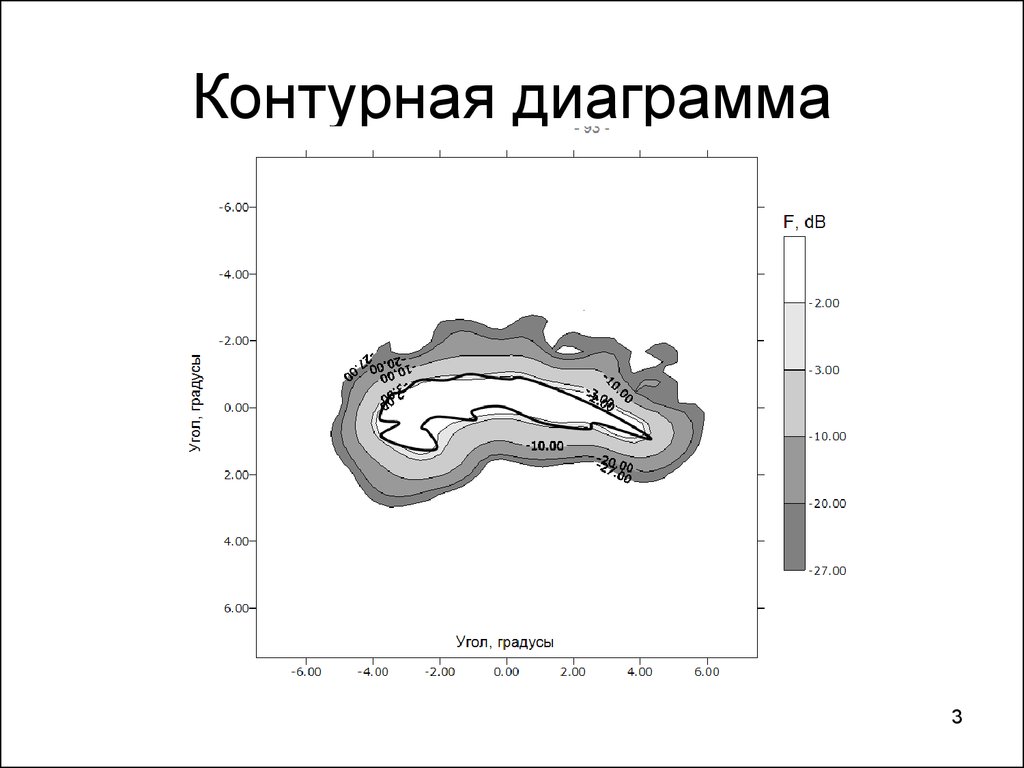
3. Контурная диаграмма

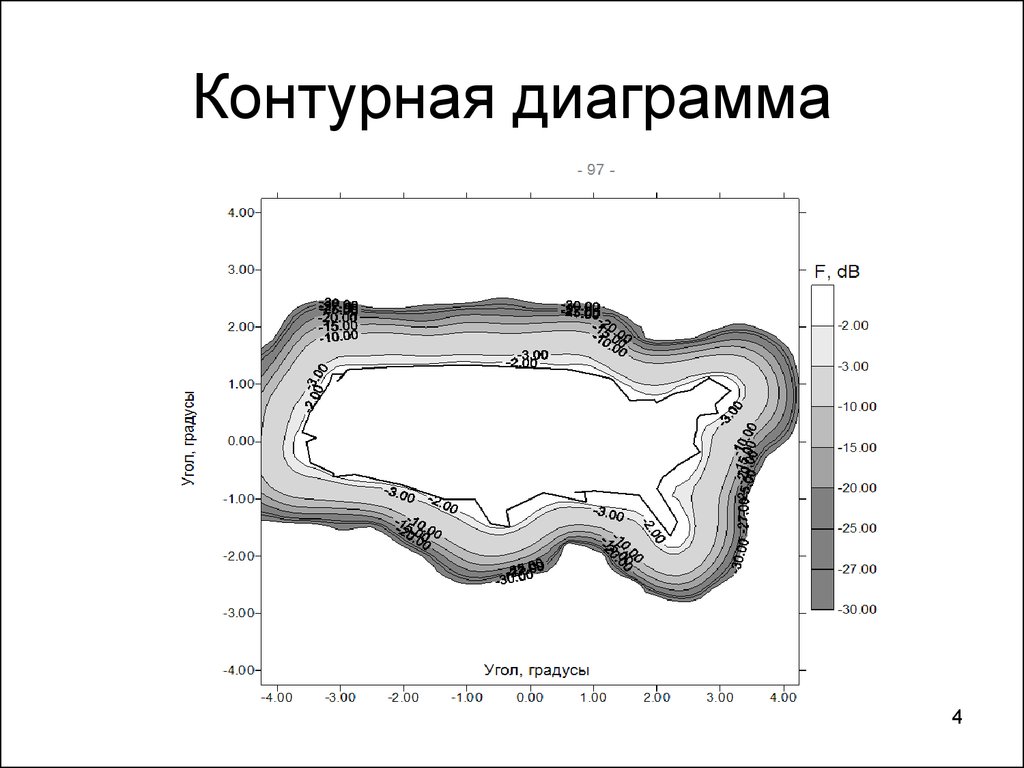
3

4. Контурная диаграмма

4

5. Еще диаграммы сложной формы

• Расширение луча
• Формирование нулей
5

6. Метод преобразования Фурье

• Задать требуемую форму диаграммы
• Провести преобразование Фурье
• Полученную функцию использовать как
амплитудное распределение
В общем случае – не работает
6

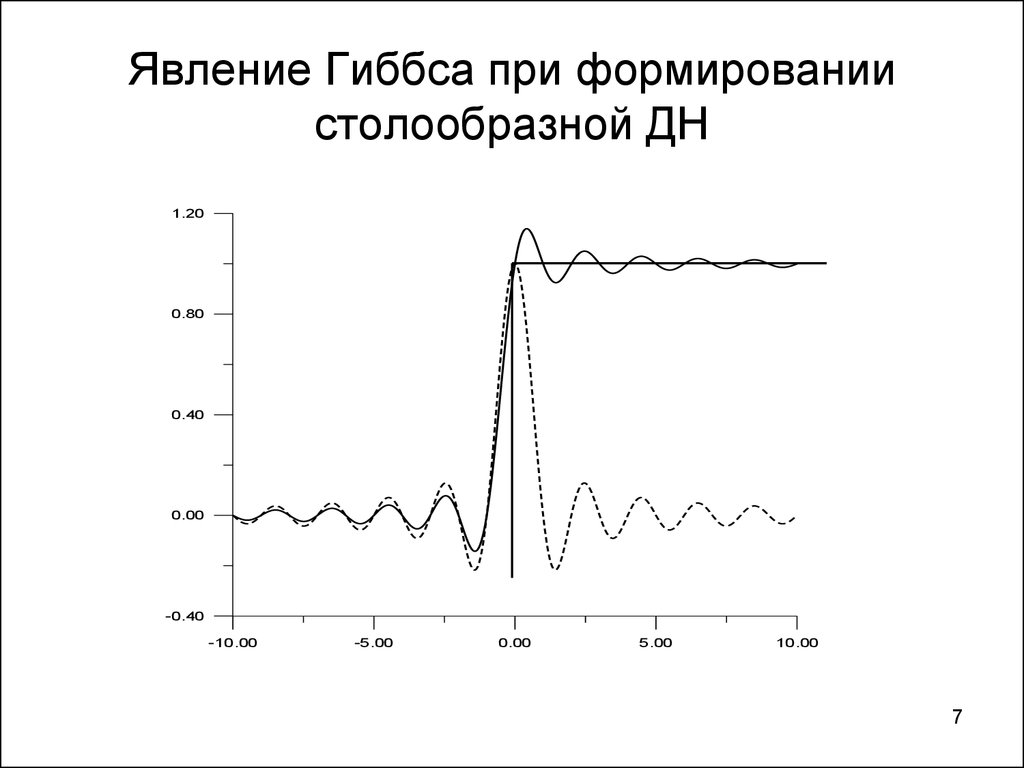
7. Явление Гиббса при формировании столообразной ДН

1.20
0.80
0.40
0.00
-0.40
-10.00
-5.00
0.00
5.00
10.00
7

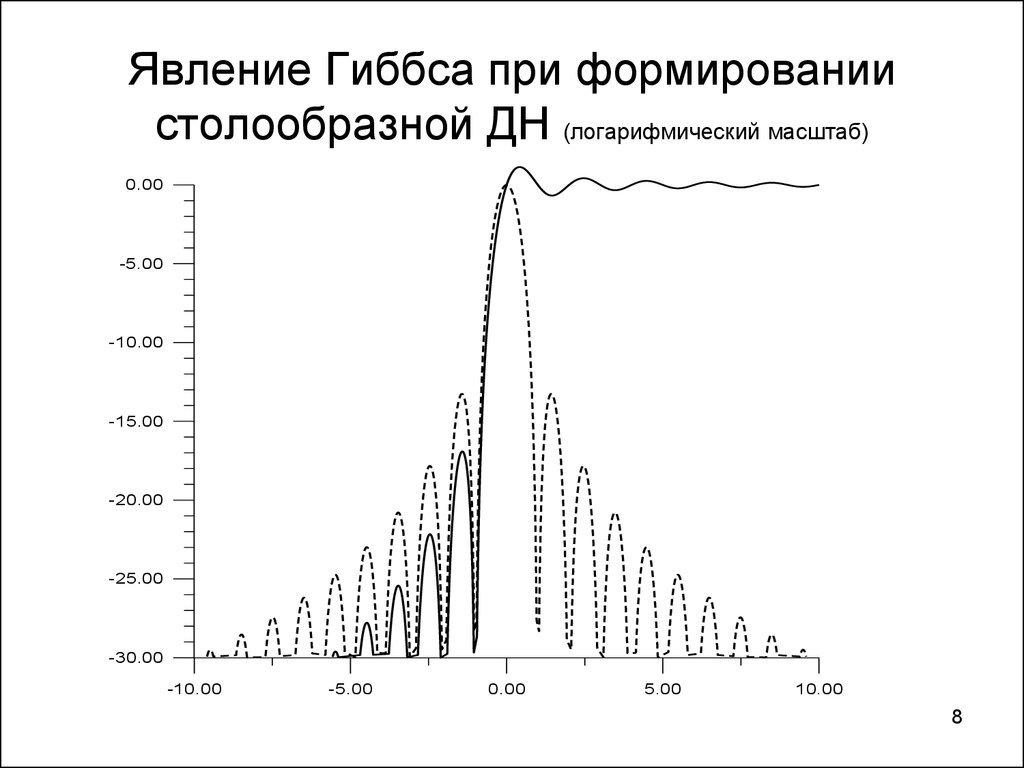
8. Явление Гиббса при формировании столообразной ДН (логарифмический масштаб)

0.00
-5.00
-10.00
-15.00
-20.00
-25.00
-30.00
-10.00
-5.00
0.00
5.00
10.00
8

9. Метод парциальных диаграмм (Вудворта-Лоусона)

• ДН сложной формы представляется как взвешенная
сумма парциальных ДН
• Парциальные ДН – остронаправленные ДН,
формируемые апертурой
• Амплитудное распределение в раскрыве есть
взвешенная сумма распределений контурных ДН
Работает с оговорками
(оптимизация весов, подавление БЛ)
9

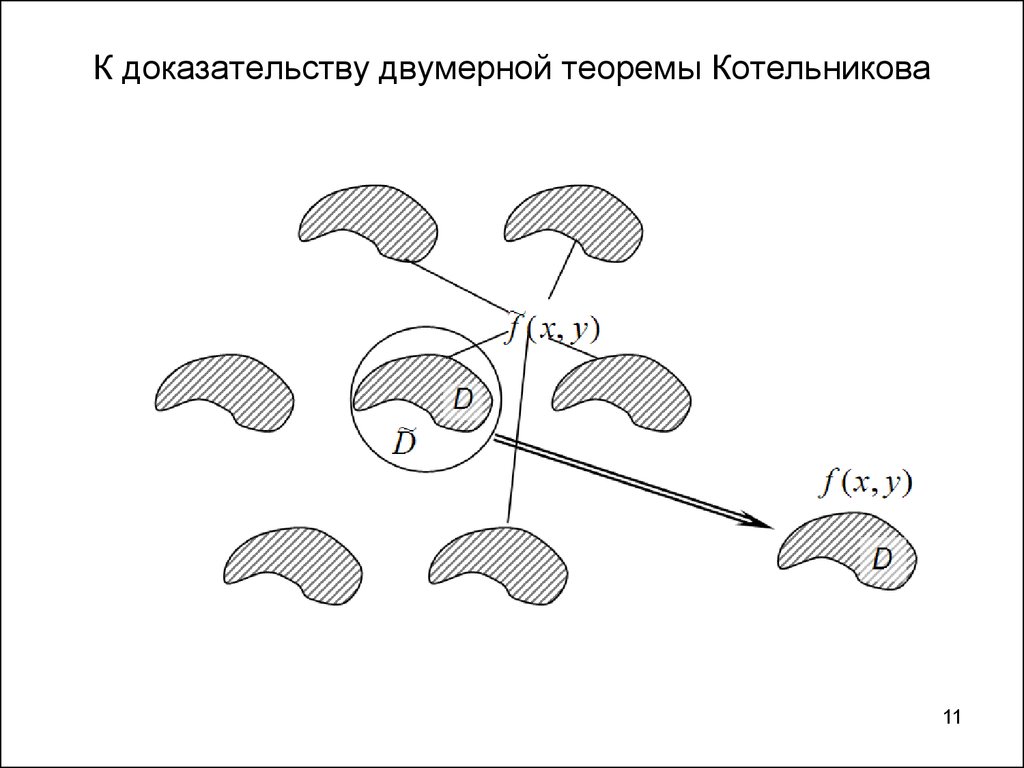
10. Двумерная теорема Котельникова

Откуда брать веса парциальных ДН? С каким шагом расставлять?
Двумерная теорема
Котельникова
• ДН сложной формы представляется как взвешенная
сумма парциальных ДН
• Парциальные ДН расположены на регулярной сетке
• Парциальные ДН – остронаправленные ДН,
формируемые апертурой
• Амплитудное распределение в раскрыве есть
взвешенная сумма распределений для
парциальныхДН
10

11. К доказательству двумерной теоремы Котельникова

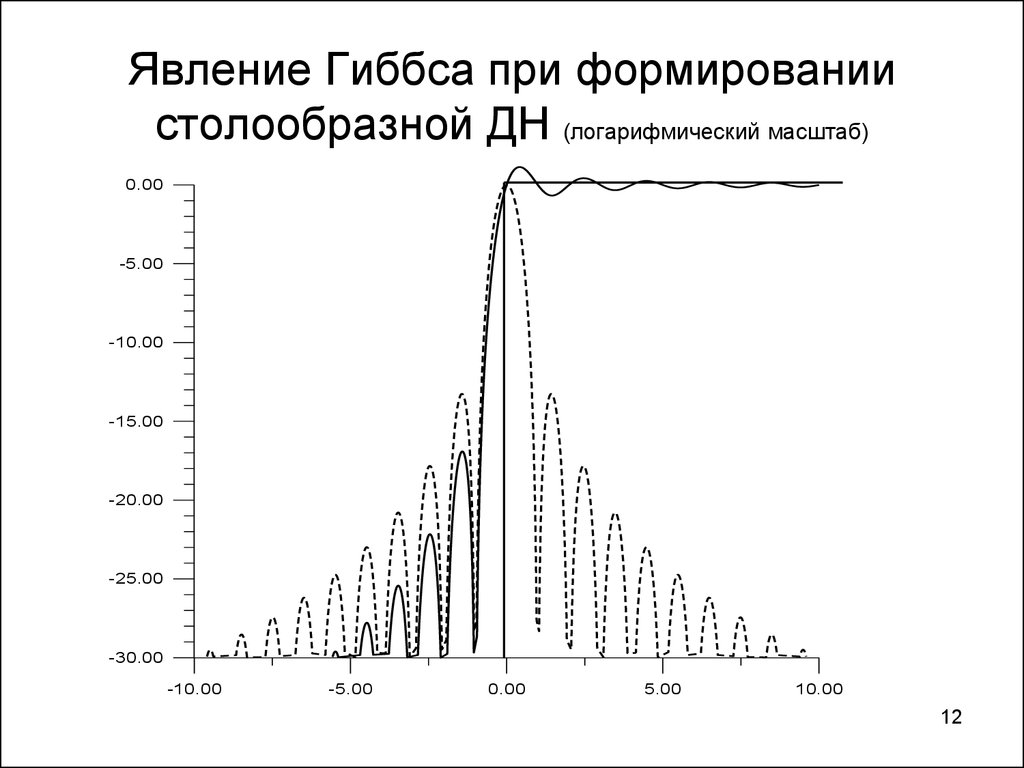
11

12. Явление Гиббса при формировании столообразной ДН (логарифмический масштаб)

0.00
-5.00
-10.00
-15.00
-20.00
-25.00
-30.00
-10.00
-5.00
0.00
5.00
10.00
12

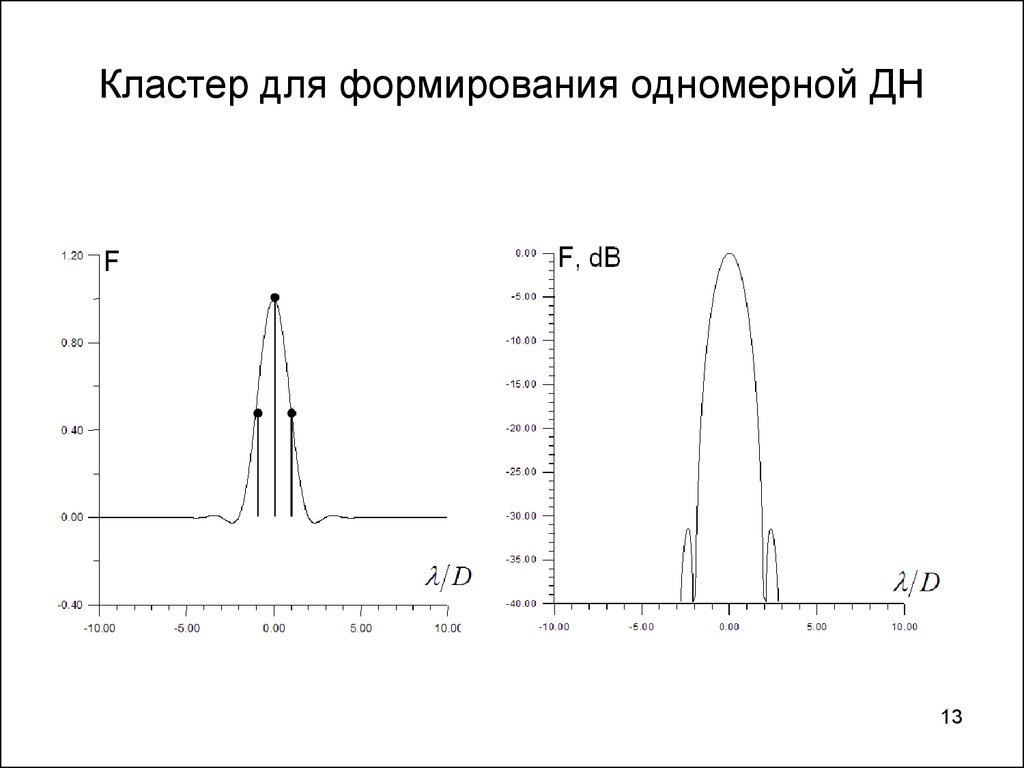
13. Кластер для формирования одномерной ДН

13

14. Формирование одномерной диаграммы из кластеров

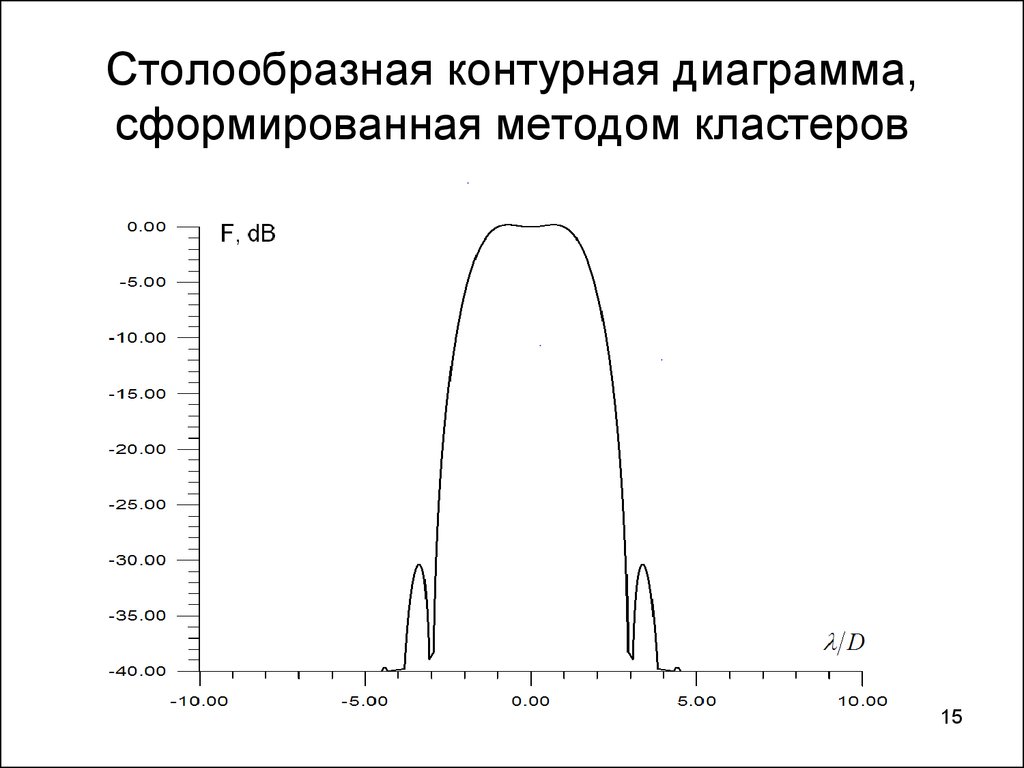
14

15. Столообразная контурная диаграмма, сформированная методом кластеров

15

16. Представление Щелкунова

N 1
Поле эквидистантной линейной решетки:
Пусть
Пусть
x j jd
e
ikud
z
ikux
E (u ) A j e j
j 0
N 1
тогда
E (u) A j eikujd
тогда
E (u ) A j z j
j 0
N 1
j 0
Итак, поле может быть представлено полиномом:
N 1
E ( z z1 )( z z 2 )...( z z N 1 ) ( z z j )
j 1
… и полностью определяется набором комплексных нулей
z j
16

17. Единичная окружность

Модуль величины z exp( jkud) всегда равен единице
Аргумент величины arg( z ) 2 d u
При
d
2
arg( z ) u
Связь между arg( z ) и
не прямая и даже не линейная!!!
Классически u dN
17

18. Для различного шага элементов

При
d
2
arg( z ) ..
При d
При d
2
перекрытие
2
безопасно
arg( z ) 2
d
u
18

19. Управление положением второго нуля

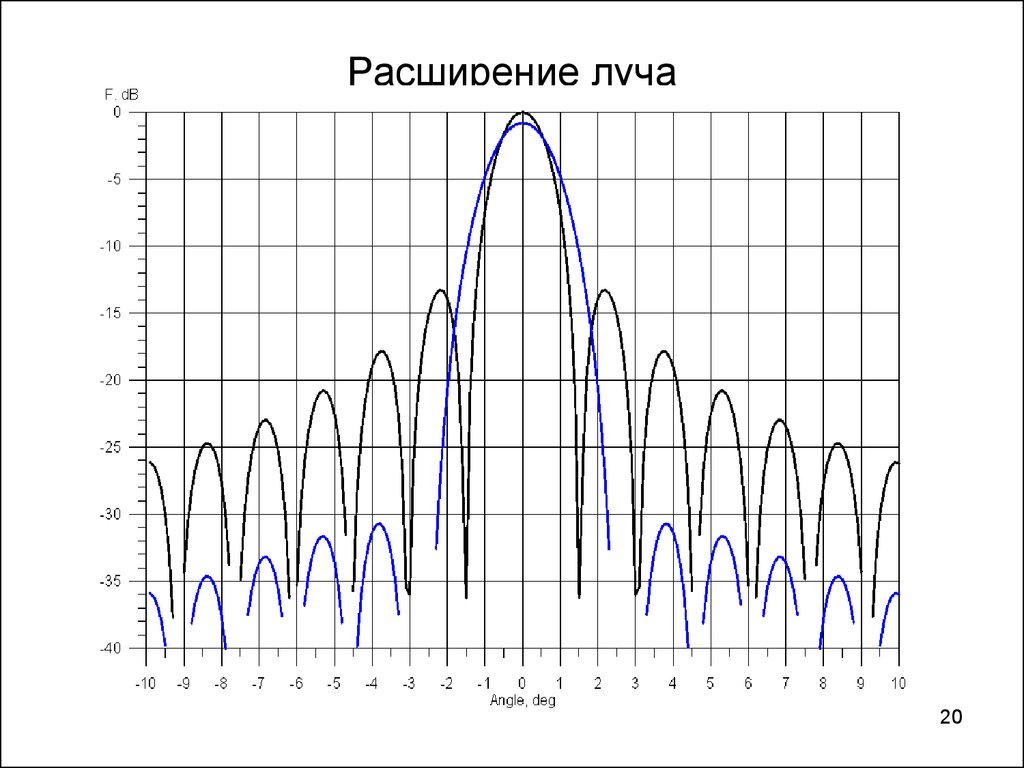
19

20. Расширение луча

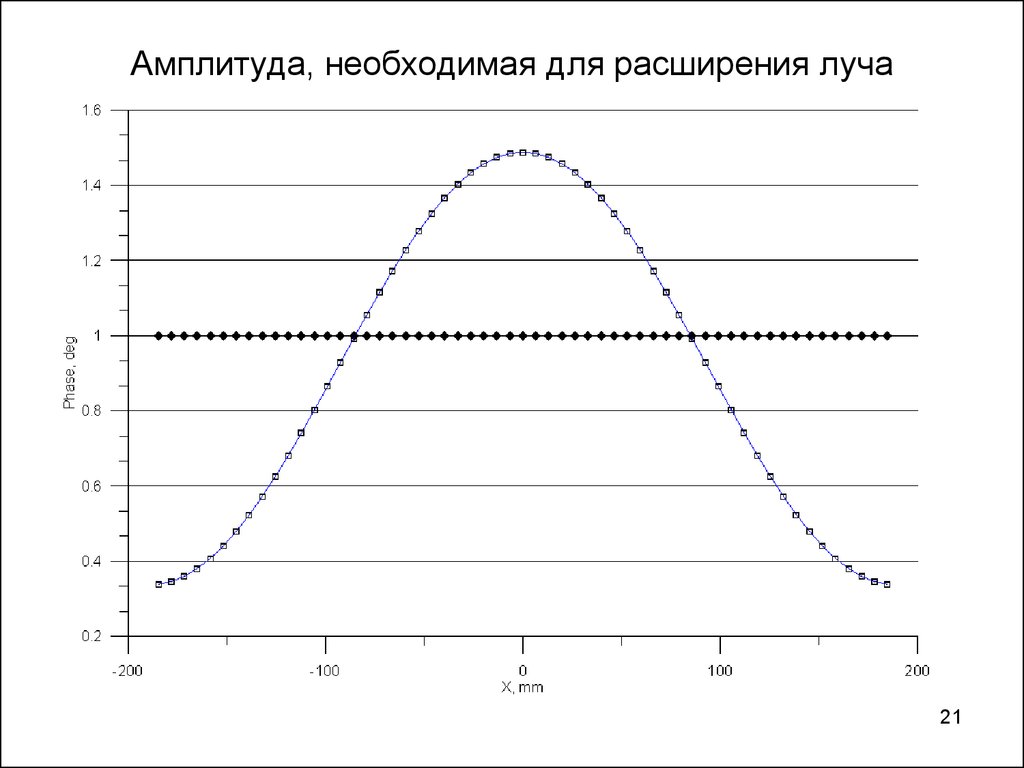
20

21. Амплитуда, необходимая для расширения луча

21

22. Попытка формирования контурной диаграммы

22

23. Приведенные до сих пор примеры касались только линейных решеток

• Представление по Щелкунову затруднительно
распросттранить на двумерный случай
• Метод парциальных диаграмм распространяется с
легкостью
23

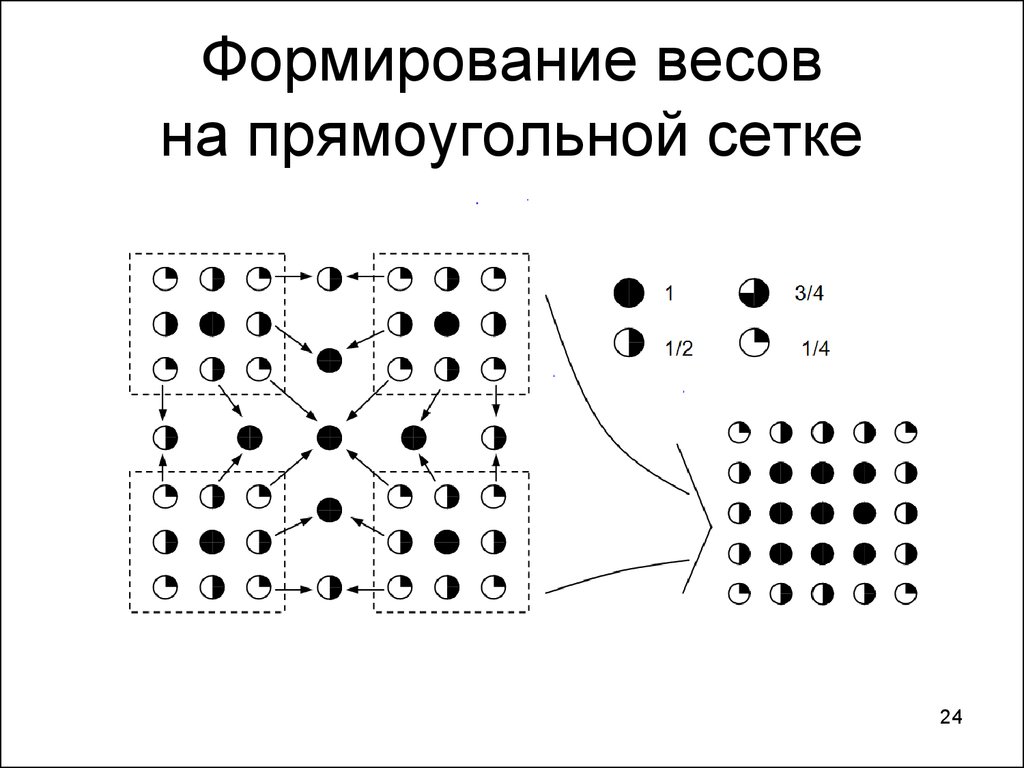
24. Формирование весов на прямоугольной сетке

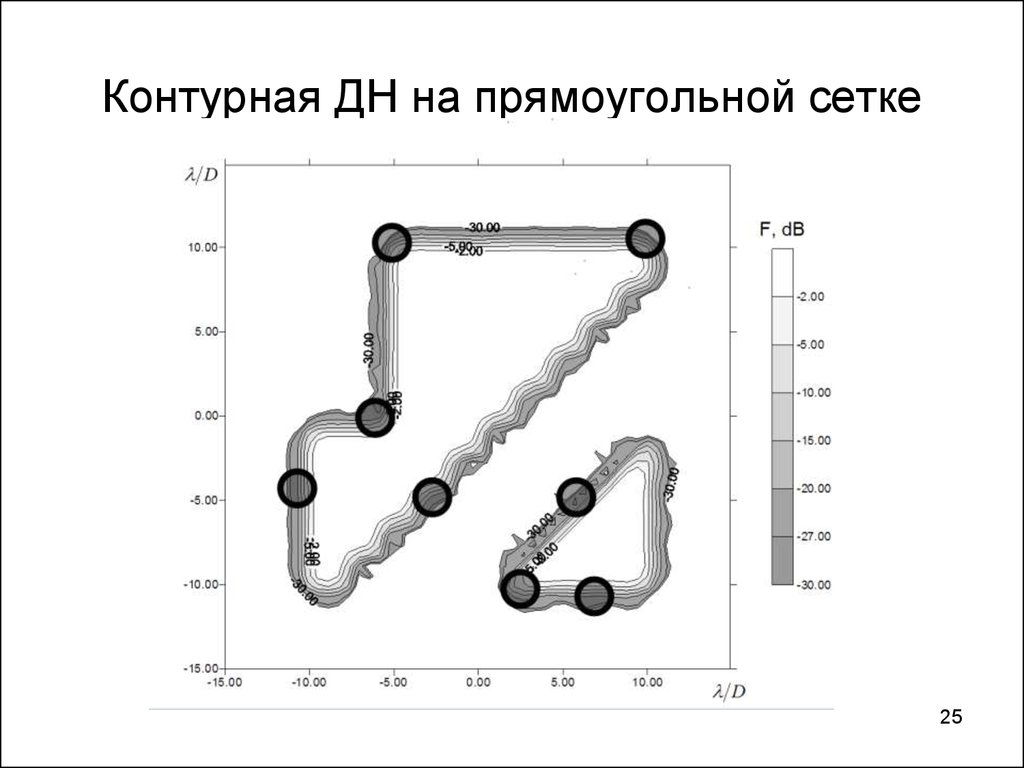
24

25. Контурная ДН на прямоугольной сетке

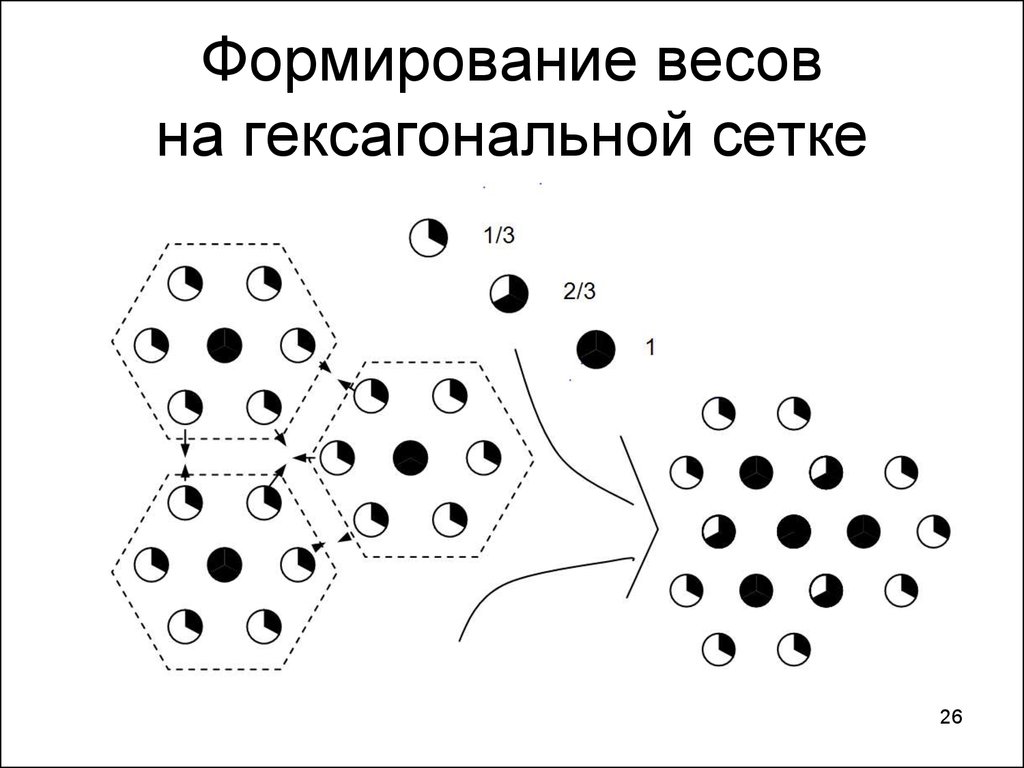
25

26. Формирование весов на гексагональной сетке

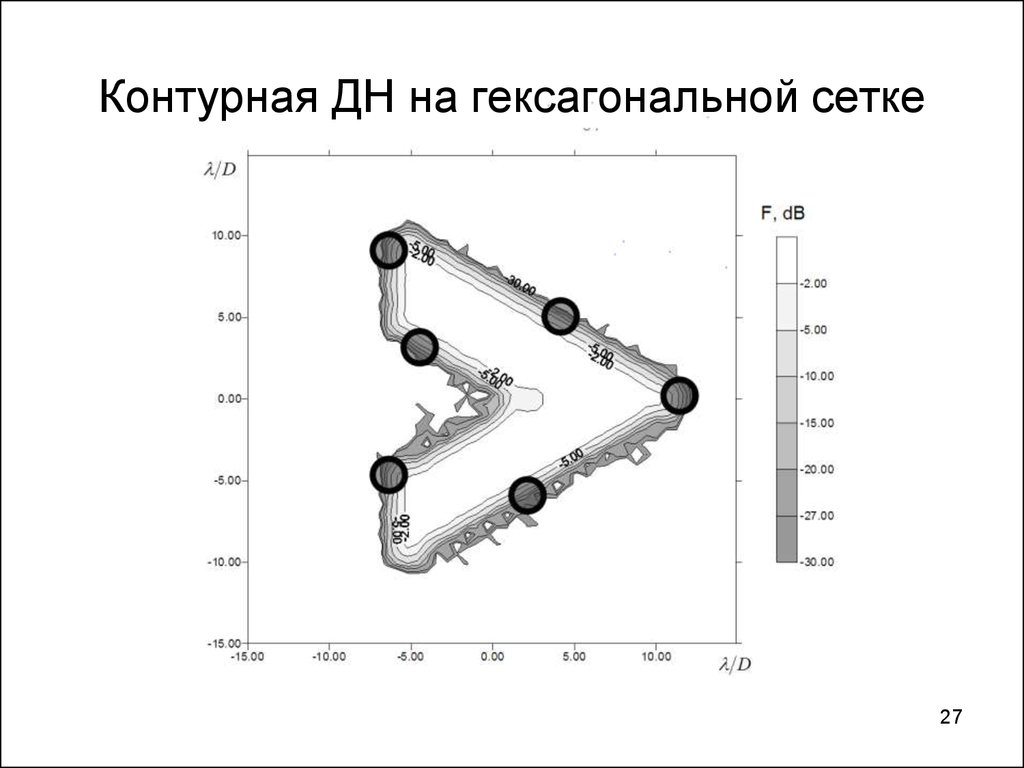
26

27. Контурная ДН на гексагональной сетке

27

28. Типы диаграммоформирования

• Формирование остронаправленного
луча (лучей)
• Создание ДН сложной формы
• Формирование нуля (нулей) в
диаграмме направленности
28

29. Формирование узкого нуля представлением Щелкунова:

• Просто установить в этом направлении
один из нулей полинома
29

30. Формирование узкого нуля методом парциальных диаграмм: (sidelobe canceller)

Сформировать ДН в направлении сигнала
Получить поле E1 направлекния помехи
Сформировать ДН в направлении помехи
Получить поле Е2 с направления помехи
Вычислить Е3 – комплексное отношение полей
Вычислить сумму распределений для ДН в направлении цели и
в направлении помехи – с коэффициентом минус Е3
• Полученная сумма сформирует ДН с нулем в направлении
помехи.
30

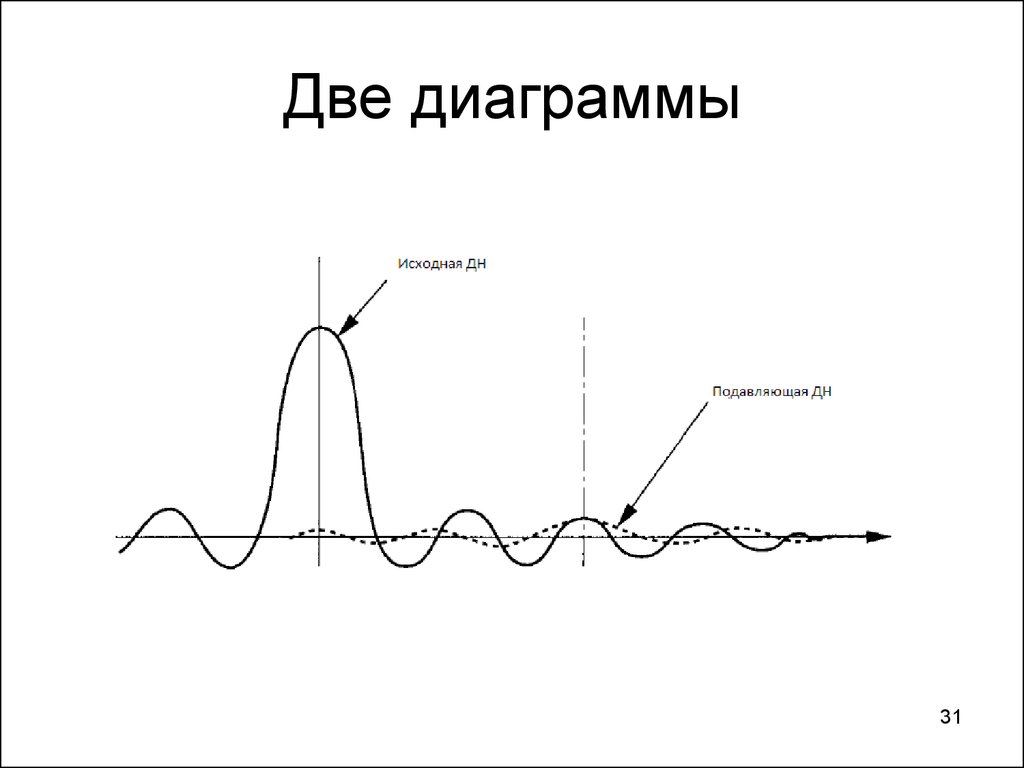
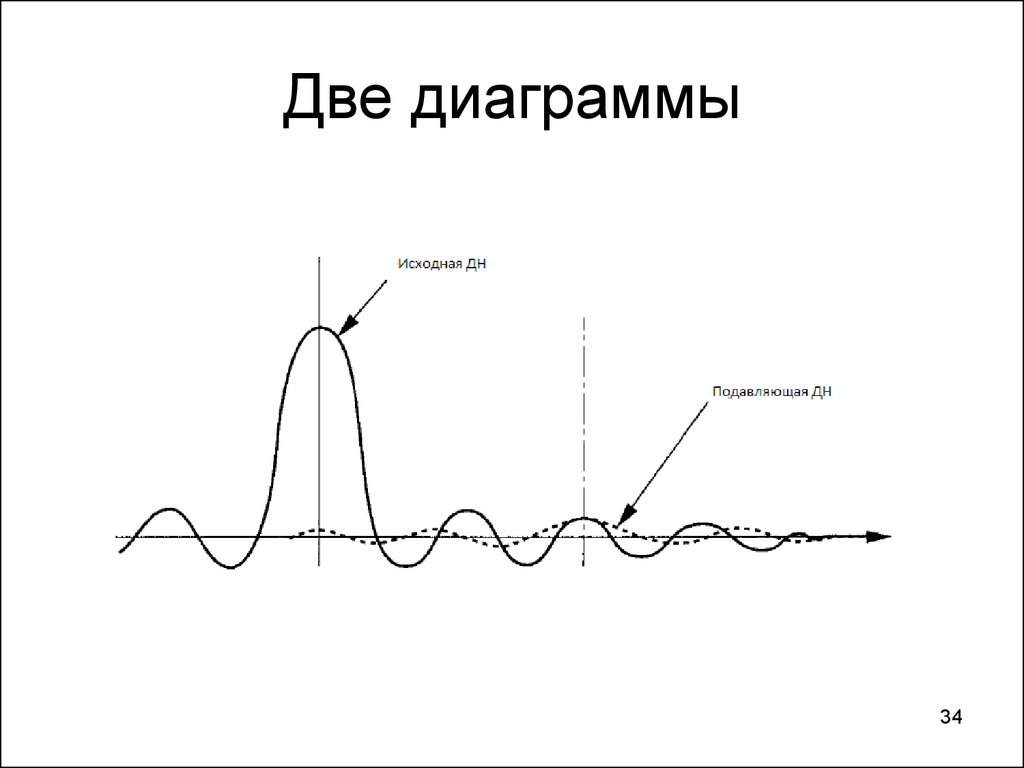
31. Две диаграммы

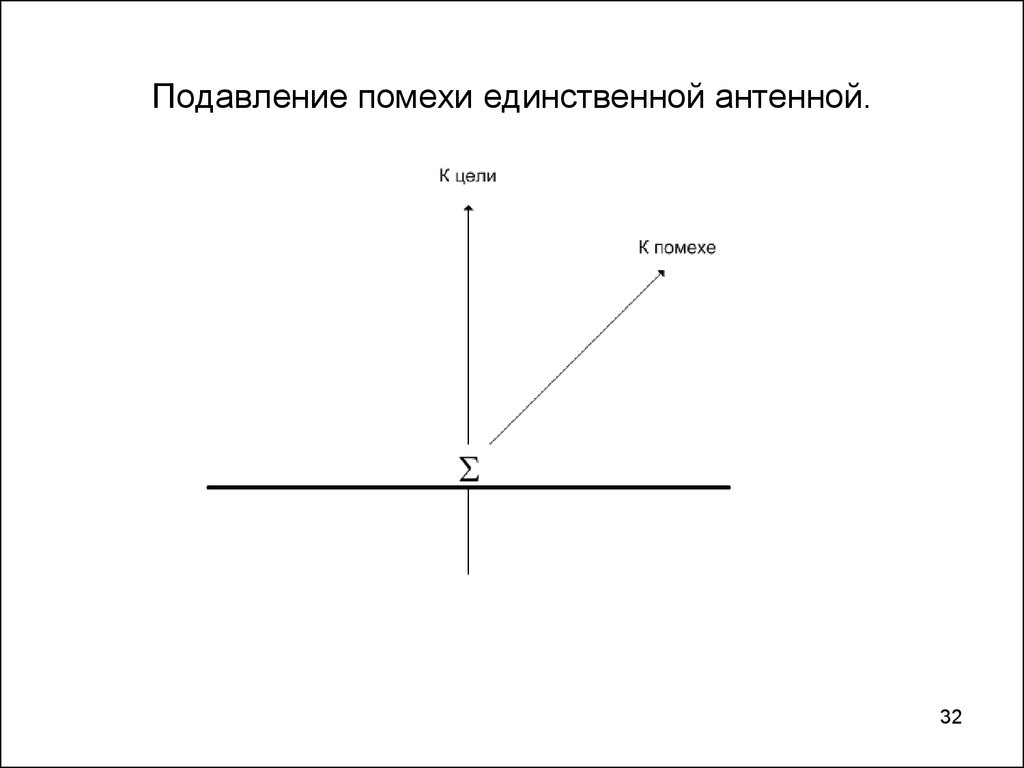
31

32. Подавление помехи единственной антенной.

32

33. Дополнительная антенна для подавления помехи

33

34. Две диаграммы

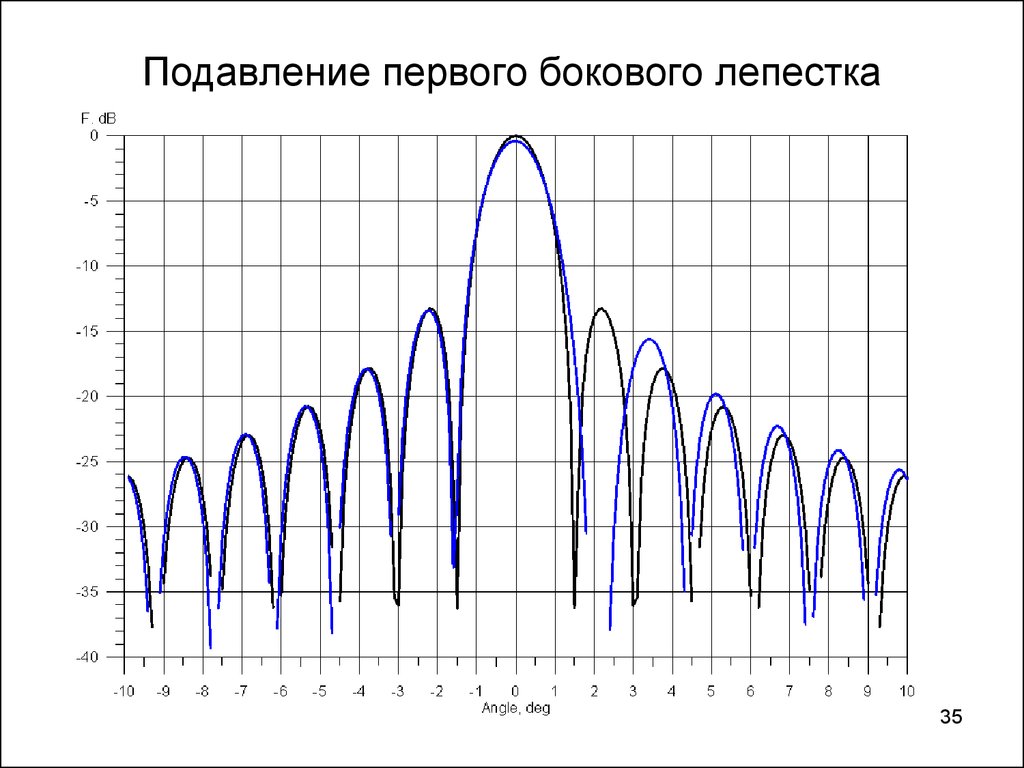
34

35. Подавление первого бокового лепестка

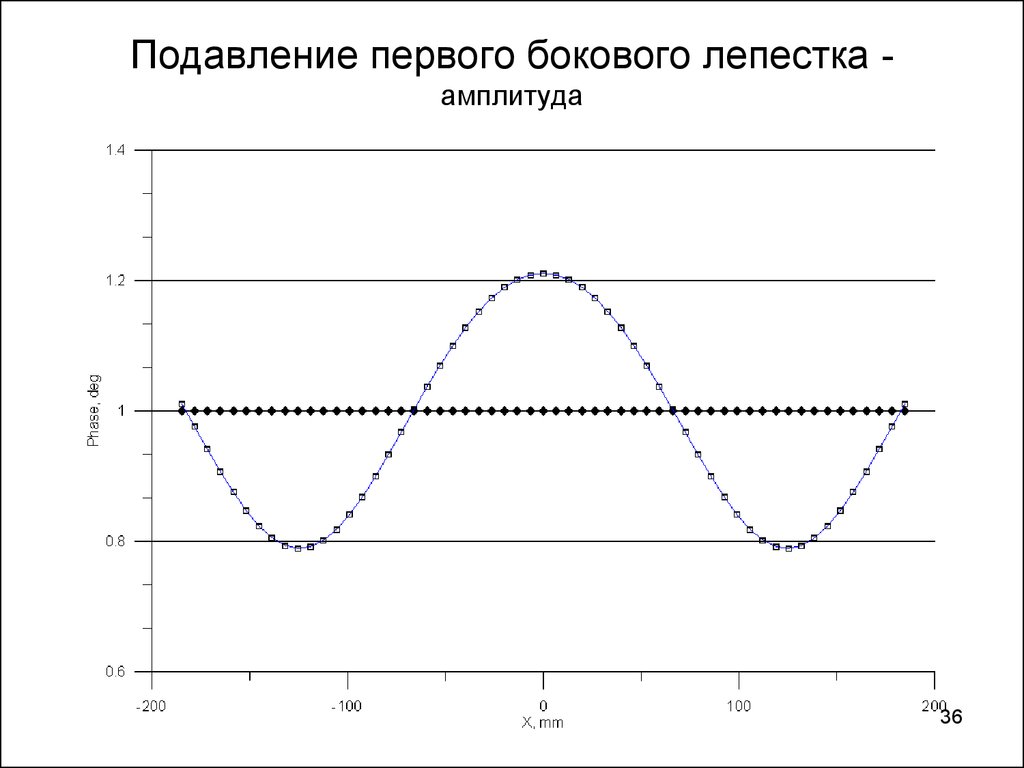
35

36. Подавление первого бокового лепестка - амплитуда

Подавление первого бокового лепестка амплитуда
36

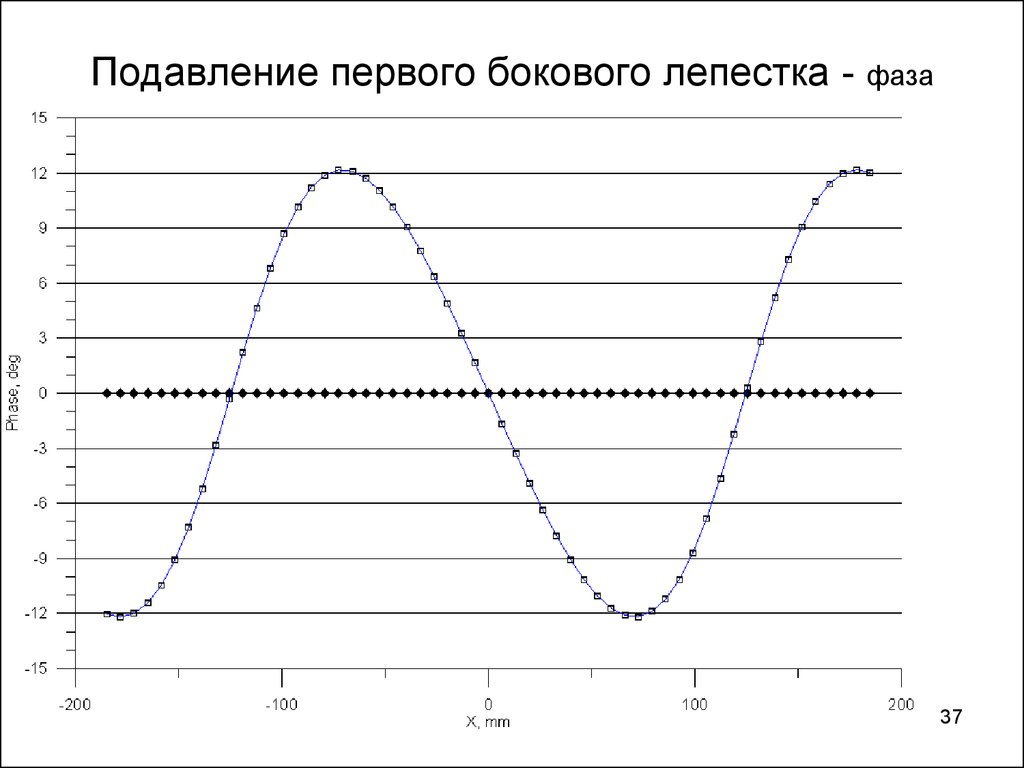
37. Подавление первого бокового лепестка - фаза

37

38. Сумма двух полей в апертуре

38

39. К вопросу о точности установки корректирующей диаграммы (точность определения направления на помеху)

39

40. Подавление первого бокового лепестка

40

41. Подавление помехи в главном луче

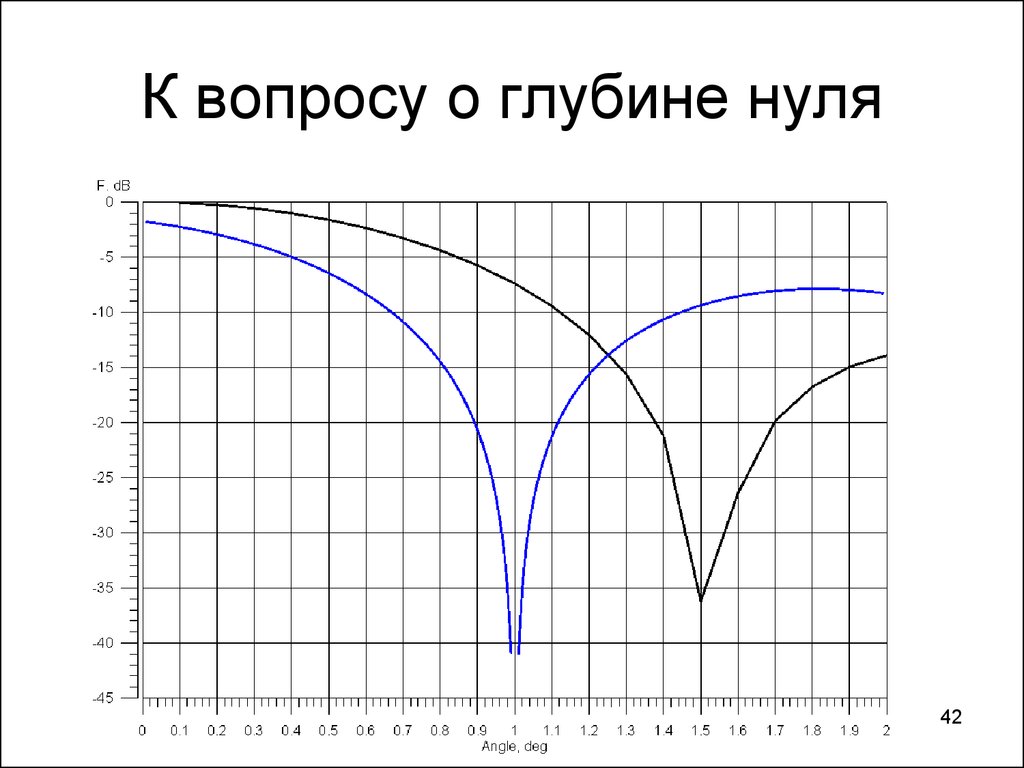
41

42. К вопросу о глубине нуля

42

43. Факторы, влияющие на глубину нуля

• Точность установки фазы
• Точность установки амплитуды
• Количество каналов антенны
• Точность определения отношения
полей.
Ошибка в один градус в первом боковом лепестке «стоит» -50 дБ
43

44. К вопросу о глубине нуля

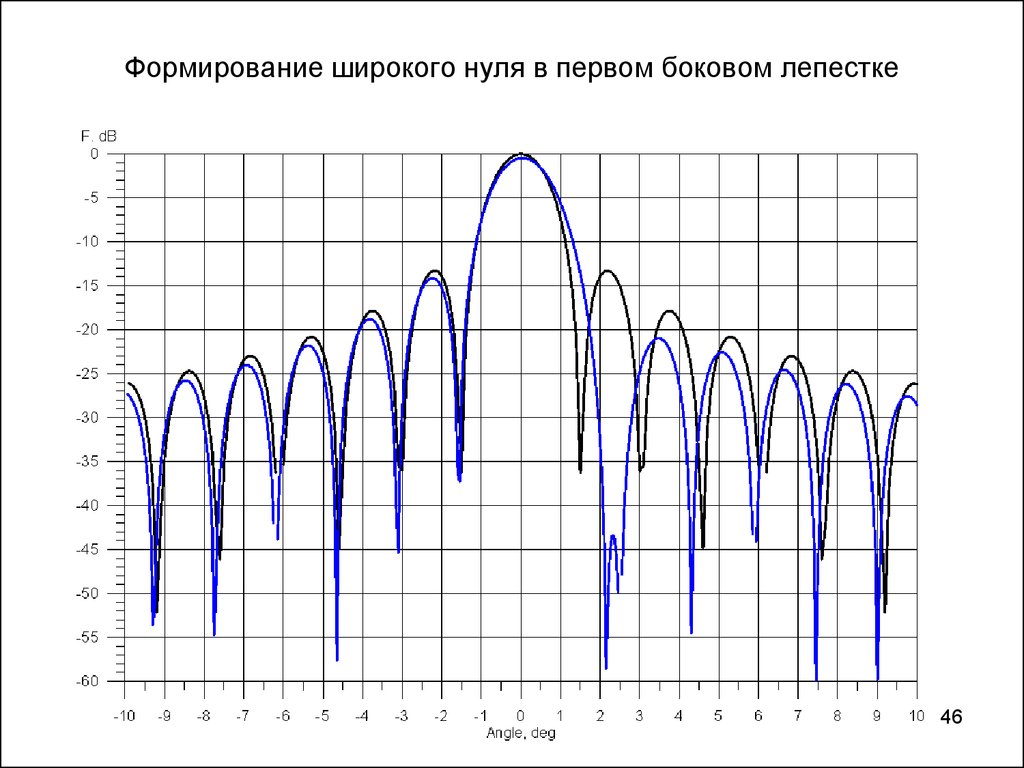
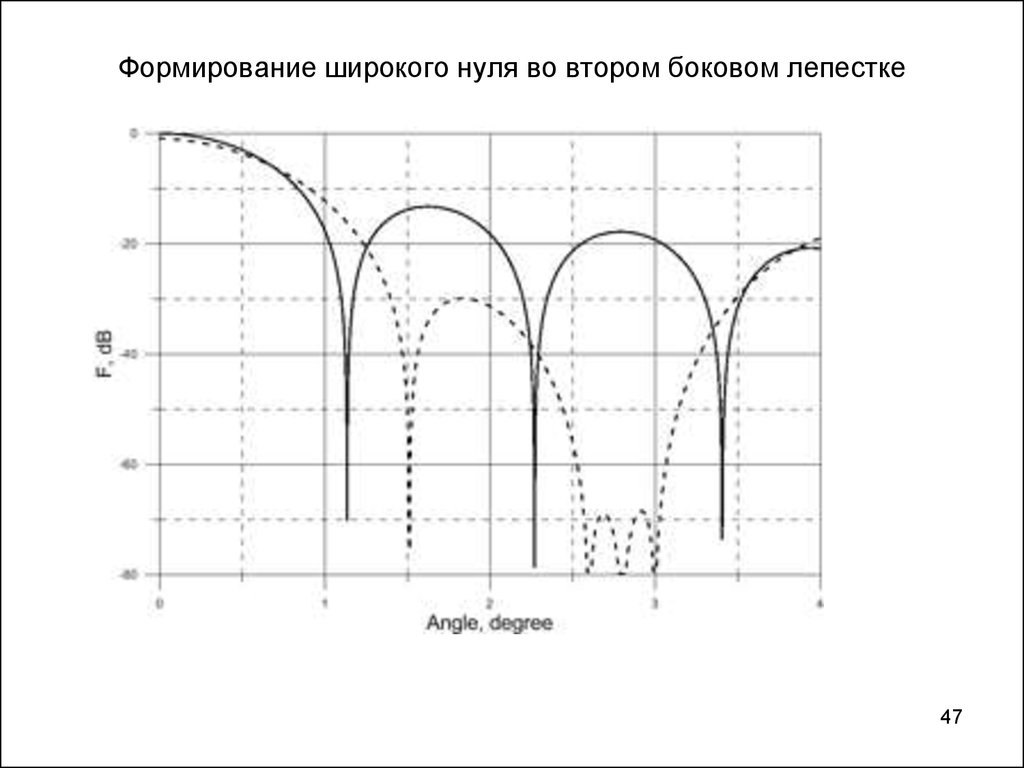
44

45. Для антенн с конечной шириной полосы

• Диаграмма масштабируется с частотой
• Необходимо формировать не только глубокий, но и
широкий ноль.
• Для этого, можно использовать несколько близко
расположенных нулей.
45

46. Формирование широкого нуля в первом боковом лепестке

46

47. Формирование широкого нуля во втором боковом лепестке

47