Похожие презентации:
Фазированные антенные решетки и их назначение. Лекция 2
1. Структура курса
• Введение– Фазированные антенные решетки и их назначение
• Теория ФАР
– Основные характеристики ФАР
– Диаграммоформирование в ФАР
• Техника ФАР
–
–
–
–
Схемы возбуждения ФАР
Широкополосные ФАР
Принципы конструирования ФАР
Калибровка и контроль ФАР
1
2. Фазированные антенные решетки
Антенная решетка – система токов,разнесенных в пространстве,
имеющая дискретную структуру
2
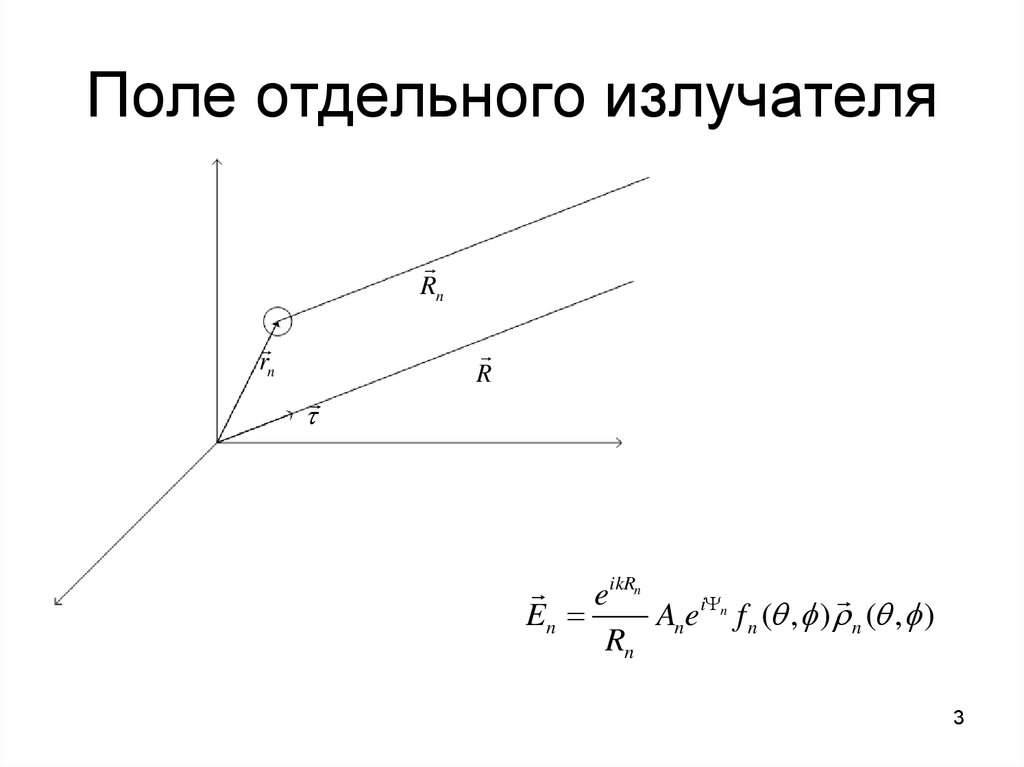
3. Поле отдельного излучателя
Rnrn
R
eikRn
En
An ei n f n ( , ) n ( , )
Rn
3
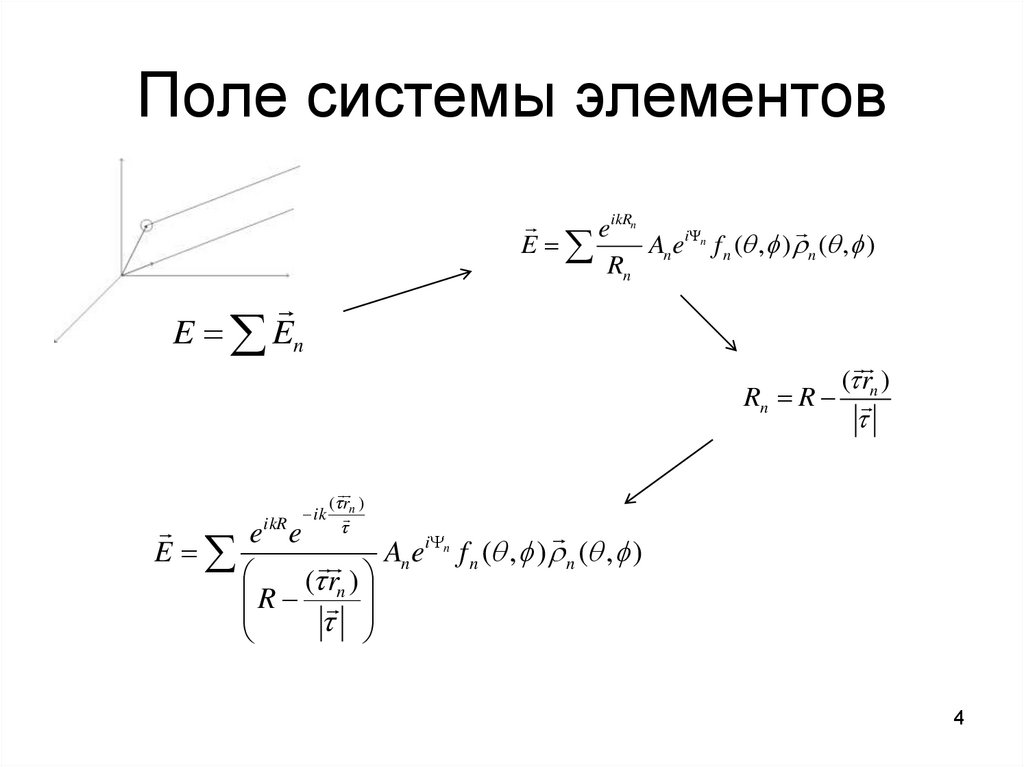
4. Поле системы элементов
eikRnE
An ei n f n ( , ) n ( , )
Rn
E En
( rn )
Rn R
( rn )
ik
ikR
e e
i n
E
A
e
f
(
,
)
n
n
n ( , )
(
r
)
n
R
4
5. Поле системы элементов
Упрощая :eikR
E
R
e
ik ( rn )
An e
i n
f n ( , ) n ( , )
Член перед суммой представляет собой типовое
амплитудное ослабление и фазовый набег. Итого, для ДН ФАР имеем
i n
ik ( rn )
f ( , ) An e f n ( , ) n ( , )e
5
6. Поле системы элементов
Если все элементы одинаковы, то :Итого :
f n ( , ) f ( , )
n ( , ) ( , )
i n ik ( rn )
f ( , ) f ( , ) ( , ) An e e
Или, проще :
ik ( rn )
f ( , ) f ( , ) ( , ) An e
6
7. ДН ФАР
Диаграмма направленности ФАРik ( rn )
f ( , ) f ( , ) ( , ) An e
Есть произведение ДН элемента
(парциальная ДН)
На множитель решетки
f ( , ) ( , )
A e
ik ( rn )
n
7
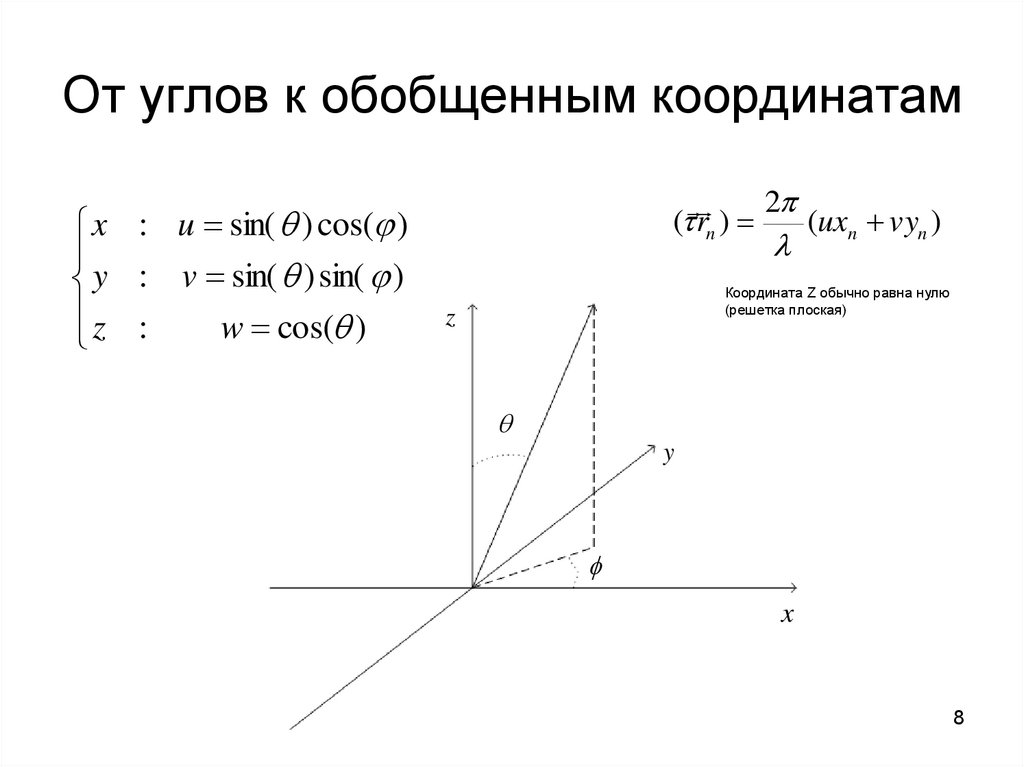
8. От углов к обобщенным координатам
x : u sin( ) cos( )y : v sin( ) sin( )
z :
w cos( )
2
( rn )
(uxn vyn )
Координата Z обычно равна нулю
(решетка плоская)
z
y
x
8
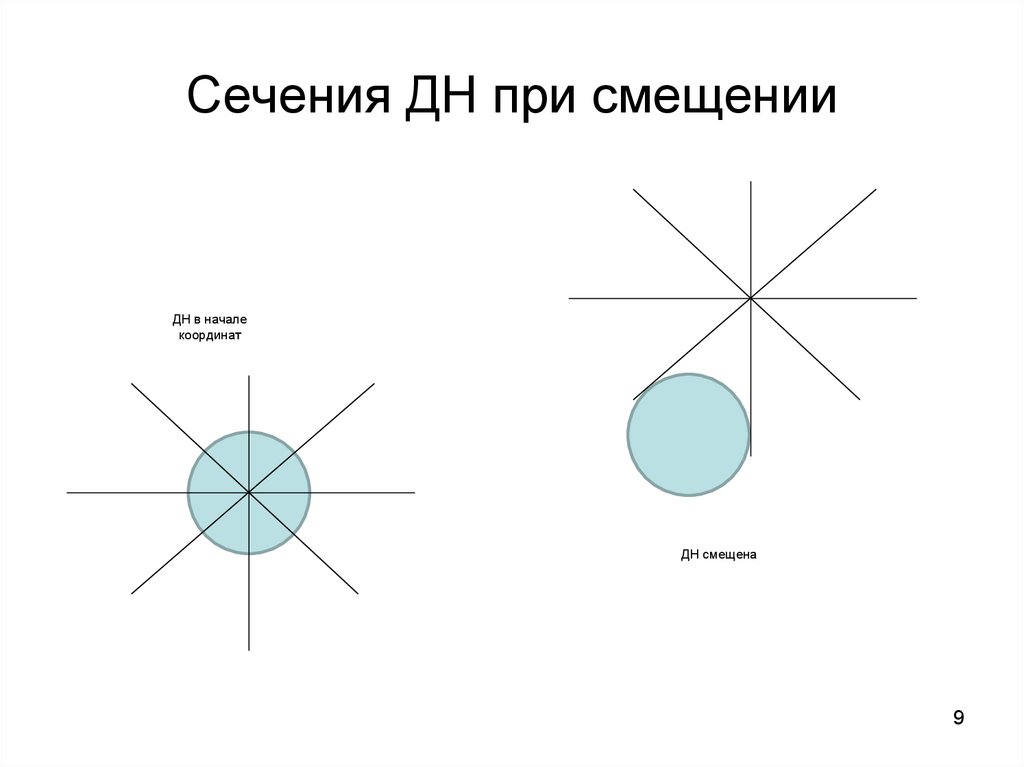
9. Сечения ДН при смещении
ДН в началекоординат
ДН смещена
9
10. От углов к обобщенным координатам
x : u cos( El ) sin( Az )v sin( El )
y :
z : w cos( El ) cos( Az )
y
x
El
Az
z
2
( rn )
(uxn vyn )
Координата Z обычно равна нулю
(решетка плоская)
10
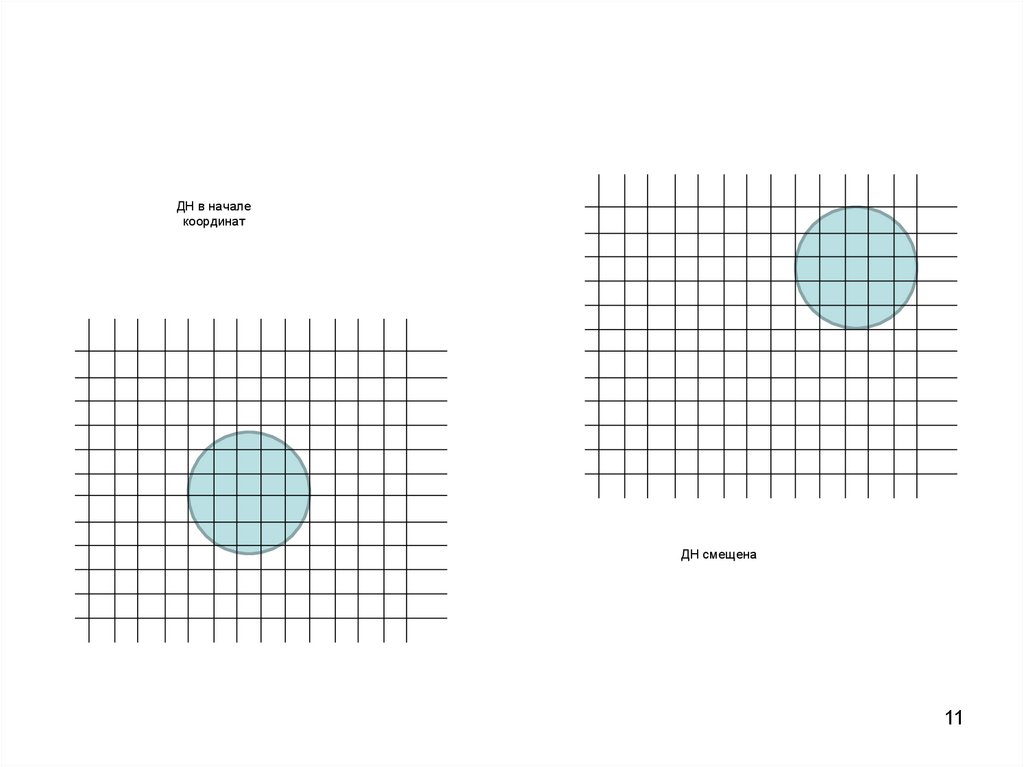
11.
ДН в началекоординат
ДН смещена
11
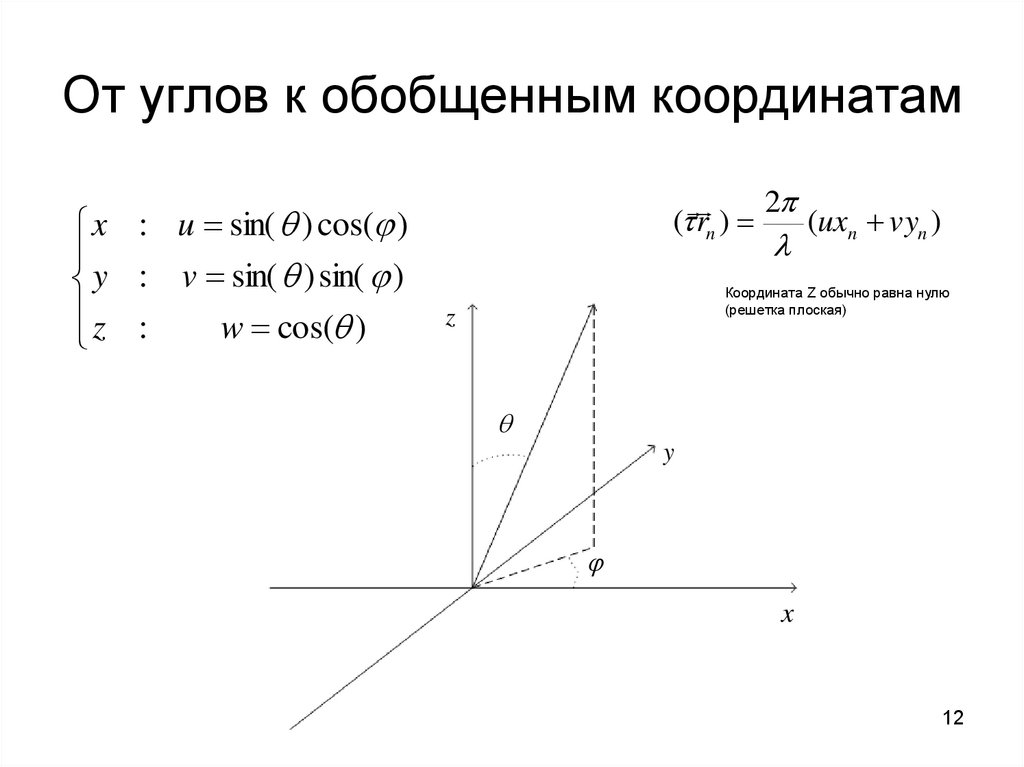
12. От углов к обобщенным координатам
x : u sin( ) cos( )y : v sin( ) sin( )
z :
w cos( )
2
( rn )
(uxn vyn )
Координата Z обычно равна нулю
(решетка плоская)
z
y
x
12
13. От углов к обобщенным координатам
x : u cos( El ) sin( Az )v sin( El )
y :
z : w cos( El ) cos( Az )
y
x
El
Az
z
2
( rn )
(uxn vyn )
Координата Z обычно равна нулю
(решетка плоская)
13
14. Множитель решетки
A en
ik ( rn )
A n e
i
2
( uxn vy n )
Перепишем, с использованием дельта-функций :
A ne
i
2
( uxn vyn )
A ( x, y) ( x xn , y yn )e
i
2
( ux vy )
dxdy
2
i ( ux vy )
~
E (u, v) A ( x, y)e
dxdy
Итак, множитель решетки есть преобразование Фурье
от распределения в апертуре (двумерное)
14
15. Линейная решетка
xn nd x (n N ... N )2
2
yn 0
Нечетное число элементов, числом N+1
zn 0
xn n 1 d x (n N ... N 1)
2
2
2
Четное число элементов, числом N
yn 0
zn 0
15
16. Равномерное амплитудное распределение в линейной решетке конечных размеров
Амплитудное распределение A представляет собой произведениегребенки Дирака (она бесконечна)
на высекающую функцию (она столообразная)
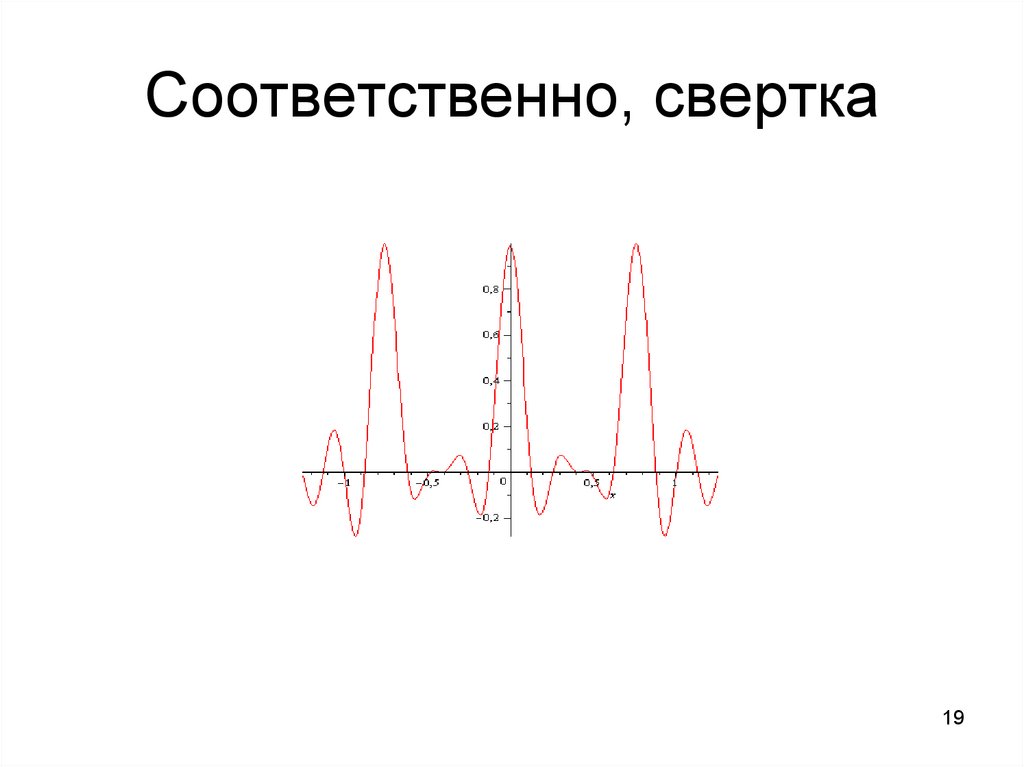
Соответственно, фурье-образ произведения – это свертка образов
16
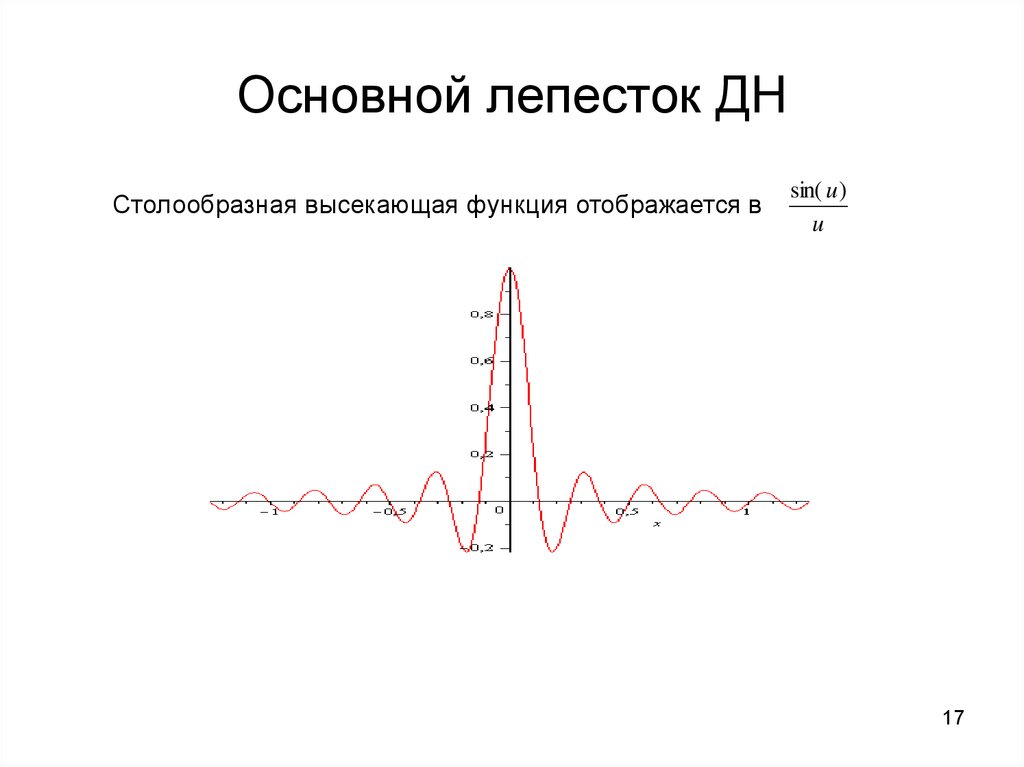
17. Основной лепесток ДН
Столообразная высекающая функция отображается вsin( u)
u
17
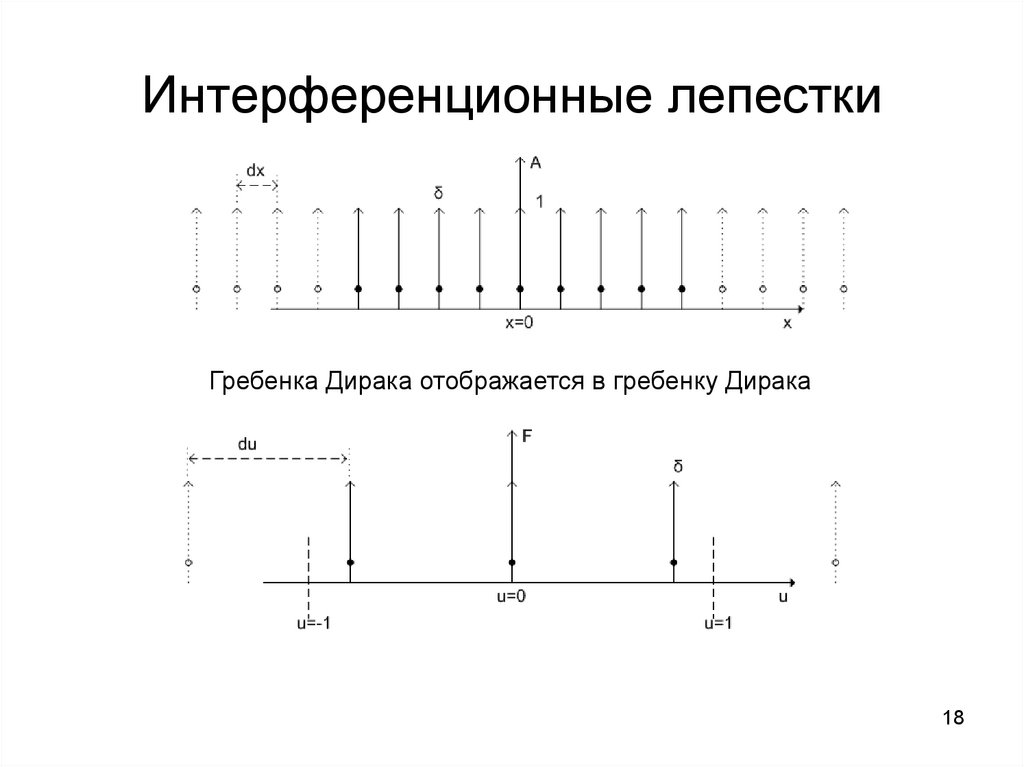
18. Интерференционные лепестки
Гребенка Дирака отображается в гребенку Дирака18
19. Соответственно, свертка
1920. Равномерное амплитудное распределение в линейной решетке конечных размеров
Амплитудное распределение A представляет собой произведениегребенки Дирака (она бесконечна)
на высекающую функцию (она столообразная)
Соответственно, фурье-образ произведения – это свертка образов
20
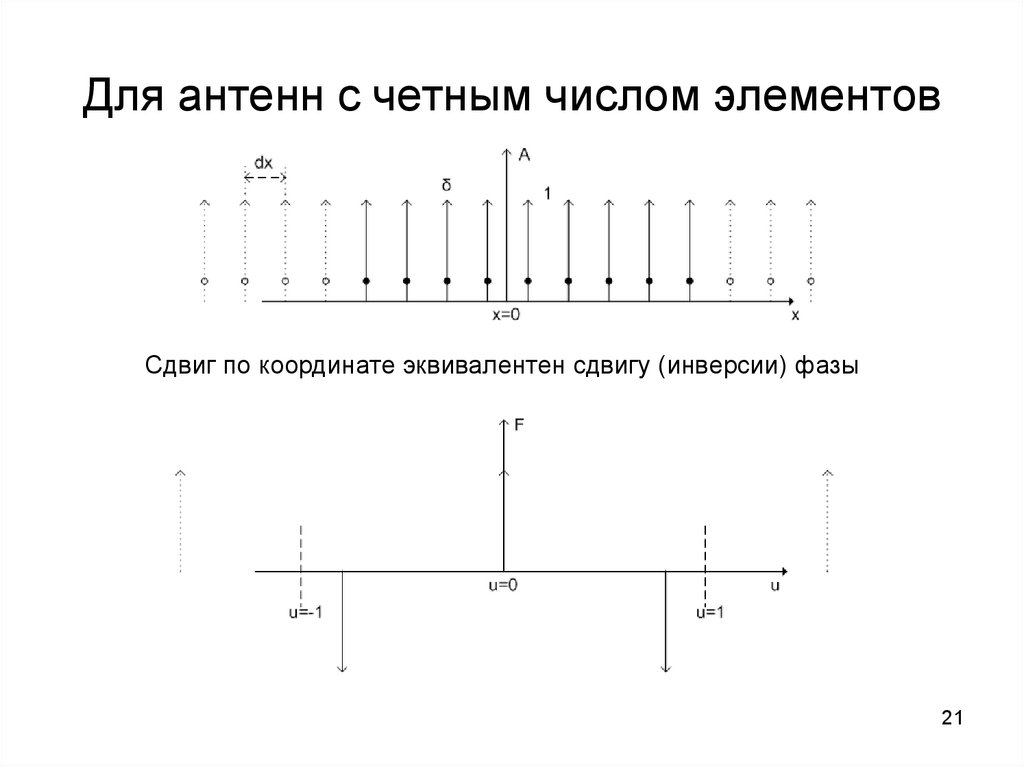
21. Для антенн с четным числом элементов
Сдвиг по координате эквивалентен сдвигу (инверсии) фазы21
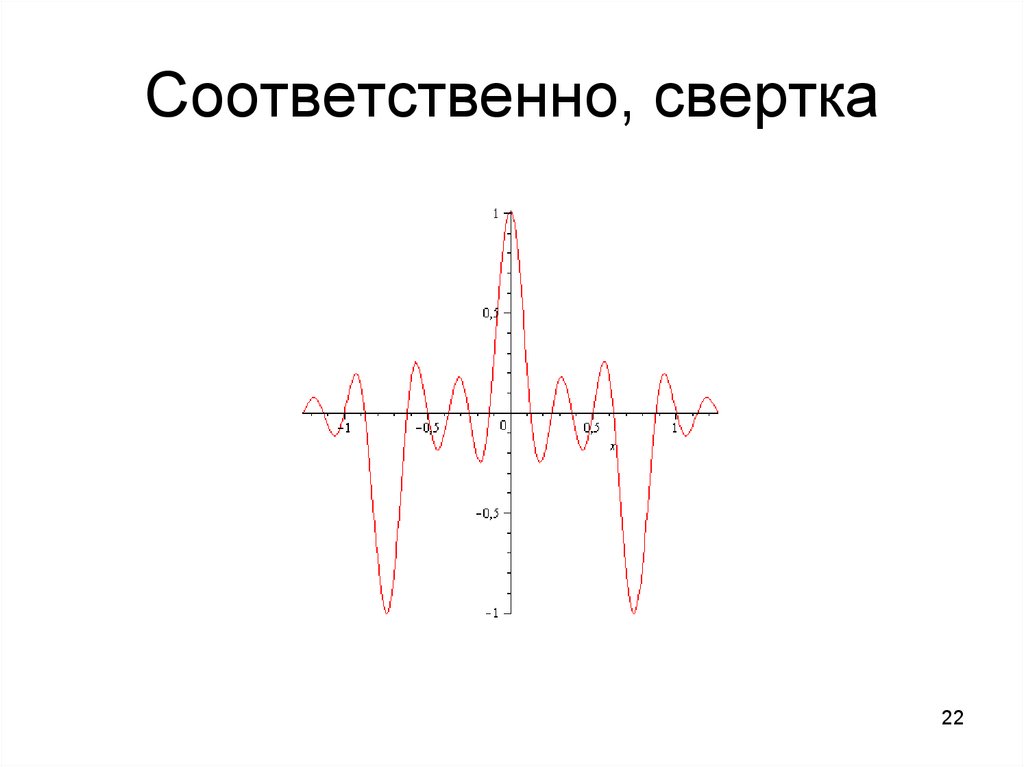
22. Соответственно, свертка
2223. Количественные соотношения
Ширина основного луча - 0.88 (линейная решетка или прямоугольная)D
Вообще форма луча определяется апертурой и распределением в ней
Расстояние между интерференционниками: см фазу
i
2
( uxn vy n )
23
24. Количественные соотношения
Расстояние между интерференционниками: см фазуi
2
( uxn vy n )
Условие возникновения:
2
( u1 d x )
2
(u 2 d x ) 2
- фазовый набег на один шаг решетки
одинаков (с точностью до 360) для соседних направлений
dx
( u 2 u1 ) 1
или
dx
u 1
24
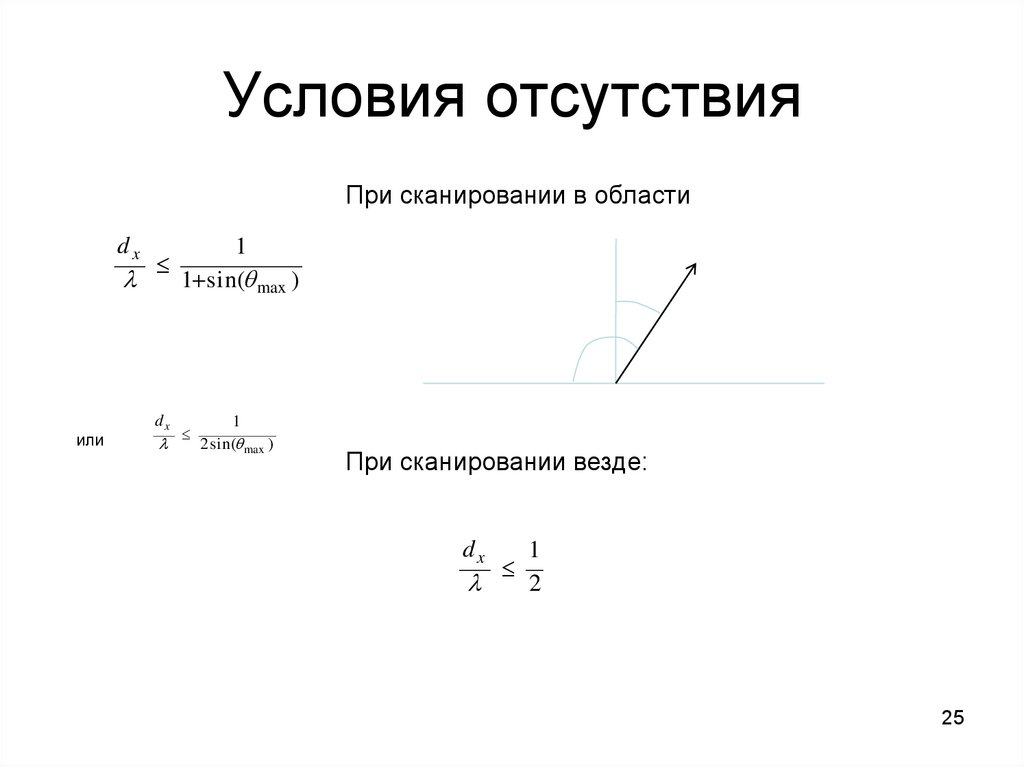
25. Условия отсутствия
При сканировании в областиdx
1
1 sin( max )
или
dx
1
2 sin( max )
При сканировании везде:
dx
1
2
25
26. Интерференционные лепестки оказывают существенное влияние на характеристики антенны
(в большинстве случаев отрицательное)• Помехоустойчивость (ЭМС)
• Коэффициент усиления (КНД)
• Область сканирования
26
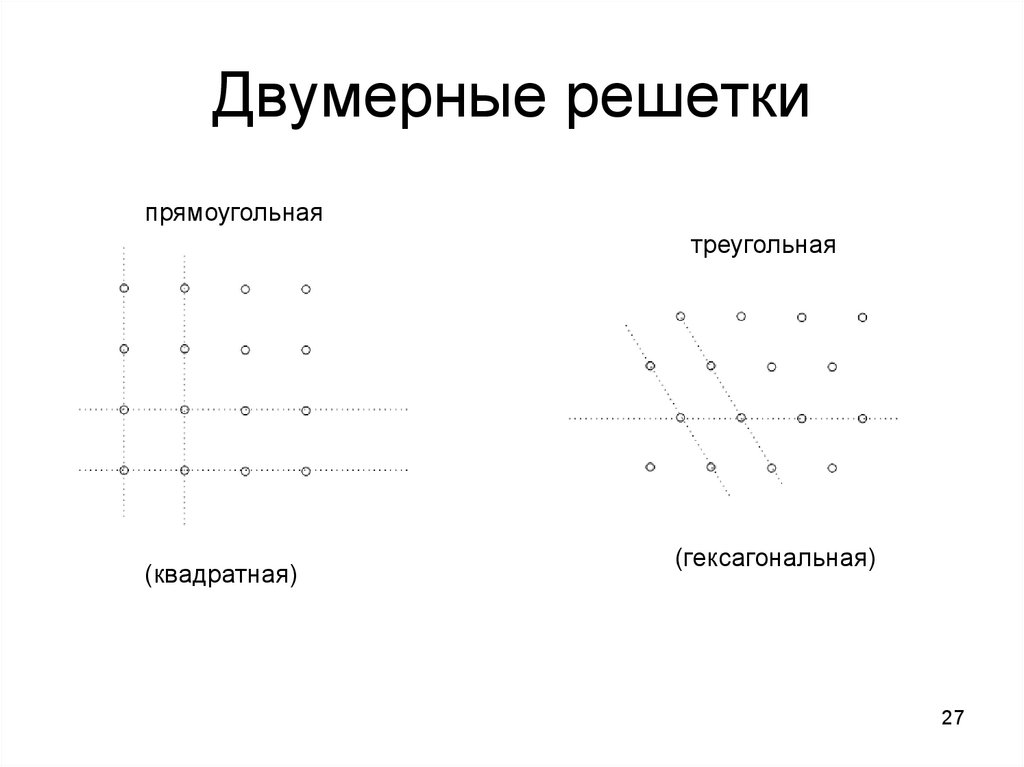
27. Двумерные решетки
прямоугольнаятреугольная
(квадратная)
(гексагональная)
27
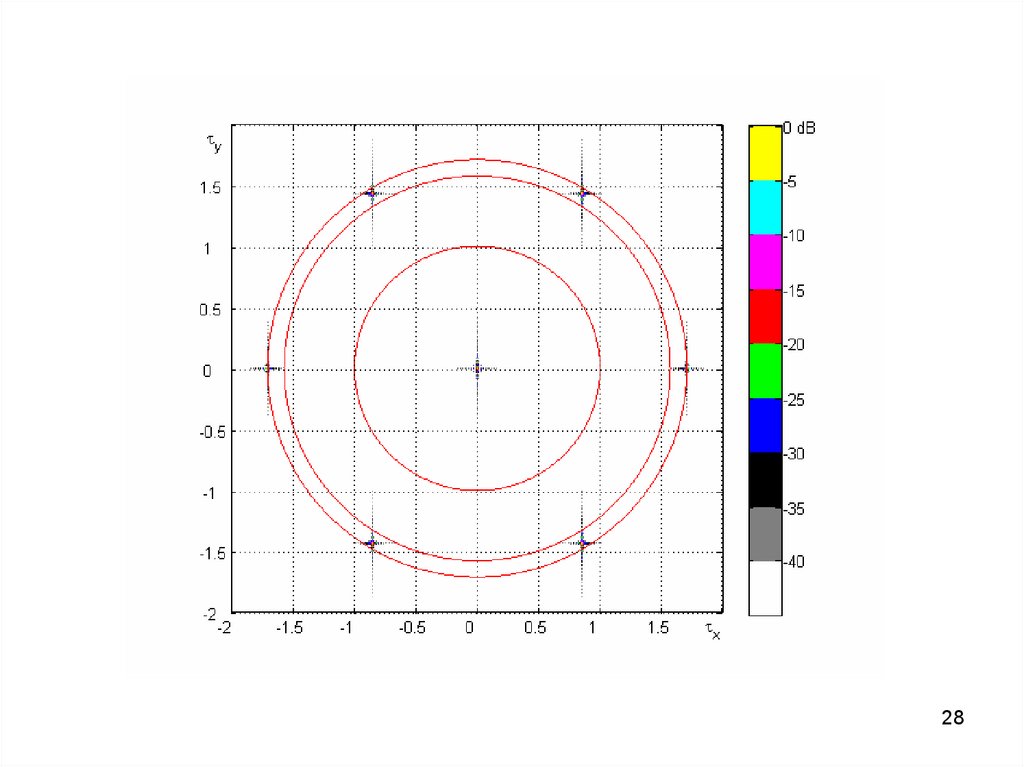
28.
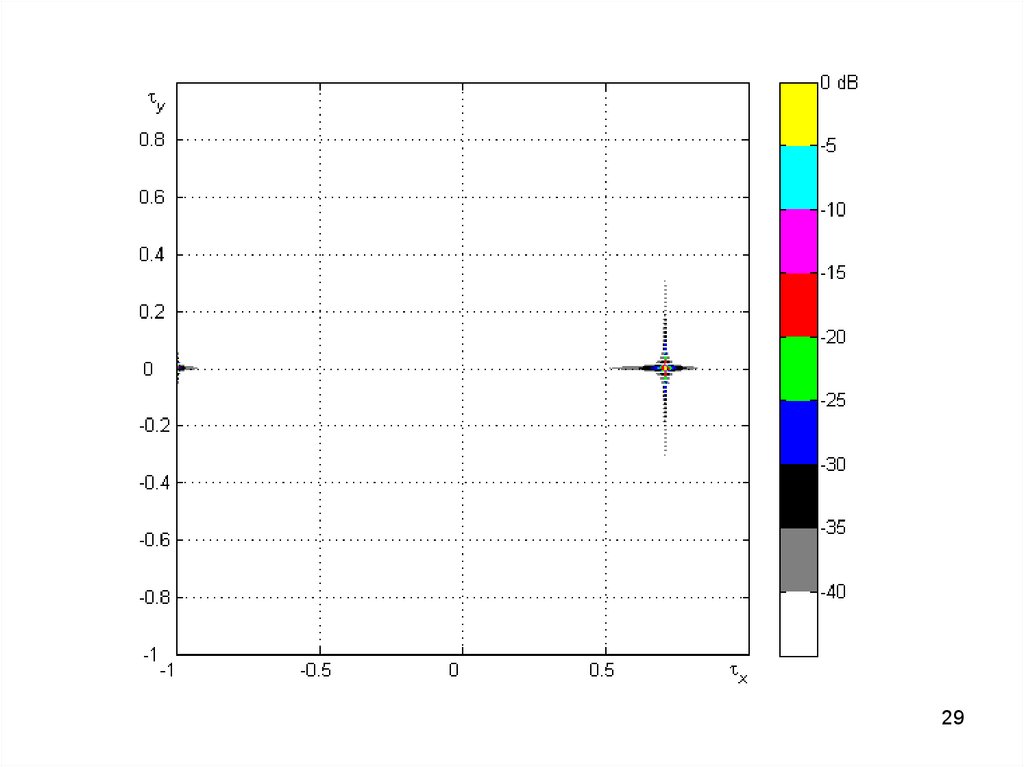
2829.
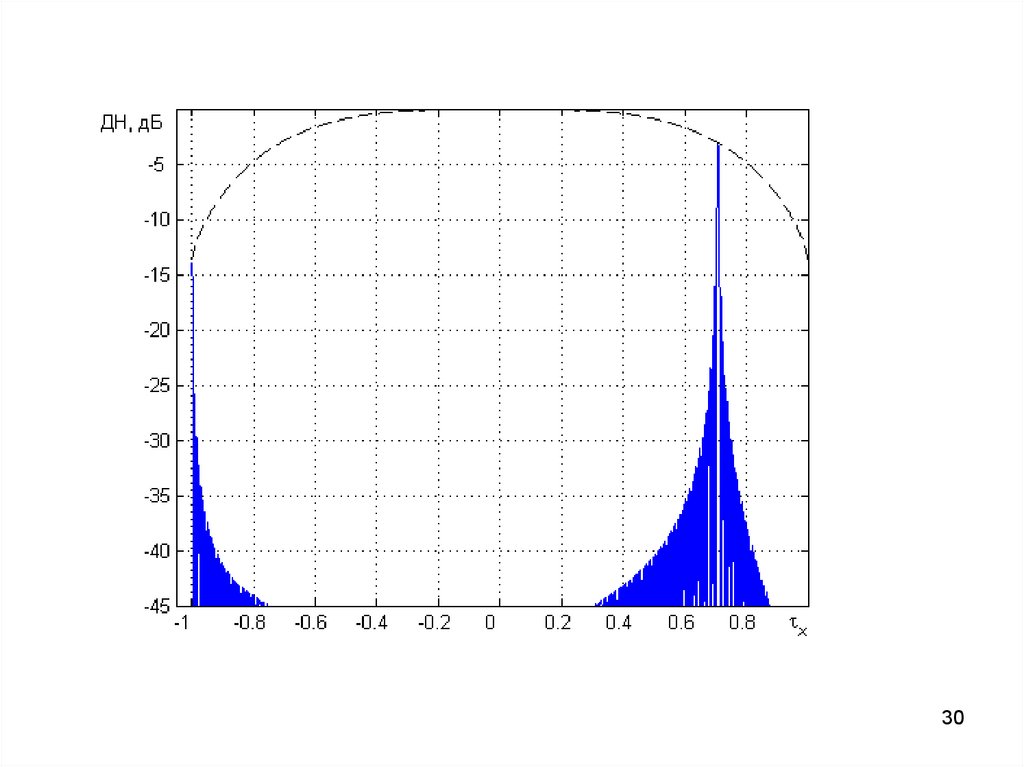
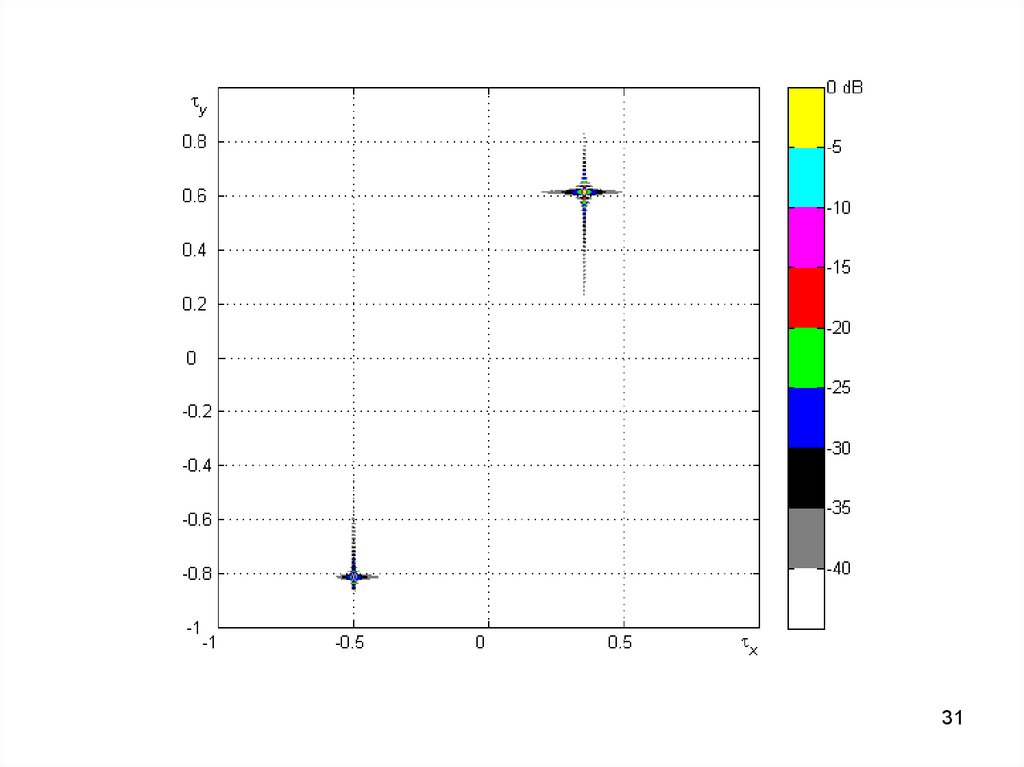
2930.
3031.
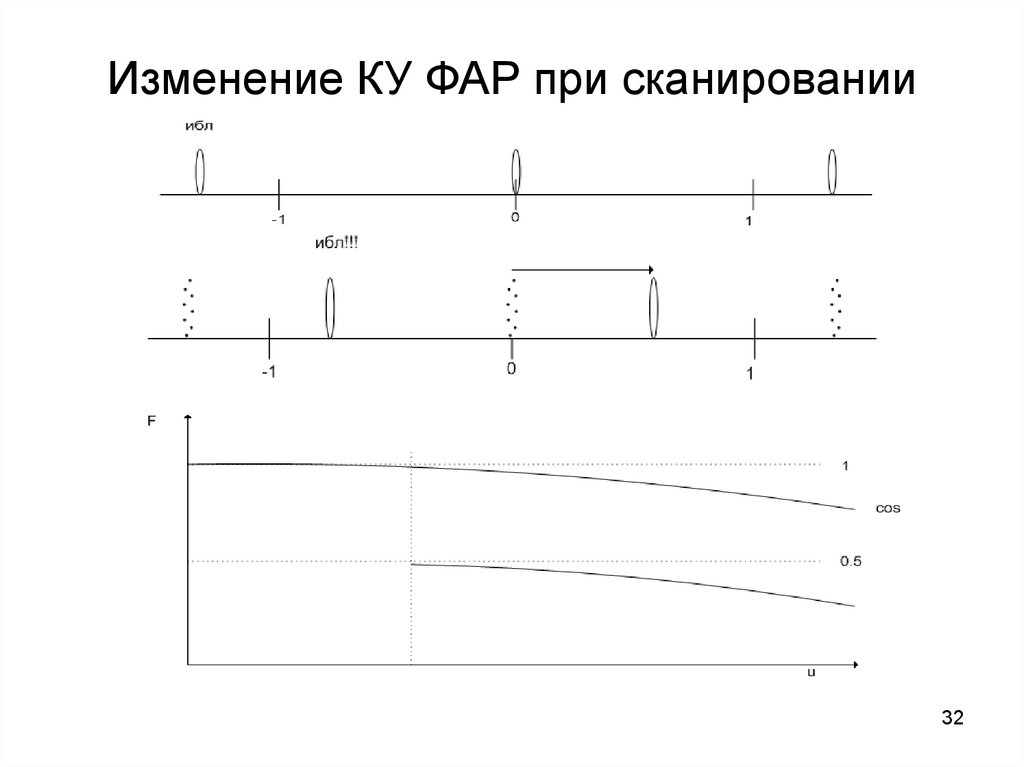
3132. Изменение КУ ФАР при сканировании
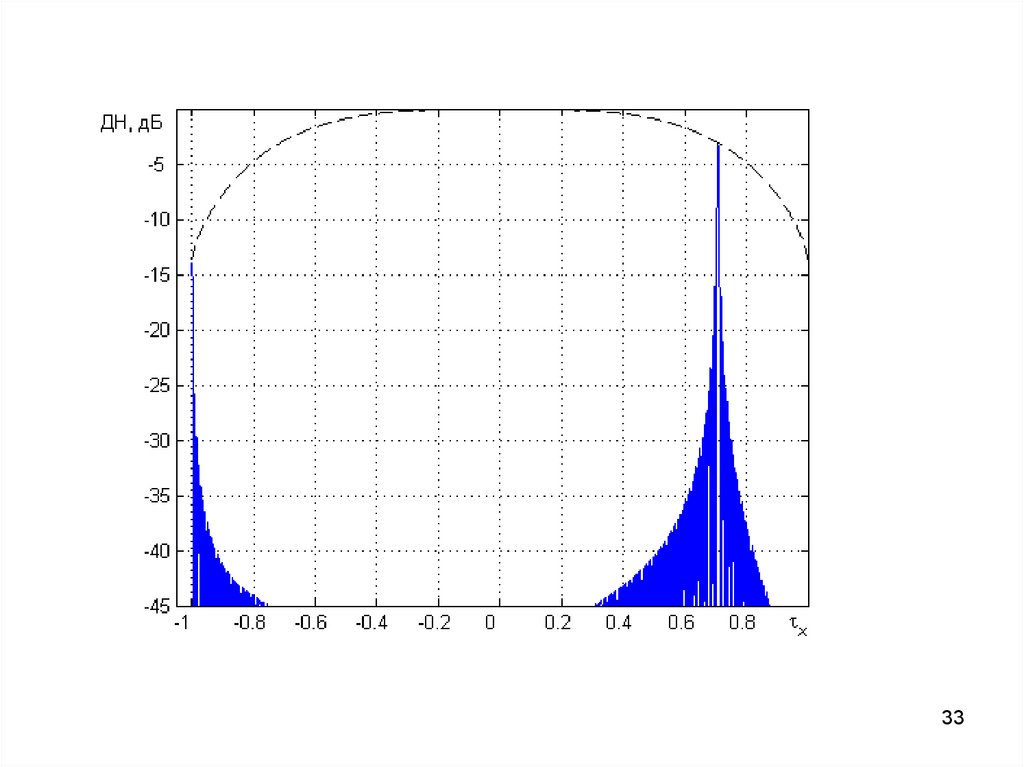
3233.
3334. Методы подавления ИБЛ
За счет уменьшения шага решетки
За счет подбора ДН излучателя
За счет неэквидистантной расстановки
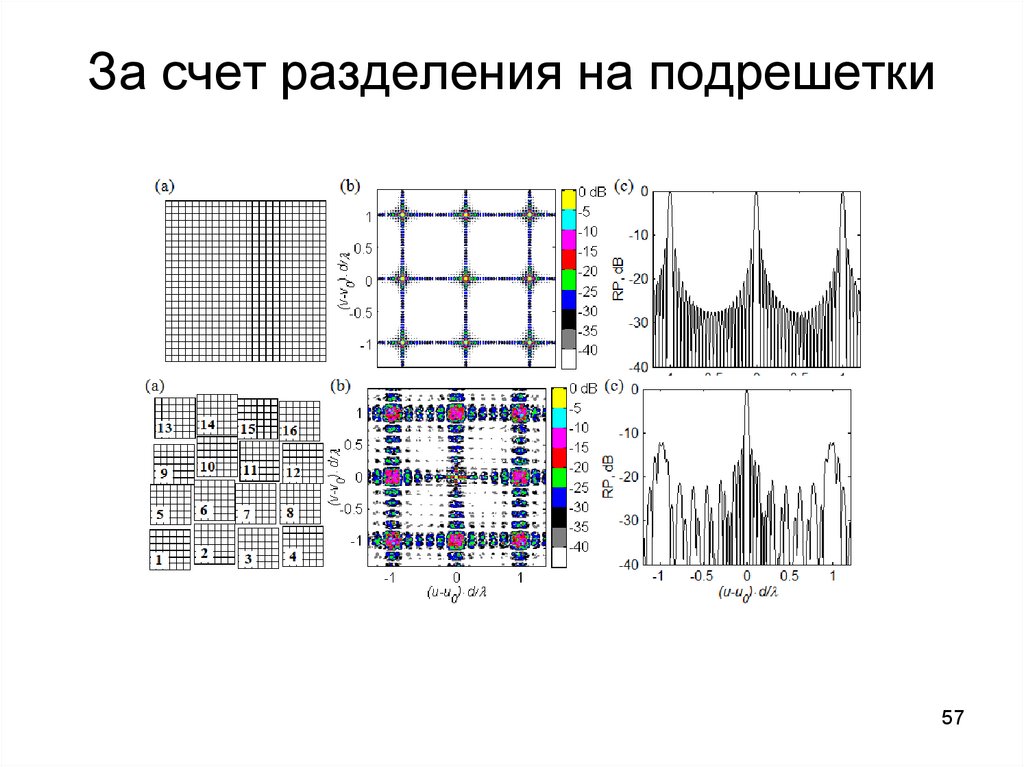
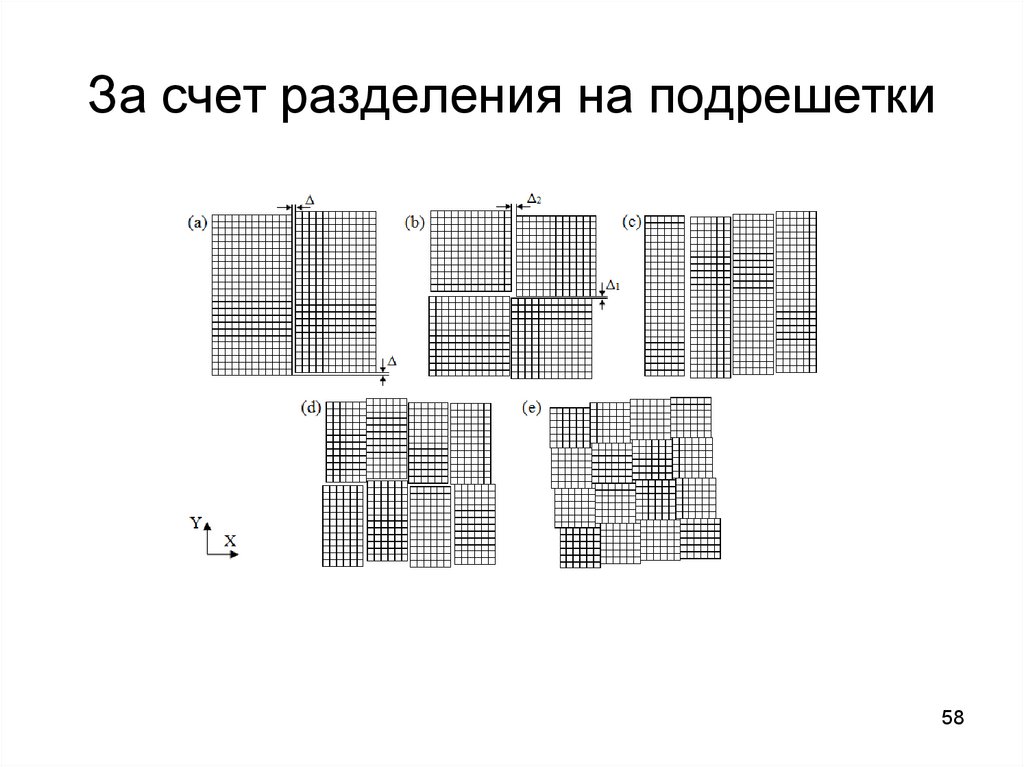
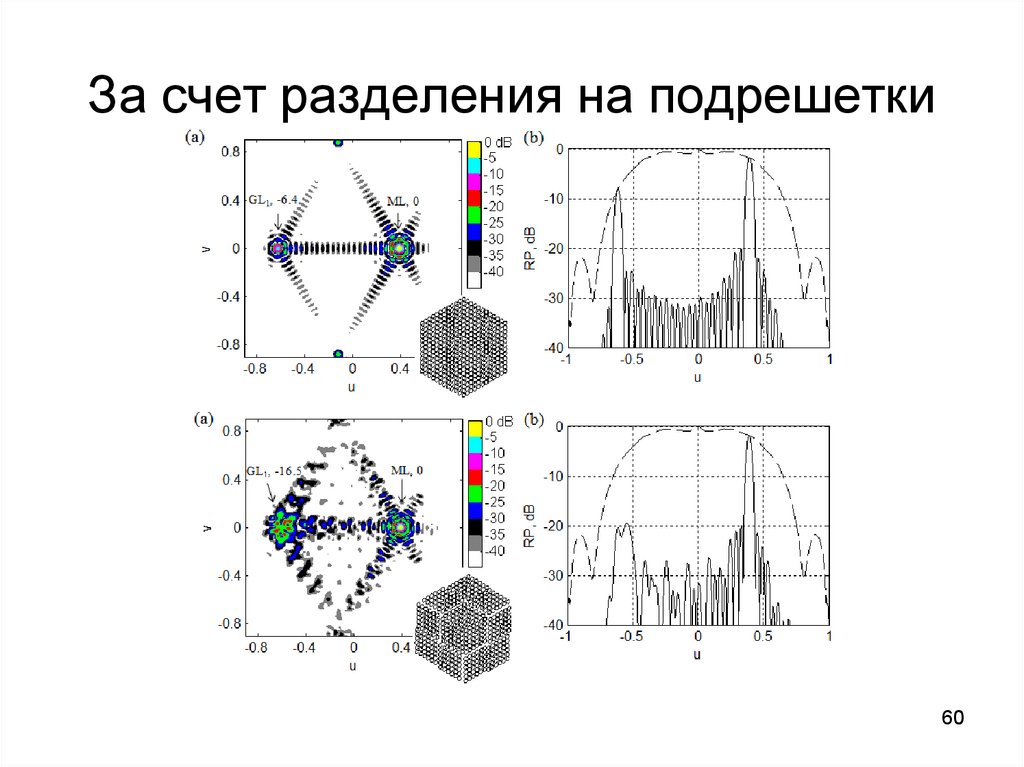
За счет разделения на подрешетки
34
35. Подавление ИБЛ
• За счет уменьшения шага решеткиРасстановка излучателей с шагом, ненамного превышающим
половину длины волны (или меньше)
Недостаток - при шаге элементов меньше половины длины волны,
решетка может «запираться»
Существенный недостаток –
избыточность количества элементов
35
36. Оптимальное количество элементов
N minS
G0
4
грубо говоря, сколько поместится ортогональных лучей ФАР
в заданной области сканирования
Альтернатива - сколько поместится элементов в области при данном шаге
• КУ задает размер антенны (ШДН)
• Область задает шаг между элементами
36
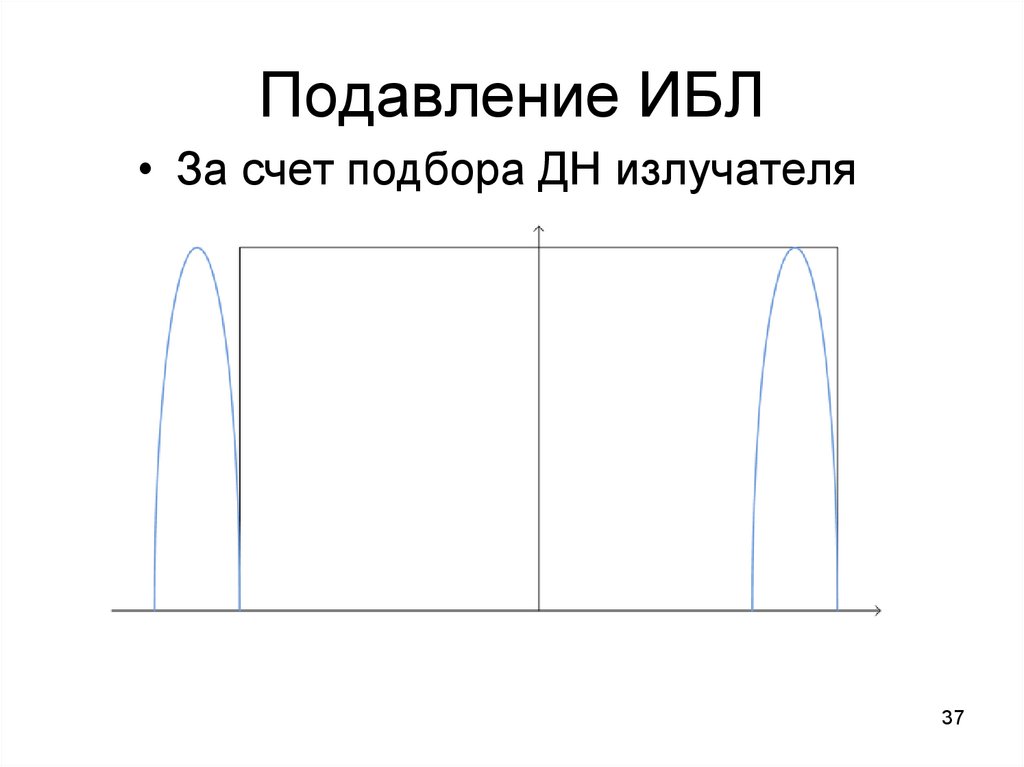
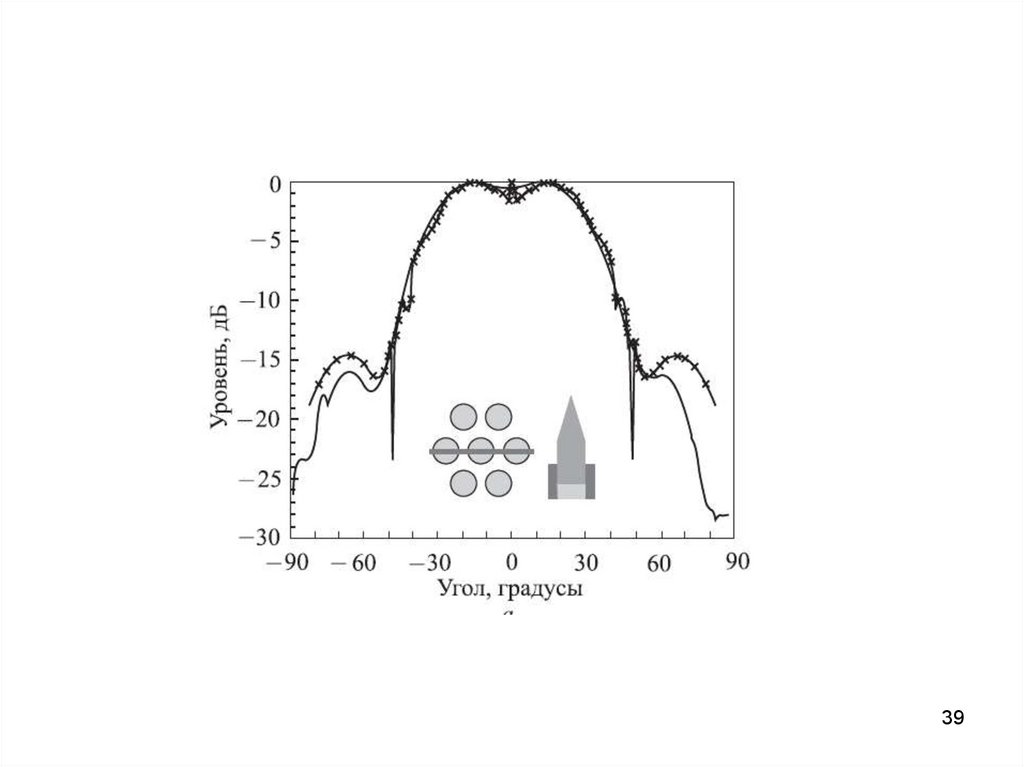
37. Подавление ИБЛ
• За счет подбора ДН излучателя37
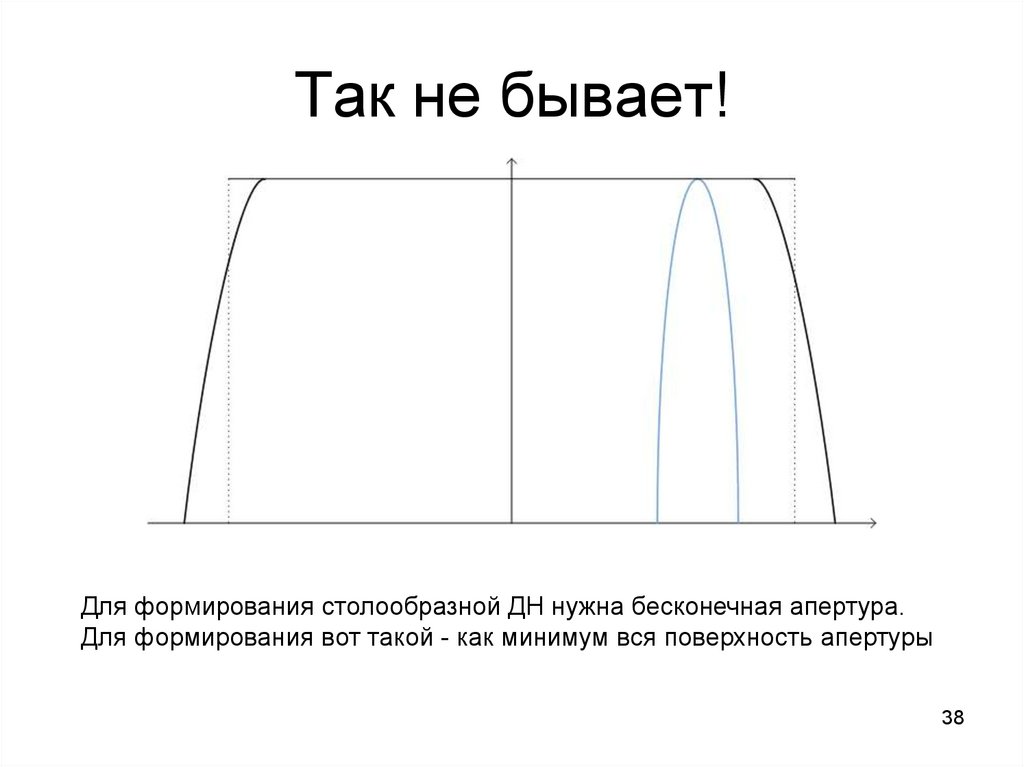
38. Так не бывает!
Для формирования столообразной ДН нужна бесконечная апертура.Для формирования вот такой - как минимум вся поверхность апертуры
38
39.
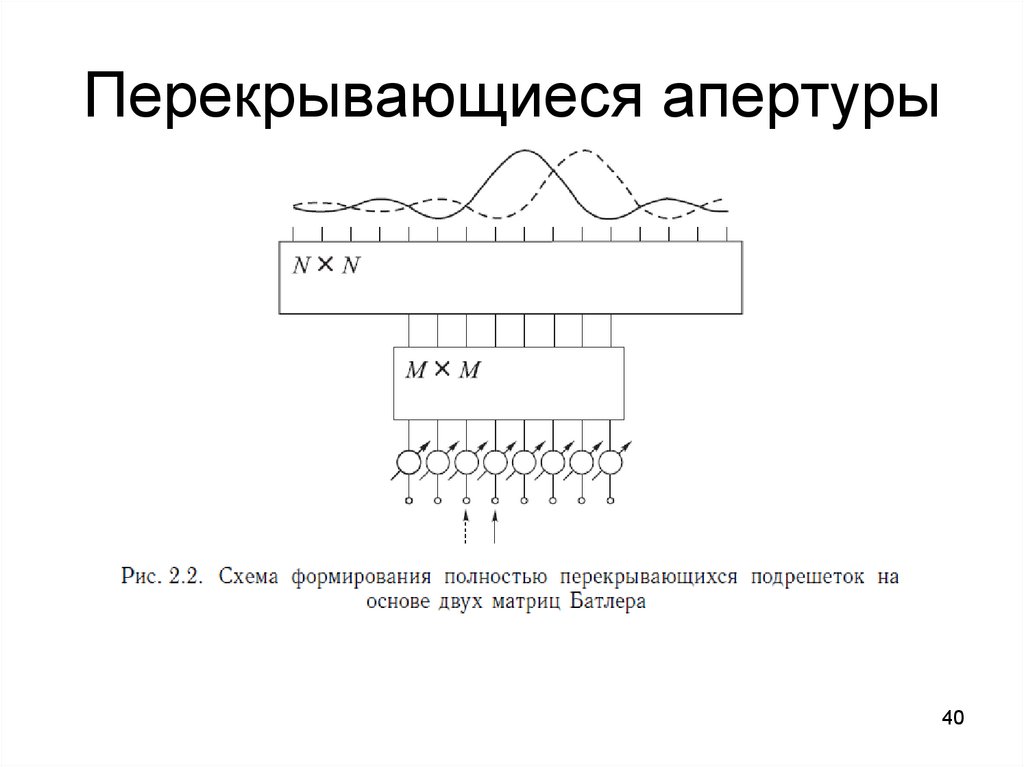
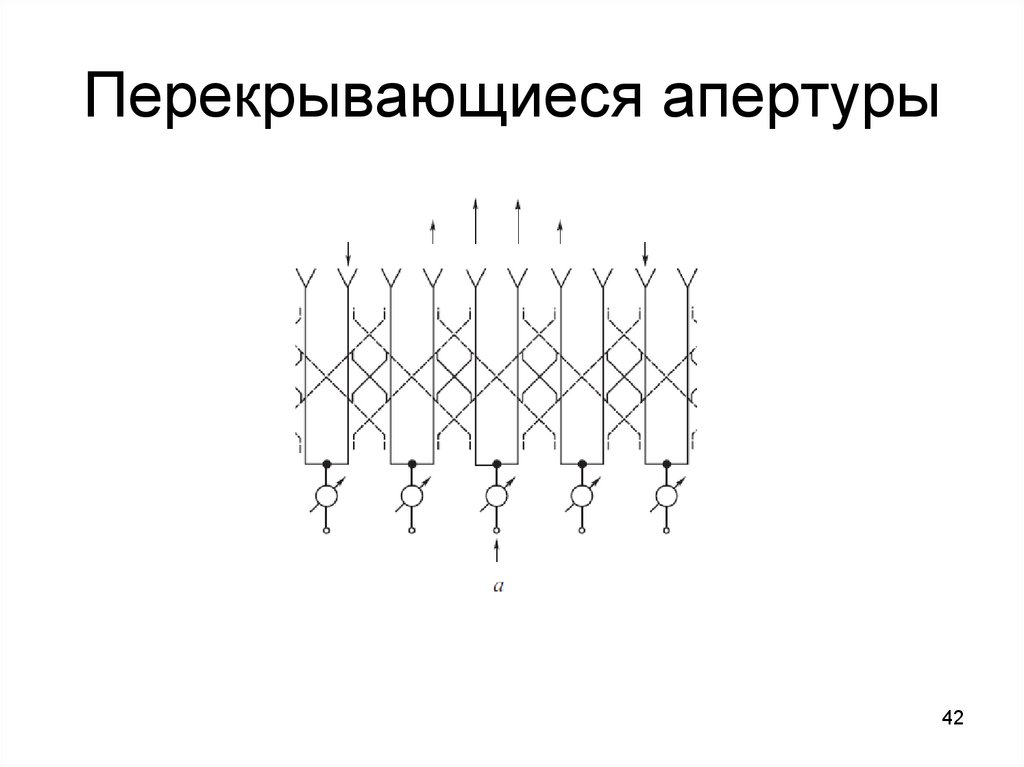
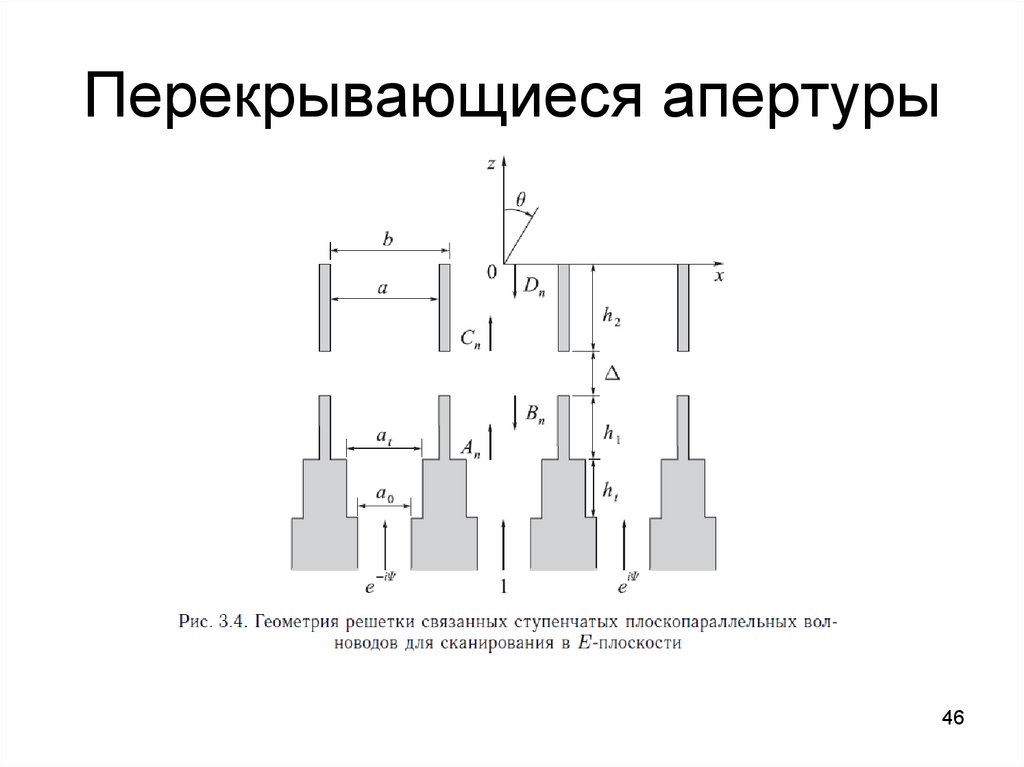
3940. Перекрывающиеся апертуры
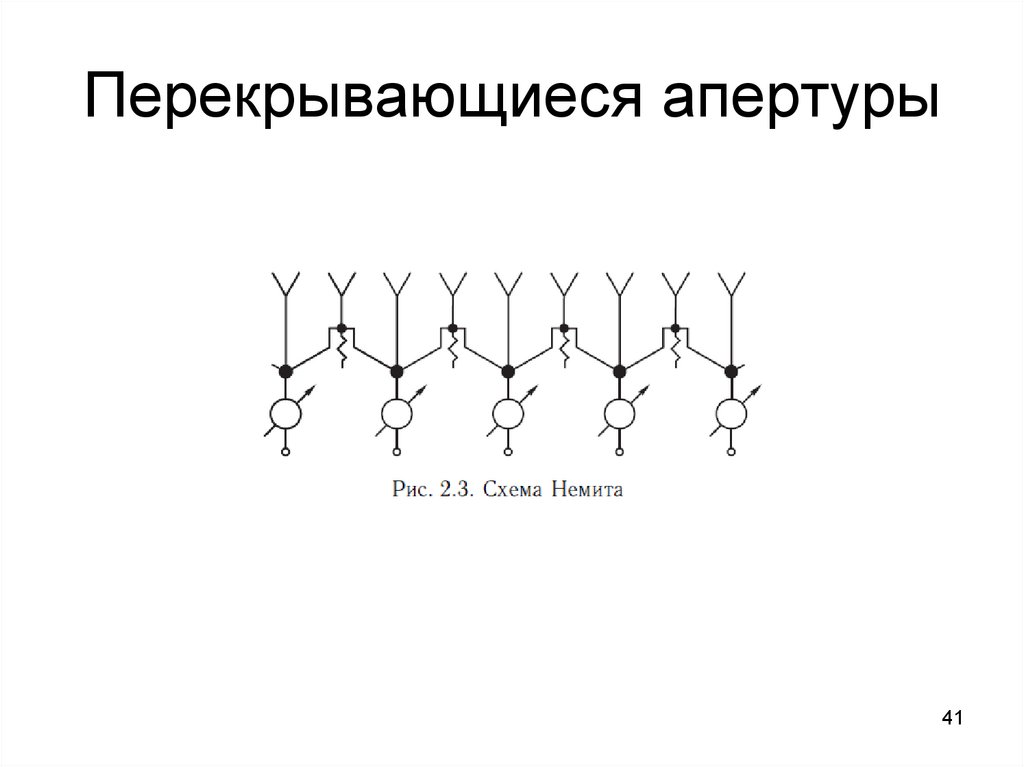
4041. Перекрывающиеся апертуры
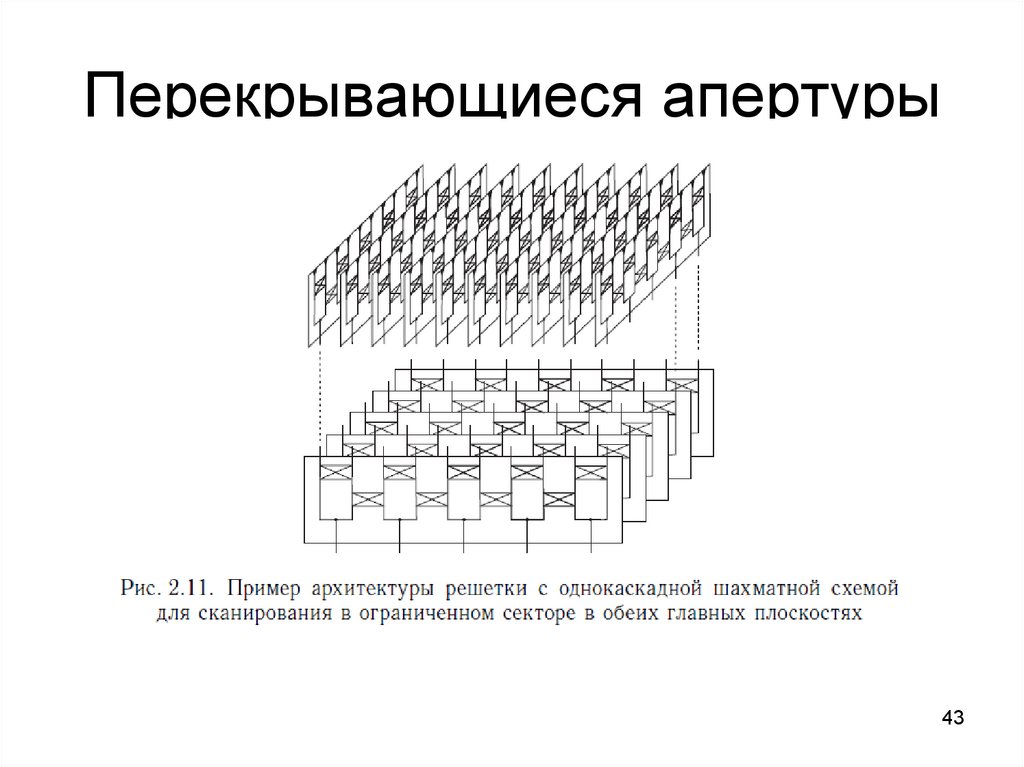
4142. Перекрывающиеся апертуры
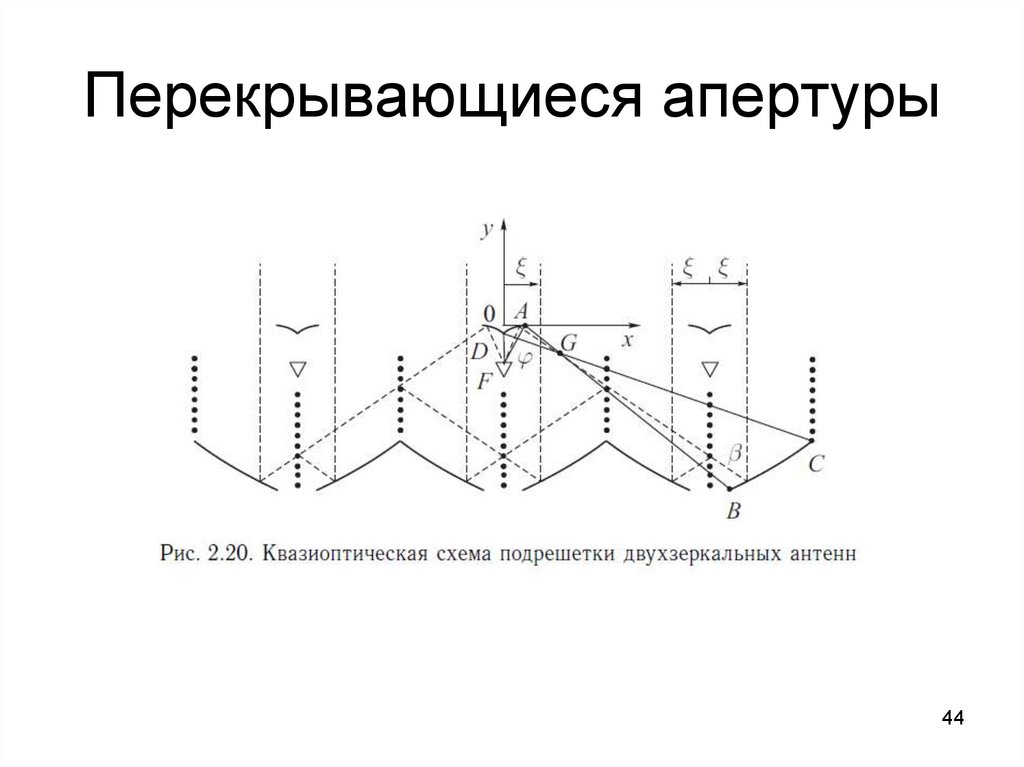
4243. Перекрывающиеся апертуры
4344. Перекрывающиеся апертуры
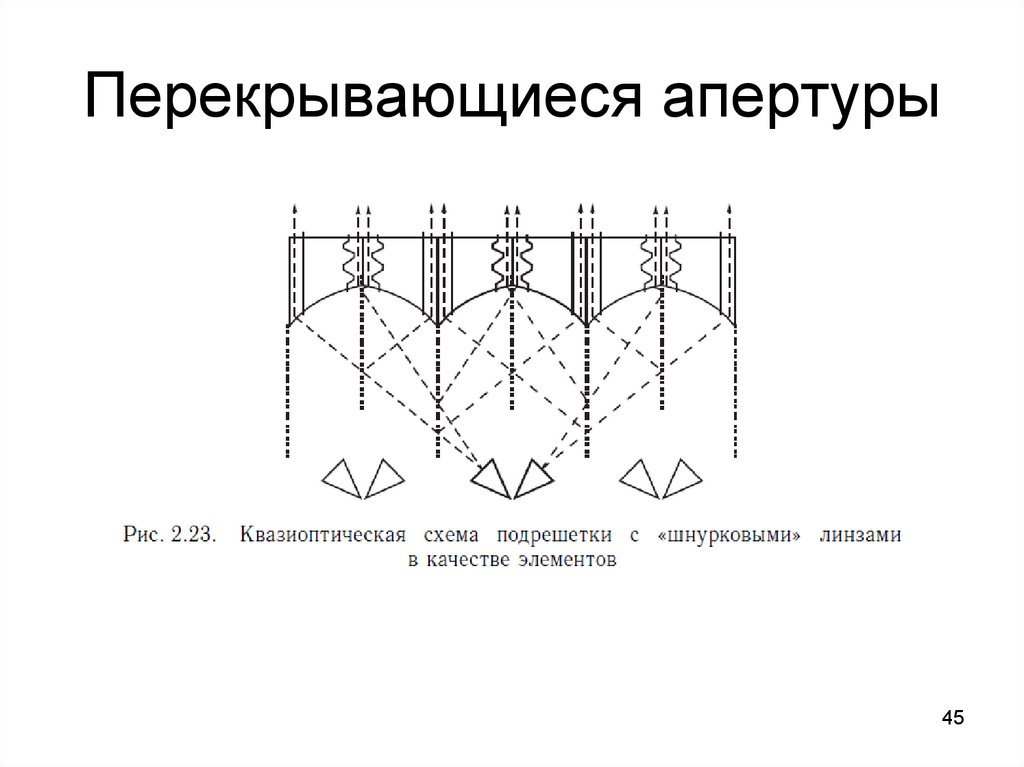
4445. Перекрывающиеся апертуры
4546. Перекрывающиеся апертуры
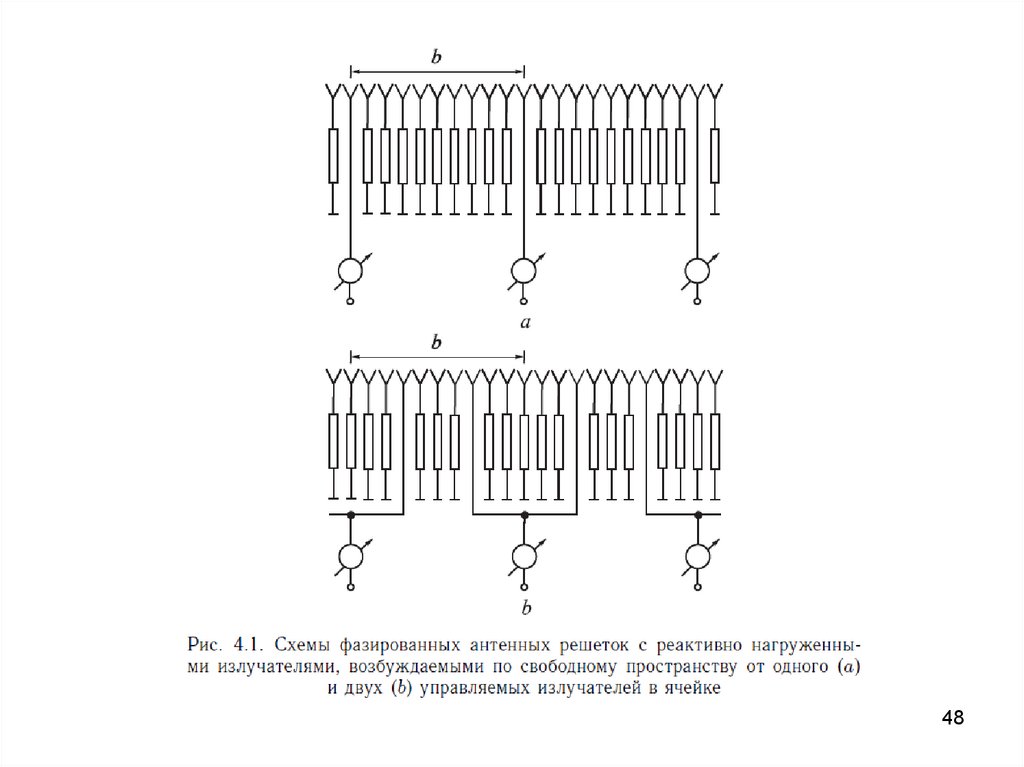
4647.
4748.
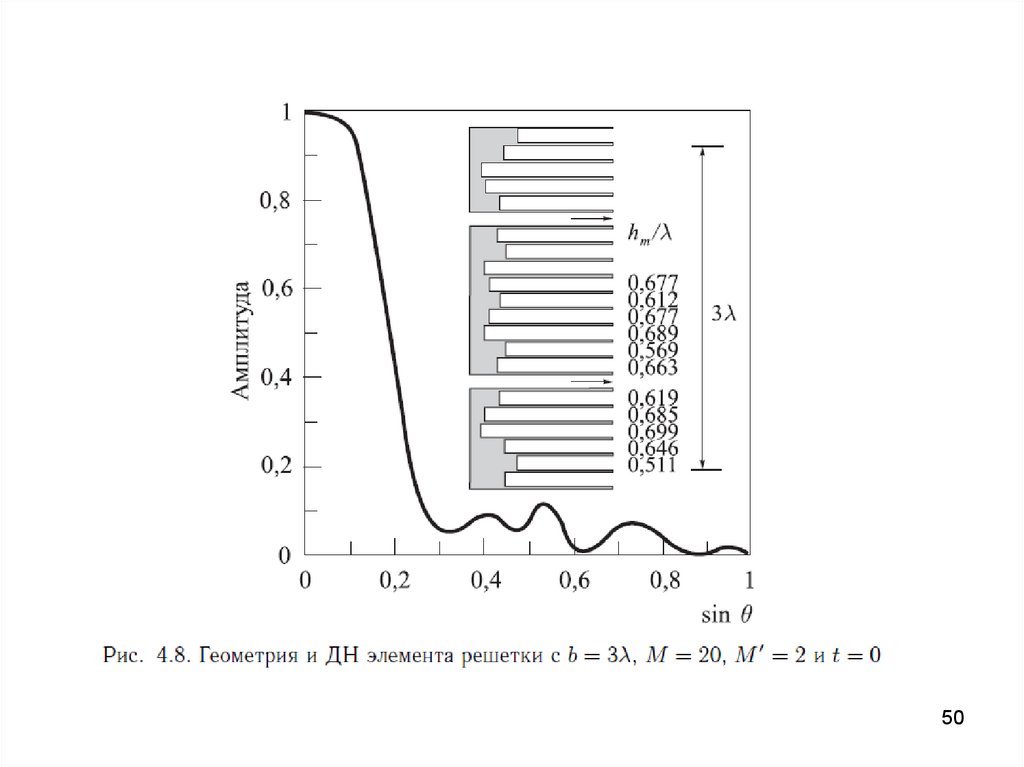
4849.
4950.
5051.
5152. Подавление ИБЛ
• За счет подбора ДН излучателяДля формирования ДН используется вся поверхность апертуры элемента
При формировании столообразной ДН элемента, апертура элемента недоиспользуется
52
53. Выводы
• Наиболее эффективная форма ДН близка к столообразной• Для эффективной формы ДН нужно организовать связь между
каналами
• Чем больше связь – тем сложнее схема
• Компромисс – связь излучателей по эфиру (получилось то, что
получилось)
Заметки
• Крайние элементы имеют другую ДН
(иногда даже используют ряд или два пассивного окружения)
• КУ антенны вовсе не «скачет» при появлении видимого ИБЛ
• Нули парциальной ДН – место, где ФАР может «запереться»
53
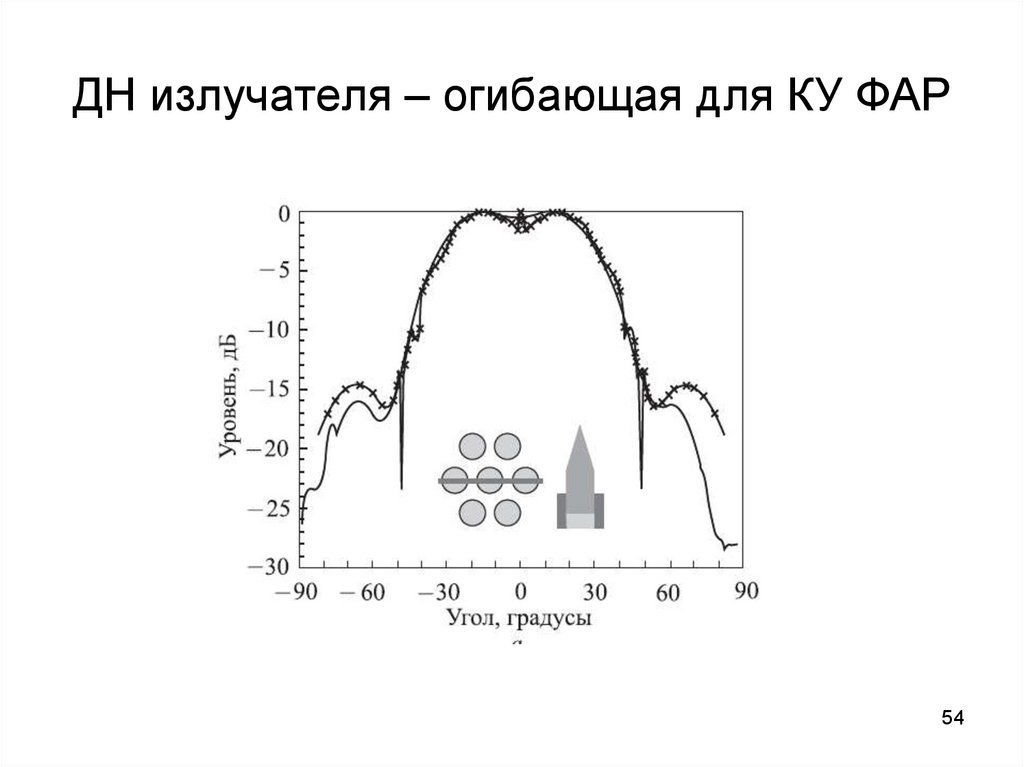
54. ДН излучателя – огибающая для КУ ФАР
5455. Подавление ИБЛ
• Неэквидистантная расстановка элементов55

























 Физика
Физика








