Линейные антенные решетки

1.

Линейные
антенные решетки

2.

ДН АР определяется произведением ДН одного
излучающего элемента на множитель системы:
f ( , ) = f 0( , ) · f с( , )

3.

Множитель системы:
sin N k d cos 2
f с
.
sin k d cos 2
N – число элементов АР;
d – шаг решётки;
ψ – фазовый сдвиг токов соседних элементов;
k = 2π / λ – волновое число.

4.

В зависимости от фазового сдвига токов ψ изменяется
положение максимума излучения. Различают режимы
нормального, наклонного и осевого излучения.

5.

Режим нормального излучения (ψ = 0)
Элементы решётки возбуждаются синфазно.
Максимум излучения ориентирован по
нормали к решетке ( 90 ).
гл

6.

Нормированная ДН (множитель системы):

7.

Пример:
множитель системы
Fс при
N = 7; d = 0,5

8.

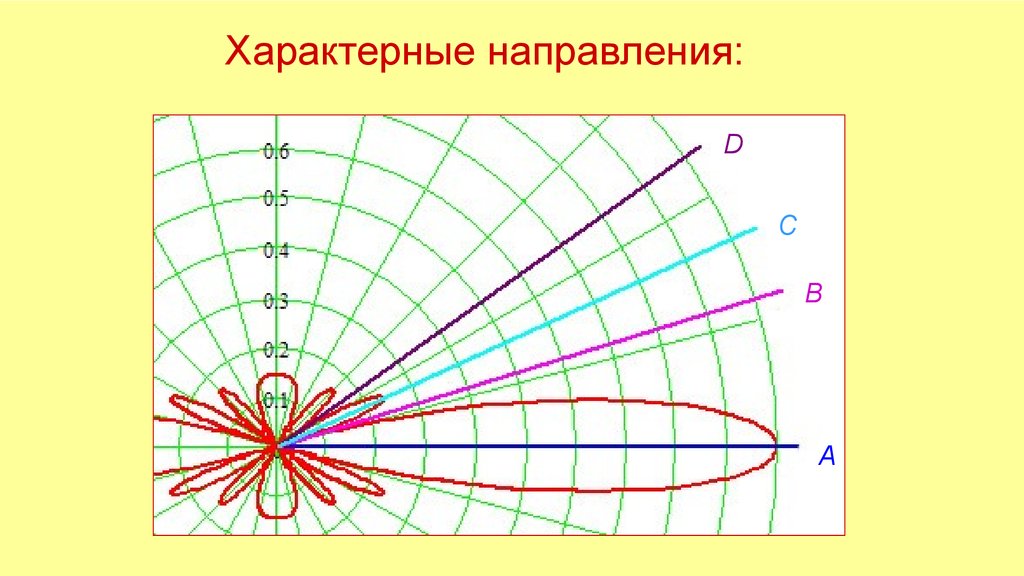
Характерные направления:
D
C
B
A

9.

Первый нуль ДН определяется из условия:
cos 01 Nd .
Чем больше элементов N содержит АР, тем
меньше 01 , т.е. уже ДН.

10.

При увеличении числа
элементов ширина ДН
уменьшается.
Пример:
d = 0,5 ;
---- N = 5;
---- N = 15.

11.

Для предотвращения появления дополнительных
главных максимумов ДН расстояние d между
элементами АР должно быть меньше длины волны:
d <

12.

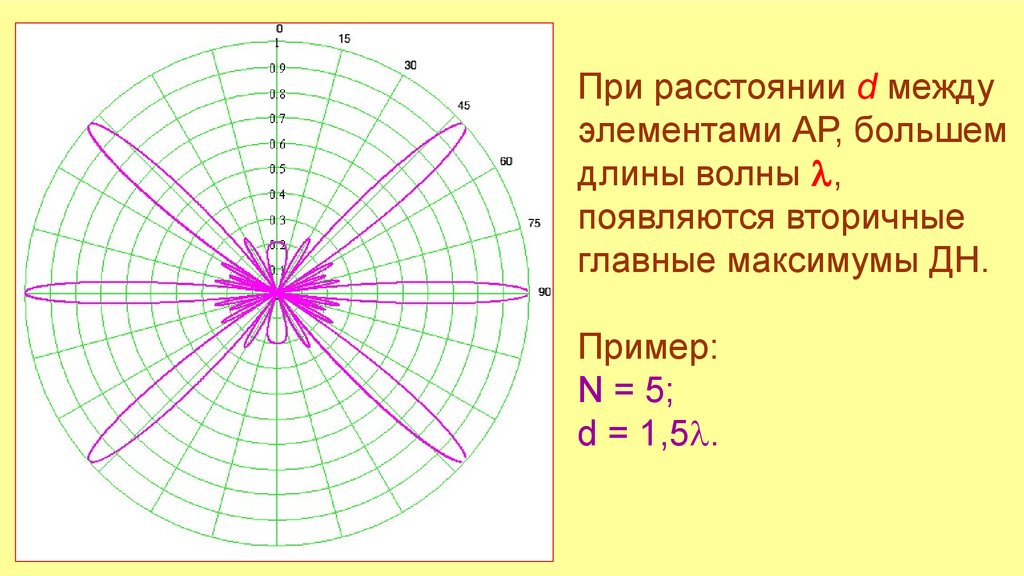
При расстоянии d между
элементами АР, большем
длины волны ,
появляются вторичные
главные максимумы ДН.
Пример:
N = 5;
d = 1,5 .

13.

Ширина главного лепестка ДН по нулевому уровню:
2 0 2 гл 01 2 Nd 115 Nd .
Ширина ДН по уровню половинной мощности:
2 0 ,5 0,89 Nd 51 Nd .

14.

Режим наклонного излучения ( 0 < ψ < kd )
Элементы решетки возбуждаются токами с фазовыми
сдвигами ψ. Максимум излучения отклоняется от
нормали к плоскости решетки.
ДН решетки (множитель системы) описывается
формулой:
sin N k d cos 2
Fс
.
N sin k d cos 2

15.

Направление главного максимума излучения может
быть найдено из выражения :
cos гл k d .
При изменении фазовых сдвигов ψ изменяется
отклонение от нормали к плоскости решетки главного
максимума ДН, т.е. осуществляется сканирование ДН.

16.

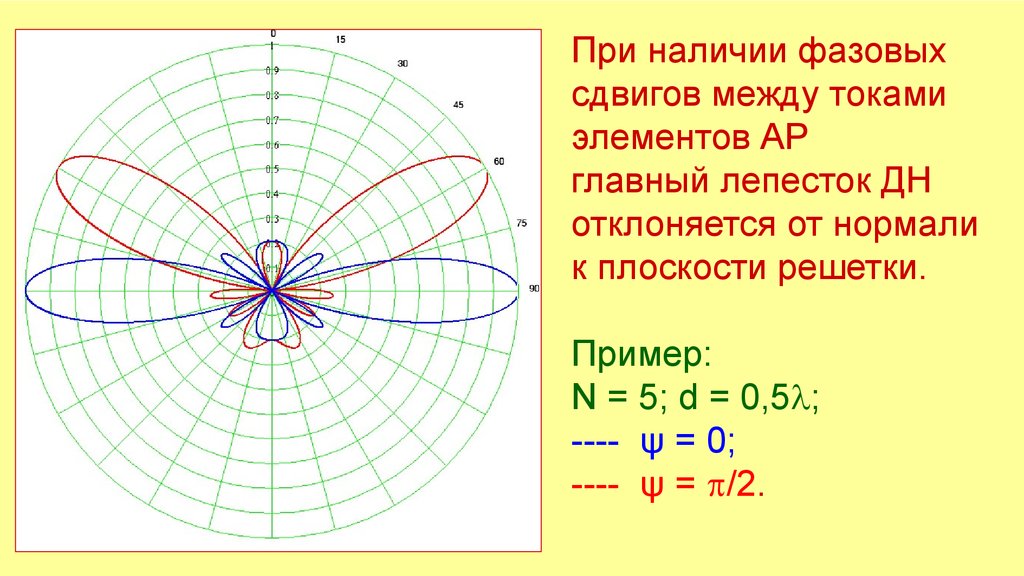
При наличии фазовых
сдвигов между токами
элементов АР
главный лепесток ДН
отклоняется от нормали
к плоскости решетки.
Пример:
N = 5; d = 0,5 ;
---- ψ = 0;
---- ψ = /2.

17.

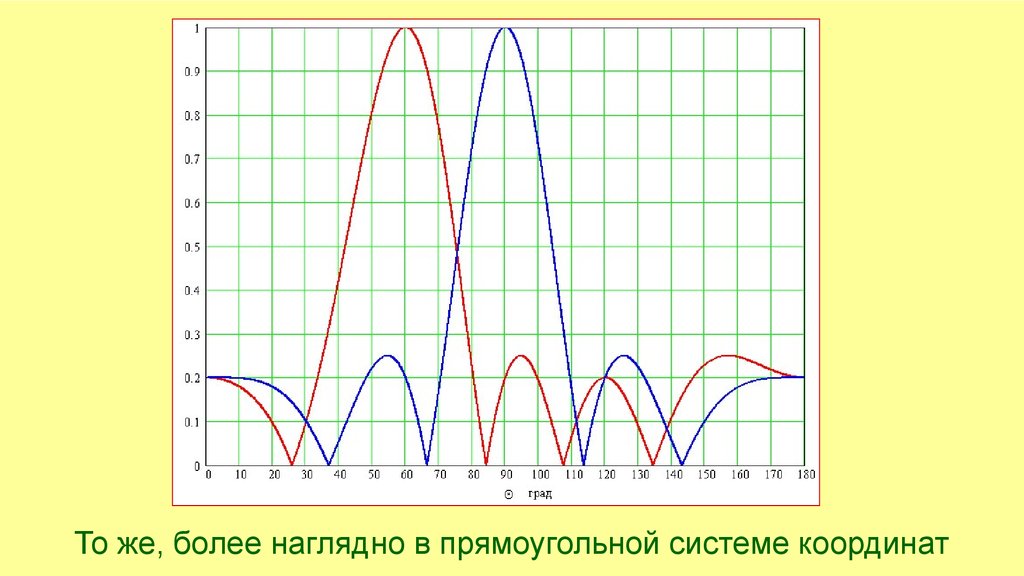
То же, более наглядно в прямоугольной системе координат

18.

РЛС SCR-270 (США)

19.

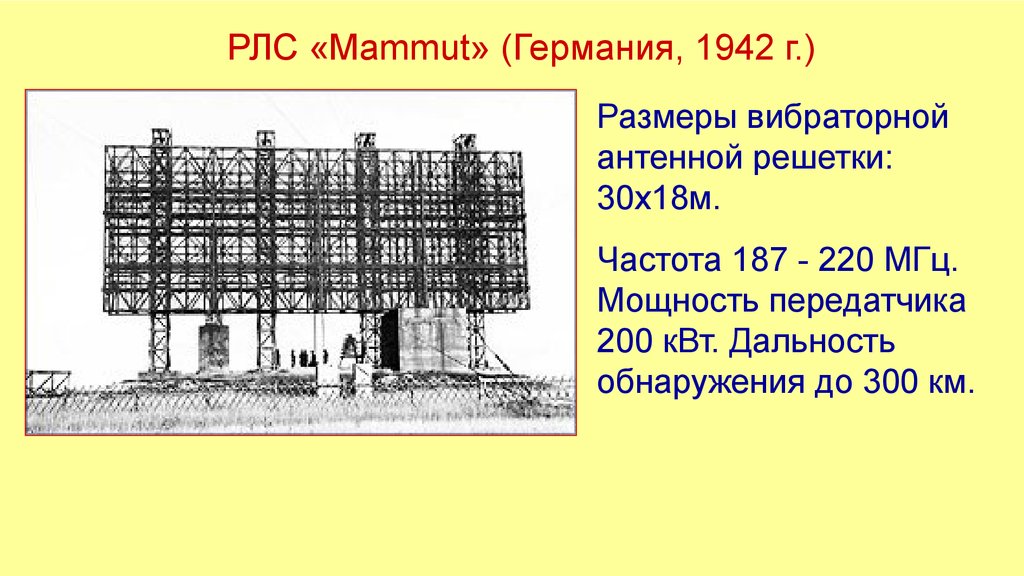
РЛС «Mammut» (Германия, 1942 г.)
Размеры вибраторной
антенной решетки:
30x18м.
Частота 187 - 220 МГц.
Мощность передатчика
200 кВт. Дальность
обнаружения до 300 км.

20.

Синфазные антенные решетки: в радиолокации

21.

в радио- и телевещании

22.

в системах мобильной связи

23.

Типовая базовая станция
мобильной связи

24.

Панельные антенны

25.

26.

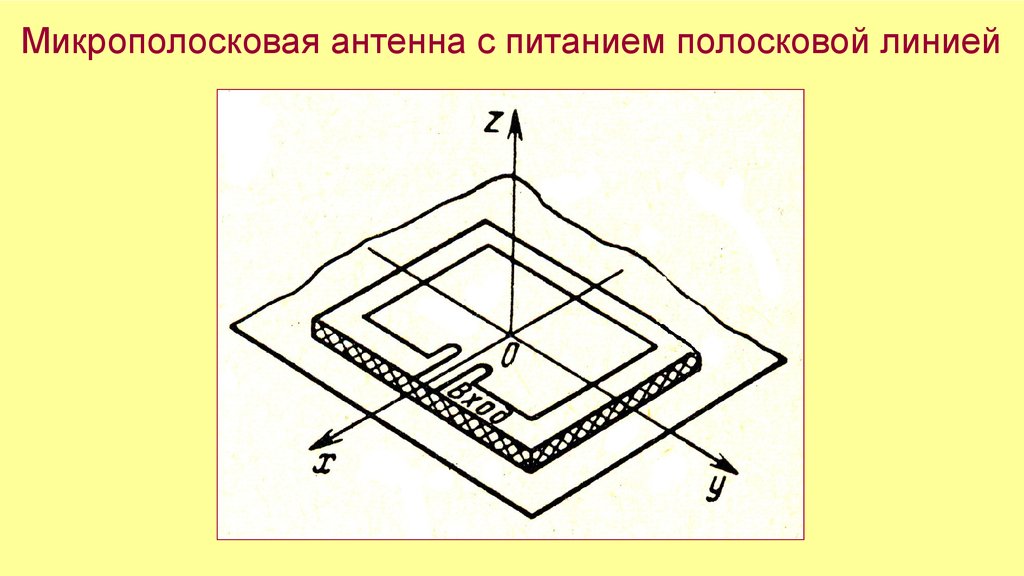
Микрополосковая антенна с питанием полосковой линией

27.

Режим осевого излучения ( ψ ≥ kd )
Вдоль АР распространяется бегущая волна.
Максимум излучения направлен вдоль оси АР.

28.

Директорные антенны
(антенны «волновой канал»,
антенны Яги или Уда-Яги)

29.

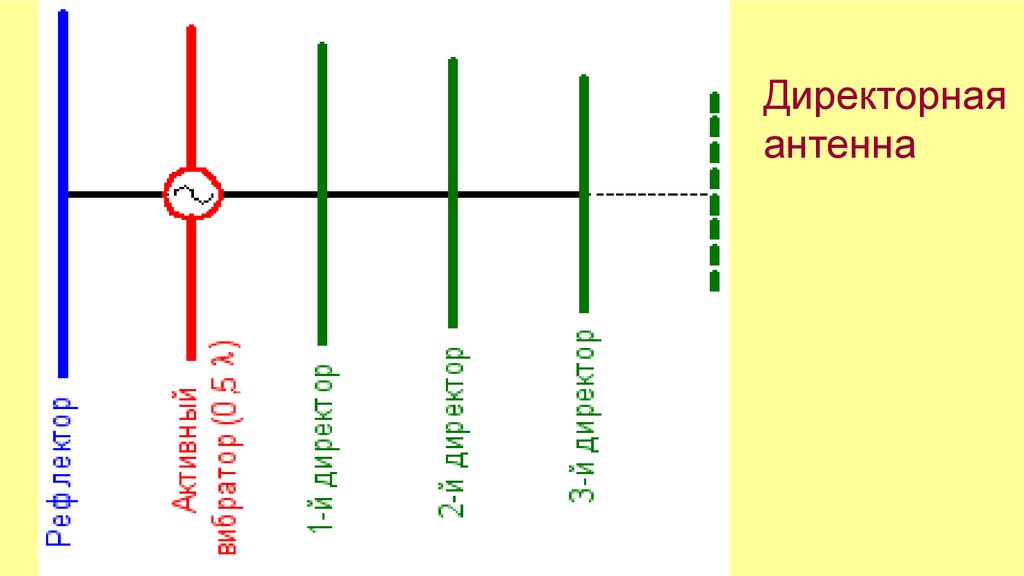
Директорная
антенна

30.

31.

Спиральные антенны

32.

33.

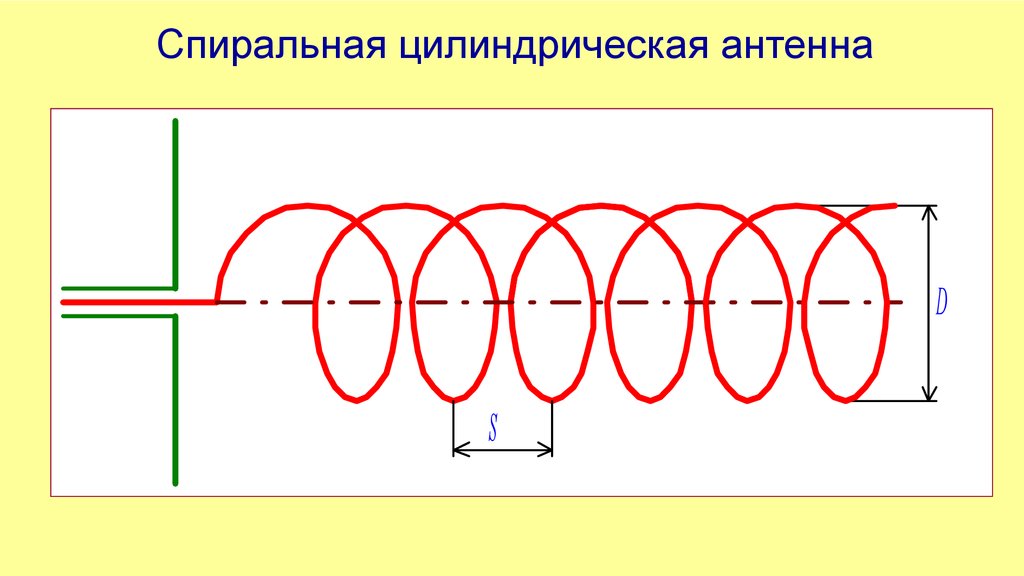
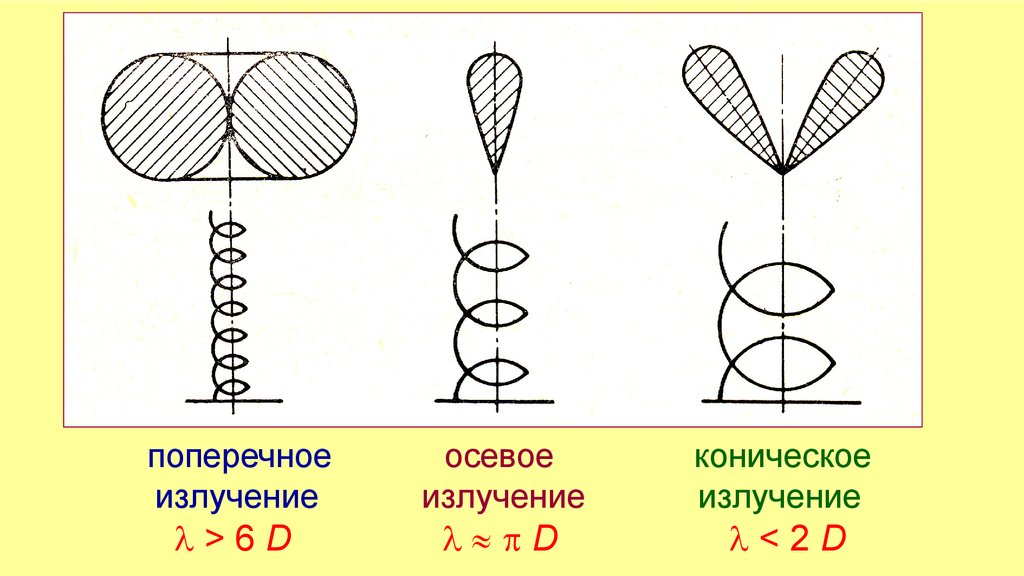
Спиральная цилиндрическая антенна
D
S

34.

поперечное
излучение
>6D
осевое
излучение
D
коническое
излучение
<2D

35.

36.

Плоская спиральная антенна системы распознавания
«свой – чужой»

37.

Диэлектрическая
стержневая
антенна

38.

Диэлектрические
стержневые антенны в
фазированной антенной
решётке.

39.

40.

Волноводно-щелевые
антенны

41. Апертурные антенны

42.

Рупорные антенны

43.

Пирамидальный рупор

44.

Ширина ДН пирамидального рупора по уровню
половинной мощности:
- в плоскости Е:
- в плоскости Н:
2 0 ,5 51 b ;
2 0 ,5 67 ,6 a .

45.

Зеркальные
параболические
антенны

46.

РЛС
Wurzburg-Riese
(Германия,
1940 г.)
Частота 560 МГц.
Диаметр зеркала
7,5 м.

47.

48.

Для преобразования сферической волны в плоскую
зеркало должно иметь форму параболоида вращения.
Все лучи, идущие из фокуса F, после отражения от
зеркала параллельны его оси и приходят в плоскость
раскрыва антенны в одной фазе (длины всех лучей
одинаковы).

49.

50.

51.

Офсетные зеркальные антенны

52.

53.

Радиотелескоп МГТУ:
двухзеркальная антенна
Кассегрена; диаметр
зеркала 7,5 метров,
диапазон длин волн:
1 - 4 мм.

54.

Рупорно-параболическая антенна