Общие методы решения уравнений

1.

«Правильному применению
методов можно научиться только
применяя их на разнообразных
примерах»
Г. Цейтен
11 класс
Общие методы
решения уравнений
УМК А.Г. Мордкович
(профильный уровень)

2. Цели урока:

Рассмотреть общие методы
решения уравнений.
Научиться применять эти методы
при решении уравнений.
Формировать навыки применение
наиболее рациональных способов
решения уравнений.

3. Рассмотрим уравнения:

1) х² - 2 х = 0;
2) sin²x + sinx = 0;
х
5
х
3) 7
49;
2

4. Рассмотрим уравнения:

4) log
2
2
x 4 log 2 x 3 0;
1
5) х
х

5. Общие методы решения уравнений:

Замена уравнения h(f(x)) = h(g(x))
уравнением f(x) = g(x).
Метод разложения на множители.
Метод введения новой переменной.
Функционально-графический метод.

6.

1. Замена уравнения h(f(x)) = h(g(x))
уравнением f(x) = g(x).
Этот метод мы применяем:
при решении показательных уравнений,
f ( x)
g ( x)
когда переходили от уравнения a
a
(а>0, а≠1) к уравнению f(x) = g(x);
при решении логарифмических уравнений,
когда переходили от уравнения
logа f(x) = logаg(x) к уравнению f(x) = g(x);
при решении иррациональных уравнений,
когда переходили от уравнения n h( x) n g ( x)
к уравнению f(x) = g(x).

7. Пример 1:

Решить уравнение
2 х 3 х 1
5
5 0
2 х 3 х 1
5
5;
2
2
2 х 3х 1 1;
2
2 х 3х 0;
х 0; х 1,5.
2
Ответ: 0; 1,5.

8. Пример 2:

log 3 x 3x 5 log 3 7 2 x ;
2
х 3х 5 7 2 х;
2
х х 12 0;
х1 4, х2 3.
2
Проверка :
х 2 3х 5 0,
7 2 х 0.
х 4 посторонний
Ответ : 3.
корень

9.

2. Метод разложения на
множители.
Уравнение f(x)g(x)h(x) = 0 можно заменить
совокупностью уравнений:
f ( x ) 0;
g ( x ) 0;
h( x ) 0.
Решив уравнения этой совокупности, нужно
взять те их корни, которые принадлежат
ОДЗ исходного уравнения, а остальные
отбросить как посторонние.

10. Пример 3:

Решить уравнение
х 2 3 2
х 6 х 5
2
х 2 3 0;
х 2 6 х 5
1;
2
ln(
х
8
)
0
.
1 ln( х 8) 0.
х 2 9;
2
х
6
х
5
0
;
х 8 1.

11. Пример 3:

х1 7;
х 1; х 5;
3
2
х 4 9.
Проверка : ОДЗ :
х 2 0,
х 8 0.
Из найденных корней этой системе
неравенств удовлетворяет только
х = 9, остальные являются
посторонними для данного уравнения.
Ответ: 9.

12.

3. Метод введения новой
переменной.
Если уравнение f(x)= 0 удалось
преобразовать к виду p(g(x)) = 0, то нужно
ввести новую переменную u = g(x), решить
уравнение p(u) = 0, а затем решить
совокупность уравнений: g ( x ) u ;
1
g ( x) u ;
2
....
g ( x) un
где и1 , и2 ,… ип - корни уравнения р(и) = 0.

13. Пример 4:

Решить уравнение
1
2
7
.
2
2
х 3х 3 х 3х 1 5
Введём новую переменную
Получим:
у х 3х .
1
2
7
.
у 3 у 1 5
2
Освободившись от знаменателей,
получим:
2
7 у 29 у 4 0;

14. Пример 4:

Найдём корни квадратного
1
уравнения:
у1 4; у 2
7
.
Выполним проверку корней на
выполнение условия:
5(у – 3)(у + 1) ≠ 0.
Оба корня удовлетворяют данному
условию.

15. Пример 4:

Вернёмся к замене переменной и
решим два уравнения:
х 3х 4
2
х 1 1; 4.
2
Ответ:
1; 4;
и
х3
4
1
х 3х .
7
2
21 469
.
14
21 469
.
14

16. 3. Функционально-графический метод.

Чтобы графически решить
уравнение f(x) = g(x) нужно
построить графики функций
у = f(x) и у = g(x) и найти точки их
пересечения. Корнями уравнения
служат абсциссы этих точек.

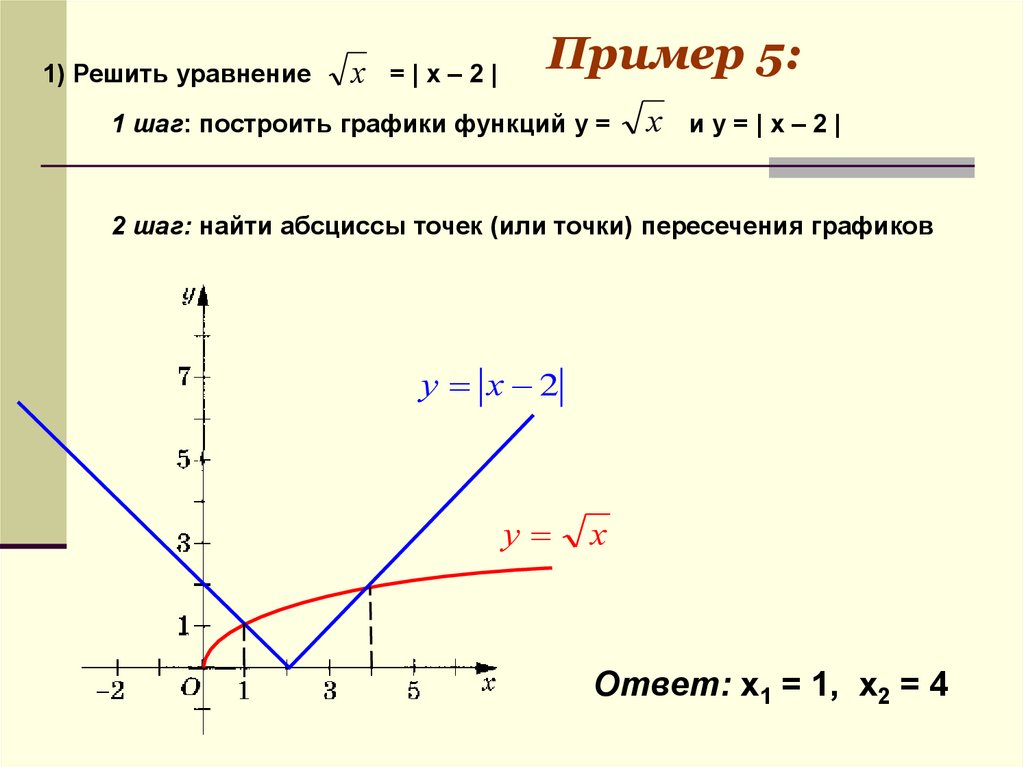
17.

1) Решить уравнение
х =|x–2|
Пример 5:
1 шаг: построить графики функций у =
х иу=|x–2|
2 шаг: найти абсциссы точек (или точки) пересечения графиков
у х 2
у
х
Ответ: x1 = 1, х2 = 4

18.

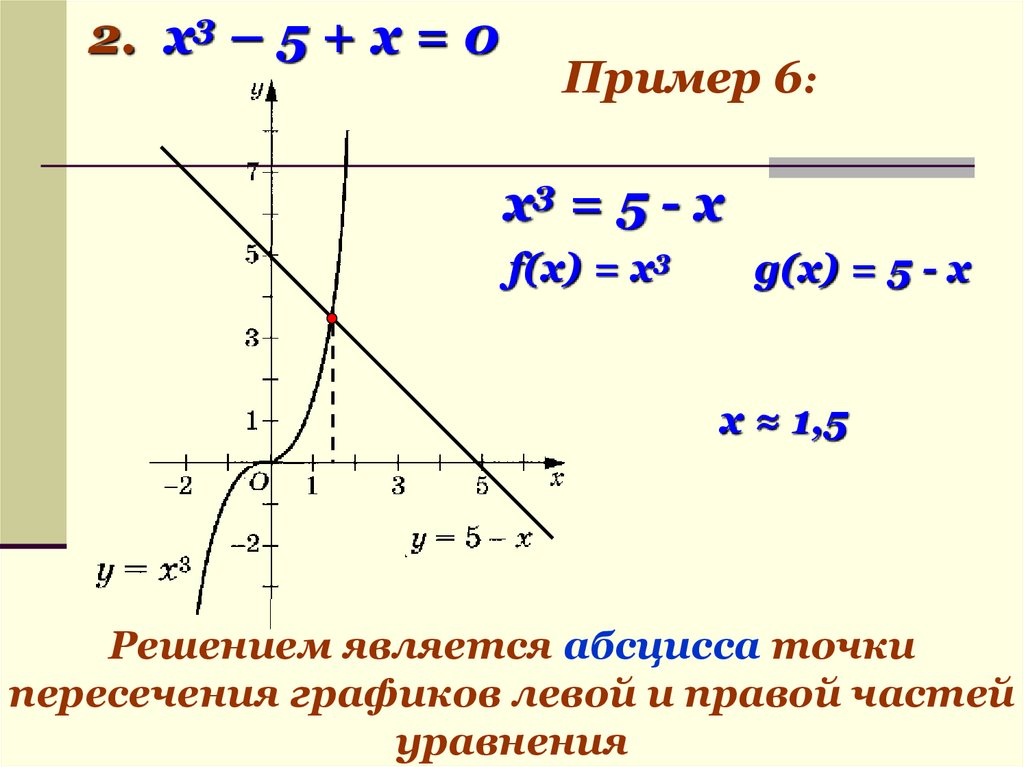
2. x3 – 5 + х = 0
Пример 6:
х3 = 5 - х
f(x) = х3
g(x) = 5 - х
х ≈ 1,5
Решением является абсцисса точки
пересечения графиков левой и правой частей
уравнения

19.

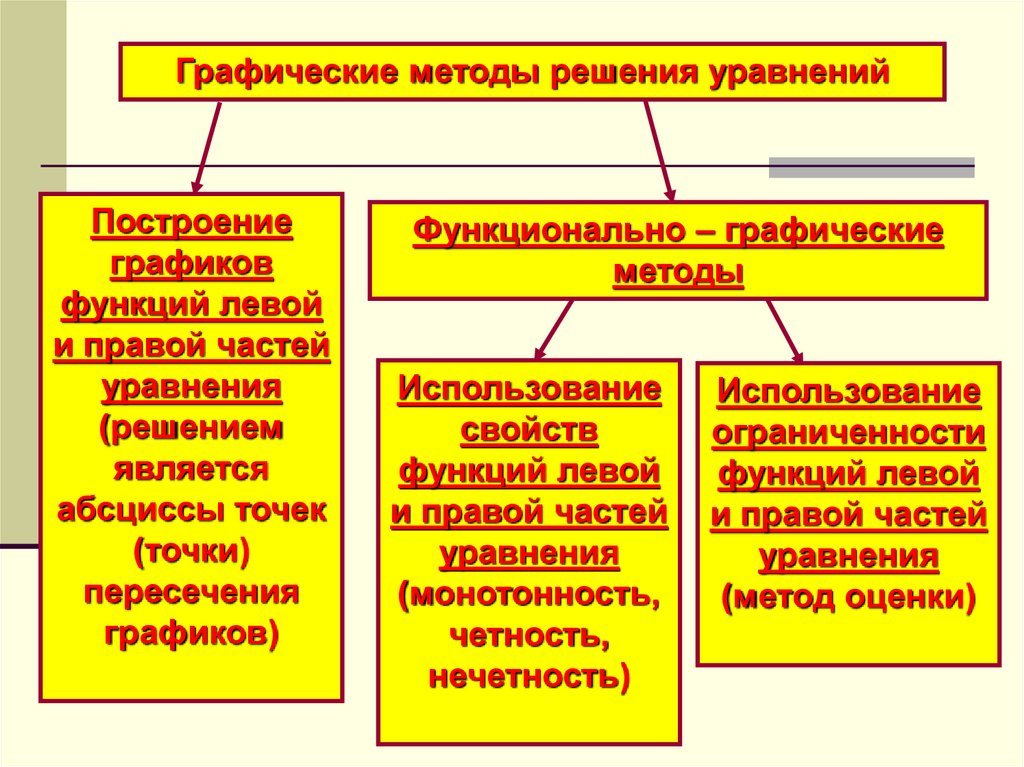
Графические методы решения уравнений
Построение
графиков
функций левой
и правой частей
уравнения
(решением
является
абсциссы точек
(точки)
пересечения
графиков)
Функционально – графические
методы
Использование
свойств
функций левой
и правой частей
уравнения
(монотонность,
четность,
нечетность)
Использование
ограниченности
функций левой
и правой частей
уравнения
(метод оценки)

20. Пример 7:

Решить уравнение
cos 2 x х 2 х 2.
2
Рассмотрим функцию у = х² - 2х + 2.
Её графиком является парабола,
ветви которой направлены вверх.
В вершине параболы функция
достигает своего наименьшего
значения.

21. Пример 7:

Найдём координаты вершины параболы.
b
х0 ; у 0 у ( х0 );
2a
(1;1)
Для функции у = х² - 2х + 2 у наим. 1.
Функция у = cos 2πx обладает
свойством: у
1.
наиб.

22. Пример 7:

Задача сводится к решению системы
уравнений
х² - 2х + 2 = 1,
cos 2πx = 1.
Решив 1 уравнение получили: х = 1.
Это значение удовлетворяет и 2
уравнению системы,
следовательно, является
единственным корнем заданного
уравнения.
Ответ: 1.

23.

Мы рассмотрели общие
методы решения уравнений,
примеры применения этих
методов.
Перейдём к практической
работе.
Решаем № 27.5 (в), 27.9 (б),
27.12 (б), 27.14 (а), 27.19 (б),
27.21 (а), 27.25 (а,б).

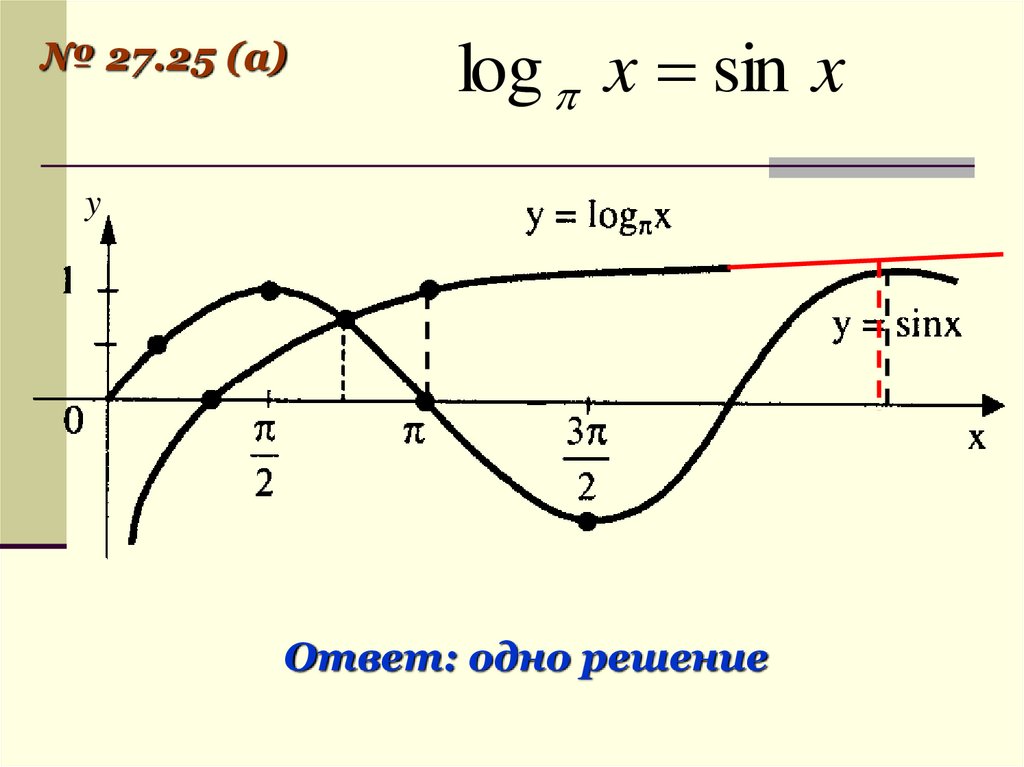
24.

№ 27.25 (а)
log x sin x
y
Ответ: одно решение

25.

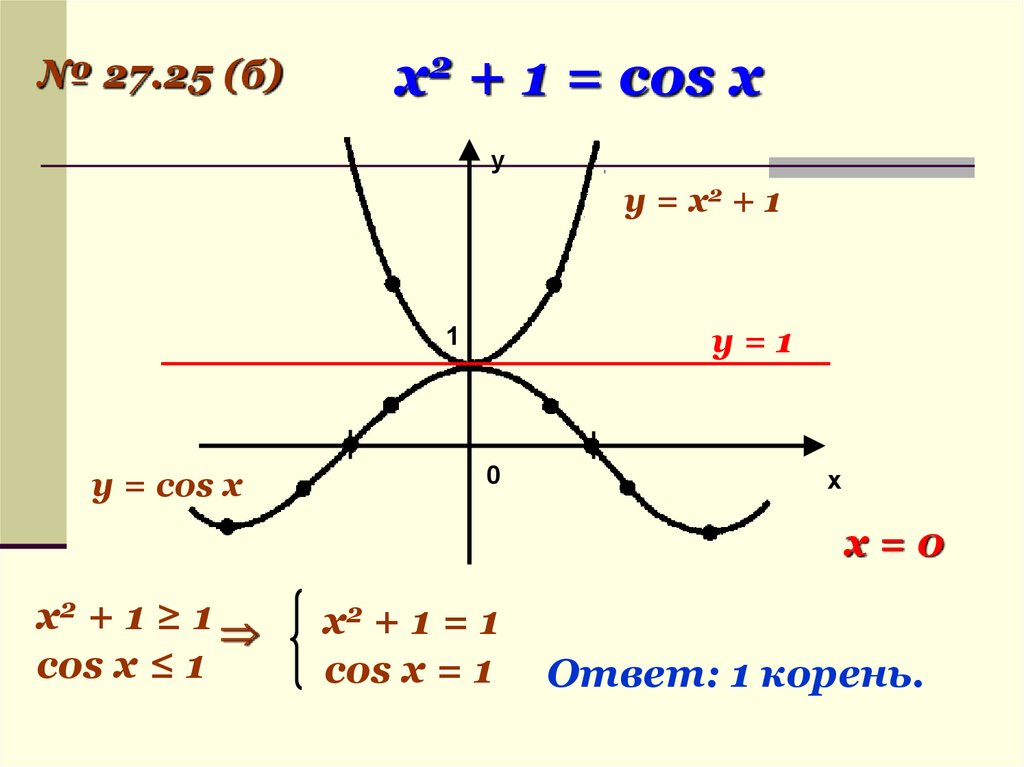
№ 27.25 (б)
x2 + 1 = cos x
у
y = x2 + 1
y=1
1
y = cos x
0
х
x=0
x2 + 1 ≥ 1
cos x ≤ 1
x2 + 1 = 1
cos x = 1
Ответ: 1 корень.

26.

Подведем
итоги
Общие методы решения
уравнений
Функционально-графические
Аналитические
1
2
3
По
графику
По
свойствам