Похожие презентации:
Теория вероятностей и математическая статистика
1. Теория вероятностей и математическая статистика
12.
Лекция 112
3. Математическое ожидание биномиальной случайной величины
34.
Теорема.Если X-биномиальная СВ с
параметрами n и p, то
М X = np
4
5. Пример
Вероятность попадания в цель пристрельбе из орудия р = 0,6. Найти
математическое ожидание общего
числа попаданий, если будет
произведено 10 выстрелов.
5
6. Решение
M ( X ) np 10 0,6 66
7.
Теорема.Математическое ожидание
случайной величины , имеющей
распределение Пуассона с
параметром
, равно .
7
8. Математическое ожидание СВ, имеющей геометрическое распределение
89.
ТеоремаМатематическое ожидание
случайной величины ,
имеющей геометрическое
распределение с параметром
p, равно 1/p.
9
10.
Дисперсия дискретнойслучайной величины
10
11. Отклонение случайной величины от её мат. ожидания
Пусть Х – случайная величина и М(Х) –её мат. ожидание.
Рассмотрим в качестве новой случайной
величины разность
Х – М(Х), которая называется
отклонением.
11
12.
Пусть закон распределения Х известен:Х
р
x1
p1
x2
p2
…
xn
…
pn
12
13.
Закон распределения отклонения:Х–М(Х)
р
x1 M ( X ) x 2 M ( X )
p1
p2
…
x n M (X )
…
pn
13
14. Теорема. Математическое ожидание отклонения равно нулю: M (Х – М (Х)) = 0.
Док-во:М (Х – М(Х)) = М (Х) – М (М (Х)) =
= М (Х) – М (Х) = 0.
14
15. Дисперсия дискретной случайной величины
Дисперсией (рассеянием) дискретнойслучайной величины называют мат.
ожидание квадрата отклонения
случайной величины от её мат.
ожидания:
D( X ) M X M ( X ) .
2
15
16.
Свойства дисперсии16
17.
Свойство 1Дисперсия постоянной C равна
нулю.
D(C) = 0
17
18. Доказательство:
D(C ) M C M (C ) .2
D(C ) M C C M (0) 0.
2
18
19. Свойство 2
D(CX ) C D( X ).2
19
20. Доказательство:
D(CX ) M CX CM ( X )2
C M X M ( X ) C D( X ).
M C X M ( X )
2
2
2
2
2
20
21. Свойство 3
Дисперсия суммы двух независимыхслучайных величин равна сумме
дисперсий этих величин:
D(X + Y) = D (X) + D(Y).
21
22. Следствие 1
Дисперсия суммы нескольких взаимнонезависимых случайных величин
равна сумме дисперсий этих величин.
22
23. Следствие 2
Дисперсия суммы постояннойвеличины и случайной равна
дисперсии случайной величины:
D (C + X) = D (X).
23
24. Следствие 3
Дисперсия разности двухнезависимых случайных величин
равна сумме их дисперсий:
D (X – Y) = D (X) + D (Y).
24
25. Дисперсия биномиальной случайной величины
2526.
ТеоремаДисперсия биномиальной случайной
величины X с параметрами n и p
равна npq :
D (X) = npq.
26
27.
Дисперсия случайной величины, имеющей распределение
Пуассона с параметром ,
равна .
27
28.
Непрерывные случайныевеличины
28
29. Функция распределения
Определение.Функцией распределения случайной величины X называют
функцию F(x):
F(X) = P(X<x)
29
30.
Случайную величину называют непрерывной, еслиеё функция распределения есть непрерывная,
кусочно-дифференцируемая функция с кусочнонепрерывной производной.
30
31. Свойства функции распределения
Свойство 1.Значения функции распределения
принадлежат отрезку 0,1
0 F ( x) 1.
31
32. Свойство 2.
F(X) – неубывающая функция, т.е.F ( x 2 ) F ( x1 ),
если
x2 x1.
32
33. Следствие 1
P(a X b) F (b) F (a)33
34.
Пример. Случайная величина Х заданафункцией распределения
0
x 1
F ( x)
4 4
1
при
x 1,
при
1 x 3,
при
х 3.
Найти вероятность того, что в
результате испытания Х примет
значение, принадлежащее интервалу
[0, 2).
34
35.
РешениеТак как на интервале (0,2)
x 1
F ( x) ,
4 4
то
2 1 0 1 1
F (2) F (0) .
4 4 4 4 2
Итак,
1
P(0 X 2) .
2
35
36. Следствие 2
Вероятность того, что непрерывнаяслучайная величина Х примет одно
определённое значение, равна
нулю:P(X=x)=0.
36
37. Следствие 3
Для непрерывной случайной величиныP ( a X b) P ( a X b)
P(a X b) P(a X b).
37
38. Свойство 3
Если возможные значения случайнойвеличины принадлежат интервалу
(a, b), то:
x
a
;
1) F(x) = 0 при
2) F(x) = 1 при
x b.
38
39. Следствие
lim F ( x) 0;x
lim F ( x) 1.
x
39
40. Плотность распределения вероятностей непрерывной случайной величины
4041.
Плотностью распределения непрерывнойслучайной величины X называют функцию f(x) –
первую производную от функции распределения
F(x):
f ( x) F ( x).
41
42. Вероятность попадания непрерывной СВ в заданный интервал
bP(a X b) f ( x)dx.
a
42
43.
ПримерЗадана плотность вероятности случайной
величины Х
0
f ( x ) 2 х
0
при
х 0,
при
0 x 1,
при
х 1.
Найти вероятность того, что в результате
испытания Х примет значение,
принадлежащее интервалу (0,5 ; 1 ).
43
44. Решение
Искомая вероятность1
P(0,5 X 1) 2 xdx x
,
0 5
2 1
,
0 5
1 0,25 0,75
44
45. Нахождение функции распределения по известной плотности распределения
xF ( x)
f (t )dt.
45
46.
ПримерНайти функцию распределения по
данной плотности распределения:
при
0
1
f ( x)
при
b
a
при
0
х а,
a x b,
x b.
46
47. Решение
xF ( x)
f (t )dt
Если
x a
, то f(x) = 0
F(x) = 0.
47
48.
Еслиa x b, то
1
f ( x)
b a
1
x a
F ( x) f (t )dt 0dt
dt
.
b
a
b
a
a
x
a
x
Если x > b, то
dt
b a
F ( x) 0dt
0dt
1.
b a b
b a
a
a
b
x
48
49.
Итак, искомая функция распределенияпри
0
x a
F ( x)
при
b
a
при
1
х а,
а x b,
x b.
49
50. Свойства плотности распределения
Свойство 1f ( x) 0
50
51.
Свойство 2f ( x)dx 1
51
52. Следствие
Если все возможные значения случайнойвеличины принадлежат интервалу (a, b),то
b
f ( x)dx 1.
a
52
53. Пример
Плотность распределения Х :f ( x)
a
e
x
e
x
Найти постоянный параметр a.
53
54.
Решениеa
dx
e
x
e
x
1.
54
55.
e xdx
e
x
x
e dx
1 e
0
2x
arctg e .
x
c
dx
dx
dx
lim x x
x
x
e x e x blim
e
c e
e
e
b
0
arctg1 lim (arctg eb ) lim(arctg ec ) arctg1
b
c
a
1
.
55
56. Числовые характеристики непрерывных случайных величин
5657. Математическим ожиданием НСВ Х называют определённый интеграл
M (X )xf ( x)dx
57
58.
Предполагается, что несобственныйинтеграл сходится абсолютно, т.е.
существует
xf x dx.
58
59. Дисперсией непрерывной случайной величины называют мат. ожидание квадрата её отклонения.
D( X )2
x
M
(
X
)
f ( x)dx.
59
60.
Среднее квадратическоеотклонение непрерывной случайной
величины определяется равенством
(X )
D( X ).
60
61.
Замечание 1Свойства математического ожидания и дисперсии
дискретных величин сохраняются и для непрерывных
величин.
61
62.
Замечание 2D( X )
x f ( x)dx M ( X ) .
2
2
62
63.
Пример 1Найти мат. ожидание и дисперсию
случайной величины Х, заданной
функцией распределения
0
F ( x) х
1
при
х 0,
при
0 x 1,
при
х 1.
63
64. Решение
0f ( x) F ( x) 1
0
при
при
при
х 0,
0 x 1,
х 1.
64
65.
2 11
x
M ( X ) x 1 dx
2
0
2
0
1
.
2
3 1
x
1
D( X ) x 1 dx
3
2
0
1
2
0
1 1
.
4 12
65
66.
Пример 2Найти мат. ожидание и дисперсию
непрерывной случайной величины Х,
распределённой равномерно в интервале
(a, b).
66
67. Решение
Плотность равномерногораспределения
1
f ( x)
b a
b
b
1
M ( X ) xf ( x)dx
xdx.
b aa
a
67
68.
a bM (X )
.
2
2
2
1
a b
2
D( X ) x f ( x)dx M ( X )
x dx
.
b aa
2
a
b
b
2
b a
D( X )
12
2
.
68
69. Нормальное распределение
Нормальным называютраспределение вероятностей НСВ с
плотностью
f ( x)
1
2
e
( x a ) 2
2 2
69
70.
Вероятностный смысл параметров:а - математическое ожидание,
- среднее квадратическое отклонение
нормального распределения.
70
71. Вероятность попадания в заданный интервал нормальной случайной величины
7172.
P( X )f ( x)dx.
72
73.
Ф0 ( x )1
2
z
x
e 2
2 0
dz,
a
a
P( X ) Ф0
Ф0
73
74.
ПримерСлучайная величина Х распределена по
нормальному закону. Мат. ожидание и
среднее квадратическое отклонение
этой величины соответственно равны
30 и 10.
Найти вероятность того, что Х примет
значение, принадлежащее интервалу
(10, 50).
74
75.
РешениеПо условию,
10, 50, a 30, 10,
50 30
10 30
P(10 X 50) Ф0
Ф0
2Ф0 (2).
10
10
0 (2) 0,4772.
P(10 X 50) 2 0,4772 0,9544 .
75
76. Вычисление вероятности заданного отклонения
7677.
X a ,X a ,
a X a .
P( X a ) P(a X a )
(a ) a
(a ) a
Ф0
Ф0
Ф0 Ф0
.
77
78.
Приняв во внимание равенствоФ0 Ф0
P( X a ) 2Ф0 .
В частности, при a = 0
P( X ) 2Ф0 .
78
79.
ПримерСлучайная величина Х распределена
нормально. Математическое ожидание и
среднее квадратическое отклонение Х
соответственно равны 20 и 10.
Найти вероятность того, что отклонение
по абсолютной величине будет меньше
трёх.
79
80. Решение
P( X a ) 2Ф .3, a 20, 10.
3
P( X 20 3) 2Ф0 2Ф0 (0,3).
10
0 (0,3) 0,1179.
P( X 20 3) 0,2358 .
80
81. Правило трёх сигм
P( X a ) 2Ф0 ,3 ,
P( X a 3 ) 2Ф0 (3) 2 0,49865 0,9973,
81
82.
Вероятность того, что абсолютная величинаотклонения превысит утроенное среднее
квадратическое отклонение, очень мала, а именно равна
0,0027.
Такие события, исходя из принципа невозможности
маловероятных событий, можно считать практически
невозможными.
82
83.
В этом и состоит сущность правилатрёх сигм:
Если случайная величина распределена нормально,
то абсолютная величина её отклонения от
математического ожидания не превосходит
утроенного среднего квадратического отклонения.
83
84. Показательное распределение
Показательным (экспоненциальным)называют распределение НСВ с
плотностью
0
f ( x ) x
e
при
при
х 0,
0 x,
0
84
85.
F ( x)x
x
0
f ( x)dx e
x
dx 1 e
x
при
х 0,
0
F ( x)
x
при 0 x.
1 e
85
86. Числовые характеристики
0f ( x ) x
e
при
при
х 0,
0 x,
86
87.
M (X )xf ( x)dx xe
dx
0
D( X )
x
x
f
(
x
)
dx
M
(
X
)
2
2
1
.
1
.
2
87
88. Два важных примера стандартных распределений
Пусть X i i 1, 2, ..., n - нормальныенезависимые случайные величины с
нулевым математическим ожиданием и
единичной дисперсией.
88
89.
Тогда случайная величинаn
2
i 1
2
Xi
распределена по закону
(хи
2
квадрат) с n степенями свободы.
89
90.
Теперь пусть X i i 0, 1, 2, ..., nнормальные независимые случайные
величины с нулевым математическим
ожиданием и единичной дисперсией.
90
91.
Тогда случайная величинаT
X0
n
i 1
Xi
n
имеет распределение, которое
называется
распределением Стьюдента с n
степенями свободы.
91
92. Вопросы к лекции 11
Какая случайная величина называетсянепрерывной?
Функция и плотность распределения
непрерывной случайной величины
Математическое ожидание и дисперсия
непрерывной с.в.
Распределение Пуассона
Нормальное распределение
92
93.
Конец лекции 1193





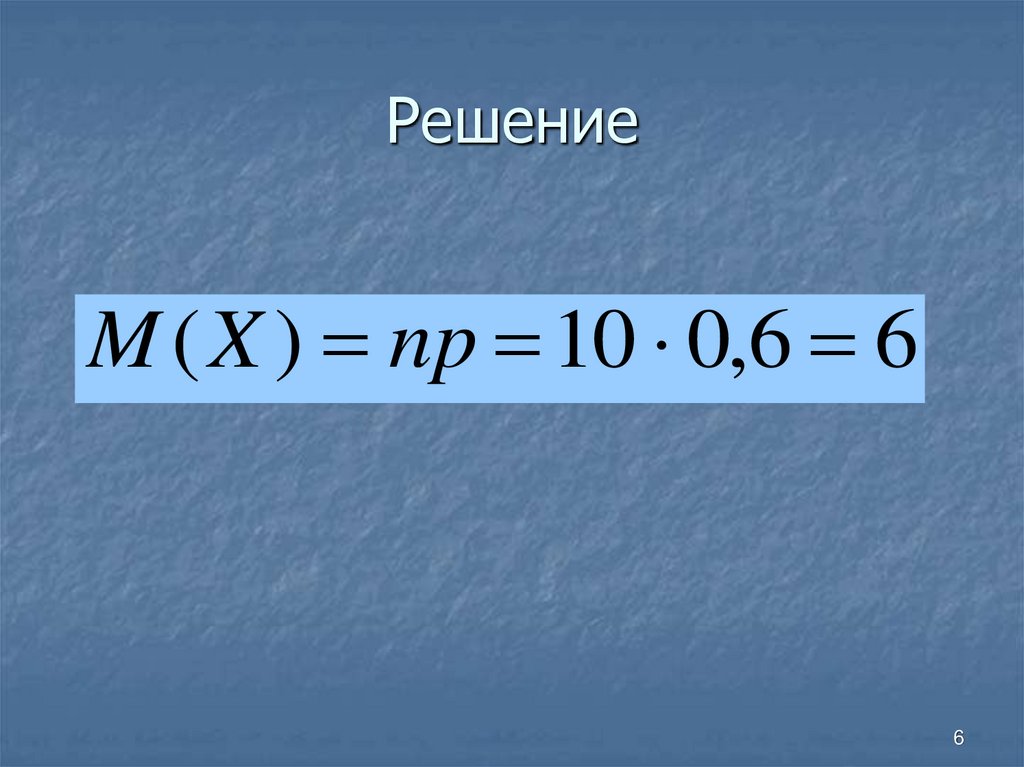











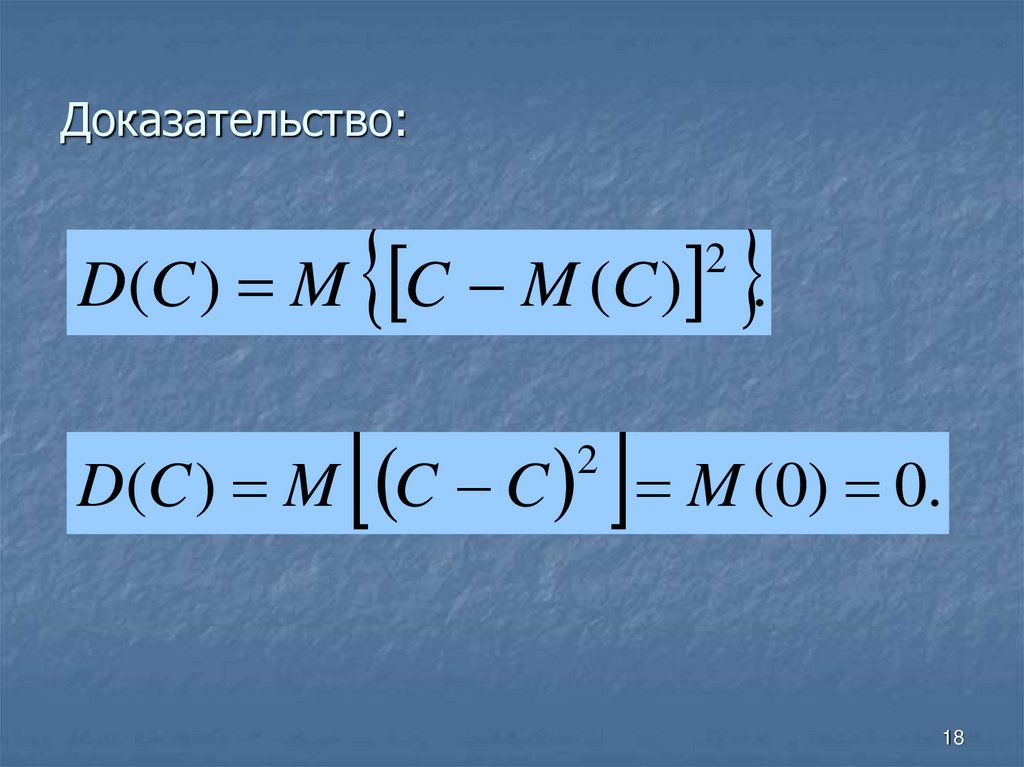

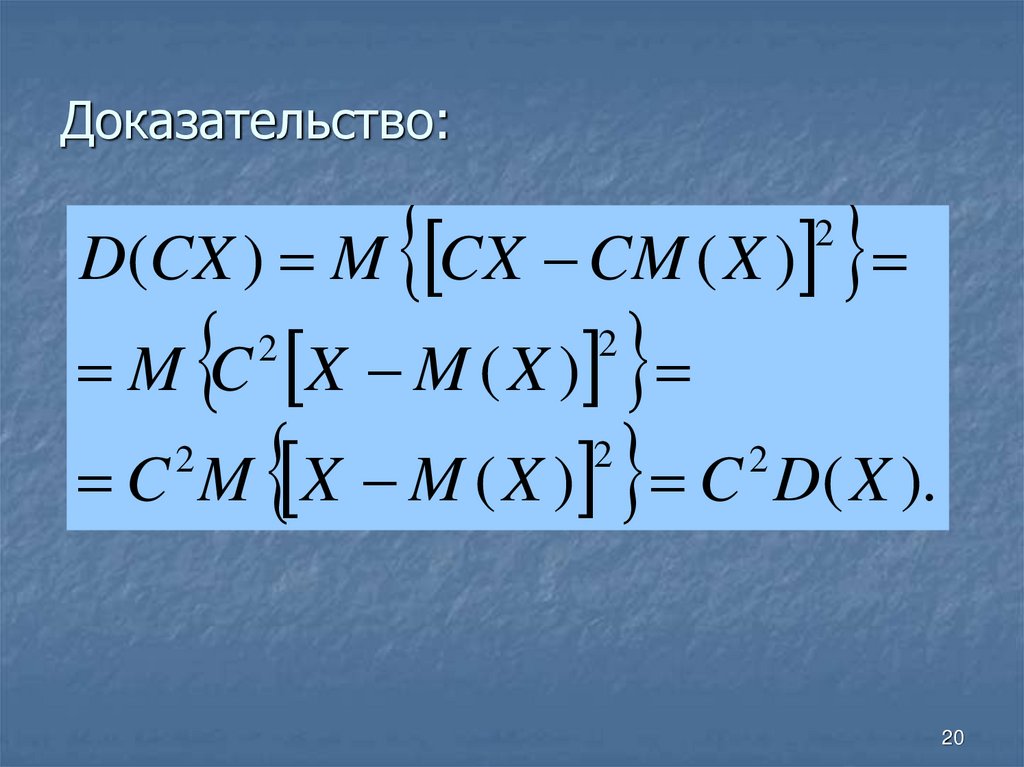












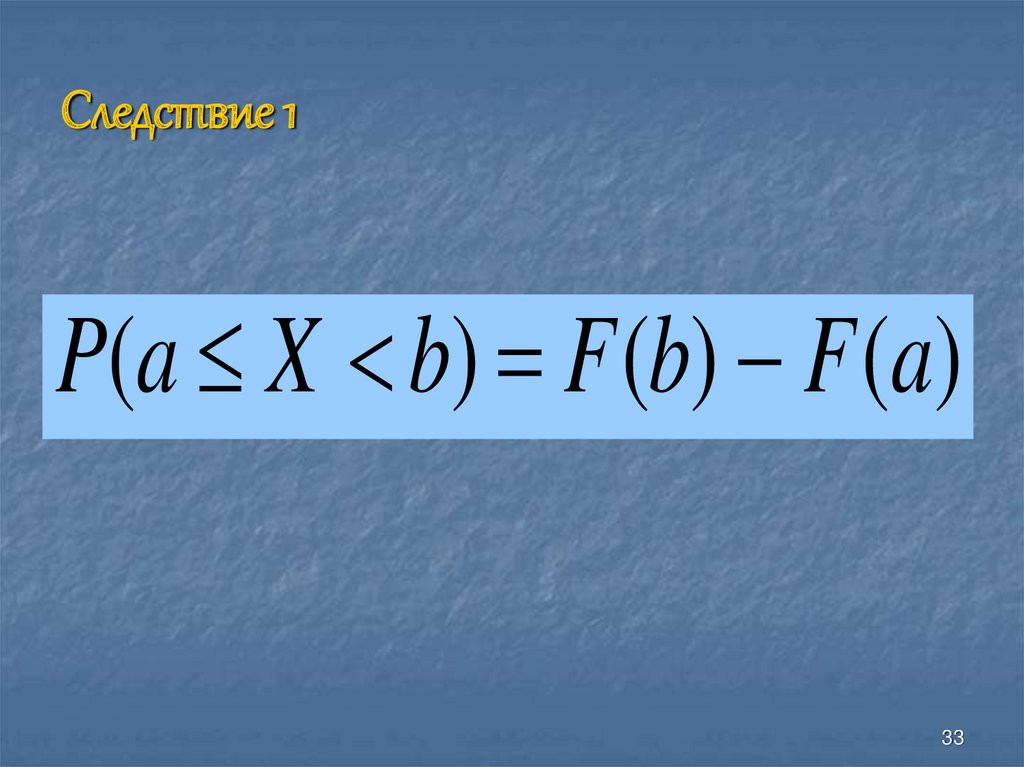











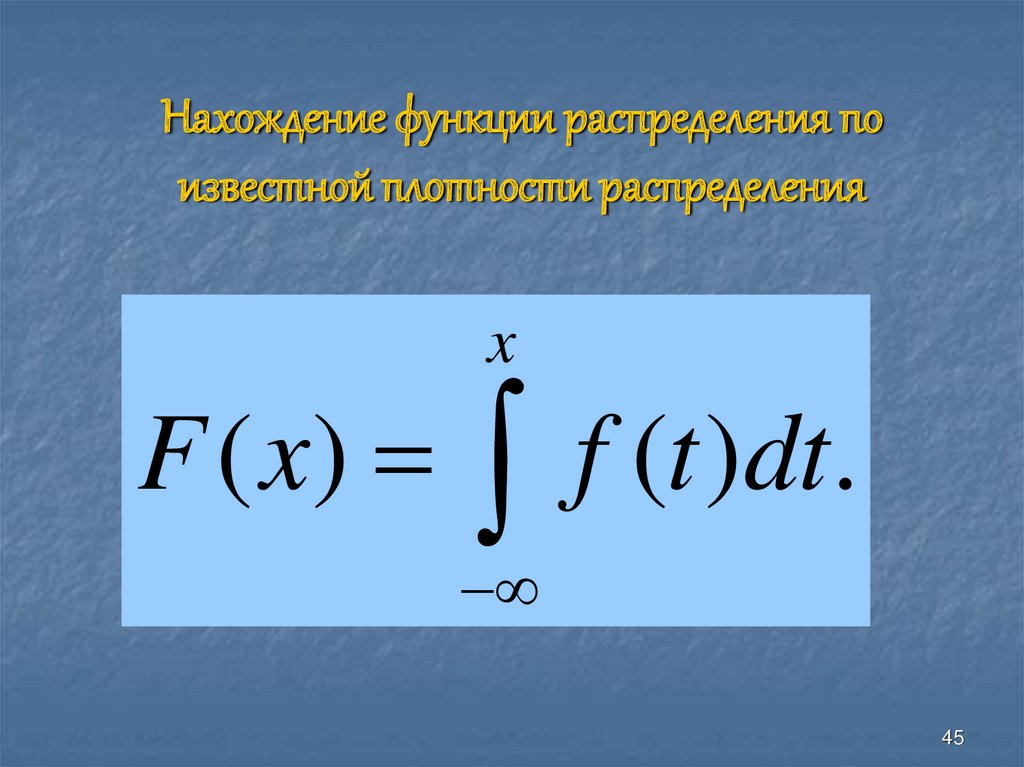

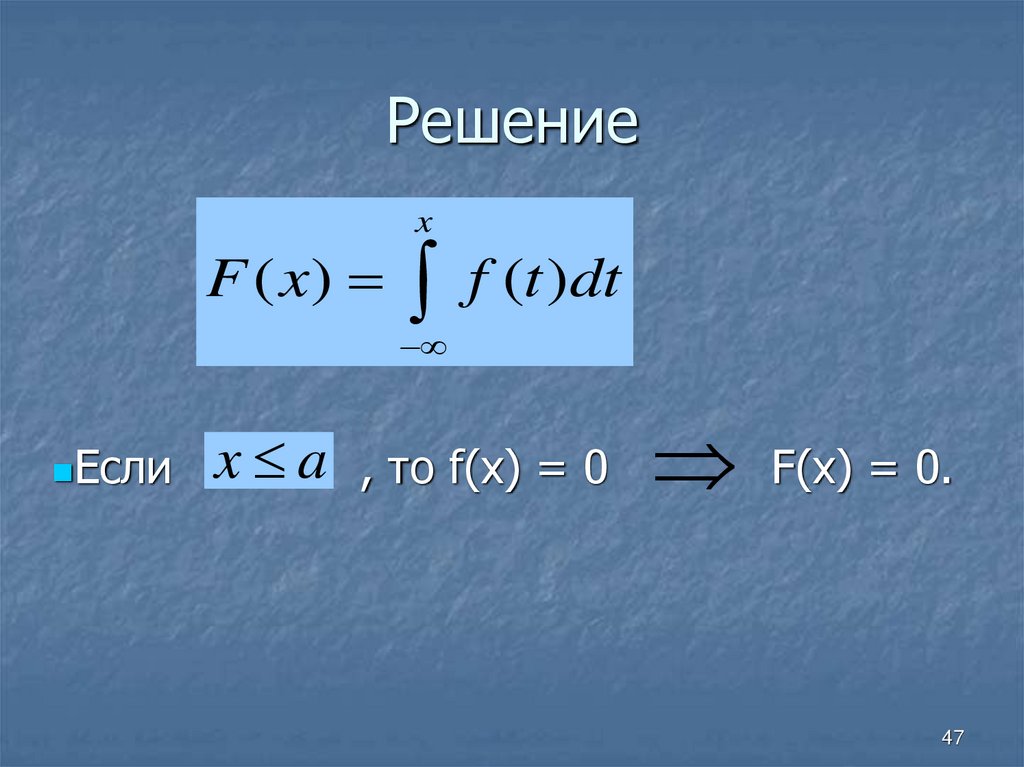
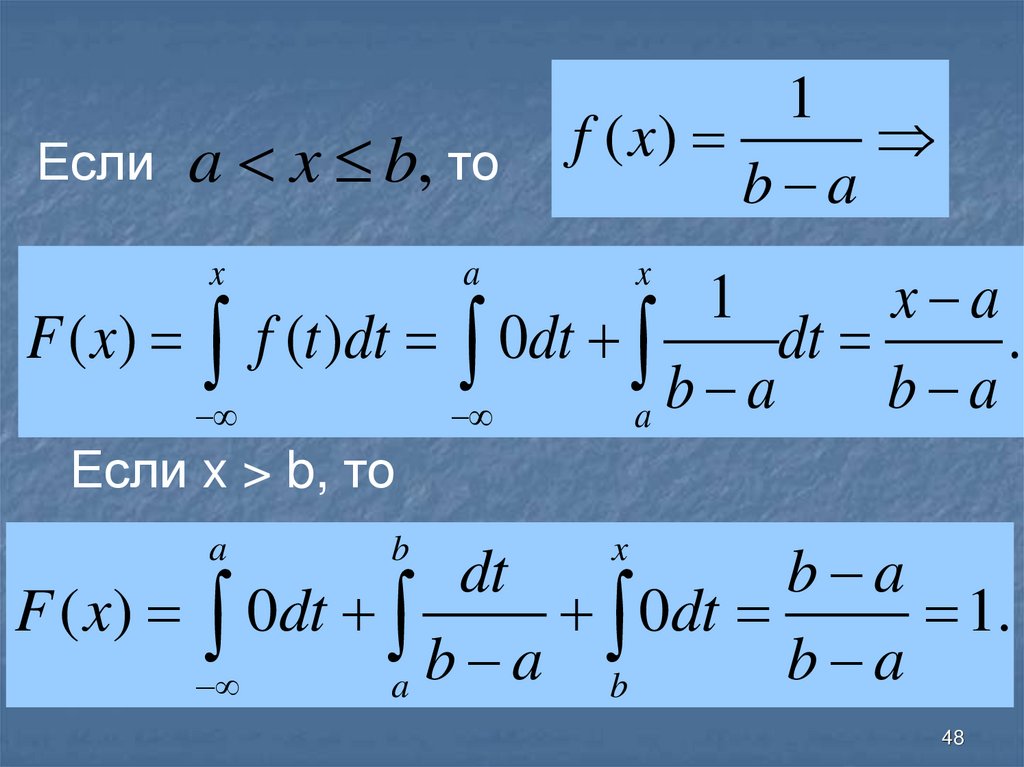






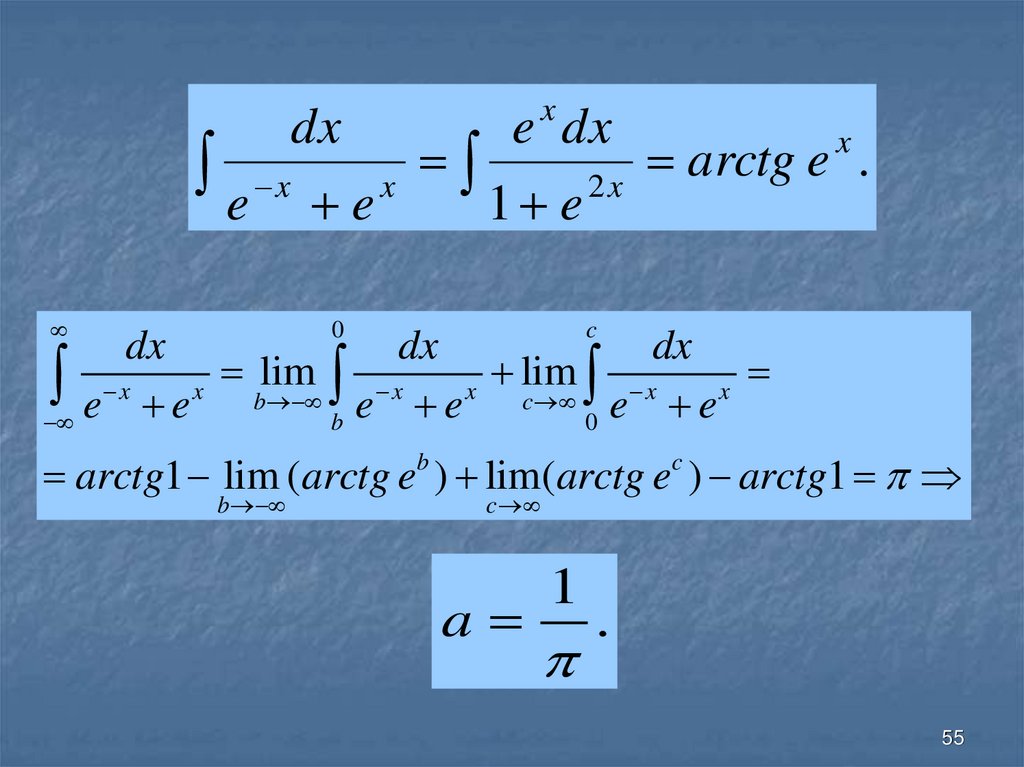

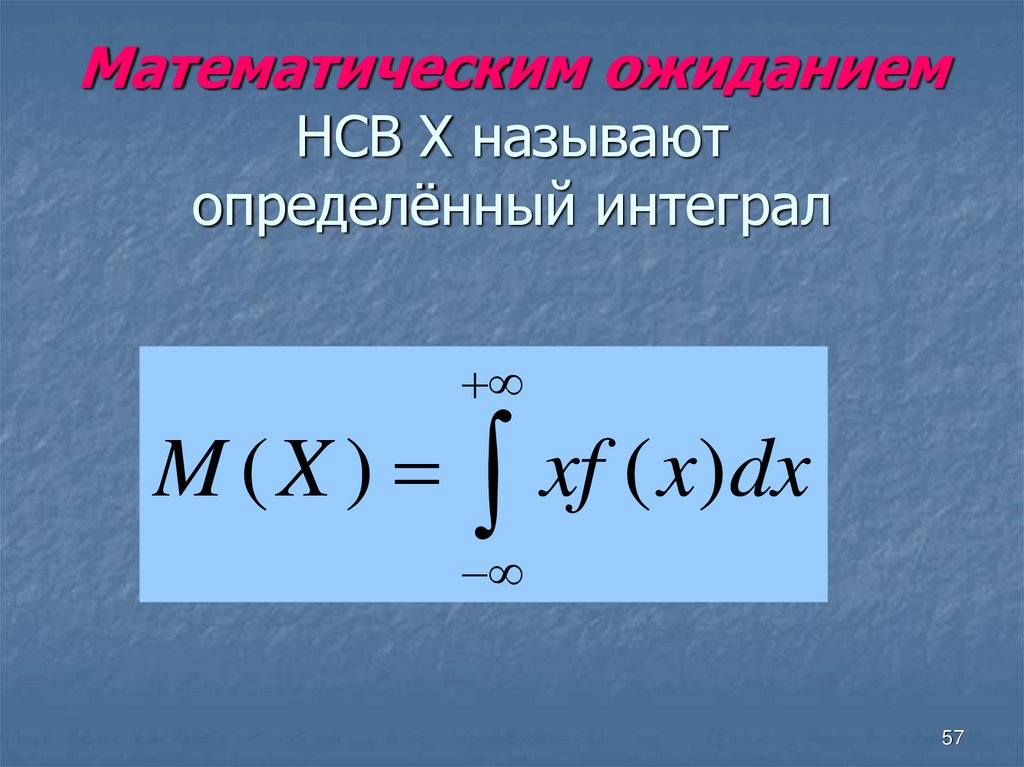




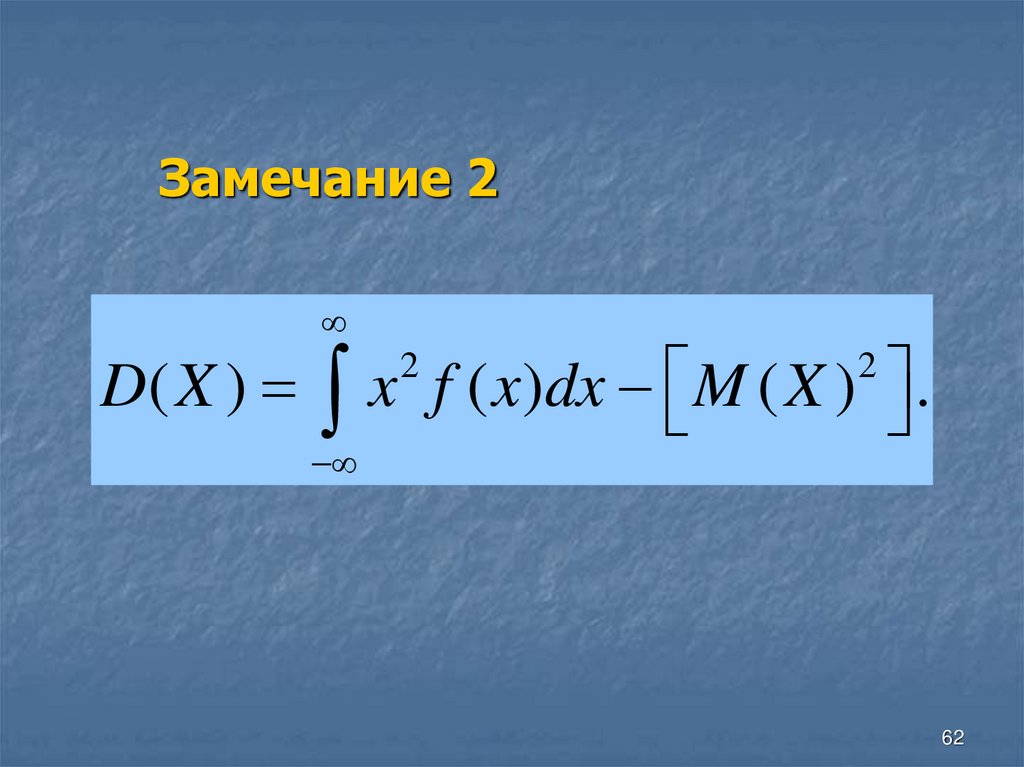


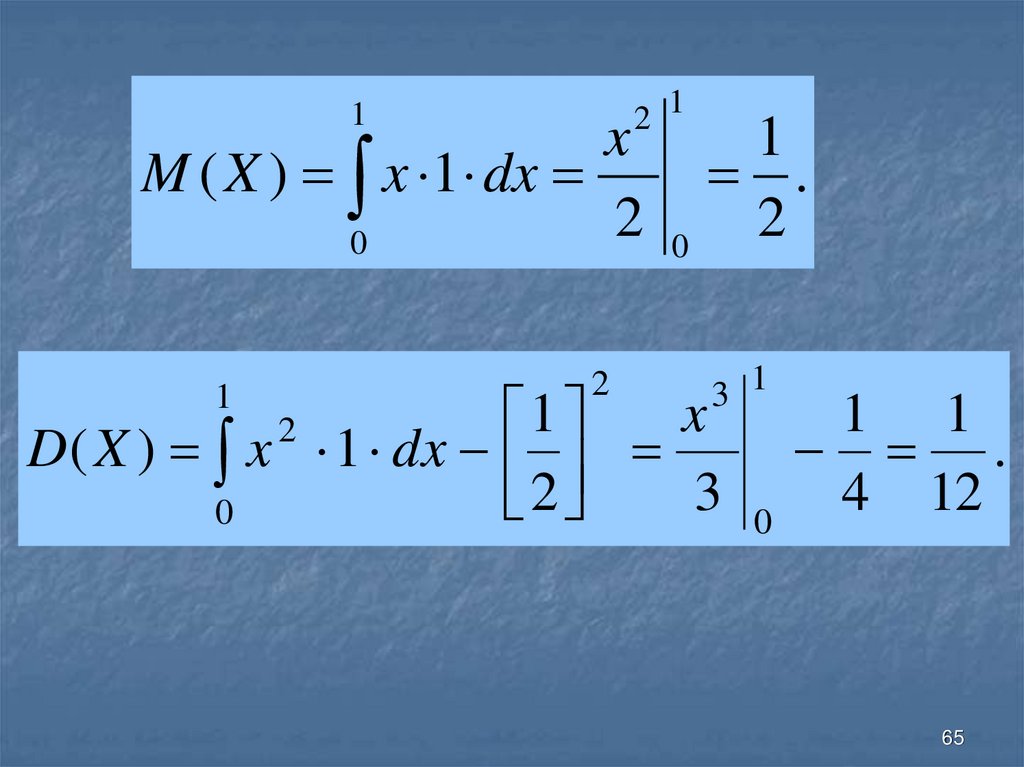


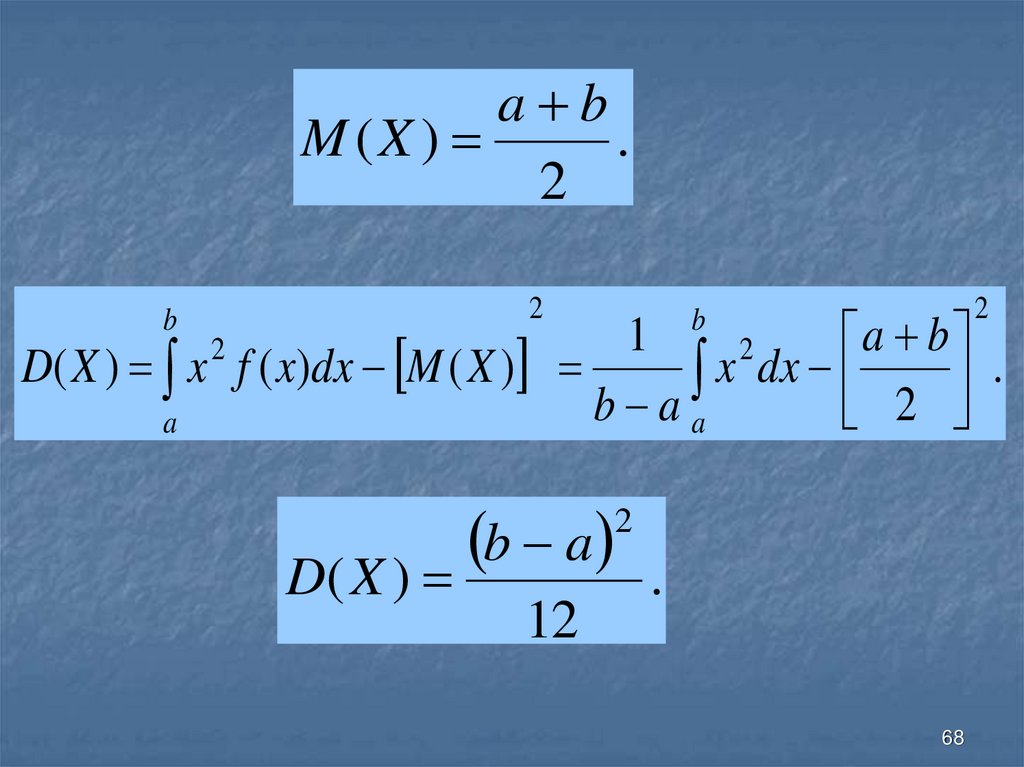



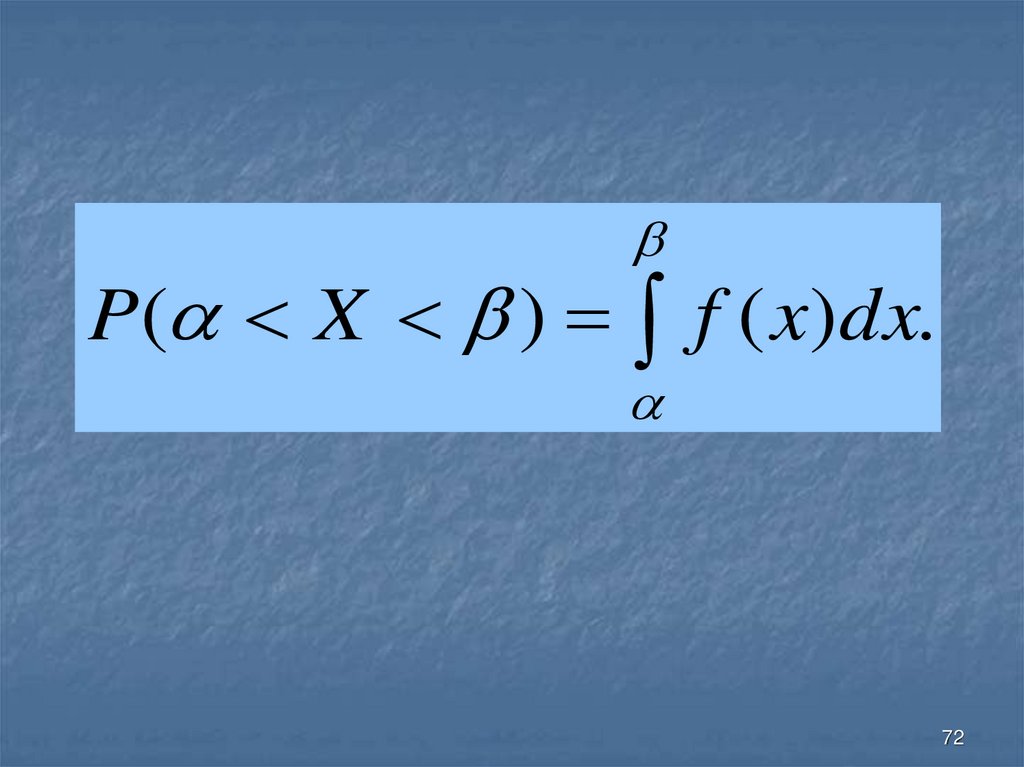
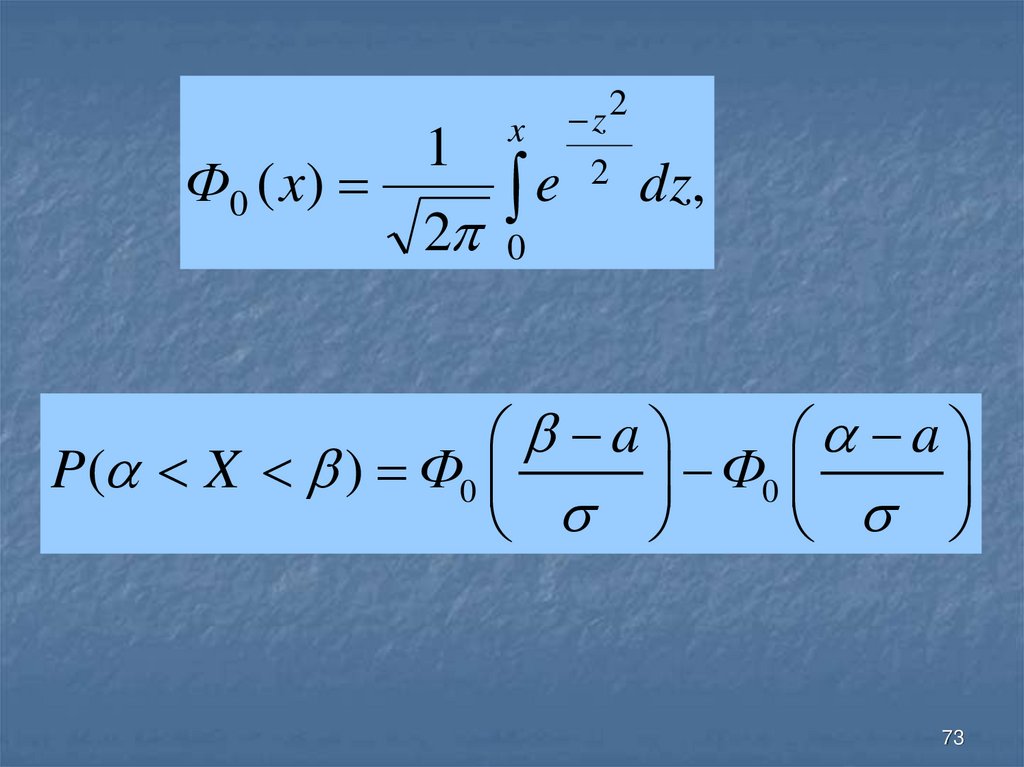



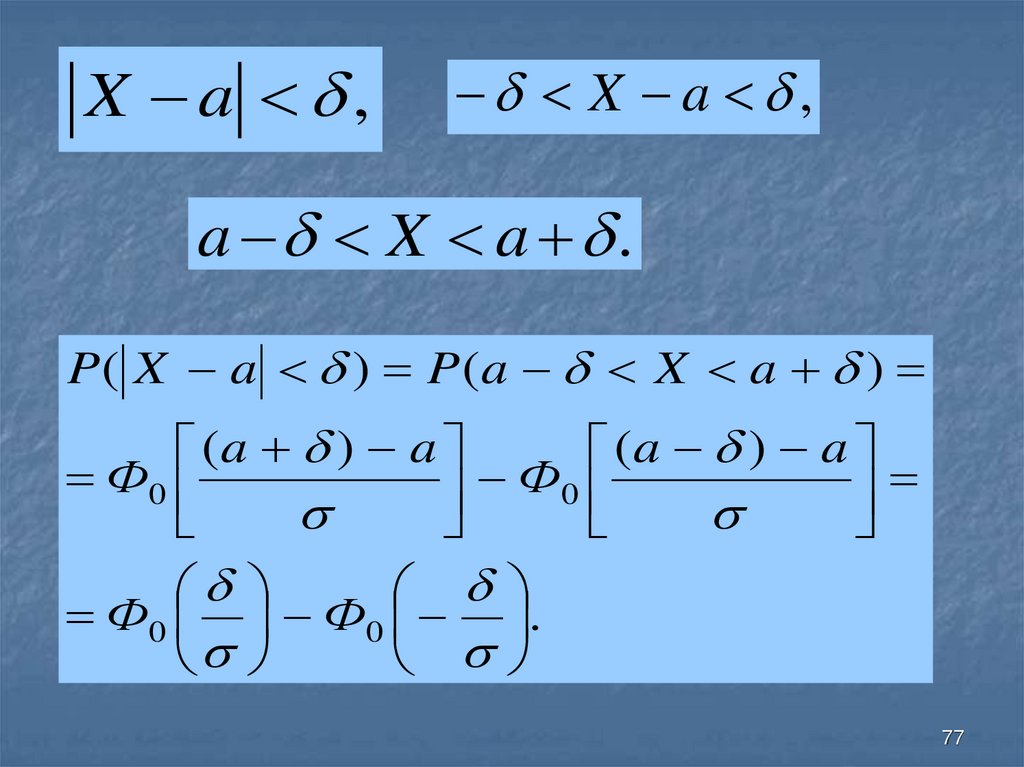







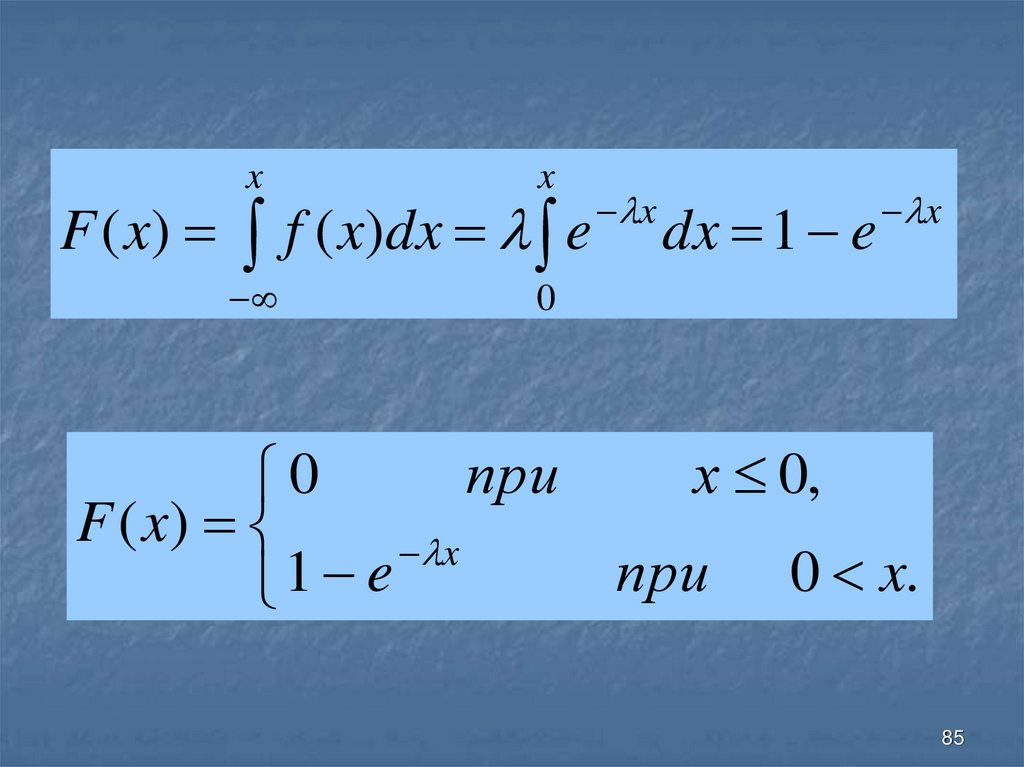

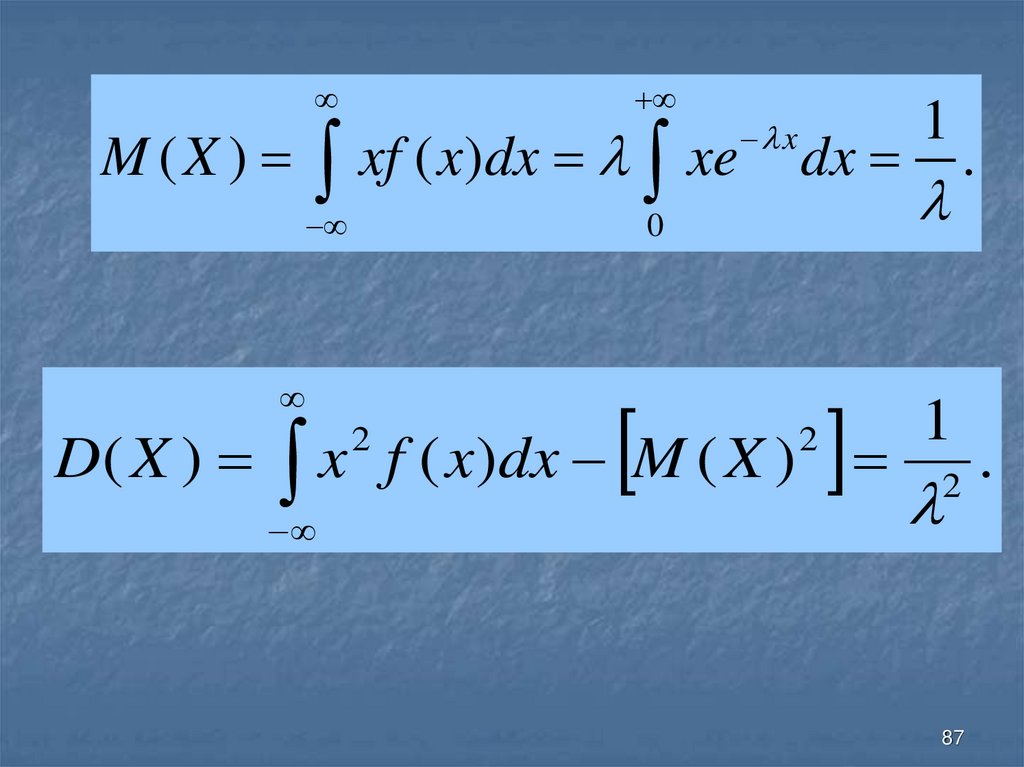






 Математика
Математика








