Похожие презентации:
Теория вероятностей и элементы математической статистики
1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
2. Раздел 2. Случайные Величины
Раздел 2. СлучайныеВеличины
Глава 1. Одномерные СВ
3. УЧЕБНЫЕ ВОПРОСЫ
1. Определенияи
классификация
случайных
величин.
2. Ряд распределения. Функция распределения СВ,
ее свойства и график.
3. Плотность распределения вероятностей.
4. Числовые
характеристики
непрерывной случайных величин.
дискретной
и
4. ЛИТЕРАТУРА
1. Баврин И. И. Высшая математика. – М.:Академия, 2004, стр. 531 – 545.
2. Письменный Д. Т. Конспект лекций по теории
вероятностей и математической статистике. – М.:
Айрис-пресс, 2004, стр. 60 – 83.
5.
§1. Основные определения6.
Случайной величиной называется величина,которая в результате опыта может принять то
или иное значение, причем заранее
неизвестно какое именно.
Обозначения: X, Y, Z…
7.
Случайныевеличины
дискретные
непрерывные
8.
9.
• Определение. Непрерывной случайнойвеличиной называют такую случайную
величину, которая может принять любое
значение из некоторого конечного или
бесконечного интервала (интервалов).
10. ПРИВЕДИТЕ ПРИМЕРЫ СЛУЧАЙНЫХ ВЕЛИЧИН
11.
Закон распределения – всякое соответствиемежду
возможными
значениями
случайной
величины и соответствующими им вероятностями.
12. § 2. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
13. ТАБЛИЧНЫЙ СПОСОБ
14.
• ПустьX x1
и
P( X x1 ) p1 ;
X x2
и
P( X x2 ) p2 ;
X x3
и
P ( X x3 ) p 3 ;
…………………………………
X xn ,
P( X xn ) pn .
n
p
i 1
i
1.
15. РЯД РАСПРЕДЕЛЕНИЯ ДСВ
Закон распределения или ряд распределениядискретной
случайной
величины
X,
принимающей конечное число значений
x 1 < x2 < … < xn ,
с соответствующими вероятностями
pi (i = 1, 2,…, рn ), задается в виде таблицы
X
x1
x2
x3
P
p1
p2
p3
……
xn
……
pn
16.
РЯД РАСПРЕДЕЛЕНИЯДСВ
Ряд распределения дискретной случайной величины,
принимающей счетное число значений задается в виде
таблицы, где
x1 < x2 < … < xm < … –
возможные значений величины Х, а pm (m = 1, 2,…) – их
вероятности.
p
m 1
m
1.
17.
18.
Ноль попаданий:P(0) 0, 4 0,3 0,12.
19.
Одно попадание:P(1) 0,6 0,3 0, 4 0,7 0, 46.
20.
Два попадания:P(2) 0,6 0,7 0, 42.
21.
Р(0)= 0,1 ; Р(1)= 46 ; Р(2)=Ряд распределения:
X
P
0,12 0, 46 0, 42 1.
22. ГРАФИЧЕСКИЙ СПОСОБ
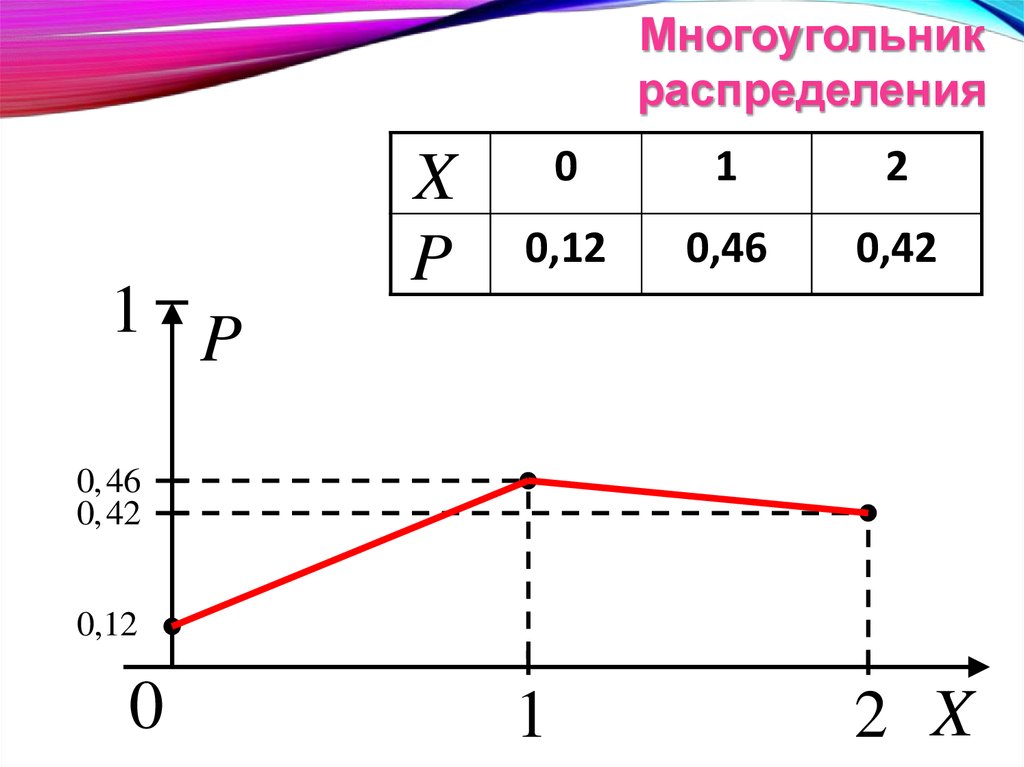
23.
Многоугольникраспределения
1 P
X
P
0
1
2
0,12
0,46
0,42
0, 46
0, 42
0,12
0
1
2 X
24. АНАЛИТИЧЕСКИЙ СПОСОБ
25. С ПОМОЩЬЮ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ F(X)
26. § 3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
27.
Функция распределенияОпределение. Функцией распределения
случайной величины Х называется
вероятность того, что случайная величина Х
примет значение меньше, чем х:
F ( x) P( X x)
28.
F ( x)для ДСВ Х
определяется формулой
0,
p,
1
F ( x)
p1 p2 ,
1,
если
x x1 ,
если x1 x x2 ,
если x2 x x3 ,
если
x xn .
29.
График –ступенчатая функция
1 F ( x)
p1 p2 p3
p1 p2
p1
0
x1
x2 x3
xn
30.
Свойства функциираспределения
1)
l im F x 0; li m F x 1.
x
2)
x
F ( x) неубывающая функция на
( ; ).
3) P( X ) F ( ) F ( ).
31.
4. Если X - непрерывная случайнаявеличина, то P( X ) 0
P( X ) P( X )
P( X ) P( X ).
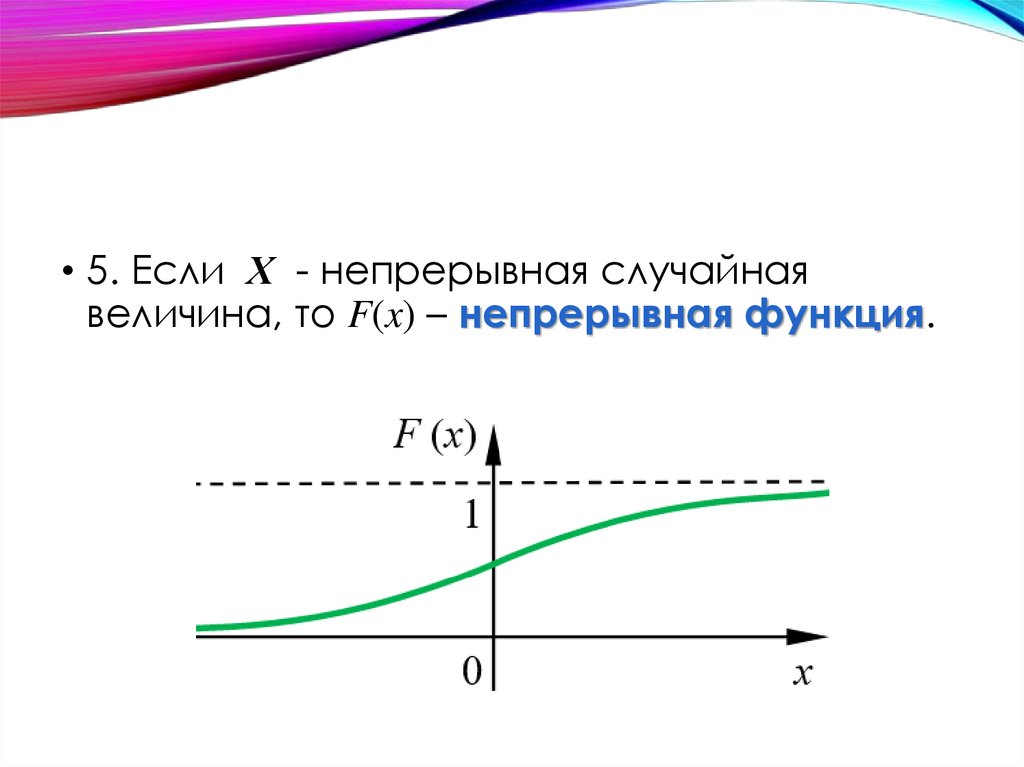
32.
• 5. Если Х - непрерывная случайнаявеличина, то F(x) – непрерывная функция.
33. § 4. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
34.
• Определение. Дифференциальнойфункцией распределения или плотностью
распределения вероятностей наз. первая
производная интегральной функции
распределения
f ( x) F ( x).
• Иногда плотность распределения
вероятностей обозначают
р( x) F ( x).
35.
• График дифференциальной функциираспределения f (x ) наз. кривой
распределения:
36. СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
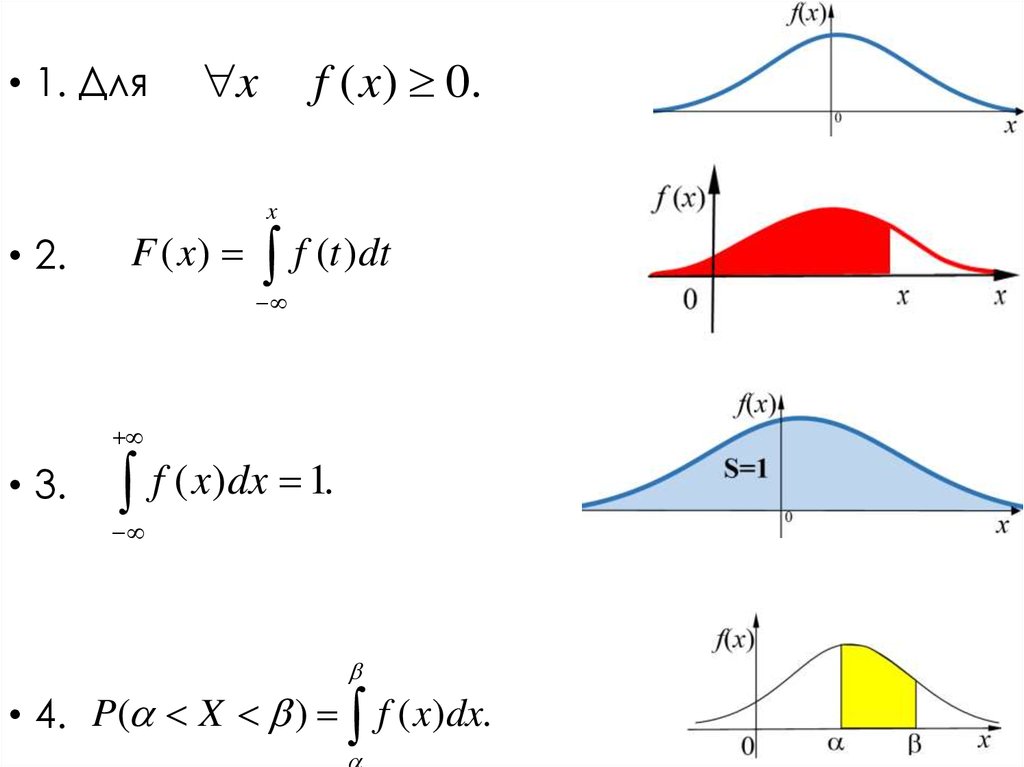
37.
• 1. Дляx
f ( x) 0.
x
• 2.
F ( x)
f (t )dt
• 3.
f ( x)dx 1.
• 4. P( X ) f ( x)dx.
38.
39.
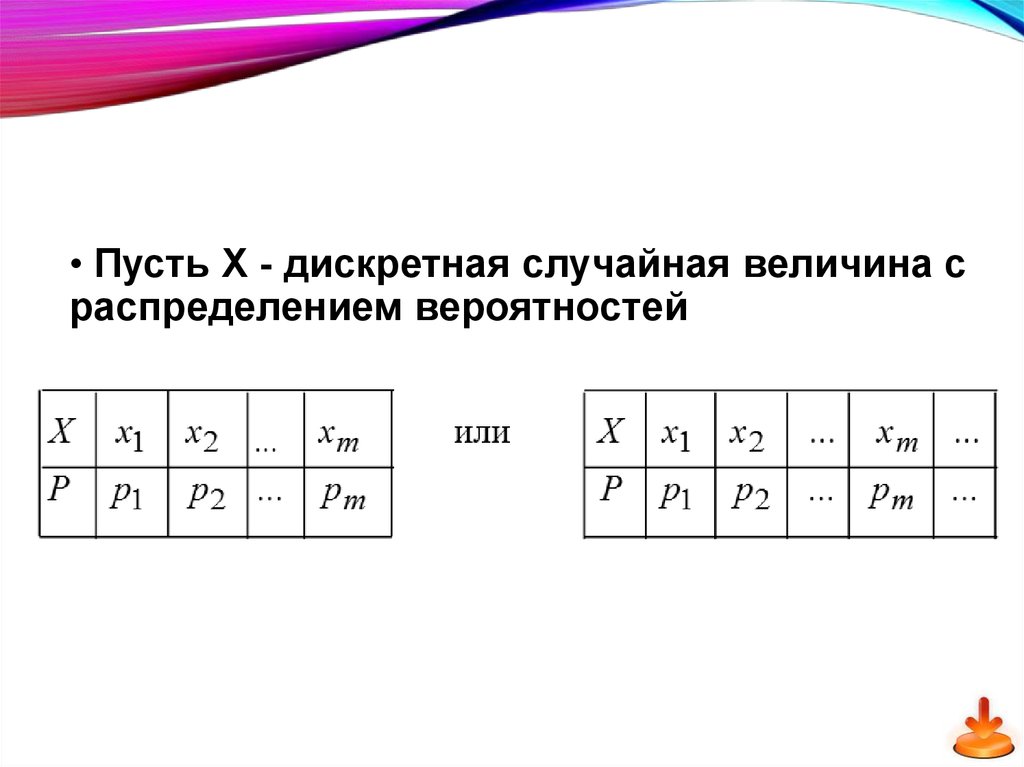
• Пусть Х - дискретная случайная величина сраспределением вероятностей
40.
Математическимназывается число
MX
ожиданием
ДСВ
m
p x
k 1
k
k
для конечного множества значений Х,
MX
p x
k 1
k
k
для счетного множества значений Х.
Х
41.
Рассмотрим случайнуювеличину с рядом распределения:
X
P
9
10
11
0,4
0,1
0,5
X
42.
Математическое ожидание случайнойвеличины X в нашем примере:
М ( Х ) = x1· p1 + x2 · p2 + x3· p3
43. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Определение. Математическим ожиданием
непрерывной случайной величины Х,
называется несобственный интеграл
M (X )
xf ( x)dx
44. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
В случае, когда все возможные значения НСВ Х
принадлежат отрезку [a,b], ее математическое
ожидание вычисляется по формуле
b
M ( X ) xf ( x)dx
a
45.
Свойства математического ожидания•1. Если X С = const, то МC = С.
•2. Если k – константа, то М(kХ) = kMХ .
•3. Если k – константа, то М(k + Х) = k + MХ .
•4. М(Х ± У) = MХ ± MУ
•5. Если СВ Х и У независимы, то
М(ХУ) = МХ МУ
46.
ДИСПЕРСИЯОпределение. Дисперсией (рассеиванием)
случайной величины называется математическое
ожидание квадрата отклонения случайной величины от
ее математического ожидания.
D( X ) M X M ( X )
2
47.
D( X ) M X M ( X )2
48.
Вычислениедисперсии
Теорема. Дисперсия равна разности
между математическим ожиданием
квадрата случайной величины Х и
квадратом ее мат. ожидания.
D( X ) M ( X ) M ( X )
2
2
49.
D( X ) M ( X ) M ( X )2
2
Вычисление
дисперсии
50.
ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СВДисперсия непрерывной случайной
величины вычисляется по формуле
D( X ) [ x M ( X )] f ( x)dx
2
51.
ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СВДля практического вычисления дисперсии
используется формула
D( X )
x
2
f ( x)dx [ M ( X )]
2
52. СВОЙСТВА ДИСПЕРСИИ
10. D [ a ] = 0, a = const;20. D [ a Х ] = a2 D[Х];
30. D [Х ] 0;
40. если Х, У независимы, то
D [ Х±У ] = D [Х ] + D [У].
53. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Определение. Средним квадратическимотклонением (СКО) случайной величины
называется корень квадратный из ее дисперсии.
СКО является мерой рассеяния случайной
величины и обозначается σ(х)
( x) D( X )
СКО имеет ту же размерность, что и случайная величина.
54. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
• Пример. Случайным образом бросают точку наотрезок [ 0,1 ]. Х– координата точки попадания.
• Найти: дисперсию и среднеквадратическое
отклонение.
• Решение.
0 , если x 0
f ( x) 1 , если х (0,1]
1
0 , если х 1
3 1
x
1
2
2
M ( X ) x dx
1
2 1
3 0 3
x
1
0
M ( X ) x dx
2 0 2
1 1 1
0
D( X )
Из формулы:
3 4 12
D( X )
2
2
x
f
(
x
)
dx
[
M
(
X
)]
1
1
(X )
12 2 3
55.
МОДАОпределение. Модой М0 дискретной
случайной величины называется ее наиболее
вероятное значение.
Для непрерывной случайной величины мода –
такое значение случайной величины, при
которой плотность распределения имеет
максимум.
56.
МЕДИАНА• Определение. Медианой MD случайной величины Х
называется такое ее значение, относительно которого
равновероятно получение большего или меньшего
значения случайной величины
P( X M D ) P( X M D )
Геометрически медиана – абсцисса точки, в которой
площадь, ограниченная кривой распределения делится
пополам S1=S2.
S1 S2
57.
НАЧАЛЬНЫЕ ИЦЕНТРАЛЬНЫЕ МОМЕНТЫ
• Определение. Начальным моментом k k-го
порядка СВ Х называется
k MX .
k
• Определение. Центральным моментом k
k-го порядка СВ Х называется
k M ( X MX ) .
k
58.
НАЧАЛЬНЫЕ МОМЕНТЫ59.
ЦЕНТРАЛЬНЫЕ МОМЕНТЫ60.
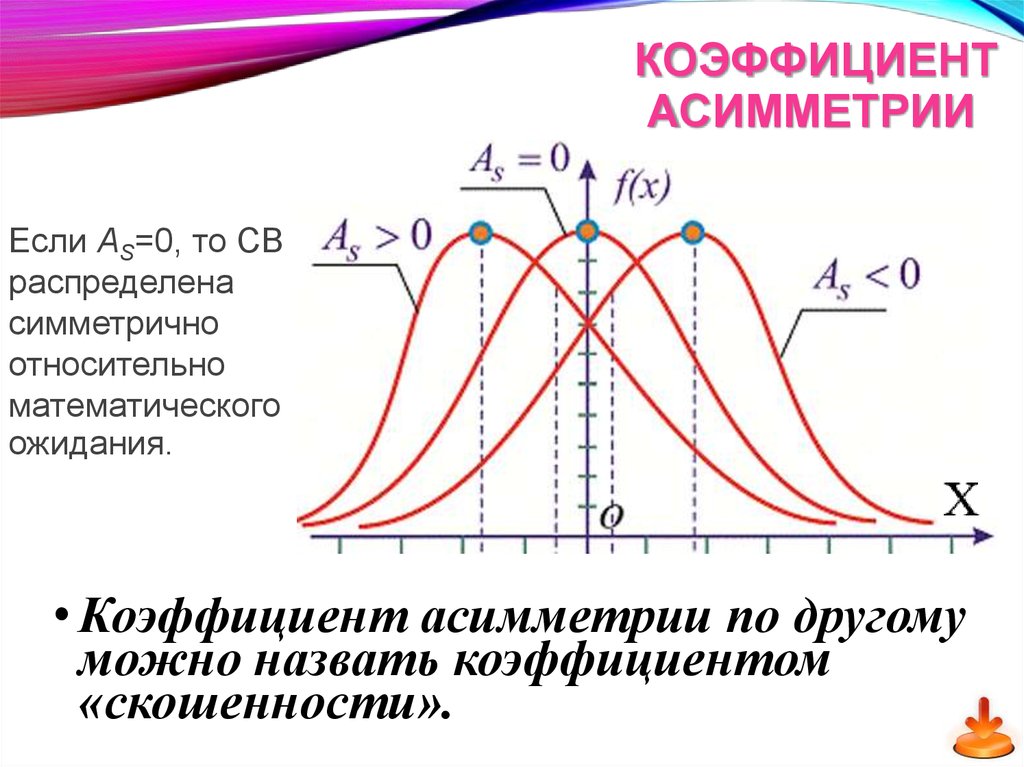
КОЭФФИЦИЕНТАСИММЕТРИИ
• Определение. Коэффициентом асимметрии AS
называется величина
3
S 3.
x
61.
КОЭФФИЦИЕНТАСИММЕТРИИ
Если АS=0, то СВ
распределена
симметрично
относительно
математического
ожидания.
• Коэффициент асимметрии по другому
можно назвать коэффициентом
«скошенности».
62.
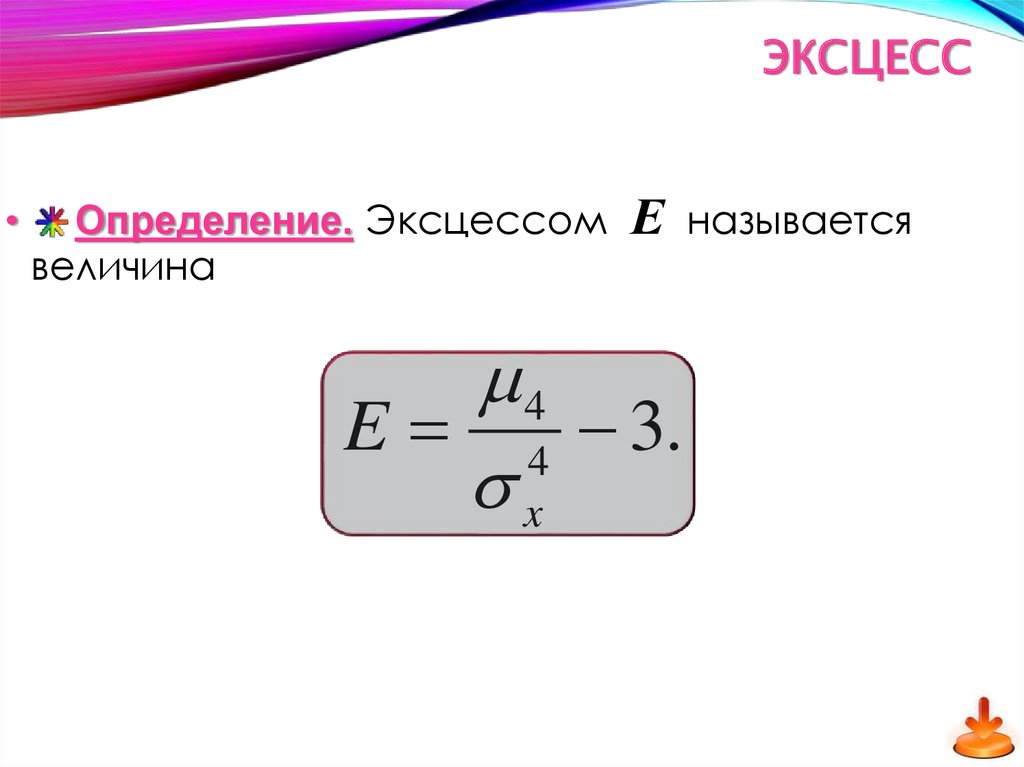
ЭКСЦЕССОпределение. Эксцессом
величина
Е
4
E 4 3.
x
называется
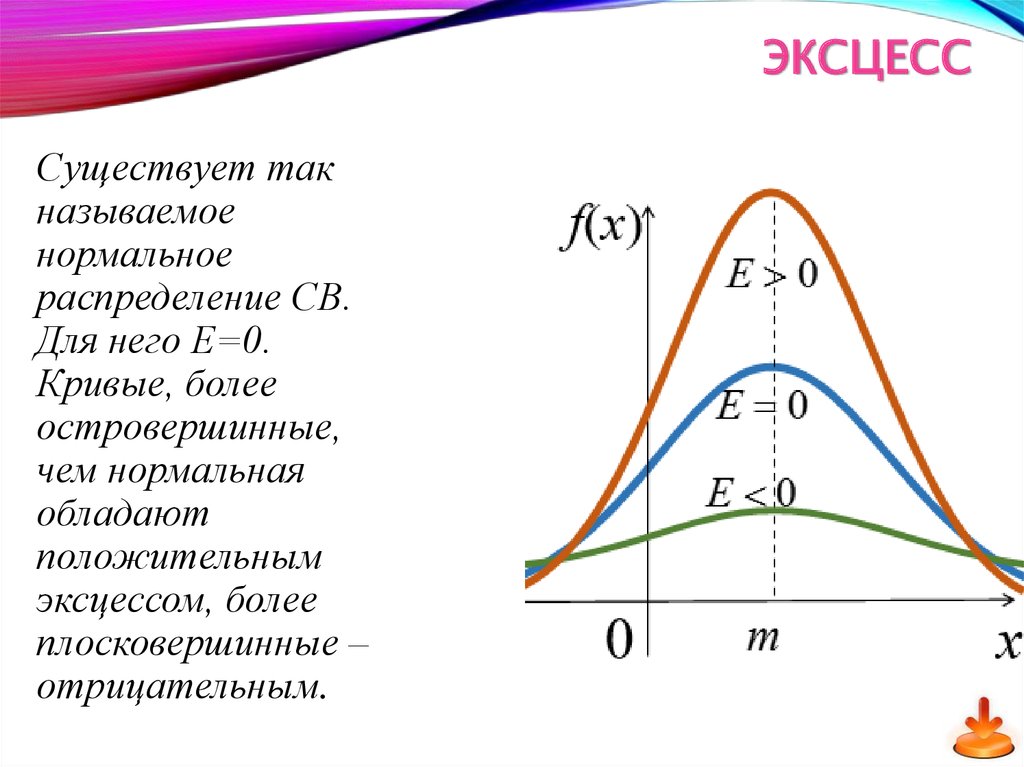
63. Существует так называемое нормальное распределение СВ. Для него Е=0. Кривые, более островершинные, чем нормальная обладают
ЭКСЦЕСССуществует так
называемое
нормальное
распределение СВ.
Для него Е=0.
Кривые, более
островершинные,
чем нормальная
обладают
положительным
эксцессом, более
плосковершинные –
отрицательным.












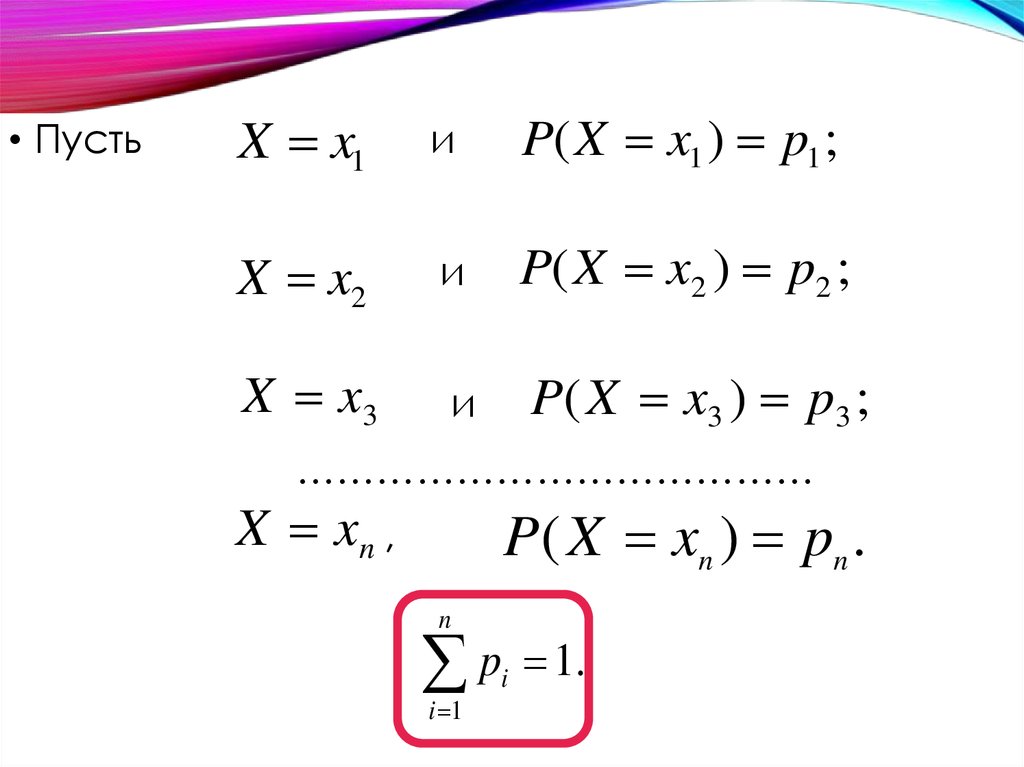











































 Математика
Математика








