Усеченная пирамида

1. «Усеченная пирамида»

2. Содержание

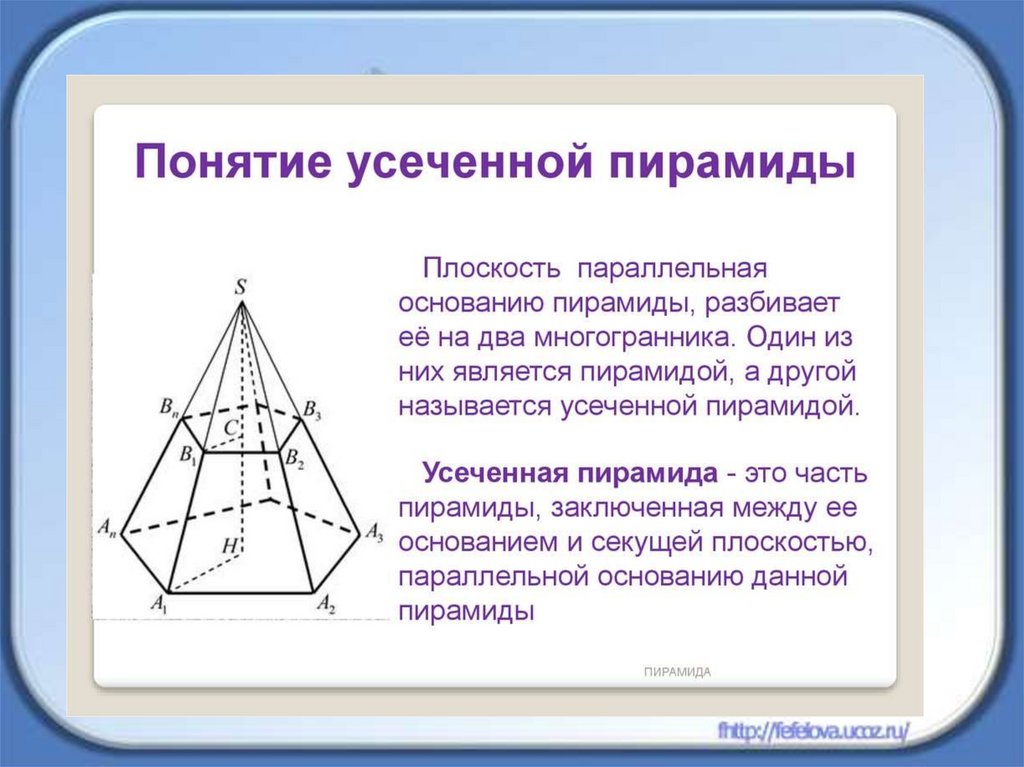
• Понятие усеченной пирамиды
• Правильная усеченная пирамида
• Площадь поверхности усеченной
пирамиды

3.

4.

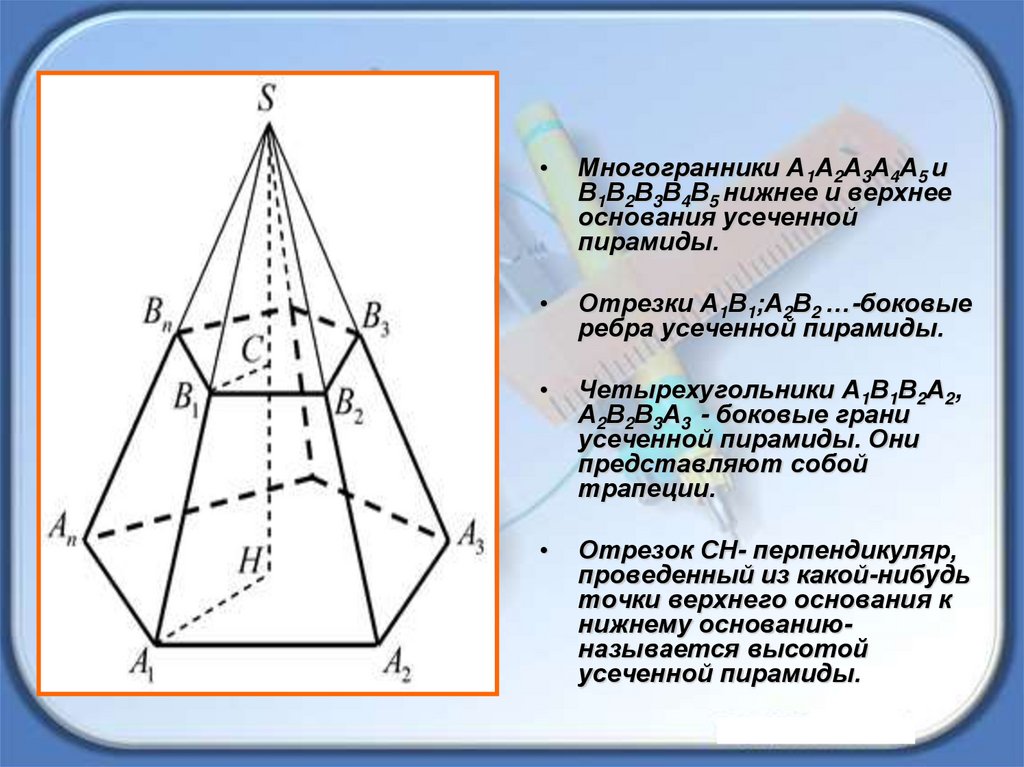
Многогранники А1А2А3А4А5 и
В1В2В3В4В5 нижнее и верхнее
основания усеченной
пирамиды.
Отрезки А1В1;А2В2 …-боковые
ребра усеченной пирамиды.
Четырехугольники А1В1В2А2,
А2В2В3А3 - боковые грани
усеченной пирамиды. Они
представляют собой
трапеции.
Отрезок СН- перпендикуляр,
проведенный из какой-нибудь
точки верхнего основания к
нижнему основаниюназывается высотой
усеченной пирамиды.

5. Правильная усеченная пирамида

Усеченная пирамида
называется правильной,
если она получена сечением
правильной пирамиды
плоскостью, параллельной
основанию.
Основания- правильные
многоугольники.
Боковые грани- равные
равнобедренные трапеции.
Высоты этих трапеций
называются апофемами.

6. Площадь поверхности усеченной пирамиды

• Площадью полной поверхности (Sполн) пирамиды
называется сумма площадей всех ее граней: основания и
всех боковых граней.
• Площадью боковой поверхности (Sбок) пирамиды
называется сумма площадей её боковых граней.
• Sполн =Sбок + Sосн
• Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на
апофему.
• Площадь боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы переметров
оснований на апофему
• Sполн.усеч. = Sбок. + Sверх.осн. + Sнижн.осн.

7.

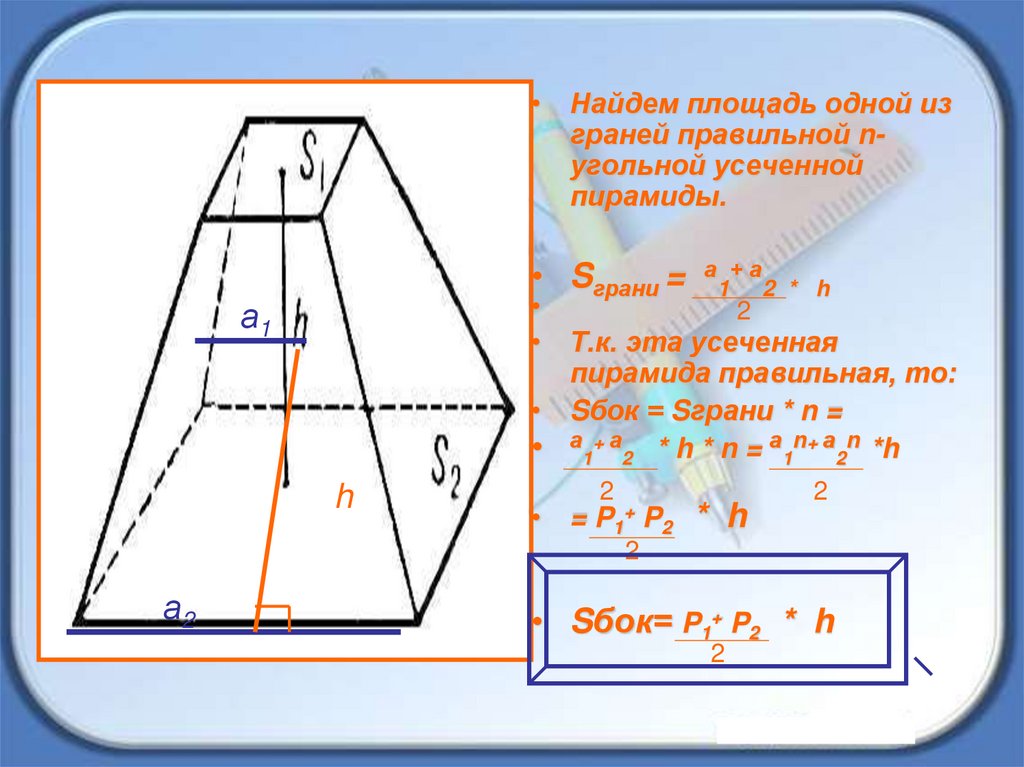
• Найдем площадь одной из
граней правильной nугольной усеченной
пирамиды.
• Sграни =
а +а
1 2 * h
2
• Т.к. эта усеченная
пирамида правильная, то:
• Sбок = Sграни * n =
• а1+ а2 * h * n = а1n+ а2n *h
а1
h
2
• = P1+ P2 * h
2
2
а2
• Sбок= P1+ P2 * h
2

8. Практическая работа

• 1 задание
• А) Нарисуйте правильную усеченную
четырёхугольную пирамиду со
сторонами оснований 3 см и 7 см.
• Б) Найдите площадь боковой
поверхности этой пирамиды, зная,
что высота грани равна 8 см.

9. 2 задание

Решите задачу: Дана правильная 4угольная усеченная пирамида.
Периметр верхнего основания равен
12, а периметр нижнего основания 24. Найдите площадь боковой
поверхности этой пирамиды, если ее
апофема равна 4.

10. 3 задание

Сделайте тест