Моделирование систем и процессов на основе свертки двух функций

1.

Моделирование систем и процессов
на основе свертки двух функций
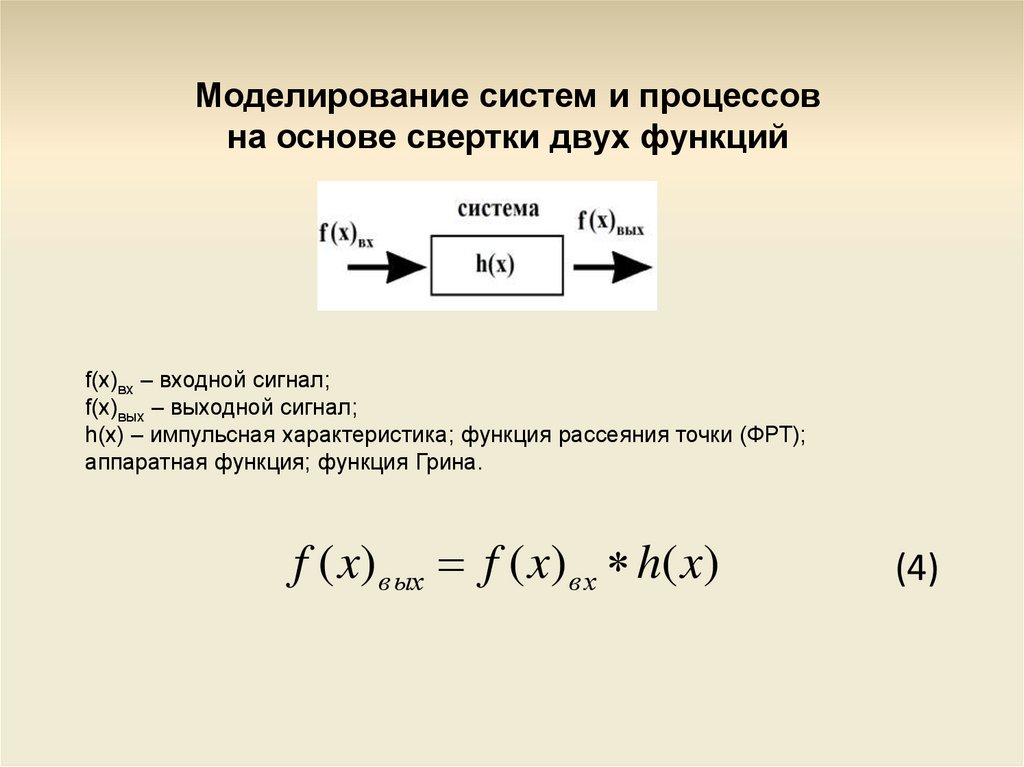
f(x)вх – входной сигнал;
f(x)вых – выходной сигнал;
h(x) – импульсная характеристика; функция рассеяния точки (ФРТ);
аппаратная функция; функция Грина.
f ( x) вых f ( x) вх h( x)
(4)

2.

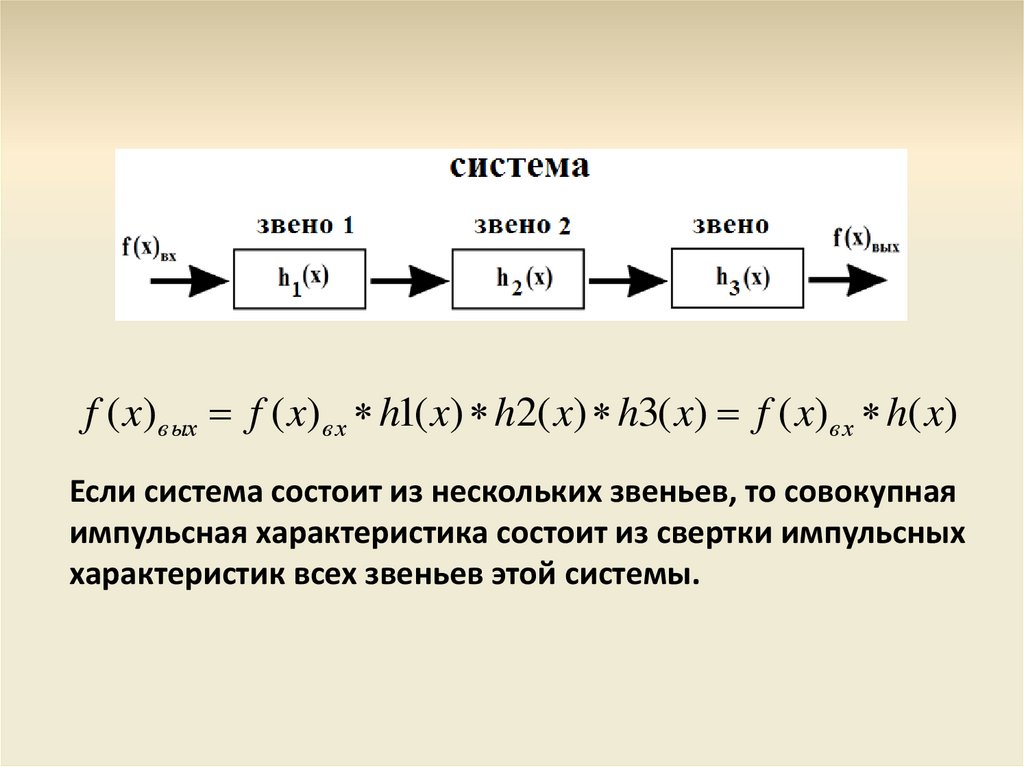
f ( x)вых f ( x)вх h1( x) h2( x) h3( x) f ( x)вх h( x)
Если система состоит из нескольких звеньев, то совокупная
импульсная характеристика состоит из свертки импульсных
характеристик всех звеньев этой системы.

3.

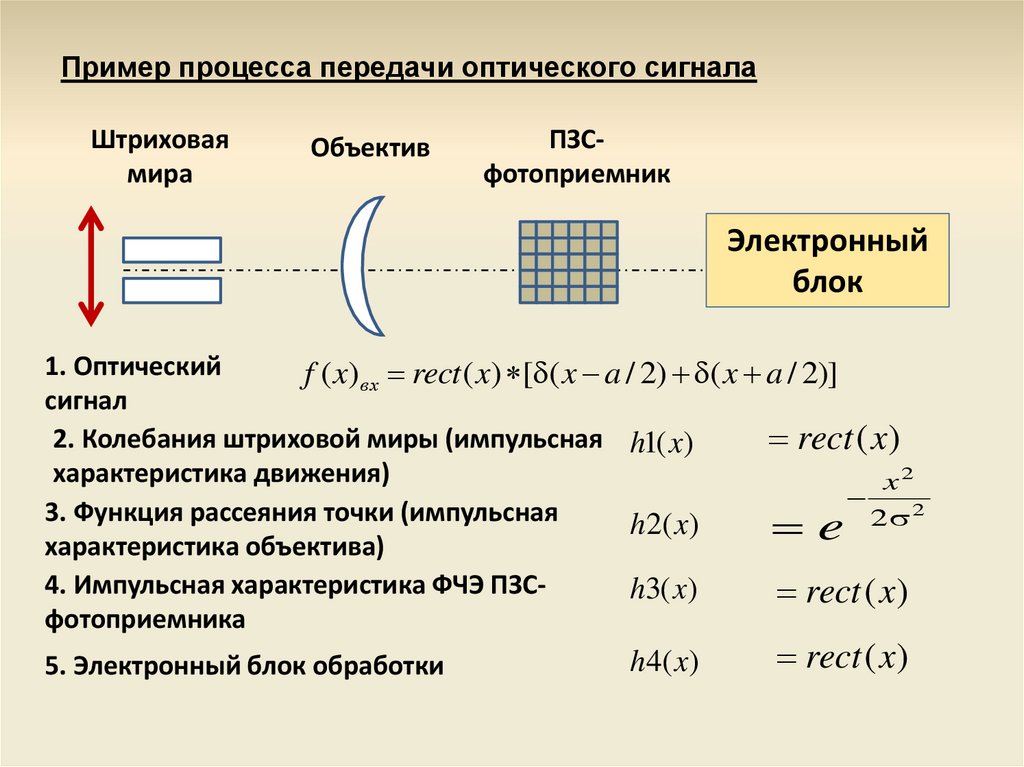
Пример процесса передачи оптического сигнала
Штриховая
мира
Объектив
ПЗСфотоприемник
Электронный
блок
1. Оптический
f ( x)вх rect ( x) [ ( x a / 2) ( x a / 2)]
сигнал
2. Колебания штриховой миры (импульсная h1( x)
rect (x)
характеристика движения)
x2
3. Функция рассеяния точки (импульсная
2 2
h2( x)
e
характеристика объектива)
4. Импульсная характеристика ФЧЭ ПЗСh3( x)
rect (x)
фотоприемника
5. Электронный блок обработки
h4( x)
rect (x)

4.

Математическое представление передачи оптического сигнала
Входной - оптический сигнал
f ( x)вых rect ( x) [ ( x a / 2) ( x a / 2)]
rect (x) e
x2
2 2
rect (x) rect (x )
совокупная импульсная характеристика состоит из свертки
импульсных характеристик всех звеньев системы.

5.

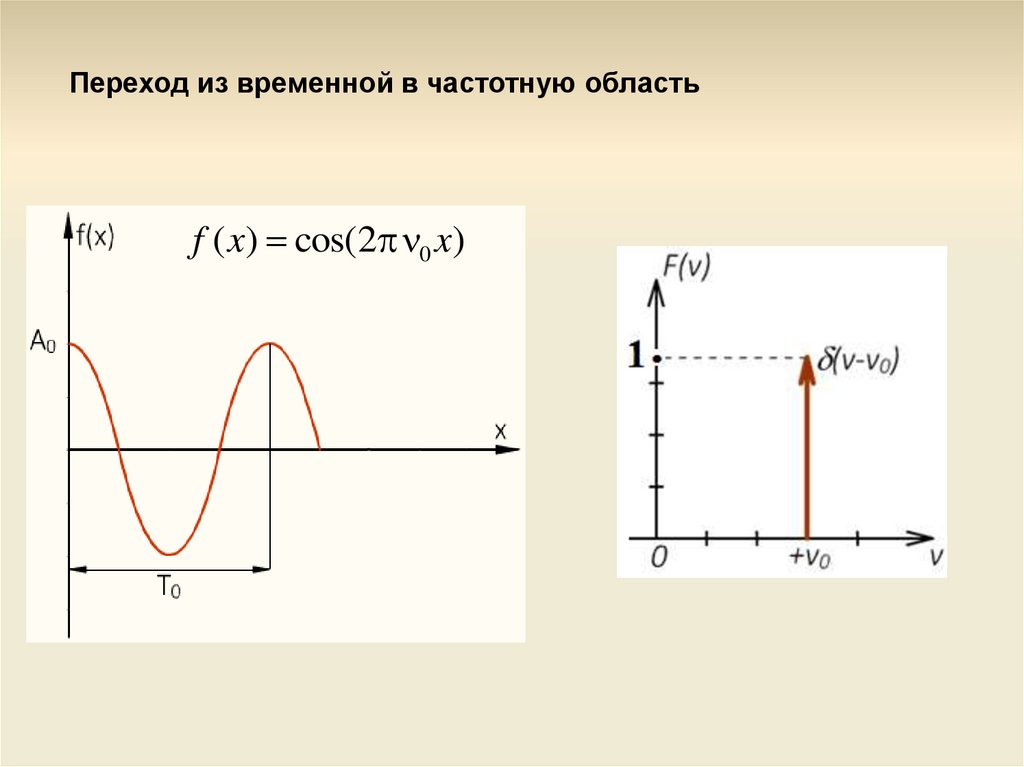
Переход из временной в частотную область
f ( x) cos(2 0 x)

6.

Анализ системы и сигналов в
частотной области
f ( x) вых f ( x) вх h( x)
Фурье-преобразование от входного сигнала называют
амплитудным спектром входного сигнала:
F( )вх= {f(x)вх}
(31)
Фурье-преобразование от выходного сигнала называют
амплитудным спектром выходного сигнала:
F( )вых= {f(x)вых}
(32)
Фурье-преобразование от импульсной характеристики
системы называют передаточной функцией:
H( )вых= {h(x)}
(33)

7.

Согласно теореме Бореля свертка двух функций преобразуется
в произведение двух функций
f ( x)вых f ( x)вх h( x)
Фурье-преобразование
F ( )вых F ( )вх H ( )
(34)

8.

Фурье-преобразование сигналов
Прямое преобразование Фурье для одномерного случая:
Обратное преобразование Фурье для одномерного случая:

9.

Вычисление амплитудного спектра от гармонической функции
Формула Эйлера для гармонической функции:

10.

Решение
Таким образом, преобразование Фурье от гармонической
функции представляет сумму двух δ-функций:
(35)

11.

Таблица фурье-преобразований
некоторых функций
Функция
f ( x ) ( x )
Фурье - преобразование
F ( ) 1
(36)

12.

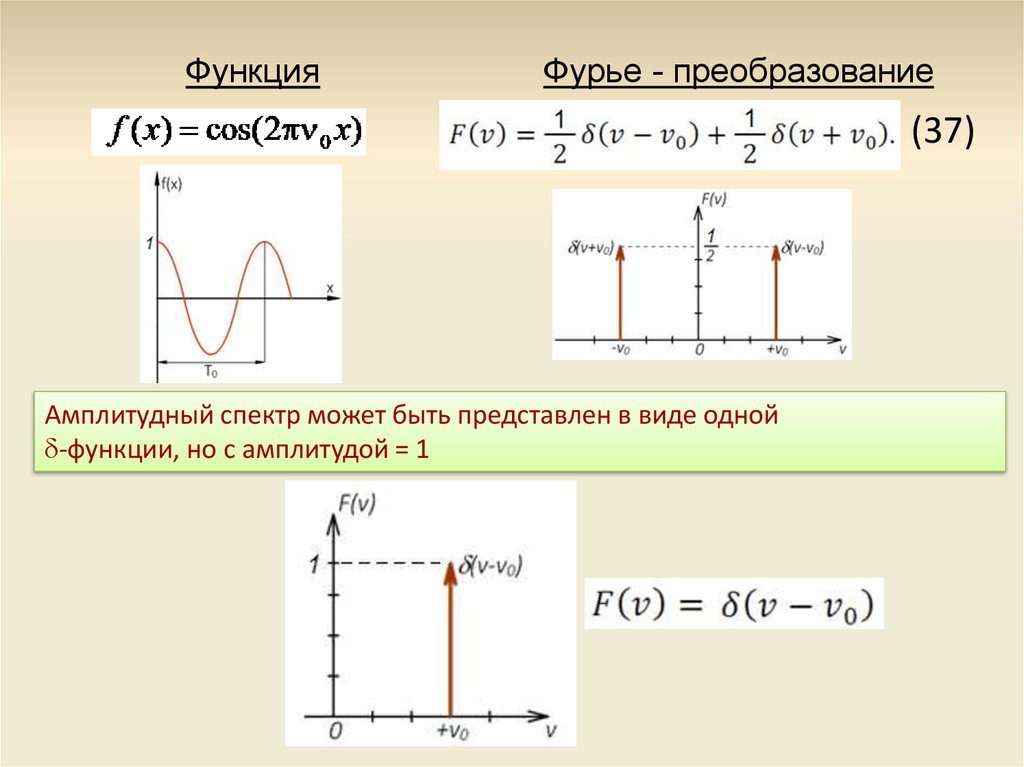
Функция
Фурье - преобразование
(37)
Амплитудный спектр может быть представлен в виде одной
-функции, но с амплитудой = 1

13.

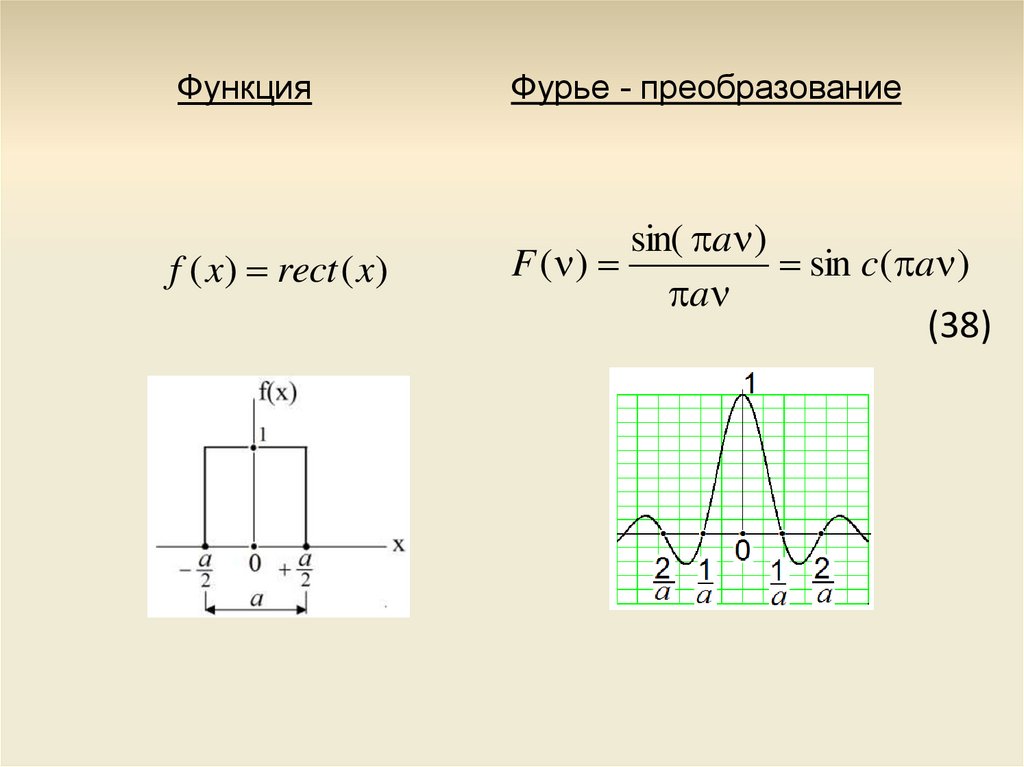
Функция
Фурье - преобразование
f ( x) rect ( x)
sin( a )
F ( )
sin c( a )
a
(38)

14.

Анализ систем
Имеем входной сигнал:
f (x)вх
Импульсная характеристика: h(x)
Выходной сигнал определяется как:
f ( x)вых f ( x)вх h( x)
Соответственно в частотной области:
F ( )вых F ( )вх H ( )

15.

Примеры решения задач
1. Имеем входной гармонический сигнал с частотой 0 и
амплитудой = 1. Импульсная характеристика системы
имеет вид дельта-функции. Определить амплитудный
спектр выходного сигнала.
f ( x)вх cos( 2 0 x)
h ( x ) ( x )
f ( x)вых cos(2 0 x) ( x)
F ( )вых ( 0 ) 1
На выходе системы получим аналогичный гармонический
сигнал (вид) с единичной амплитудой и неизменной
частотой (параметры):

16.

2. Имеем входной гармонический сигнал с частотой 0 и
амплитудой = 1. Импульсная характеристика системы имеет
вид функции прямоугольного импульса с шириной а=Т0.
Будет ли система пропускать входной сигнал? Если «да», то
определить амплитудный спектр выходного сигнала и
сделать вывод
f ( x)вх cos( 2 0 x)
h( x) rect ( x)
f ( x)вых cos(2 0 x) rect ( x)
F ( )вых ( 0 )
sin( a )
a

17.

Определяем нули функции sin на оси частот:
a
1 1
0
a T0
Следовательно передаточная функция равна нулю на
частоте 0 =1/Т0 . Причем эта точка совпадает с частотой
гармоники
Дельта-функция ( 0 ) тоже определена на
частоте 0
Поэтому выходной сигнал равен нулю!
Выходной сигнал равен нулю для частот,
совпадающих с нулями передаточной
функции!