Замена непрерывной передаточной функции дискретной передаточной функцией

1.

При малом ∆t можно использовать ступенчатую аппроксимацию импульсной
характеристики и криволинейную трапецию заменить прямоугольником.
Тогда
( i 1) t
g (n t )d t * g[(n i) t ]
i t
и формула дискретной свертки
n 1
y (n t ) t x(i t ) g[( n i ) t ].
i 0
3. Замена непрерывной передаточной функции дискретной передаточной
функцией
Первый путь – использование дискретного преобразования Лапласа (Zпреобразования
Дискретизация
L
K(p)
g(t)
Z
g[n]
K(z)
Непрерывная передаточная функция K(p) связана с импульсной
характеристикой g(t) преобразованием Лапласа. Дискретизацией импульсной
характеристики получается весовая функция g[n]. Z-преобразование от
весовой функции даст дискретную передаточную характеристику K(z).

2.

Второй путь – замена непрерывного интегрирования дискретным. Для этого в
передаточной функции
bm p m bm 1 p m 1 ... b0
K ( p)
a n p n a n 1 p n 1 ... a0
перейдем от оператора дифференцирования p к оператору интегрирования 1/p,
поделив числитель и знаменатель на pn.
1
bm
p
K ( p)
t
Значения интеграла y (t )
x(t )dt ,
t0
отстоящие друг от друга на интервал
времени ∆t, связаны соотношением
t
y(t ) y(t t )
x(t )dt.
n m
1
bm 1
p
n m 1
1
...
p
n
2
1
1
1
a n a n 1 a n 2 ... a 0
p
p
p
n
x
G
xn
C
D
x(t)
B
xn-1
F
t t
С учетом обозначений, принятых на
рисунке
y(n t ) y(( n 1) t ) S ABCDE ,
(n-2)∆t
A
(n-1)∆t
E
n∆t
t

3.

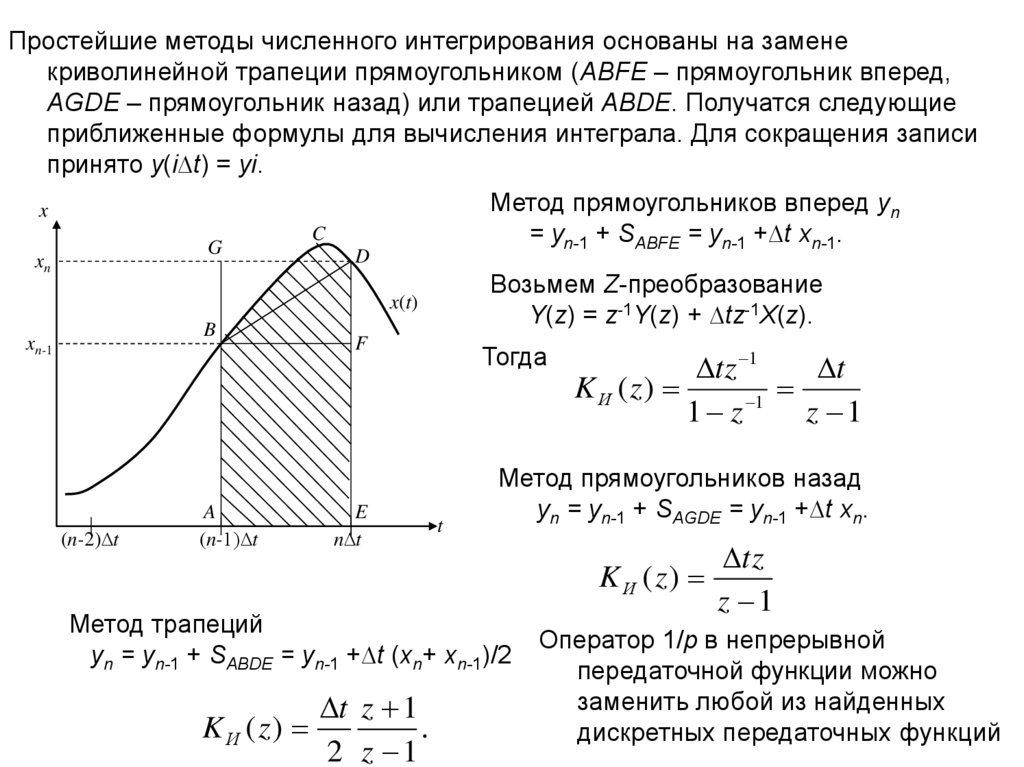
Простейшие методы численного интегрирования основаны на замене
криволинейной трапеции прямоугольником (ABFE – прямоугольник вперед,
AGDE – прямоугольник назад) или трапецией ABDE. Получатся следующие
приближенные формулы для вычисления интеграла. Для сокращения записи
принято y(i∆t) = yi.
Метод прямоугольников вперед yn
x
C
= yn-1 + SABFE = yn-1 +∆t xn-1.
G
D
xn
Возьмем Z-преобразование
Y(z) = z-1Y(z) + ∆tz-1X(z).
x(t)
B
xn-1
(n-2)∆t
A
(n-1)∆t
F
E
n∆t
Тогда
t
Метод прямоугольников назад
yn = yn-1 + SAGDE = yn-1 +∆t xn.
Метод трапеций
yn = yn-1 + SABDE = yn-1 +∆t (xn+ xn-1)/2
t z 1
K И ( z)
.
2 z 1
tz 1
t
K И ( z)
1 z 1 z 1
tz
K И ( z)
z 1
Оператор 1/p в непрерывной
передаточной функции можно
заменить любой из найденных
дискретных передаточных функций

4.

Как видим, дискретная модель непрерывной системы может быть получена
различными путями. Целесообразно выбрать самый точный.
Сравним эти методы на примере переходной характеристики интегрирующей цепи.
Разностное уравнение интегрирующей цепи. α = ∆t/T, Т – постоянная времени
№
п/п
Метод
1
Прямой Эйлера
Разностное уравнение
y n 1 (1 ) y n xn
y n 1
1
yn
x n 1
1
1
2
Обратный Эйлера
3
Усредненный Эйлера
4
Дискретная формула свертки
5
Z-преобразование
6
Прямоугольников «вперед»
y n 1 (1 ) y n xn
7
Прямоугольников «назад»
y n 1 (1 ) y n xn 1
8
Трапеций
y n 1
1 2
2
yn
( x n 1 x n )
1 2
1 2
y n 1 e y n e x n
y n 1 e y n x n 1
y n 1 (1 ) y n
2
( x n 1 x n )

5.

6.

Как видим, дискретная модель непрерывной системы может быть получена
различными путями. Целесообразно выбрать самый точный. Практика
моделирования показывает, что наименьшую ошибку обеспечивают методы
численного интегрирования дифференциальных уравнений.

7.

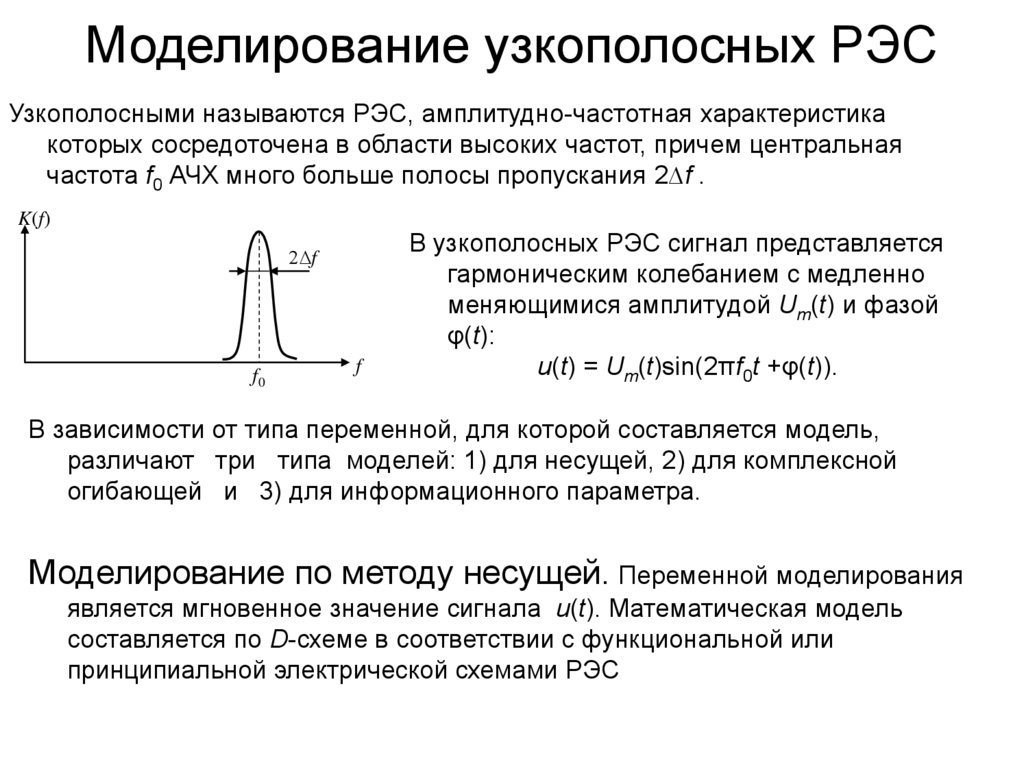
Моделирование узкополосных РЭС
Узкополосными называются РЭС, амплитудно-частотная характеристика
которых сосредоточена в области высоких частот, причем центральная
частота f0 АЧХ много больше полосы пропускания 2∆f .
K(f)
2∆f
f0
f
В узкополосных РЭС сигнал представляется
гармоническим колебанием с медленно
меняющимися амплитудой Um(t) и фазой
φ(t):
u(t) = Um(t)sin(2πf0t +φ(t)).
В зависимости от типа переменной, для которой составляется модель,
различают три типа моделей: 1) для несущей, 2) для комплексной
огибающей и 3) для информационного параметра.
Моделирование по методу несущей. Переменной моделирования
является мгновенное значение сигнала u(t). Математическая модель
составляется по D-схеме в соответствии с функциональной или
принципиальной электрической схемами РЭС

8.

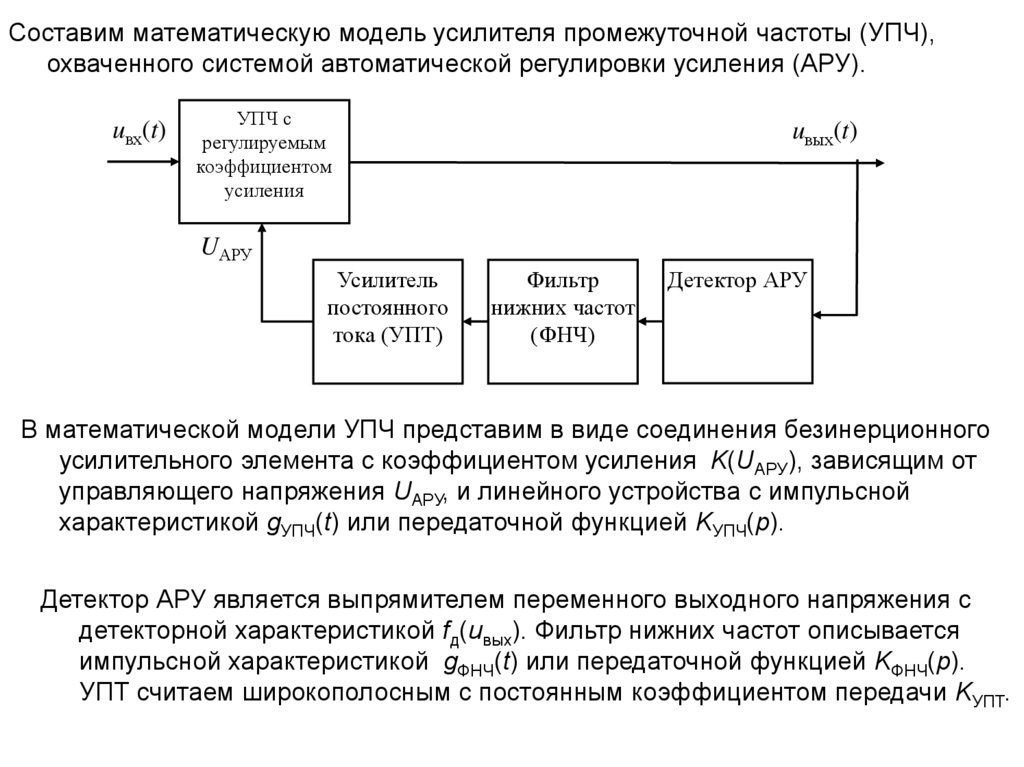
Составим математическую модель усилителя промежуточной частоты (УПЧ),
охваченного системой автоматической регулировки усиления (АРУ).
uвх(t)
УПЧ с
регулируемым
коэффициентом
усиления
uвых(t)
UАРУ
Усилитель
постоянного
тока (УПТ)
Фильтр
нижних частот
(ФНЧ)
Детектор АРУ
В математической модели УПЧ представим в виде соединения безинерционного
усилительного элемента с коэффициентом усиления K(UАРУ), зависящим от
управляющего напряжения UАРУ, и линейного устройства с импульсной
характеристикой gУПЧ(t) или передаточной функцией KУПЧ(p).
Детектор АРУ является выпрямителем переменного выходного напряжения с
детекторной характеристикой fд(uвых). Фильтр нижних частот описывается
импульсной характеристикой gФНЧ(t) или передаточной функцией KФНЧ(p).
УПТ считаем широкополосным с постоянным коэффициентом передачи KУПТ.

9.

uвх(t)
gУПЧ(t)
K(UАРУ)
uвых(t)
KУПЧ(p)
UАРУ
KУПТ
gФНЧ(t)
fд(uвых)
KФНЧ(p)
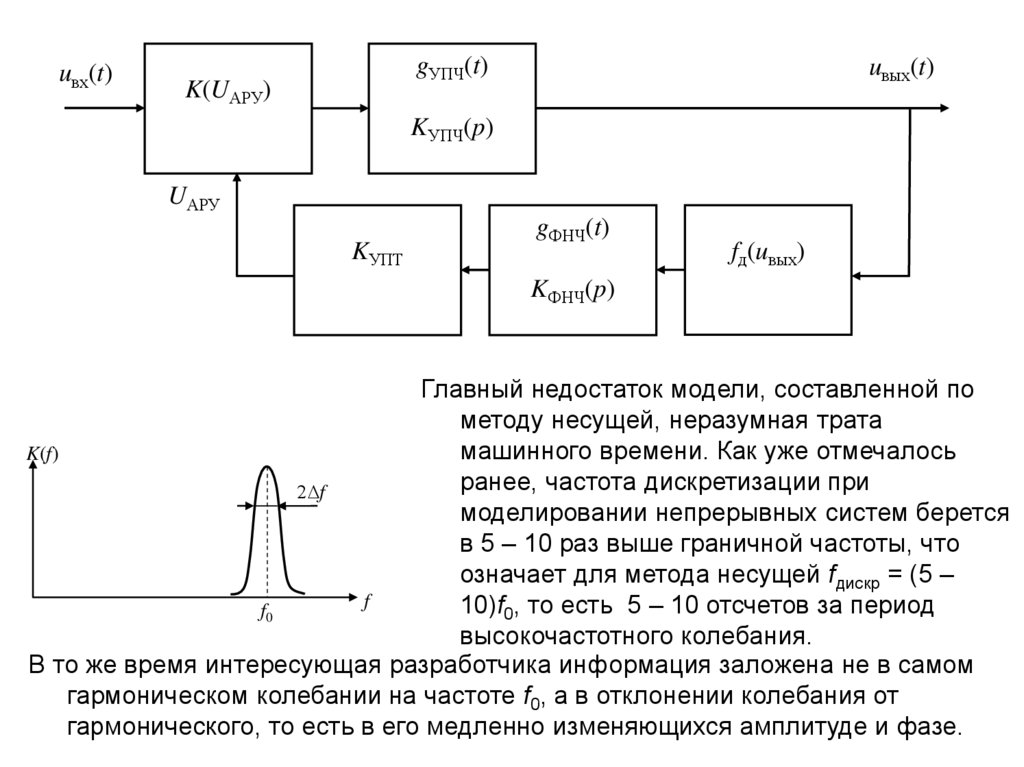
Главный недостаток модели, составленной по
методу несущей, неразумная трата
машинного времени. Как уже отмечалось
K(f)
ранее, частота дискретизации при
2∆f
моделировании непрерывных систем берется
в 5 – 10 раз выше граничной частоты, что
означает для метода несущей fдискр = (5 –
f
10)f0, то есть 5 – 10 отсчетов за период
f0
высокочастотного колебания.
В то же время интересующая разработчика информация заложена не в самом
гармоническом колебании на частоте f0, а в отклонении колебания от
гармонического, то есть в его медленно изменяющихся амплитуде и фазе.

10.

Модель, построенная по методу комплексной огибающей, как раз
и позволяет исследовать амплитудно-фазовые изменения, не моделируя
само несущее колебание. Частота дискретизации в этой модели
определяется уже не несущей частотой f0, а шириной спектра сигнала,
который близок к полосе пропускания АЧХ РЭС : fдискр = (5 – 10)∆f.
Комплексная амплитуда сигнала:
U m (t ) U m (t )e j (t ) U m (t ) cos (t ) jU m (t ) sin (t ) U c (t ) jU s (t ).
Нелинейные преобразования совершаются над амплитудой сигнала Um(t), а
линейные над действительной Uc(t) и мнимой Us(t) составляющими сигнала.
Импульсная характеристика узкополосного УПЧ
g (t ) G (t ) sin( 0 t g (t ))
Ее комплексная огибающая
j ( t )
G (t ) G(t )e g Gc (t ) jGs (t ),
При использовании передаточной функции K(p) для моделирования линейного
звена ее необходимо заменить низкочастотным эквивалентом для
комплексной огибающей.

11.

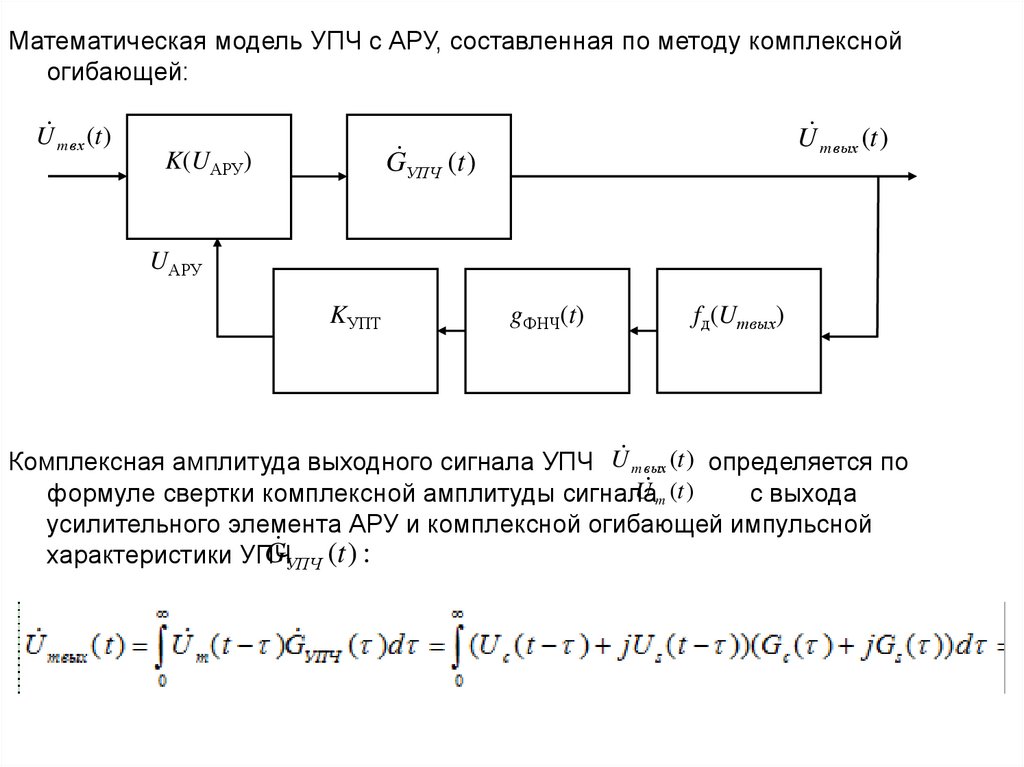
Математическая модель УПЧ с АРУ, составленная по методу комплексной
огибающей:
U m вх (t )
U m вых (t )
G УПЧ (t )
K(UАРУ)
UАРУ
KУПТ
gФНЧ(t)
fд(Umвых)
Комплексная амплитуда выходного сигнала УПЧ U m вых (t ) определяется по
U m (t )
формуле свертки комплексной амплитуды сигнала
с выхода
усилительного элемента АРУ и комплексной огибающей импульсной
G УПЧ (t ) :
характеристики УПЧ

12.

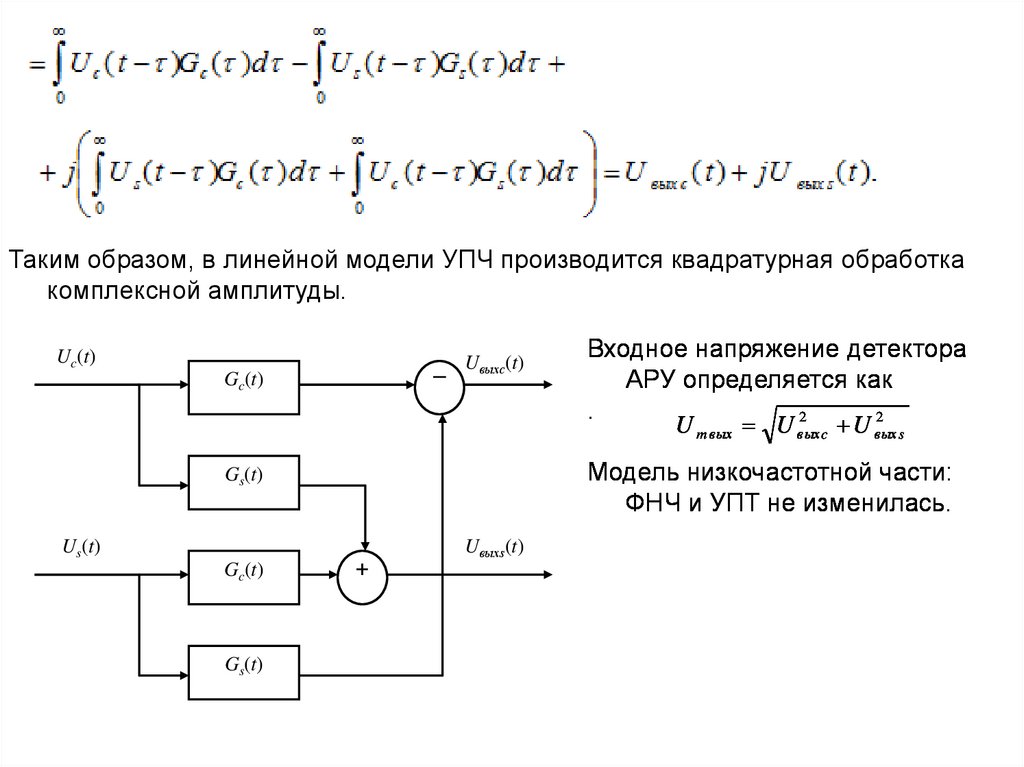
Таким образом, в линейной модели УПЧ производится квадратурная обработка
комплексной амплитуды.
Uc(t)
_
Gc(t)
Uвыхс(t)
Модель низкочастотной части:
ФНЧ и УПТ не изменилась.
Gs(t)
Us(t)
Gc(t)
Gs(t)
Входное напряжение детектора
АРУ определяется как
.
2
2
U m вых U вых
c U вых s
+
Uвыхs(t)

13.

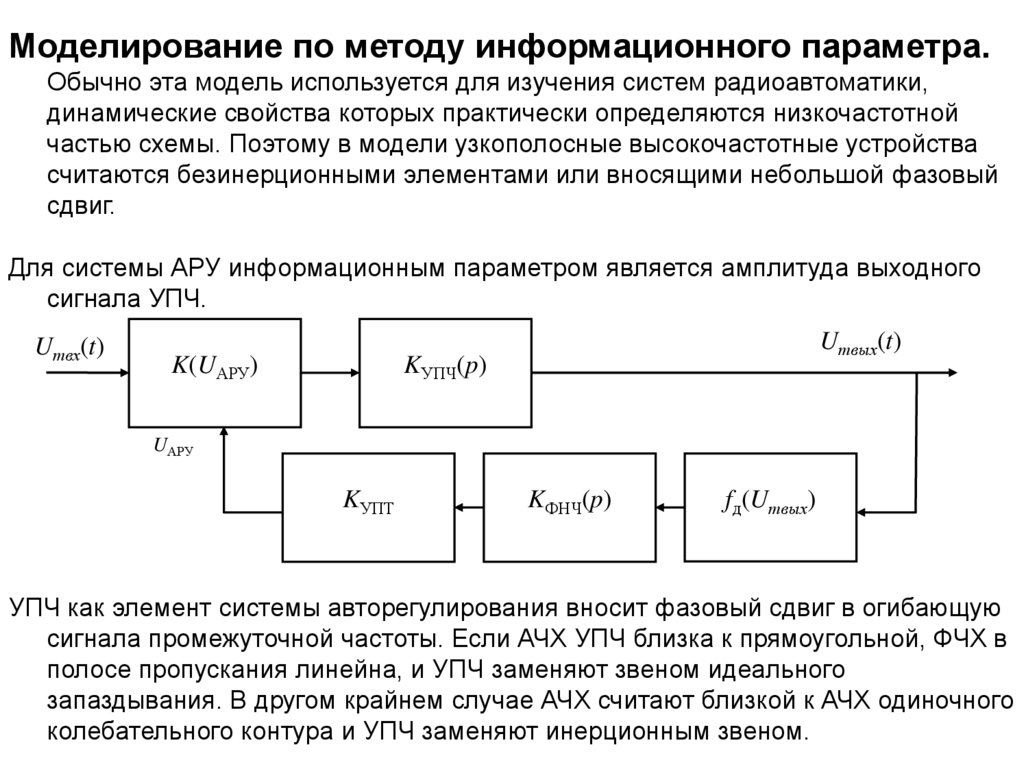
Моделирование по методу информационного параметра.
Обычно эта модель используется для изучения систем радиоавтоматики,
динамические свойства которых практически определяются низкочастотной
частью схемы. Поэтому в модели узкополосные высокочастотные устройства
считаются безинерционными элементами или вносящими небольшой фазовый
сдвиг.
Для системы АРУ информационным параметром является амплитуда выходного
сигнала УПЧ.
Umвх(t)
K(UАРУ)
Umвых(t)
KУПЧ(p)
UАРУ
KУПТ
KФНЧ(p)
fд(Umвых)
УПЧ как элемент системы авторегулирования вносит фазовый сдвиг в огибающую
сигнала промежуточной частоты. Если АЧХ УПЧ близка к прямоугольной, ФЧХ в
полосе пропускания линейна, и УПЧ заменяют звеном идеального
запаздывания. В другом крайнем случае АЧХ считают близкой к АЧХ одиночного
колебательного контура и УПЧ заменяют инерционным звеном.

14.

Частота дискретизации