Похожие презентации:
Системна оптимізація
1.
СистемнаОптимізація
Нормативний курс
2.
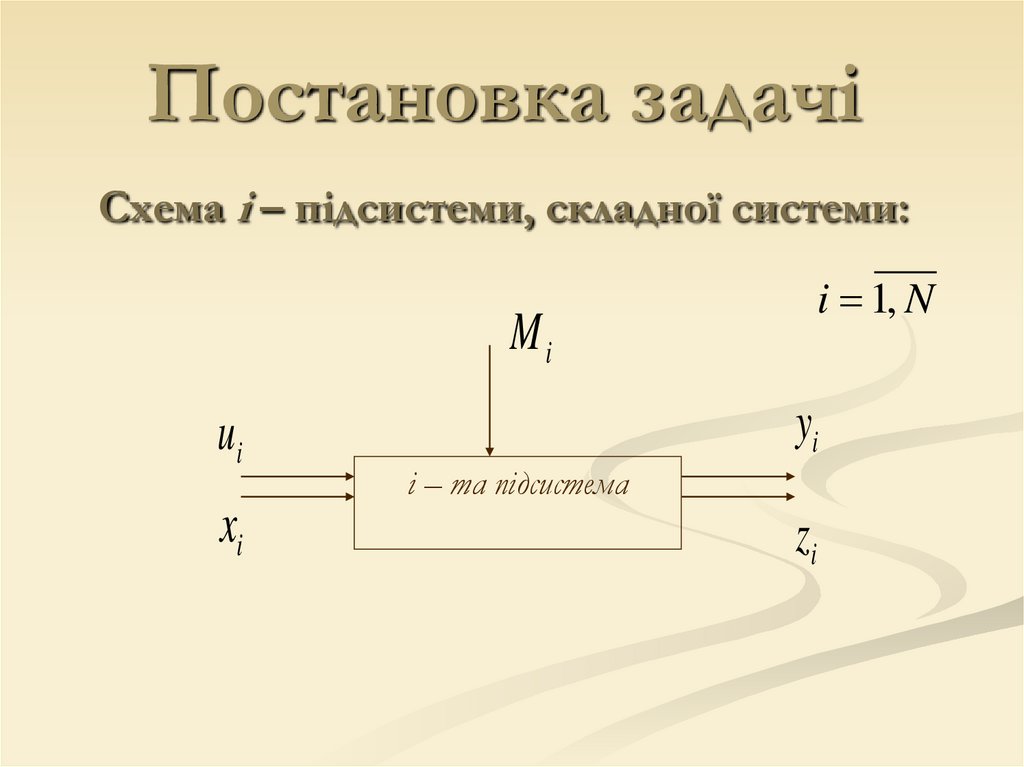
Постановка задачіСхема і – підсистеми, складної системи:
Mi
ui
xi
i 1, N
yi
і – та підсистема
zi
3.
Постановка задачіВектор
розмірність
ui mui
xi mxi
M i mM i
yi m y i
z i m zi
f i M i , xi
i 1, N
Вхідні сигнали, як на систему, так і на і-ту
підсистему, на які неможливо впливати;
Проміжні вхідні сигнали з інших підсистем;
Управління і-ю підсистемою;
Вихідні сигнали і-ої підсистеми, що входять в
загальний набір вихідних сигналів системи;
Проміжні вихідні сигнали і-ої підсистеми, які
надходять на входи інших підсистем;
4.
Постановка задачіі-підсистеми, i 1, N ,
визначається при заданому векторі вхідних
сигналів u векторними рівняннями:
Поведінка
zi Ti M i , xi , i 1, N
yi S i M i , xi , i 1, N
(1)
(2)
Ti - вектор-функція розмірності mz
S i - вектор-функція розмірності m y
i
(2) Можна не враховувати, якщо
на
yi
i
не накладені обмеження.
5.
Постановка задачіВзаємодія між N підсистемами
визначається лінійними взаємозв’язками:
N
xi cij z j , i 1, N
(3)
j 1
cij - елементи матриці розмірності mz mx
i
i
6.
Постановка задачіНехай цільова функція F складної системи
задана в аддитивно-сепарабельному виді:
N
F f i M i , xi max
(4)
i 1
Потрібно визначити вектори M i , xi , i 1, N,
що максимізують (4) при обмеженнях (1), (3)
7.
Зведемо задачу умовної оптимізації (1), (3), (4)до задачі безумовної оптимізації:
N
T
L f i M i , xi i Ti zi pi xi cij z j
i 1
i 1
i 1
j 1
N
N
N
(5)
L – Функція Лагранжа задачі (1), (3), (4)
8.
ipi
L, f i , Ti , i 1, N
Lxi , LM i , Lzi , L i , Lpi
Вектор множників Лагранжа розмірності
mzi , i 1, N
Вектор множників Лагранжа розмірності
mxi , i 1, N
Неперервні функції, що мають неперервні
перші похідні.
Частинні похідні від функції Лагранжа
9.
Оптимальний розв’язокзадовольняє умовам:
T
Lxi
Ti
f i
L
i pi 0, i 1, N
xi
xi
xi
LM i
Ti
f i
L
M i
M i
M
i
(6)
T
i 0, i 1, N
N
L
Lzi
i cijT p j 0, i 1, N
zi
j 1
L
L i
Ti zi 0, i 1, N
i
N
L
L pi
xi cij z j 0, i 1, N
pi
j 1
(7)
(8)
(9)
(10)
10.
Оптимальний розв’язокзадовольняє умовам:
Ti1
x1
i
Ti
...m z
xi
Ti i
1
x
i
Ti1
M 1
i
Ti
...m z
M i
Ti i
1
M
i
...
...
...
...
...
...
Ti1
m
xi xi
...
m
Ti zi
m xi
xi
Ti1
mM i
M i
...
m
Ti zi
m
M i M i
11.
Приклад 1“Система водосховищ”
12.
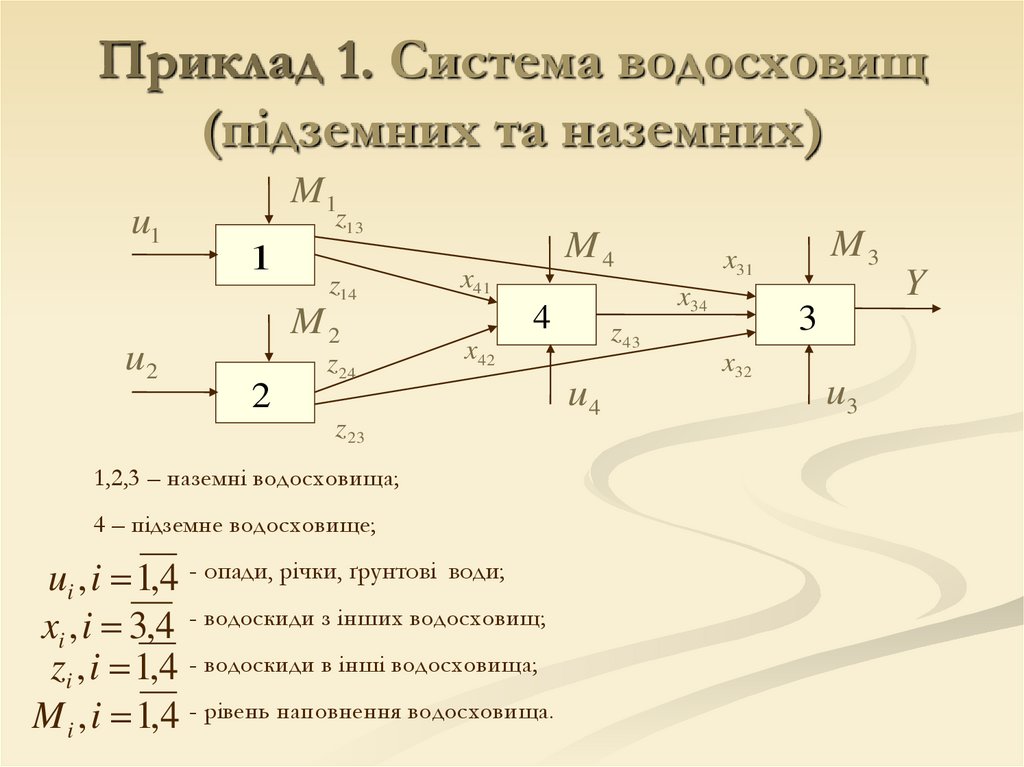
Приклад 1. Система водосховищ(підземних та наземних)
u1
u2
M1
z13
1
z14
M2
z 24
M4
x41
x34
4
2
z23
1,2,3 – наземні водосховища;
4 – підземне водосховище;
ui , i 1,4 - опади, річки, ґрунтові води;
xi , i 3,4 - водоскиди з інших водосховищ;
zi , i 1,4 - водоскиди в інші водосховища;
M i , i 1,4 - рівень наповнення водосховища.
3
z43
x42
u4
M3
x31
x32
u3
Y
13.
Приклад 2“Туристична агенція”
14.
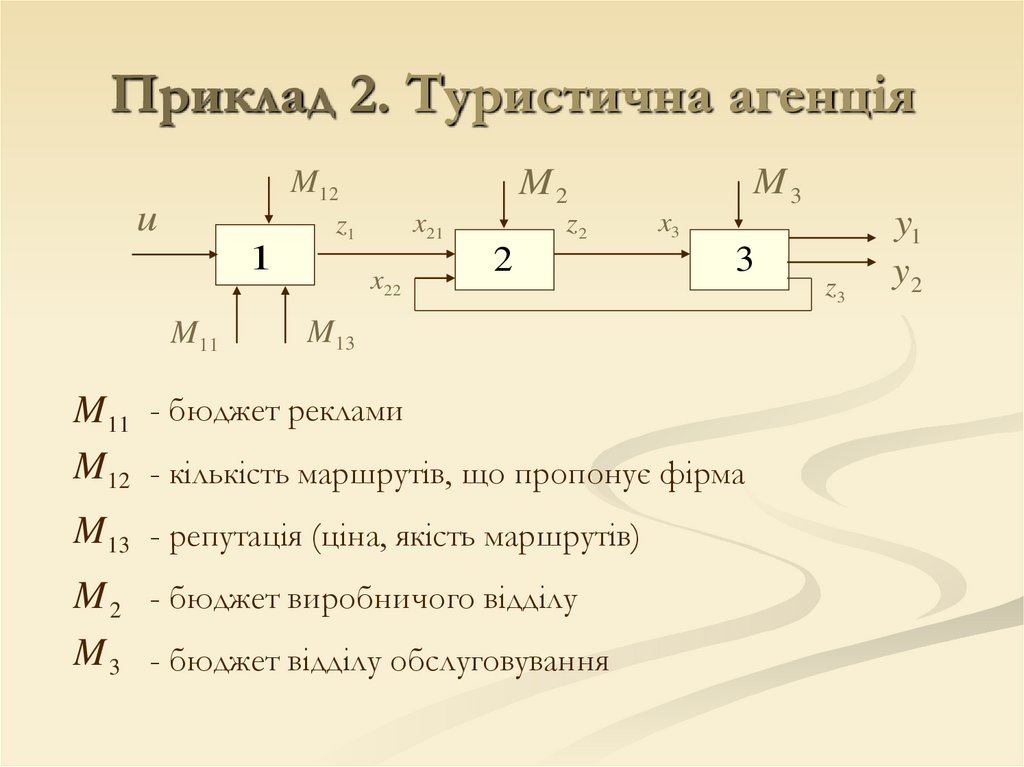
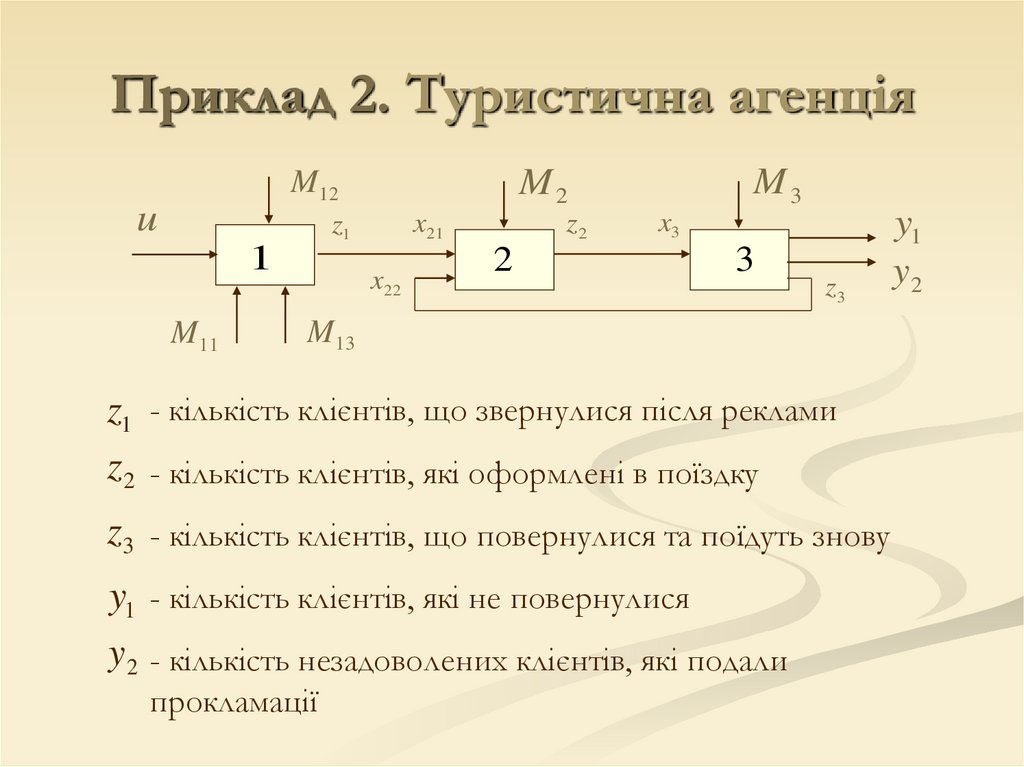
Приклад 2. Туристична агенціяНехай туристичне агенство має три відділи:
1. Відділ реклами
2.
Виробничий відділ
(підготовка до поїздок: візи, білети, угоди і т.п.)
3.
Відділ обслуговування на маршрутах
(під час поїздок: гіди, водії, транспортні засоби, готелі,
екскурсії, ресторани і т.п.)
15.
Приклад 2. Туристична агенціяu
M 11
z2
x21
z1
1
M3
M2
M12
x22
2
x3
3
M 13
M 11 - бюджет реклами
M12 - кількість маршрутів, що пропонує фірма
M 13 - репутація (ціна, якість маршрутів)
M 2 - бюджет виробничого відділу
M 3 - бюджет відділу обслуговування
z3
y1
y2
16.
Приклад 2. Туристична агенціяu
M 11
z2
x21
z1
1
M3
M2
M12
x22
2
x3
3
z3
y1
y2
M 13
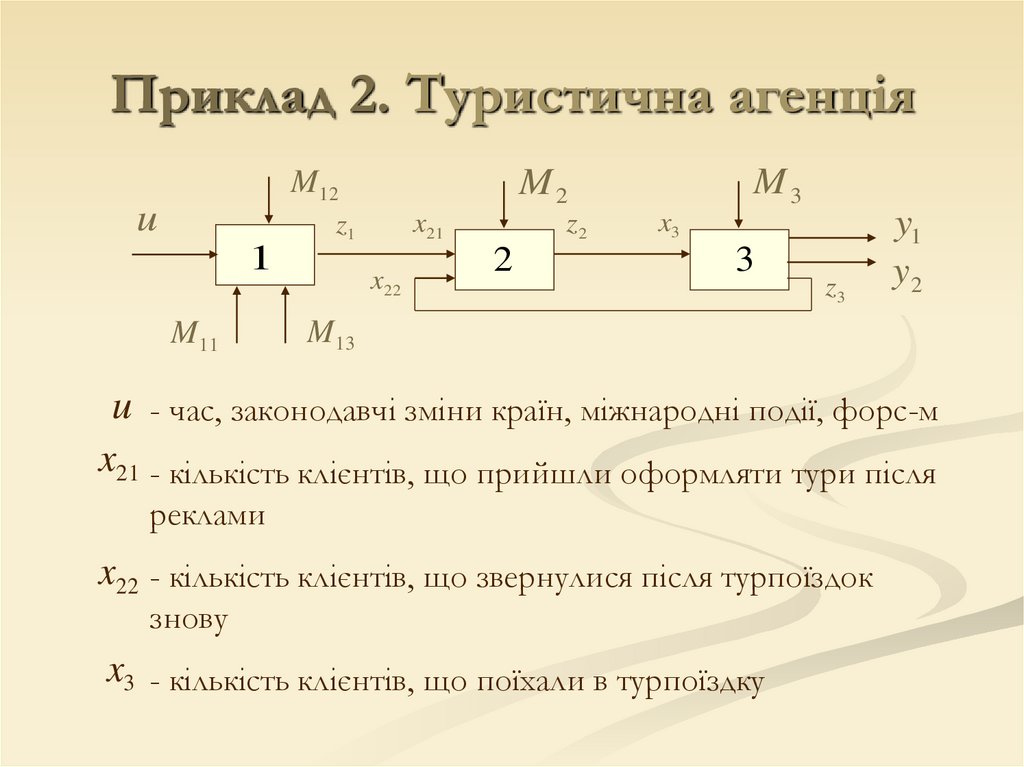
u - час, законодавчі зміни країн, міжнародні події, форс-м
x21 - кількість клієнтів, що прийшли оформляти тури після
реклами
x22 - кількість клієнтів, що звернулися після турпоїздок
знову
x3 - кількість клієнтів, що поїхали в турпоїздку
17.
Приклад 2. Туристична агенціяu
M 11
z2
x21
z1
1
M3
M2
M12
x22
2
x3
3
z3
M 13
z1 - кількість клієнтів, що звернулися після реклами
z2 - кількість клієнтів, які оформлені в поїздку
z3 - кількість клієнтів, що повернулися та поїдуть знову
y1 - кількість клієнтів, які не повернулися
y2 - кількість незадоволених клієнтів, які подали
прокламації
y1
y2
18.
Приклад 2. Туристична агенція3
F1 f1i M i , xi min
i 1
мінімізація витрат агенції
3
F2 f 2i M i , xi max
i 1
максимізація долі ринку за
всіма маршрутами агенції
19.
Приклад 2. Туристична агенціяz1 l11u1 l12u2 l13u3 l14 M11 l15M12 l16 M13
z2 l2 x21 x22 2 M 2
l2
- статистичний коефіцієнт врахування
відсіву клієнтів
2 - коефіцієнт залежності кількості
оформлених клієнтів від бюджету
20.
Приклад 2. Туристична агенціяz3 l3 x3 3 M1 M 2 M 3
l3 - статистичний коефіцієнт фірми
3 - коефіцієнт залежності повторних
клієнтів від бюджету
y1 11x3 12u2 13u3
y2 21x3 22 M 3 23u4
21.
Ітераційні алгоритмикоординації (ІАК)
22.
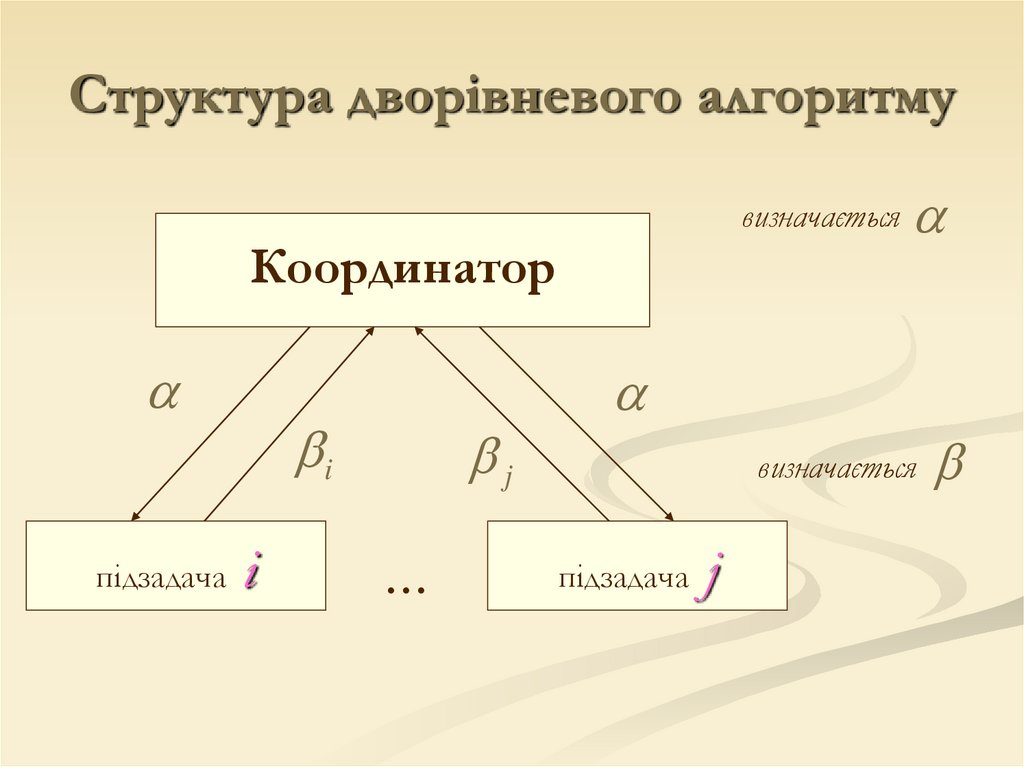
Принцип ієрархічної оптимізаціїв ІАК:
Розподіл процедур розв’язання рівнянь (6)-(10) між
двома рівнями – центром (координатором) та
нижнім рівнем підсистем ( під задач). Лагранжіан
розглядають в адитивно – сепарабельній формі
N
-
L Li i ,
i 1
вектор змінних параметрів координації;
i , i 1, N - вектор змінних і – під задачі
(підсистеми) нижнього рівня.
23.
Структура дворівневого алгоритмувизначається
Координатор
підзадача
i
i
j
…
визначається
підзадача
j
24.
Розподіл процедур розв’язання рівнянь (6)-(10)між верхнім (ВР) та нижнім (НР) рівнями в
ітераційних алгоритмах координації (МЦК, МКМ,
ЗМ) та порівняння алгоритмів:
МЦК
МКМ
ЗМ
Умова
Lx 0
LM 0
Lz 0
L 0
Lp 0
ВР
НР
НР
ВР
НР
*
*
*
*
*
*
*
*
*
МЦК – метод цільової координації;
МКМ – метод координації моделей;
ЗМ – змішаний метод.
ВР
*
*
*
*
*
*
25.
Метод цільової координації(МЦК)
26.
Метод цільової координації (МЦК)T pT ,
x , M , z , , i 1, N
T
i
T
i
T
i
T
i
T
i
I. Зміст i–підзадачі нижнього рівня:
Знайти для заданих pi , i 1, N
iT xiT , M iT , ziT , iT
N
N
N
N
i 1
j 1
i 1 j 1
T
T
p
c
z
p
i ij j j c ji zi
27.
Метод цільової координації (МЦК)Локальна оптимізація
N
T
T
f i pi xi p j c ji zi
j 1
max f i M i , xi f i (12)
xi p , zi p
zi Ti M i , xi
28.
Метод цільової координації (МЦК)Аналітично j знаходять з системи (6)-(9):
T
з (8) знаходять
i для фіксованих pi , i 1, N
з (6), (7) знаходять x , M для відомих pi , i
i
i
з (9) знаходять zi для відомих xi , M i
29.
Метод цільової координації (МЦК)II. Зміст задачі координації:
знайти
T pTз (10):
Lpi 0, i 1, N
Алгоритм градієнтного типу в дискретній формі:
pi t 1 pi t k L pi t
N
pi t k xi cij z j , i 1, N
j 1
k 0
t
- ітераційний індекс координатора
N
f 0 - в оптимальних розв’язках
i 1
i
модифікація критерія дорівнює 0.
(13)
30.
Метод цільової координації (МЦК)III. Інформаційний обмін між рівнями:
N
pi t 1 pi t k xi cij z j , i 1, N
j 1
k 0
pi , i 1, N
координатор
zi p
xi p
N T
T
max f i M i , xi pi xi p j c ji zi
j
1
zi Ti M i , xi
підсистема
i
i 1, N
31.
Метод цільової координації (МЦК)Критерій закінчення МЦК:
L Lp
T
p
- вибирають з міркувань прийнятного часу
та точності рішення задачі
32.
Метод координації моделей(МКМ)
33.
Метод координації моделей (МКМ)T zT ,
x , M , p , , i 1, N
T
i
T
i
T
i
T
i
T
i
I. Зміст i–підзадачі нижнього рівня:
Знайти для заданих zi , i 1, N
x , M , p ,
T
i
T
i
T
i
T
i
T
i
34.
Метод координації моделей (МКМ)Локальна оптимізація
max f i M i , xi
zi Ti M i , xi
N
xi cij z j
j 1
(14)
35.
Метод координації моделей (МКМ)Аналітично T знаходять з системи (6), (7),
j
(9), (10):
mM i mzi : з (10) знаходять xi для заданих zi , i 1, N
з (9), (7) знаходять M i , i для відомих zi , xi
з (6) знаходять
pi
для відомих
M i , i
mM i mzi : (9) не має розв’язку, МКМ не працює
mM i mzi : (9) може не мати розв’язку, мати один або
багато розв’язків
36.
Метод координації моделей (МКМ)II. Зміст задачі координації:
знайти
z
T
Tз
(8):
Lzi 0, i 1, N
Алгоритм градієнтного типу в дискретній формі:
zi t 1 zi t k Lzi t
N
T
zi t k i cij p j , i 1, N
j 1
k 0
(15)
37.
Метод координації моделей (МКМ)III. Інформаційний обмін між рівнями:
N
T
zi t 1 zi t k i cij p j , i 1, N
j 1
k 0
координатор
i z
pi z
zi , i 1, N
max f i M i , xi
zi Ti M i , xi
N
xi cij z j
j 1
підсистема
i
i 1, N
38.
Метод координації моделей (МКМ)Умова використання МКМ:
mM i mzi , i 1, N
Критерій закінчення МКМ:
L Lz
T
z
- вибирають з міркувань прийнятного часу
та точності рішення задачі
39.
Змішаний метод (ЗМ)40.
Змішаний метод (ЗМ)T pT , z T
x , M , , i 1, N
T
i
T
i
T
i
T
i
I. Зміст i–підзадачі нижнього рівня:
Знайти для заданих pi , zi , i 1, N
x , M ,
T
i
T
i
T
i
T
i
41.
Змішаний метод (ЗМ)Локальна оптимізація
N
T
T
max f i M i , xi pi xi pi cij z j
j 1
(16)
zi Ti M i , xi
42.
Змішаний метод (ЗМ)Аналітично T знаходять з системи (6), (7),
j
(9):
mxi mM i mzi :
з (6), (7), (9) знаходять
для відомих
zi , pi
xi , M i , i
43.
Змішаний метод (ЗМ)II. Зміст задачі координації:
знайти
T pT , z T
з (8), (10): Lzi 0, L pi 0, i 1, N
Алгоритм градієнтного типу в дискретній формі:
N
pi t 1 pi t k L pi t pi t k xi z j t (17)
j 1
N
T
zi t 1 zi t k Lzi t zi t k i cij p j t
j 1
i 1, N , k 0
44.
Змішаний метод (ЗМ)III. Інформаційний обмін між рівнями:
N
pi t 1 pi t k xi z j t
j 1
N
zi t 1 zi t k i cijT p j t
j 1
i 1, N , k 0
pi , zi
i 1, N
координатор
i p, z
xi p, z
N
T
T
max f i M i , xi pi xi pi cij z j
j 1
zi Ti M i , xi
підсистема
i
i 1, N
45.
Змішаний метод (ЗМ)Умова використання ЗМ:
mxi mM i mzi , i 1, N
Критерій закінчення ЗМ:
L Lp
T
p
L Lz
T
z
- вибирають з міркувань прийнятного часу
та точності рішення задачі
46.
Приклади розв’язання задачкоординації ітераційними
методами
47.
Приклад 148.
Розв’язокM1
U
x1
M2
z12 x2
1
z13
2
M3
z2 x32
x31
Y
3
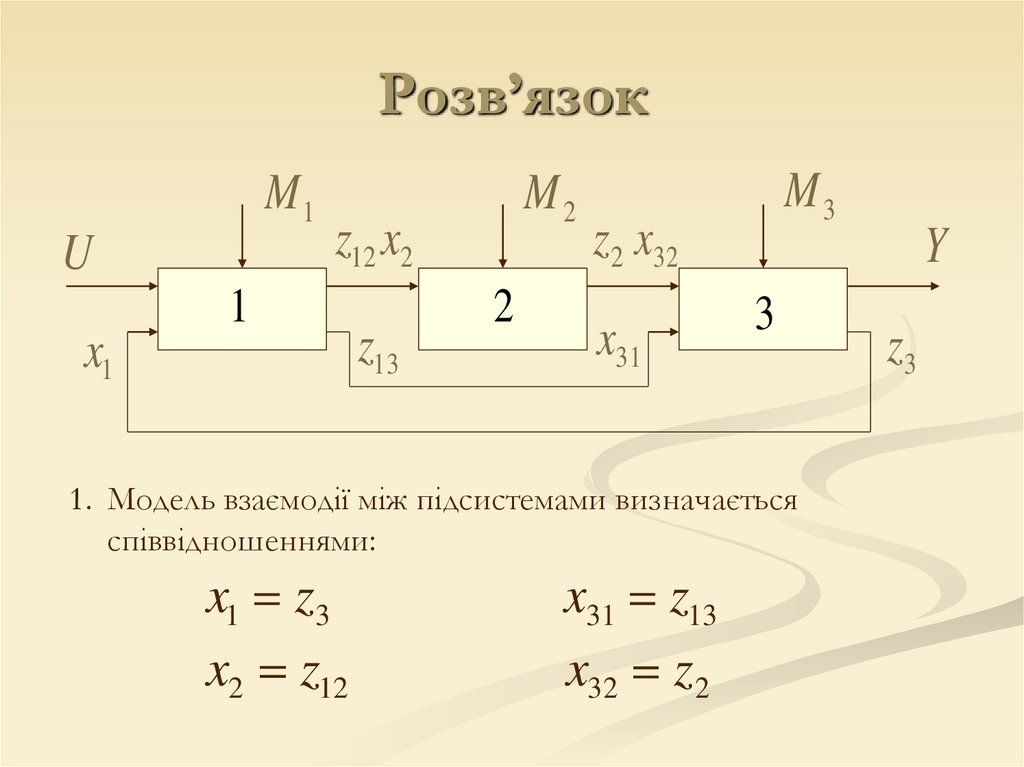
1. Модель взаємодії між підсистемами визначається
співвідношеннями:
x1 z3
x2 z12
x31 z13
x32 z2
z3
49.
Розв’язок2. Проведемо аналіз застосування кожного з методів для даної
задачі.
Випишемо розмірності векторів:
mM1 1
mz1 2
mx1 1
mM 2 1
mz 2 1
m x2 1
mM 3 1
m z3 1
mx3 2
a) Метод цільової координації можна застосовувати без
обмежень;
50.
Розв’язокb) Метод координації можна застосовувати, якщо mM mz , i 1,3
i
підсистема 1:
підсистема 2:
підсистема 3:
i
mM1 1 , mz1 2
mM 2 1 , mz2 1
mM 3 1 , mz3 1
Метод координації моделей для розв’язку задачі
використовувати не можна, оскільки для першої підсистеми
умова не виконується;
51.
Розв’язокc) Змішаний метод можна використовувати за умови
mxi mM i mzi , i 1,3
підсистема 1:
підсистема 2:
підсистема 3:
mx1 mM1 2
mx2 mM 2 2
mx3 mM 3 3
,
,
,
mz1 2
mz 2 1
m z3 1
Отже, змішаний метод можна використовувати для
розв’язку даної задачі.
52.
Приклад 253.
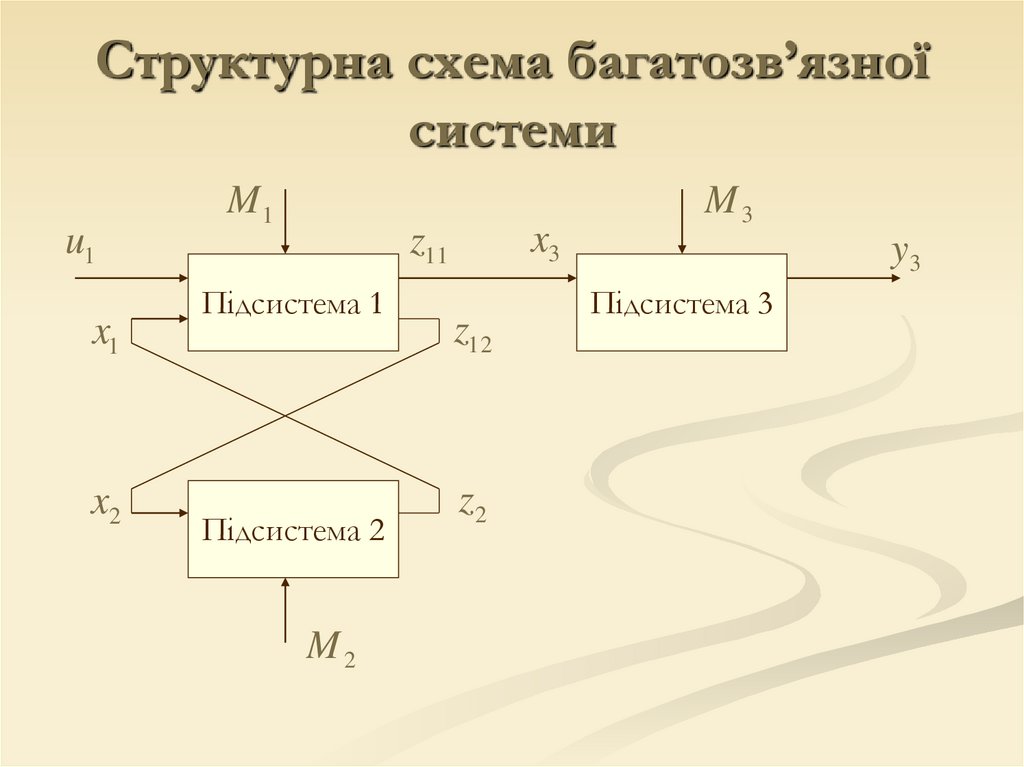
Структурна схема багатозв’язноїсистеми
u1
x1
x2
M1
x3
z11
Підсистема 1
Підсистема 2
M2
z12
z2
M3
y3
Підсистема 3
54.
Постановка задачіu x M x M x M min
2
1
2
1
2
1
2
2
2
2
2
3
2
z
x
11
1 M 1 u1 ;
3
2
z
x
M
12 1
1 u1 ;
z x2 M ;
2
2
2
при
_
умовах
x1 z 2 ;
x2 z12 ;
x3 z11.
Зрозуміло, що даній задачі умова
2
3
mM i mzi не виконується
mM1 1, mz1 2 . Отже, можна застосовувати лише метод
цільової координації або змішаний метод.
55.
Задача координаціїЛагранжіан може бути записаний у вигляді:
L u12 x12 M 12 11 x12 M 1 u1 z11 12 x13 M 12 u1 z12
x22 M 22 2 x22 M 2 z2 x32 M 32 p1 x1 z2 p2 x2 z12
p3 x3 z11 ,
де 11, 12 , 2 , pi i 1,2,3 - множники Лагранжа.
56.
Цільова координаціяДля заданого p лагранжіан переписується наступним
чином:
L Li u x M p1 x1 p2 z12 p3 z11
i 1
L1
11 x12 M 1 u1 z11 12 x13 M 12 u1 z12
x22 M 22 p2 x2 p1 z2 2 x22 M 2 z 2 L2
3
2
1
2
1
2
1
x M p3 x3 L3
2
3
2
3
Досліджуючи кожний доданок Li , можна визначити
окремі підзадачі:
57.
Цільова координаціяПідзадача 1. Для заданих p1 , p2 , p3 потрібно знайти
u
2
1
x M p1 x1 p2 z12 p3 z11 min
2
1
2
1
при умовах
z11 x12 M 1 u1 ;
3
2
z
x
M
12
1
1 u1
58.
Цільова координаціяПідзадача 2. Для заданих p1 , p2 потрібно знайти
x
2
2
M p2 x2 p1 z2 min
2
2
при умові
z2 x M 2
2
2
59.
Цільова координаціяПідзадача 3. Для заданого p3 потрібно знайти
x
2
3
M p3 x3 min
2
3
60.
Цільова координаціяРозв’язавши ці підзадачі, отримаємо значення x* , M * , z * ,
які задовольняють всім умовам стаціонарності для L (за
виключенням умови L p 0 , що розглядається на другому
рівні).
При використанні градієнтного алгоритму координації (t
– ітераційний індекс координатора) можна записати
p1 t 1 p1 t kLp1 p1 t k x1* z2* ;
*
*
p2 t 1 p2 t k x2 z12 ;
k 0
*
p3 t 1 p3 t k x3* z11
;
Глобальний розв’язок досягається, якщо LTp Lp , -
деяке завчасно вибране мале число.
61.
Змішана координаціяУ випадку змішаної координації,
координуючими змінними є вектори p та z .
Для яких лагранжіан стає роздільним, що
веде до появи наступних підзадач:
62.
Змішана координаціяПідзадача 1. Для заданих p1, z11, z12 , z2 потрібно знайти
u
2
1
x M p1 x1 z2 min
2
1
2
1
при умовах
z11 x12 M 1 u1 ;
3
2
z
x
M
12 1
1 u1
63.
Змішана координаціяПідзадача 2. Для заданих p2 , z12 , z2 потрібно знайти
x
2
2
M p2 x2 z12 min
2
2
при умові
z2 x M 2
2
2
64.
Змішана координаціяПідзадача 3. Для заданого p3 , z11
x
2
3
потрібно знайти
M p3 x3 z11 min
2
3
65.
Змішана координаціяКоординація оптимальних рішень:
Градієнтний метод:
p t 1 p t k x z
p t 1 p t k x z
p1 t 1 p1 t k x1* z 2
2
3
2
*
2
3
*
3
12
11
z t 1 z t k p
z t 1 z t k p
*
z11 t 1 z11 t k p3 11
12
2
12
2
2
1
Метод прямих ітерацій:
p1 t 1 2* t
z11 t 1 x3* t
p3 t 1 11* t
z 2 t 1 x1* t
p2 t 1 12* t
*
12
z12 t 1 x2* t
*
2
66.
Безітераційні алгоритмикоординації (БАК)
67.
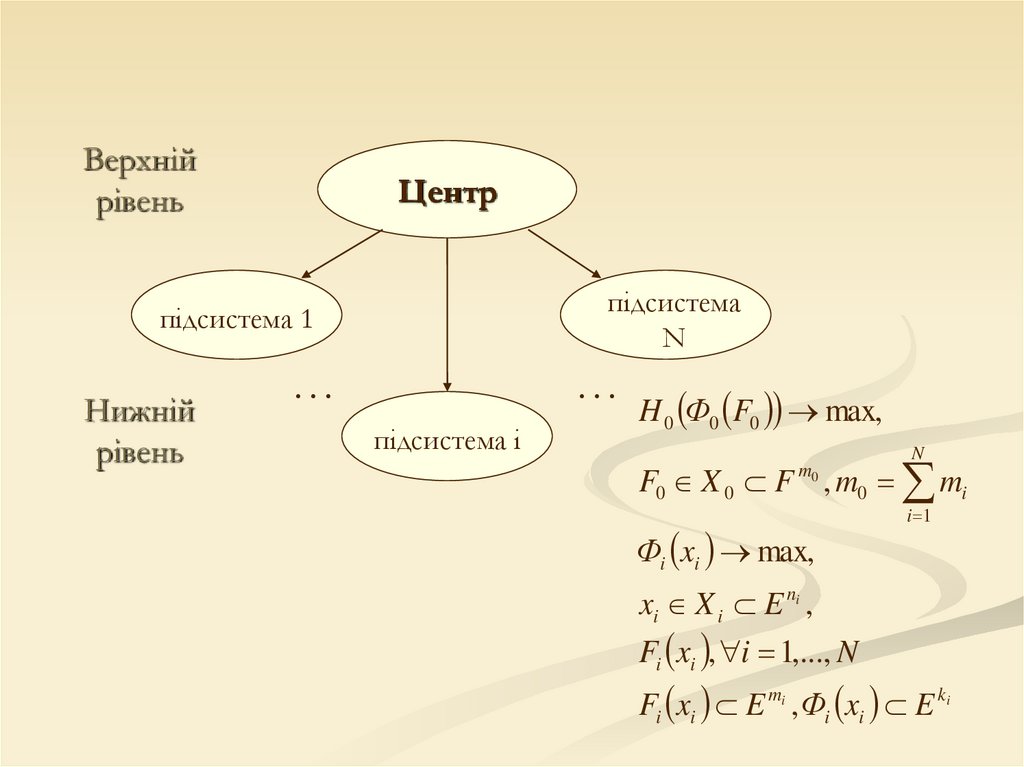
Верхнійрівень
Центр
підсистема
N
підсистема 1
Нижній
рівень
…
…
підсистема i
H 0 Ф0 F0 max,
N
F0 X 0 F , m0 mi
m0
Фi xi max,
xi X i E ni ,
Fi xi , i 1,..., N
i 1
Fi xi E mi , Фi xi E ki
68.
i підсистема нижнього рівняi 1,..., N
стан і-ої підсистеми:
показники роботи і-ої
підсистеми:
локальні інтереси і-ої
підсистеми:
1
2
F f x ,..., f x
Ф x x ,..., x max 3
xi xi1 ,..., xini X i E
i
i
i1
i
i
imi
i1
i
ni
i
iki
i
ni - кількість змінних і-ої підсистеми;
mi - кількість показників роботи і-ої підсистеми;
ki - кількість критеріїв і-ої підсистеми.
mi ni
ki ni
69.
ЦентрF0 F1 ,..., FN X 0 E m0
стан центра:
4
N
Fi Fi xi , m0 mi
інтереси центра:
узагальнений критерій:
k0
Ф0 F0 01 F0 ,..., 0k0 F0 max
i 1
H 0 Ф0 F0 max
5
6
- кількість критеріїв центра;
Фi xi Fi xi , i 1, N
X 0 F0 : H F0 b, b b1 ,..., bM
7
8
70.
Схема безітераційного алгоритмукоординації (БАК)
H 0 F1 ,..., FN max
H j F1 ,..., FN b j , j 1,..., M
Fi QiF Fi : xi QiX або xi X i , i 1,..., N
Q1F
F1 x1 max
x1 X 1
2
1
F1 x1 F1*
x1 X 1
FN*
QNF
F1*
12
1
…
FN xN max
xN X N
6
8
9
2
1
FN xN FN*
xN X N
12
1
71.
Способи визначення множиниQ , i 1, N
F
i
1.
2.
Q Fit , t 1,..., Ti
F
i
10
Q Fi : Fi it Fit , it Ti 11
t 1
Ti
Ti it : it 1, it 0
t 1
F
i
Ti
72.
Задача координації в БАК длялінійних систем
H a , F , j 0,..., M
13
N
j
N
i 1
i 1 t 1
i max
14
jit
i b j , j 1,..., M
15
Ti
z
i 1 t 1
i
0 it
Ti
z
N
ji
t
t
mi
де z jit a ji , f it a jil f itl ,
l 1
Ti
t 1
it
1, i 1,..., N
i 0,1
t
i 0
t
16
17
18
73.
Позначенняj
-
номер загального критерію та обмежень центра,
j 0, M
i
t
-
номер підсистеми, i 1, N
-
номер ефективної точки,
l
-
номер локального критерію підсистеми, l 1, mi
t 1, Ti
74.
Приклад розв’язання задачікоординації для лінійних
систем за допомогою
безітераційного алгоритму
координації
75.
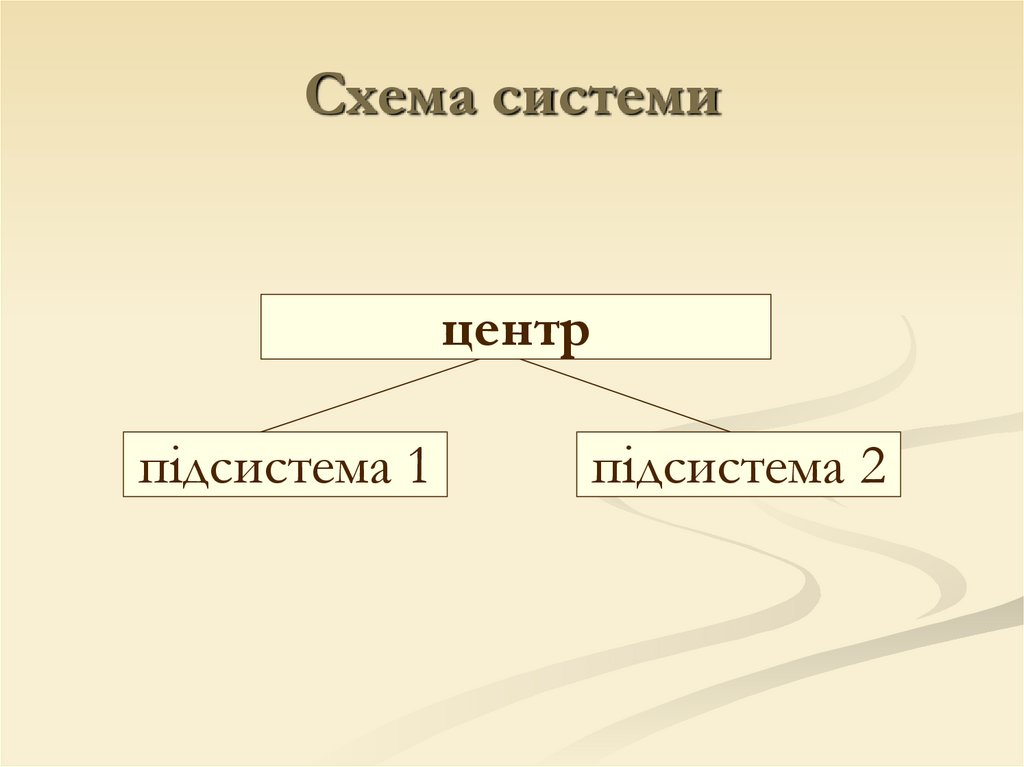
Схема системицентр
підсистема 1
підсистема 2
76.
Математична модель першоїпідсистеми нижнього рівня
Ф1 F 1 f11, f12 - векторний критерій
f11 x1 2 x2 max
f12 2 x1 x2 max
Множина допустимих розв’язків першої підсистеми:
x : x1 x2 4
x x 2
1
2
X1
x1 2 x2 1
x1 , x2 0
(19)
77.
Математична модель другоїпідсистеми нижнього рівня
Ф2 F2 f 21, f 22 - векторний критерій
f 21 y1 y2 max
f 22 y1 5 y2 max
Множина допустимих розв’язків другої підсистеми:
y : y1 2 y2 4
y 2y 8
1
2
X2
2 y1 y2 10
y1 , y2 0
(20)
78.
Математична модель верхньогорівня (центра)
Глобальна цільова функція:
H 0 x1 2 x2 y1 y2 max
Глобальне обмеження:
H1 2 x1 x2 y1 5 y2 23
79.
Позначенняj
-
номер глобального критерію та обмежень, j 0, M
i
t
-
номер підсистеми, i 1, N
-
номер крайньої ефективної точки, t 1, Ti
l
-
номер локального критерію, l 1, mi
80.
I етапПозначимо:
1
- оптимальний розв’язок задачі (19) за критерієм
f11
x2
- оптимальний розв’язок задачі (19) за критерієм
f12
1
- оптимальний розв’язок задачі (20) за критерієм
f 21
- оптимальний розв’язок задачі (20) за критерієм
Знаходимо ефективні крайні точки задач (19) та (20) за
допомогою симплекс-методу.
f 22
x
y
y2
81.
I етапОтримаємо:
x1 1,3
x 3,1
2
2
Врахуємо обмеження
it
i 1
y1 4,2
y 2 2,3
1 , перепозначимо
i i , i 1 i , i 1,2
1
2
F
Q
Множини ефективних значень критеріїв i , i 1,2
використовують на II етапі алгоритму формування задачі
центра.
82.
I етапВизначимо, відповідно (11), множину ефективних значень
F
Q
критеріїв підсистеми 1 :
2
F1 : F1 f11 , f12 1t F1t
t 1
F
1
2
Q1 1 F1 x 1 1 F1 x
1
2
1 f11 x 1 1 f11 x f11 x
1
2
f
x
1
f
x
f
x
1 12
12
1 12
83.
I етапВизначимо, відповідно (11), множину ефективних значень
F
Q
критеріїв підсистеми 2 :
2
F2 : F2 f 21, f 22 2t F2t
t 1
F
1
2
Q2 2 F2 y 1 2 F2 y
1
2
2 f 21 y 1 2 f 21 y f 21 y
f y1 1 f y 2 f y
2
22
22
2 22
84.
II етапВизначимо вектори a ji , j 0,1, i 1,2 в позначеннях
a ji , Fi , введених в задачі координації безітераційного
алгоритму координації для лінійних систем.
1
1
a0i : a01 ; a02
0
0
0
0
a1i : a11 ; a12
1
1
85.
II етапВідповідно (13), задача центра набуває вигляд (14), (15):
H 0 a01, F1 a02 , F2
1 f11 x 0 f12 x 1 f 21 y 0 f 22 y
x x 2 x x x x 2 x x 1
y y y y y y y y 1
f11 x1 1 f11 x 2 1 1 f 21 y1 2 f 21 y 2 1 2
1
1
1
2
1
1
2
1
1
1
2
2
2
2
2
1
1
2
2
2
1 6 1 3 2 1 1 4 2 2 2 3 1 2
7 1 5 5 1 6 2 5 5 2 2 1 2 10 max
86.
II етапПри глобальному обмеженні:
H1 a11 , F1 a12 , F2
0 f11 x 1 f12 x 0 f 21 y 1 f 22 y
2 x x x x 2 x x x x 1
y y 5 y y y y 5 y y 1
f12 x 1 f12 x 1 1 f 22 y 2 f 22 y 1 2
1
2
1
1
1
2
1
1
1
2
1
1
1
2
2
2
1
2
2
1
2
2
2
2
2 3 1 6 1 1 1 4 10 2 2 15 1 2
2 1 7 3 2 17 2 1 3 2 24 23
2 1 3 2 1
87.
II етапМаємо задачу лінійного програмування:
2 1 2 10 max
2 1 3 2 1
1 , 2 0
Розв’язок:
1
1/ 2
1 1 / 2
2 0
1/ 3
1
2
88.
II етап*
*
Підрахуємо оптимальні значення критеріїв підсистем F1 , F2 :
1
1
*
1
1
2
2
f
x
x
2
x
x
x
x
2
x
x
11
1
2
1
2
1
/
2
2
2
F1* 1
1
1
1
1
2
2
f*
2
x
x
x
x
2
x
x
x
x
2
1
2
12 1 1/ 2 2 1
2
1
7 5
1
1
6
3
2
6
2
2
2
1 2 3 1 6 1 5 7 6
2
2
2
89.
II етап*
*
Підрахуємо оптимальні значення критеріїв підсистем F1 , F2 :
f 21*
y1 y 2 y2 x 2 2 3 5
2 0
*
F2 *
2
2
f
y
x
5
y
x
2 15 17
22 0
1
2
2
90.
II етапВектори F1* та F2* передаємо у відповідні підсистеми нижнього
рівня:
*
f11
6
*
F1 *
f12 1 1/ 2 6
f
F
f
*
2
*
21
*
22 2 0
5
17
91.
III етапЗнаходимо локальні розв’язки xi* , i 1,2 в підсистемах.
Для першої підсистеми:
*
*
x
f
x
2
x
6
f
11 1
1 2
*
2
11
F1
*
*
f12 2 x1 x2 6 f12 x2 2
Для другої підсистеми:
*
*
y
f
y
y
5
f
21 1 2
1 2
*
11
F2
*
*
f 22 y1 5 y2 17 f12 y2 3
92.
Постановка задачі прийняттярішень (ЗПР) в термінах
багатокритеріальної оптимізації
93.
fi x , i II 1,..., M
M
I1 1,..., m
- множина критеріїв
- множина індексів критеріїв
- кількість критеріїв
- множина індексів критеріїв, що
максимізуються
I 2 m 1,..., M - множина індексів критеріїв, що
I I1 I 2
D0
мінімізуються
- множина допустимих альтернатив
opt f i x , i I
x D0
1
94.
ВизначенняАльтернатива x0 називається ефективною, якщо на
множині допустимих альтернатив D0 не існує іншої
альтернативи x , для якої виконуються нерівності:
f i x f i x0 , i I1
f i x f i x0 , i I 2
та хоча б одна нерівність була строгою.
95.
Додаткова інформація в ЗПУР.Перший евристичний аспект в
задачах БО
(2)
f i 0 f i x
, i I1
f0 f
i min
i
wi f i x
0
f i x f i , i I
2
f i max f i 0
96.
Додаткова інформація в ЗПУР.Перший евристичний аспект в
задачах БО
0 wi f i x 1, i I , x D0 ,
wi x wi fi x , i I - монотонні перетворення значень
критеріїв f i x , що призводять критерії до безрозмірного
вигляду та одного напрямку оптимізації;
f i min , f i max
fi
W
0
- відповідно, найменші та найбільші значення
критеріїв, що оптимізуються, на множині
допустимих альтернатив D0 ;
- оптимальне значення критерію i на множині
допустимих розв’язків D0 ;
- простір перетворених значень критеріїв f x , i I
i
97.
Другий евристичний аспект взадачах БО
i , i I i : i 1, i 0, i I 3
i I
Переваги ОПР на множині функцій цілі
fi x , i I
98.
Процедури виявлення переваг ОПР намножині критеріїв
1.
2.
3.
4.
5.
Ранжування критеріїв
Попарне порівняння
Безпосередня оцінка
, i I
*
i
*
x D0
f *, i I
i w j f j x* / w j f j x* , i I
j I
j i
q I j I
j q
4
99.
Три способи визначення множиниефективних альтернатив
1.
min
x D0
i I
i
wi x
5
i Г i : i 0, i I , i 1 ,
i I
D
відносно параметрів
де wi x , i I - увігнуті неперервні функції,
замкнена множина.
2.
min max i wi x
x D0
i I
0
є опукла
6
відносно параметрів i Г i : i 0, i I , i 1 ,
i I
де wi x , i I - монотонні перетворення (2) критеріїв f i x , i I
100.
Три способи визначення множиниефективних альтернатив
3.
f i x zi , i I1 , i l
f i x zi , i I 2
x D0
max f l x
відносно параметрів z Z M 1
f
i I1
i l
7
0
0
,
f
f
i , fi max
i min
i
i I 2
101.
ВизначенняРішення задачі БО називають компромісним
рішенням. Нехай додаткова інформація від ОПР
задана у вигляді (2), (3), то компромісним рішенням
*
задачі БО буде
ефективний розв’язок
x D0
для заданого в просторі W вектора переваг критеріїв
i , i I
102.
Метод обмежень(метод знаходження компромісного рішення )
Визначення
Під компромісним рішенням задачі БО в методі обмежень
розуміють ефективну альтернативу x* D0, що знаходиться
на заданому вектором i , i I напрямку в просторі W , та
забезпечує однакові мінімальні зважені відносні відхилення
від оптимальних значень по всім критеріям одночасно:
1 w1 x* ... M wM x*
компромісне рішення для заданих i , i I можна знайти при
розв’язуванні задачі параметричного програмування відносно
параметра k0 :
103.
Метод обмежень(метод знаходження компромісного рішення)
min k0
i wi x k0 , i I
8
x D0
k0 0
xn 1 k0
min xn 1
w x x
i i
n 1
x D0
xn 1 0
9
104.
Ітераційний процес в методіобмежень
k0 0,1 M
k0 0 i wi x 0, i I f i x f i , i I
0
l - ітераційний індекс
, 0 - заданий параметр закінчення ітераційного процесу
l
- номер ітерації, на якій система нерівностей в (8)
сумісна
l 1- номер ітерації, на якій система нерівностей в (8)
несумісна
k0 l k0 l 1
процесу
- критерій закінчення ітераційного
105.
Геометрична інтерпретація методаобмежень
w2
1
k0 1
j
w2 j
k0 j
w2 l l
k0 l
l
1
WD0
w2 l 1
k0 l 1
w1 l 1 w1 l w1 j w1 1
w2 1
w1
106.
Геометрична інтерпретація методаобмежень
WD0- множина перетворених значень критеріїв на множині
допустимих розв’язків D0
j i wi x k0 j , i I
j - номер ітерації
WD0 j 0, j 1, l
WD0 l 1 0, j l 1
107.
Метод обмеженьбагатокритеріальної задачі
лінійного програмування
n
f f i x cij x j , i I
j 1
n
D0 x : aij x j bi , i 1, p, x j 0, j 1, n
j 1
n
n
0
cij x j cij x j
j 1
n j 1
, i I1
n
0
x
c
j cij x j min
ij
j 1
j 1
wi x n
n
cij x j cij x 0j
j 1
j 1
,i I2
n
n
cij x j max cij x 0j
j 1
j 1
arg max f i x , i I1 ,
x D0
0
xj
arg min f i x , i I 2 , j 1, n
x D0
x j min arg min f i x , i I1 , j 1, n
x D0
x j max arg max f i x , i I 2 , j 1, n
x D0
108.
min k0n
k0 n
0
cij x j cij x cij x j cij x j min , i I1
i j 1
j 1
j 1
j 1
n
n
n
n
k
0
0
0
cij x j cij x j cij x j max cij x j , i I 2
i j 1
j 1
j 1
j 1
n
n
0
j
n
a
j 1
ij
x j bi , i 1, p
x j 0, j 1, n
k0 0
i , i I - заданий ОПР вектор переваг на множині
критеріїв
109.
Прийняття рішень прикоаліційному об’єднанні критеріїв
110.
F , D0топ-менеджер
f , D0
X Fl , wq x k
X Fl X l
менеджери
q 1,..., Q
f
1
, D0
Xl
f Ufq
q X
p, q , p q :
…
X 1l 1 , w1 x1
f p fq 0
f
q
, D0
…
X ql q , wq xq
f
Q
, D0
X Q Q , wQ xQ
111.
Постановка задачі багаторівневоїбагатокритеріальної оптимізації
при коаліційному об’єднанні
критеріїв
112.
f f i x , i II 1,..., M
M
D0
- множина критеріїв
- множина індексів критеріїв
- кількість критеріїв
- множина допустимих альтернатив
f , D0 opt fi x , i I - задача багатокритеріальної оптимізації
x D0
l
X
1,..., Q
- множина ефективних рішень задачі
f , D0
- множина індексів коаліцій критеріїв
f q , q , на які декомпозована множина f
Q
- кількість коаліцій критеріїв, на які
розділена множина критеріїв f
f U f q , p, q , p q : f p f q 0
q X
113.
- множина критеріїв в коаліції q, q1,..., i ,..., M - множина індексів критеріїв в коаліції q
f f , iq I q
iq
q
Iq
q
Mq
iq
q
- кількість критеріїв в коаліції q
q
- поточний індекс критерія в коаліції
iq
f , D0 opt f , iq I q - задача багатокритеріальної оптимізації
x D0
q
q
для коаліції
X
l
q
q
- множина ефективних рішень задачі f , D0
Знайти розв’язок задачі багаторівневої
багатокритеріальної оптимізації f , D0 при
коаліційному об’єднанні критеріїв
114.
Пошук внутрішньокоаліційнихкомпромісних розв’язків задач
f
q
, D0 , q
115.
iq : iq 0, iq I q , iq 1 , qiq I q
q
- заданий вектор переваг критеріїв в коаліції
wq wiq x , iq I q
q
- задані монотонні перетворення значень критеріїв f q
коаліції q , що призводять до їх мінімізації та
безрозмірного виду з інтервалом зміни значень (0,1).
116.
xq , xq Xl
q
- внутрішньокоаліційний компромісний розв’язок
задачі f q , D0 при заданих q, w q , який можна
знайти методом обмежень:
xq arg min max iq wiq x , q
x D0 iq I q
- з узагальненим критерієм для коаліції q:
1
117.
Fq , x max iq wiq x , qq
iq I q
k Fq , xq max iq wiq xq , q
*q
0
q
- значення
iq I q
2
3
Fq q , x в компромісному розв’язку xq
118.
Пошук міжкоаліційногокомпромісного розв’язку задачі
F , D0
119.
F Fq , x , qq
- множина всіх узагальнених критеріїв коаліцій
F , D0
min F , x , q
q
x D0
q
- нова міжкоаліційна задача багатокритеріальної
оптимізації
X
l
F
- множина ефективних рішень задачі
F , D0
120.
q : q 0, q , q 1q
- заданий вектор переваг коаліцій
wq Fq , x
q
max iq wiq x k
iq I q
1
k0*q
Mq
*q
0
, q
4
- побудовані монотонні перетворення значень
критеріїв Fq q , x , q , де
1 *q
та оптимальні значення
, k0 - відповідно найбільші
q
Mq
F
, x , q на множині допустимих
критеріїв q
альтернатив D0
121.
x ,x Xk
k
l
F
-компромісний розв’язок міжкоаліційної задачі
F , D0
який можна знайти методом обмежень:
x arg min max q wq Fq , x
k
x D0
q
q
5
122.
Загальна схема розв’язання задачіміжкоаліційного прийняття
управлінських рішень
123.
I етапЗнайти внутрішньокоаліційні компромісні
розв’язки xq , q задачі багатокритеріальної
оптимізації f q , D0 для кожної коаліції q, q
q
q
w
, q , наприклад, методом
при заданих
та
обмежень:
min Fq , x max iq wiq x , q 6
x D0
q
124.
II етапЗнайти міжкоаліційний компромісний розв’язок
задачі багатокритеріальної оптимізації F , D0 з
числом критеріїв (2), рівним кількості коаліцій
при заданих та wq , наприклад, методом
обмежень:
min max q wq Fq , x
x D0
x X
k
q
w
F
,x
- з монотонності
q
q
l
F
X X
l
F
q
q
l
- при фіксованих векторах переваг
критеріїв
q , кожної коаліції q
xk
7
125.
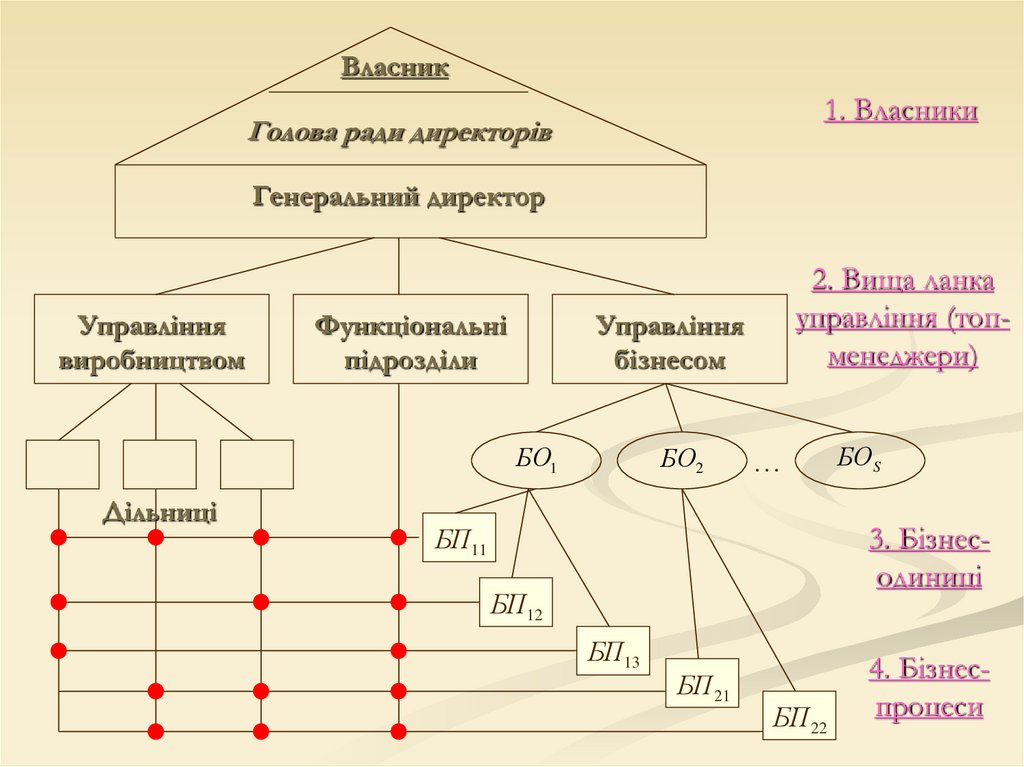
Матрична структура підприємства126.
Власник1. Власники
Голова ради директорів
Генеральний директор
Управління
виробництвом
Функціональні
підрозділи
Управління
бізнесом
БО1
Дільниці
2. Вища ланка
управління (топменеджери)
БО2
…
БОS
3. Бізнесодиниці
БП11
БП12
БП13
БП 21
БП 22
4. Бізнеспроцеси
127.
Бізнеси (бізнес-процеси - БП) – організованіза продуктовим ланцюгом платежі –
постачання сировини – реалізація – повернення
грошей.
Бізнес-одиниці – підрозділи, що
управляють бізнесами.
Виробничі та функціональні підрозділи
виконують замовлення бізнес одиниць.
128.
Схема інформаційної таматематичної підтримки
управління розвитком
129.
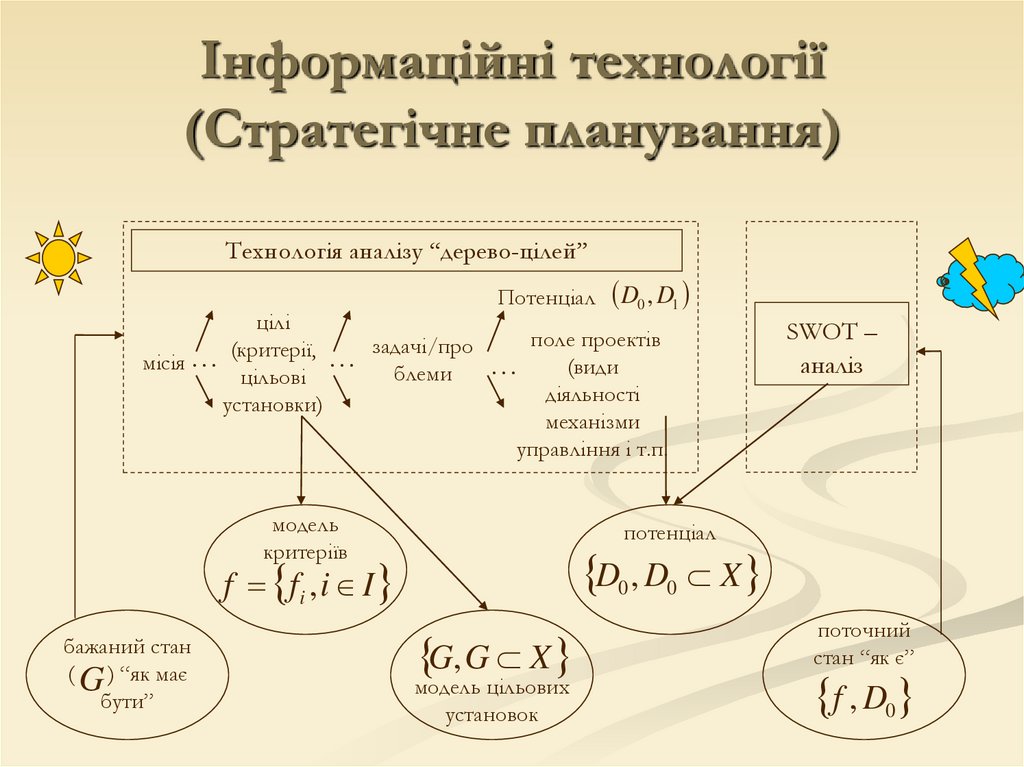
Інформаційні технології(Стратегічне планування)
Технологія аналізу “дерево-цілей”
цілі
(критерії, … задачі/про
місія …
блеми
цільові
установки)
Потенціал
поле проектів
(види
…
діяльності
механізми
управління і т.п.
модель
критеріїв
SWOT –
аналіз
потенціал
D0 , D0 X
f fi , i I
бажаний стан
( G ) “як має
бути”
D0 , D1
G, G X
модель цільових
установок
поточний
стан “як є”
f , D0
130.
Метод аналізу “витрати-ефект”131.
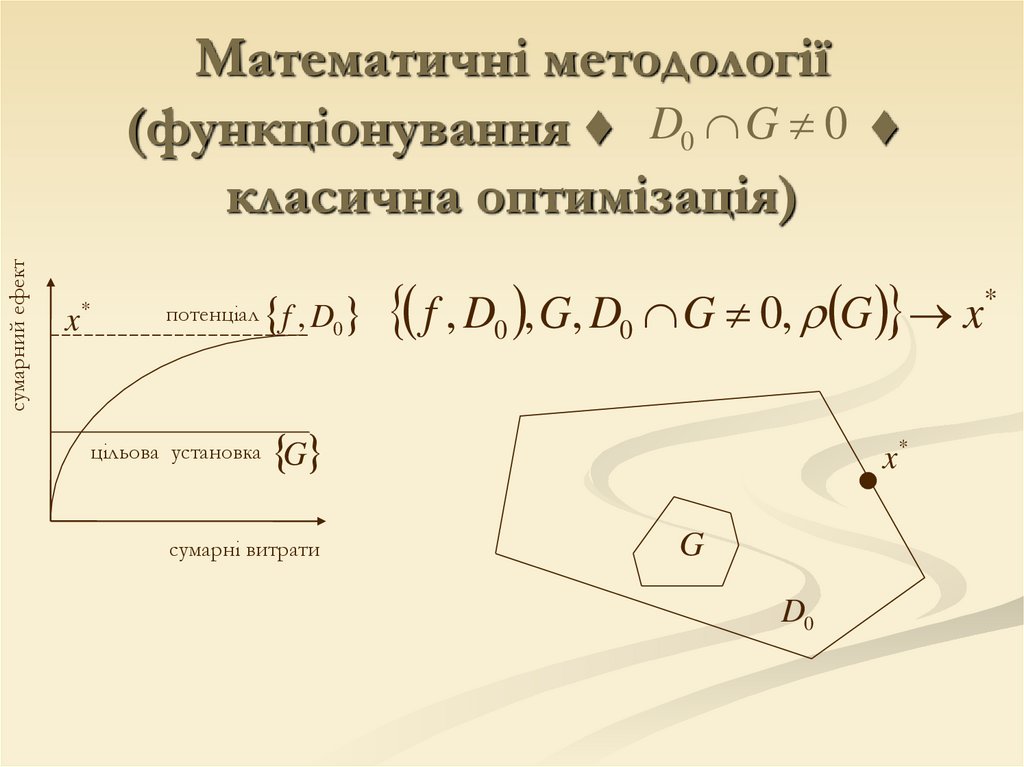
сумарний ефектМатематичні методології
(функціонування ♦ D0 G 0 ♦
класична оптимізація)
x
*
потенціал
цільова установка
f , D0
f , D0 , G, D0 G 0, G x*
G
сумарні витрати
x*
G
D0
132.
сумарний ефектМатематичні методології
(розвиток ♦ D0 G 0 ♦ системна
оптимізація)
x
*
цільова установка
потенціал
G
f , D0
f
f
, D , G, D G 0, G x
0
1
, D0 , G, D0 G 0
1
1
1
x*
сумарні витрати
x*
G
D0
G
G
D0 D1
D1
*
133.
Постановка задачі системноїоптимізації для оргсистем, що
формалізуються в класі
багатокритеріальних задач
лінійного програмування
134.
Модель оргсистемиf , D0
n 0
0
D0 x : alj x j bl , l Q 1,..., m , j J 1,..., n
j 1
n
f f i x cij x j opt , i I 1,..., M I1 I 2
j 1
135.
Модель цільових установокG
Задача системної оптимізації виникає, якщо:
1. G D0 0;
2. alj0 , bl0 , cij , l Q, j J , i I
alj , bl , cij , l Q, j J , i I
a alj , l Q0 , Q0 Q, j J
b bl , l Q0 , Q0 Q
c ci , i I 0 , I 0 I
P0 a, b, c - задає ОПР на основі реальних
можливостей задачі в процесі її рішення
136.
Потрібно побудувати нову модельоргсистеми
f , D1
при якій D1 G 0 на основі зміни початкової моделі
оргсистеми f , D0 у відповідності з
в межах P0
G
f x f x , i I
x k , x k D1 : f i x k f i x , i I1
k
i
i
x G
з урахуванням специфіки реальної задачі.
2
137.
Алгоритм системної оптимізації змоделлю цільових установок у
просторі рішень
138.
Постановка задачіG x , x D
f f x f
*
*
0
*
i
*
i min
i
, f i max ,
f i min min f i x
x D0
f i max max f i x , i I
x D0
I I1 , f i 0 f i max , i I
Потрібно побудувати D1 шляхом зміни D0 в межах P0 , в якій
x D1 , x D1 : f i x f i x , i I
*
k
k
*
139.
Алгоритм1. Визначення узгодженості цілей оргсистеми з G
x0k - ефективний розв’язок f , D0 , знайдений методом *
обмежень при заданому векторі переваг критеріїв
f
wi x* f i 0 f i x
0
i
f i min , i I
*
*
*
i w j x wh x , i, j, h I , i j, h q
q I
x* f x* f 0 , f min w x* * x0k
i w j f j x* / w j f j x* , i I
*
Вважаємо
j I
j i
q I j I
j q
f i x* f i x0k , i I , x* D0
і хоча б одна з нерівностей строга.
140.
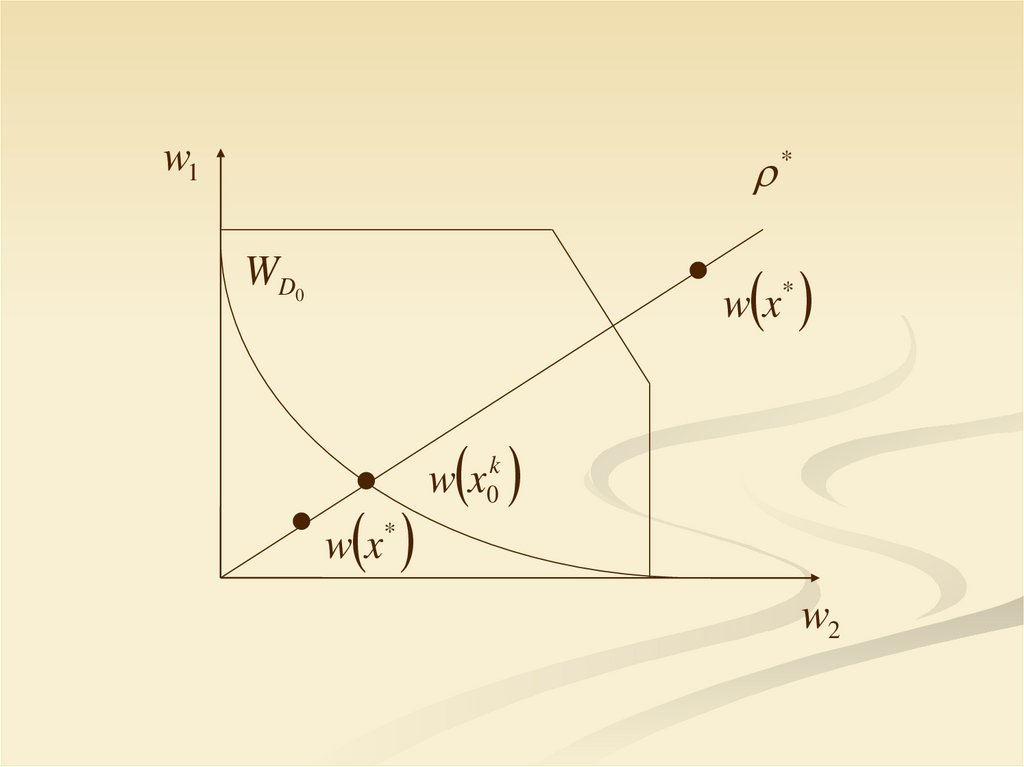
w1*
WD0
w x*
wx
w x0k
*
w2
141.
n2. Визначимо Q l : a x* b , l Q , Q Q
lj j
0
0
l
Теорема
j 1
Якщо f i x* f i x0k , i I , і хоча б одна нерівність
строга, то допустимі розв’язки D , які знаходяться на
0
гіперплощинах з номерами з множини Q , є
0
ефективними розв’язками по множині критеріїв f
3. Побудуємо область варіацій параметрів для Q0
142.
alj , bl , l Q0 , j J :alj , bl , l Q0 , j J :
n
n
x* a b b 0 a 0 x , l Q
j
lj
l
l
lj
j
0
j 1
j 1
bl bl0 , bl0 0, l Q0
P
bl bl0 , bl 0, l Q0
alj alj0 , alj0 0, l Q0 , j J
alj alj0 , alj0 0, l Q0 , j J
143.
P P0 0 :4. Задачі вибору варіацій параметрів
.
min
a , b P P0
alj , bl , l Q0 , j J :
C a, b
C a, b - функція витрат, пов’язаних зі змінами
параметрів D
0
. opt F
a , b P P0
F alj , blj , l Q0 , j J - множина критеріїв,
де величина зміни кожного параметра суттєвих обмежень Q0
виступає як окремий критерій, який в залежності від
фізичної суті може максимізуватися або мінімізуватися.
144.
alj0 , l Q / Q0alj 0
alj alj , l Q0 , j J
bl0 , l Q / Q0
bl 0
bl bl , l Q0
n
D1 x : alj x j bl , l Q, j 1, n
j 1
145.
Твердження 1Якщо серед обмежень D0 є:
Q l : alj0 0, bl0 0, j 1, n, l Q 0,
то область D1 побудована за рахунок зміни параметрів обмежень
Q0 згідно з P є обмеженою та замкнутою.
Якщо Q 0, D0 - замкнута та обмежена, то, щоб D1 була
обмеженою та замкнутою, додамо до D0
n
x j bm 1 0 - наслідок системи D0
j 1
n
bm 1 max x j
x D0
j 1
n
n
*
*
a
x
b
b
x
m 1
m 1
j
m 1 j j
j 1
j
P : am 1 j 1, j 1, n
bm 1 bm 1
146.
P P0 P 0 : alj , bl , l Q0 m 1 , j Jn
D1 x : alj x j bl , l Q, j J ,
j 1
n
am 1 j x j bm 1
j 1
am 1 j am 1 j 1,
bm 1 bm 1 bm 1
1
*
*
k
x* f x* , f 0 1 , f min
w
f
x
w
x
x
1
1 1
147.
Твердження 2x k , x k D1 : f i x k f i x* , i I ,
x arg min max i 1 wi 1 x ,
k
x D1
де
i I
wi 1 x , i 1 wi 1 x побудовані для f , D1
148.
Загальна постановка задачісистемної оптимізації
149.
Модель оргсистемиf , D0
D0 x : gl x 0, l Q 1,..., m , x x j , j J 1,..., n
f f i x max, i I1 , f i x min, i I 2 , I1 I 2 I 1,..., M
150.
Модель цільових установокG
f , f , i I : G x : f f x f , i I , x
x x , j J : G x : x x , j J
x , x , j J : G x x x , j J
f * f i * , i I : G x : f i * f i x , i I1 , f i * f i x , i I 2 , x j 0, j J
i Н
*
i В
i Н
*
j
j Н
X:
opt L x :
x X
*
j
j
j В
j Н
j
G X
G arg opt L x
x X
i В
i
j В
j
0, j J
151.
Задача системної оптимізаціївиникає, якщо
G D0 0 або G 0
Q0 l : l Q, D0 G 0 , Q0 Q
- множина індексів обмежень D0 , через які G D0 0 :
I 0 i : i I , G 0 , I 0 I
- множина індексів критеріїв f , через які G 0 :
2. pl , l Q0
- вектори варіацій параметрів обмежень
з індексами з множини Q0
pi , i I 0 - вектори варіацій параметрів критеріїв
з індексами з множини I 0
P0 pl , l Q0 , pi , i I 0
Обмежену область обмежень на варіації параметрів задає ОПР
на основі реальних можливостей задачі в процесі її
рішення.
1.
152.
P pl , l Q0 , pi , i I 0-
область обмежень на варіації параметрів з індексами з
множин Q0, I 0 , яка математично забезпечує побудову D1
так, що D1 G 0
, або переформування множини
критеріїв f при G 0 на f1 таким чином, що G 0 , без
врахування реальних можливостей P0 по зміні параметрів
системи.
Задача системної оптимізації полягає в побудові f1 , D1
шляхом зміни параметрів f , D0 в межах P0 , що D1 G 0
,
(при D0 G 0), або G 0 (при f1 ) з урахуванням
специфіки задачі.
153.
1.2.
3.
4.
Специфічні особливості задачі
системної оптимізації
Модель оргсистеми представлена f , D0 ,
або D0 .
Необхідний ступінь узгодженості цілей
оргсистеми з моделлю цільових установок G.
Необхідний ступінь узгодженості D1 та G :
G D1 , або G D1 0.
В практичних задачах ОПР має різні
можливості по формуванню P0 .










































































































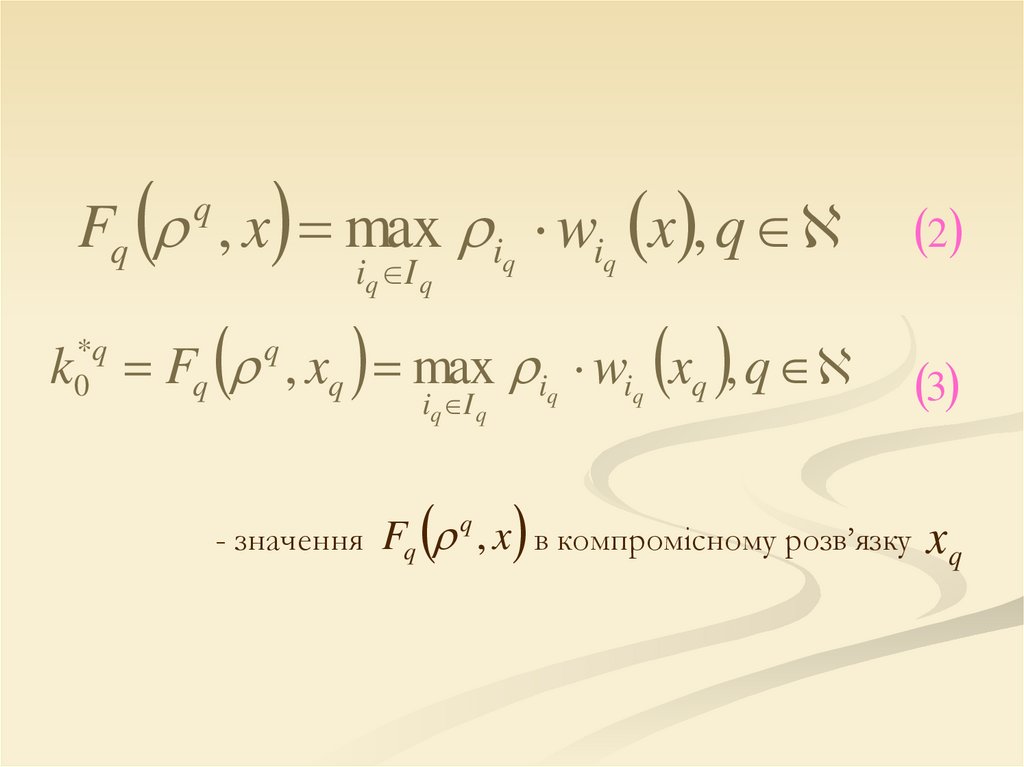




















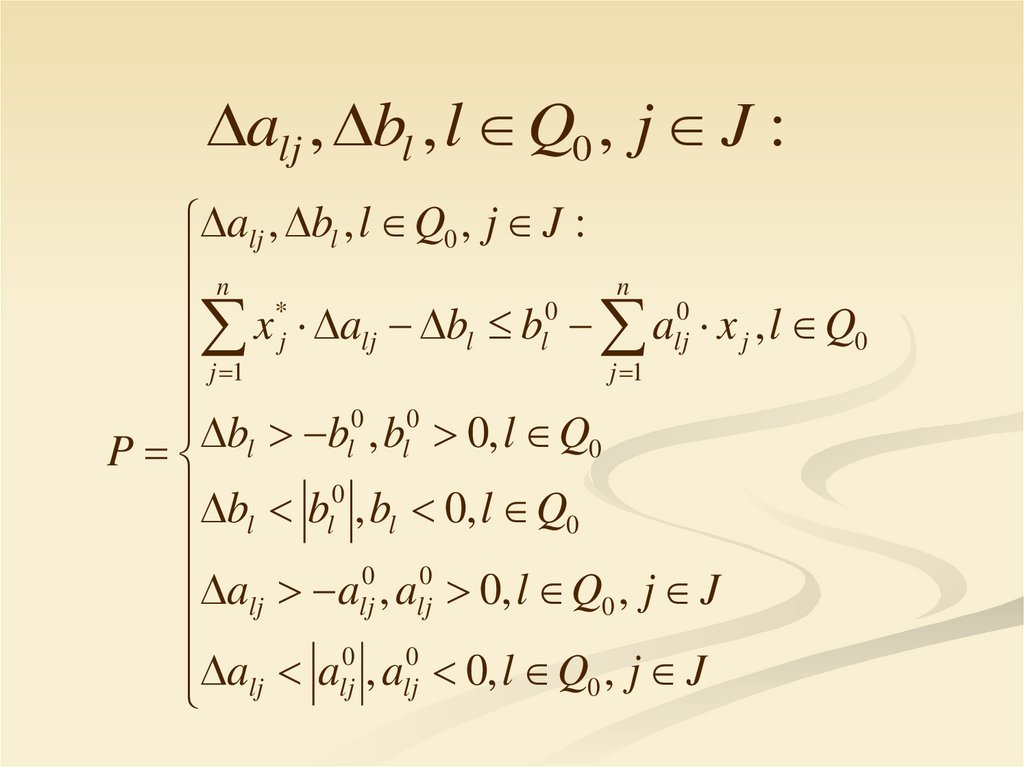

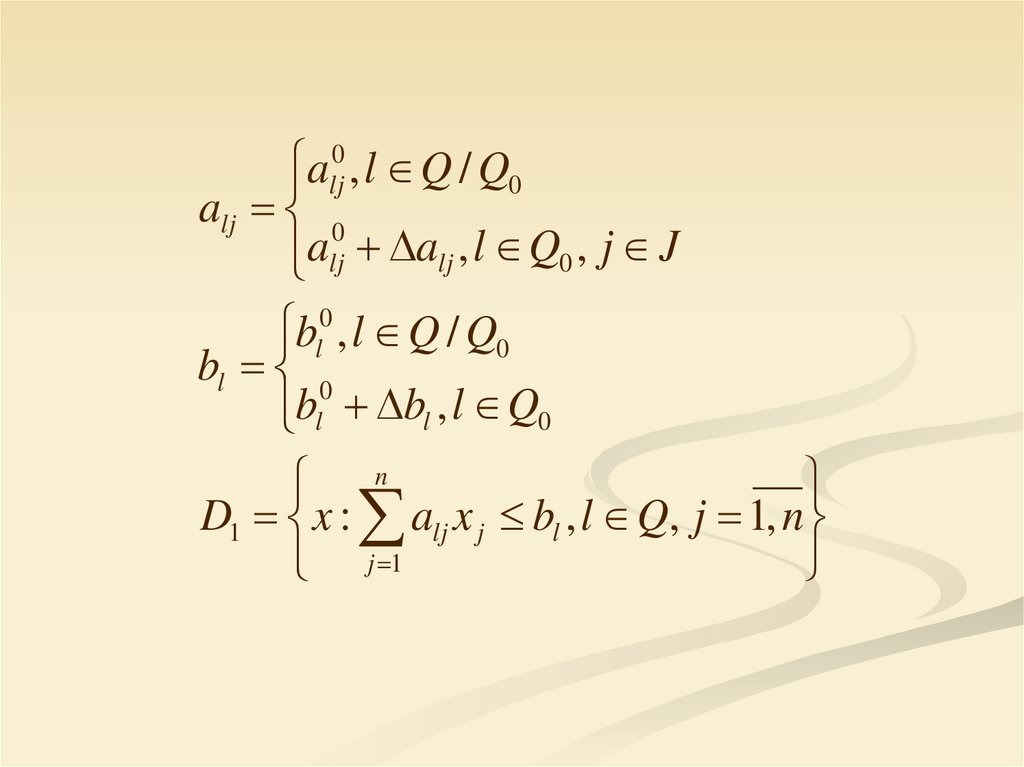

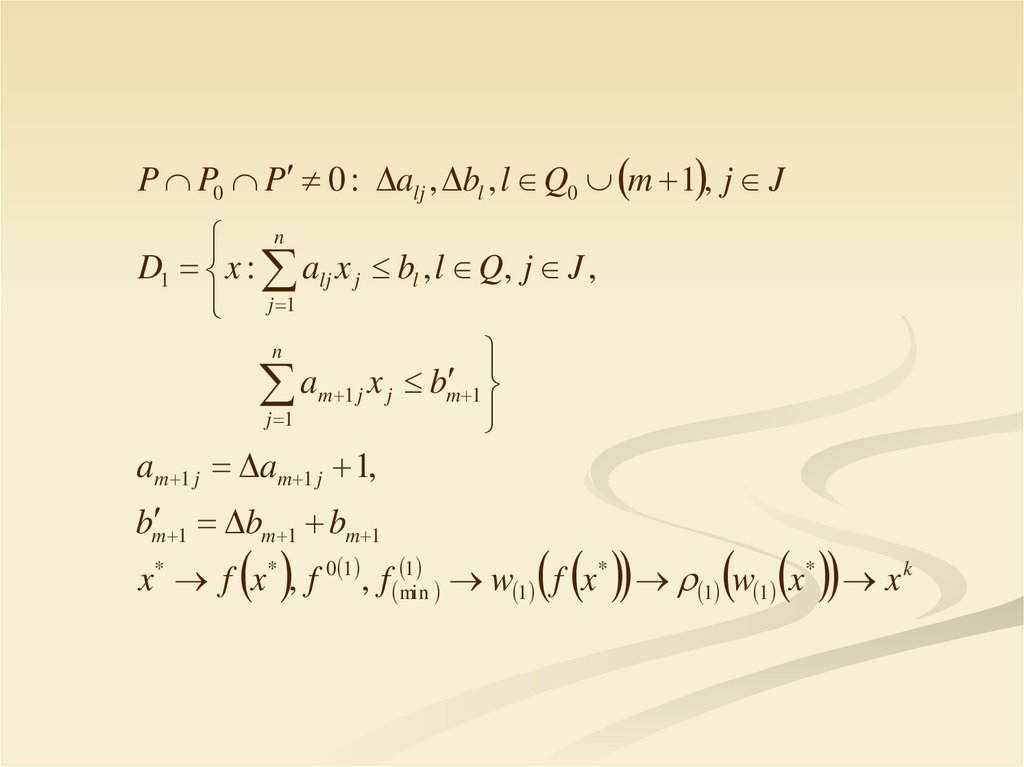
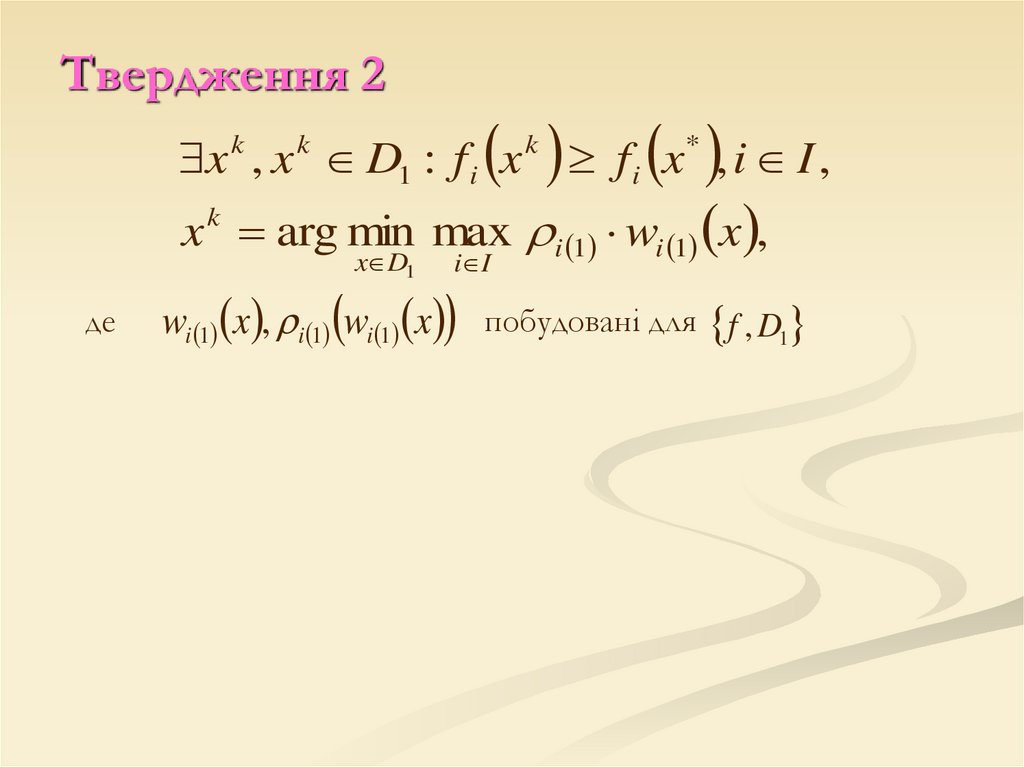







 Математика
Математика








