Програмування чисельних методів. Лекція 8

1.

2.

• Вступ
• Задача Коші
• Методи Рунге-Кутти
• Крайова задача
• Розв'язок ДУ в скінчених різницях
2

3.

• Щоб знайти розв’язок диференціального рівняння
необхідно мати значення залежної змінної і (або) її
похідних при деяких значення незалежної змінної.
Якщо ці додаткові умови задаються при одному
значення незалежної змінної, то така задача
називається задачею з початковими умовами або
задачею Коші. Якщо ж умови задаються при двох або
більше значення незалежної змінної, то задача
називається крайовою. В задачі Коші додаткові умови
називаються початковими, а в крайовій – граничними.
3

4.

• З теорії звичайних диференціальних рівнянь відомо, що
рівняння n-го порядку можна звести до систем з n
рівнянь першого порядку.
y f ( x, y, y )
z y
y z
z f ( x, y, z )
• Тому головну увагу ми будемо приділяти саме рівнянням
першого порядку
4

5.

• Задача Коші формулюється наступним чином: треба
знайти функцію y (x) , яка задовольняє
диференціальному рівнянню
dy
y f ( x, y ) (1)
dx
• і початковій умові y ( x0 ) y 0
• Чисельне рішення цієї задачі полягає в обчисленні
значень функції в дискретній послідовності точок
y ( x1 ), y ( x 2 ),..., x( y n )
5

6.

• Найпростішим з методів розв’язку цієї задачі є метод
Ейлера, який виходить з розкладення функції в ряд
Тейлора в околі точки xn , в якій рішення відоме
1 2
1 k (k )
y ( xn 1 ) y ( xn h) y ( xn ) hy ( xn ) h y ( xn ) ... h y ( xn ) ...(2)
2!
k!
• де h xn 1 xn
– відстань між вузлами інтегрування
6

7.

• В силу співвідношення (1) формули для похідних в (2)
набудуть вигляду
y f
y
f f y
fx f y f
x y x
(3)
y f xx 2 f xy f f yy f 2 ( f x f y f ) f y
• де всі обчислення проводяться в точці ( xn , yn ) .
• Після підстановки (3) в (2) знаходимо значення функції y в
точці xn 1 . Такий підхід є дуже ефективним для розробки
методів інтегрування ДУ, але на практиці в силу складності
і необхідності виконувати ці обчислення для кожної
конкретної функції f(x,y), застосовується вкрай рідко.
7

8.

• Утримуючи в (2) тільки лінійну по частину, одержуємо
робочу формулу методу Ейлера
yn 1 yn hf ( xn , yn ) (4)
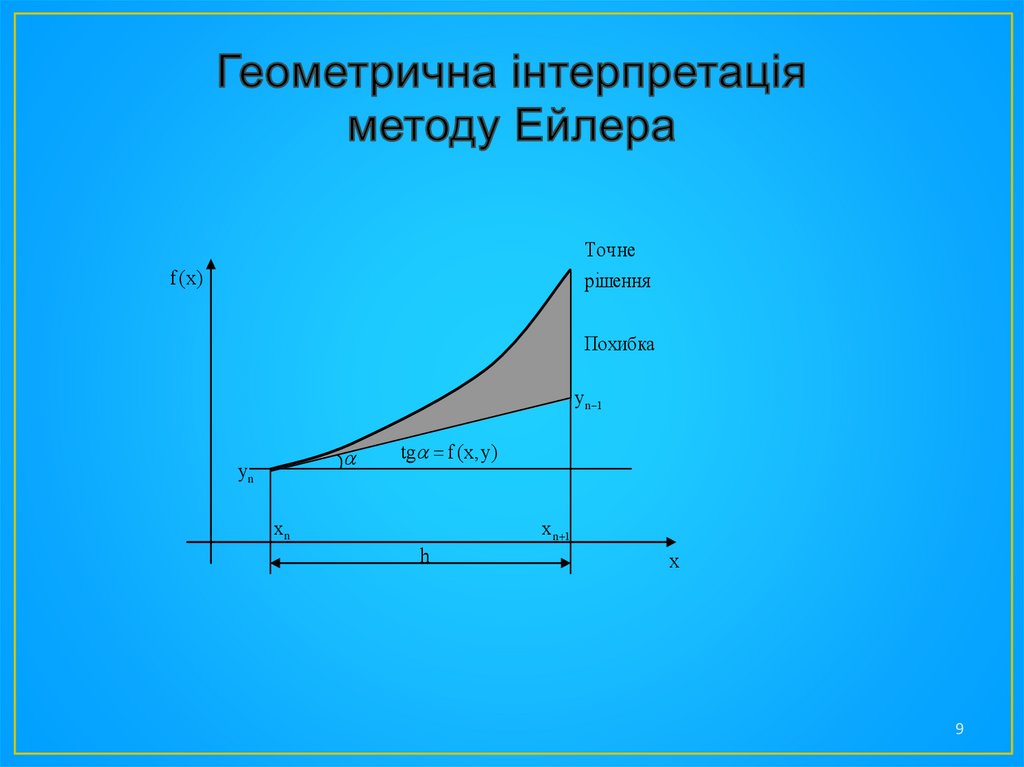
• З геометричної інтерпретації методу Ейлера видно,
що точне рішення буде одержано тільки у випадку
лінійної функції f(x,y)
8

9.

Точне
рішення
f (x)
Похибка
y n 1
yn
tg f ( x, y)
xn
x n 1
h
x
9

10.

• Ці методи призначені для отримання розв’язку
• на основі рядів Тейлора, але без явного обчислення
похідних, за винятком першої. Шляхом безпосереднього
xn h
xn h
• інтегрування
y dx f ( x, y )dx
xn
xn
• з врахуванням умови y ( xn ) y n розв’язок задачі Коші у
точці можна записати у вигляді
yn 1 yn
xn h
f ( x, y )dx
xn
• Тоді загальна формула чисельних методів рішення задачі
Коші може бути представлена у вигляді
yn 1 yn y
(5)
10

11.

• У методах Рунге-Кутти величина y обчислюється як
q
y Ak k ,
k 0
• де Ak набір констант, k – набір допоміжних функцій.
Якщо ввести ще два набори констант
1 , 2 ,..., q
10
20 , 21
.......... .......... ........
q 0 , q1 ,..., qq 1 .
• І визначити q як
11

12.

0 h f x, y ,
1 h f x 1 h, y 10 0 ,
2 h f x 2 h, y 20 0 21 1 ,
.......... .......... .......... .......... .......... .......... .......... .......... .......... ....
q h f x q h, y q 0 0 q1 1 ... qq 1 q 1 ,
• то q можна послідовно обчислити по відомих і .
• Оскільки (2) і (5) мають однакову структуру, то
параметри A, і можна знайти шляхом порівняння
коефіцієнтів при однакових ступенях h в (2) і в
розкладенні y в ряд Тейлора в околі h=0.
12

13.

• Порядок метода буде визначатися найвищим
ступенем h утриманим в цих розкладеннях.
• При q=0 необхідно обчислити
(h) A0 hf ( xn , y n )
(0) 0
(h) A0 f ( xn , y n )
(0) A0 f ( xn , y n )
• Тоді y n hf y n hA0 f, звідки визначаємо A0 f ( xn , y n ) ,
тобто метод Рунге-Кутти першого порядку і метод
Ейлера співпадають.
13

14.

• Аналогічні обчислення при q=1дають
(h) A0 hf ( xn , yn ) A1hf ( xn 1h, yn 10 hf ) A0 hf ( xn , yn ) A1hf (h)
(h) A0 f A1 f (h) A1h 1 f x (h) 10 f y (h) f (h)
1 f x (h) 10 f y (h) f (h)
( h) 2 A1 A1 h
(0) 0
(0) ( A0 A1 ) f
d
dh
(0) 2 A1 2 A1 1 f x 10 f y f
14

15.

• Порівнюючи (2) і (5)
h2
yn hf ( f x f y f ) yn h( A0 A1 ) f h 2 A1 ( 1 f x 10 f y f )
2
1
1
• отримаємо A0 A1 1, 1 A1 , 10 A1
2
2
• Починаючи з q>1 характерною є ситуація коли число
невідомих більше числа рівнянь для їх визначення.
• Тобто A, , неможливо знайти однозначно.
15

16.

• Тоді звичайно одну з невідомих приймають як
незалежну змінну. Якщо за незалежну змінну взяти у
даному випадку A1 , то отримаємо
1
1
A 1 A ,
,
0
1
1
2 A1
10
2 A1
• Конкретні значення A1 вибирають з міркувань
простоти або симетрії робочих формул. Якщо
1
A
0
,
• прийняти, що , A1 1 то 0
і отримаємо
1
10
2
формулу Рунге другого порядку
h
h
hf ( x n , y n f )
2
2
16

17.

• При A1
1
маємо A0 1 , 1 10 1, що приводить до
2
2
• іншої формули цього ж порядку
1
( 0 1 ), 1 hf ( xn h, yn 0 )
2
• Для найбільш поширеного метода Рунге-Кутти
четвертого порядку маємо
1
y n 1 y n ( 0 2 1 2 2 3 )
6
h
0 hf ( xn , y n ),
1 hf ( xn , y n 0 ),
2
2
h
3 hf ( xn h, yn 2 )
2 hf ( xn , y n 1 ),
2
2
17

18.

• Методи типа Рунге відносяться до одно крокових
(самостартуючих), постільки для обчислення функції в
наступній точці досить мати її значення у попередній.
Так як, для методів одного порядку точність рішення
залежить від кроку це дає можливість проводити
обчислення з заданою точністю. Наприклад критерієм
зменшення величини кроку h в два рази є виконання
умови
h
y n y n ( h)
,
1
2
2 N 1 ,
• де N-порядок методу.
18

19.

• Розглянемо крайову задачу
y F ( x, y, y ) (6)
,
y (a) , y (b) (7)
• У випадку лінійної задачі будь-яка лінійна комбінація
часткових рішень диференціального рівняння є також його
рішенням. Розв’язок задачі шукається у вигляді
y( x) k1 y1 ( x) k 2 y2 ( x)
• Коефіцієнти k1 і k2 визначаються шляхом розв’язку двох
задач Коші для рівняння (6) з початковими умовами
y1 (a) , y1 (a) 1
• ,
,
y2 (a) , y2 (a) 2
19

20.

• Якщо отримані рішення у точці b мають значенняy1 (b) 1
і y2 (b) 2 , то умова (7) утворює систему алгебраїчних
рівнянь відносно невідомих k1 і k 2
k1 k 2 1
k1 1 k 2 2
• І остаточне рішення лінійної крайової задачі має
вигляд
y ( x)
1
( 2 ) y1 ( x) ( 1 ) y2 ( x)
1 2
20

21.

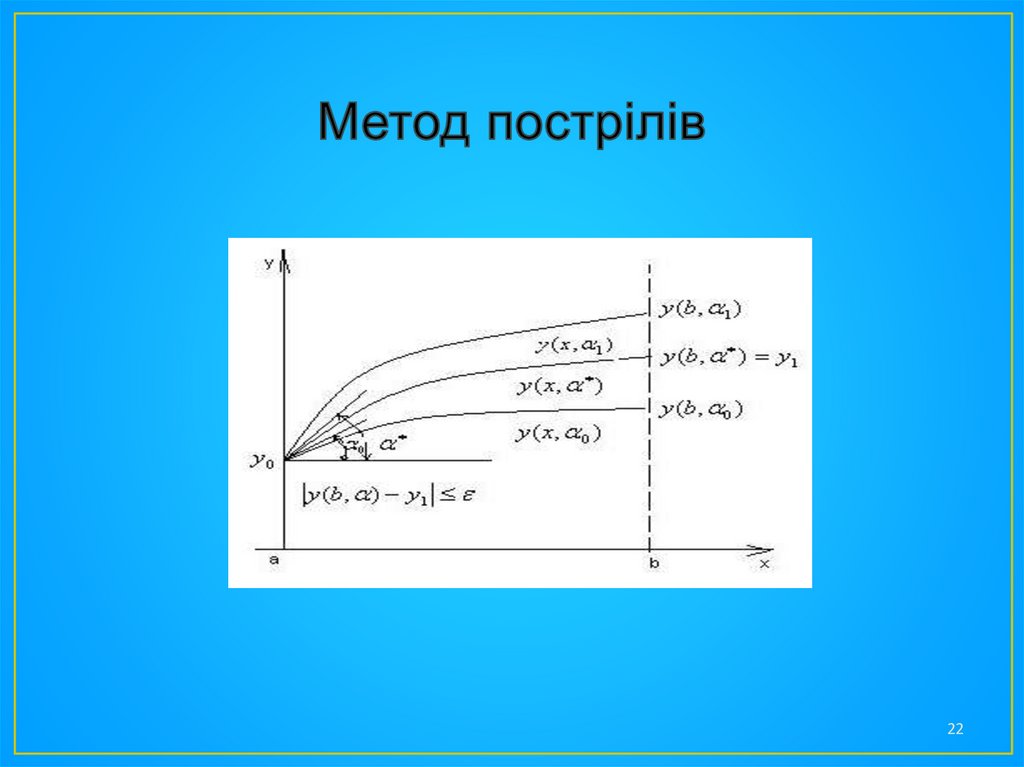
• Для рішення нелінійної задачі звичайно
використовується метод пострілів, у якому крайова
задача зводиться до послідовності задач Коші.
Знайдемо розв’язок двох задач Коші для рівняння (6),
у яких друга початкова умова має вигляд y1 (a) 1 і y2 (a) , 2
а рішення при x=b відповідно y1(b) 1, y2 (b) 2
• Завжди можна підібрати такі значення 1, 2 , щоб
• виконувалась умова
( 1 )( - 2 ) 0
• тобто 1, 2 і утворюють інтервал невизначеності для
21

22.

22

23.

• нелінійного рівняння
y ( k , b) 0
• де y - рішення задачі Коші
y F ( x, y, y )
y (a) , y (a) k
23

24.

• Досить поширеним і ефективним підходом до рішення
лінійних диференціальних рівнянь є зведення диференціальних залежностей до алгебраїчних за допомогою
скінчено-різницевої апроксимації похідних(формул
чисельного диференціювання)
f i
f i 1 f i 1
f 2f f
f ( xi ) fi i 1 2i i 1 (8)
h
2h
• Якщо застосувати формули(8) до диференціального
рівняння
y p( x) y g ( x) y z ( x)
(9)
• отримуємо його дискретний (наближений) аналог
24

25.

(2 pi h) yi 1 (2h 2 gi 4) yi (2 pi h) yi 1 2h 2 zi
(10)
yi y ( xi ), pi p( xi ), g i g ( xi ), zi z ( xi )
• записаного у послідовності xi , i 2,3,..., n - 1
• внутрішніх точок інтервалу [a,b], на якому шукається
розв'язок. Рівняння () після введення позначень
Ai (2 pi h), Bi (2h2 gi 4), Ci (2 pi h), Di 2h2 zi
• приймає більш компактну форму
Ai yi 1 Bi yi Ci yi 1 Di
(11)
25

26.

• У випадку задачі Коші для (9) маємо початкові умови,
y(a)
y (a)
• які в скінчено-різницевій формі запишуться як
y0
y1 y0 h
• Якщо рівняння (10) розрішити відносно величини
yi 1 отримаємо
• просту рекуретну формулу для визначення всіх значень функції y
yi 1 ( Di - Ai yi 1 Bi yi )/Ci
.
26

27.

• Для крайової задачі граничні умови мають вид
або y1 , y n
y(a) , y(b)
• то з (11) отримуємо наступну СЛАР
• Постільки матриця системи має трьох діагональну
структуру, то для її розв’язку доцільно застосувати
метод прогонки
27