Похожие презентации:
Параллелограмм, решение задач по готовым рисункам
1.
2.
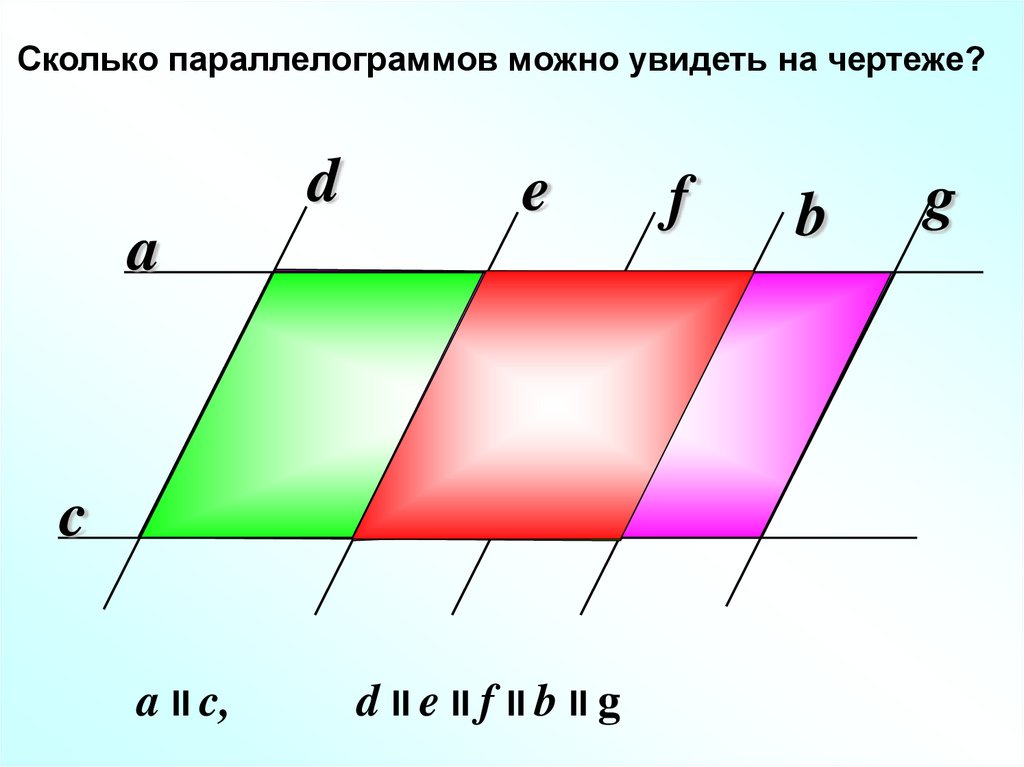
Сколько параллелограммов можно увидеть на чертеже?d
e
a
c
a II c,
d II e II f II b II g
f
b
g
3.
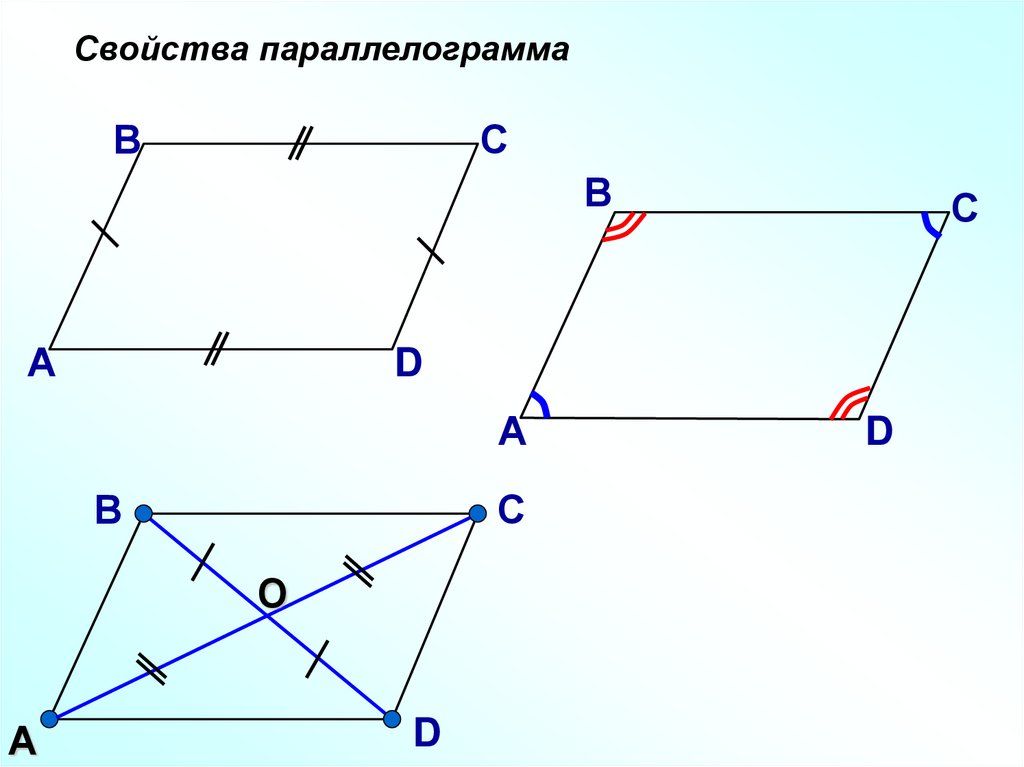
Свойства параллелограммаВ
С
В
А
D
А
В
С
О
А
С
D
D
4.
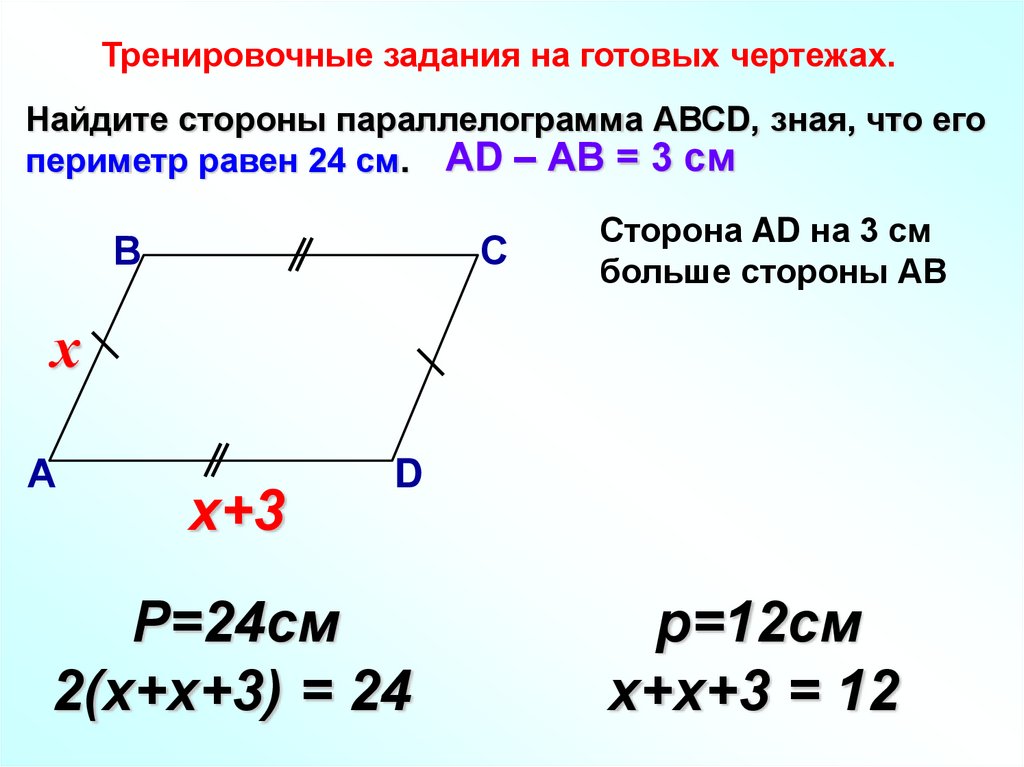
Тренировочные задания на готовых чертежах.Найдите стороны параллелограмма АВСD, зная, что его
периметр равен 24 см. АD – АВ = 3 см
В
С
Сторона AD на 3 см
больше стороны АВ
х
А
х+3
D
Р=24см
2(х+х+3) = 24
р=12см
х+х+3 = 12
5.
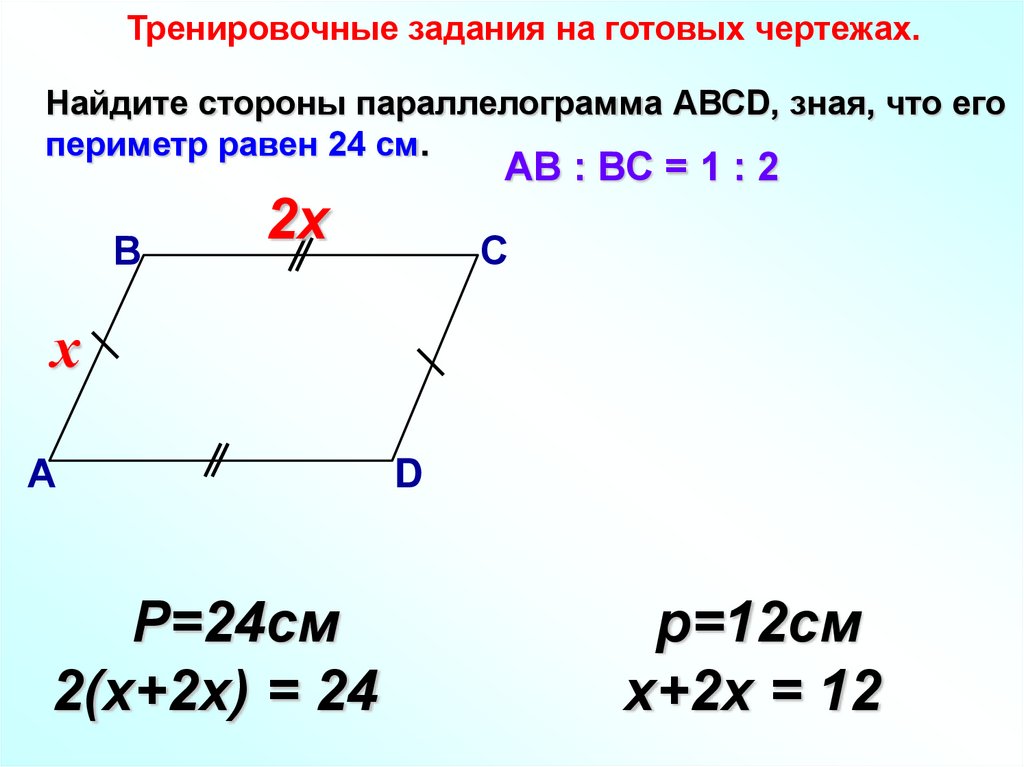
Тренировочные задания на готовых чертежах.Найдите стороны параллелограмма АВСD, зная, что его
периметр равен 24 см.
В
АВ : ВС = 1 : 2
2х
С
х
А
Р=24см
2(х+2х) = 24
D
р=12см
х+2х = 12
6.
Тренировочные задания на готовых чертежах.В
1
4
3
А
2
Дано: ABCD
четырехугольник
С
1 = 2, 3 = 4
D
Доказать: АВСD –
параллелограмм.
Докажите
По определению
параллелограмма
АВС = СDА по второму признаку равенства
треугольников
По признаку 10
По признаку 20
7.
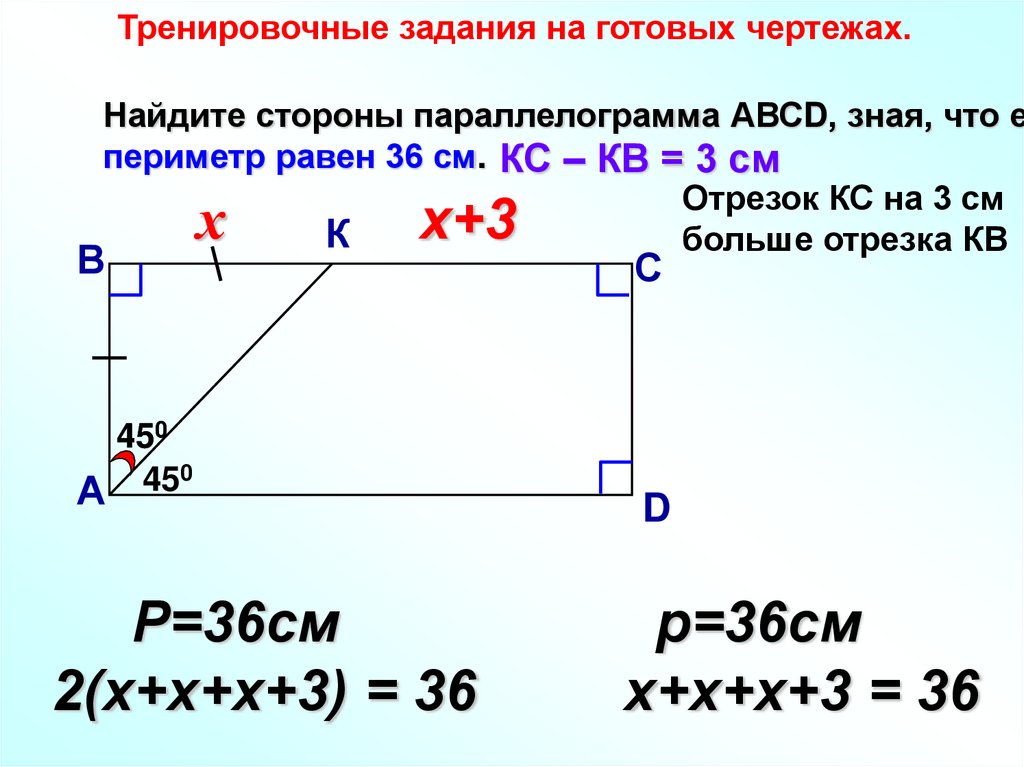
Тренировочные задания на готовых чертежах.Найдите стороны параллелограмма АВСD, зная, что е
периметр равен 36 см. КС – КВ = 3 см
Отрезок КС на 3 см
К
больше отрезка КВ
В
х
х+3
450
0
45
А
Р=36см
2(х+х+х+3) = 36
С
D
р=36см
х+х+х+3 = 36
8.
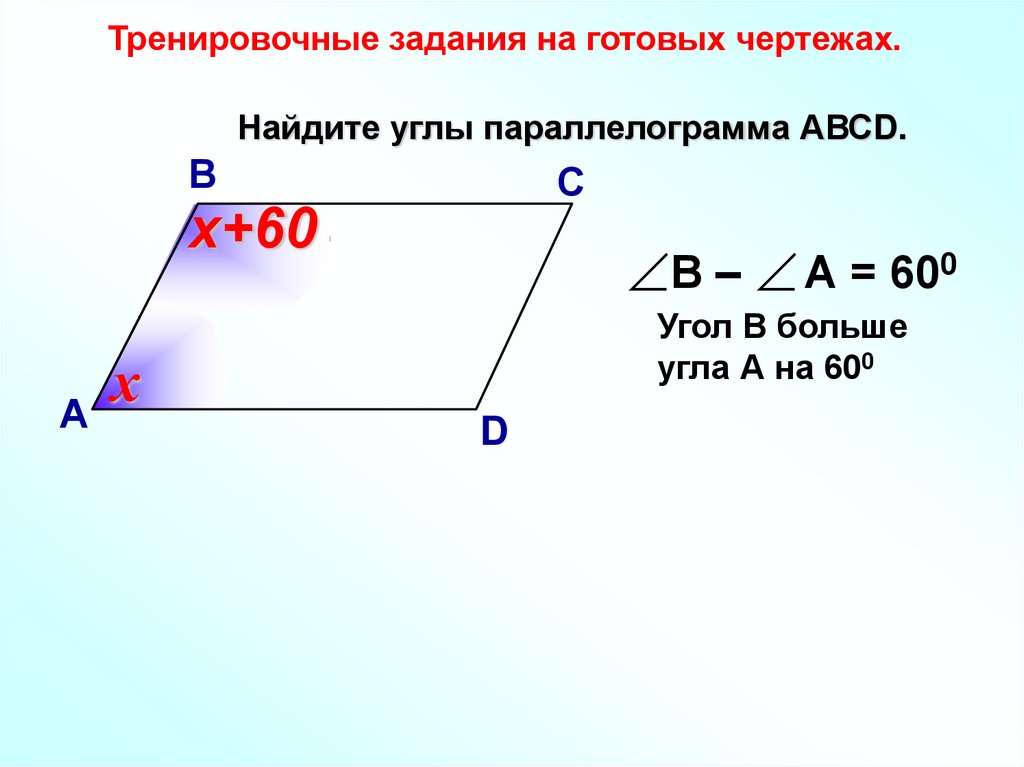
Тренировочные задания на готовых чертежах.Найдите углы параллелограмма АВСD.
В
С
х+60
А
В – А = 600
Угол В больше
угла А на 600
х
D
9.
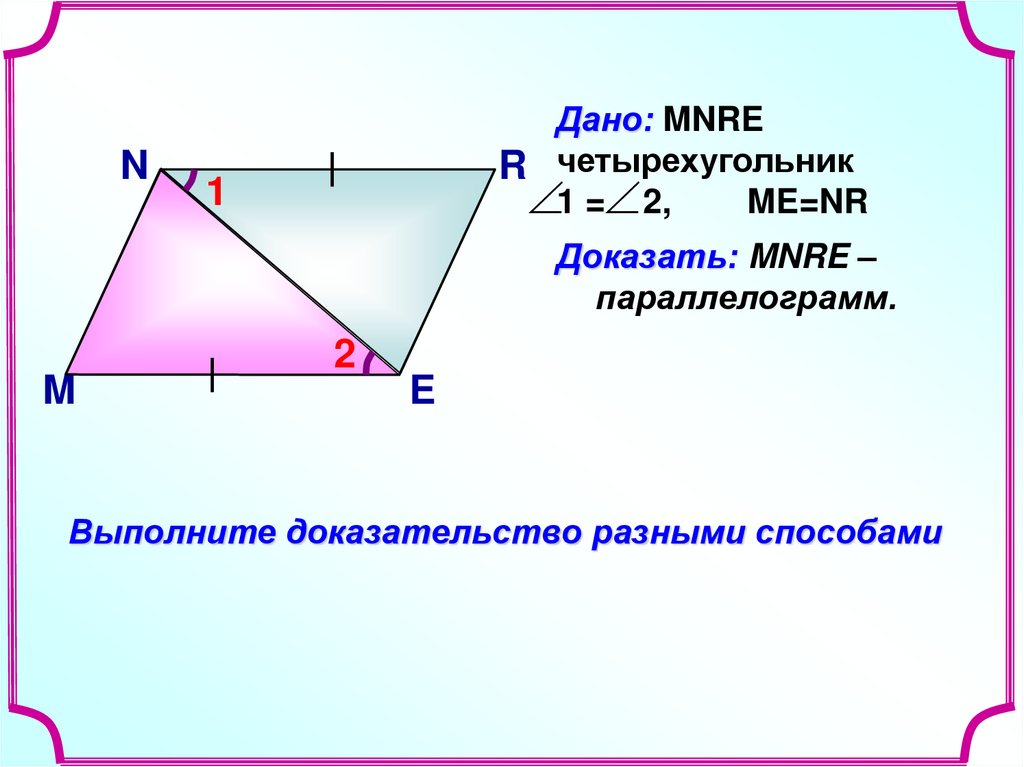
NДано: MNRE
R четырехугольник
1 = 2,
ME=NR
1
Доказать: MNRE –
параллелограмм.
M
2
E
Выполните доказательство разными способами
10.
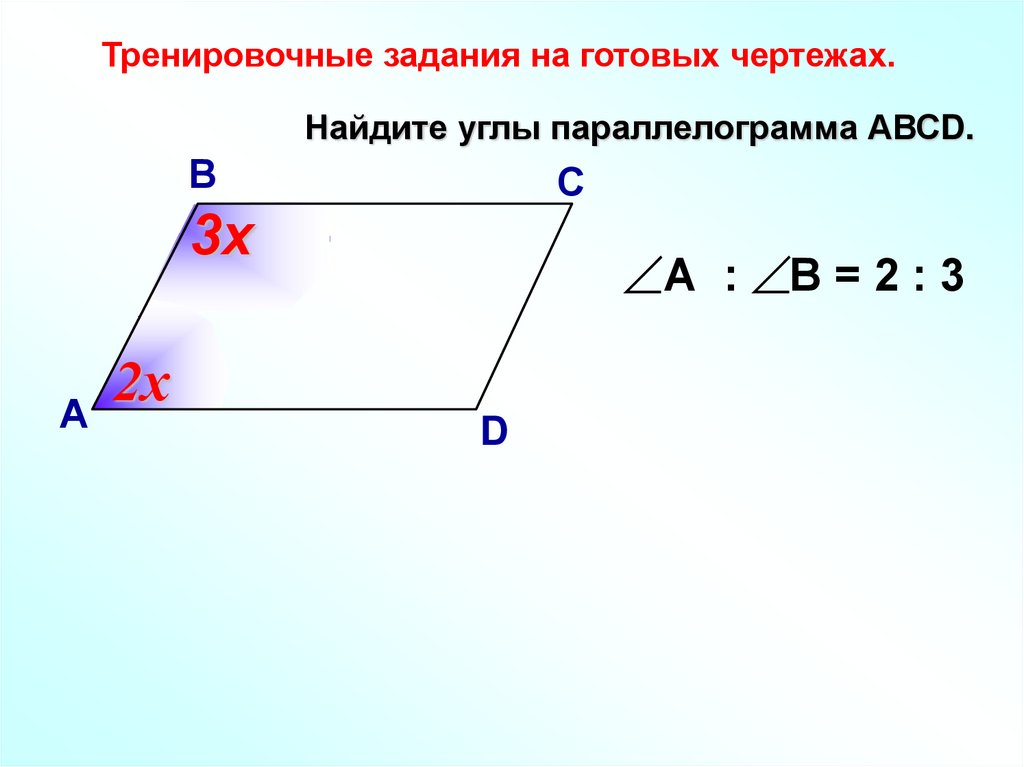
Тренировочные задания на готовых чертежах.Найдите углы параллелограмма АВСD.
В
С
3х
А
А : В = 2 : 3
2х
D
11.
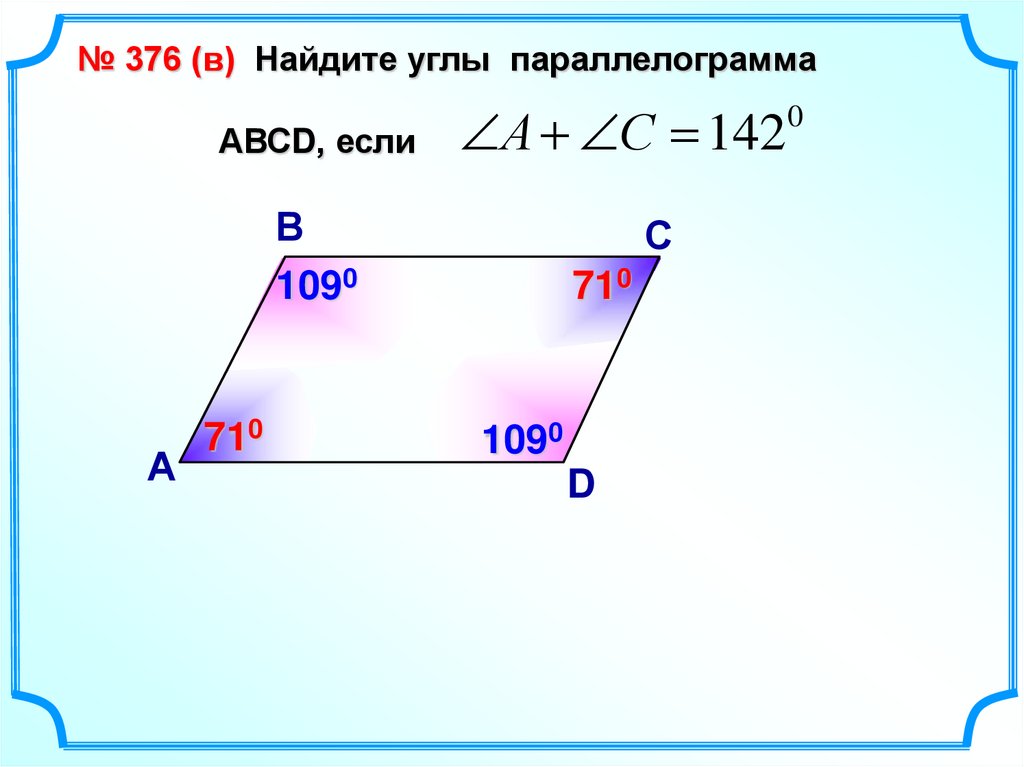
№ 376 (в) Найдите углы параллелограммаАВСD, если
А С 142
В
1090
А
710
С
710
1090
D
0
12.
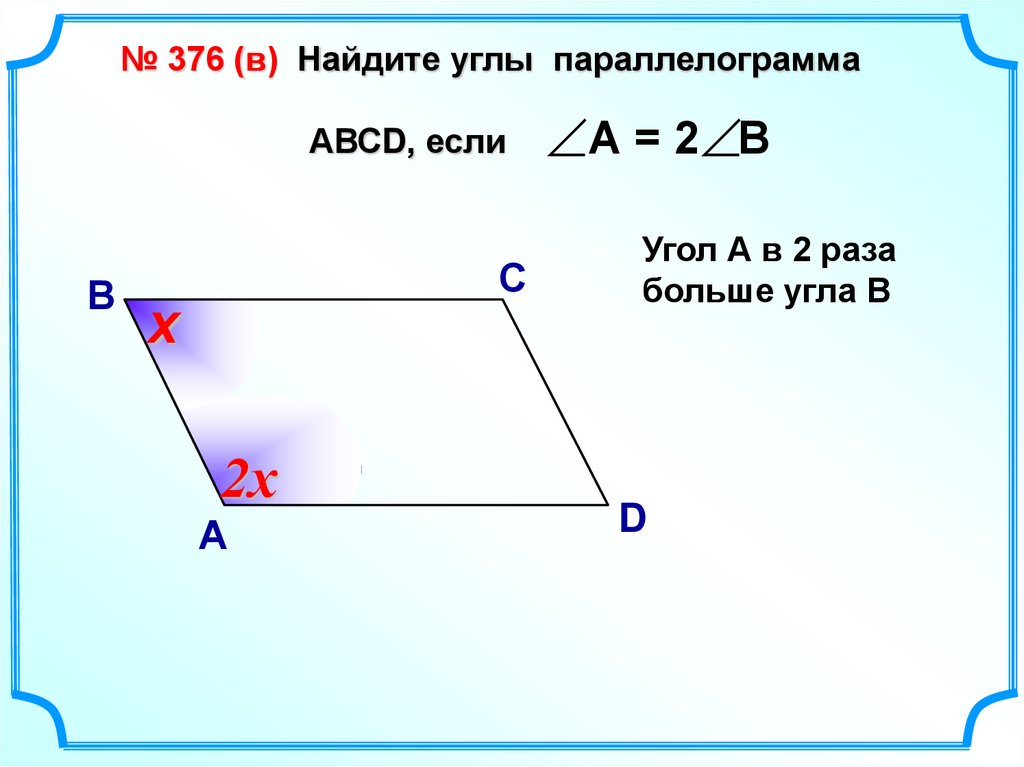
№ 376 (в) Найдите углы параллелограммаАВСD, если
В
С
х
2х
А
А = 2 В
Угол А в 2 раза
больше угла В
D
13.
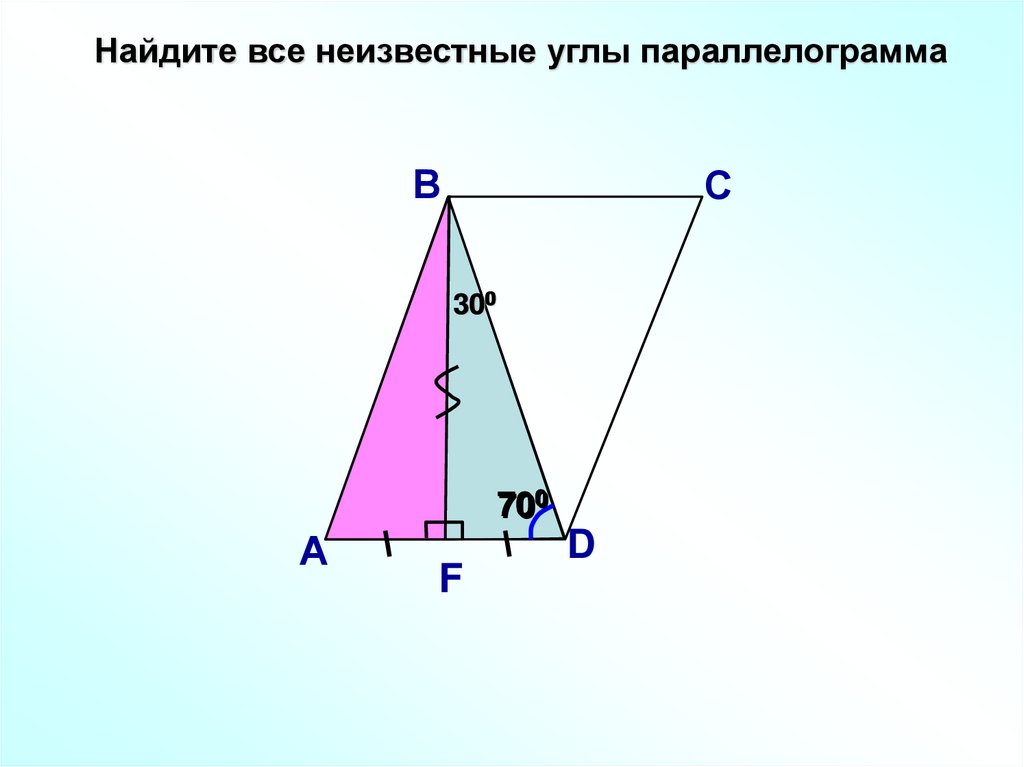
Найдите все неизвестные углы параллелограммаВ
С
300
700
А
F
D
14.
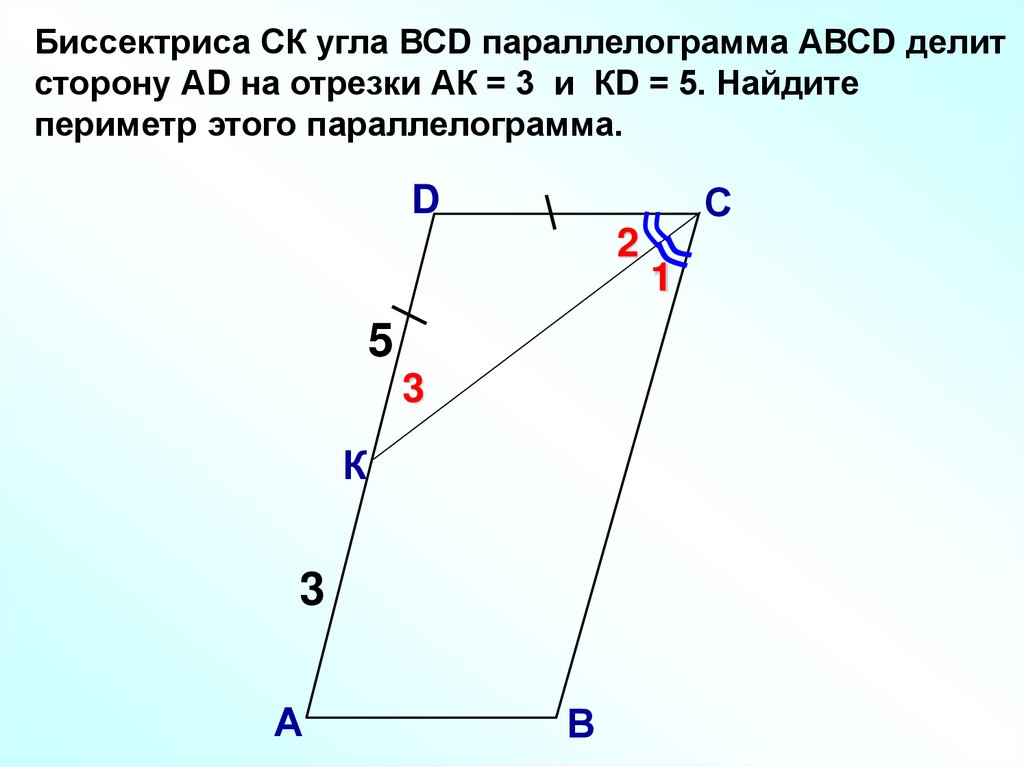
Биссектриса СК угла ВСD параллелограмма АВСD делитсторону АD на отрезки АК = 3 и КD = 5. Найдите
периметр этого параллелограмма.
С
D
2
5
3
К
3
А
В
1
15.
Дано: ABCDчетырехугольник
С
АВС = СDA
В
Доказать: АВСD –
параллелограмм.
А
D
Выполните доказательство разными способами
По признаку 10
По признаку 20
По определению параллелограмма
16.
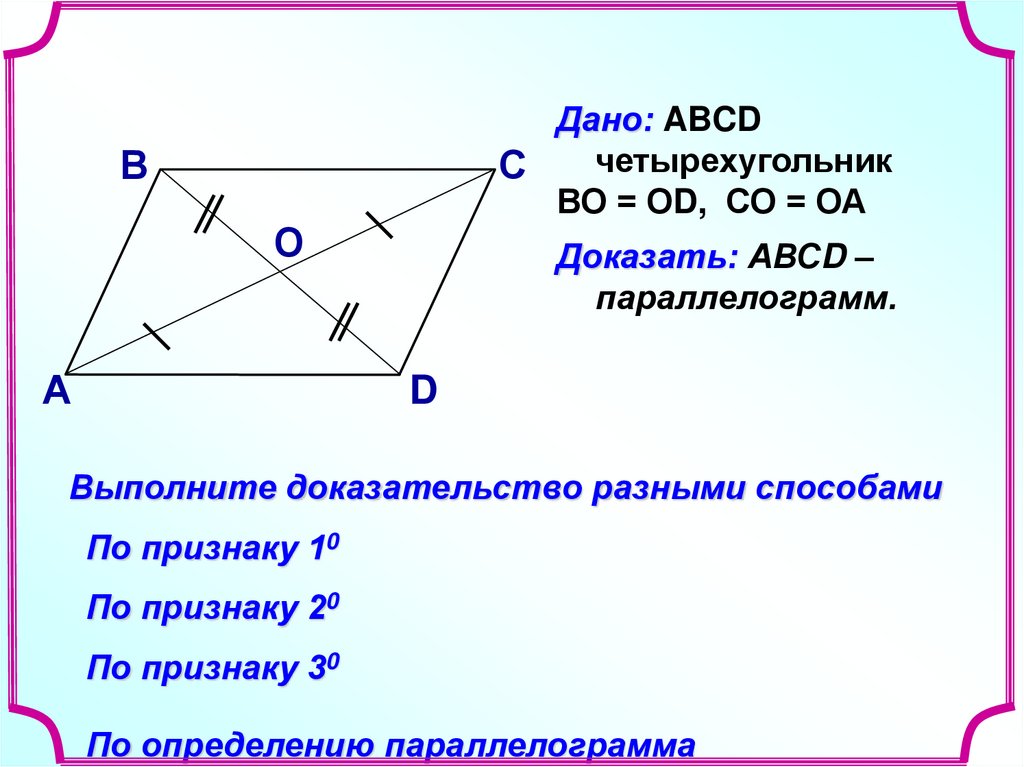
Дано: ABCDчетырехугольник
С
ВО = ОD, СО = ОА
В
О
А
Доказать: АВСD –
параллелограмм.
D
Выполните доказательство разными способами
По признаку 10
По признаку 20
По признаку 30
По определению параллелограмма
17.
№ 383Дано: ABCD параллелограмм, BD – диагональ, BP=QD.
Доказать, что АPCQ – параллелограмм.
В
С
Р
О
Q
А
D




 Математика
Математика








