Решение задач на параллельность прямых и плоскостей

1. Решение задач по теме «Параллельность прямых и плоскостей. Взаимное расположение прямых в пространстве».

2.

• 1) Дано: точки А,В,С,Д не принадлежат
одной плоскости.
• Доказать: любые три точки являются
• вершинами треугольника.

3. Метод от противного

Предположим, что
три точки А, В и С не являются
вершинами треугольника,
А В
т.е. лежат на одной прямой
a
С
Д
Тогда существует пл ( а, Д ) . И все
четыре точки принадлежат одной
плоскости. Это противоречит условию.
Следовательно, наше предположение
неверно. Любые три точки из четырех
могут являться вершинами треугольника.

4.

Дано : a | | b, c a K , c b Д .
2)
Д
К
a
с
Доказать : прямая с лежит
в одной плоскости с прямыми
b
a и b
Доказательство :
1.Существует пл. (а, b)
2. К а, а К
Д b, b Д
К , Д
3.
с ( Аксиома 2)
К с, Д с

5.

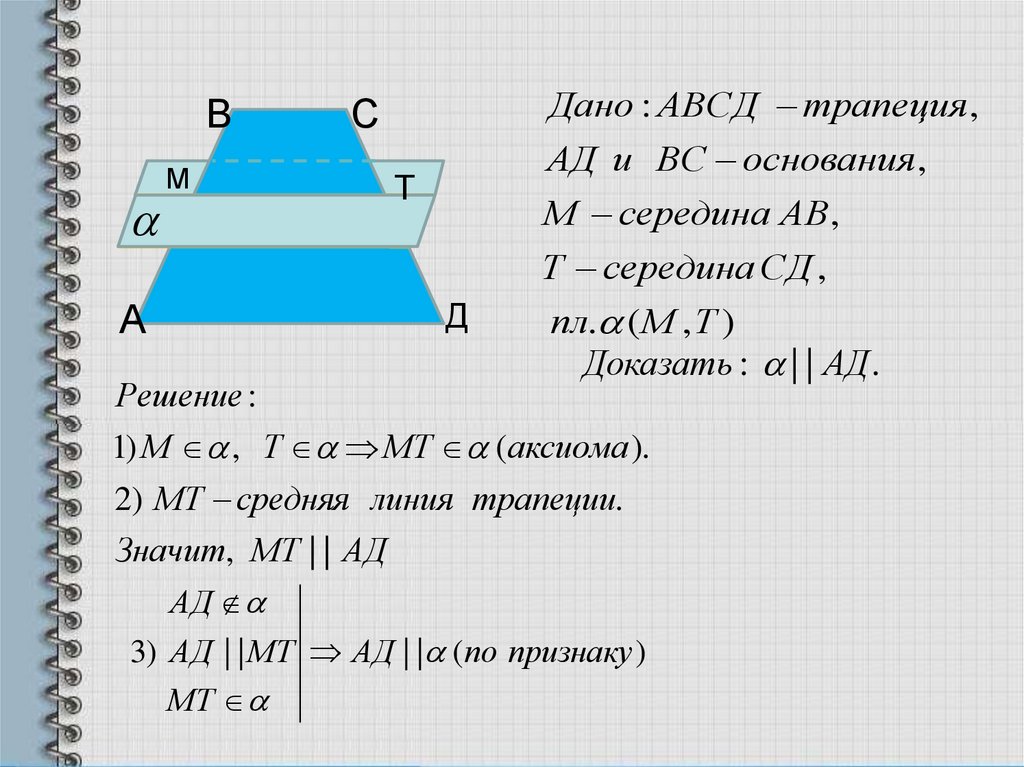
3). Дана трапеция АВСД с основаниями
АД и ВС. Через середины боковых сторон
проведена плоскость .
Докажите, что | | АД .

6.

В
М
А
Решение :
Дано : АВСД трапеция ,
С
АД и ВС основания ,
Т
М середина АВ,
Т середина СД ,
Д
пл. ( М , Т )
Доказать : | | АД .
1) М , Т МТ (аксиома ).
2) МТ средняя линия трапеции.
Значит, МТ | | АД
АД
3) АД | | МТ АД | | (по признаку )
МТ

7.

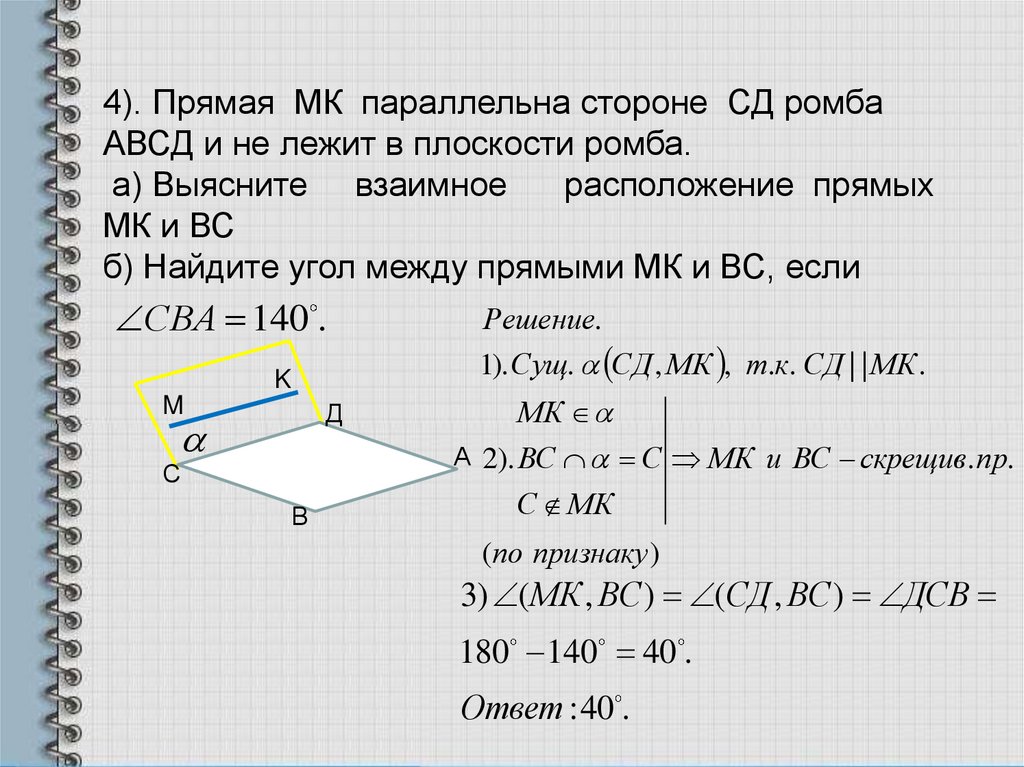
4). Прямая МК параллельна стороне СД ромба
АВСД и не лежит в плоскости ромба.
а) Выясните взаимное
расположение прямых
МК и ВС
б) Найдите угол между прямыми МК и ВС, если
СВА 140 .
K
M
Д
Решение.
1). Сущ. СД , МК , т.к. СД | | МК .
МК
А 2). ВС С МК и ВС скрещив. пр.
С
В
С МК
(по признаку )
3) ( МК , ВС ) (СД , ВС ) ДСВ
180 140 40 .
Ответ :40 .