Решение задач по теме «Параллельность прямых и плоскостей. Взаимное расположение прямых в пространстве». 10 класс

1. Решение задач по теме «Параллельность прямых и плоскостей. Взаимное расположение прямых в пространстве».

РЕШЕНИЕ ЗАДАЧ
ПО ТЕМЕ
«ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И
ПЛОСКОСТЕЙ. ВЗАИМНОЕ
РАСПОЛОЖЕНИЕ ПРЯМЫХ В
ПРОСТРАНСТВЕ».

2.

3.

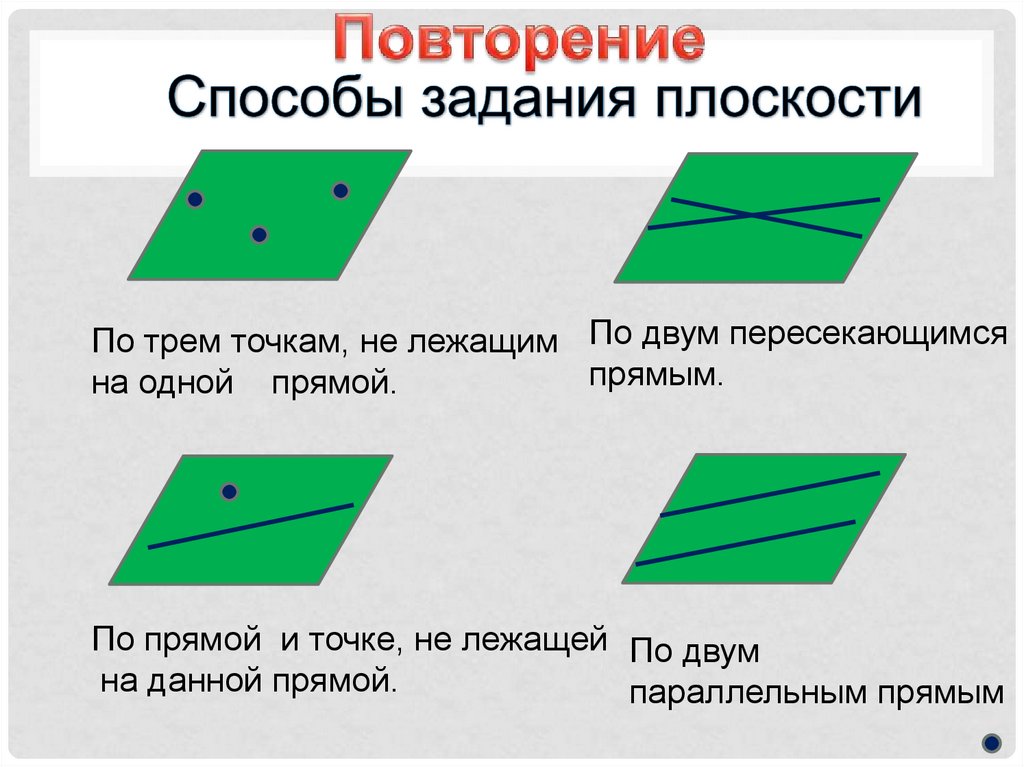
По трем точкам, не лежащим По двум пересекающимся
прямым.
на одной прямой.
По прямой и точке, не лежащей По двум
на данной прямой.
параллельным прямым

4.

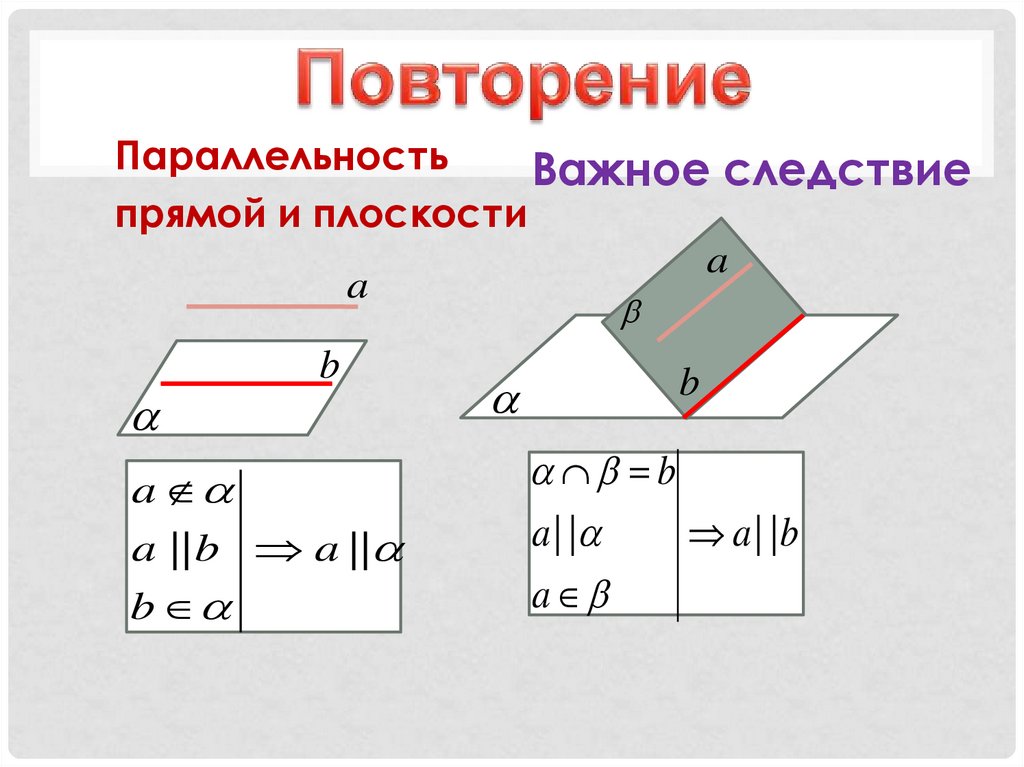
Параллельность
Важное следствие
прямой и плоскости
a
a
b
a
a | | b a | |
b
b
b
a | |
a | |b
a

5.

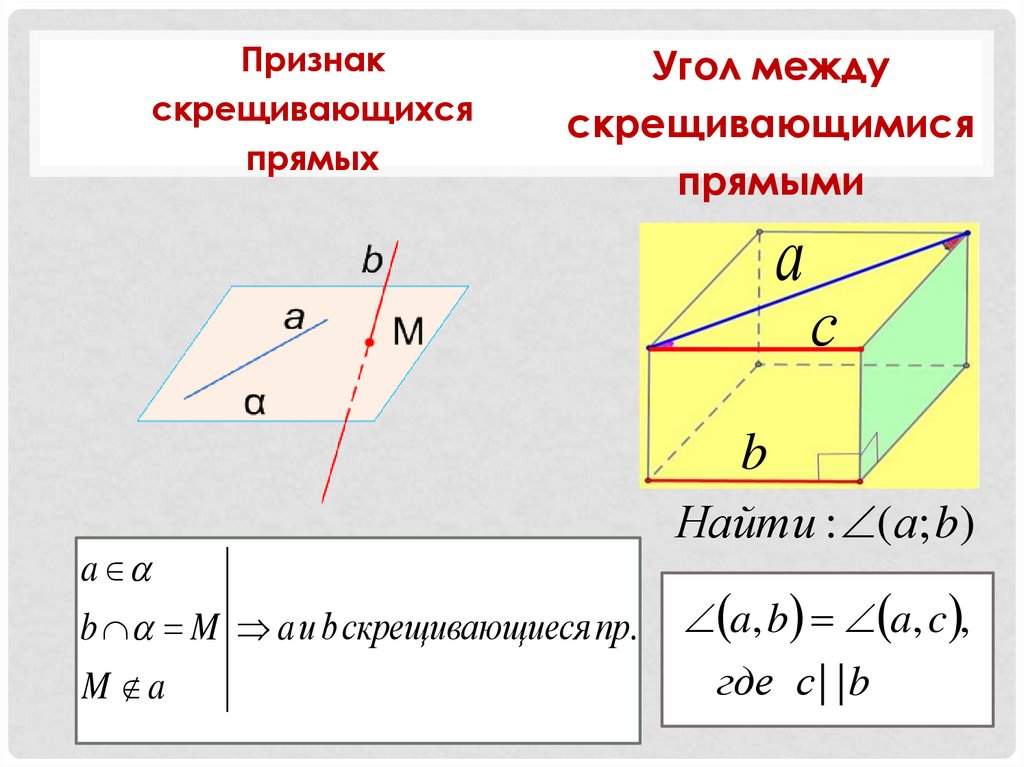
Признак
скрещивающихся
прямых
Угол между
скрещивающимися
прямыми
а
с
b
a
b M a и b скрещивающиеся пр.
M a
Найти : (а; b)
a, b a, c ,
где с | | b

6.

• 1) Дано: точки А,В,С,Д не принадлежат одной
плоскости.
• Доказать: любые три точки являются
• вершинами треугольника.
Треугольником называется фигура,
образованная тремя точками,
не лежащими на одной прямой и
соединенными отрезками.

7. Метод от противного

МЕТОД ОТ ПРОТИВНОГО
Предположим, что
три точки А, В и С не являются
вершинами треугольника,
А В
т.е. лежат на одной прямой
a
С
Д
Тогда существует пл ( а, Д ) . И все
четыре точки принадлежат одной
плоскости. Это противоречит условию.
Следовательно, наше предположение
неверно. Любые три точки из четырех
могут являться вершинами треугольника.

8. Устная работа

2)
Д
К
a
b
Дано : a | | b, c a K , c b Д .
с Доказать : прямая с лежит
в одной плоскости с прямыми
a и b
Доказательство :
1.Существует пл. (а, b)
2. К а, а К
Д b, b Д
К , Д
3.
с ( Аксиома 2)
К с, Д с

9. Устная работа

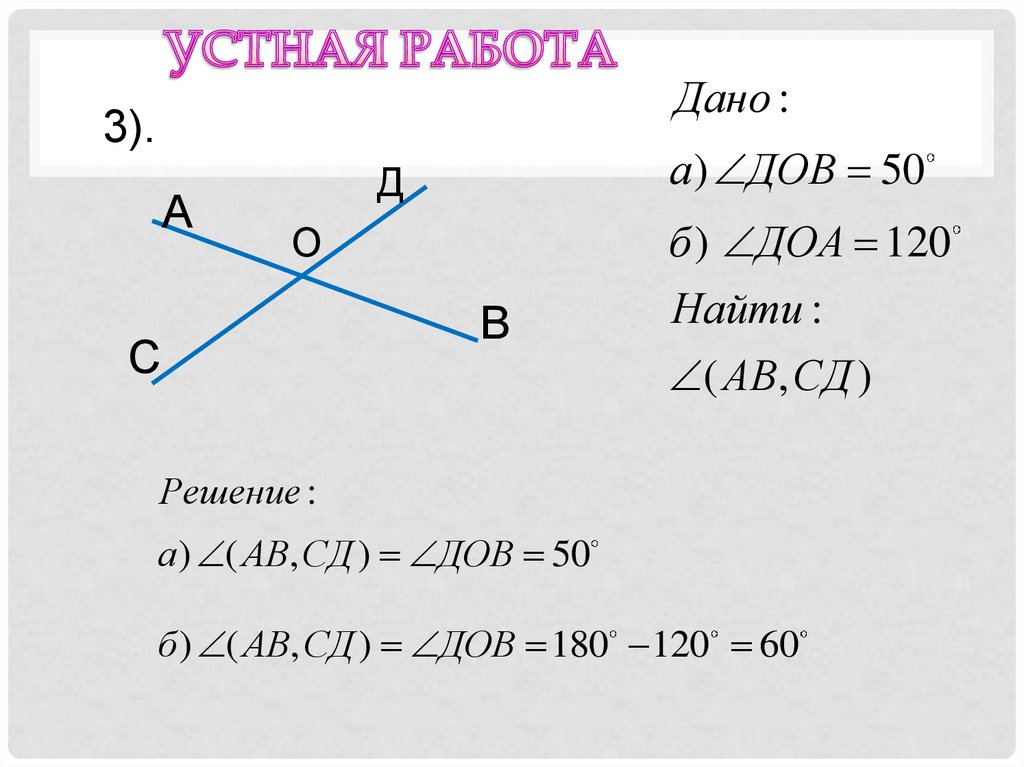
Дано :
3).
А
а ) ДОВ 50
Д
О
С
В
б ) ДОА 120
Найти :
( АВ, СД )
Решение :
а) ( АВ, СД ) ДОВ 50
б ) ( АВ, СД ) ДОВ 180 120 60

10.

Дана трапеция АВСД с основаниями АД и
ВС. Через середины боковых сторон
проведена плоскость .
Докажите, что | | АД .

11. Проверьте свое решение.

ПРОВЕРЬТЕ СВОЕ РЕШЕНИЕ.
В
А
М
С
Т
Д
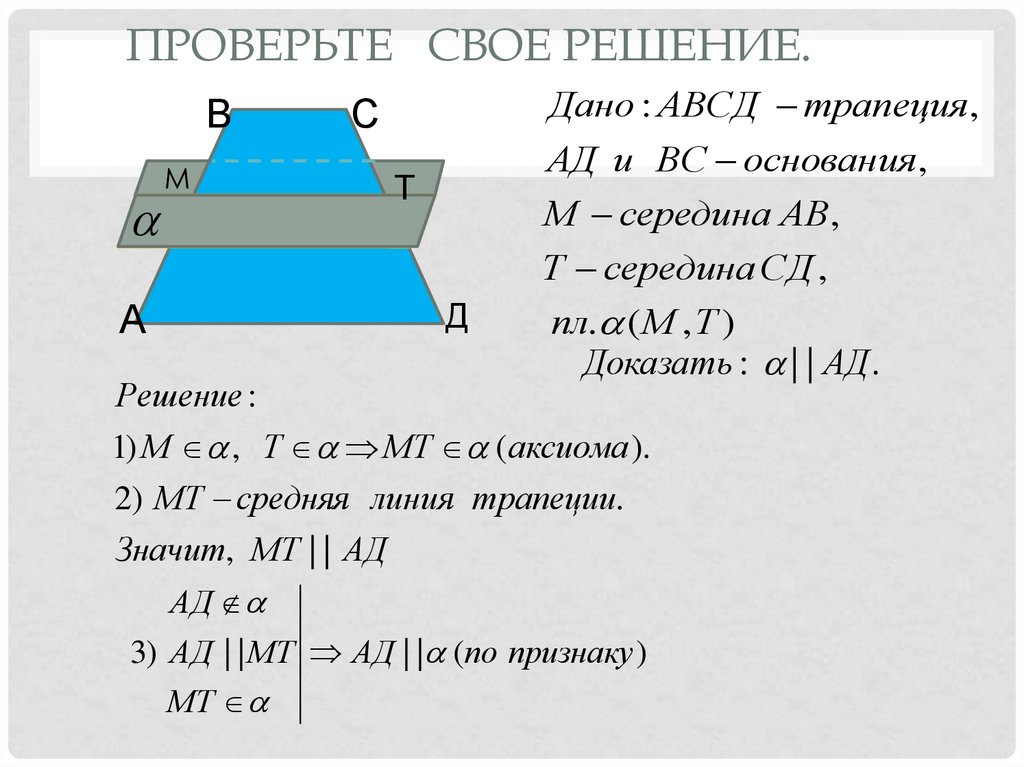
Дано : АВСД трапеция,
АД и ВС основания,
М середина АВ,
Т середина СД ,
пл. ( М , Т )
Доказать : | | АД .
Решение :
1) М , Т МТ (аксиома ).
2) МТ средняя линия трапеции.
Значит, МТ | | АД
АД
3) АД | | МТ АД | | (по признаку )
МТ

12. Задача №2

ЗАДАЧА №2 Дано : ДМС , | | МС ,
Д
ДМ К , ДС О,
1
К
М
О
2
ДК 1
, КО 4 см
ДМ 3
Выполните рисунок к
Найти : задаче.МС
Длину какого
С
отрезка можно найти
Решение.
ДМС КО
1) МС | |
КО | | МС (следствие)
МС ДМС
2) КДО~ МДС , т.к.
1 2 (соответственные углы при КО | | МС ),
ДК 1
Д общий; k
ДМ 3
3) МС 4 3 12 см
Ответ : МС 12 см.

13.

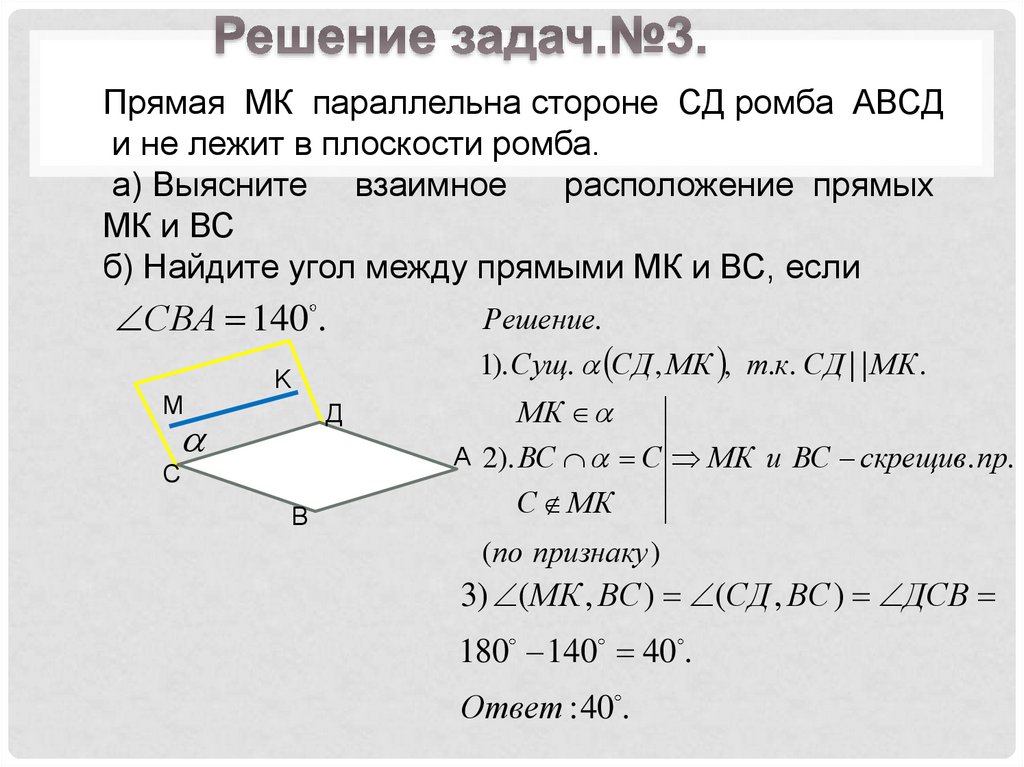
Прямая МК параллельна стороне СД ромба АВСД
и не лежит в плоскости ромба.
а) Выясните взаимное
расположение прямых
МК и ВС
б) Найдите угол между прямыми МК и ВС, если
СВА 140 .
K
M
Д
С
В
Решение.
1). Сущ. СД , МК , т.к. СД | | МК .
МК
А 2). ВС С МК и ВС скрещив. пр.
С МК
(по признаку )
3) ( МК , ВС ) (СД , ВС ) ДСВ
180 140 40 .
Ответ :40 .

14.

Аксиомы и следствия
Определения
Признаки
Параллельности прямой и
плоскости
Скрещивающихся прямых
Важное следствие 1

15.

1) Кто испытывает трудности - поднимет учебник.
2) Кто усвоил практически всё, но есть задания,
где помощь необходима – поднимет тетрадь.
3) Кто хорошо усвоил тему и может применять
полученные знания на практике - поднимет руку,
показывая «пять».

16.

• Повторить п.1 – 9.
• Решить №Повторить №11,23,26.