Линейная функция y=kx и ее график

1. ЛИНЕЙНАЯ ФУНКЦИЯ y=kx И ЕЕ ГРАФИК.

2.

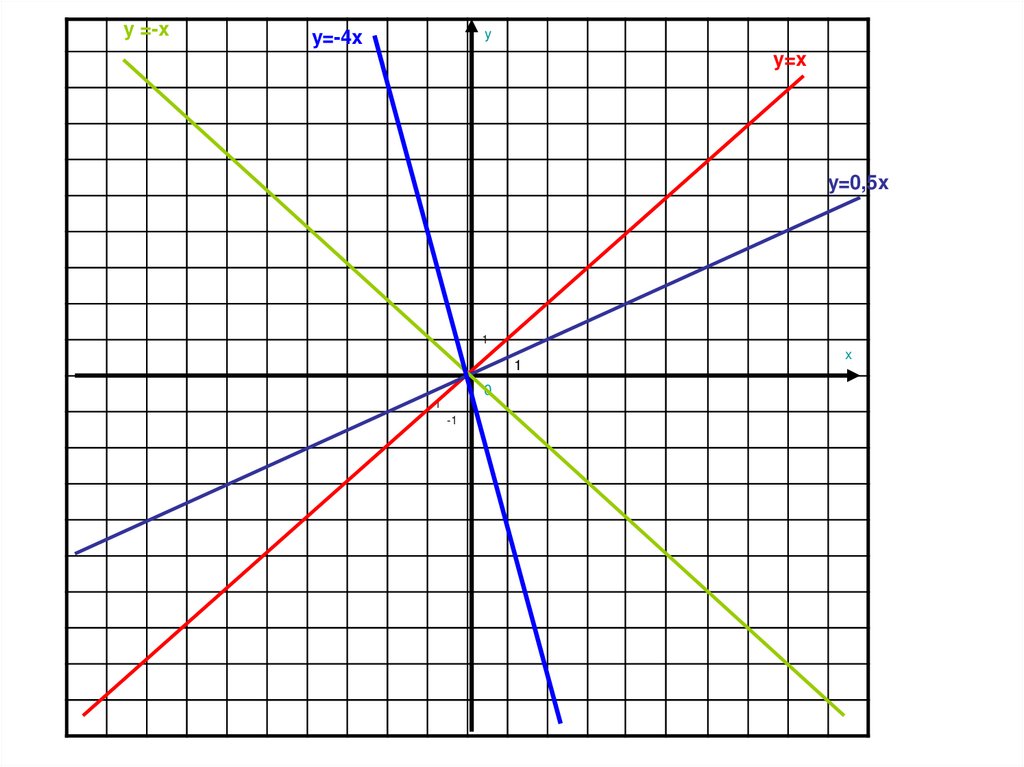
На координатной плоскости построить
графики линейных функций:
х02
y=x, у 0 2
y=0,5x;
y=-x;
y=-4x
х02
у 01
х02
у 0 -2
х02
у 0 -8

3.

y =-x
y
y=-4x
y=x
y=0,5x
1
1
0
-1
-1
x

4.

Определите, что общего в данных
графиках?
Чем отличаются графики данных
линейных функций?

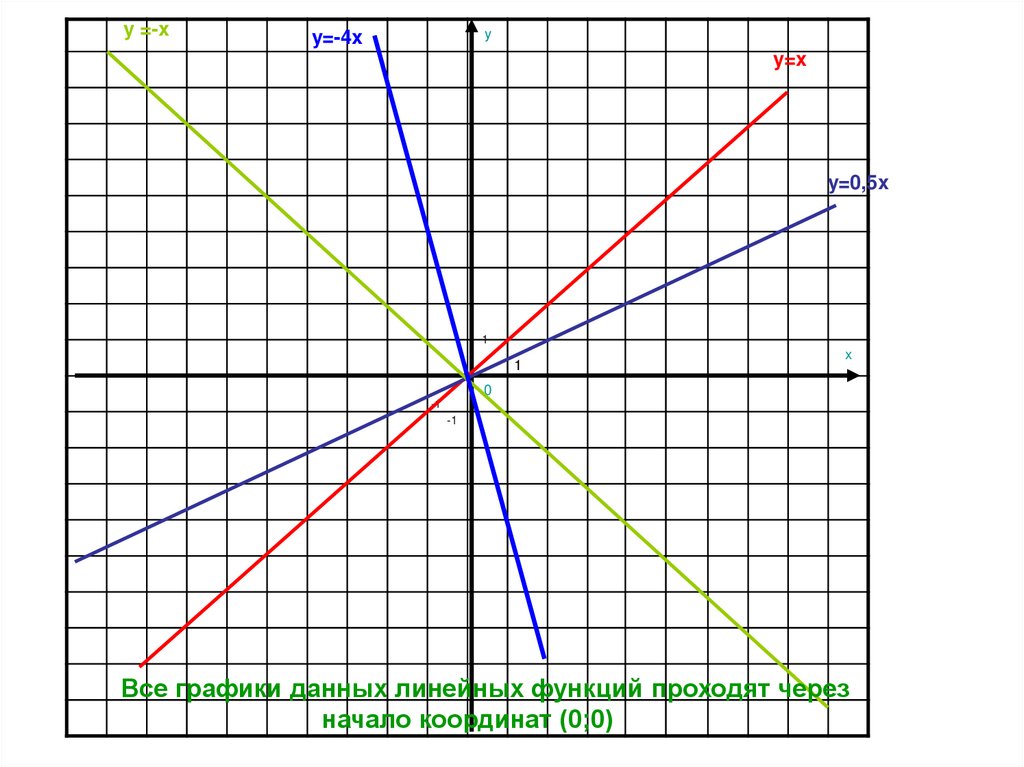
5.

y =-x
y
y=-4x
y=x
y=0,5x
1
1
x
0
-1
-1
Все графики данных линейных функций проходят через
начало координат (0;0)

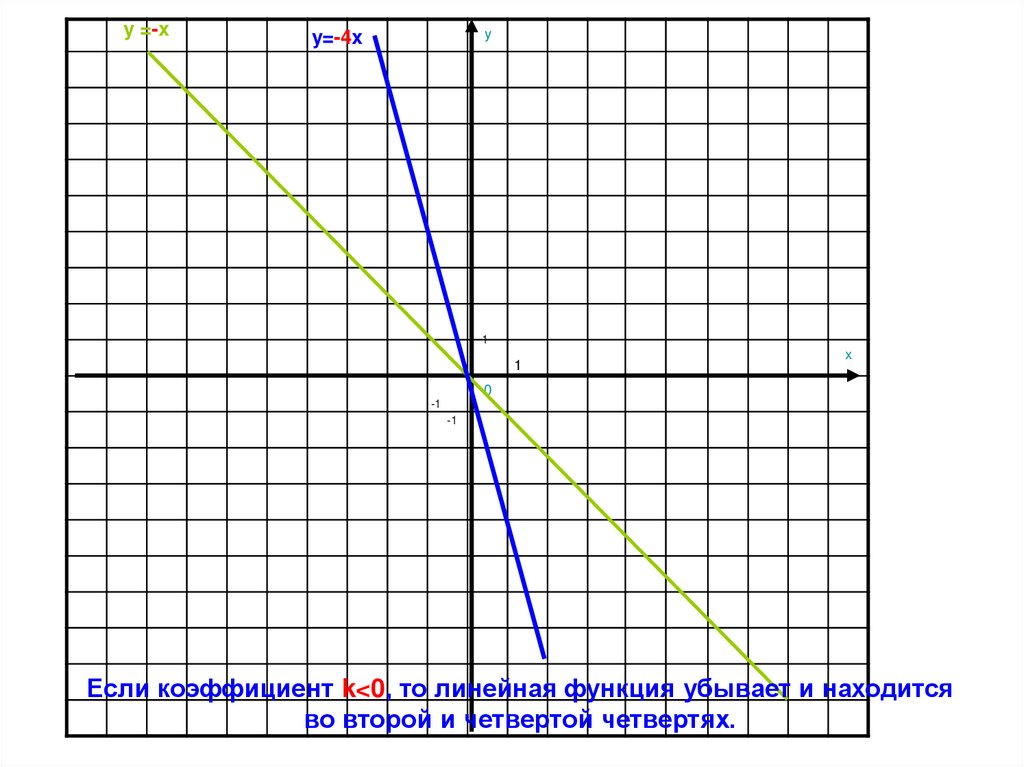
6.

y =-x
y
y=-4x
1
1
x
0
-1
-1
Если коэффициент k<0, то линейная функция убывает и находится
во второй и четвертой четвертях.

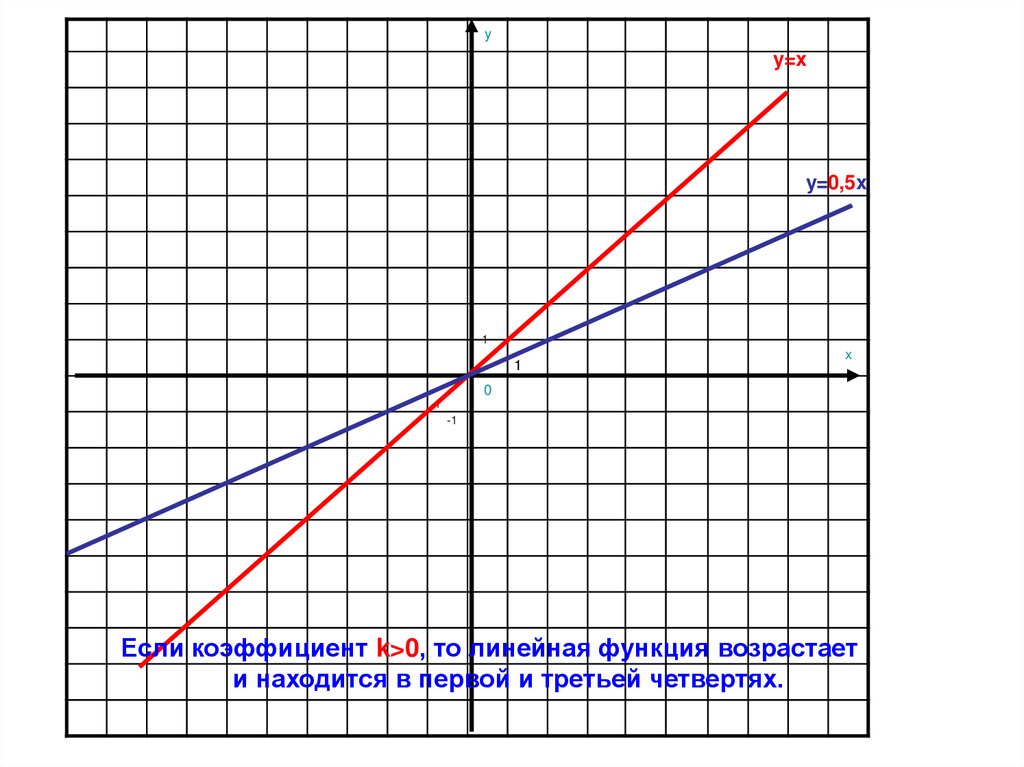
7.

y
y=x
y=0,5x
1
1
x
0
-1
-1
Если коэффициент k>0, то линейная функция возрастает
и находится в первой и третьей четвертях.

8. Задача Постройте график линейной функции: а) y=2x, б) y=-3x. На одной координатной плоскости. Что вы можете сказать про графики

данных линейных функций?

9. Решение.

Находим координаты точек для
линейной функции y=2x:
y=2·0=0; О(0;0)
y=2·3=6; А(3;6).
Переносим точки на координатную
плоскость.
• Строим график данной линейной
функции и, обязательно, его
подписываем.
X 0 3
y 0 6

10.

y
y=2x
А
6
1
x
1
0
-1
-1
3

11. Решение.

• Находим координаты точек для
линейной функции y=-3x:
y=-3·0=0; О(0;0)
y=-3· (-3)=9; В(-3;9).
• Переносим точки на координатную
плоскость. Строим график данной
линейной функции и, обязательно,
его подписываем.
X 0 -3
y 0 9

12.

y
В
y=2x
9
А
6
1
x
1
-3
0
-1
3
-1
y=-3x

13. Задача

Постройте график линейной функции
y=0,4x. Найдите по графику:
а) значение y, соответствующее
значению x, равному 0;5;-10;-5;
б) значение x, соответствующее
значению y, равному 0;2;4;-2;
в) решение неравенства: 0,4x>0;
г) решение неравенства: -2≤у≤0

14. Вопросы:

1. Что вы можете сказать про график
данной линейной функции: y=0,4x?
2. Какую абсциссу лучше взять, чтобы
координаты точек были целыми
числами?
3. Для чего, координаты точек должны
являться целыми числами?
4. Что значит: 0,4x>0?

15. Решение:

1. Находим координаты точек для
линейной функции y=0,4x:
y=0,4·0=0; О(0;0)
y=0,4·5=2; А(5;2).
• Переносим точки на координатную
плоскость. Строим график данной
линейной функции и, обязательно, его
подписываем.
x 0 5
y 0 2

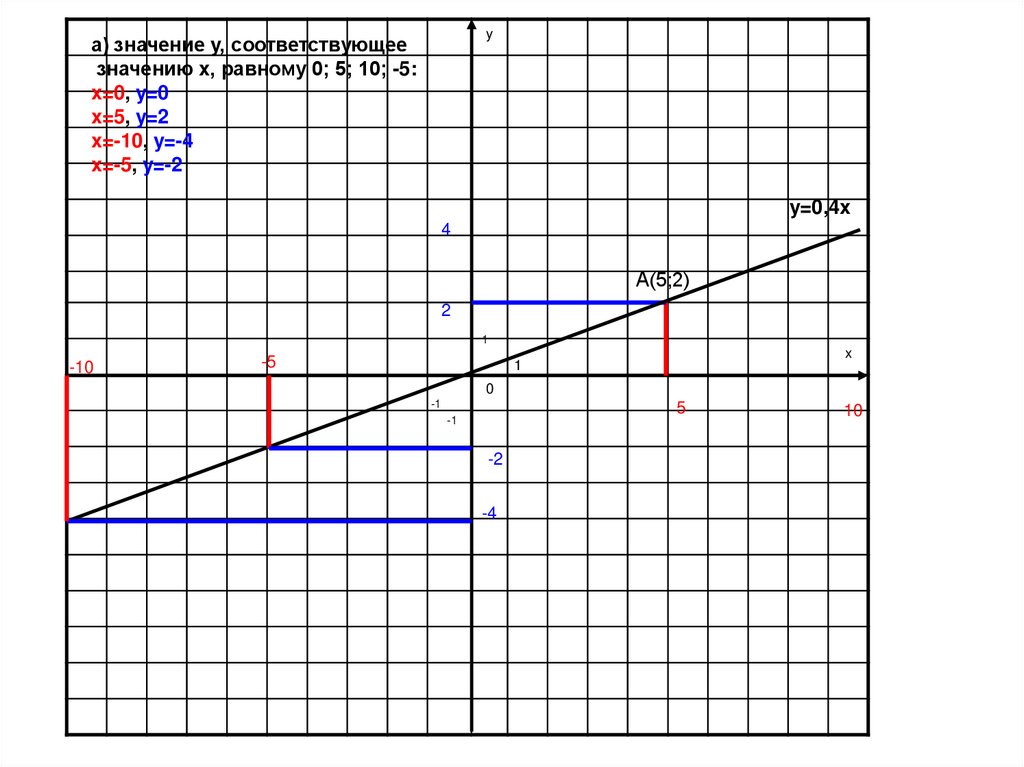
16.

y
а) значение y, соответствующее
значению x, равному 0; 5; 10; -5:
x=0, y=0
x=5, y=2
x=-10, y=-4
x=-5, y=-2
y=0,4x
4
А(5;2)
2
1
-10
-5
x
1
0
-1
5
-1
-2
-4
10

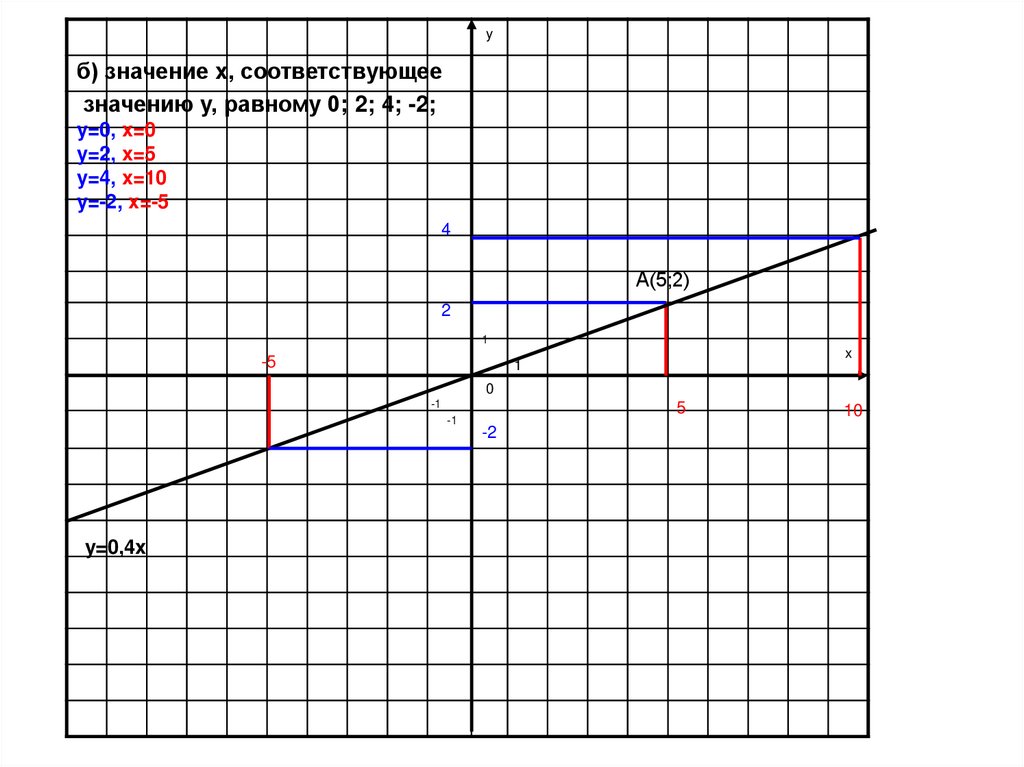
17.

y
б) значение x, соответствующее
значению y, равному 0; 2; 4; -2;
y=0, x=0
y=2, x=5
y=4, x=10
y=-2, x=-5
4
А(5;2)
2
1
-5
x
1
0
-1
-1
y=0,4x
5
-2
10

18.

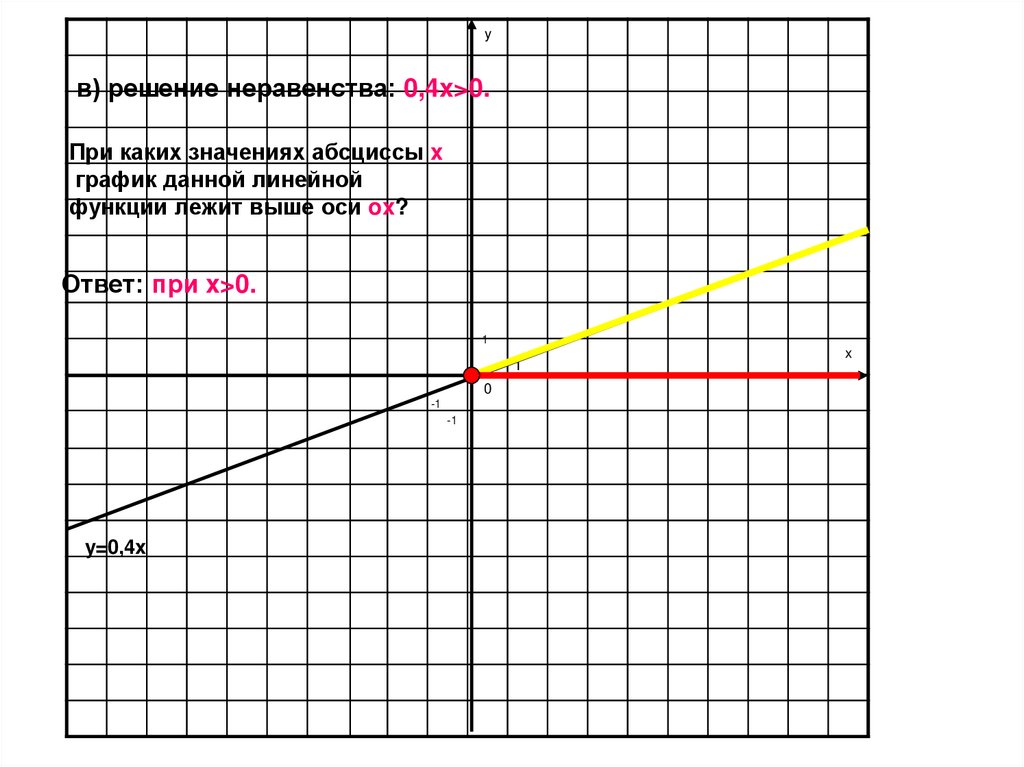
y
в) решение неравенства: 0,4x>0.
При каких значениях абсциссы x
график данной линейной
функции лежит выше оси ox?
Ответ: при x>0.
1
1
0
-1
-1
y=0,4x
x

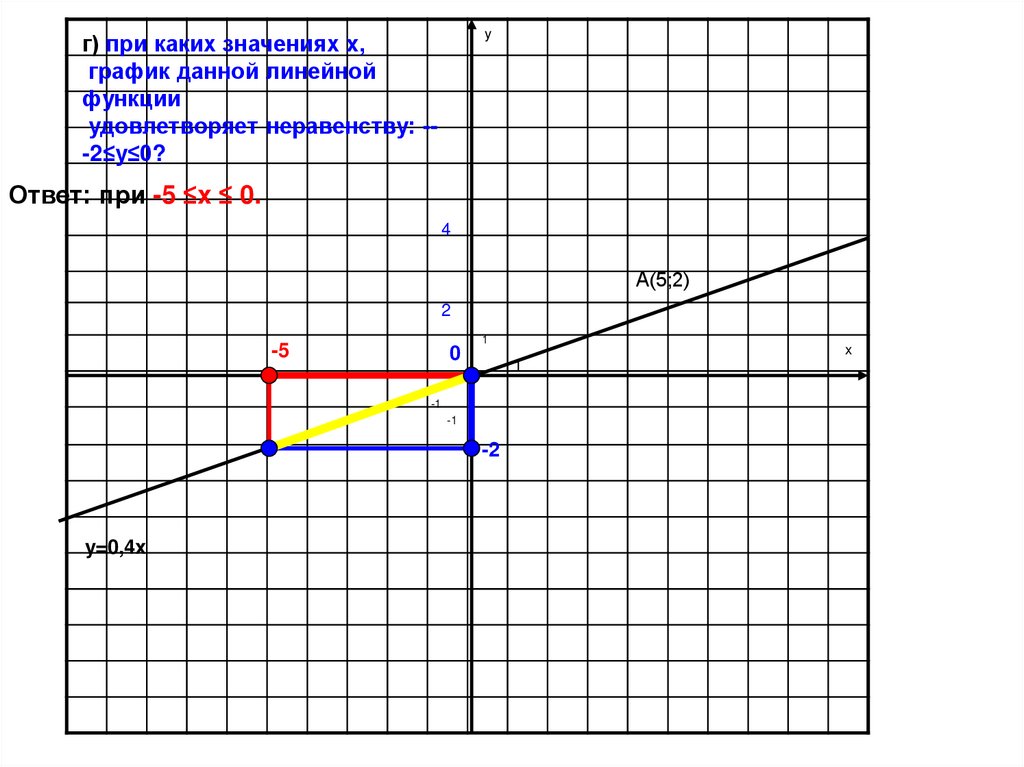
19.

y
г) при каких значениях x,
график данной линейной
функции
удовлетворяет неравенству: --2≤y≤0?
Ответ: при -5 ≤x ≤ 0.
4
А(5;2)
2
-5
0
1
-1
-1
-2
y=0,4x
x
1

20. Алгоритм нахождения значений абсциссы, по графику линейной функции, удовлетворяющих неравенству -2≤y≤0 :

1.Отметим на оси oy точки y=-2 и y=0.
2. Получим отрезок прямой, который лежит в
пределах значений -2 ≤ y ≤ 0 :
Из ординаты, равной -2 и ординаты равной 0
опустим перпендикуляр к графику данной
линейной функции.
3. Из концов отрезка графика прямой, опустим
перпендикуляры на ось ox.
4. Получили значения абсциссы, в пределах
которой лежит график данной прямой:
-5 ≤ x ≤0. Этот промежуток и будет являться
решением данного задания .

21. Домашнее задание: № 9.9. Данное задание, аналогично только что выполненному, поэтому, если вы будете четко следовать алгоритму,

то
решите его без ошибок.