Графики функций. Линейная функция y=kx+b

1.

Муниципальное бюджетное общеобразовательное учреждение
«Лицей №8 имени Жени Попова»
Графики функций
учитель: Тлехурай Ю.В.,
учитель математики,
информатики.
Майкоп, 2021 год

2.

Линейная функция
y=kx+b
Что является графиком данной функции?

3.

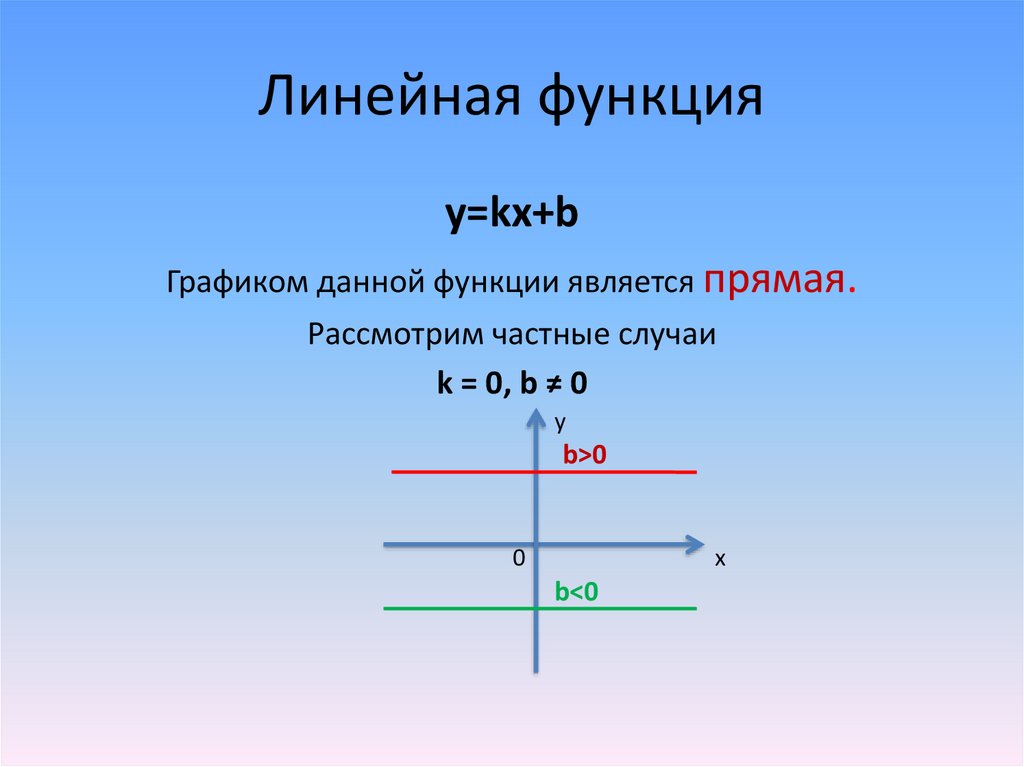
Линейная функция
y=kx+b
Графиком данной функции является прямая.
Рассмотрим частные случаи
k = 0, b ≠ 0
y
b>0
0
x
b<0

4.

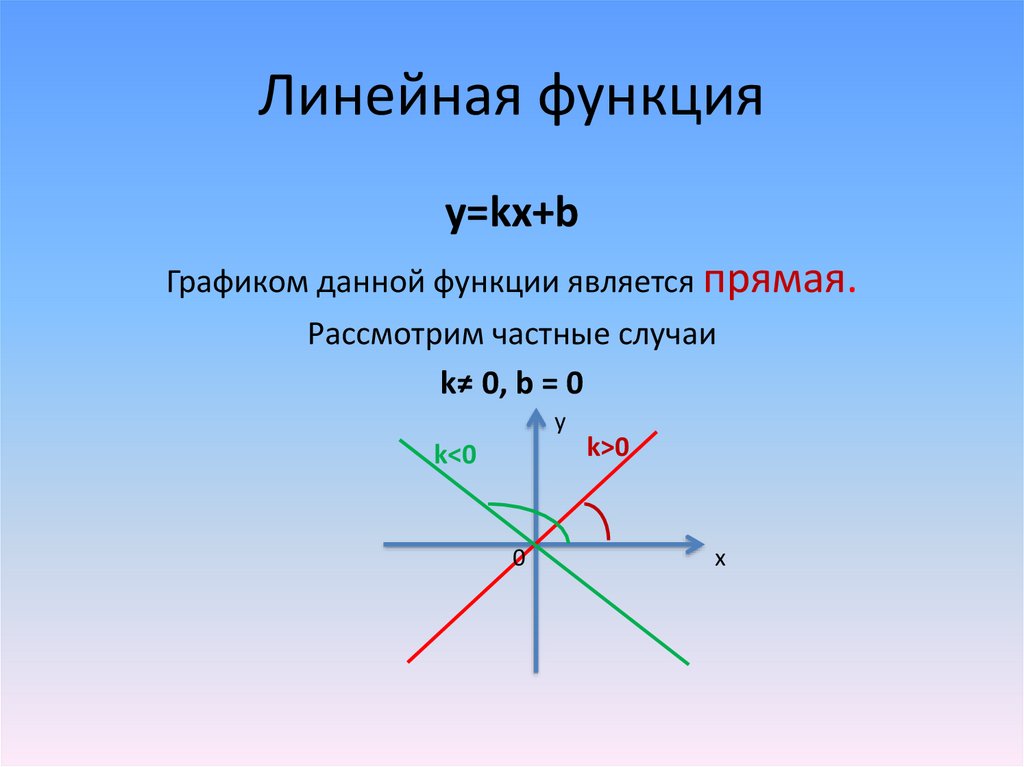
Линейная функция
y=kx+b
Графиком данной функции является прямая.
Рассмотрим частные случаи
k≠ 0, b = 0
y
k<0
0
k>0
x

5.

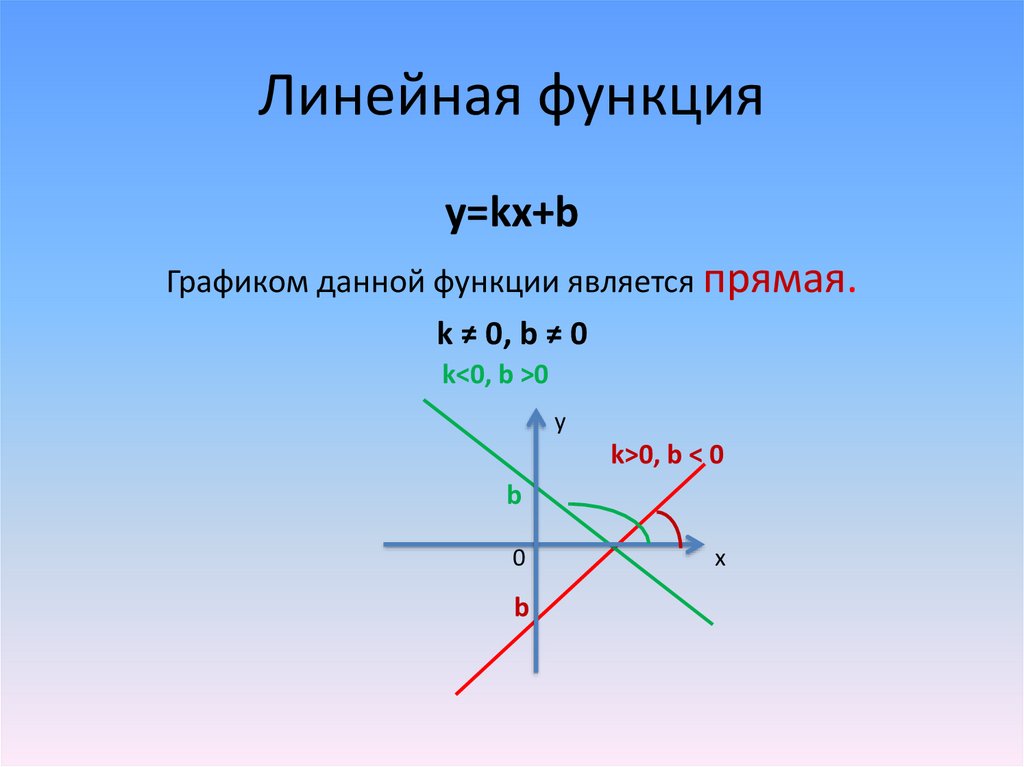
Линейная функция
y=kx+b
Графиком данной функции является прямая.
k ≠ 0, b ≠ 0
k<0, b >0
y
k>0, b < 0
b
0
b
x

6.

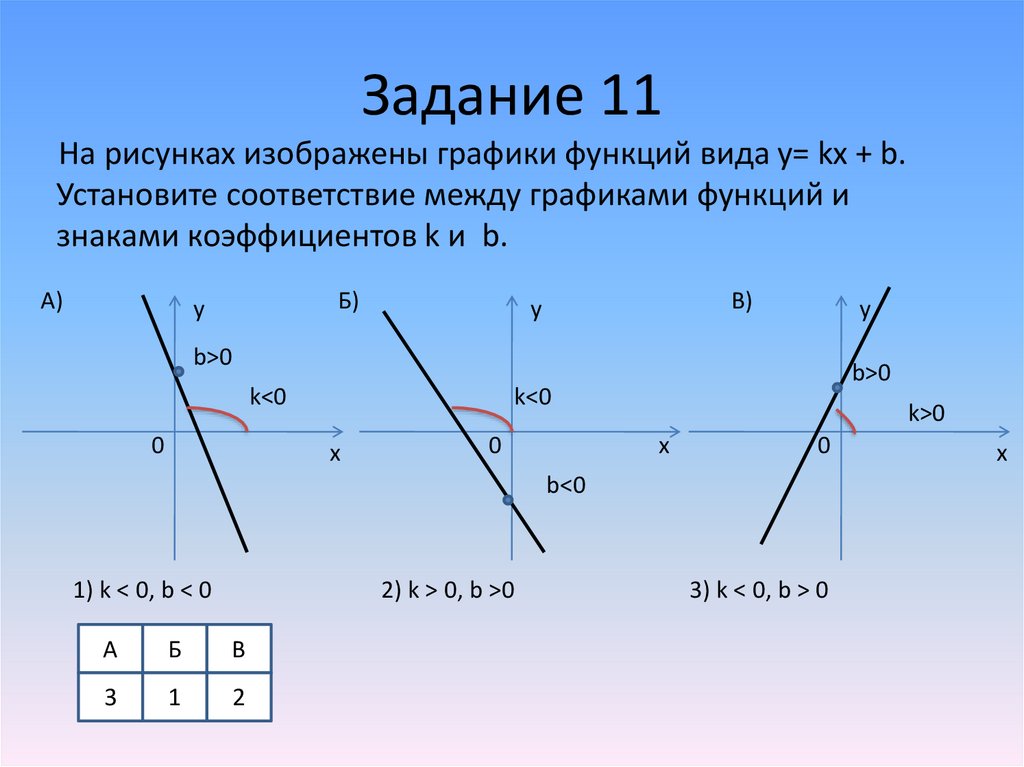
Задание 11
На рисунках изображены графики функций вида y= kx + b.
Установите соответствие между графиками функций и
знаками коэффициентов k и b.
A)
Б)
y
В)
y
y
b>0
k<0
0
b>0
k<0
x
0
k>0
x
0
b<0
1) k < 0, b < 0
2) k > 0, b >0
А
Б
В
3
1
2
3) k < 0, b > 0
x

7.

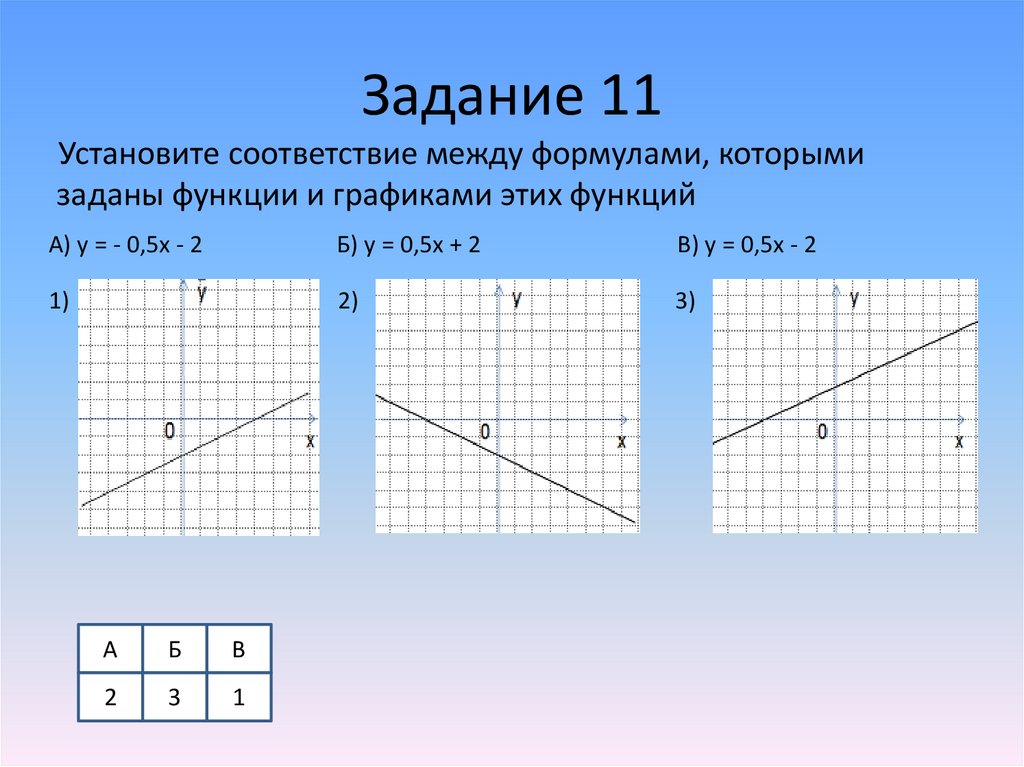
Задание 11
Установите соответствие между формулами, которыми
заданы функции и графиками этих функций
А) y = - 0,5x - 2
Б) y = 0,5x + 2
В) y = 0,5x - 2
1)
2)
3)
А
Б
В
2
3
1

8.

Квадратичная функция
y = аx² + bx + c
Что является графиком данной функции?

9.

Квадратичная функция
y = аx² + bx + c
Графиком данной функции является парабола,
ветви которой направлены вверх если а
>0и
вниз, если а < 0.
Вершина параболы
Точка (m;n)
b
m =
,
2a
Точка пересечения с осью OY
(0; c)
b 2 4ac
n=
4a

10.

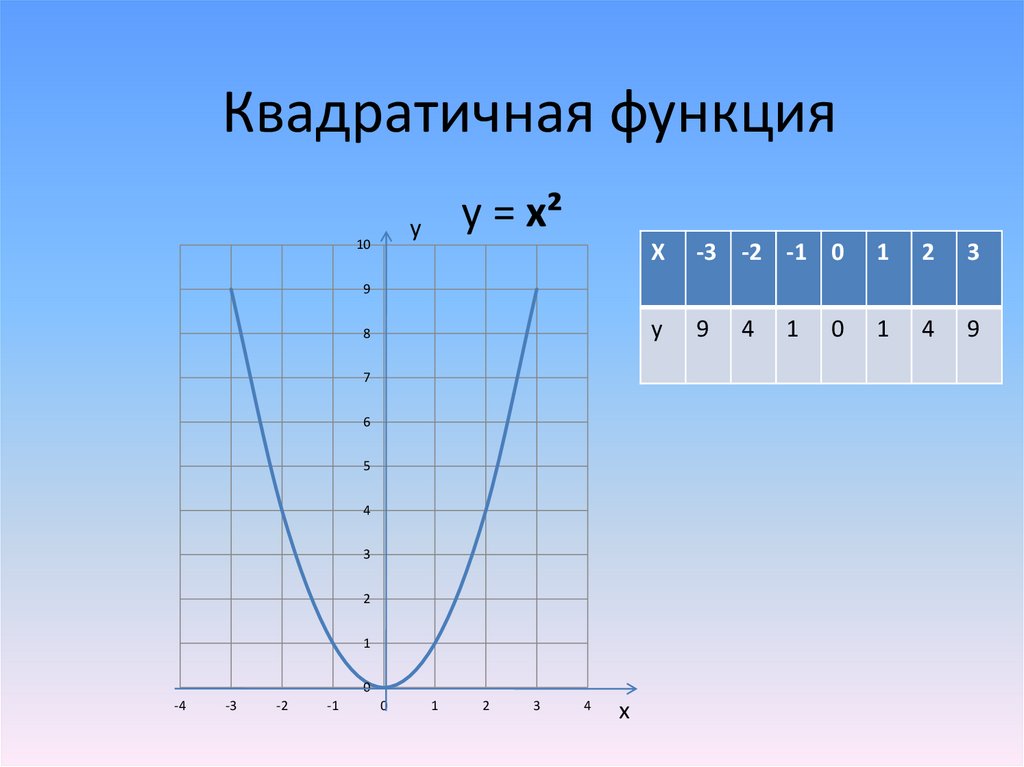
Квадратичная функция
y = x²
y
10
X
-3 -2 -1 0
1
2
3
y
9
1
4
9
9
8
7
6
5
4
3
2
1
0
-4
-3
-2
-1
0
1
2
3
4
x
4
1
0

11.

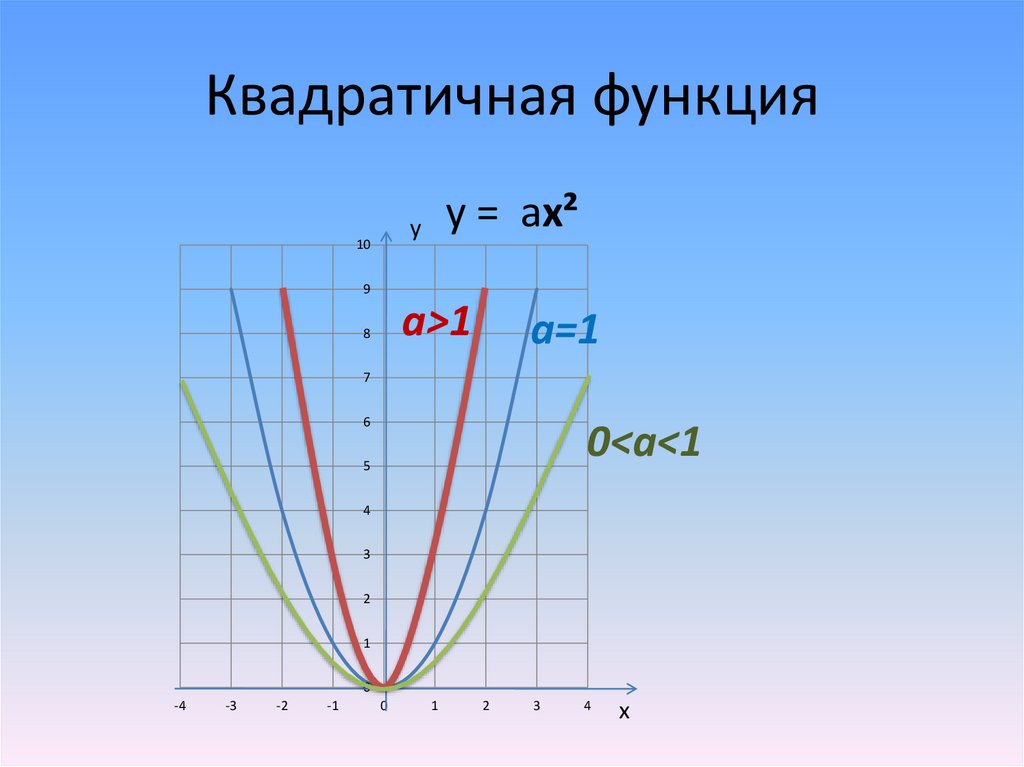
Квадратичная функция
y = ax²
y
10
9
a>1
8
a=1
7
6
0<a<1
5
4
3
2
1
0
-4
-3
-2
-1
0
1
2
3
4
x

12.

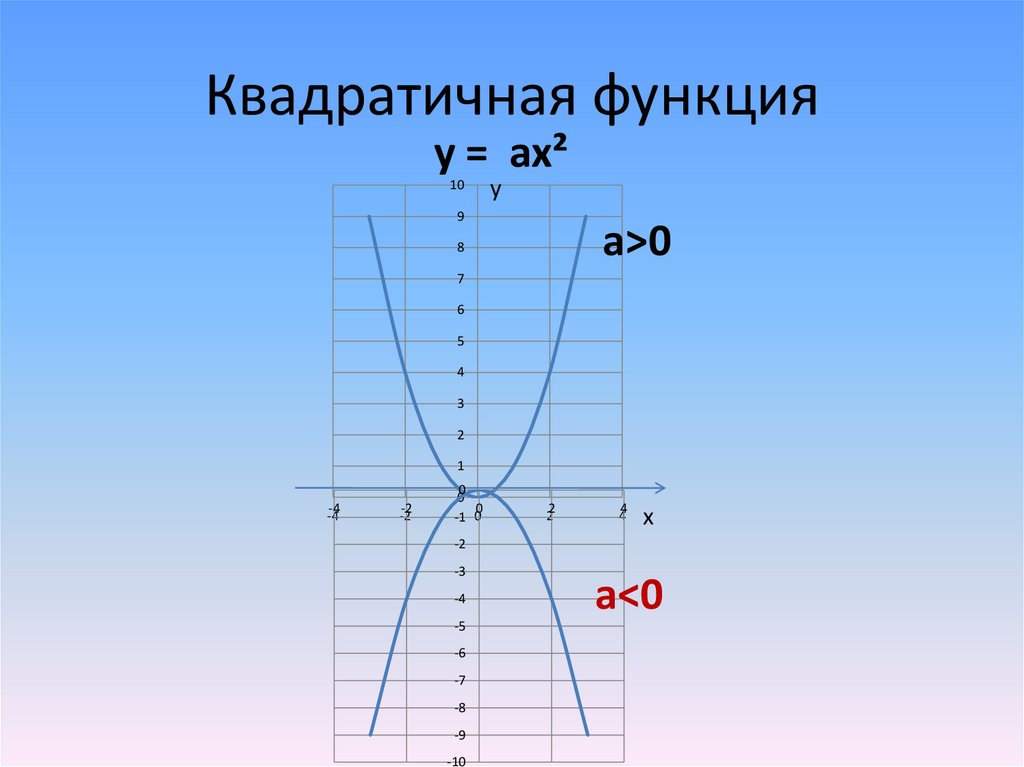
Квадратичная функция
y = ax²
10
y
9
a>0
8
7
6
5
4
3
2
1
-4
-4
-2
-2
0
0
0
-1 0
2
2
4
4
x
-2
-3
-4
-5
-6
-7
-8
-9
-10
a<0

13.

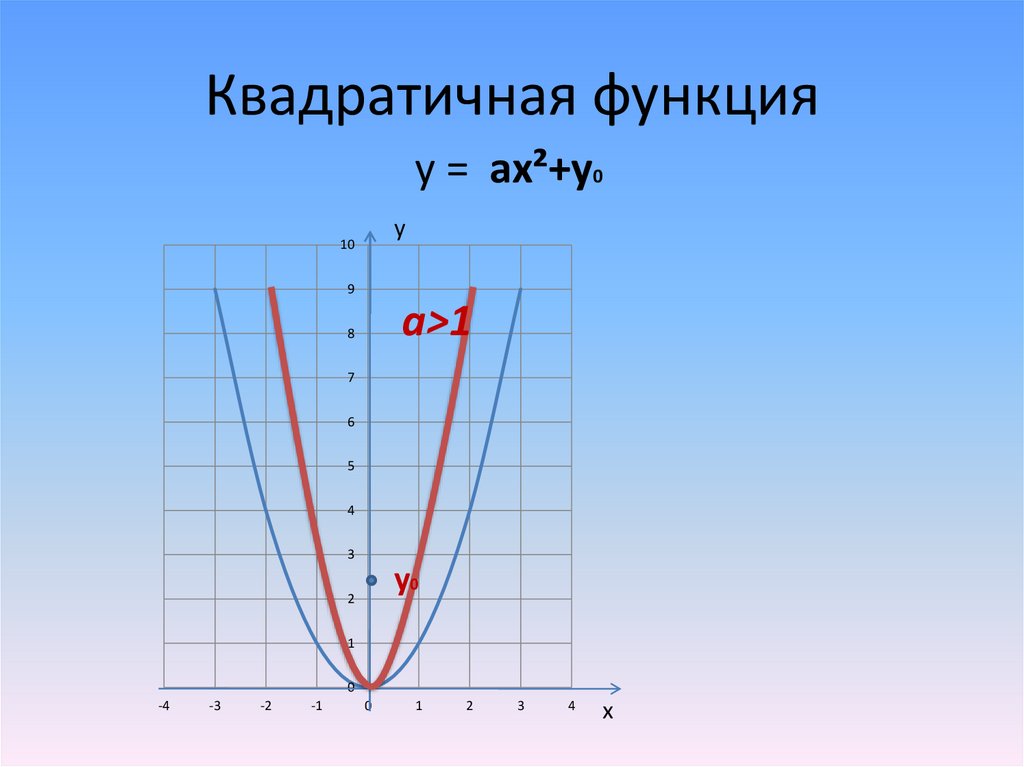
Квадратичная функция
y = ax²+y0
y
10
9
a>1
8
7
6
5
4
3
y0
2
1
0
-4
-3
-2
-1
0
1
2
3
4
x

14.

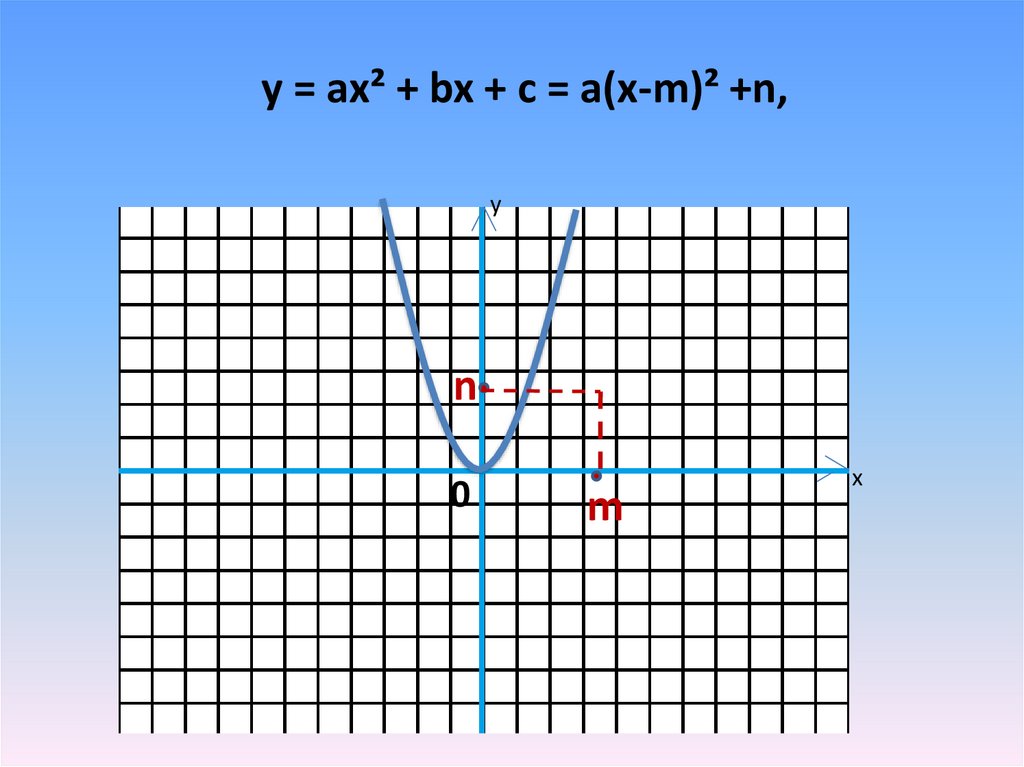
y = аx² + bx + c = a(x-m)² +n,
y
n
0
m
x

15.

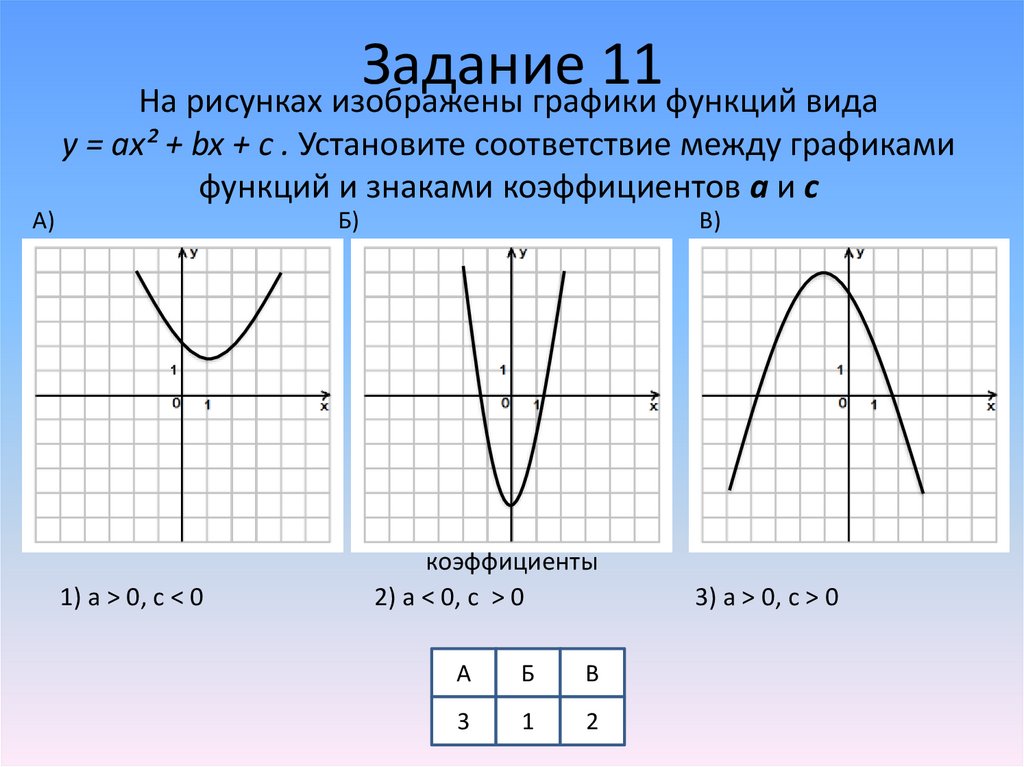
Задание
11
На рисунках изображены графики функций вида
y = аx² + bx + c . Установите соответствие между графиками
функций и знаками коэффициентов а и с
A)
Б)
1) a > 0, c < 0
В)
коэффициенты
2) a < 0, c > 0
А
Б
В
3
1
2
3) a > 0, c > 0

16.

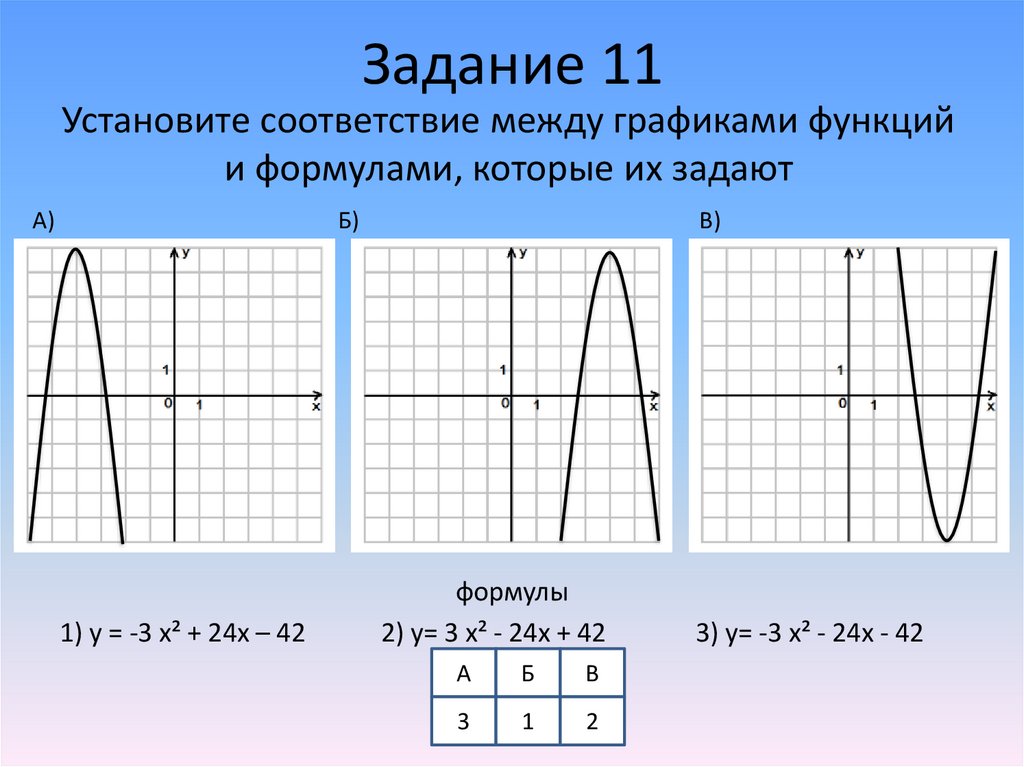
Задание 11
Установите соответствие между графиками функций
и формулами, которые их задают
A)
Б)
1) y = -3 x² + 24x – 42
В)
формулы
2) у= 3 x² - 24x + 42
А
Б
В
3
1
2
3) у= -3 x² - 24x - 42

17.

Обратная пропорциональность
k
y=
x
Что является графиком данной функции?

18.

Обратная пропорциональность
y=
k
x
, k≠0
Графиком данной функции является гипербола
Гипербола состоит из двух ветвей
Если к > 0, то ветви гиперболы расположены в 1 и 3
координатных четвертях
Если k < 0, то ветви гиперболы расположены во 2 и 4
координатных четвертях.
Точка (0;0) — центр симметрии гиперболы, оси
координат — асимптоты гиперболы.

19.

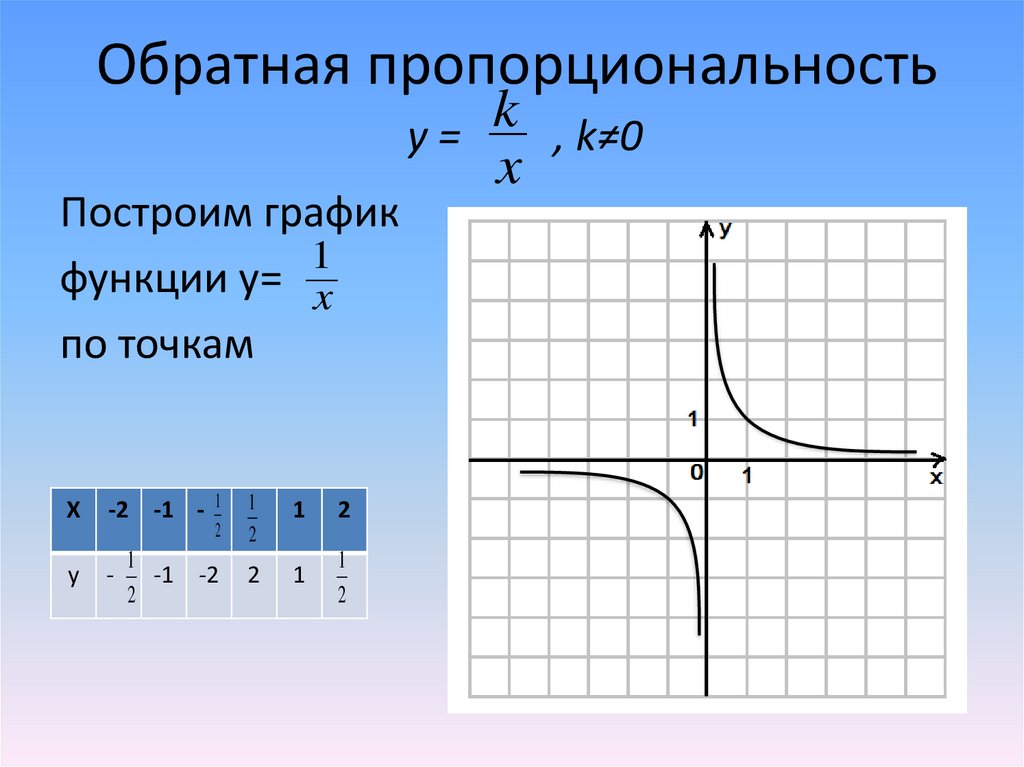
Обратная пропорциональность
Построим график
1
функции y= x
по точкам
1
2
1
2
1
2
1
-1 -2
2
2
1
1
2
X
-2 -1 -
y
-
k
y=
, k≠0
x

20.

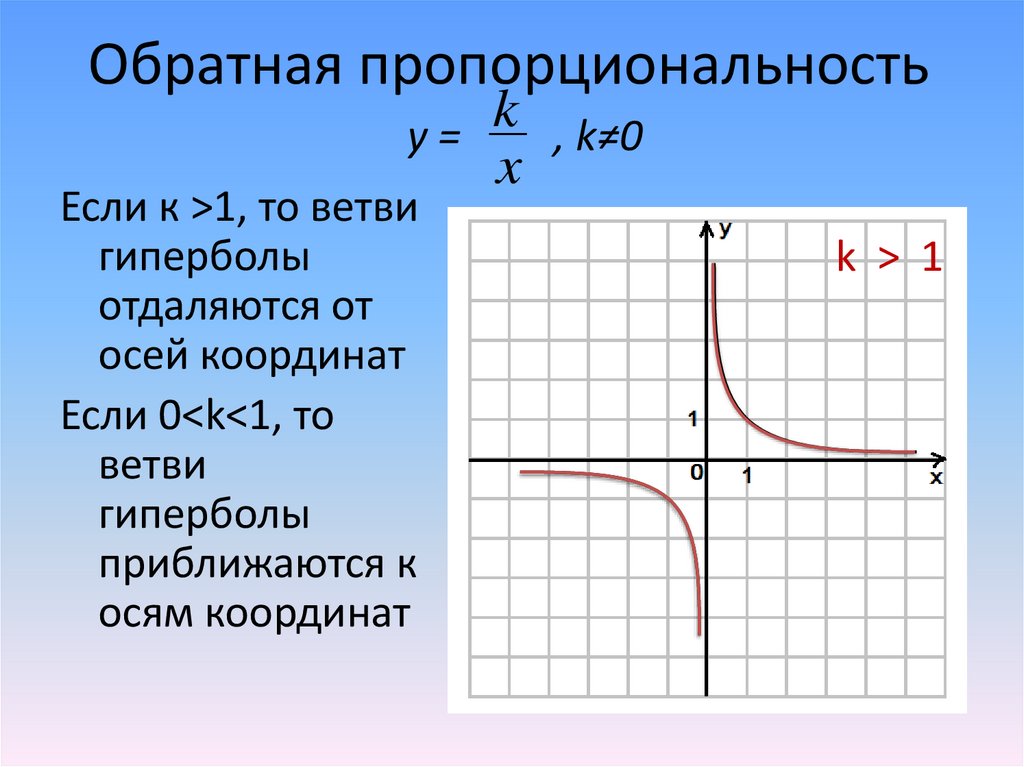
Обратная пропорциональность
k
y=
, k≠0
x
Если к >1, то ветви
гиперболы
отдаляются от
осей координат
Если 0<k<1, то
ветви
гиперболы
приближаются к
осям координат
k > 1

21.

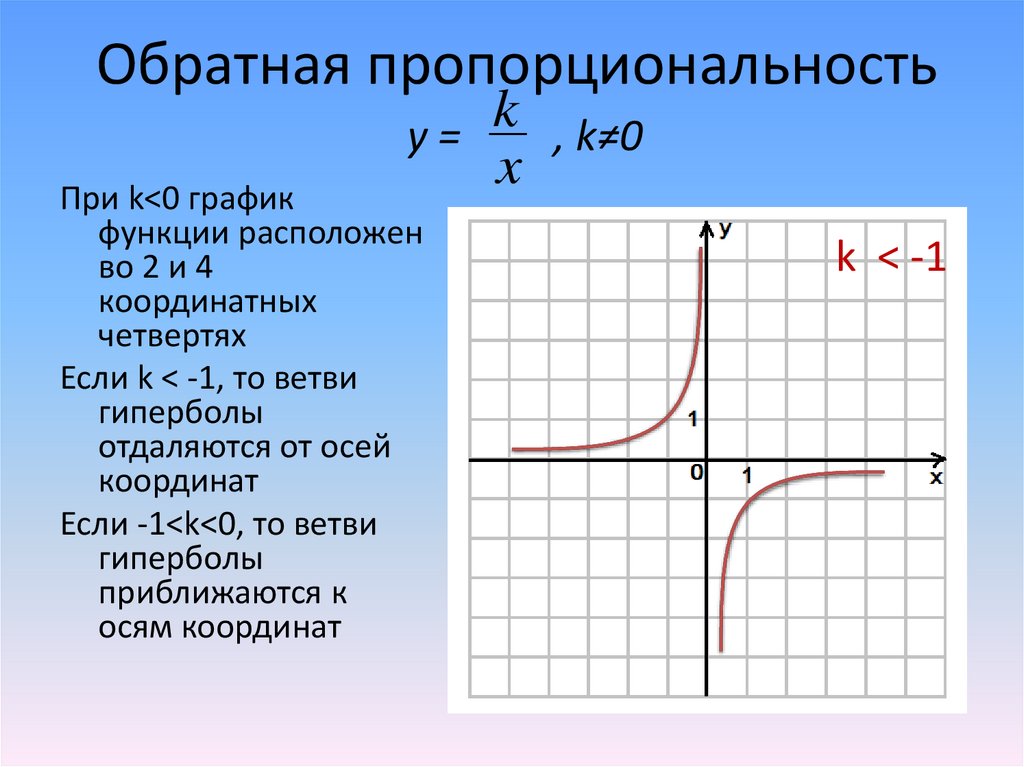
Обратная пропорциональность
k
y=
, k≠0
x
При k<0 график
функции расположен
во 2 и 4
координатных
четвертях
Если k < -1, то ветви
гиперболы
отдаляются от осей
координат
Если -1<k<0, то ветви
гиперболы
приближаются к
осям координат
k < -1

22.

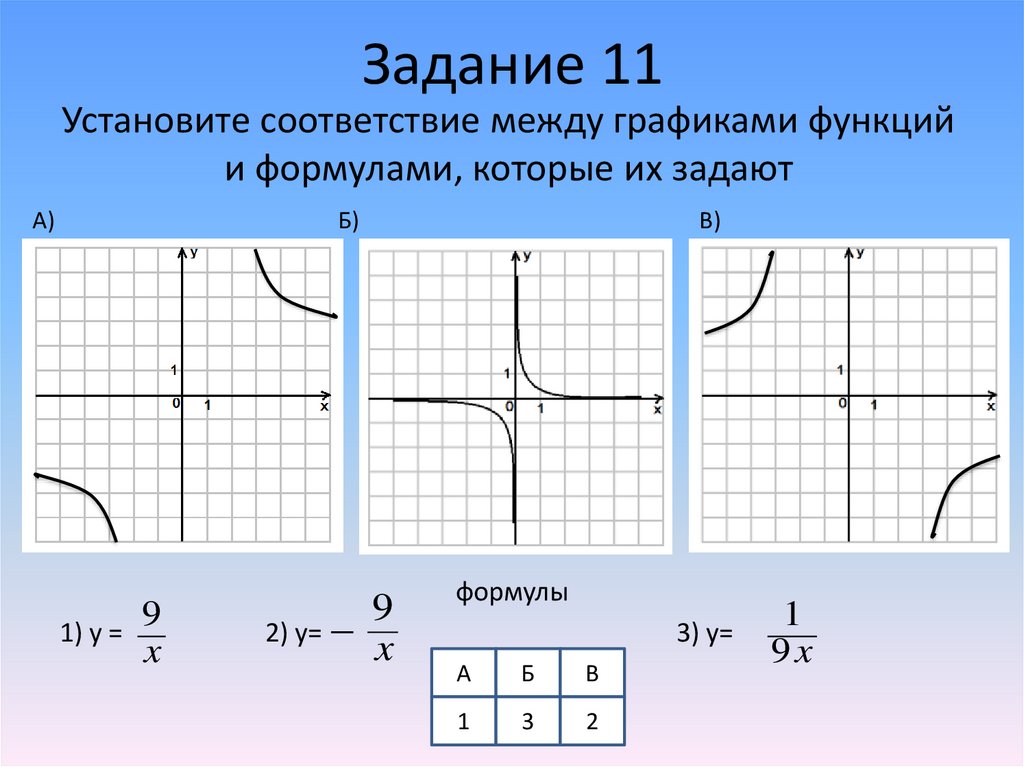
Задание 11
Установите соответствие между графиками функций
и формулами, которые их задают
A)
Б)
1) y =
9
x
9
2) у=
x
В)
формулы
3) у=
А
Б
В
1
3
2
1
9x

23.

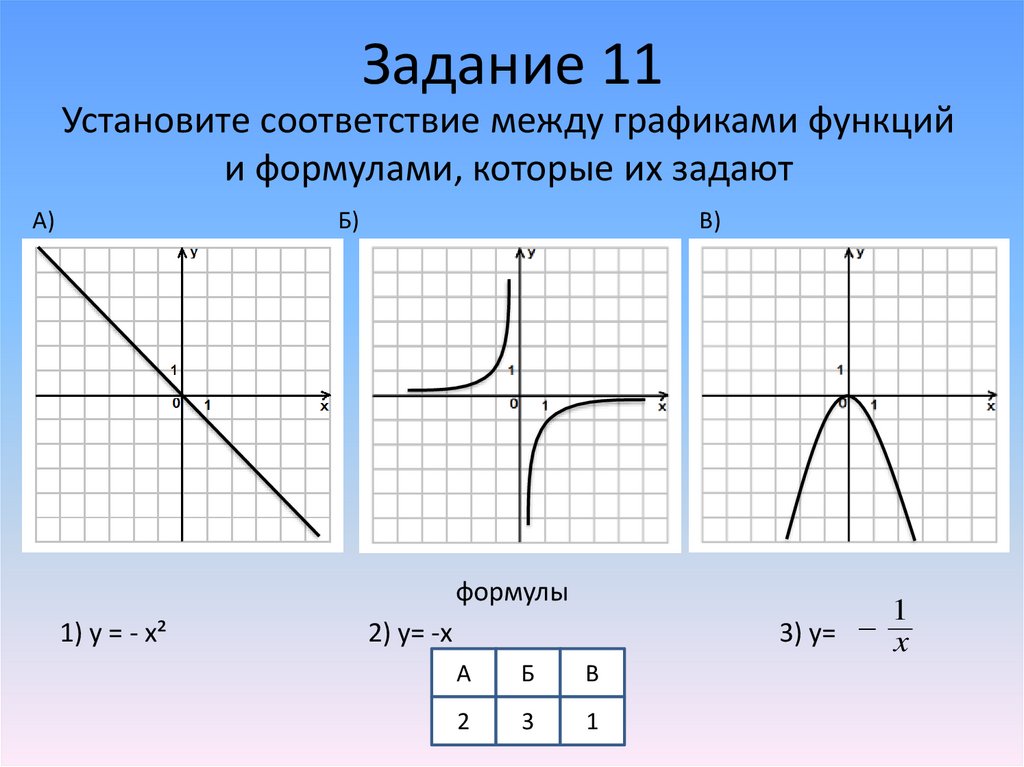
Задание 11
Установите соответствие между графиками функций
и формулами, которые их задают
A)
Б)
В)
формулы
1) y = - x²
1
3) у=
x
2) у= -x
А
Б
В
2
3
1

24.

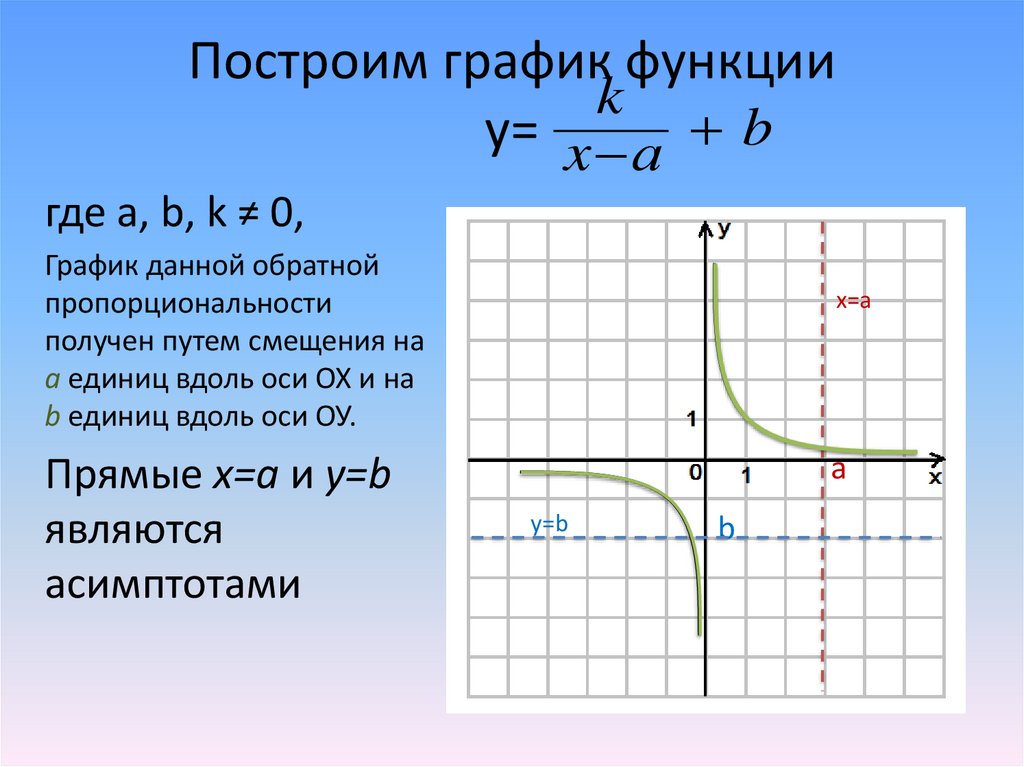
Построим график функции
k
у= x а b
где а, b, k ≠ 0,
График данной обратной
пропорциональности
получен путем смещения на
а единиц вдоль оси ОХ и на
b единиц вдоль оси ОУ.
Прямые х=а и у=b
являются
асимптотами
x=a
a
y=b
b