Похожие презентации:
Простейшие задачи в координатах
1.
2.
№929 Точка А лежит на положительной полуоси Ох, аточка В – на положительной полуоси ОУ. Найдите
координаты вершин треугольника АВО, если
y
а) ОА = 5, ОВ = 3;
б) ОА = a, ОВ = b
B
3
x
O
5
A
3.
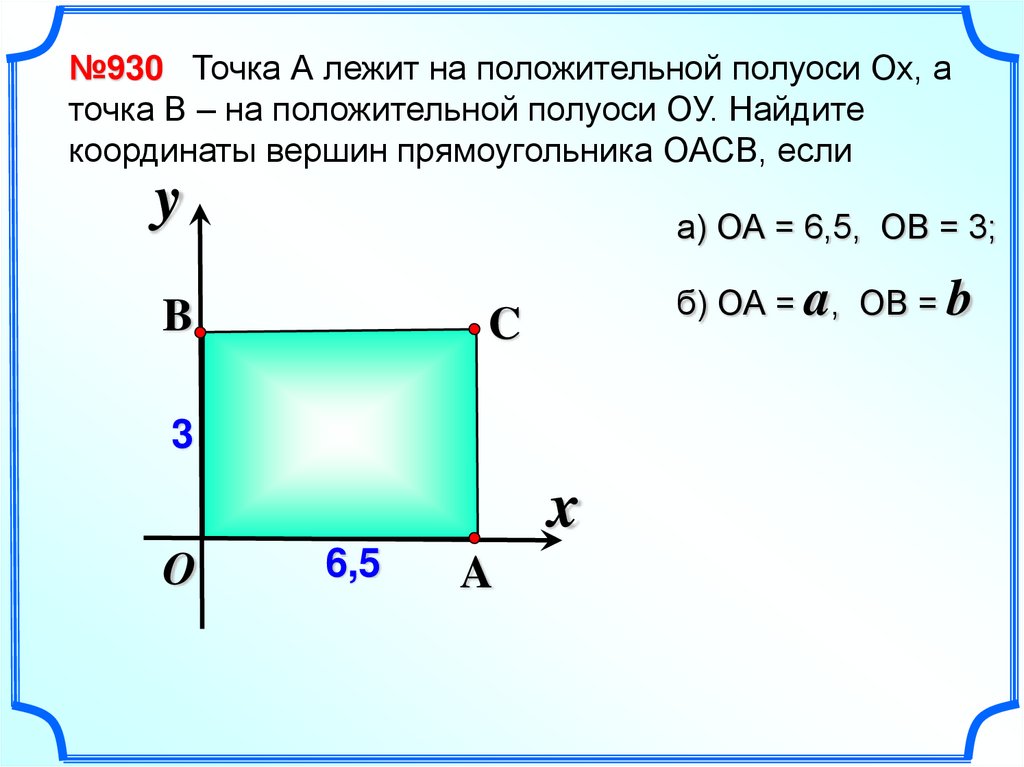
№930 Точка А лежит на положительной полуоси Ох, аточка В – на положительной полуоси ОУ. Найдите
координаты вершин прямоугольника ОАСВ, если
y
а) ОА = 6,5, ОВ = 3;
B
б) ОА = a, ОВ = b
C
3
x
O
6,5
A
4.
№932 Найдите координаты вершин равнобедренноготреугольника АВС, изображенного на рисунке, если
АВ = 2a, а высота СО равна
y
C
x
A
O
B
b.
5.
Выразимкоординаты
вектора
АВ равна
через координаты
Каждая
координата
вектора
разности его
начала А и конца В.
соответствующих координат его конца и начала.
AB = ОВ - OА
из ОАВ
y
B (x2;y2)
A(x1;y1)
O
x
6.
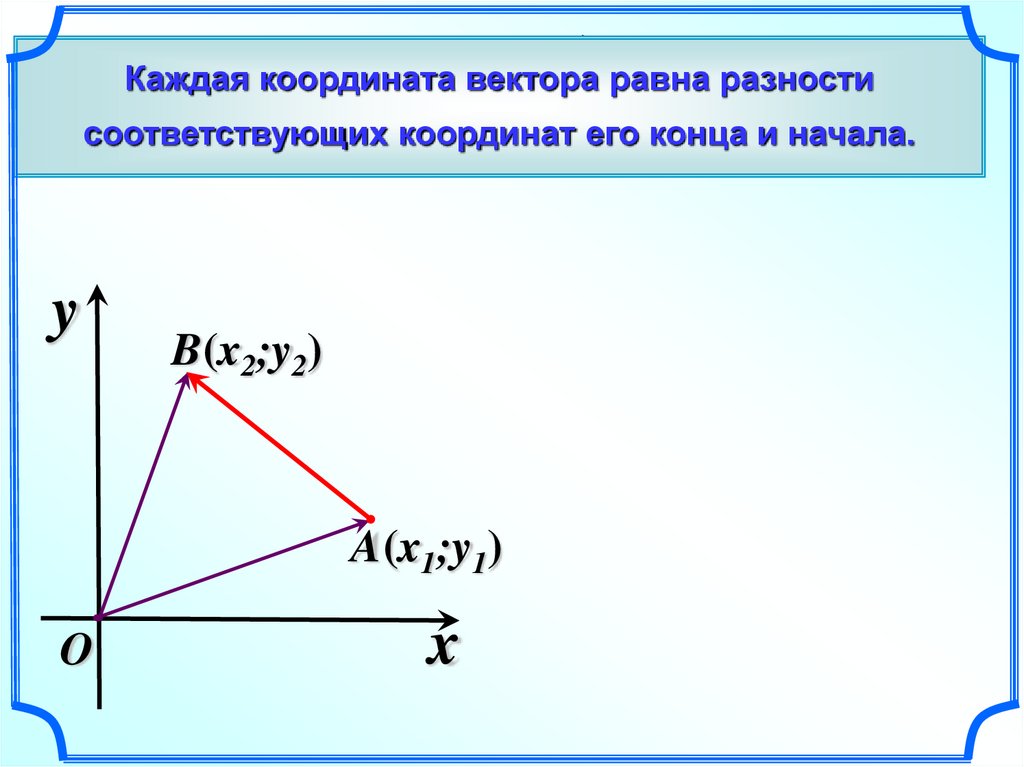
Каждая координата вектора равна разностисоответствующих координат его конца и начала.
y
A(x1;y1) B(x2;y2)
B (x2;y2)
A(x1;y1)
O
x
7.
yT (0;5) A(3;5)
B (5;4)
N(3;2)
x
О
R(-4;0)
D(-3;-4)
1
P (2;-1)
C (4;-4)
8.
Обратные задачи.Дано: AB{2;-1},
Найти:
A(x;y)
B(5;4)
Дано: AB{2;-1},
Найти:
B(x;y)
A(2;-4)
9.
ПовторениеB
C
A
1
ОС (ОА ОВ )
2
O
10.
Координаты середины отрезка1
ОС (ОА ОВ )
2
+
OA{x1;y1}
OB{x2;y2}
OA+OB {x1+x2; y1+y2}
y
B(x2;y2)
1
2
:2
x1+x2 y1+y2
(OA+OB) {
;
}
2
C (x0;y0)
2
x1+x2 y1+y2
OC {
;
}
2
2
A(x1;y1)
О
x
x0=
x1+x2
2
; y0 =
y1+y2
2
11.
Каждая координата середины отрезка равнаполусумме соответствующих координат его концов.
x1+x2 y1+y2
OC {
;
}
2
y
2
B(x2;y2)
Полусумма абсцисс
x1+x2 y1+y2
C(
C
;
)
2
2
A(x1;y1)
О
x
x0=
x1+x2
2
;
Полусумма ординат
y0=
y1+y2
2
12.
Каждая координата середины отрезка равнаполусумме соответствующих координат его концов.
A(x1;y1) B(x2;y2) C – середина отрезка АВ
B(x2;y2)
C(x0;y0)
C
A(x1;y1)
13.
yПолусумма абсцисс
T (0;5) A(3;5)
C
B(5;4)
N(3;2)
S
1
R(-4;0)
Q
D(-3;-4)
2
P (2;-1)
V
C (4;-4)
;
Полусумма ординат
y0=
y1+y2
x
F
О
x0=
x1+x2
2
323 +0
+5
2-1+(-4)
5 +0
+4
+4
0+(-4)
5+0;;
xxx00=
=
;
;
y
y
=
=
0+(-3)
0+(-4)
0
0
=
;
y
=
xx000== 22222 ;; 0yy00==22 222
C(4;
4,5)
F(1,5;
1)
V(3;-2,5)
Q(-1,5;-2)
S(-2;2,5)
14.
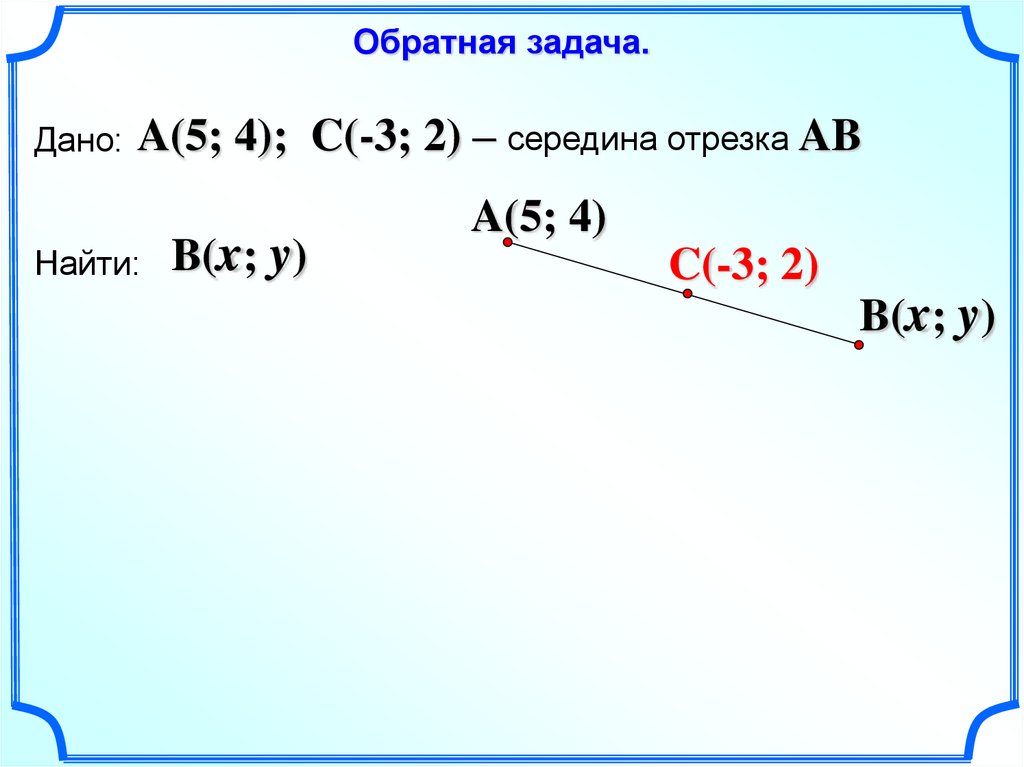
Обратная задача.Дано:
A(5; 4); C(-3; 2) – середина отрезка AB
Найти:
B(x; y)
A(5; 4)
C(-3; 2)
B(x; y)
15.
Вычисление длины вектора по его координатамOA2=OA12 + AA12
y
OA2= x2 + y2
OA
OA= a{x;y}
A (x;y)
A2
y
О
a
OA = x2 + y2
=
x
A1
x
=
16.
Вычисление длины вектора по его координатамвычисляется по формуле
17.
Расстояние между двумя точкамиy
M2(x2;y2)
–
d
M2(x2;y2)
M1(x1;y1)
M1M2 {x2–x1; y2–y1}
M1(x1;y1)
O
x
a = x2 + y2
M1M2 = (x2–x1)2+(y2–y1)2
d = (x2–x1)2+(y2–y1)2
18.
Расстояние между двумя точкамии
вычисляется по формуле
M1M2 = (x2–x1)2+(y2–y1)2
d = (x2–x1)2+(y2–y1)2
19.
№ 940Найдите расстояние между точками
A(2;7)
и
B(-2;7)
20.
Домашнее задание:1. Разобрать по учебнику 91,92;
2. Выучить формулы (слайд 11,15,17).
3. Выполнить задание на Якласс.
Прислать фотоотчет решений задач № 8,9,10

















 Математика
Математика








