Преобразование графиков функции

1. Тема: «Преобразование графиков функции»

2. Вопросы на повторение:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Графиком линейной функции является _______________ .
Графиком квадратичной функции является _______________ .
Если в квадратичной функции , коэффициент а >0, то ветви параболы
направлены _______________ .
Если в квадратичной функции , коэффициент а <0, то ветви параболы
направлены _______________ .
Если при решении квадратного уравнения D >0, то парабола
пересекает ось Ох в _______ точках.
Если при решении D=0, то точка пересечения параболы и оси Ох
является _____________ параболы.
Если при решении квадратного уравнения D <0, то парабола
__________________ ось Ох. Значит, парабола расположена либо в
_____________ полуплоскости, если а >0, либо в ______________
полуплоскости, если а <0 оси Оу.
Графиком обратной пропорциональности является
_________________ .
Если k >0 в уравнении , то ветви гиперболы расположены в _____
четверти и в _____ четверти.
Если k <0 в уравнении , то ветви гиперболы расположены в _____
четверти и _____ четверти.

3. Рассмотрим основные правила преобразования графиков на примерах элементарных функций

4. 1) y=-f(x) Cимметрия относительно OX для y=f(x)

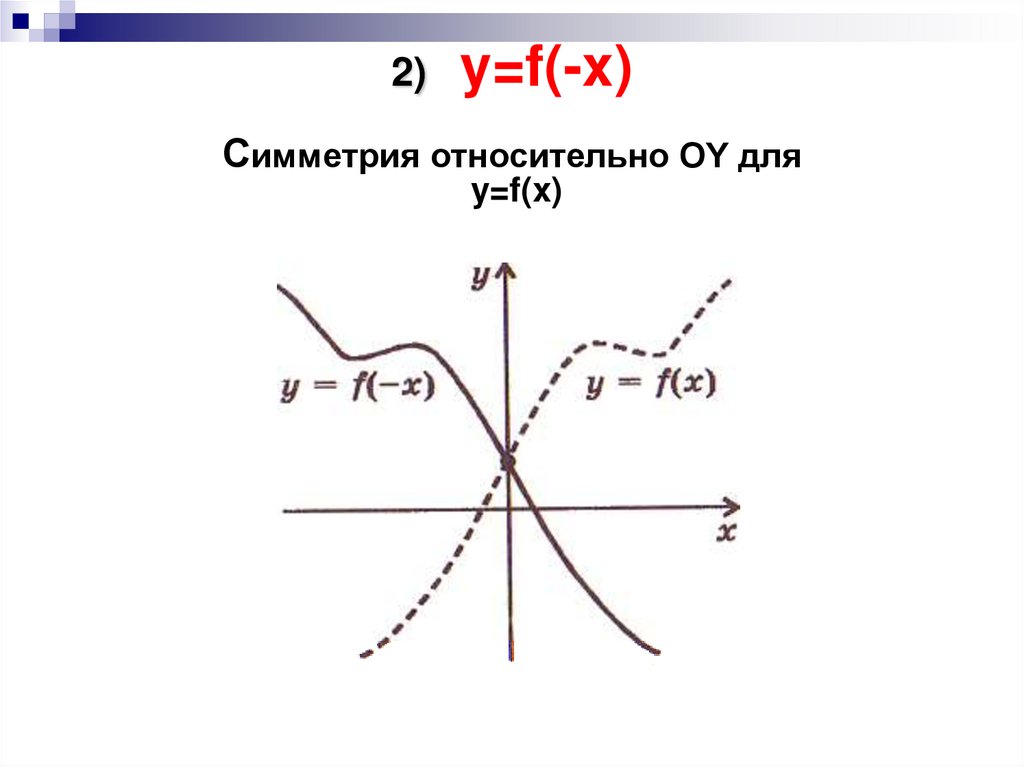
5. 2) y=f(-x) Симметрия относительно OY для y=f(x)

6. 3) y=f(x-a) Параллельный перенос вдоль OX y=f(x) влево при a<0 вправо при a>0

3)
y=f(x-a)
Параллельный перенос вдоль OX
y=f(x)
влево при a<0
вправо при a>0

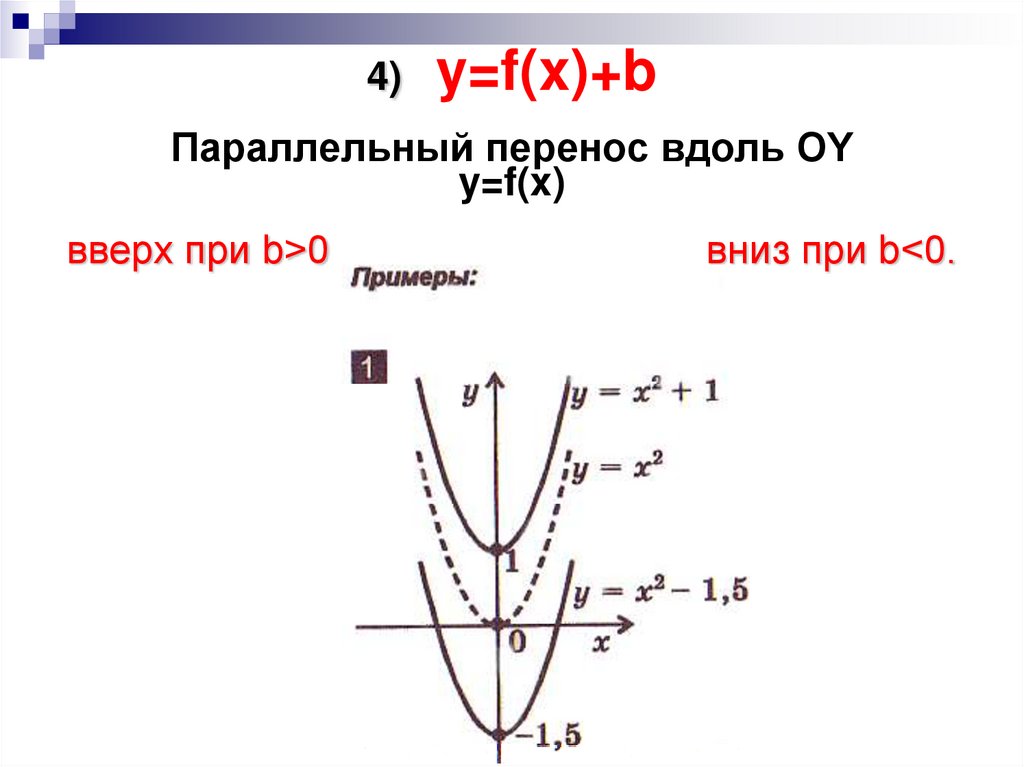
7. 4) y=f(x)+b Параллельный перенос вдоль OY y=f(x) вверх при b>0 вниз при b<0.

4)
y=f(x)+b
Параллельный перенос вдоль OY
y=f(x)
вверх при b>0
вниз при b<0.

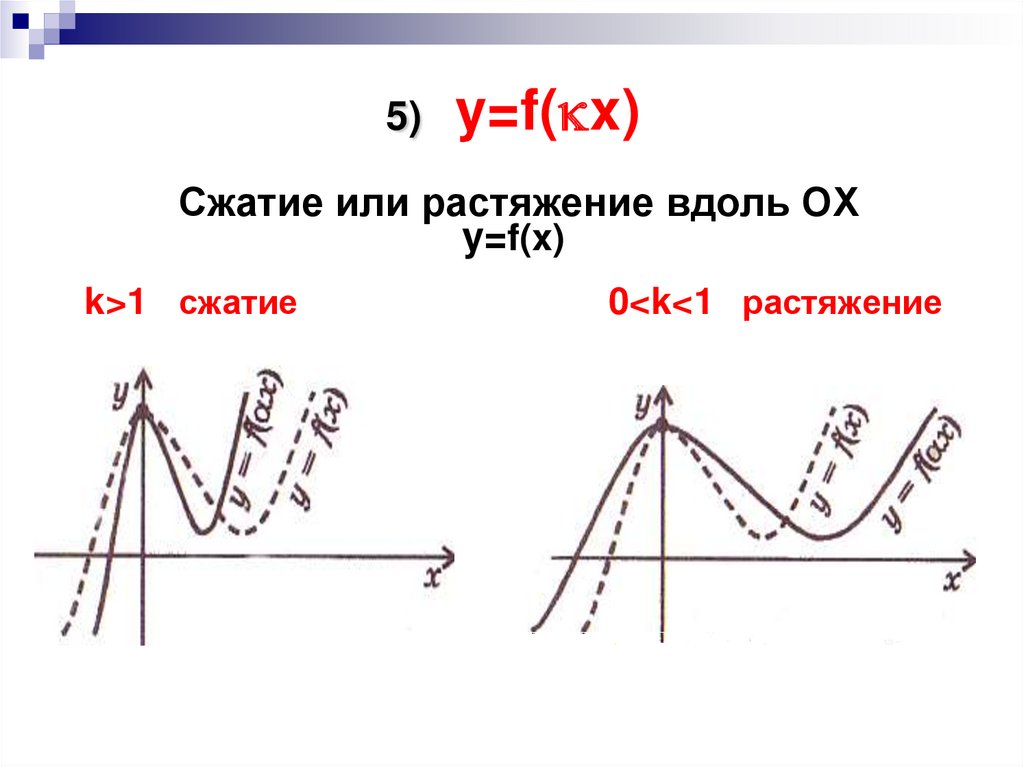
8. 5) y=f(kx) Сжатие или растяжение вдоль OX y=f(x) k>1 cжатие 0<k<1 растяжение

5)
y=f(kx)
Сжатие или растяжение вдоль OX
y=f(x)
k>1 cжатиеK
0<k<1 растяжение

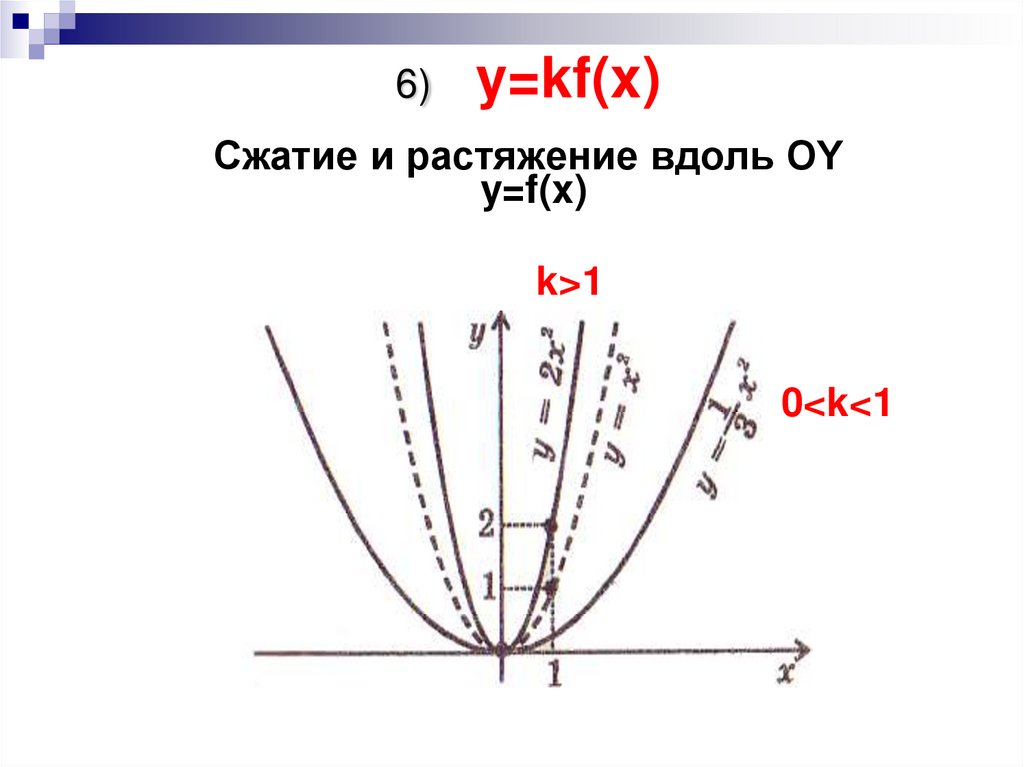
9. 6) y=kf(x) Сжатие и растяжение вдоль OY y=f(x)

k>1
0<k40<1
0<k<1

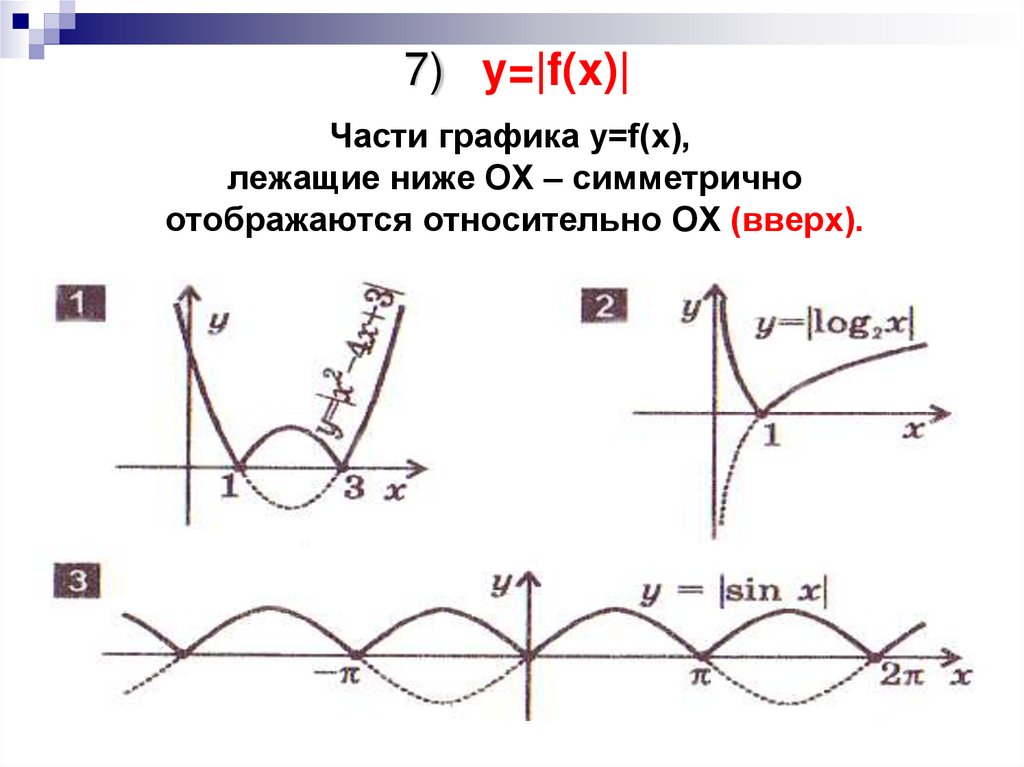
10. 7) y=|f(x)|

Части графика y=f(x),
лежащие ниже OX – симметрично
отображаются относительно OX (вверх).

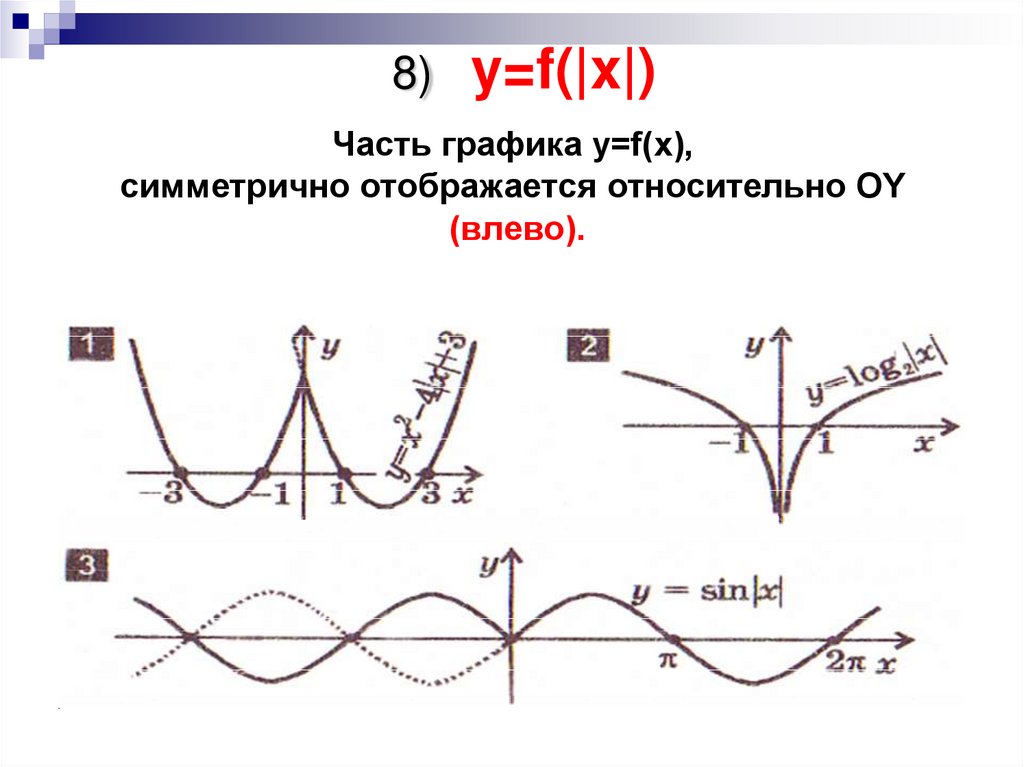
11. 8) y=f(|x|)

Часть графика y=f(x),
симметрично отображается относительно OY
(влево).

12.

Построим график функции:
у 2 х 2 12 х 19
Решение: Сначала выделим полный квадрат для
данного трехчлена:
у 2 х 12 х 19 2( х 6 х) 19
2
2
2(( х 6 х 9) 9) 19
2
2( х 3) 18 19
2
2( х 3) 1
2

13.

Выполним следующие преобразования:
2
построим график функции у х
;
параболу параллельно перенесем вдоль оси Ох в
положительном направлении на три единицы;
полученную параболу растянем от оси Ох в 2 раза;
затем к полученной параболе применим симметричность
относительно прямой у=0;
последнюю параболу параллельно перенесем вдоль оси Оу на
одну единицу в отрицательном направлении.

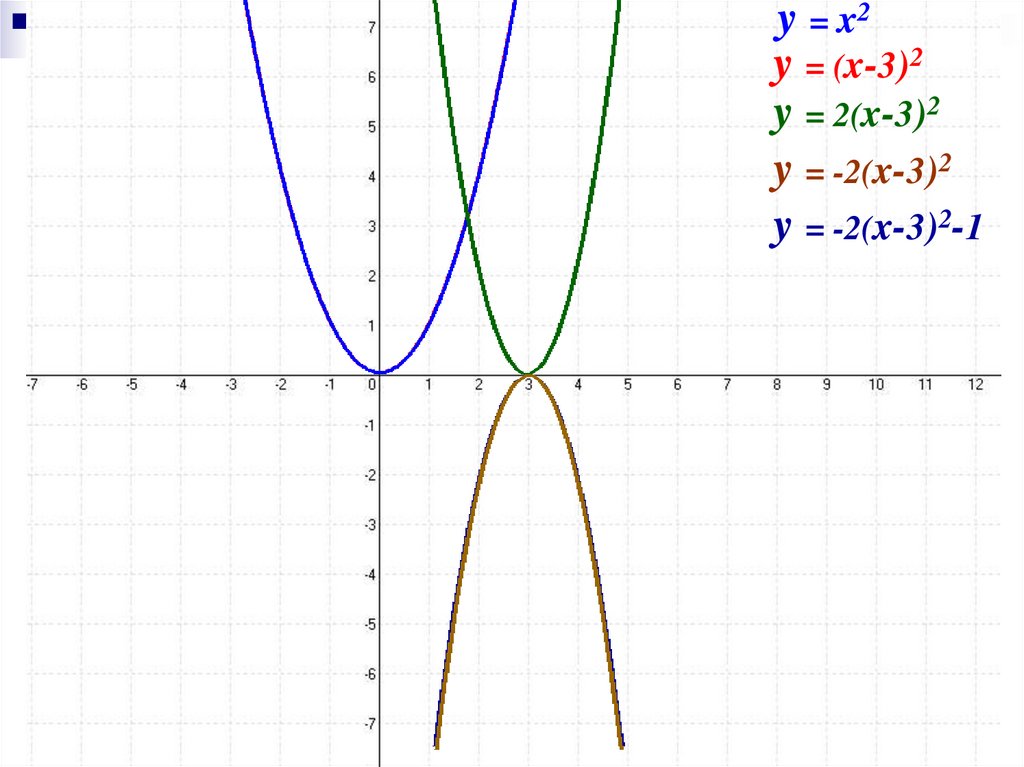
14.

y = x2
y = (x-3)2
y = 2(x-3)2
y = -2(x-3)2
y = -2(x-3)2-1

15.

Рядом с графиками напишите его функцию:
y =x
y = 2x
y = -3x
y = x - 1,5
y = -2x + 3,5

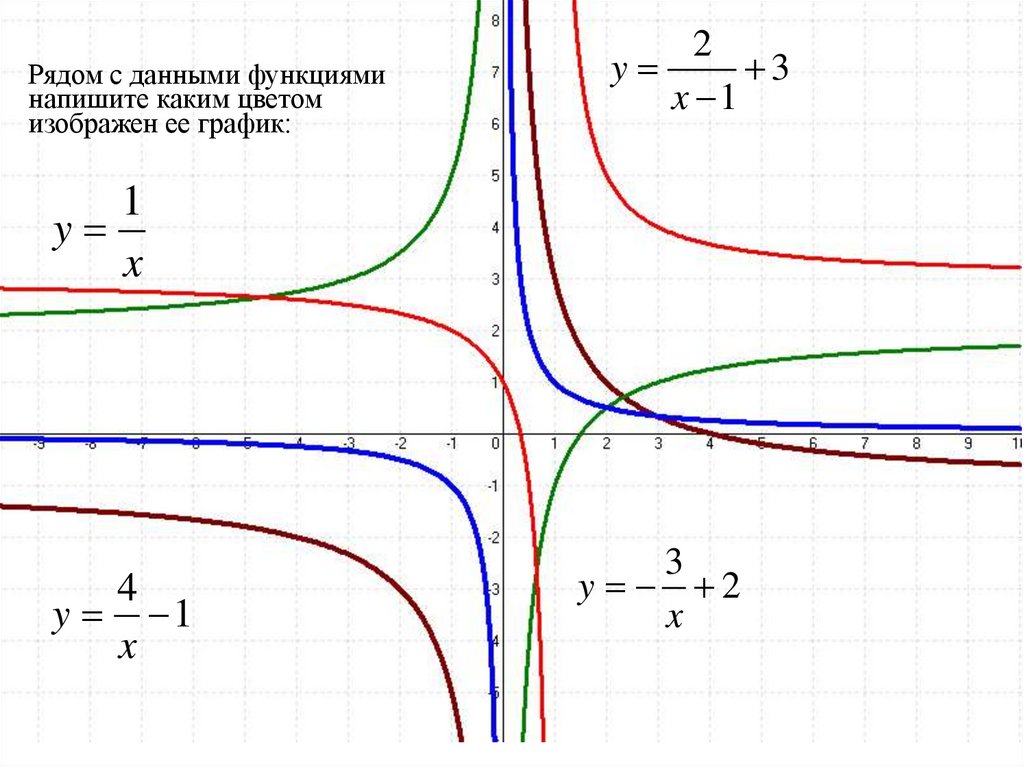
16.

Рядом с данными функциями
напишите каким цветом
изображен ее график:
2
y
3
x 1
1
y
x
4
y 1
x
3
y 2
x

17. Какой кривой являются графики следующих функций:

а ) у сos
3
5x
1
б ) у 7 sin
2
x
1 3
в ) у sin
x
6
2
x
г) у
tg
3
4
2

18.

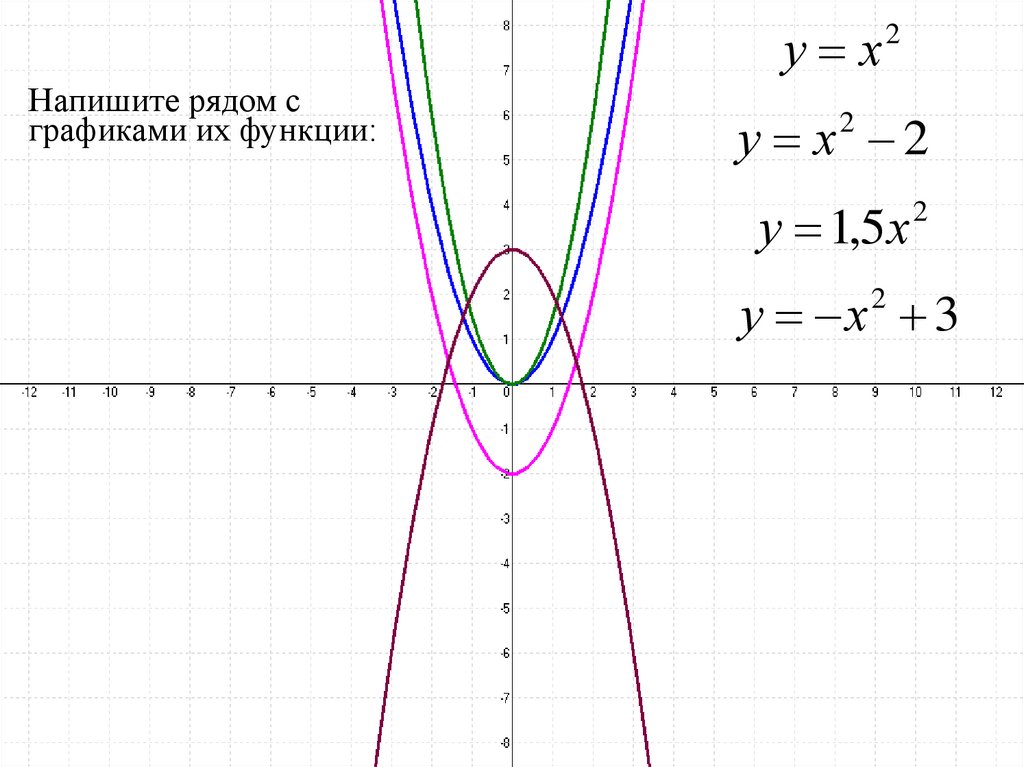
у х
Напишите рядом с
графиками их функции:
2
у х 2
2
у 1,5 х
2
у х 3
2

19.

Самостоятельная работа учащихся
С помощью шаблона графика
функции
у х
2
построить график функции
у 3х 12 х 8
2
и рассказать о выполненных преобразованиях.

20.

Проверка самостоятельной работы:
Сначала выделим полный квадрат для данного трехчлена:
3х 2 12 х 8 3( х 2 4 х) 8
3( х 4 х 4 4) 8 3(( х 2) 4) 8
2
2
3( х 2) 2 12 8 3( х 2) 2 4.

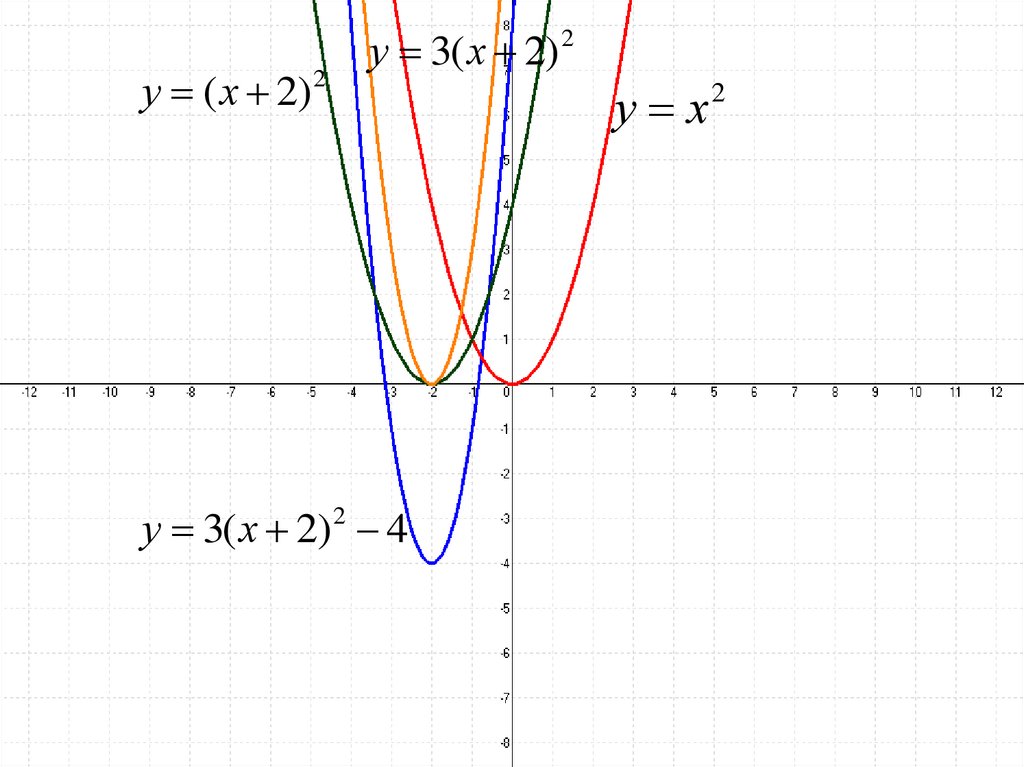
21.

у ( х 2) 2
у 3( х 2) 2
у 3( х 2) 2 4
у х2

22.

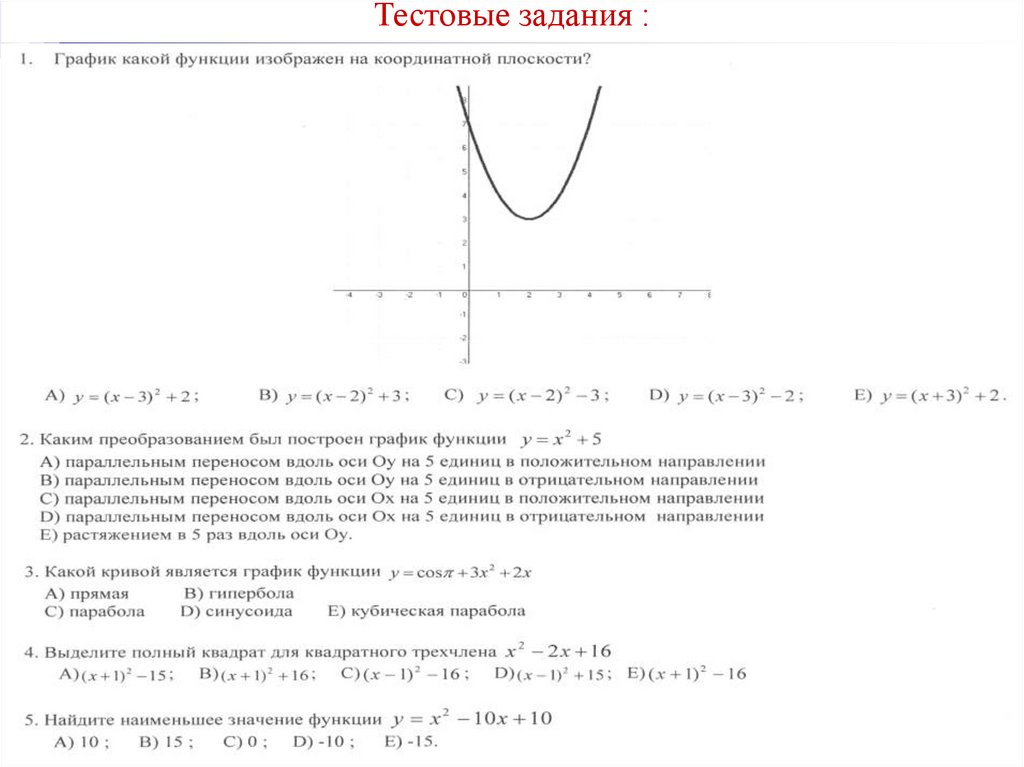
Тестовые задания :

23.

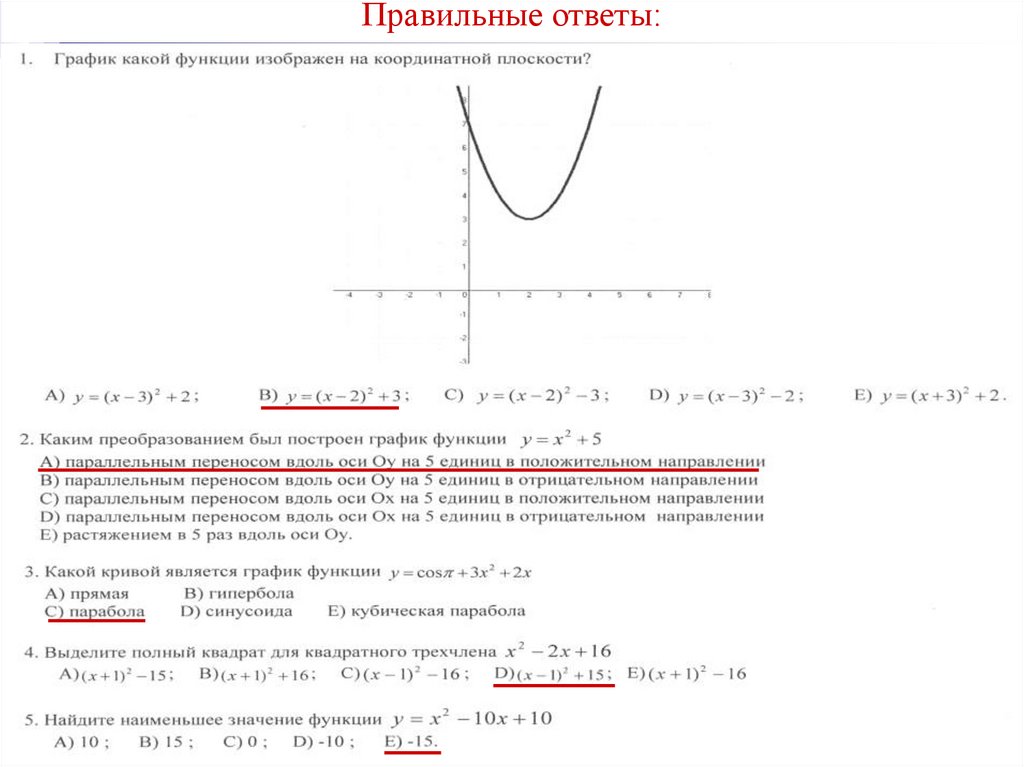
Правильные ответы:

24.

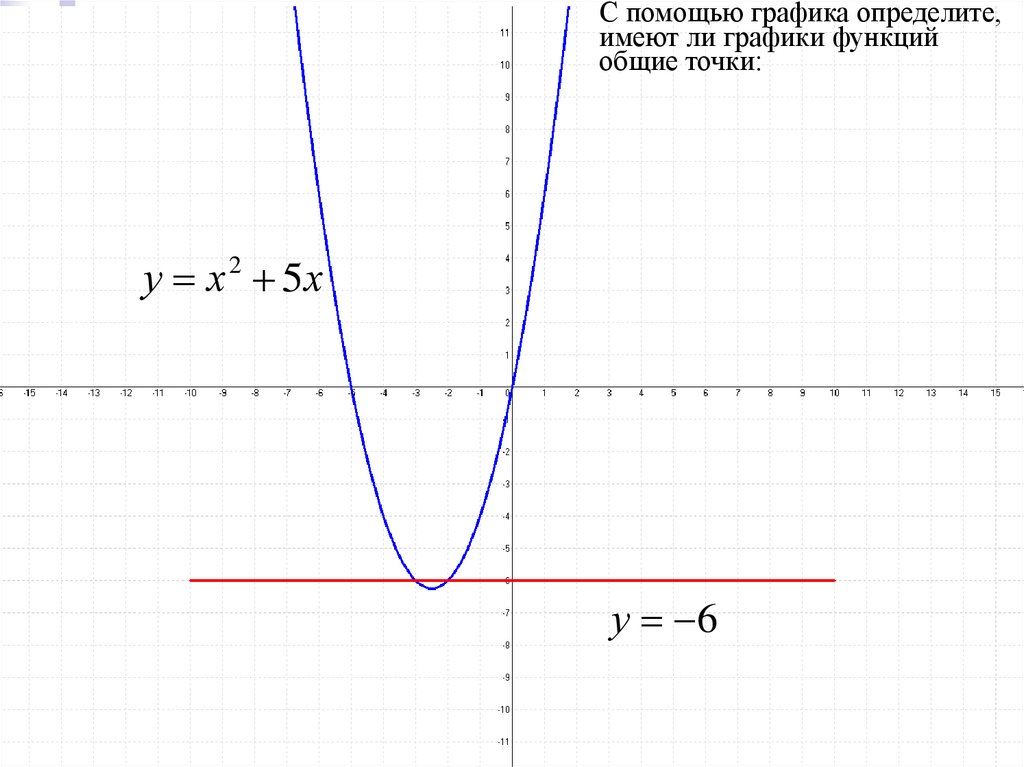
С помощью графика определите,
имеют ли графики функций
общие точки:
у х 2 5х
у 6

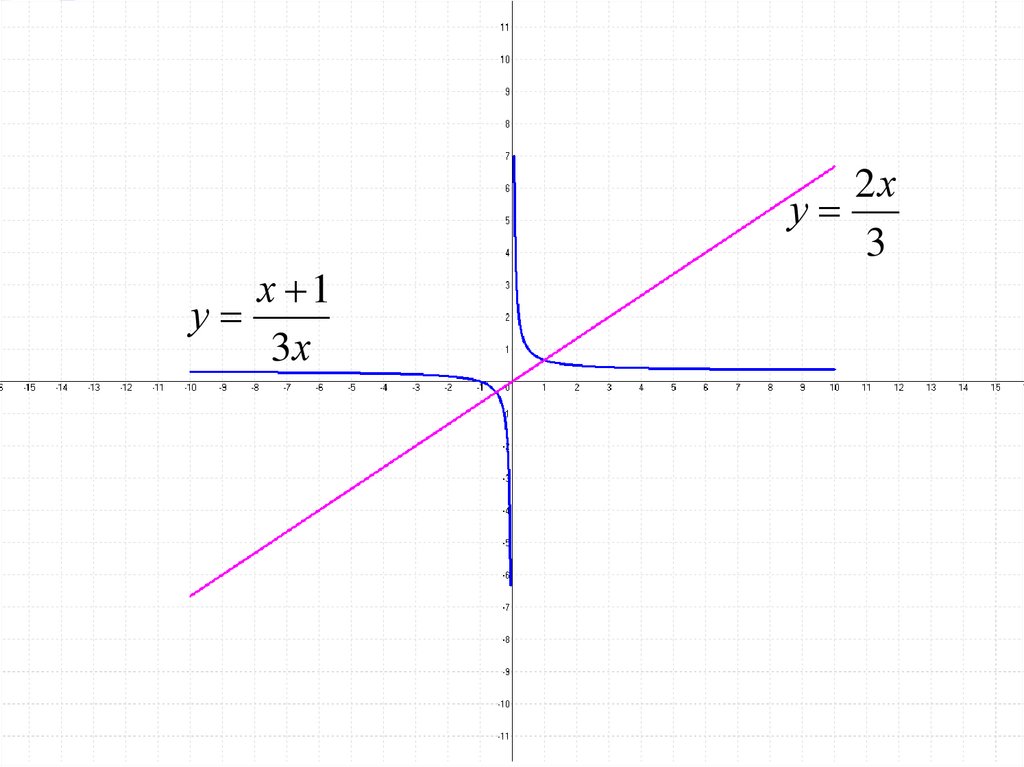
25.

х 1
у
3х
2х
у
3