Моделирование эпидемии гриппа

1. Моделирование ЭПИДЕМИИ ГРИППА

22 декабря 2021 г.
Моделирование
ЭПИДЕМИИ
ГРИППА

2.

Модель Ферхюльста.
Рост популяции, ограниченный ресурсами
dN
N
kN (1 )
dt
L
N - численность популяции,
t - время,
K - максимальная скорость прироста,
L –емкость популяции
Пьер Ферхюльст
1804 - 1849
Ограниченный рост. Зависимость
величины скорости роста от
численности (а) и численности от
времени (б)

3.

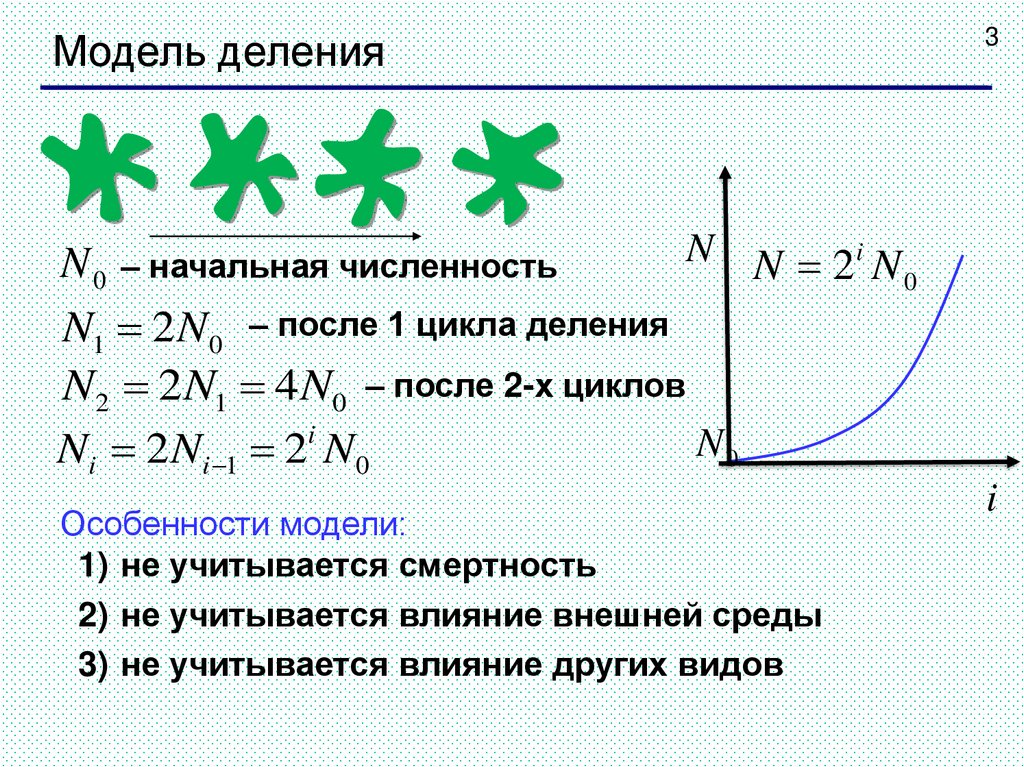
Модель деления
3
N N 2i N
N 0 – начальная численность
0
N1 2N 0 – после 1 цикла деления
N2 2 N1 4N0 – после 2-х циклов
i
N0
Ni 2 Ni 1 2 N0
Особенности модели:
1) не учитывается смертность
2) не учитывается влияние внешней среды
3) не учитывается влияние других видов
i

4. Параметры модели

В(1)- количество больных начальная,
В(n) - количество больных через n дней
k - коэффициент заражения = 0,5 ,
L=300 - всего людей,
Модель ограниченного роста:
4

5.

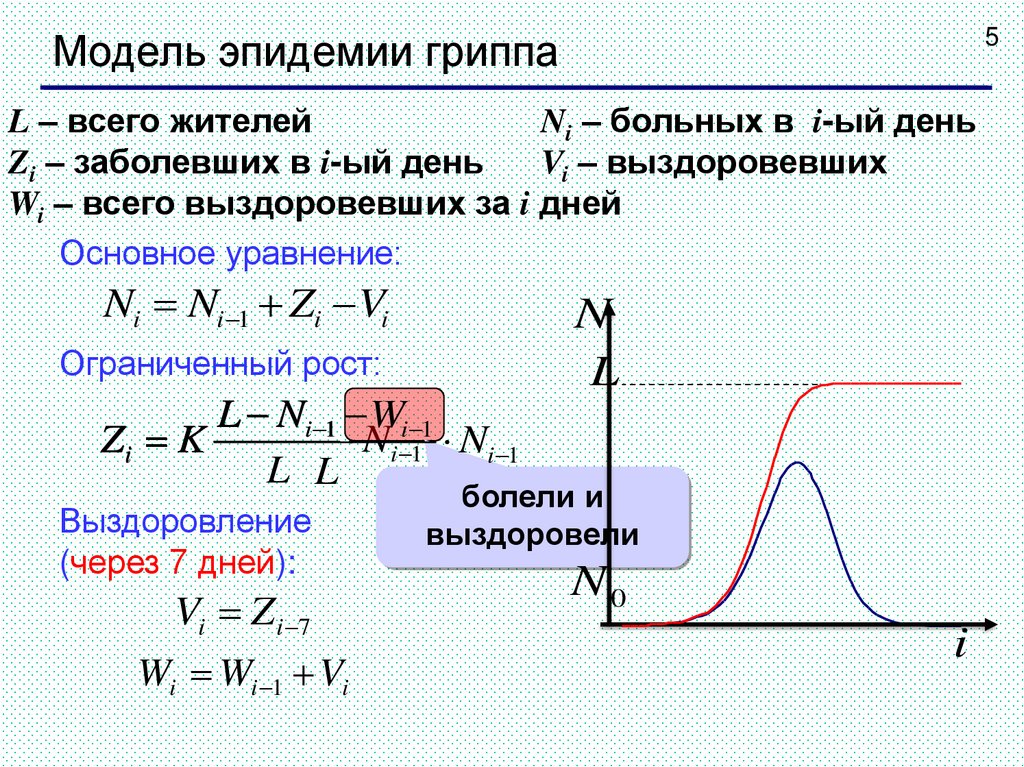
5
Модель эпидемии гриппа
L – всего жителей
Ni – больных в i-ый день
Zi – заболевших в i-ый день
Vi – выздоровевших
Wi – всего выздоровевших за i дней
Основное уравнение:
Ni Ni 1 Zi Vi
Ограниченный рост:
L Ni 1 Wi 1
Ni 1 Ni 1
Zi K
L L
Выздоровление
(через 7 дней):
Vi Zi 7
Wi Wi 1 Vi
N
L
болели и
выздоровели
N0
i

6. Параметры модели

В(1)- количество больных начальная =1,
В(n) - количество больных через n дней
k - коэффициент заражения = 0,5 ,
L=300- всего людей,
• V(n) –количество выздоровевших,
N(i)-число больных в i-й день
Z(i)- число заболевших в i-й день
W(i)-число выздоровевших за i дней
v(i)- выздоровевших в i-й день
6

7. Математическая модель

7

8. Практическая работа №14

1. ЦЕЛЬ: создать компьютерную модель
эпидемии гриппа, (график)
2. Реализация
Использовать табличный процессор Microsoft
Excel
1. Определить на каком шаге
вычислений (год) когда эпидемия
достигнет максимума.
2. Когда эпидемия закончится.
8