Похожие презентации:
Физическая кинетика явления переноса (лекция № 15)
1. ЛЕКЦИЯ № 15. Физическая кинетика Явления переноса
1591
2. ВОПРОСЫ 43. Средняя длина свободного пробега молекул. Эффективный диаметр молекулы. Среднее число соударений в единицу времени.
44. Явления переноса – диффузия,теплопроводность и вязкость в газах.
Коэффициенты диффузии,
теплопроводности, вязкости.
159
2
3. 43. Средняя длина свободного пробега молекул. Эффективный диаметр молекулы. Среднее число соударений в единицу времени.
1593
4. Микроскопическую теорию процессов, происходящих в неравновесных системах, называют физической кинетикой. Физическая кинетика
используетпредставления об
атомно-молекулярном
строении веществ.
159
4
5. Она изучает процессы переноса массы вещества, импульса, энергии, заряда и т. д. в различных физических системах (газах,
жидкостях, твердых телах, плазме) ивлияние на них внешних полей.
159
5
6. Молекулы реальных газов хотя и малы, имеют конечные размеры и, находясь в состоянии непрерывного хаотического теплового
движения,неизбежно сталкиваются друг с
другом и со стенками сосуда.
159
6
7.
1597
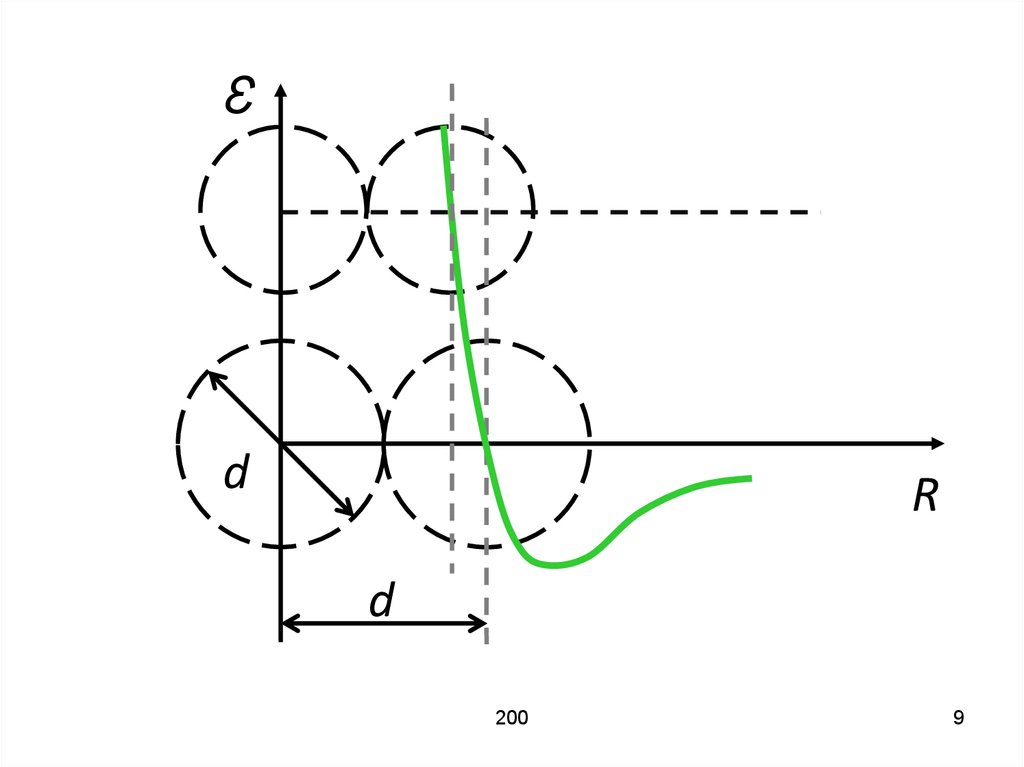
8. Под столкновением двух молекул не будем понимать столкновение двух абсолютно упругих шаров. Рассмотрим процесс столкновения
двух молекул с помощьюзависимости энергии их
взаимодействия от расстояния
между их центрами.
159
8
9.
Ԑd
R
d
200
9
10. d – диаметр молекулы или эффективный диаметр. σ = π d2 – эффективное сечение молекулы. Если молекула движется со средней
скоростью ʋср и претерпевает всреднем ν столкновений за секунду,
то средняя длина свободного
пробега будет равна
λ
ср
ν
159
ν
10
11. Предположим, что все молекулы, кроме одной покоятся. Двигающаяся молекула изменяет своё направление, если центр неподвижной
молекулы находится нарасстоянии меньшем эффективного
диаметра от линии движения.
159
11
12. Таким образом, число столкновений за 1секунду равно числу молекул, центры которых попали в объём V = σ ʋср = π d2 ʋср, то есть
ν' = π d2 ʋср n,n – концентрация.
159
12
13.
d159
13
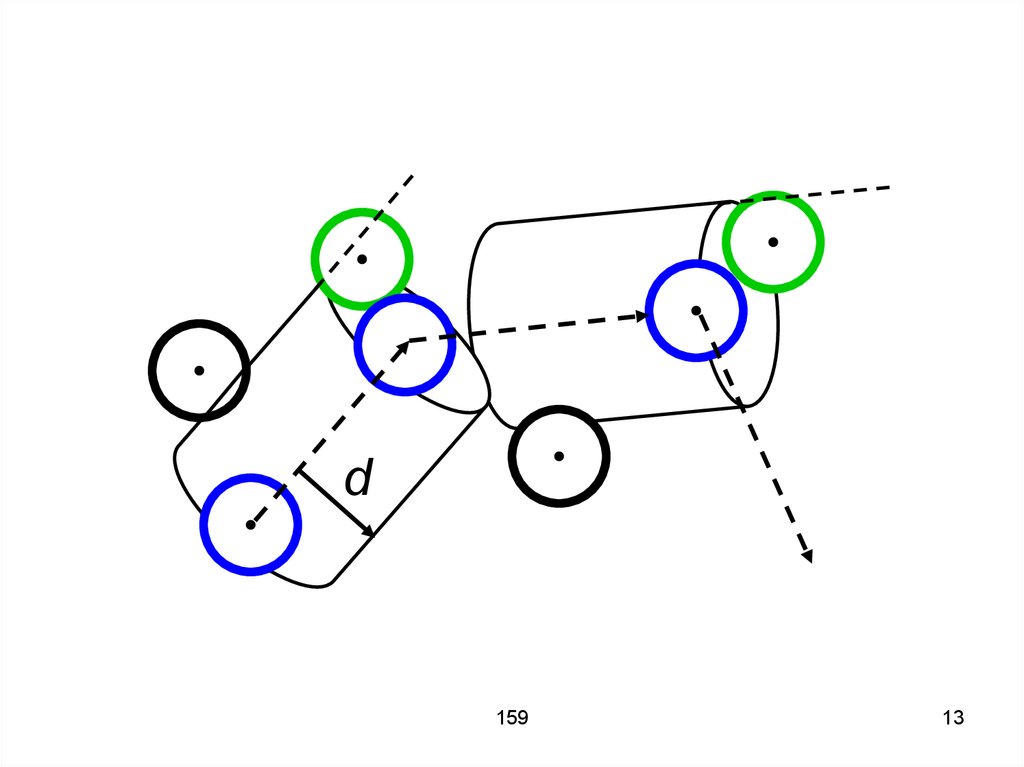
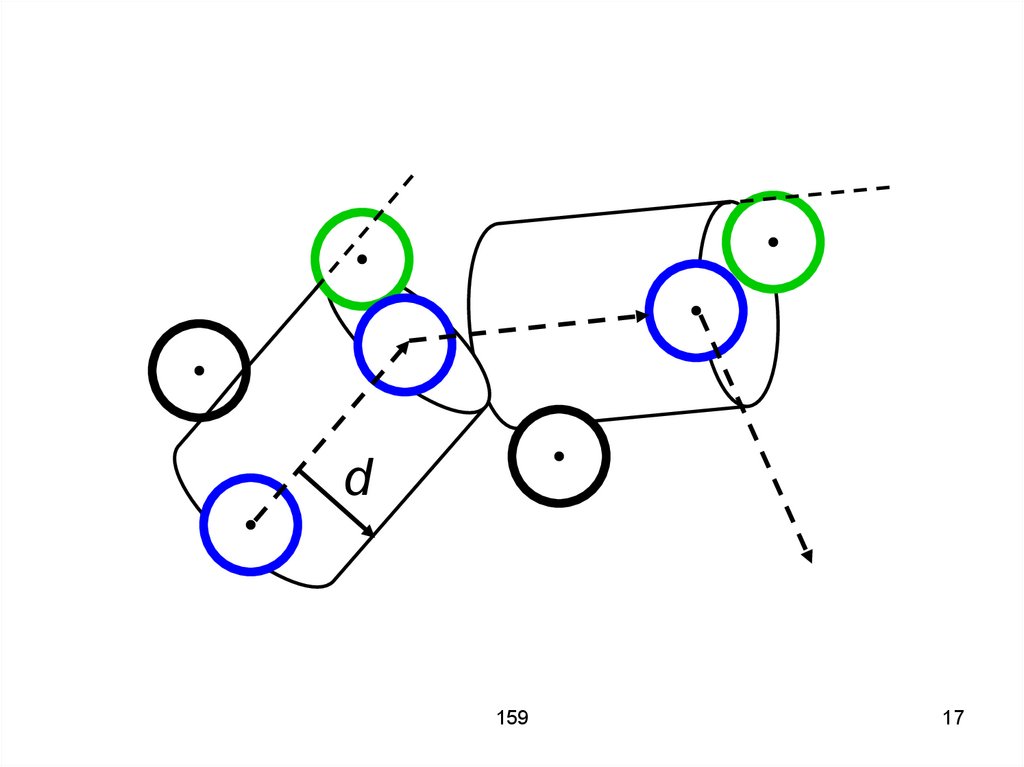
14. Столкновение происходит тогда, когда расстояние между центрами молекул становится меньше диаметра молекулы d. Иными словами,
при движении молекулаописывает некоторый цилиндр,
площадь основания которого
равняется эффективному сечению
σ = πd2, а ось совпадает с вектором
скорости молекулы.
159
14
15. Учёт движения всех молекул даст поправку в виде сомножителя √2: ν = √2πd2ʋсрn. Отсюда получаем
1λ
2
2 πd n
159
15
16. Длина свободного пробега – расстояние, которое проходит молекула между двумя последовательными соударениями.
15916
17.
d159
17
18. Связь длины свободного пробега с коэффициентами. Коэффициент диффузии Коэффициент теплопроводности Коэффициент вязкости
Связь длины свободного пробега скоэффициентами.
Коэффициент диффузии
1
D λ
3
Коэффициент теплопроводности
1
1
уд
об
k λρCV λCV
3
3
Коэффициент вязкости
1
η λρ
3
159
18
19. Здесь ρ – плотность газа, CVоб – теплоёмкость газа при постоянном объёме на единицу объёма, CVуд – теплоёмкость газа при
постоянном объёме на единицумассы.
159
19
20.
15920
21. 44. Явления переноса – диффузия, теплопроводность и вязкость в газах. Молекулярный механизм процессов переноса. Коэффициенты
диффузии, теплопроводности,вязкости; связь между ними.
159
21
22. В случае нарушения равновесия возникают потоки либо молекул, либо теплоты и т.п. Этими процессами занимается физическая
кинетика.159
22
23. Диффузия – самопроизвольное выравнивание концентраций в смеси нескольких различных веществ, обусловленное тепловым движением
молекул.159
23
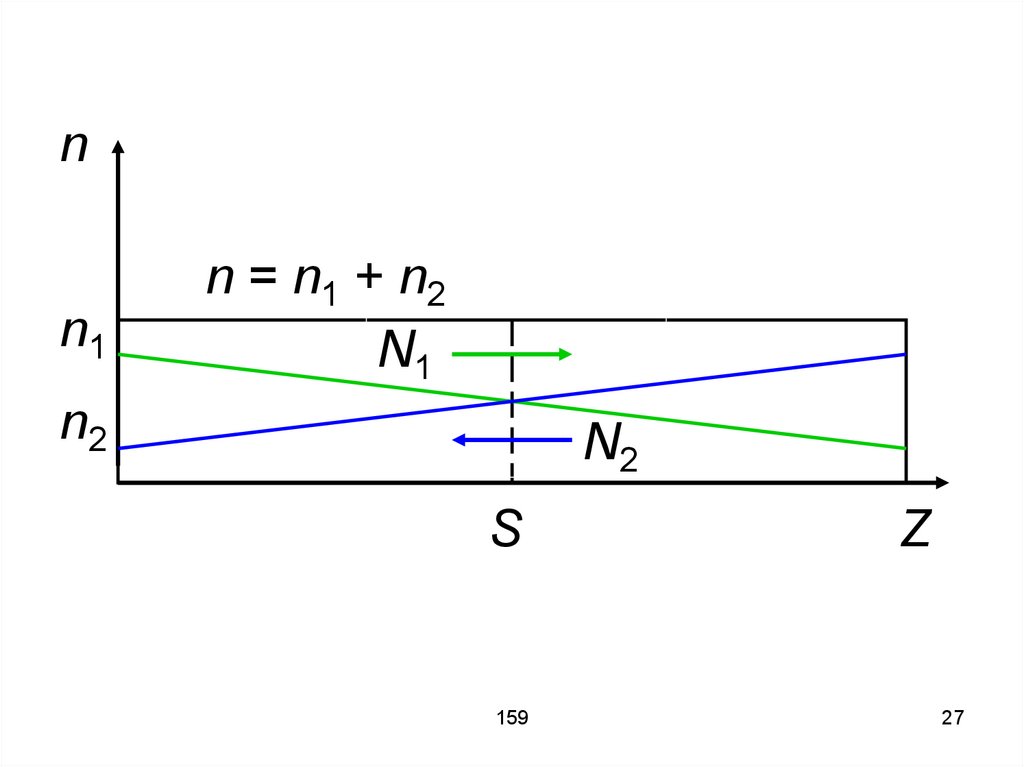
24. Рассмотрим сосуд, содержащий газ из двух компонент: n1 – концентрация молекул одного вида, n2 – концентрация молекул другого
вида. Полное число молекул наединицу объёма n = n1 + n2.
159
24
25. Предположим, что молекулы разных газов распределены неравномерно, но n = const, и как следствие p = nkT = const. Поэтому потоки
невозникают, но переносятся
компоненты, поскольку имеются
градиенты концентрации компонент,
равные друг другу
dn
dn1
dn2 dn1 dn2
0,
,
0.
dz
dz
dz
dz
dz
159
25
26. Сосуд длинный и узкий. На рисунке верхний край сосуда совпадает с величиной «n». S – поперечное сечение сосуда. N1 и N2 – число
молекул первого и второго типа,переносимых в сторону меньшей
концентрации данного вещества
(этому соответствует знак минус в
формуле).
159
26
27.
nn1
n = n 1 + n2
N1
n2
N2
S
159
Z
27
28. Это явление описывается законом Фика Ni – число частиц переносимых за 1 секунду через поперечное сечение S. D – коэффициент
Это явление описывается закономФика
dni
Ni D
S
dz
Ni – число частиц переносимых за 1
секунду через поперечное сечение
S. D – коэффициент
пропорциональности – коэффициент
диффузии (размерность – м2/с).
159
28
29. Теплопроводность – перенос тепла (тепловой энергии) от более горячего участка системы к более холодному (по направлению,
противоположному градиентутемпературы).
159
29
30. Закон Фурье (одномерный и общий случай) k – коэффициент теплопроводности (размерность – Вт/м*К)
Закон Фурье (одномерный и общийслучай)
dT
q k
S
dz
T T T
q kgradTS kS i
j
k
y
z
x
k – коэффициент теплопроводности
(размерность – Вт/м*К)
159
30
31. Воспользуемся соотношением и продифференцируем закон Фурье по координате dz:
Воспользуемся соотношениемQ
q
mCV T Sdzρ CV dT
t t
t
и продифференцируем закон Фурье
по координате dz:
dT
dzSρ CV T k S ,
t
dz
k d dT
T
,
t
ρCV dz dz
159
31
32. В итоге получим уравнение температуропроводности – коэффициент температуро-проводности среды, ρ – плотность, CV – удельная
В итоге получим уравнениетемпературопроводности
T
T
k
χ 2 , χ
,
t
z
ρCV
2
χ – коэффициент температуропроводности среды, ρ – плотность,
CV – удельная теплоёмкость при
постоянном объёме.
159
32
33.
15933
34. Вязкость (вязкое трение) – процесс переноса импульса в газе или жидкости от одного слоя к другому. В жидкостях вязкость
осуществляется непосредственнымвзаимодействием молекул между
собой. Чем меньше подвижность
молекул, тем выше коэффициент
вязкости – с уменьшением
температуры вязкость
увеличивается.
159
34
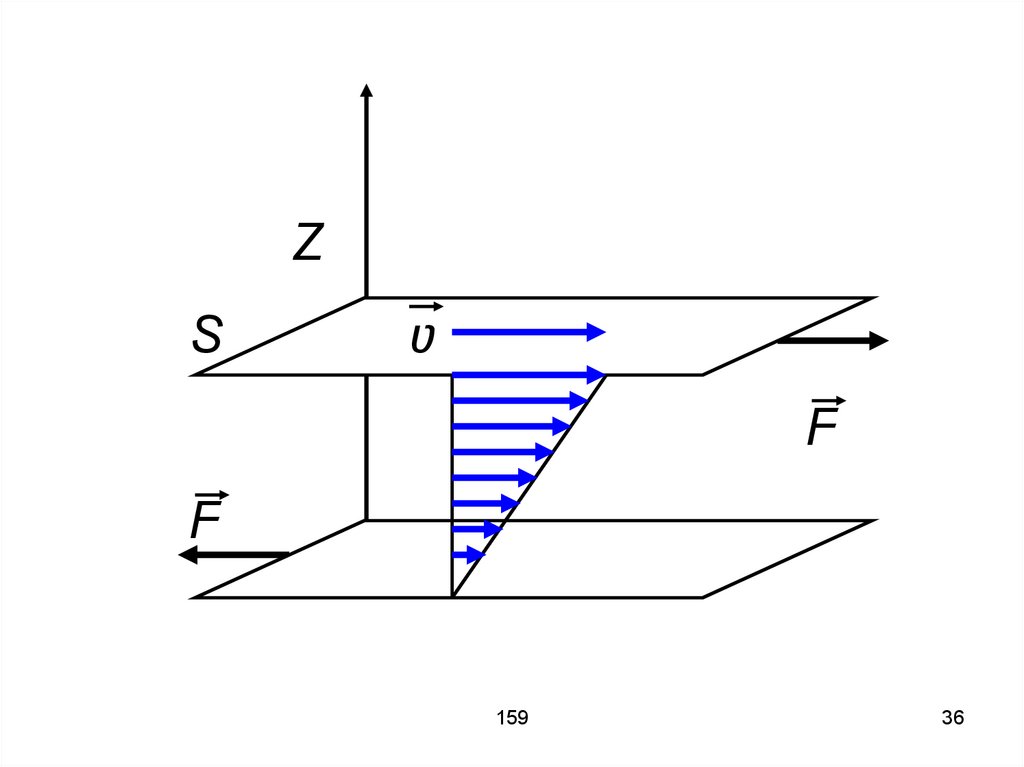
35. Рассмотрим две параллельные пластины площадью S, одна неподвижна и прикреплена к динамометру, другая подвижна. Она движется со
скорость ʋ по действиемнекоторой силы F. Динамометр у
нижней пластины спустя некоторое
время покажет усилие, действующие
на неподвижную пластину, равное F.
159
35
36.
ZS
ʋ
F
F
159
36
37. Формула вязкого трения для газов η – коэффициент вязкости или внутреннего трения (размерность – Па*с (СИ), Пуаз (СГС), 1 Па*с =
Формула вязкого трения для газовd
F η S
dz
η – коэффициент вязкости или
внутреннего трения (размерность –
Па*с (СИ), Пуаз (СГС),
1 Па*с = 10 П).
159
37
38. В газах передача импульса происходит за счёт того, что молекулы перелетают из одного слоя в другой, с ростом температуры
вязкость в газах увеличиваетсяпотому, что растёт скорость молекул
и они более эффективно переходят
из слоя в слой, передавая импульс.
159
38
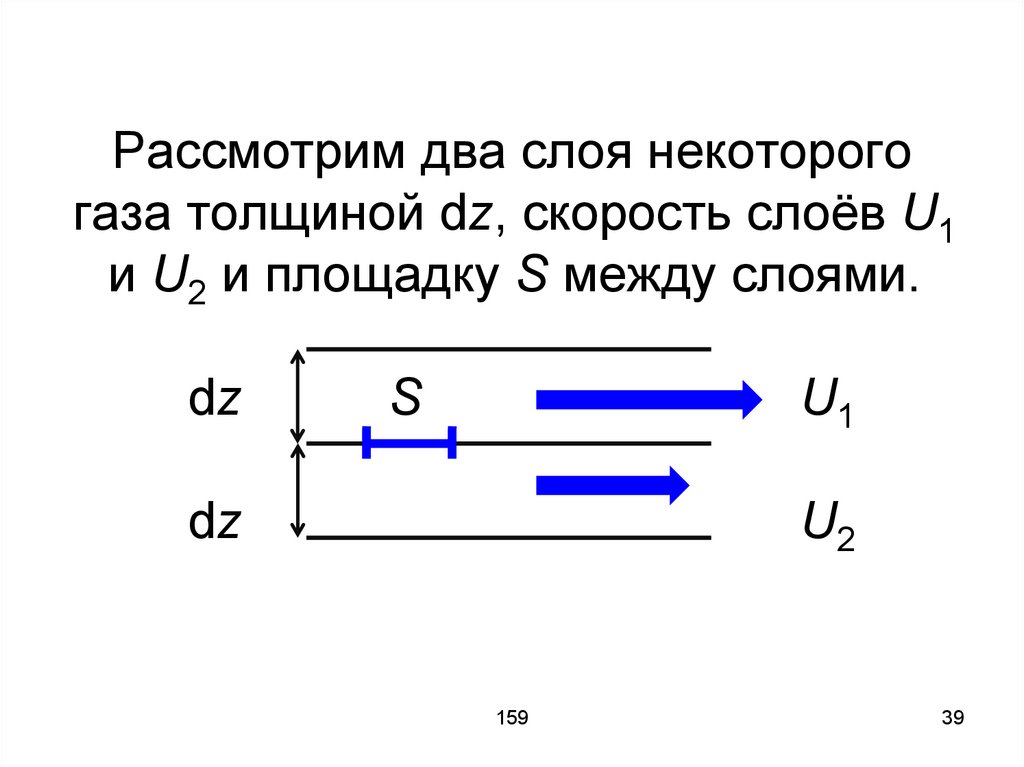
39. Рассмотрим два слоя некоторого газа толщиной dz, скорость слоёв U1 и U2 и площадку S между слоями. dz S U1 dz U2
15939
40. Пусть в какой-то момент времени слои обладают импульсами K1 и K2. Они постоянно меняются, благодаря переходу молекул из одного
слоя вдругой. Число молекул, прошедших
через площадку S за 1 секунду
1
N n S
6
159
40
41. В итоге, больший импульс уменьшается (он получает молекулы с меньшей упорядоченной скоростью), меньший – увеличивается. Запишем
импульс, которыйпередаётся от одного слоя к другому
через площадку S в единицу
времени (m – масса молекулы)
K N mU 1 mU 2
159
41
42. Или Реально, скорость изменяется непрерывно, так как молекула пролетает расстояние λ от удара до удара, перепишем последнее
Или1
K n Sm U1 U 2
6
Реально, скорость изменяется
непрерывно, так как молекула
пролетает расстояние λ от удара до
удара, перепишем последнее
уравнение
1
1
dU
K n Sm U z λ U z λ n Sm
2λ
6
6
dz
159
42
43. Перепишем следующим образом η – коэффициент вязкости.
11
dU
K n Sm U z λ U z λ n Sm
2λ
6
6
dz
Перепишем следующим образом
nm ρ,
dU
1
dU
K λρ
S η
S,
dz
3
dz
1
η λρ
3
η – коэффициент вязкости.
159
43
44.
15944
45. ЛЕКЦИЯ № 16. Элементы физической кинетики
15945
46. ВОПРОСЫ 45. Броуновское движение. 46. Элементы неравновесной термодинамики. Кинетической коэффициенты. Теорема Онсагера.
15946
47. 45. Броуновское движение.
15947
48. Термодинамика неравновесных процессов Классическая термодинамика даёт полное количественное писание равновесных (обратимых)
процессов. Для неравновесныхпроцессов она устанавливает лишь
неравенства, которые указывают
возможное направление этих
процессов.
159
48
49. Задача термодинамики неравновесных процессов – количественное изучение неравновесных процессов для состояний, несильно
отличающихсяот равновесного, в частности
определение скоростей
неравновесных процессов в
зависимости от внешних условий.
159
49
50. Здесь применяют следующий метод: систему представляют состоящей из элементарных объёмов, которые всё же настолько велики, что
содержатбольшое число частиц.
159
50
51. Рассматривают следующие равновесия: Неполное равновесие – параметры системы, характеризующие состояние системы, очень слабо
зависят от времени.159
51
52. Локальное равновесие – равновесие в элементарых объёмах среды, можно характеризовать температурой, химическим потенциалом и
другимитермодинамическими параметрами,
но не постоянными, а зависящими от
координат и времени.
159
52
53. При локальном термодинамическом равновесии элементов среды состояние среды в целом неравновесно. На основе локального
равновесия вфизической кинетики получают
уравнения диффузии,
теплопроводности.
159
53
54. Время релаксации Релаксационные явления: равномерное распределение по всей макросистеме температуры, давления, концентрации,
установление ламинарного теченияили полное прекращение движения
слоёв жидкости относительно друг
друга.
159
54
55. Время релаксации – время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в «е»
раз.159
55
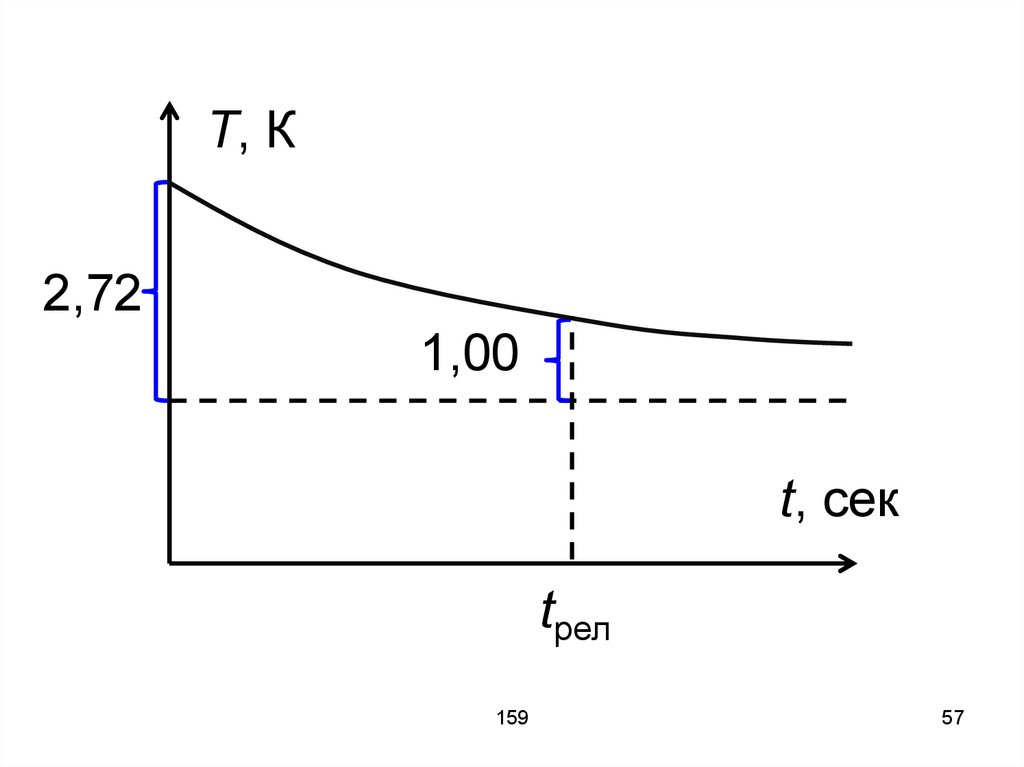
56. Пример: пуст в теплоизолированном поршне (цилиндрический сосуд) создадим в некотором месте скачёк давления, что приведёт к
возрастанию температуры в этойобласти, допустим на 2,72 К.
временем релаксации здесь будет
время, за которое эта разность
температур уменьшится в «е» раз и
станет равной 1,00 К.
159
56
57.
T, К2,72
1,00
t, сек
tрел
159
57
58. Броуновское движение – хаотическое движение взвешенных микрочастиц в газах или жидкостях. Теорию движения броуновских частиц
разработали А. Эйнштейн иМ. Смолуховский.
159
58
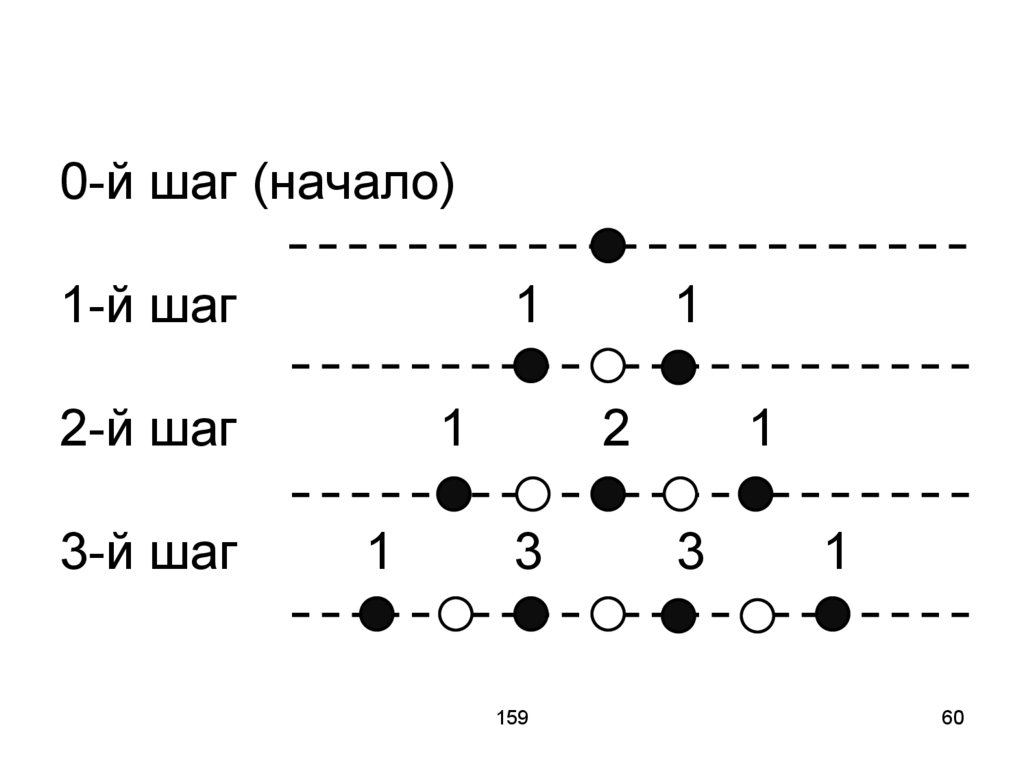
59. Модель: Блуждание «абсолютно пьяного человек». Каждый раз человек смещается на 1 шаг вправо или влево.
15959
60. 0-й шаг (начало) 1-й шаг 1 1 2-й шаг 1 2 1 3-й шаг 1 3 3 1
0-й шаг (начало)1-й шаг
1
2-й шаг
3-й шаг
1
1
1
2
3
159
1
3
1
60
61. Среднее смещение равно нулю, но средний квадрат пропорционален числу шагов или времени. То же и для броуновской частицы.
15961
62. Уравнение движения F0 – сила, действующая на броуновскую частицу, m – масса броуновской частицы, B – коэффициент – подвижность
Уравнение движения2
dx
dx dt
m 2 F0
dt
B
F0 – сила, действующая на
броуновскую частицу, m – масса
броуновской частицы, B –
коэффициент – подвижность
частицы.
159
62
63. Движение броуновской частицы определяется хаотически меняющейся силой f, поэтому от постоянной силы F0 перейдём к f.
15963
64. Используем следующие выражения умножим на x уравнение движения и получим:
Используем следующие выраженияd x
dx d x
d x dx
2x ,
2 x 2 2 ,
2
dt
dt
dt
dt
dt
2
2
2
2
2
умножим на x уравнение движения
2
d x
dx dt
m 2 f
dt
B
и получим:
1 d x
d x dt
dx
m
m xf
0
2
2
dt
2B
dt
2
2
2
159
2
64
65. Усредним полученное выражение по времени: Перепишем энергию теплового движения:
Усредним полученное выражение повремени:
x 0,
f 0,
x f 0.
Перепишем энергию теплового
движения:
2
dx
m kT
dt
159
65
66. Получаем: Если пропорционален времени ( ~ t), то первый член исчезает, и мы получаем формулу Эйнштейна:
Получаем:2
2
2
d x dt
1 d x
m
kT
0
2
2
dt
2B
2
Если x пропорционален времени
2
( x ~ t), то первый член исчезает, и
мы получаем формулу Эйнштейна:
x 2kTBt
2
159
66
67. В случае движения в плоскости в объёме
В случае движения в плоскостиr x y 4kTBt
2
2
2
в объёме
R x y z 6kTBt
2
2
2
159
2
67
68. Броуновское движение как диффузия Рассмотрим броуновское движение в поле сил тяжести;
15968
69. в стационарном состоянии, когда установится больцмановское распределение концентрации частиц поток частиц, движущихся по
в стационарном состоянии, когдаустановится больцмановское
распределение концентрации частиц
Mgh
fx
n n0 exp
n0 exp
RT
kT
поток частиц, движущихся по
направлению силы со скоростью Bf,
должен компенсироваться
диффузионным потоком в
направлении уменьшения
концентрации,
159
69
70. То есть Dбр – коэффициент диффузии броуновских частиц.
То естьdn
nBf Dбр
dt
Dбр – коэффициент диффузии
броуновских частиц.
159
70
71. Отсюда формула Эйнштейна принимает вид
fx dnf
fx
n n0 exp
n0
,
exp
kT dx
kT
kT
Отсюда
fD
Bf
D BkT ,
kT
формула Эйнштейна принимает вид
R 6Dt
2
159
71
72.
15972
73. 46. Элементы неравновесной термодинамики. Кинетической коэффициенты. Теорема Онсагера.
15973
74. В случае изолированной системы выполняется второе начало термодинамики и в случае равновесного состояния энтропия максимальна
В случае изолированной системывыполняется второе начало
термодинамики
dS
0
dt
и в случае равновесного состояния
энтропия максимальна (тепловая
смерть вселенной).
159
74
75. В открытых системах происходит постоянный обмен с окружающей средой энергией и веществом. Здесь даже малые воздействия могут
привести к значительнымпоследствиям. В описании
неравновесных процессов
используют понятие возрастание
энтропии системы
dS dt σ
159
75
76. При определённых условиях суммарное уменьшение энтропии за счёт обмена с внешней средой может превысить её внутреннее
производство. Появляетсянеустойчивость предшествующего
неупорядоченного однородного
состояния, возникают и возрастают
крупномасштабные флуктуации.
159
76
77. При этом оказывается возможной самоорганизация – создание определённых структур из хаоса, неупорядоченности (примеры: тайфун,
торнадо, смерчи).Эти структуры могут
последовательно переходить во всё
более упорядоченные состояния. В
таких системах энтропия убывает.
159
77
78. Принцип Онсагера Онсагер, на основе выше сказанного, предположил, что при небольших отклонениях от равновесия существует
линейная связь междупотоками Ii и термодинамическими
силами Xj.
m
I i Lij X j
j 1
Lij – кинематический или
феноменологический коэффициент.
159
78
79. В термодинамике необратимых процессов скорость приращения энтропии (производство энтропии) за счёт необратимых процессов может
быть представлена в видеm
σ Ii X i
i 1
159
79
80. Коэффициент Lij отражает факт существования перекрёстных эффектов (процессов) перенос одной величины (заряд, масса, энергия и
т.д.) неразрывно связан спереносом другой (импульс,
температура и т.д.).
159
80
81. Шумы флуктуации накладывают ограничение на чувствительность приборов. Как правило, чувствительность не достигает уровня
флуктуаций (напримердавление).
159
81
82. Тепловой шум: электроны в электрических приборах ведут себя подобно молекулам идеального газа, соответственно, их концентрация,
вразличных частях электрической
системы, испытывает флуктуации,
что приводит к скачкам напряжения и
силы тока.
159
82
83. Если отношение «сигнал/шум» мало, то сигнал идёт с большим искажением либо его невозможно обнаружить.
15983
84. Дробовой шум: шум, определяемый дискретностью электрического заряда. В полупроводниках два типа носителей заряда: дырки и
электроны, которые могутгенерироваться и рекомбинировать.
Поэтому величина шума в
полупроводниках в два раза выше,
чем в проводниках.
159
84
85.
15985
86. ЛЕКЦИЯ № 17.
15986
87. ВОПРОСЫ 47. Кристаллы. Кристаллическая решётка. Преобразования симметрии. Жидкие кристаллы. 48. Неравновесные процессы.
Синергетика. Бифуркация.159
87
88. 47. Кристаллы. Кристаллическая решётка. Преобразования симметрии. Жидкие кристаллы.
15988
89. Кристаллы (krystallos (греч.) – лёд) – твёрдые тела обладающие трёхмерной периодической атомной структурой и, при равновесных
условиях образования, имеющиеестественную форму правильных
симметричных многогранников.
159
89
90. Кристаллы обладают симметрией. Здесь симметрия это свойство тела совмещаться с самим собой при определённых перемещениях,
называемых преобразованиями илиоперациями симметрии.
Эти перемещения не должны
сопровождаться изменением
расстояния между атомами.
159
90
91. Преобразования симметрии: 1) параллельный перенос всех точек тела на определённое расстояние (трансляция); 2) поворот тела
вокруг некоторой осина определённый угол;
3) отражение в плоскости;
4) инверсия или отражение в точке;
а также все комбинации таких
преобразований.
159
91
92. Таким образом, можно отменить основное отличие кристаллов от жидкостей и аморфных тел: периодичность пространственного
расположения атомов, молекул илиионов, из которых состоит кристалл.
Такая периодичность получила
название дальнего порядка.
159
92
93. В аморфных и жидких телах упорядоченное расположение частиц может распространяться только на соседние атомы – ближний порядок.
15993
94. Кристаллическая решётка – упорядоченное расположение атомов, молекул или ионов, характеризующиеся периодичной повторяемостью в
трёх измерениях.159
94
95. Плоские грани кристалла, образовавшегося в равновесных условиях, соответствуют атомным плоскостям, рёбра – рядам атомов.
Расположение атомов соответствуетминимуму энергии.
159
95
96. Для описания кристаллической решётки достаточно знать размещение атомов в её элементарной ячейке, повторением которой путём
параллельныхпереносов (трансляций) образуется
кристаллическая решётка.
159
96
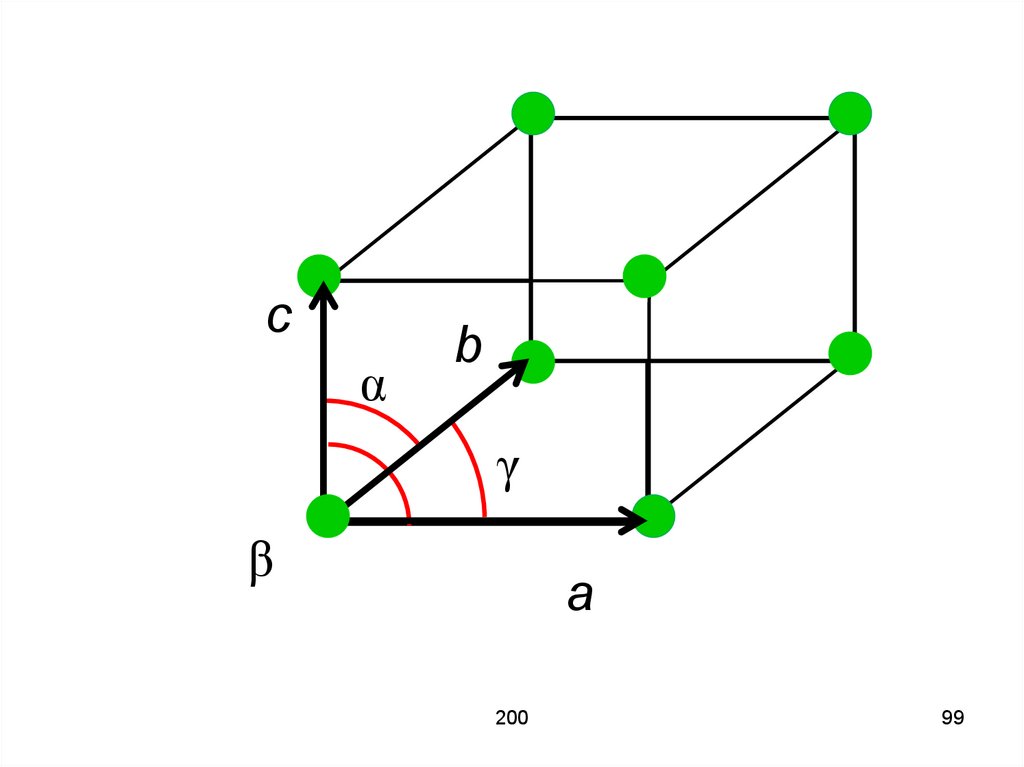
97. Элементарная ячейка имеет форму параллелепипеда. Рёбра элементарного параллелепипеда a, b, c называются постоянными или
периодами кристаллической решёткилибо векторами трансляции. Этот
параллелепипед характеризуется
также углами α, β, γ между рёбрами.
159
97
98. Параллелепипед минимального объёма, содержащий наименьшее число атомов, называется примитивной (элементарной) ячейкой. Величины
a, b, c и α, β, γ однозначноопределяют элементарную ячейку и
называются её параметрами.
159
98
99.
cα
b
γ
β
a
200
99
100.
159100
101. Кристаллическая решётка, как правило, обладает одновременно несколькими видами симметрии. Но возможны всего 230 комбинаций
элементов симметрии, которыеназываются пространственными
группами. 230 групп делятся на 32
класса. Классы, по форме
элементарной ячейки делятся на
семь кристаллических систем
(сингоний).
159
101
102. 1) Триклинная система. a ≠ b ≠ c и α ≠ β ≠ γ. Элементарная ячейка имеет форму косоугольного параллелепипеда.
159102
103. 2) Моноклинная система. a ≠ b ≠ c, α = γ = 90º, β ≠ 90º. Элементарная ячейка имеет форму прямой призмы, в основании которой
лежит параллелограмм (т.е. формупрямого параллелепипеда).
159
103
104. 3) Ромбическая система. a ≠ b ≠ c, α = β = γ = 90º. Элементарная ячейка имеет форму прямоугольного параллелепипеда.
159104
105. 4) Тетрагональная система. a = b ≠ c, α = β = γ = 90º. Элементарная ячейка имеет форму прямой призмы с квадратным основанием.
159105
106. 5) Ромбоэдрическая (или тригональная) система. a = b = c, α = β = γ ≠ 90º. Элементарная ячейка имеет форму куба,
деформированного сжатиемили растяжением вдоль диагонали.
159
106
107. 6) Гексагональная система. a = b ≠ c, α = β = 90º, γ = 120º. Если составить вместе три элементарные ячейки, то получается
правильная шестиугольная призма.159
107
108. 7) Кубическая система. a = b = c, α = β = γ = 90º. Элементарная ячейка имеет форму куба.
159108
109. Жидкие кристаллы Особое состояние некоторых органических веществ, в котором они обладают свойствами жидкости – текучестью, но
сохраняютопределённую упорядоченность в
расположении молекул и
анизотропию ряда физических
свойств, характерную для твёрдых
кристаллов.
159
109
110. Число химических соединений для которых найдены жидкие кристаллы несколько тысяч. Но для использования годятся несколько
десятков.159
110
111. По способу получения различают два типа жидких кристаллов: термотропные и лиотропные. Первые образуются при нагревании твердых
кристаллов или приохлаждении изотропных жидкостей и
существуют в некотором
температурном интервале.
159
111
112. Вторые образуются при растворении твердых органических веществ, например, в воде или других растворителях. Оба типа жидких
кристаллов имеют несколькомодификаций –
жидкокристаллических фаз, каждой
из которых на фазовой диаграмме
соответствует определенная
область.
159
112
113. Эта область зависит от типа вещества и может находиться как при низких до 60 С, так и при высоких температурах 400 С.
Эта область зависит от типавещества и может находиться как
при низких до 60 С, так и при
высоких температурах 400 С.
159
113
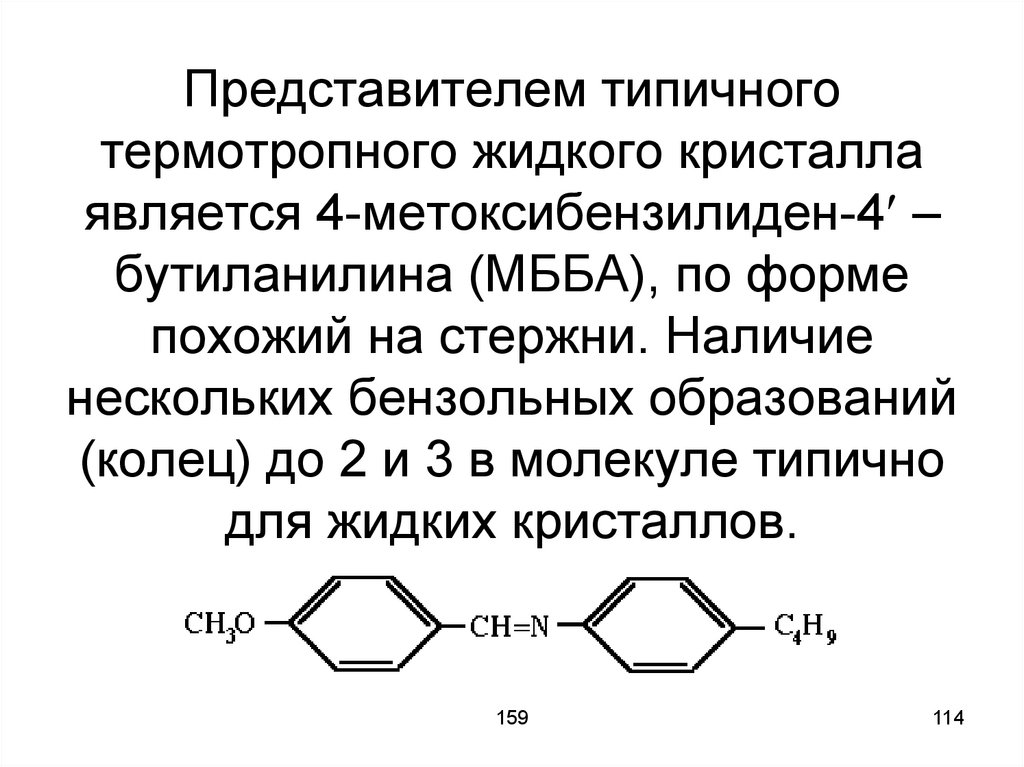
114. Представителем типичного термотропного жидкого кристалла является 4-метоксибензилиден-4 – бутиланилина (МББА), по форме
Представителем типичноготермотропного жидкого кристалла
является 4-метоксибензилиден-4 –
бутиланилина (МББА), по форме
похожий на стержни. Наличие
нескольких бензольных образований
(колец) до 2 и 3 в молекуле типично
для жидких кристаллов.
159
114
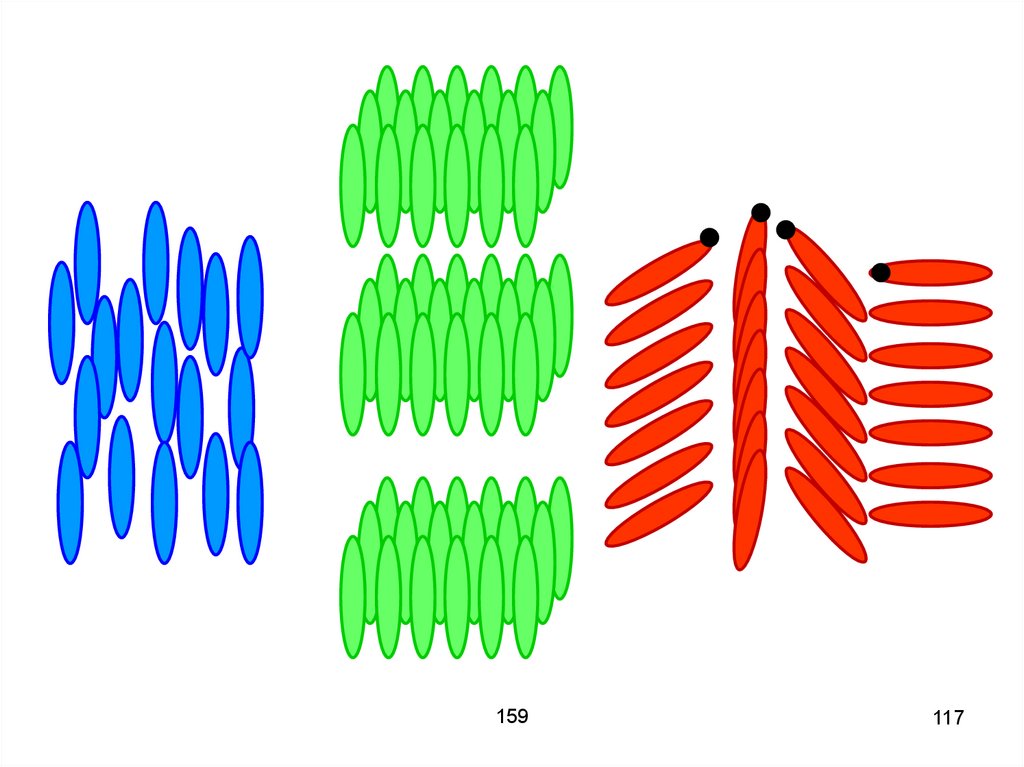
115. Нематические жидкие кристаллы – молекулы параллельны, но сдвинуты вдоль своих осей, одна относительно другой на произвольные
расстояния.159
115
116. Смектические жидкие кристаллы – молекулы параллельны друг другу и расположены слоями. Холестерические жидкие кристаллы – похожи
на нематические, ноотличаются дополнительным
закручиванием молекул в
направлении, перпендикулярном их
длинным осям.
159
116
117.
159117
118.
159118
119. 48. Неравновесные процессы. Синергетика. Бифуркация.
159119
120. Неравновесные процессы Классическая термодинамика описывает стабильность, равновесие. Вблизи равновесия система однозначно
реагирует на неслишком большое возмущение,
возвращаясь в состояние
равновесия.
159
120
121. При этом частицы, составляющие систему, взаимодействуют только на близких расстояниях и ничего «не знают» о частицах,
расположенныхдостаточно далеко. Здесь вполне
адекватна модель замкнутой
системы.
159
121
122. Однако, если система далеко отклоняется от состояния равновесия, то возврат к начальному состоянию необязателен. Здесь
целесообразно рассматриватьмодель открытых диссипативных
систем, постоянно обменивающихся
с окружающей средой энергией и
веществом.
159
122
123. Именно в открытых системах для состояний, далёких от равновесия, возникают эффекты согласования, когда частицы как бы
устанавливаютсвязь друг с другом на
макроскопических расстояниях,
через макроскопические интервалы
времени.
159
123
124. В результате согласованного взаимодействия надсистем происходят процессы упорядочения, возникновения из хаоса определённых
структур, ихпреобразования и усложнения.
159
124
125. Возникновение макроскопических структур обусловлено рождением коллективных типов движения (мод) под действием крупномасштабных
флуктуаций, их конкуренцией,отбором наиболее приспособленных
мод,
159
125
126. то есть в конечном счёте спонтанное возникновение структур в неупорядоченных системах связано с совместным коллективным
поведением подсистемы,образующих систему.
159
126
127. Область науки, изучающая эти процессы, получила название «синергетика».
159127
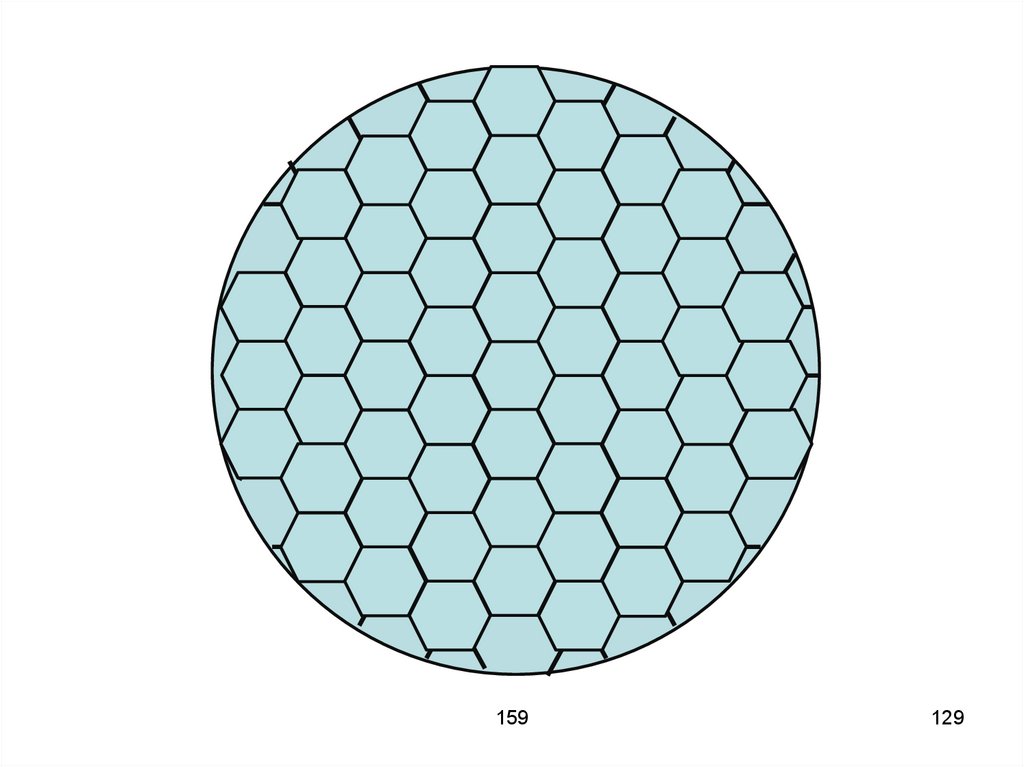
128. Пример1. Ячейка Бенара. На сковороду наливают тонкий слой минерального масла (5 мм) и подогревают снизу горячей водой. При
достижении критическогоградиента в жидкости возникают
потоки и образуются красивые
шестиугольные ячейки. В центре
ячейки конвекционный поток
движется вверх, а по краям – вниз.
159
128
129.
159129
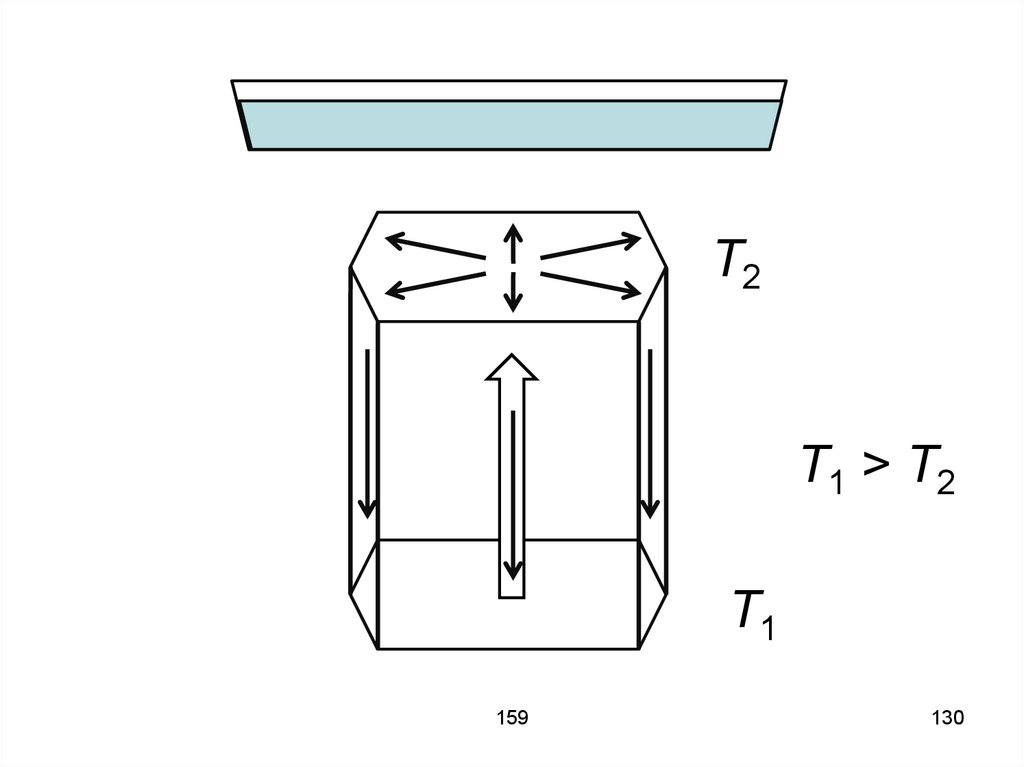
130.
T2T1 > T2
T1
159
130
131. Ячейки Бенара в неравновесной термодинамике играют исключительную роль, поскольку в этом явлении очень отчётливо проявляются
все основные чертытермодинамики необратимых
процессов.
159
131
132. По сравнению с однородным состоянием конвективные ячейки являются более высокоорганизованной структурой – открытая система
отдаёт энтропию.Образование же её связано с
неустойчивостью
крупномасштабного конвективного
движения и обусловлено
следующими обстоятельствами.
159
132
133. Если слой жидкости сильно нагреть, то возникает разность (градиент) температур ΔT между нижней и верхней поверхностями. Такой
температурный градиент называетсяинверсным, так как жидкость у
нижней поверхности вследствие
теплового расширения имеет
меньшую плотность, чем вблизи
верхней поверхности.
159
133
134. Из-за силы тяжести и архимедовой выталкивающей силы такая система оказывается неустойчивой, поскольку «лёгкий» нижний слой и
«тяжёлый» верхний стремятсяпоменяться местами.
159
134
135. Однако, вследствие вязкости жидкости, при небольших градиентах температуры движение не возникает и тепло передаётся только
путёмтеплопроводности.
159
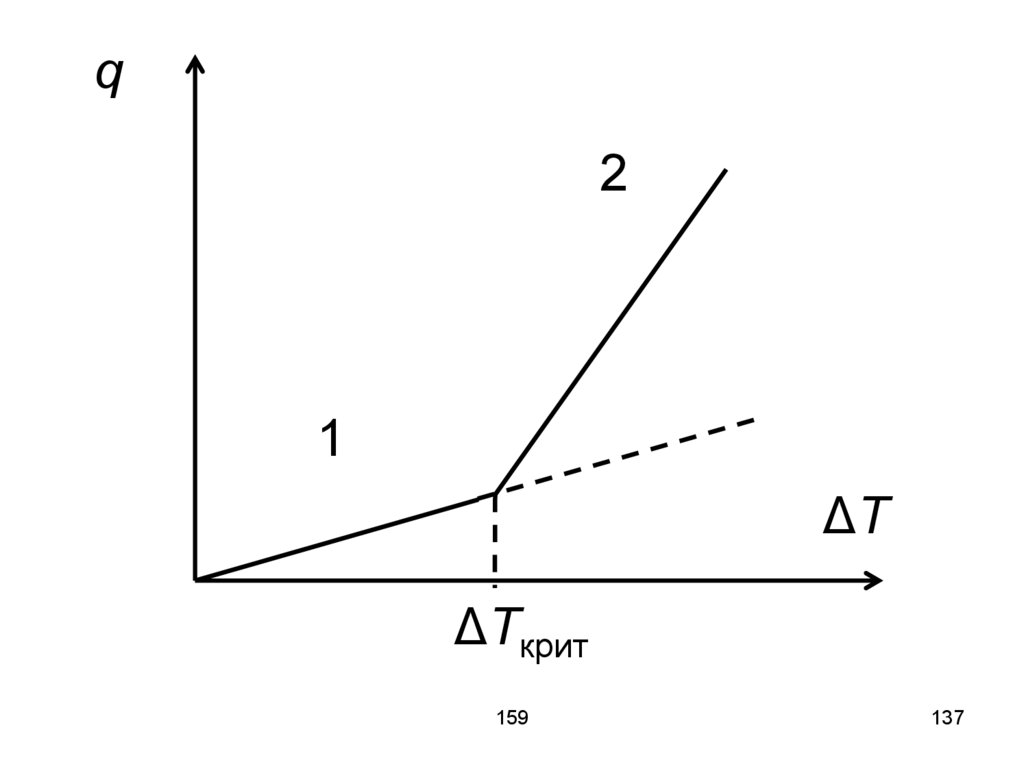
135
136. Лишь при достижении критического значения температурного градиента появляется конвекционный поток, обладающий характерной
структуройв виде шестиугольных ячеек. Внутри
ячеек жидкость поднимается вверх,
а по краям спускается вниз.
159
136
137.
q2
1
ΔT
ΔTкрит
159
137
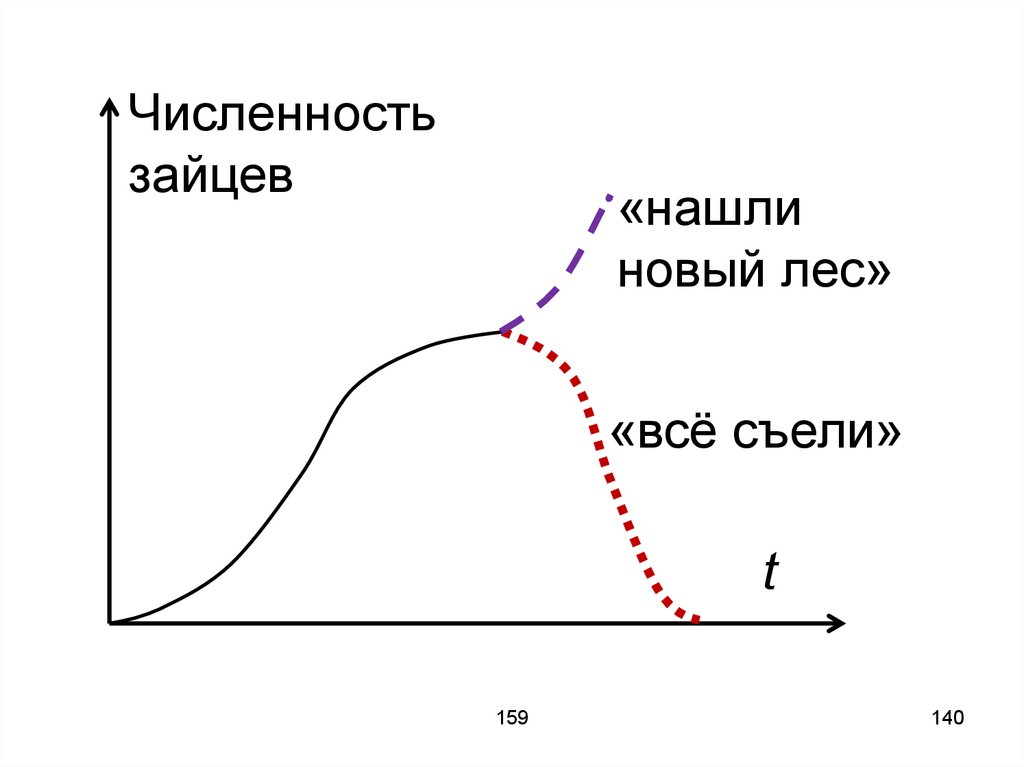
138. Бифуркация- качественное различие в поведение объекта, при незначительном изменении параметра, от которого зависит объект.
159138
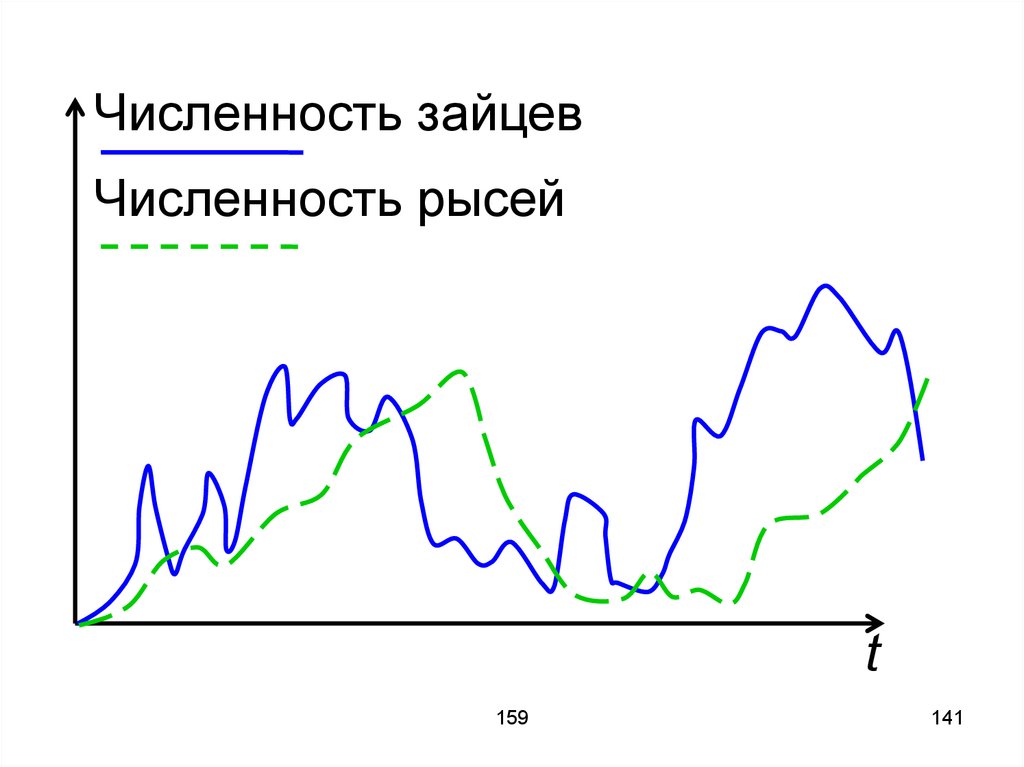
139. Пример 2. Эволюция численности зайцев и рысей. В результате взаимодействия двух биологических систем возникают периодические
колебаниячисленности особей.
159
139
140.
Численностьзайцев
«нашли
новый лес»
«всё съели»
t
159
140
141.
Численность зайцевЧисленность рысей
t
159
141
142.
159142




























































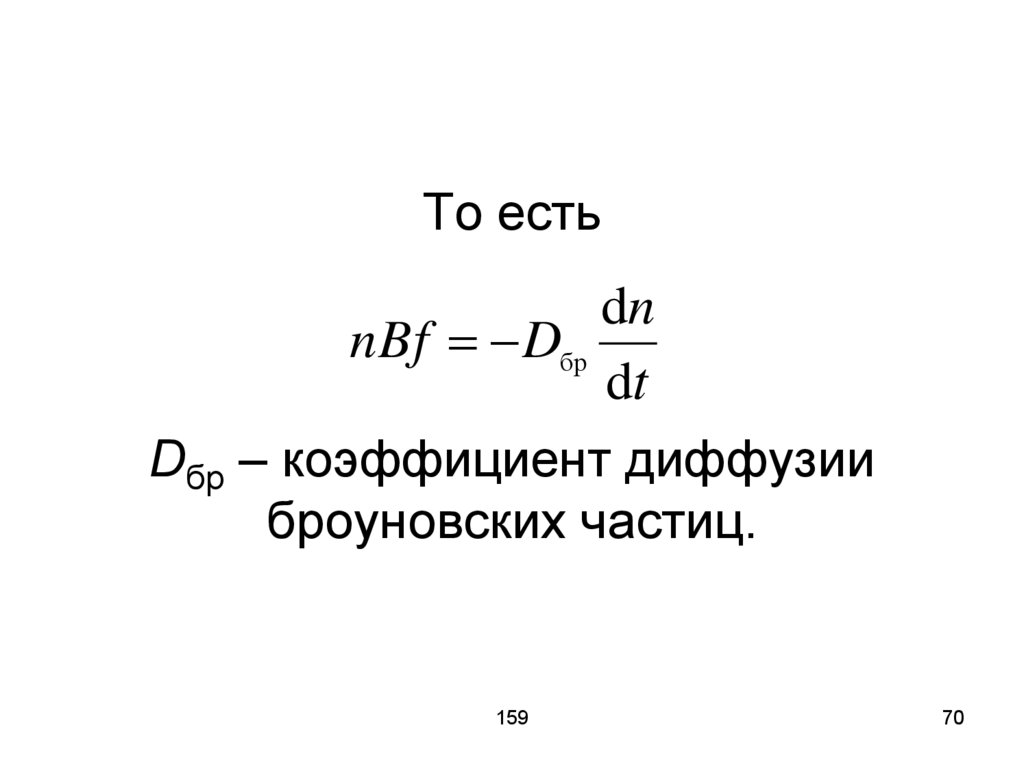































































 Физика
Физика








