Явления переноса

1. Явления переноса

ВоГУ
Лекция 7
Явления переноса
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1

2.

2

3.

Явления переноса в неравновесных системах
Определение:
Система неравновесна,
если какая-либо физическая
характеристика вещества имеет разные
значения в разных точках системы
В таких системах происходят необратимые процессы,
называемые явлениями переноса.
Следствия этих процессов – выравнивание характеристик
вещества по всему объёму

4.

Явления переноса в неравновесных системах
1) Если неодинакова концентрация частиц,
происходит перенос массы вещества; это – диффузия
2) Если неодинакова скорость направленного движения
частиц,
происходит перенос импульса;
это – вязкость (внутренне трение)
3) Если неодинакова температура,
происходит перенос энергии (теплоты)
это – теплопроводность
Законы, описывающие явления переноса, были открыты экспериментально

5.

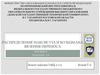
Диффузия
Пусть концентрация частиц n изменяется
вдоль оси OZ
Плотность потока частиц IN– число
частиц, перенесённых за единицу
времени через единичную площадку,
dN
перпендикулярную
I
направлению переноса: N S dt
Закон Фика:
Плотность потока частиц IN
пропорциональна градиенту
dn I D dn
концентрации
: N
dz
dz
dn
dN D S dt
dz

6.

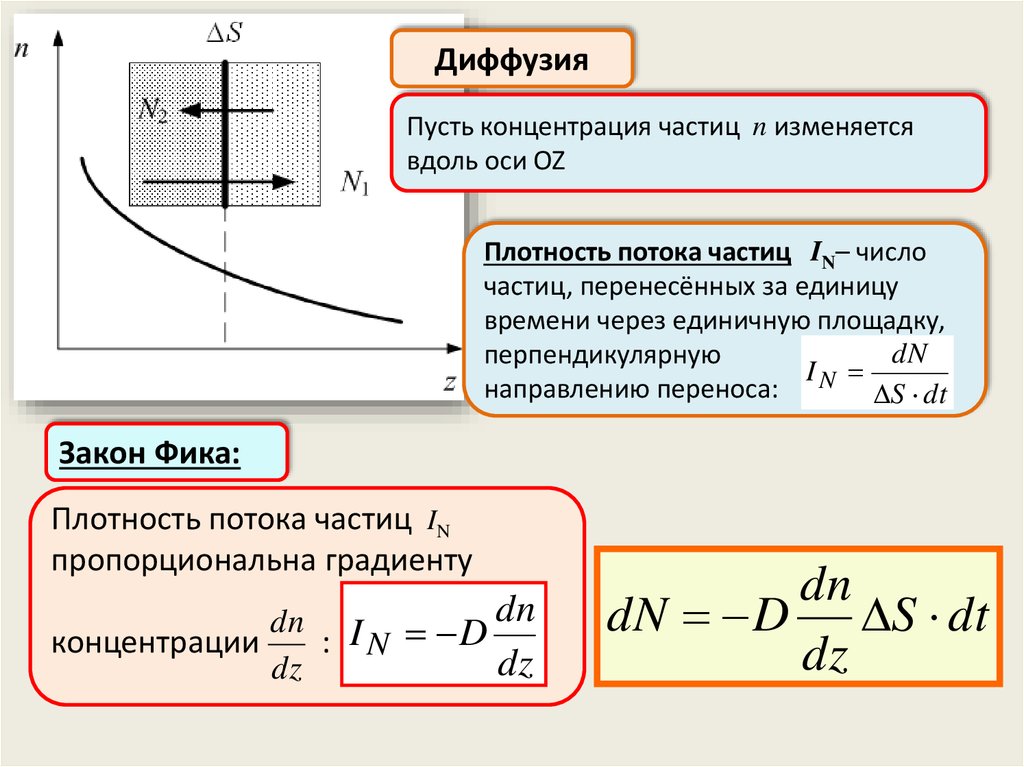
Диффузия
dn
dN D S dt
dz
Закон Фика:
Число частиц, перенесённых за время
dt через малую площадку ΔS,
пропорционально и промежутку
времени, и величине площадки, а
dn
также градиенту концентрации
,
dz
показывающему, как быстро
изменяется концентрация вдоль
оси OZ
Коэффициент диффузии
Перенос происходит в точки с меньшей
концентрацией

7.

Диффузия
d n m0
d N m0 D
S dt
dz
dn
dN D S dt
dz
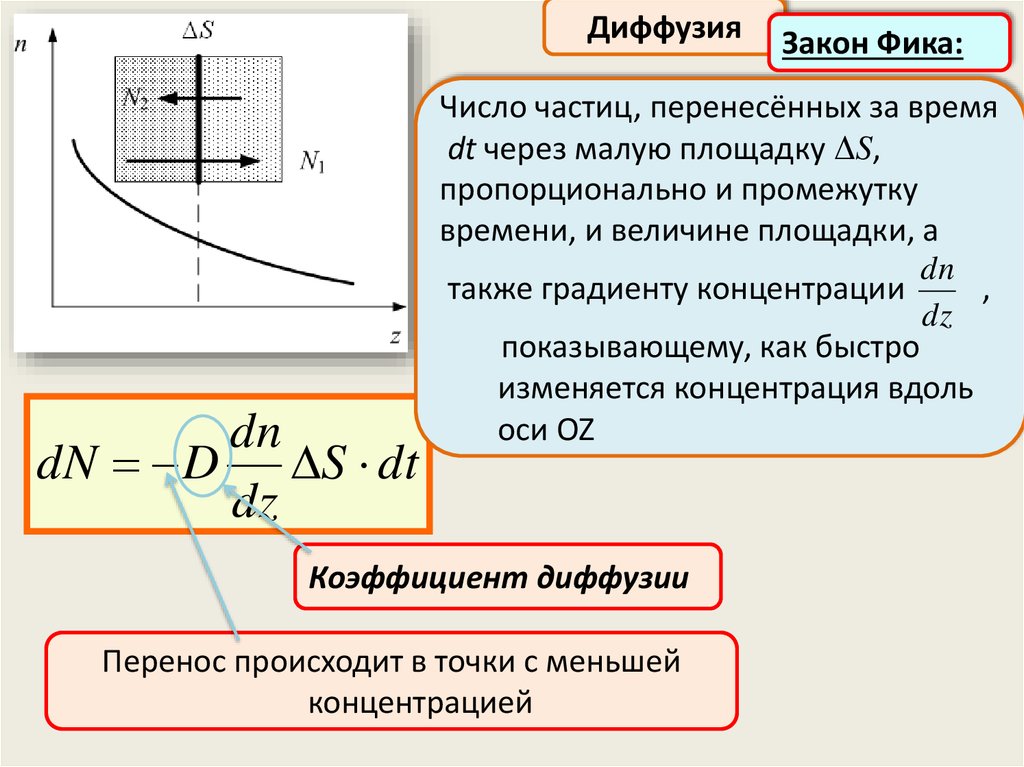
Плотность потока массы
По определению: По закону Фика:
Im
dm
S dt
d
I m D
dz
d
dm D
S dt
dz
Коэффициент диффузии D численно равен массе вещества,
перенесённого за единицу времени через единичную
площадку при единичном градиенте плотности
dm
D
d
S dt
dz
м2
кг 2
с
м
с
м4
кг

8.

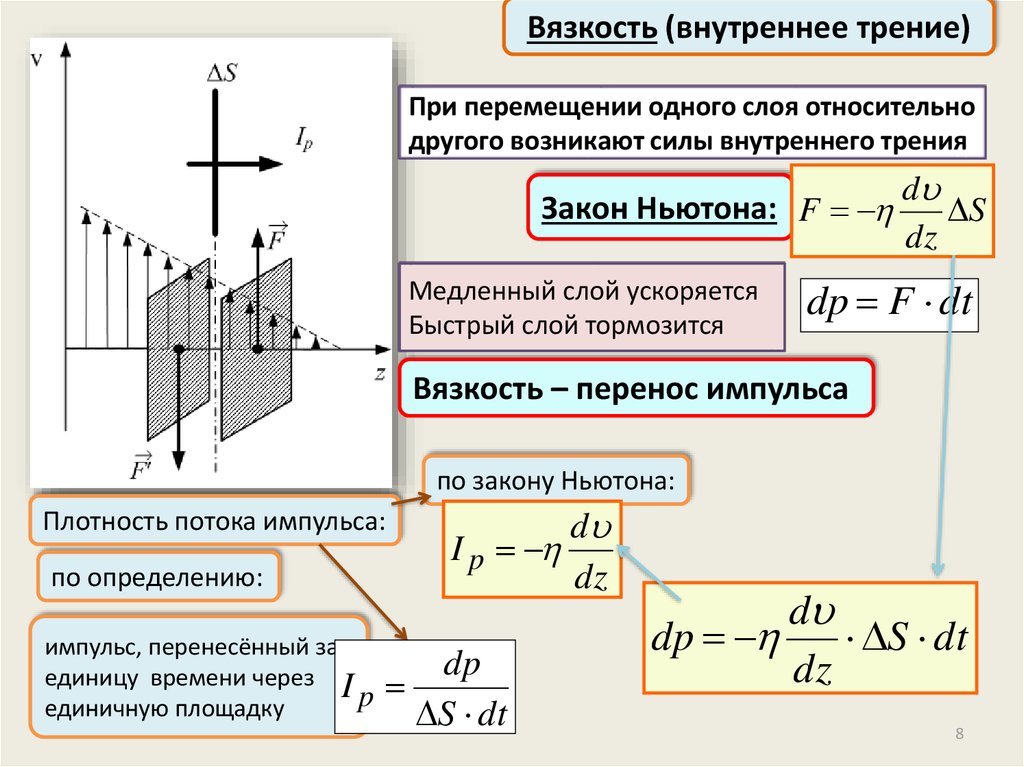
Вязкость (внутреннее трение)
При перемещении одного слоя относительно
другого возникают силы внутреннего трения
Закон Ньютона: F
Медленный слой ускоряется
Быстрый слой тормозится
d
S
dz
dp F dt
Вязкость – перенос импульса
по закону Ньютона:
Плотность потока импульса:
по определению:
импульс, перенесённый за
единицу времени через I
p
единичную площадку
d
I p
dz
dp
S dt
d
dp
S dt
dz
8

9.

Вязкость. Закон Ньютона
d
dp
S dt
dz
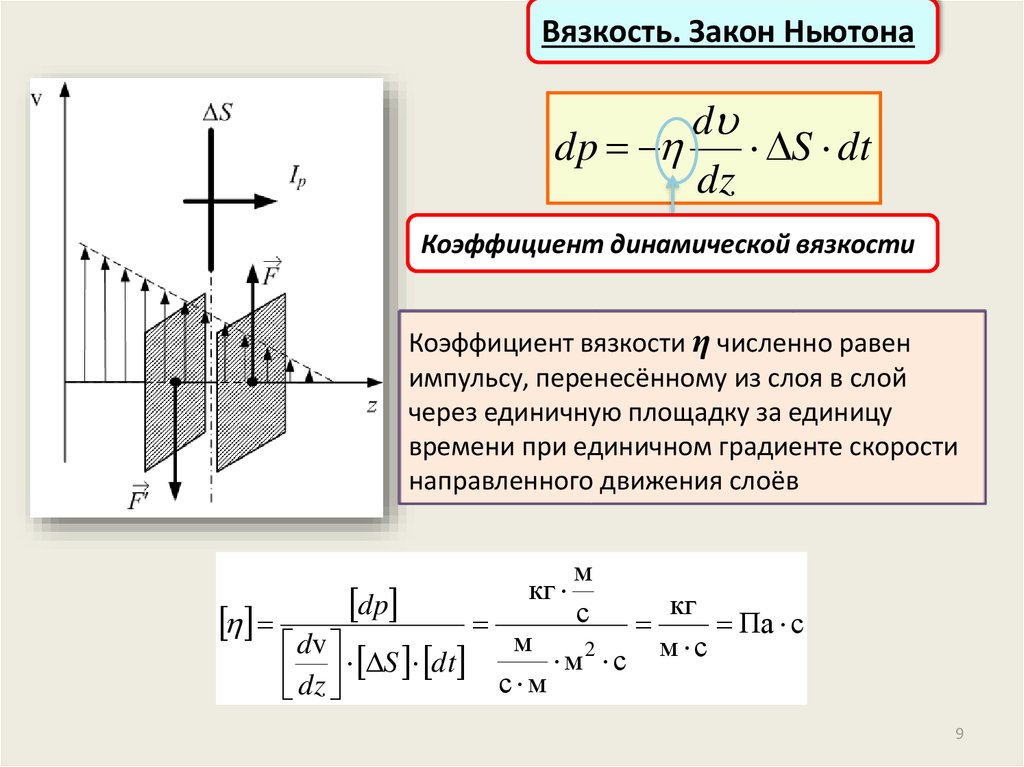
Коэффициент динамической вязкости
Коэффициент вязкости η численно равен
импульсу, перенесённому из слоя в слой
через единичную площадку за единицу
времени при единичном градиенте скорости
направленного движения слоёв
dp
d
v
S dt
dz
кг
м
с
кг
Па с
м
м2 с м с
с м
9

10.

Теплопроводность. Закон Фурье
Количество теплоты, перенесённой через площадку
dT
ΔS за время dt, пропорционально градиенту температуры
dz
dT
dQ
S dt
dz
Коэффициент теплопроводности
численно равен количеству теплоты,
перенесённой через единичную
площадку за единицу времени при
единичном градиенте температуры
dQ
Дж
Дж
К
dT
м2 с К м с
S
dt
dz
м
10

11.

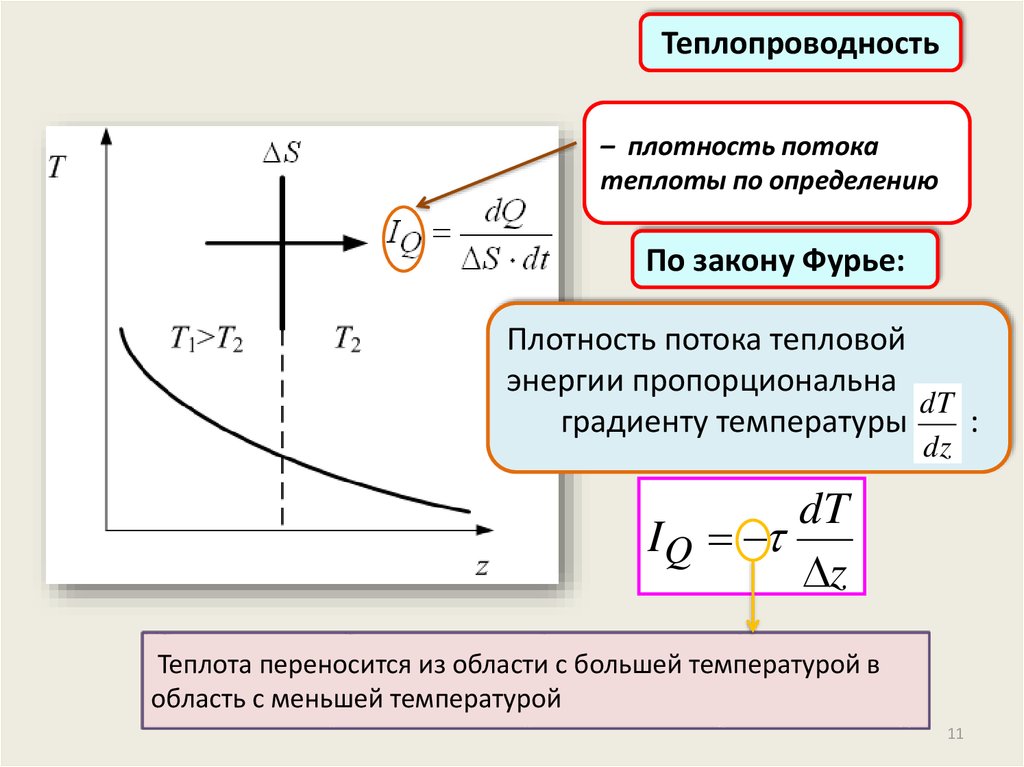
Теплопроводность
– плотность потока
теплоты по определению
По закону Фурье:
Плотность потока тепловой
энергии пропорциональна
dT
градиенту температуры
:
dz
dT
I Q
z
Теплота переносится из области с большей температурой в
область с меньшей температурой
11

12.

Явления переноса в твёрдых и жидких телах
Диффузия
– в жидкостях протекает медленнее, чем в газах
Для некоторых твёрдых тел при комнатной температуре
практически не заметна
Это объясняется меньшей подвижностью частиц в
конденсированной фазе
С ростом температуры подвижность молекул растёт
диффузии жидкости увеличивается
коэффициент

13.

Вязкость
жидкости с ростом температуры уменьшается, так как
молекулы легче меняют своё положение и, например,
при движении тела в жидкости легче «пропускают» его,
перестраиваясь в другое положение.
Сами же коэффициенты вязкости для жидкостей на несколько порядков больше,
чем для газов.
Теплопроводность жидких и твёрдых тел больше, чем газов.
Это объясняется взаимодействием частиц, в результате которого тепловая
энергия передаётся быстрее. У металлов теплопроводность большая
за счёт очень подвижных электронов

14.

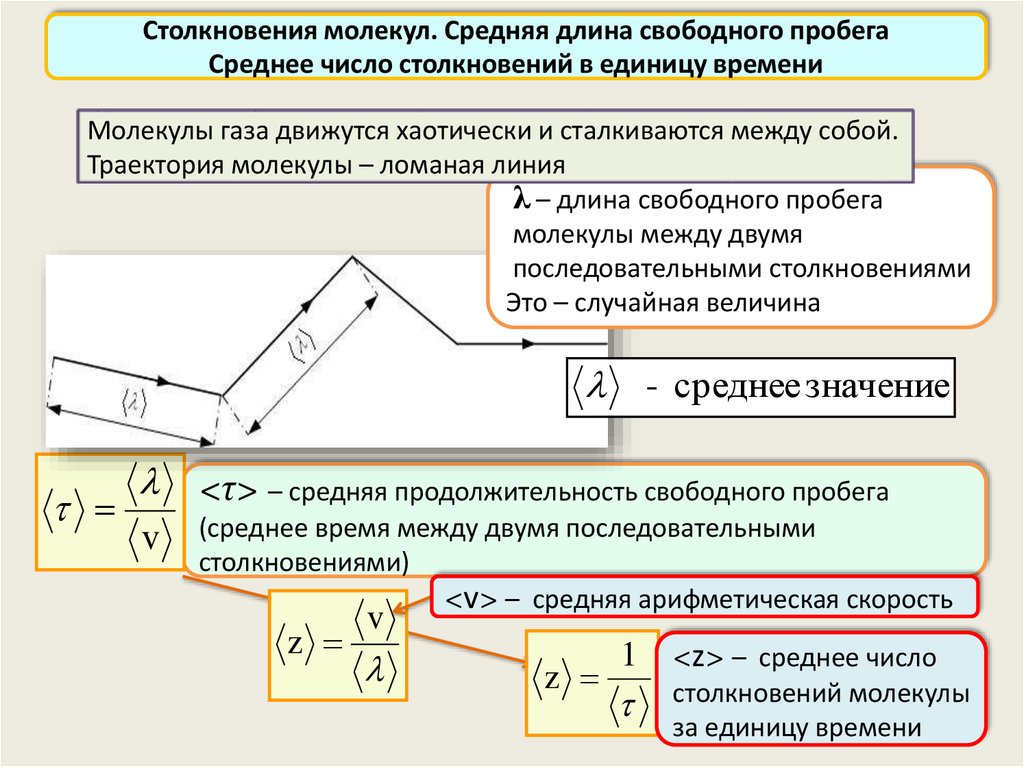
Столкновения молекул. Средняя длина свободного пробега
Среднее число столкновений в единицу времени
Молекулы газа движутся хаотически и сталкиваются между собой.
Траектория молекулы – ломаная линия
λ – длина свободного пробега
молекулы между двумя
последовательными столкновениями
Это – случайная величина
- среднее значение
<τ> – средняя продолжительность свободного пробега
(среднее время между двумя последовательными
v
столкновениями)
z
v
<v> – средняя арифметическая скорость
z
1 <z> – среднее число
столкновений молекулы
за единицу времени

15.

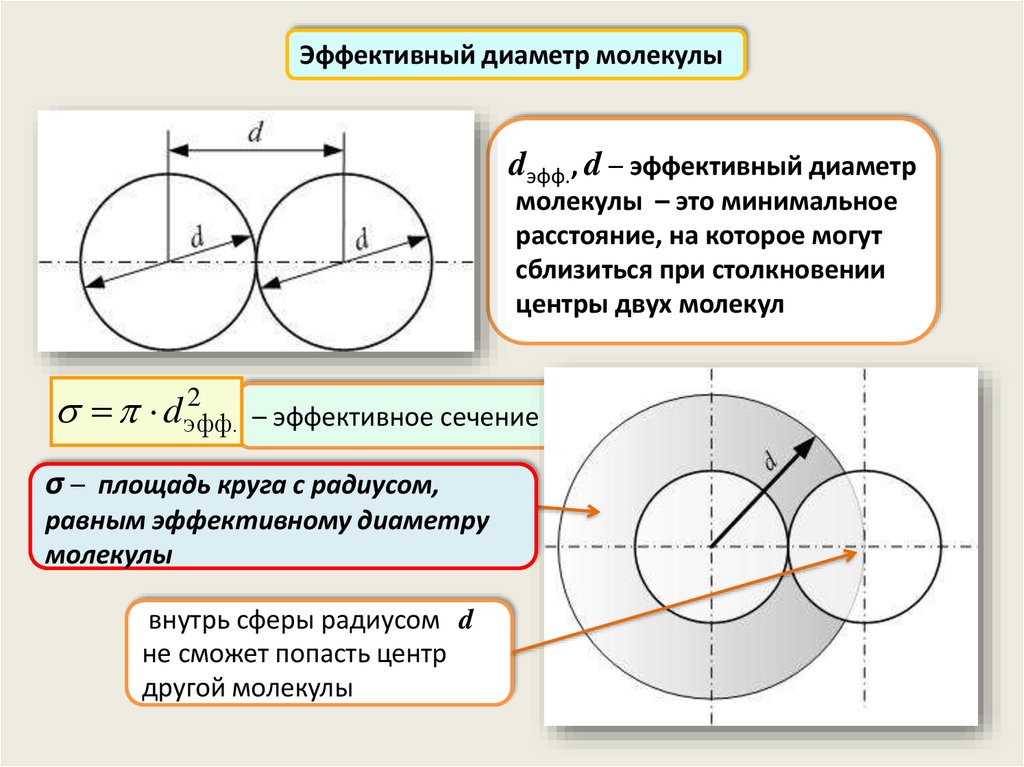
Эффективный диаметр молекулы
dэфф., d – эффективный диаметр
молекулы – это минимальное
расстояние, на которое могут
сблизиться при столкновении
центры двух молекул
2
dэфф.
– эффективное сечение
σ – площадь круга с радиусом,
равным эффективному диаметру
молекулы
внутрь сферы радиусом d
не сможет попасть центр
другой молекулы

16.

Среднее число столкновений молекулы с другими в единицу времени
z
Рассмотрим движение одной молекулы среди неподвижных молекул
Столкновение произойдёт, если центр
какой-либо молекулы попадёт в
ломаный цилиндр объёмом
V l v t
Число молекул, центры которых
попали в цилиндр:
N n V n l n v t
Число столкновений молекулы за N n v t
n v
единицу времени:
t
t
z 2 n v
– с учётом движения других молекул

17.

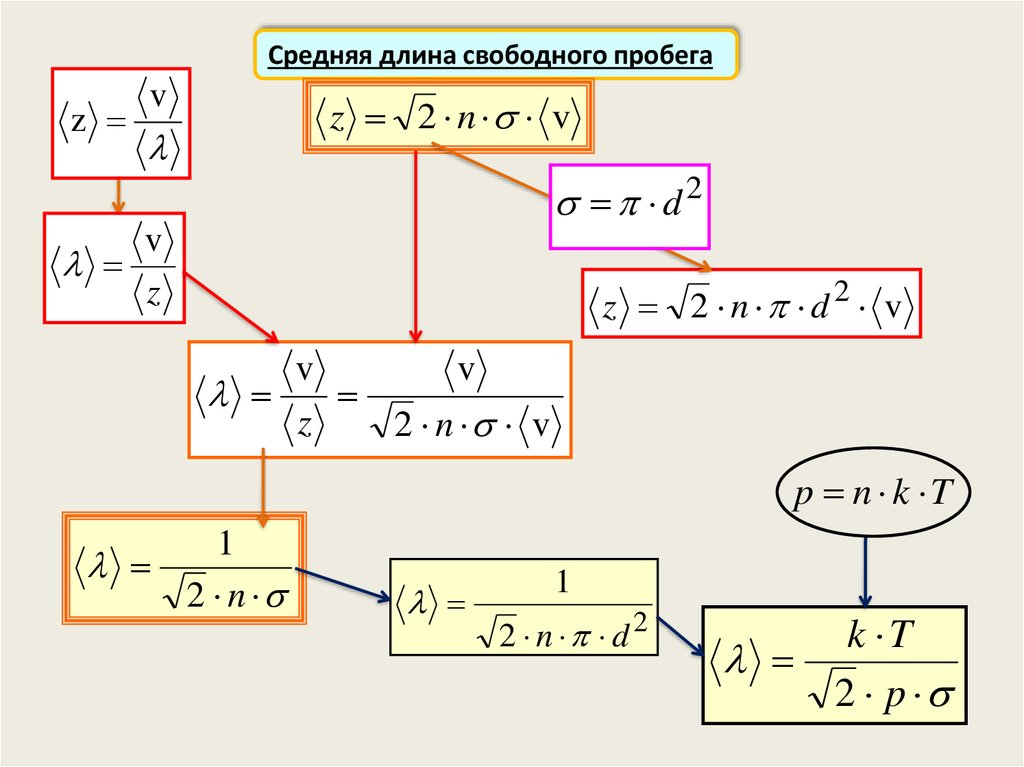
Средняя длина свободного пробега
z
v
z 2 n v
d2
v
z
z 2 n d 2 v
v
z
v
2 n v
p n k T
1
2 n
1
2 n d 2
k T
2 p

18.

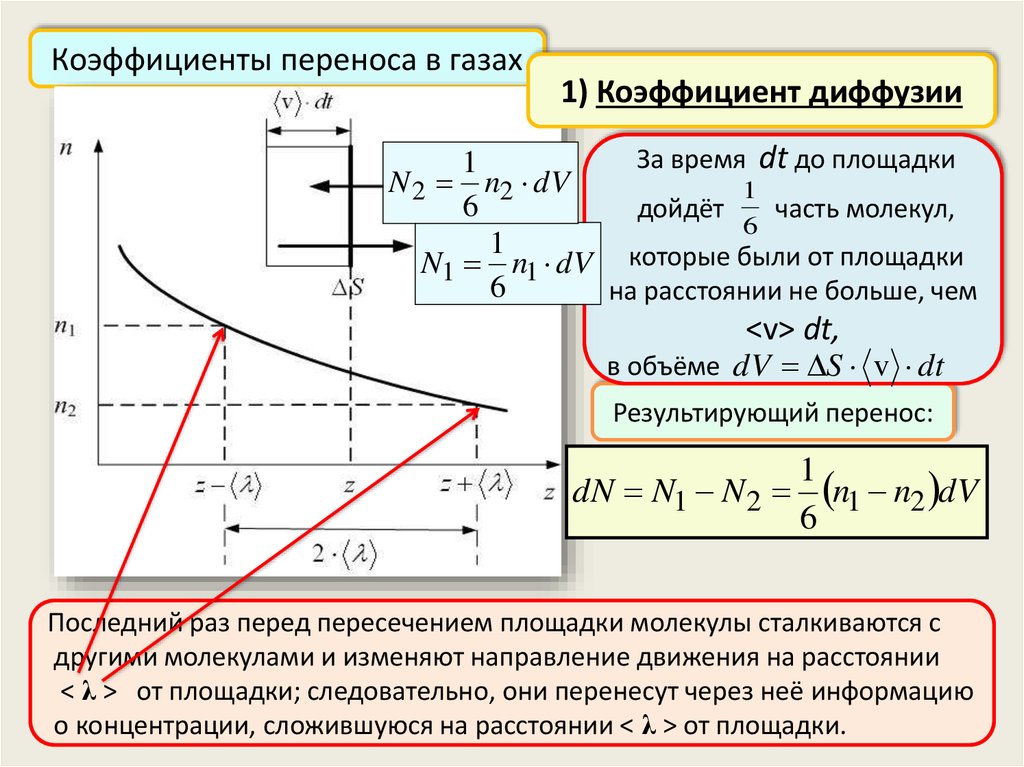
Коэффициенты переноса в газах
1) Коэффициент диффузии
За время dt до площадки
1
N 2 n2 dV
1
6
дойдёт
часть молекул,
6
1
N1 n1 dV которые были от площадки
6
на расстоянии не больше, чем
<v> dt,
в объёме dV S v dt
Результирующий перенос:
1
dN N1 N 2 n1 n2 dV
6
Последний раз перед пересечением площадки молекулы сталкиваются с
другими молекулами и изменяют направление движения на расстоянии
< λ > от площадки; следовательно, они перенесут через неё информацию
о концентрации, сложившуюся на расстоянии < λ > от площадки.

19.

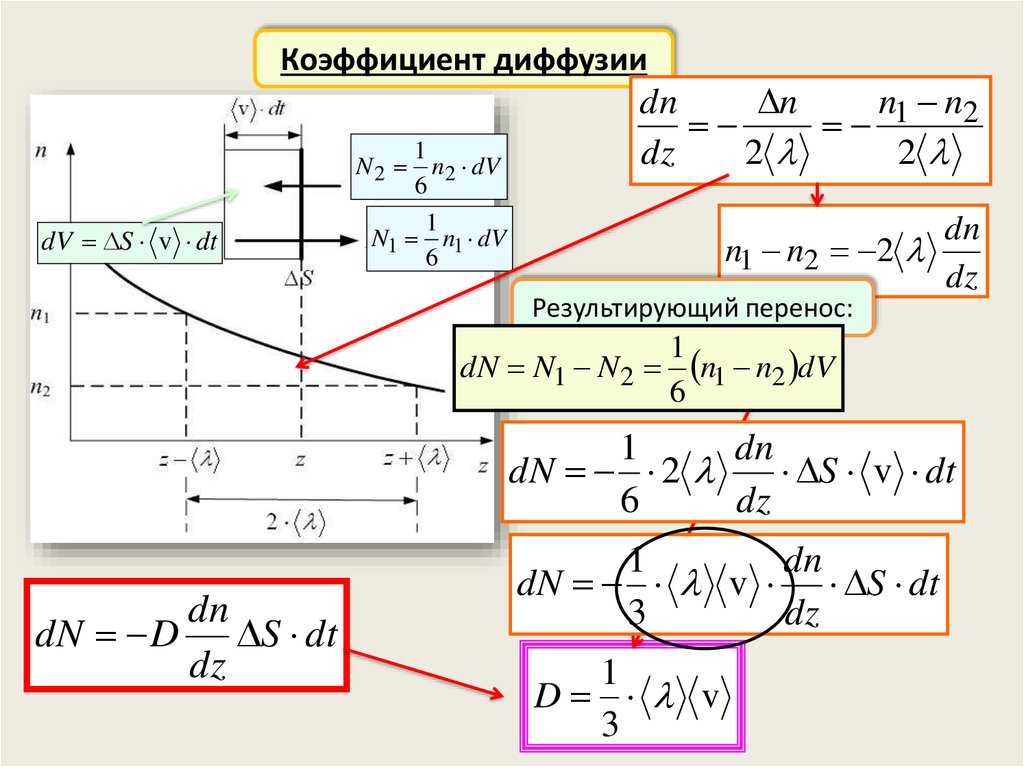
Коэффициент диффузии
dV S v dt
1
N 2 n2 dV
6
1
N1 n1 dV
6
dn
n
n1 n2
dz
2
2
dn
n1 n2 2
dz
Результирующий перенос:
1
dN N1 N 2 n1 n2 dV
6
1
dn
dN 2
S v dt
6
dz
dn
dN D S dt
dz
1
dn
dN v S dt
3
dz
1
D v
3

20.

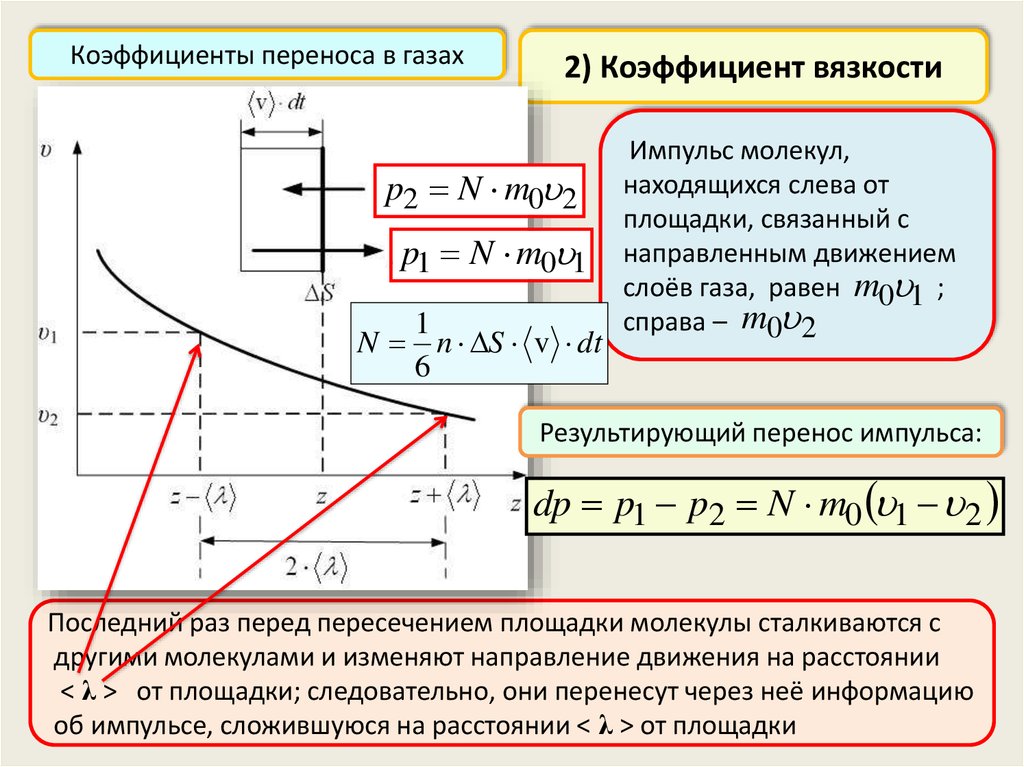
Коэффициенты переноса в газах
2) Коэффициент вязкости
p2 N m0 2
p1 N m0 1
1
N n S v dt
6
Импульс молекул,
находящихся слева от
площадки, связанный с
направленным движением
слоёв газа, равен m0 1 ;
справа – m0 2
Результирующий перенос импульса:
dp p1 p2 N m0 1 2
Последний раз перед пересечением площадки молекулы сталкиваются с
другими молекулами и изменяют направление движения на расстоянии
< λ > от площадки; следовательно, они перенесут через неё информацию
об импульсе, сложившуюся на расстоянии < λ > от площадки

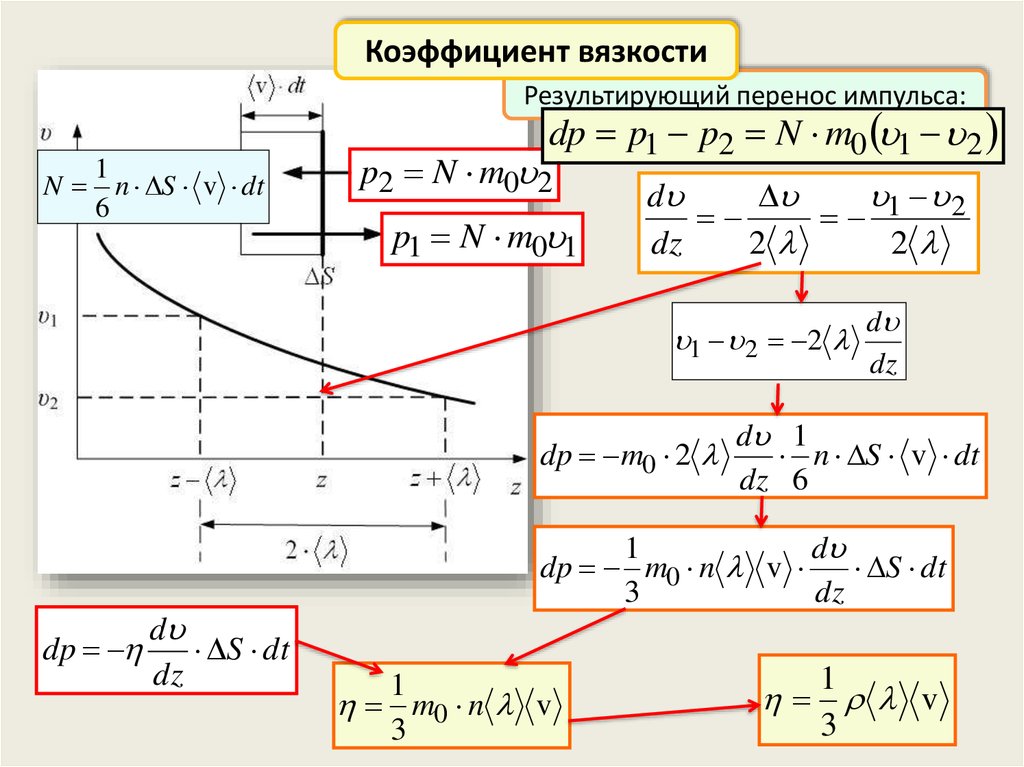
21.

Коэффициент вязкости
Результирующий перенос импульса:
1
N n S v dt
6
dp p1 p2 N m0 1 2
p2 N m0 2
p1 N m0 1
d
1 2
dz
2
2
1 2 2
dp m0 2
dp
d
S dt
dz
d
dz
d 1
n S v dt
dz 6
1
d
dp m0 n v
S dt
3
dz
1
m0 n v
3
1
v
3

22.

Коэффициент вязкости газа
1
v
3
Коэффициент вязкости газа
с ростом температуры
при постоянном давлении растёт
за счёт увеличения скорости хаотического движения:
8kT
v
m0
за счёт увеличения длины свободного пробега:
k T
2 p

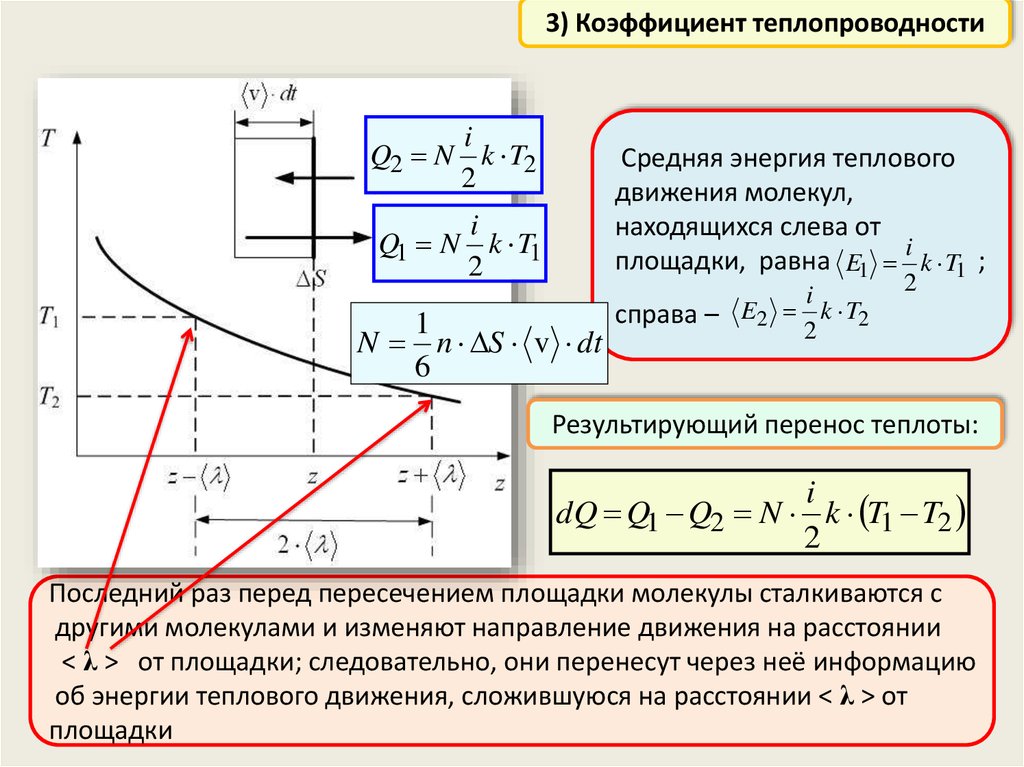
23.

3) Коэффициент теплопроводности
i
Q2 N k T2
2
Средняя энергия теплового
движения молекул,
находящихся слева от
i
площадки, равна E1 k T1 ;
i
Q1 N k T1
2
1
N n S v dt
6
i
справа – E2 k T2
2
2
Результирующий перенос теплоты:
i
dQ Q1 Q2 N k T1 T2
2
Последний раз перед пересечением площадки молекулы сталкиваются с
другими молекулами и изменяют направление движения на расстоянии
< λ > от площадки; следовательно, они перенесут через неё информацию
об энергии теплового движения, сложившуюся на расстоянии < λ > от
площадки

24.

Коэффициент теплопроводности
Результирующий перенос теплоты:
i
Q2 N k T2
2
i
Q1 N k T1
2
i
dQ Q1 Q2 N k T1 T2
2
1
N n S v dt
6
1
i
dQ n S v dt k T1 T2
6
2
dT
T
T1 T2
dz
2
2
dT
T1 T2 2
dz
1
i
dT
dQ n S v dt k 2
6
2
dz
1
i dT
dQ v n k
S dt
3
2 dz

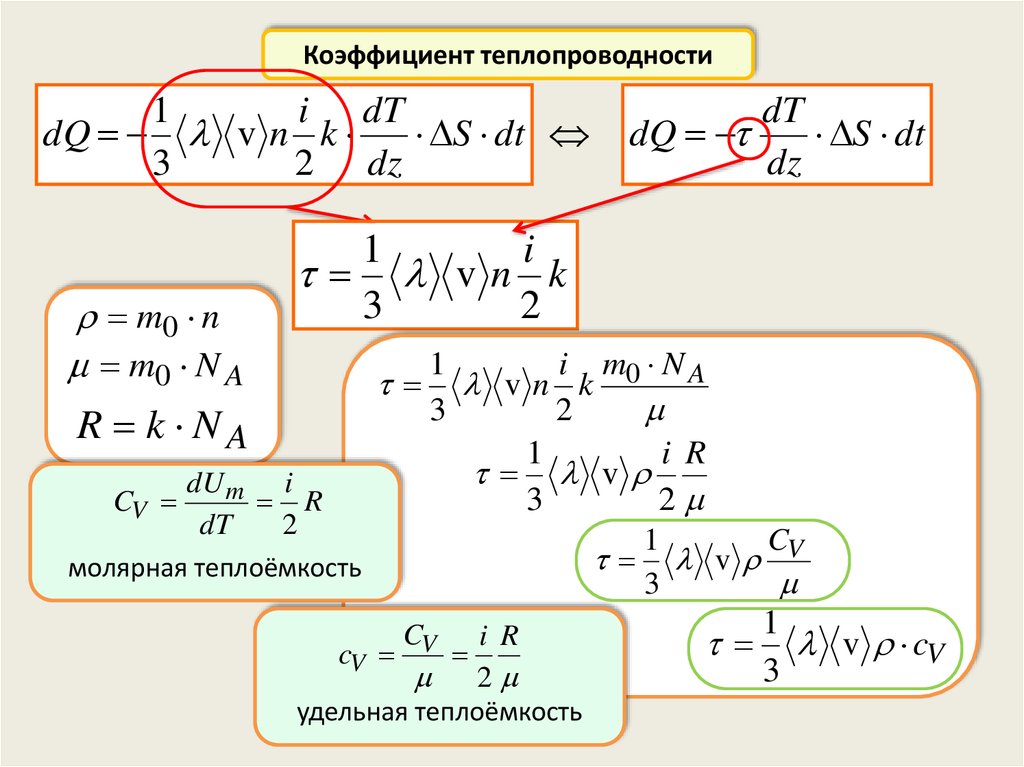
25.

Коэффициент теплопроводности
1
i dT
dQ v n k
S dt
3
2 dz
m0 n
m0 N A
dT
dQ
S dt
dz
1
i
vn k
3
2
1
i m0 N A
vn k
3
2
R k NA
1
i R
v
dU m i
3
2
CV
R
dT
2
CV
1
v
молярная теплоёмкость
3
1
CV i R
v cV
cV
3
2
удельная теплоёмкость

26.

Коэффициент теплопроводности
1
v cV
3
Коэффициент теплопроводности
при постоянной температуре не
зависит от давления:
уменьшение плотности компенсируется увеличением <λ>
1
1
v cV v
3
3
cV
1
v
2 n 3
m
cV
1
V
v
N
2 3
V
m cV
2 N
В состоянии вакуума длина свободного пробега <λ>
соизмерима с размерами сосуда
Молекулы от стенки до стенки пролетают без столкновений
При дальнейшей откачке <λ> не меняется:
lсосуда const
Теплопроводность разреженного газа уменьшается за счёт
уменьшения плотности

27.

Общность механизма явлений переноса в газах
Все явления переноса в газах обусловлены хаотическим
движением молекул
В результате теплового движения молекулы переносят по
всему объёму
массу;
импульс, связанный с направленным движением;
тепловую энергию
Вследствие этого коэффициенты переноса
связаны друг с другом

28.

Общность механизма явлений переноса в газах
Коэффициенты переноса связаны друг с другом
1
D v
3
1
v
3
1
v cV
3
D
D cV
cV