Похожие презентации:
Квадратичная функция
1.
04.10.212.
Какая из точек принадлежит из точек принадлежит точек принадлежитграфику
функции y =10 – 5x
И
К
Л
(1;5)
(5;10)
(-1;10)
3.
Какие из точек принадлежит функцийя из точек принадлежит вля из точек принадлежит ются из точек принадлежит
квадратичными
З
И
K
y = x3 + 5 x + 6
y = 2x – 6
y = x2
4.
Деятельность – единственный путьк знанию
Б.Шоу
Тема урока :
Функция y
= x2 ,
ее график и свойства
5.
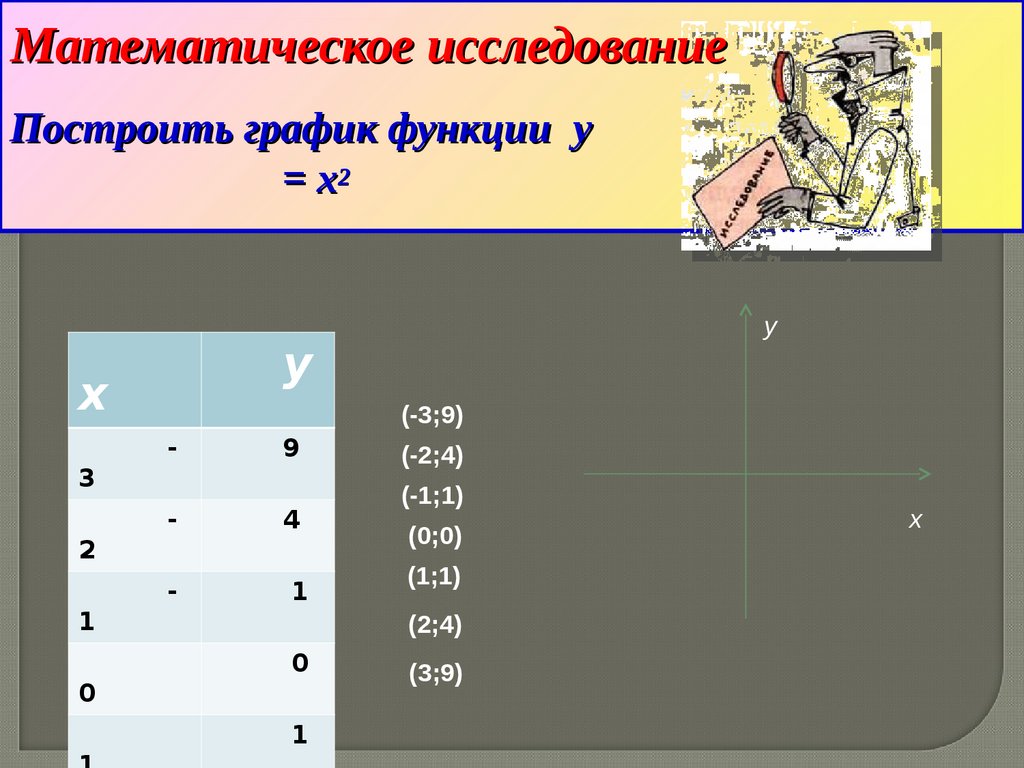
Математическое исследованиеПостроить график функции y
= x2
y
x
3
2
1
0
y
(-3;9)
-
9
4
1
(-2;4)
(-1;1)
(0;0)
(1;1)
(2;4)
0
1
(3;9)
x
6.
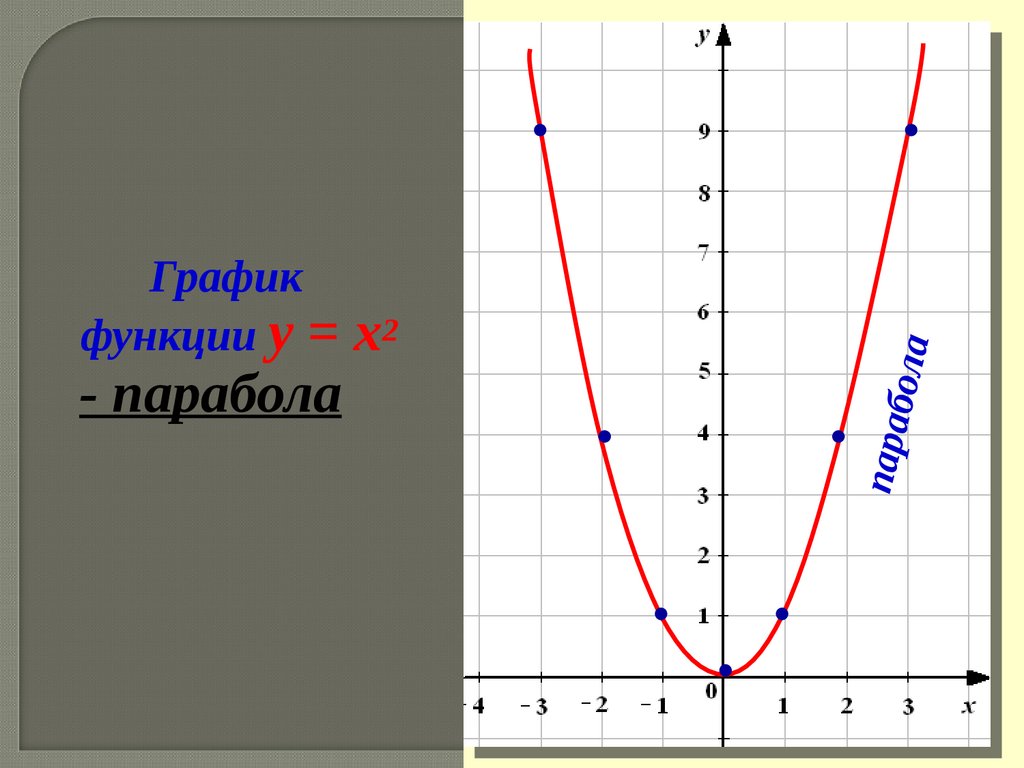
бола- парабола
x2
пара
График
функции y =
7.
8.
Схема исследования из точек принадлежитфункции:
1.
2.
3.
4.
5.
6.
Область определения определения из точек принадлежит
Область определения з точек принадлежит начений
Нули функции
Интервалы з точек принадлежит накопостоя из точек принадлежит нства
Промежутки монотонности
Наболь определенияшее и наимень определенияшее
з точек принадлежит начения из точек принадлежит функции
9.
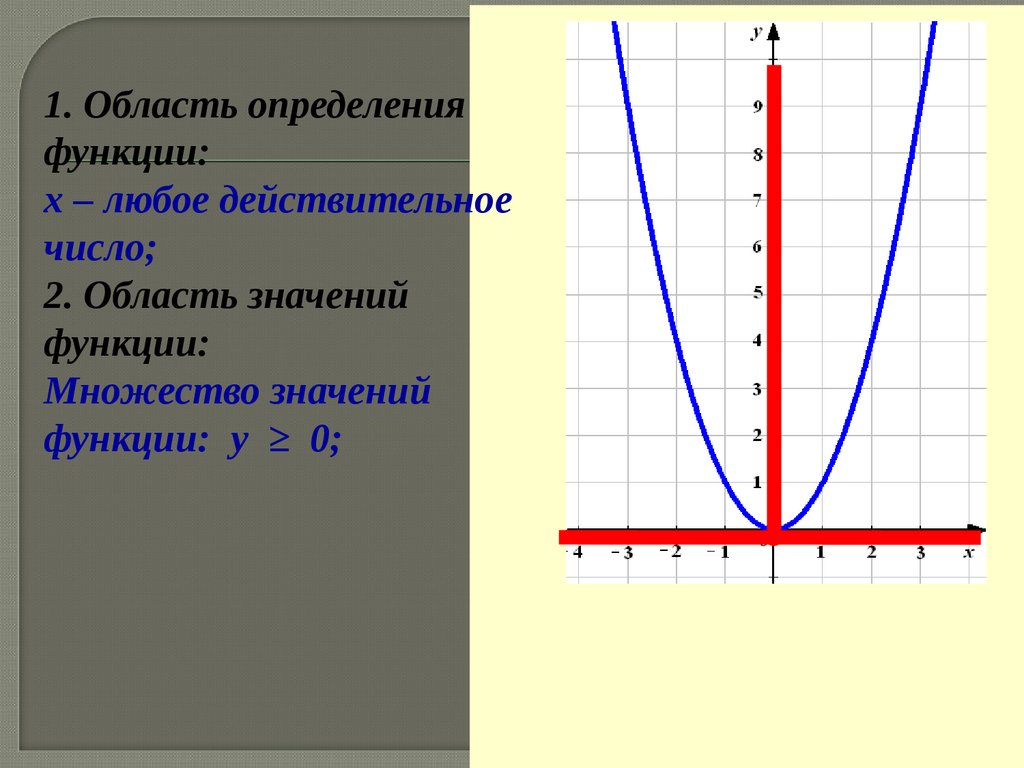
1. Область определенияфункции:
х – любое действительное
число;
2. Область значений
функции:
Множество значений
функции: у ≥ 0;
10.
3. Нули функции(это значения аргумента х, при
которых значение функции у(х) равно
нулю).
y = 0, если x = 0
График функции проходит
через начало координат
11.
III
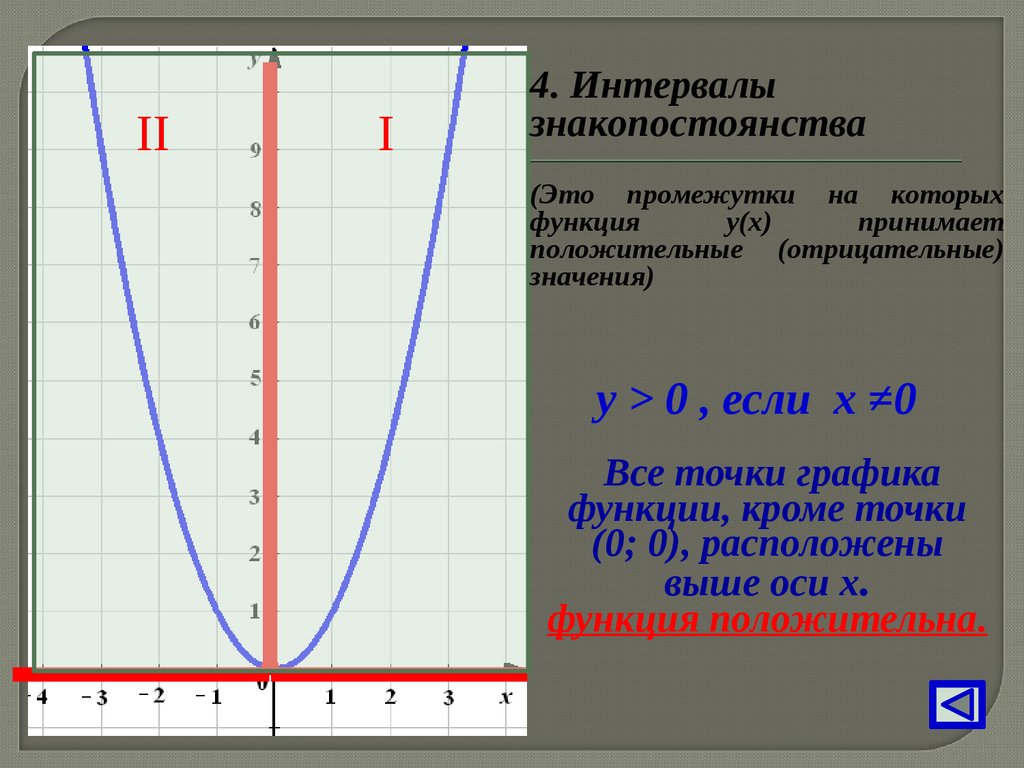
4. Интервалы
знакопостоянства
(Это промежутки на которых
функция
y(х)
принимает
положительные (отрицательные)
значения)
у > 0 , если х ≠0
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
функция положительна.
12.
5. Монотонность функцииДля неположительных значений Х неположительных значений Х значений Х Х
функция неположительных значений Х y(х)х значений Х ) убывает.
- Убывает на промежутке от минус бесконечности до 0.
Функция y(х) х) ) возрастает если для любых)
x1 и x2 из множества P (х) x1 < x2), выполнено
неравенство y (х) x2) > y (х) x1)
- Вызрастает на промежутке от 0 до плюс
бесконечности
13.
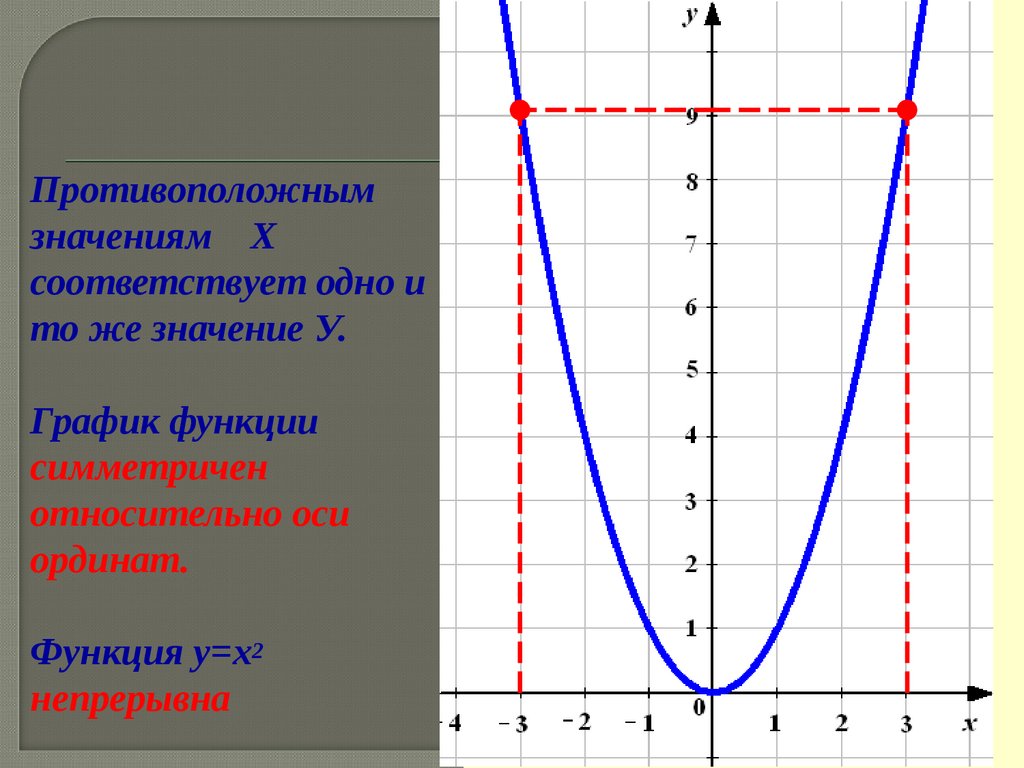
Противоположнымзначениям Х
соответствует одно и
то же значение У.
График функции
симметричен
относительно оси
ординат.
Функция у=х2
непрерывна
14.
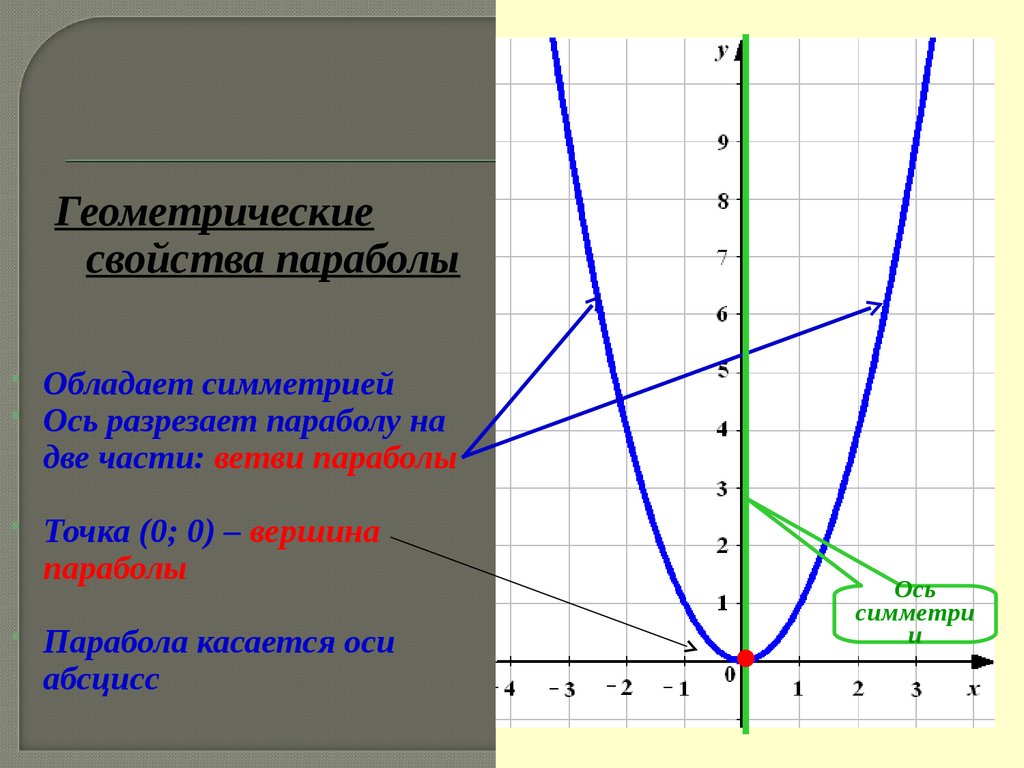
Геометрическиесвойства параболы
Обладает симметрией
Ось разрезает параболу на
две части: ветви параболы
Точка (0; 0) – вершина
параболы
Парабола касается оси
абсцисс
Ось
симметри
и
15.
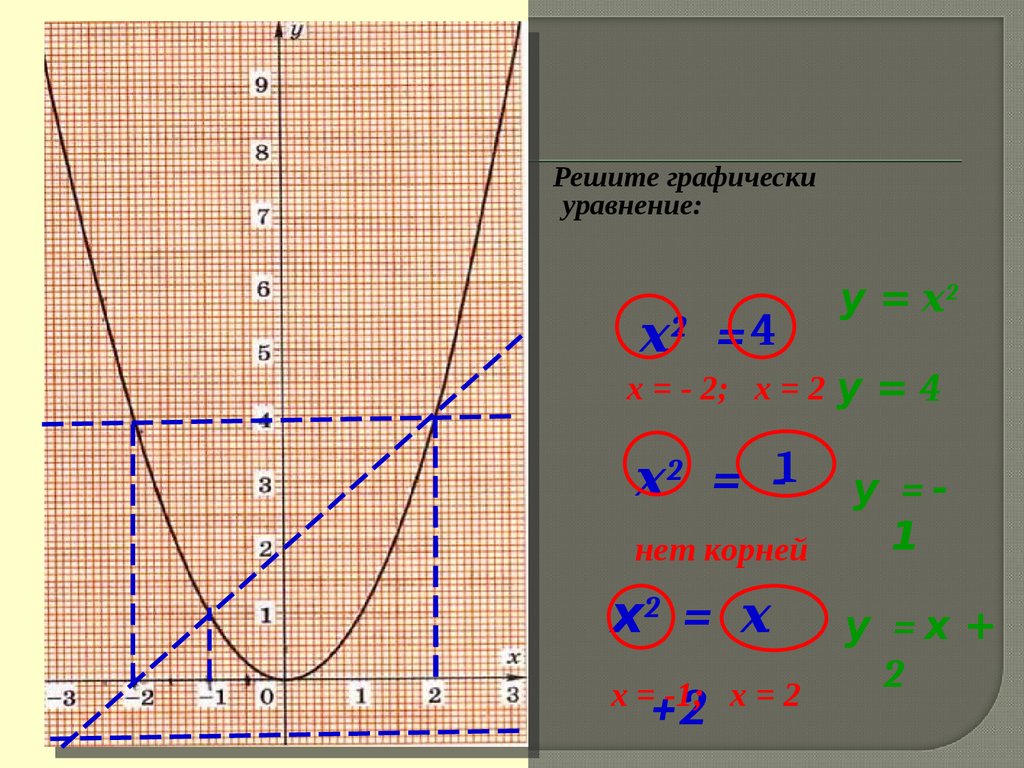
Решите графическиуравнение:
х2 = 4
y = х2
х = - 2; х = 2 y = 4
х2 = -1
нет корней
x2 = х
х = -1; х = 2
+2
y =1
y =x +
2
16.
Домашнее задание:п.2.2, п.2.3 (знать осноные
понятия)
№ 88, №89, №99
видеоурок:
https://ok.ru/video/64430630636
2









 Математика
Математика








