Магнитные свойства электрона

1. Магнитные свойства электрона

1
l iS e r 2 2 e r 2m 2m ,
r 2m pl
l e 2m pl .
l l pl e 2m
pl r 2m nh 2 n ,
l e 2m pl e 2m n n B ,
B e 2m .
B 9, 27 10 24
pl l l 1 ; l l l 1 B ,
lH ml B ,
ml l , l 1 , ..., 1, 0, 1, ..., l 1 , l.

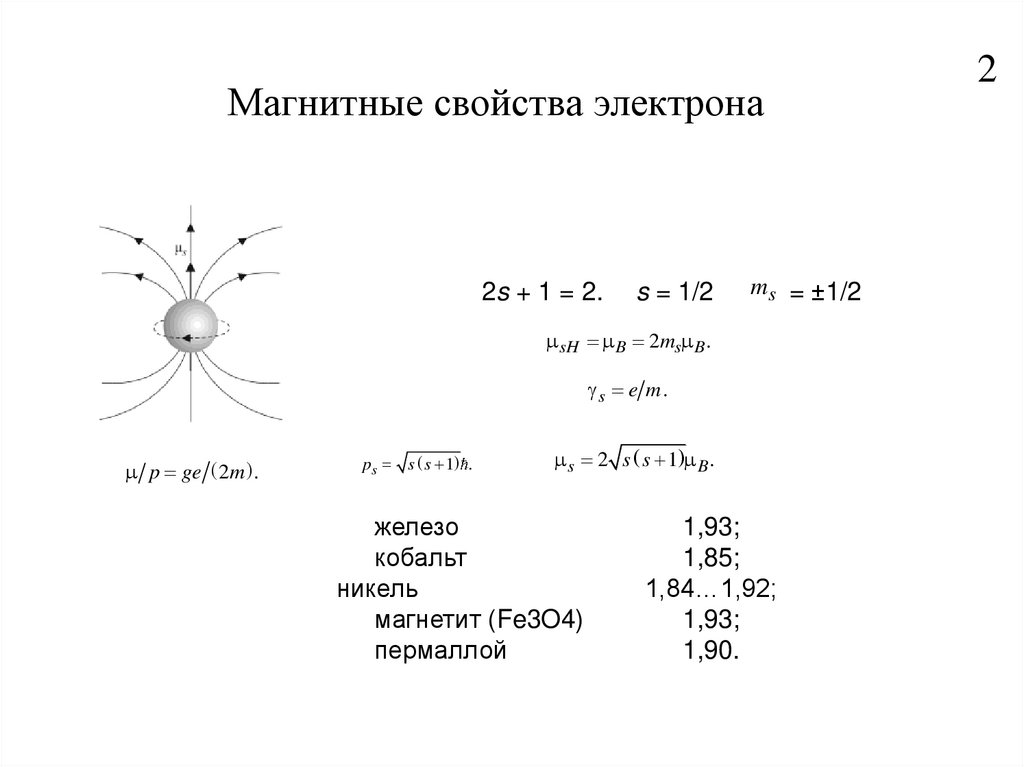
2. Магнитные свойства электрона

2s + 1 = 2.
s = 1/2
ms = ±1/2
sH B 2ms B .
s e m.
p ge 2m .
ps s s 1 .
s 2 s s 1 B .
железо
кобальт
никель
магнетит (Fe3O4)
пермаллой
1,93;
1,85;
1,84…1,92;
1,93;
1,90.
2

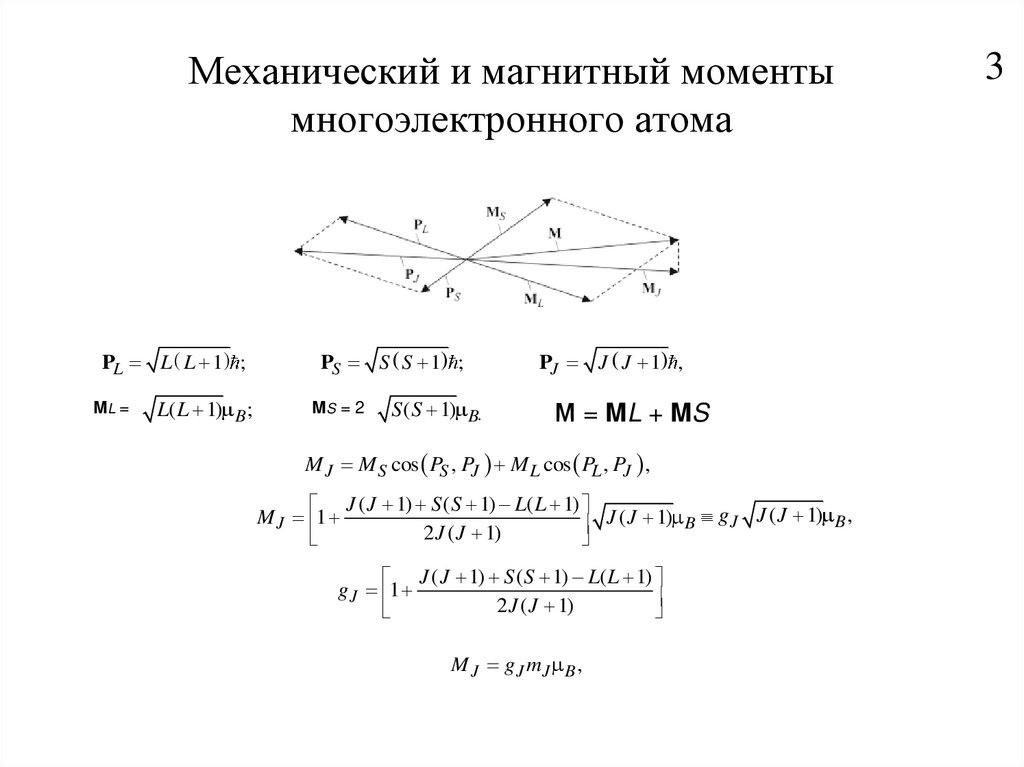
3. Механический и магнитный моменты многоэлектронного атома

PL L L 1 ;
ML =
L( L 1) B ;
PS S S 1 ;
MS = 2
S ( S 1) B.
PJ J J 1 ,
М = ML + MS
M J M S cos PS , PJ M L cos PL , PJ ,
J ( J 1) S ( S 1) L( L 1)
g J J ( J 1) B ,
M J 1
J ( J 1) B
2
J
(
J
1)
J ( J 1) S ( S 1) L( L 1)
g J 1
2 J ( J 1)
M J g J mJ B ,
3

4. Основные магнитные параметры

Напряженность магнитного поля Н [А/м]
Намагниченность
Магнитная индукция в вакууме [Тл] В = μ0Н
Магнитная индукция в веществе [Тл] В = μ0 μН
М = χH [А/м]
μ0 = 4π · 10–7 Гн/м – магнитная постоянная
μ – относительная магнитная проницаемость
χ – магнитная восприимчивость
μ = 1 + χ.
В = μ0μН = μ0 (1 + χ)Н = μ0Н + μ0χН = μ0Н + μ0М = Ве + Вi,
4

5. Основные виды магнитного состояния вещества

Диамагнетики
Парамагнетики
Ферромагнетики (а)
Антиферромагнетики (б)
Ферримагнетики (в)
5

6. Диамагнетизм

6
Диамагнетизм
F0 mv02 R m 02 R,
FH 0He 1R 0Hev1.
F F0 FH m 12 R m 02 R 0 He 1R.
2
Не
Не
Не
1 = – 0
± 0 02 0 0
2m
2m
2m
Δω = ω0 – ω1= μ0Не/(2m) = γlμ0Н
еR 2
Δμ = –
Δω
2
е2 0 Н z 2
ΔМА = –NА
Ri ,
6m i 1
χА =
е2 0 z 2
M А
= –NА
Ri .
H
6m i 1

7. Парамагнетизм

7
Парамагнетизм
Ем = μ0μмНcos θ
Суммарный магнитный момент N частиц в
поле Н
м Na
M=
2π exp( a cos )sin cos d =
4 sh a 0
=
E
Н cos
dN = Аexp м dΩ = Аexp 0 м
dΩ
kT
kT
Н
а= 0 м .
kT
N = 2πA exp( a cos )sin d 2
0
А=
Na
.
4 sh a
dM = μмdN cos θ
м Na
2
2π
4 sh a a
sh a
ch a
= μм N
a
1
cth a ,
а
μм = μB, в поле Н = 8·105 А/м при комнатной температуре
получим а ≈ 1/400.
В этом случае L(a) ≈ а/3
A
A
exp( a) exp( a) 4 sh a.
a
a
2
0 м
NH
М=
,
3kT
2
0 м
N
С
χ = М/Н =
= ,
3kT
Т
0 2м N
С=
.
3k

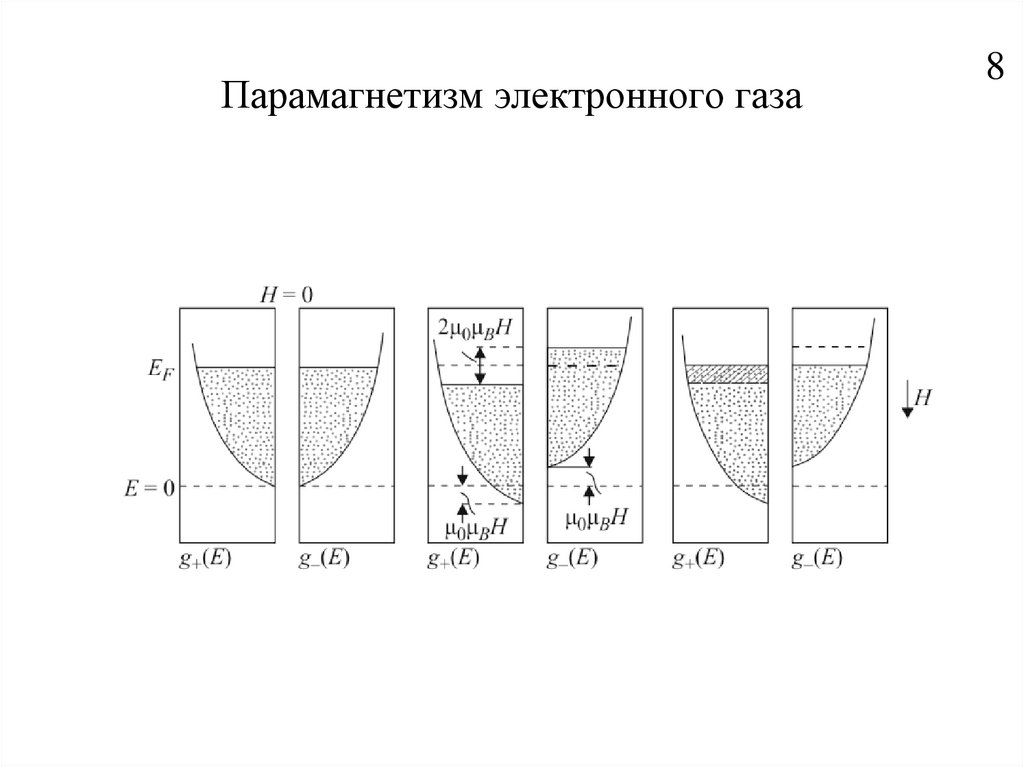
8. Парамагнетизм электронного газа

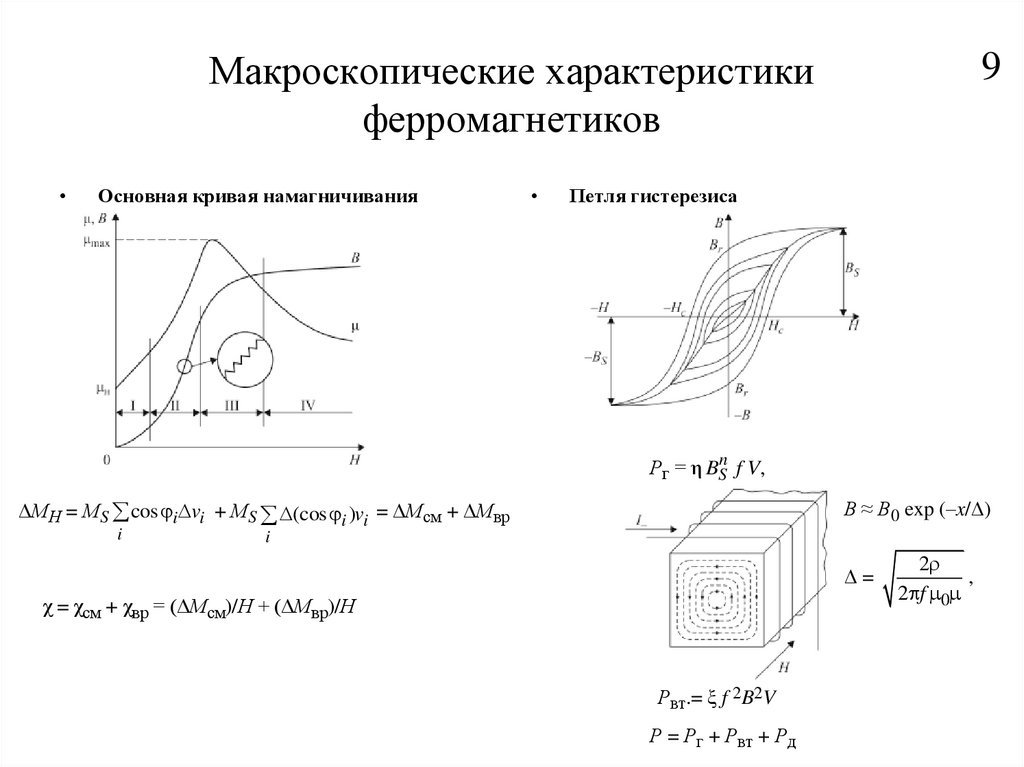
8

9. Макроскопические характеристики ферромагнетиков

Основная кривая намагничивания
9
Петля гистерезиса
Рг = η BSn f V,
ΔМН = МS cos i vi + МS (cos i )vi = ΔМсм + ΔМвр
i
В ≈ В0 exp (–x/Δ)
i
Δ=
χ = χсм + χвр = (ΔМсм)/Н + (ΔМвр)/Н
Рвт.= ξ f 2B2V
Р = Рг + Рвт + Рд
2
,
2 f 0

10. Намагничивание незамкнутых сердечников. Намагничивание переменным током

Кривая намагничивания незамкнутых
сердечников
Комплексная магнитная проницаемость
h = Hmax sin ωt
b = Bmax sin (ωt – δ).
μп =
Bmax
;
0 H max
=
Bmax1
0 H max
=
Нi = Не – Нd
NВ ≈ NМ/μ0
1
μт =
μ.
1 N M ( 1)
=
Bmax 2
0 H max
Bmax e j ( t )
0 H max e
j t
tg δм = .
= μпe–jδ = – j
10

11. Формальная теория ферромагнетизма (1)

11
В ферромагнетиках существует сильное
F = U – ST,
S = k ln W
внутреннее магнитное поле, названное
молекулярным полем, которое и приводит к
N!
S = k(ln N! – ln r! – ln l!).
W=
.
спонтанному (самопроизвольному)
r !l !
намагничиванию ферромагнетика до
N
насыщения даже при отсутствии внешнего
S=
k [(1 + y)ln(1 + y) + (1 – y) ln(1 – y)].
2
магнитного поля (первая гипотеза Вейсса).
(∂F/∂y) = 0
Ферромагнетик представляет собой «газ
1. Внутренняя энергия U не зависит от намагниченности y
электронных спинов», под которым будем
понимать совокупность
ln(1 + y) – ln(1 – y) = 0. y = 0
нескомпенсированных спиновых магнитных
2. Внутренняя энергия или ее часть является функцией
моментов N одинаковых атомов в узлах
намагниченности U = f (у).
кристаллической решетки вещества.
U(y) = –A1Ny2
Количество магнитных моментов с «правой»
ориентацией r, а количество моментов с
4 A1
1 y
у = ln
«левой» ориентацией l.
kT
1 y
y=
r=
r l
,
N
N
N
(1 + y), l =
(1 – y).
2
2

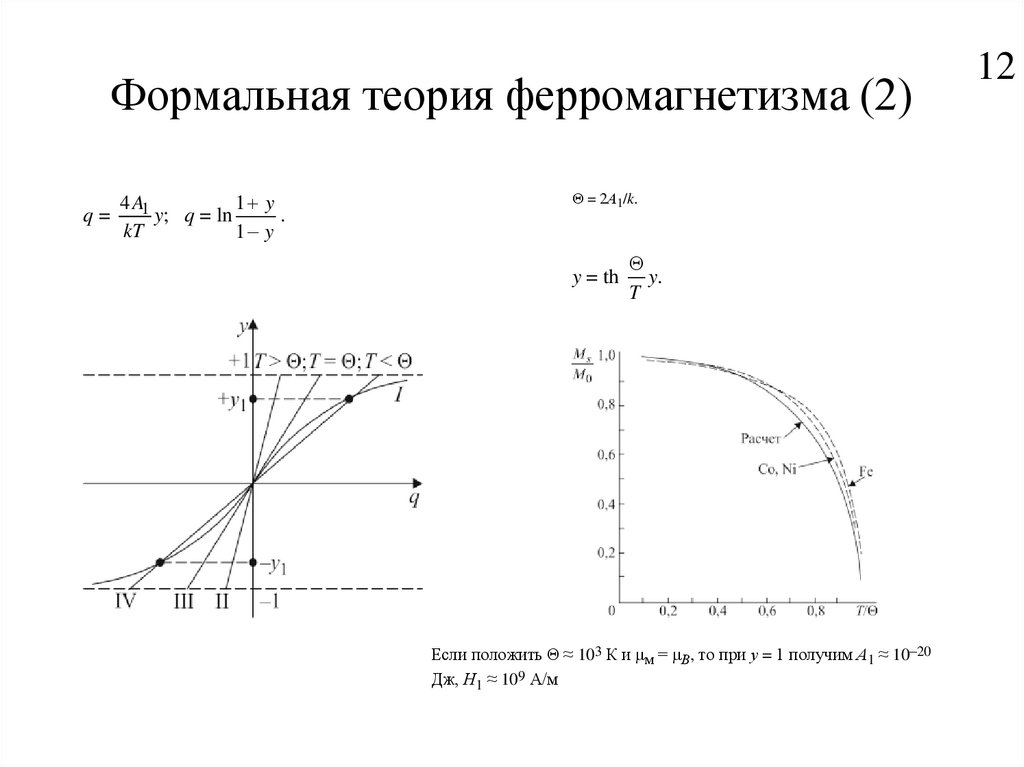
12. Формальная теория ферромагнетизма (2)

4 A1
1 y
q=
y; q = ln
.
kT
1 y
Θ = 2А1/k.
y = th
y.
T
Если положить Θ ≈ 103 К и μм = μВ, то при у = 1 получим А1 ≈ 10–20
Дж, Н1 ≈ 109 А/м
12

13. Молекула водорода и обменное взаимодействие (1)

В 1927 г. Гайтлер и Лондон провели
квантово-механическое рассмотрение
молекулы водорода и установили, что ее
энергия зависит от взаимной ориентации
спиновых магнитных моментов двух
электронов, входящих в состав молекулы.
U=
13
Задача заключается в определении энергии
системы в зависимости от расстояния между
ядрами R.
2m
1 2 2 E U R, r, ra1, ra 2 , rb1, rb2 0,
e2
e2
e2
e2
e2
e2
+
–
–
–
–
.
4 0 R 4 0r 4 0ra1 4 0ra 2 4 0rb1 4 0rb2
Ψ = Ψ(x1, y1, z1, x2, y2, z2),
x1, y1, z1, x2, y2, z2 – пространственные координаты первого и
второго электронов
Уравнение Шредингера решают методом последовательных
Приближений.

14. Молекула водорода и обменное взаимодействие (2)

14
Молекула водорода и обменное взаимодействие (2)
Нулевое приближение: R=∞. Пусть энергия
изолированного атома Е0.
2m
e2
1 2 E0
a q1 0,
4 0ra1
2m
e2
2 2 E0
b q2 0,
4 0rb1
Ψ0(q1, q2) = Ψa(q1) Ψb(q2), Ψ0(q2, q1) = Ψa(q2) Ψb(q1),
Первое приближение:.
Атомы начинают сближаться, взаимодействия
электронов и ядер приведут к изменению
собственных значений энергии системы:
E 2 E0 E ,
Теперь уравнение Шредингера имеет два
возможных решения(при том, что α = ±β):
01 q1, q2 a q1 b q2 a q2 b q1 ,
Е(1) = 2Е0 + С + А
Ψ0(q1, q2) = α Ψa(q1) Ψb(q2) + β Ψa(q2) Ψb(q1).
02 q1, q2 a q1 b q2 a q2 b q1 ,
Данная волновая функция описывает состояние
Е(2) = 2Е0 + С – А
системы, в которой каждый электрон имеет
e2
e2 1 1
1
2
2
некоторую вероятность нахождения около атома а
C
a q1 b q2 dq1dq2 ,
4 0 R 4 0 r rb1 ra1
или атома b. При этом |α|2 дает вероятность нахождения
электрона 1 у атома а, а электрона 2 у атома b, а |β|2 –
вероятность обратного распределения электронов.
2
A
e
1 *
1 1
a q1 b q1 *b q2 a q2 dq1dq2 .
4 0 r rb1 ra1

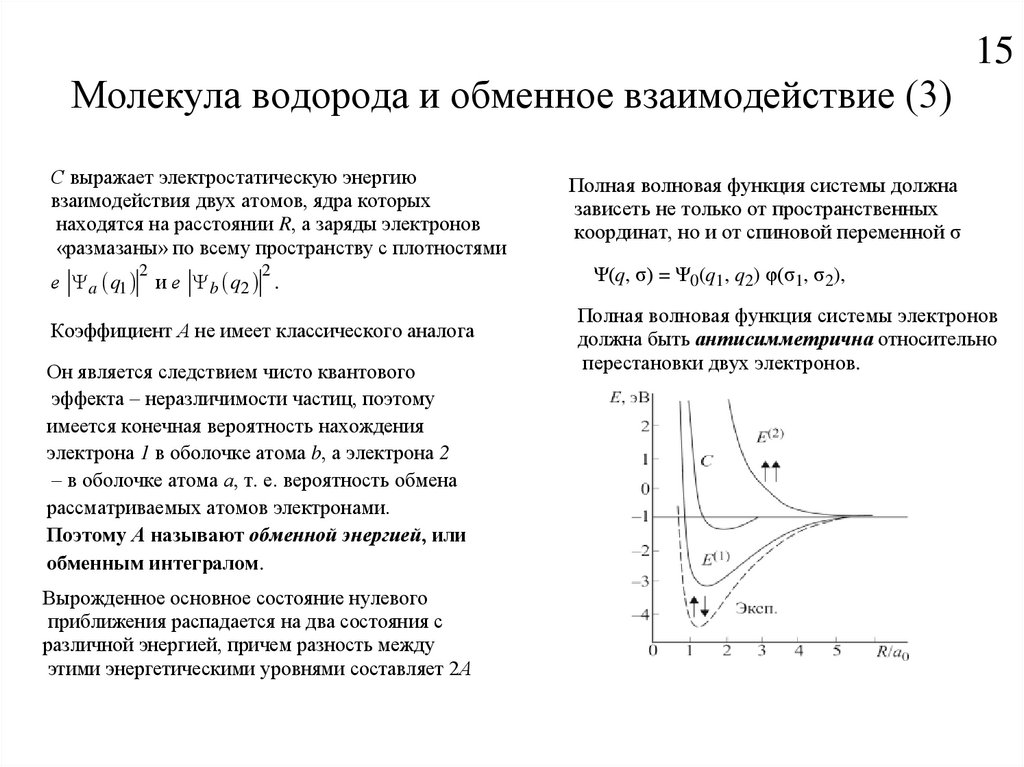
15. Молекула водорода и обменное взаимодействие (3)

15
Молекула водорода и обменное взаимодействие (3)
С выражает электростатическую энергию
взаимодействия двух атомов, ядра которых
находятся на расстоянии R, а заряды электронов
«размазаны» по всему пространству с плотностями
е a q1 и е b q2 .
2
2
Коэффициент А не имеет классического аналога
Он является следствием чисто квантового
эффекта – неразличимости частиц, поэтому
имеется конечная вероятность нахождения
электрона 1 в оболочке атома b, а электрона 2
– в оболочке атома а, т. е. вероятность обмена
рассматриваемых атомов электронами.
Поэтому А называют обменной энергией, или
обменным интегралом.
Вырожденное основное состояние нулевого
приближения распадается на два состояния с
различной энергией, причем разность между
этими энергетическими уровнями составляет 2А
Полная волновая функция системы должна
зависеть не только от пространственных
координат, но и от спиновой переменной σ
Ψ(q, σ) = Ψ0(q1, q2) φ(σ1, σ2),
Полная волновая функция системы электронов
должна быть антисимметрична относительно
перестановки двух электронов.

16. Некоторые аспекты квантовой теории самопроизвольной намагниченности ферромагнетиков

Некоторые аспекты квантовой теории
16
самопроизвольной намагниченности ферромагнетиков
Гейзенберг рассматривал систему, состоящуюя из N водородоподобных атомов, электроны которых
находятся в s-состояниях.
Для упрощения задачи учитывалось только электростатическое взаимодействие
Полная энергия системы, как и для молекулы водорода, была представлена суммой энергий изолированных атомов NЕ0, энергии кулоновского взаимодействия электронов и ионов С и обменной энергии
Еобм. Далее было получено выражение для интеграла обменной энергии Aij между атомами i и j. После
суммирования по всем парам атомов было получено выражение:
Еобм 2 Aij 2 cos ij
Еобм = –NzA
ij
А1 = Аz.
Еобм = –Nу2zA
Θ = 2zА/k.
1) если обменный интеграл А положителен, то может возникнуть
состояние с самопроизвольной намагниченностью (ферромагнетизм);
2) величина энергии обменного взаимодействия достаточна
для существования ферромагнитной упорядоченности вплоть до
температур порядка 103 К.

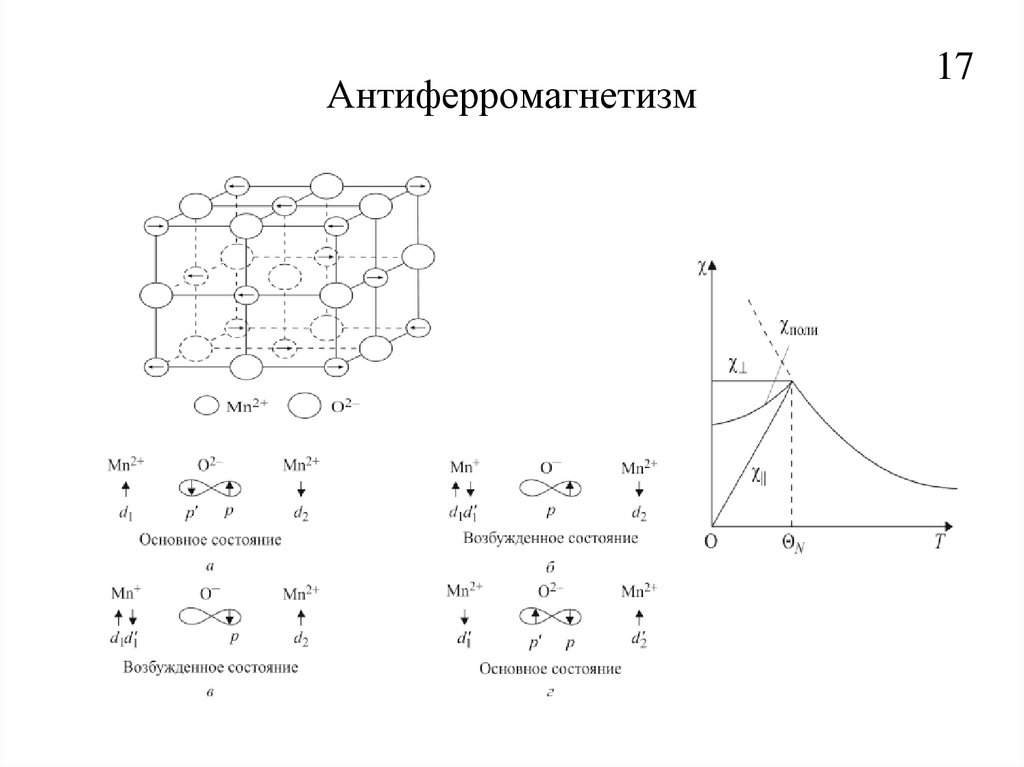
17. Антиферромагнетизм

17

18. Ферримагнетизм (1)

18
Магнитная элементарная ячейка феррита-шпинели (постоянная
Общую формулу ферритов-шпинелей можно
решетки а ≈ 0,85 нм) содержит 8 формульных единиц (8MeFe2O4) и
записать как MeO–Fe2O3 или MeFe2O4,
включает в себя 32 иона кислорода, 8 ионов металла и 16 ионов
где Ме – двухвалентные ионы одного или
нескольких металлов (Ni, Co, Mn, Fe, Cu, Mg, Zn, Cd). железа (в сумме 24 катиона). Общее количество междоузлий – 96,
из них 64 – тетраэдрических и 32 – октаэдрических. Совокупность
тетраэдрических междоузлий принято называть подрешеткой А, а
октаэдрических – подрешеткой В.
Нормальные шпинели. Все двухвалентные катионы размещаются в
тетраэдрических позициях, а все трехвалентные – в октаэдрических.
Распределение катионов по позициям принято записывать в виде
Me2 Fe32 O4
Обращенные шпинели. Все двухвалентные катионы находятся в
октаэдрических позициях, а трехвалентные поровну занимают
тетра- и октапозиции. Обращенными ферритами являются магнетит
Fe3O4, формулу которого можно записать в виде (Fe3+)[Fe2+Fe3+]O4,
Смешанные шпинели. Двух- и трехвалентные
катионы произвольно распределены по позициям,
и общую формулу можно представить в виде
Me2x Fe13 x Fe13 x Me12 x O4.

19. Ферримагнетизм (2)

19

20. Основные виды энергии в ферромагнитном кристалле

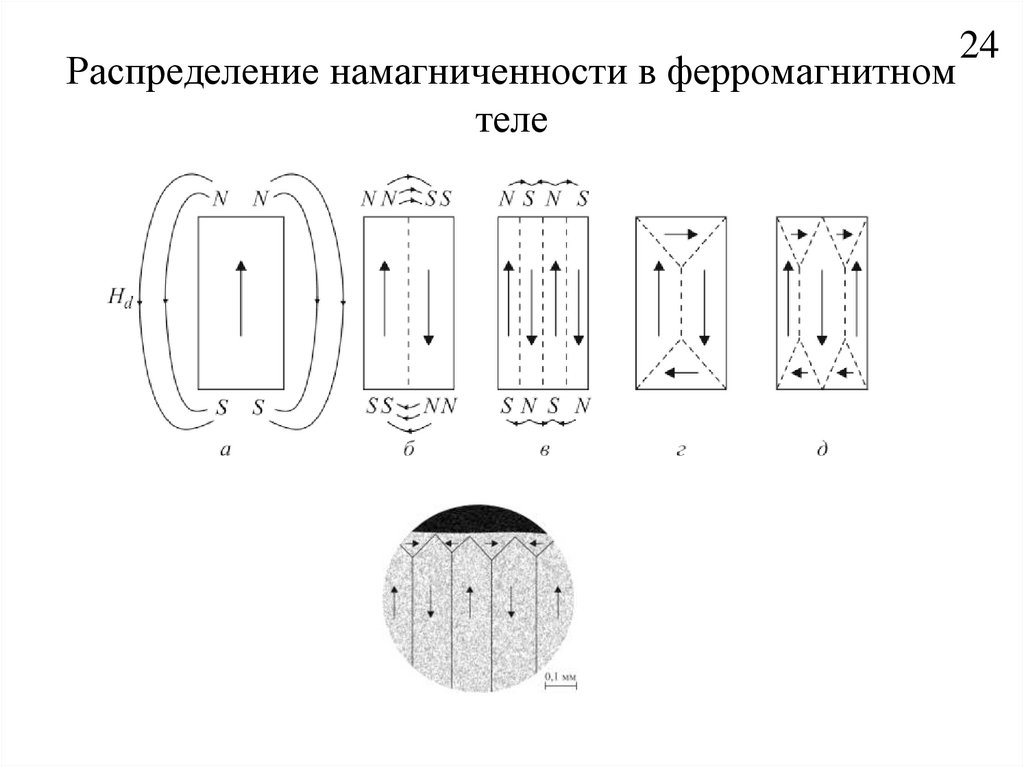
Вторая гипотеза Вейсса: ферромагнитное тело самопроизвольно разбивается на множество
макрообластей (доменов). Каждый домен намагничен до насыщения, а векторы магнитных
моментов разных доменов равновероятно расположены в пространстве, что в сумме приводит к
нулевой намагниченности.
Для объяснения возникновения доменной структуры необходимо проанализировать все возможные
виды энергии, существующие в ферромагнитном теле. Тогда устойчивому состоянию
ферромагнетика будет соответствовать минимум всех энергетических вкладов.
Можно выделить следующие возможные виды энергии:
1) энергия обменного взаимодействия Еобм;
2) энергия кристаллографической магнитной анизотропии Еk;
3) энергия магнитострикционной деформации Еλ;
4) магнитоупругая энергия Еσ;
5) магнитостатическая энергия (энергия размагничивания) Еd;
6) магнитная энергия (энергия взаимодействия с внешним магнитным полем Ем).
Еобм в 103…104 раз больше других энергий, поэтому при анализе их влияния можно предположить,
что все тело намагничено до насыщения, или рассматривать отдельно взятый домен. Величина
внешнего магнитного поля в большинстве случаев значительно меньше величины молекулярного
поля.
20

21. Энергия кристаллографической магнитной анизотропии

Магнитная анизотропия – это явление преимущественной ориентации спонтанной
намагниченности ферромагнетика вдоль особых, характерных для данного вещества,
кристаллографических осей.
Причинами возникновения кристаллографической магнитной
анизотропии являются:
– диполь-дипольное (двухионное) взаимодействие между магнитными моментами;
– спин-орбитальное (одноионное) взаимодействие между спиновым и орбитальным магнитными моментами одного электрона (атома).
Ek K0 K1 12 22 22 32 32 12 K2 12 22 32 ,
Ед = ±
1 2
4 0r
3
(1 – 3cos2 φ),
Еk = K0 + K1sin2 φ + K2sin4 φ
21

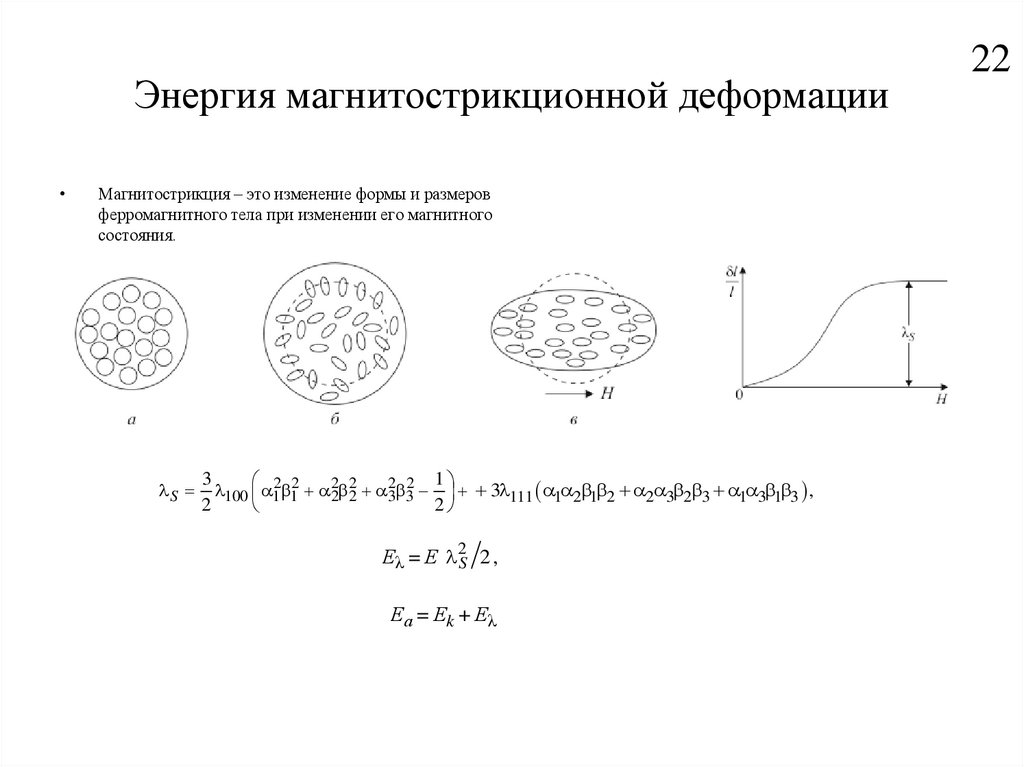
22. Энергия магнитострикционной деформации

Магнитострикция – это изменение формы и размеров
ферромагнитного тела при изменении его магнитного
состояния.
3
1
S 100 12 12 22 22 32 32 3 111 1 2 1 2 2 3 2 3 1 3 1 3 ,
2
2
Еλ = Е 2S 2 ,
Еа = Еk + Еλ
22

23. Магнитоупругая, магнитостатическая и магнитная энергии

23
Если ферромагнитное тело подвергнуть
действию внешних механических
напряжений σ (растяжение или сжатие), то
при этом возникает магнитоупругая энергия:
3
E 100 12 12 22 22 32 32 2 111 1 2 1 2 2 3 2 3 1 3 1 3 ,
2
3
100 ≈ 111 = λS,
E S cos2
2
1
1
0 NM S2
Ed 0 MH d 0M S NM S
.
2
2
2
Ем = –μ0(МSН)
Е = Еа + Еσ + Еd + Ем
Устойчивому состоянию ферромагнитного тела, т. е.
равновесному положению вектора МS при заданных значениях Н и
Нd = –NMS
σ, соответствует минимум полной энергии при выполнении условия
E i 0,

24. Распределение намагниченности в ферромагнитном теле

24

25. Переходная область между двумя доменами

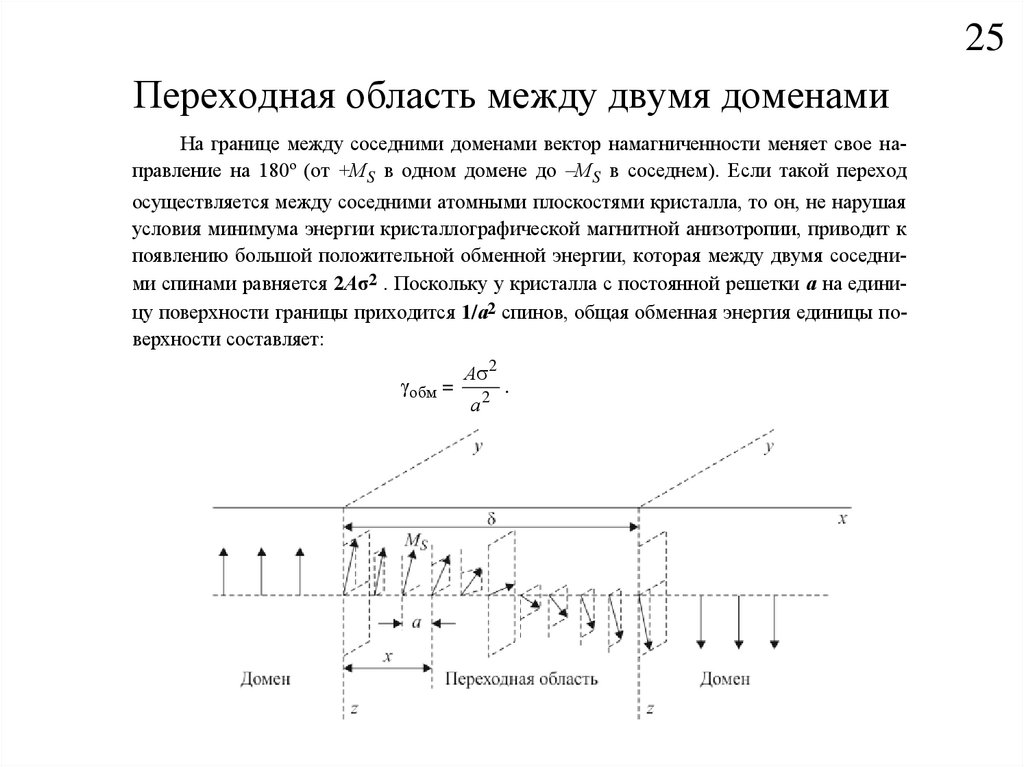
25
Переходная область между двумя доменами
На границе между соседними доменами вектор намагниченности меняет свое направление на 180º (от +МS в одном домене до –МS в соседнем). Если такой переход
осуществляется между соседними атомными плоскостями кристалла, то он, не нарушая
условия минимума энергии кристаллографической магнитной анизотропии, приводит к
появлению большой положительной обменной энергии, которая между двумя соседними спинами равняется 2Аσ2 . Поскольку у кристалла с постоянной решетки а на единицу поверхности границы приходится 1/а2 спинов, общая обменная энергия единицы поверхности составляет:
γобм =
А 2
а2
.

26. Энергия и толщина доменной границы

Если обозначить через φ угол между спиновыми моментами соседних атомных слоев, то при
малости угла φ уравнение, выражающее обменную энергию для соседних спинов, можно представить в виде
2
2
2 A cos 2 A 1
.
2
2
Введем понятие толщины доменной границы δгр . Тогда для угла φ будет справедливо следующее выражение: φ = аπ/δгр.
2
2
а гр 1
2
γобм = A
а 2 A а .
а
гр
гр
2
γгр = γобм + γа =
δгр = πσ
δгр ≈
a K1 гр ,
d гр
А 2 2
+ βK1δгр
а гр
А
.
K1а
k
;
K1a
d гр
γгр = 2πσ
γгр ≈
=0=–
А 2 2
а 2гр
+ βK1
K1А
.
а
k K1
.
a
Тогда для железа (Θ = 1043 К, K1 = 5 ∙ 104 Дж/м3, а = 2,5 ∙ 10–10 м и k = 1,38 ∙ 10–23 Дж/К) получим:
δгр ≈ 350 ∙ 10–10 м, что составляет приблизительно 140 атомных слоев, и γгр ≈ 2 ∙ 10–3 Дж/м2
26

27. Размеры доменов. Однодоменные частицы

Удельная энергия анизотропии в замыкающих
доменах: γа = K1. Объем каждой призматической
Егр = γгр S ≈
k K1 D2
,
a
4
27
области составляет Vпр = d y /4 (d – ширина домена),
а их число по обеим противоположным сторонам
3
1 1
1 11
M S2 D 3
4 D
0
тела n = 2lx/d. Суммарный объем призматических Ed 0 NM S2 V 0 NM S2
2 2
2 2 3
72
3 8
доменов в этом случае определяется выражением
36
k K1
d 2 l y 2l x
Dкр =
.
1
2
V = Vпрn =
= lx ly d,
a
М
0 S
4
2
d
для железа Dкр ≈ 0,05 мкм, для соединения Mn–Bi Dкр ≈ 8 мкм, для
K
2 l x l y L AK1
Еа = 1 lx ly d
Егр =
.
бариевого феррита Dкр ≈ 1,5 мкм.
2
a
d
2l
Величину d можно найти из условия ∂Е/∂d = 0:
d
14
А
1/2
= 2(πLσ)
.
K а
1

28. Цилиндрические магнитные домены

28
Устойчивое состояние домена соответствует минимальному
значению его полной энергии:
Е = Ем + Егр + Еd,
Ем = 2μ0НвнМSπr2h
Егр = 2πrhγгр
Егр
Е
Ем
Еd
Еd
=
+
–
= 4μ0НвнМSπrh + 2πhγгр –
r
r
r
r
r
Нвн +
гр
2 0 М S r
–
1
Еd
= Нвн + Нгр – Нd
4 0rhM S r

29. Процессы намагничивания. Смещение доменных границ.

29
Процессы намагничивания.
Смещение доменных границ.
R=–
1 E
.
S x
р(Н) + R(x) = 0
Энергия обоих доменов во внешнем
поле Н пропорциональна (V1М1 +
V2М2) Н.
Под действием поля граница смещается на δх,
при этом энергия изменяется на величину
δЕН = –μ0 (М1 – М2)НSδх = –μ0МSH(cos α1 – cos α2)Sδх.
δЕН = –2μ0МSHSδх = –2μ0МSHδV
χ=
δЕполн = δ(Е + ЕН) = 0
–δЕН = μ0МSH(cos α1 – cos α2)Sδх = δЕ
Н(х) =
1
E
.
SM S (cos 1 cos 2 ) 0 x x
р = μ0МSH(cos α1 – cos α2) = μ0(М1 – М2)Н
M
S x
=
МS (cos α1 – cos α2)
H
V H
S
dH
dM
χобр =
= μ0МS (cos α1 – cos α2)
dx
dH x V
=
S2
M 2 (cos 1 cos 2 ) 2
μ0 S
.
2
2
V
E x
1
=

30. Процессы намагничивания. Вращение вектора намагниченности.

30
Для случая α = 180º стабильны лишь положения,
отвечающие углам θ = 0 или θ = 180º, причем переворот
вектора намагниченности происходит при Н = НА.
В этом случае коэрцитивная сила Нс = НА .
Магнитное поле создает вращательный
момент Т = μ0(М Н)
Равновесный угол θ0, учитывая условия
E 0 и 2 E 2 > 0.
0
Е = K sin2 θ – μ0MSHcos(α – θ)
Для случая α = 90º находим следующее решение:
M H
H
sin θ0 = 0 S =
при Н ≤ НА
2K
HA
0M S2
M
= S при Н < НА
2K
HA
Если же Н > НА, то θ = 90º и χвр = 0
χвр =
1 0M S2
χвр =
.
3 K1

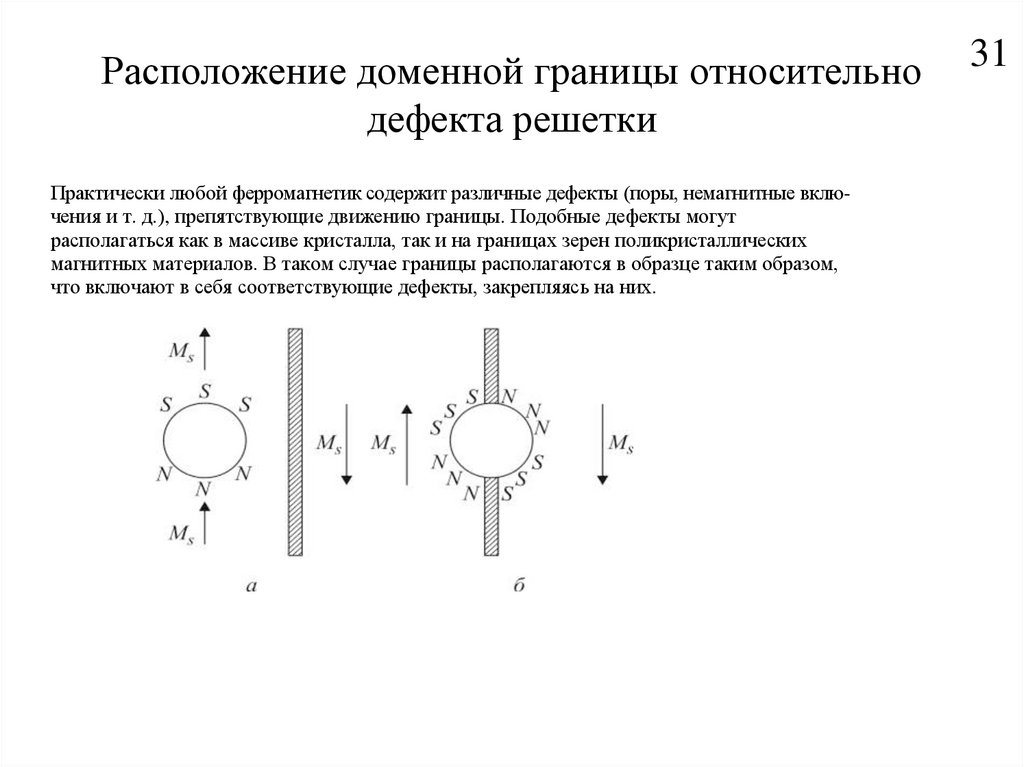
31. Расположение доменной границы относительно дефекта решетки

Практически любой ферромагнетик содержит различные дефекты (поры, немагнитные включения и т. д.), препятствующие движению границы. Подобные дефекты могут
располагаться как в массиве кристалла, так и на границах зерен поликристаллических
магнитных материалов. В таком случае границы располагаются в образце таким образом,
что включают в себя соответствующие дефекты, закрепляясь на них.
31

32. Возможные модели смещения доменной границы

Если граница проходит через дефект , то энергия размагничивания уменьшается почти
вдвое. В таком случае граница, смещаясь под действием внешнего магнитного поля, не
сохраняет строго плоскую форму, а сила, удерживающая границу в равновесии,
обусловлена изменением энергии самой границы за счет увеличения ее площади, с одной
стороны, и, с другой стороны, либо изменением энергии анизотропии искривленной
границы, либо магнитостатической энергией магнитных полюсов, возникающих на такой
границе. Оба указанных варианта иллюстрирует рис.
Условие равновесия в поле Н имеет вид
μ0Н(М1 – М2)δV = δ(Sγгр) ≈ гр S
V = 2 3 DlL,
М
χсм =
Н
0 M S2 D 2
=
.
6 грd
Н 0
χсм =
02 M S4 D
K 2d
0 M S (cos 1 cos 2 ) D 2
l=
Н.
8 гр
,
S = DL 1 8l 2 3D 2 .
32

33. Температурная зависимость начальной магнитной восприимчивости

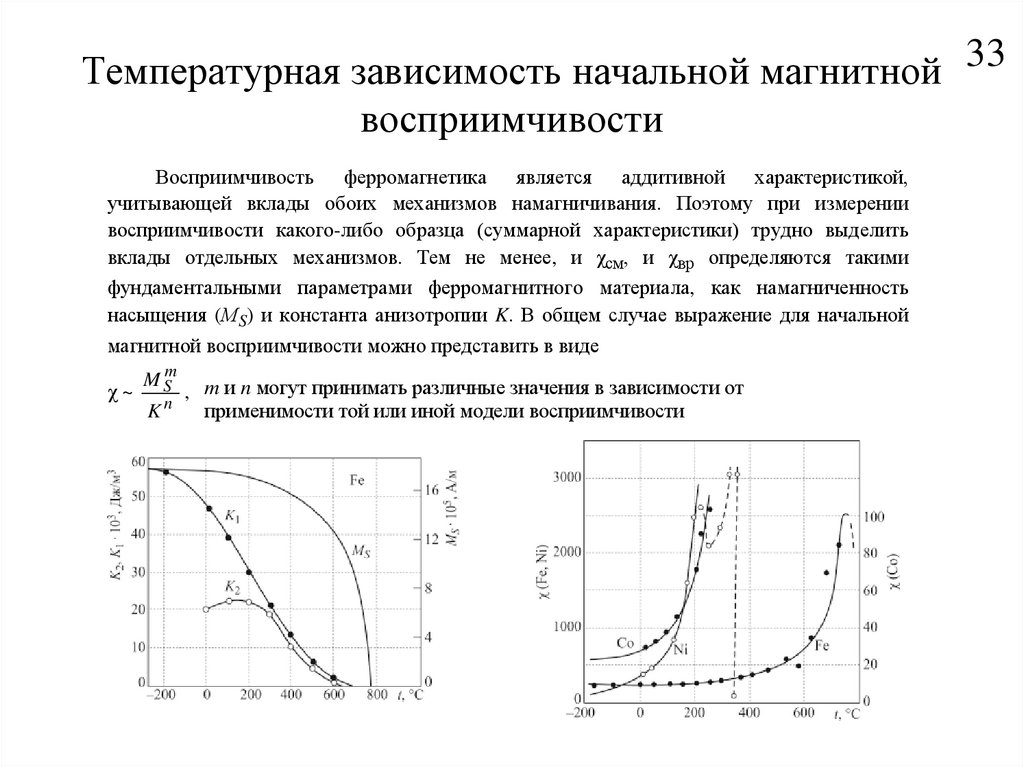
33
Температурная зависимость начальной магнитной
восприимчивости
Восприимчивость ферромагнетика является аддитивной характеристикой,
учитывающей вклады обоих механизмов намагничивания. Поэтому при измерении
восприимчивости какого-либо образца (суммарной характеристики) трудно выделить
вклады отдельных механизмов. Тем не менее, и χсм, и χвр определяются такими
фундаментальными параметрами ферромагнитного материала, как намагниченность
насыщения (МS) и константа анизотропии K. В общем случае выражение для начальной
магнитной восприимчивости можно представить в виде
χ~
M Sm
K
n
, m и n могут принимать различные значения в зависимости от
применимости той или иной модели восприимчивости

34. Процессы намагничивания. Коэрцитивная сила при смещении границ.

34
Если монотонно увеличивать значение внешнего магнитного поля, то доменная граница будет все
дальше двигаться вдоль оси x, переходя из одной потенциальной ямы в другую. Не исключено, что в
какой-то потенциальной яме эта граница встретит другую границу, пришедшую с противоположной
стороны. В этом случае две границы уничтожат друг друга и домен исчезнет. Величина критического
поля определяется максимальным значением Е x . Такое поле называется коэрцитивным полем, а
чаще – коэрцитивной силой:
Нс =
1
E
.
2 0 М S x max
Коэрцитивная сила является структурно-чувствительным параметром ферромагнитных материалов,
ее можно вычислить рассматривая конкретные причины, приводящие к удержанию (фиксации) доменной
границы в определенном положении.
Изменение энергии кристалла при смещении доменной границы можно отнести к изменению собственной энергии границы. Когда на пути смещения границы происходит существенное изменение ее площади (что имеет место, например, при обтекании ею большого количества дефектов), коэрцитивную силу можно представить в виде
Нс =
1
S
2 0 М S S x max
K
Нс = р
βn (теория включений)
0 M S
Нс ≈
S гр
,
2 0 М S x max (теория напряжений).

35. Динамика процессов намагничивания. Естественный ферромагнитный резонанс (1).

Пусть состояние равновесия нарушается
за счет быстрого изменения поля Н. В этом
случае вектор намагниченности начнет
прецессировать вокруг нового направления
Н с ларморовской частотой ωL = γμ0H.
35
Пусть состояние равновесия нарушается за счет
быстрого изменения поля Н. В этом случае вектор
намагниченности начнет прецессировать вокруг
нового направления Н
с ларморовской частотой ωL = γμ0H.
Допустим, что поле изменяется непрерывно
по закону h exp(jωt) c очень малой по сравнению
с Н амплитудой.
0
[M·(M·H)]
М
τ –1 = ωрел = γαμ0Н
t
Мх = ΔМ exp j 0t ,
t
My = ΔM exp j 0t
2
M 2
2t
Mz = M 1
exp ,
M
dM/dt = –γμ0M·H –
Для установления соотношения между
мгновенным значением намагниченности
и соответствующим значением переменного
магнитного поля заменим Н суммой Н + (h exp(jωt)),
которая вызывает появление динамической
составляющей намагниченности m << M

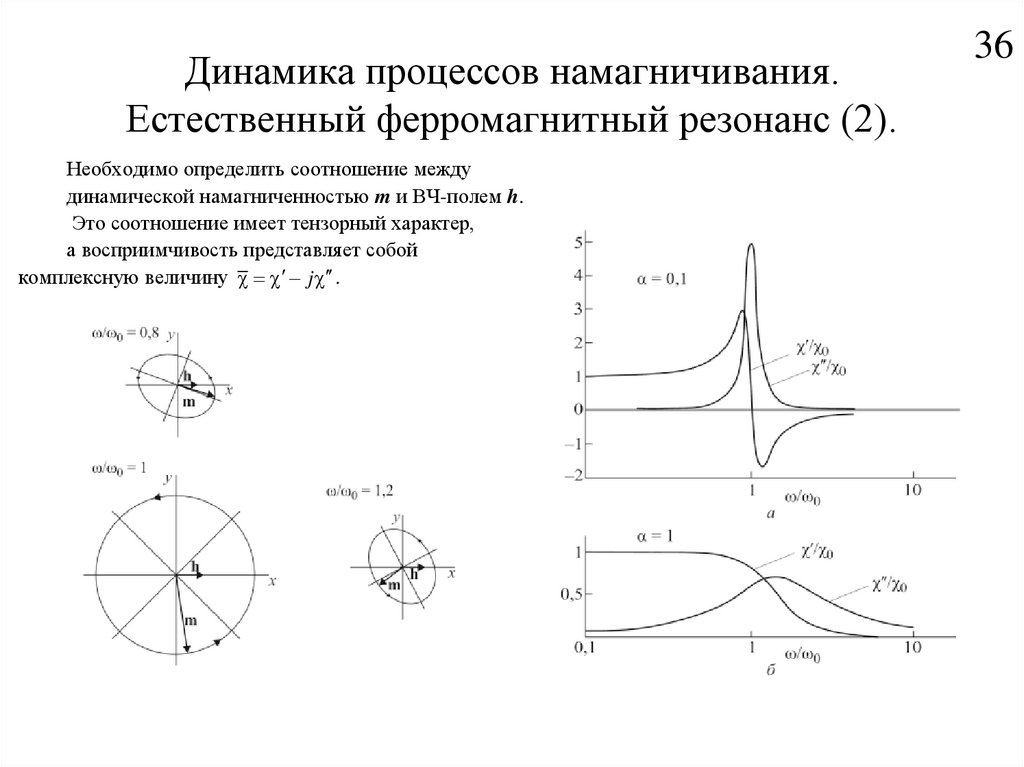
36. Динамика процессов намагничивания. Естественный ферромагнитный резонанс (2).

Необходимо определить соотношение между
динамической намагниченностью m и ВЧ-полем h.
Это соотношение имеет тензорный характер,
а восприимчивость представляет собой
комплексную величину j .
36

37. Динамика процессов намагничивания. Смещение доменных границ (1).

37
Динамика процессов намагничивания.
Смещение доменных границ (1).
Решающее влияние на поведение доменных
границ в слабых полях оказывают силы,
удерживающие границы в положениях
равновесия -точка х0
2 Е
х 2 = const = kгр
χсм =
R(х) = – kгрх
0 M S2
,
dkгр
С полем Нэф связана определенная энергия.
Поскольку эта энергия возникает в
движущейся границе, то ее можно трактовать
как дополнительную энергию
самой доменной границы Δγгр
2
1
v2
dФ
Δγгр = – μ0 М z H эфdz ≈
dz
2 2 dz
2
8
0
=
1
mгрv2
2
mгр =
2
2
0 гр
,
μ0 Н эф М dz = 8παγμ МΔγ = βv2
0
гр
2
М
dФ
β = 4παγμ0Мmгр =
dz ,
dz
0
ω=–
dФ dФ
=
v. ω ≈ μ0γНэф
dt
dz
v dФ
Нэф ≈
.
0 dz

38. Динамика процессов намагничивания. Смещение доменных границ (2).

Уравнение движения границы можно
записать в виде:
mгр
d 2z
dt 2
+β
= χсм
dz
+ kгрz = 2μ0МSHx
dt
Если приложено переменное магнитное поле
Нх = Нх exp(jωt), то решение уравнения имеет вид
0
z=
2 0 M S H x0 kгр
1 mгр kгр 2 j kгр
exp(jωt)
Вклад рассматриваемой границы в
магнитную восприимчивость равен 2zМS /Hx,
так что при параллельном расположении 180º-х
границ на расстоянии d друг от друга получаем:
m
χ(ω) = χсм 1 гр 2
k
гр
ω0 =
kгр
mгр
ωрел =
j
k
гр
kгр
= χсм
1 2
0
2
1 2
рел 2
0
рел
2
1 2 2
0
рел
Если затухание слабое, т. е. β2 << kгрmгр (ω0 << ωрел),
то частотная зависимость восприимчивости
имеет резонансный характер.
В случае сильного затухания (ω0 >> ωрел)
= χсм
1
1 рел
1
,
38
= χсм
2
рел
1 рел
2

39. Экспериментальные магнитные спектры.

39
Экспериментальные магнитные спектры.