Похожие презентации:
Магнитное поле в веществе. Тема №21
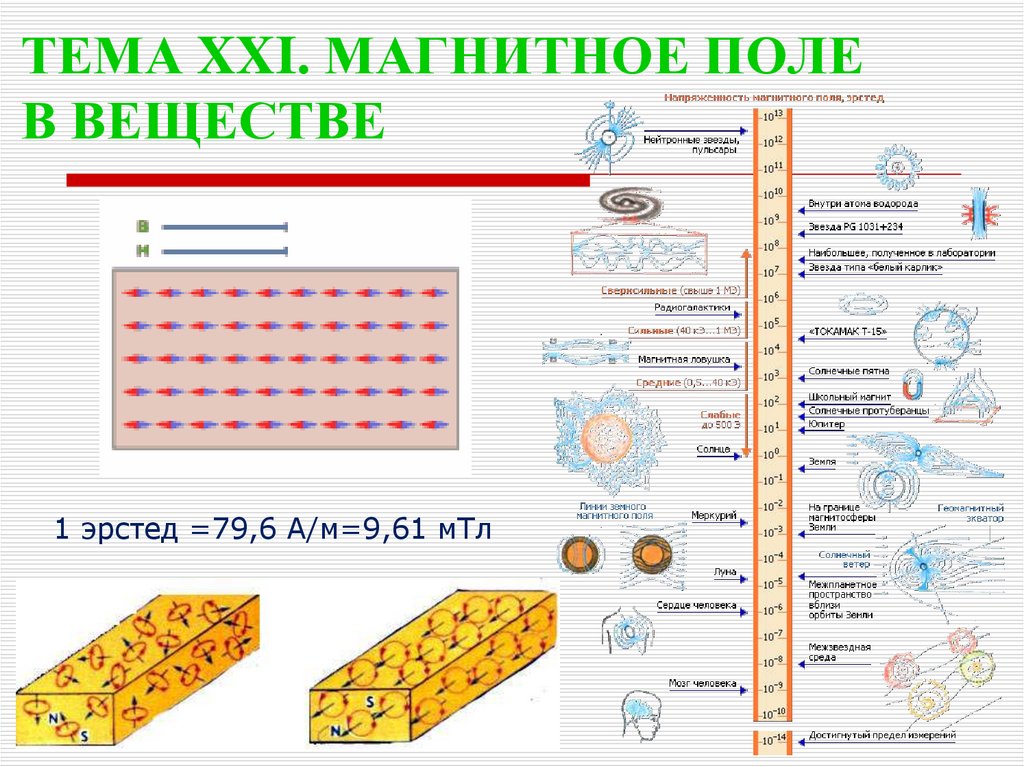
1. ТЕМА XXI. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
1 эрстед =79,6 А/м=9,61 мТл2. 1. НАМАГНИЧЕНИЕ МАГНЕТИКА
Все вещества являются магнетиками, то естьcпособны под действием поля приобретать
магнитный момент (намагничиваться).
Намагниченное вещество создает магнитное поле B , которое
накладывается на внешнее поле B0 .
Оба поля вместе дают результирующее поле B B0 B .
Для объяснения намагничения тел Ампер предположил,
что в молекулах вещества циркулируют молекулярные токи.
В отсутствие внешнего поля молекулярные токи ориентированы
беспорядочно, поэтому обусловленное ими поле равно нулю.
Под действием внешнего поля магнитные моменты молекул
ориентируются вдоль поля – происходит намагничение образца.
Намагничение магнетика характерезуют магнитным
1
pm .
моментом единицы объема – намагниченностью: J
V
V 0
3. 2. РОТОР ИНДУКЦИИ РЕЗУЛЬТИРУЮЩЕГО ПОЛЯ
Результирующее магнитное поле в магнетике это суммавнешнего поля и поля молекулярных токов (внутреннее поле)
B B0 B
B B0 B .
Ротор индукции внешнего поля определяется плотностью
макроскопического тока. Аналогично ротор индукции внутреннего
поля должен определяться плотностью микроскопических токов:
B0 0 j0 ;
B 0 j
B 0 ( j0 j ).
Чтобы определить ротор магнитной индукции суммарного поля
нужно знать плотность макроскопических и молекулярных токов.
В свою очередь плотность молекулярных (микроскопических)
токов зависит от значения индукции результирующего поля.
Для преодоления возникшего затруднения нужно найти такую
вспомогательную величину, которая определяется только
внешними макроскопическими токами (токами проводимости).
4. 3. ЦИРКУЛЯЦИЯ НАМАГНИЧЕННОСТИ
Установим связь между плотностью молекулярных токови намагниченностью магнетика. Для этого вычислим
сумму молекулярных токов, охватываемых некоторым контуром.
Вклад в сумму внесут только токи, «нанизанные» на контур.
Элемент контура dl , образующий с намагниченностью J угол
нанизывает на себя те молекулярные токи, центры которых
попадают внутрь косого цилиндра с объемом dV Sm cos dl.
Суммарный ток, охватываемый элементом
I m Sm pm ; pm n J
dI J cos dl Jdl
I dI
L
Jdl .
L
,
dl : dI I m nSm cos dl.
5. 4. РОТОР НАМАГНИЧЕННОСТИ
Сумма молекулярных токов, охватываемых замкнутымконтуром равна циркуляции вектора намагниченности вдоль
этого контура
I
Jdl .
L
I j dS
Выразим суммарный ток через
плотность молекулярных токов
S
j dS Jdl .
S
По теореме Стокса
L
Jdl J dS
L
j dS J dS
S
S
S
j J .
6. 5. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ
Плотность молекулярных токов отлична от нуля в тех точках, гдене равен нулю ротор намагниченности, причем j rotJ .
Подставим выражение для плотности молекулярных токов
в формулу для ротора магнитной индукции результирующего поля:
B 0 j0 0 j ; j J B 0 j0 0 J .
Объединим слагаемые, содержащие роторы:
B 0 J 0 j0
B
( J ) j0 ;
0
H
B
0
( B 0 J ) 0 j0
J H
– напряженность магнитного поля;
H j0 j .
А
H J 1 .
м
7. 6. ЦИРКУЛЯЦИЯ НАПРЯЖЕННОСТИ ПОЛЯ
Ротор напряженности магнитостатического поля равен плотностимакроскопических токов (токов проводимости)
H j .
Вычислим поток ротора напряженности магнитного поля через
произвольную поверхность натянутую на некоторый контур
H dS jdS .
S
По теореме Стокса
H dS Hdl
S
L
S
N
Hdl jdS I .
L
S
k 1
Теорема о циркуляции вектора напряжённости:
циркуляция вектора напряженности магнитного поля
по произвольному контуру равна алгебраической сумме
макроскопических токов, охватываемых этим контуром.
k
8. 7. МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ
Намагниченность принято связывать не с магнитной индукцией,а с напряженностью магнитного поля.
Для каждой точки изотропного магнетика справедливо J H ,
где
– характерная для данного магнетика величина,
называемая магнитной восприимчивостью.
Опыт показывает, что для слабомагнитных (неферромагнитных)
не зависит от H .
веществ при не слишком сильных полях
Размерность
H
и
J
совпадают,
В анизотропных средах направления
– безразмерная величина.
H и J могут не совпадать.
Для таких сред связь между намагниченностью и напряженностью
поля задается тензором магнитной восприимчивости ij :
J i ij H j ;
j
J
x
xx H x xy H y xz H z .
9. 8. МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
HB
0
H H
J H
J;
B
0
H 1
B
0
H
B
0
H
B
H
.
0 1
1
Безразмерная величина
называется относительной магнитной проницаемостью,
или просто магнитной проницаемостью вещества.
H
B
0
;
B 0 H .
10. 9. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ (I)
Рассмотрим поле бесконечно длинногокруглого намагниченного стержня.
Намагниченность J будем считать всюду
одинаковой и направленной по оси стержня.
Разобьем мысленно стержень на перпендикулярные к оси слои
Каждый слой разобьем на малые цилиндрические элементы.
Каждый такой элемент обладает магнитным моментом
dl.
dpm JdldS dpm dI dS dI Jdl.
Каждый элемент создаёт поле, которое бы создавал ток dI Jdl ,
dpm JdSdl ,
обтекающий элемент по боковой поверхности.
Воображаемые токи, текущие по общему для двух соседних
элементов участку, одинаковы по величине и противоположны по
направлению, поэтому их сумма равна нулю.
Таким образом, некомпенсированными оказываются лишь токи,
текущие по внешней боковой поверхности стержня.
11. 10. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ (II)
Слой стержня толщиной dl создаётмагнитное поле, которое создавал бы ток
dI Jdl , обтекающий этот слой
по внешней боковой поверхности стержня.
Линейная плотность этого тока равна
j лин dI dl J .
Весь бесконечно длинный стержень создает магнитное поле,
эквивалентное полю цилиндра,
обтекаемому током
j лин J .
с линейной плотностью
Вне бесконечно длинного цилиндра (соленоида)
поле равно нулю, а внутри цилиндра однородно и равно
0 jлин .
Таким образом, вне однородного стержня поле равно нулю.
Внутри намагниченного стержня поле однородно:
B 0 J .
12. 11. ПОЛЕ НАМАГНИЧЕННОГО СТЕРЖНЯ (III)
Пусть однородное поле B0 , создано макротоками в вакууме.Напряженность этого поля равна H 0 B0 0
( 1).
Внесем в это поле бесконечно длинный круглый стержень
из однородного магнетика, расположив его ось вдоль поля B0 .
Из соображений симметрии следует, что возникающая
намагниченность J совпадает по направлению с индукцией B0 .
Намагниченный стержень создает внутри себя поле B J .
В результате поле внутри стержня станет равным
B B0 B B0 0 J ;
H
B
0
J
B0
0
0
0 J
J H0.
0
Напряженность поля в стержне такая же как в вакууме.
B 0 H ;
H H 0 B0 0
B 0 B0 0 B0 .
Относительная магнитная проницаемость показывает, во
сколько раз возрастает магнитная индукция в магнетике.
13. 12. УСЛОВИЯ НА ГРАНИЦЕ ДВУХ МАГНЕТИКОВ (НОРМАЛЬНЫЕ К-Ы)
Возьмём на границе двух магнетиковвоображаемую цилиндрическую
поверхность, расположенную
по разные стороны от границы раздела.
По теореме Гаусса
BdS 0
B1n1 S B2 n2 S Bn Sбок 0.
B1n1 B2 n2 .
Если проецировать B1 и B2 на одну и ту же нормаль, то B1n B2 n .
H
Выразив магнитную индукцию
0 1H1n 0 2 H 2 n 1n 2 .
через напряжённость, получим:
H 2 n 1
Устремляя высоту цилиндра к нулю (h 0), получим:
То есть, при переходе через границу раздела двух магнетиков
нормальный компонент вектора B изменяется непрерывно.
Нормальный компонент вектора
H
претерпевает разрыв.
14. 13. УСЛОВИЯ НА ГРАНИЦЕ ДВУХ МАГНЕТИКОВ (ТАНГЕНЦИАЛЬНЫЕ К-Ы)
Возьмём на границе двух магнетиковвоображаемый прямоугольный контур,
расположенный по разные стороны от границы раздела.
По теореме о циркуляции вектора напряжённости
Hdl I .
Будем считать, что по границе раздела
не текут макроскопические токи, тогда H1 b H 2 b H 2a 0.
Устремляя высоту контура к нулю (a 0), получим: H1 H 2 .
Выразив напряжённость магнитного поля через магнитную
индукцию, получим:
B
B
B
1
0 1
2
0 2
1
B2
1
2
.
То есть, при переходе через границу раздела двух магнетиков
тангенциальный компонент вектора H изменяется непрерывно.
Тангенциальный компонент вектора
B
претерпевает разрыв.
15. 14. ПРЕЛОМЛЕНИЕ МАГНИТНЫХ ЛИНИЙ
B1n B2 n ,H 1n 2
,
H 2 n 1
H1 H 2 ,
B1 1
.
B2 2
При переходе через границу раздела двух магнетиков компоненты
магнитного поля Bn
1
и H изменяются непрерывно.
Компоненты B и H n
претерпевают разрыв.
Обозначим углы между линиями B
и нормалью к поверхности как 1 , 2 .
B1
B2
, tg 2
Тогда tg 1
B2n
B1n
tg 1 B1 B1n B1 1
.
tg 2 B2 B2 n B2 2
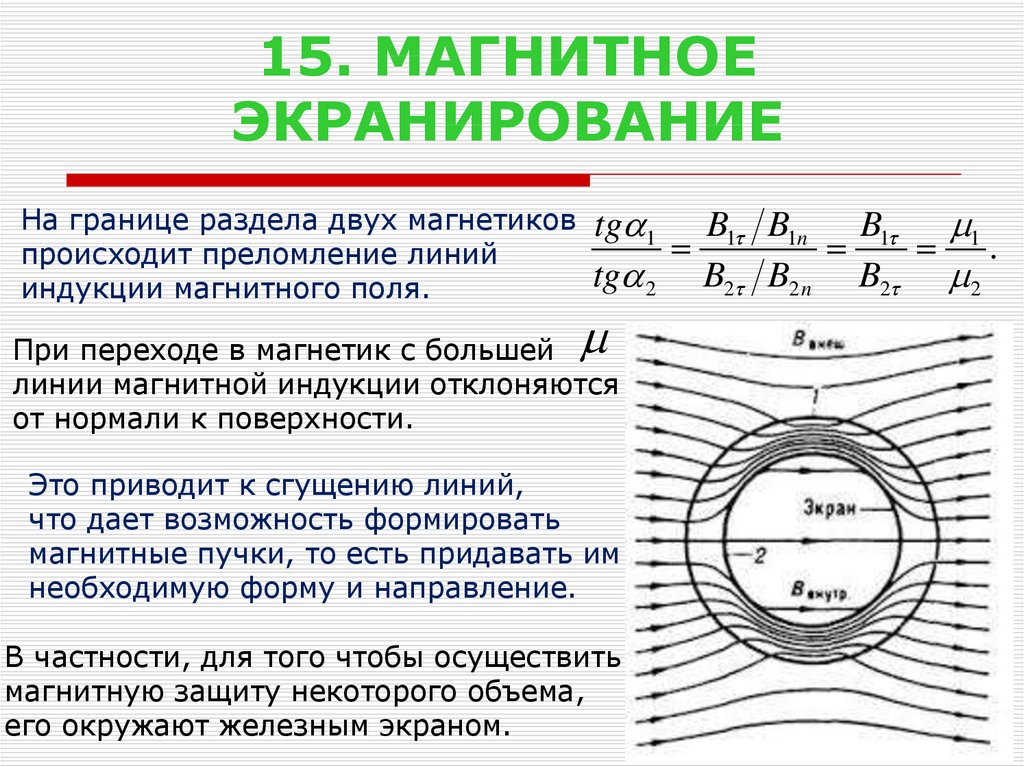
16. 15. МАГНИТНОЕ ЭКРАНИРОВАНИЕ
На границе раздела двух магнетиковпроисходит преломление линий
индукции магнитного поля.
tg 1 B1 B1n B1 1
.
tg 2 B2 B2 n B2 2
При переходе в магнетик с большей
линии магнитной индукции отклоняются
от нормали к поверхности.
Это приводит к сгущению линий,
что дает возможность формировать
магнитные пучки, то есть придавать им
необходимую форму и направление.
В частности, для того чтобы осуществить
магнитную защиту некоторого объема,
его окружают железным экраном.
17. 16. МАГНИТНОЕ ПОЛЕ В ЗАЗОРЕ ЭЛЕКТРОМАГНИТА
Простейший электромагнит состоит из железного сердечника,на который насажены катушки с током.
Линии магнитной индукции сосредоточены
внутри сердечника.
Применим теорему о циркуляции
к контуру, идущему по оси сердечника.
H жlж H вlв NI ,
Hж
Bж Bв B
Blж
B
0 NI
lв в lж
0 ж
Bж
0 ж
Blв
Hв
,
0 в
Bв
0 в
NI
0 NI
; lв
ж lв lж ж
lж
ж
;
B 0 I
N
.
lв
18. 17. ВИДЫ МАГНЕТИКОВ
J H,J ( 1) H .
В зависимости от знака и величины
магнитной восприимчивости все
магнетики делятся на три вида:
1. Диамагнетики
2. Парамагнетики
3. Ферромагнетики
(10 4 10 6 ).
(10 4 10 6 ).
(H )
1.
Молекулы диамагнетиков не обладают
собственным магнитным моментом.
Молекулы парамагнетиков обладают
орбитальным магнитным моментом,
у ферромагнетиков – спиновым м-ом.
19. 18. МАГНИТОМЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
e 2 2 rpm IS r ;
V
T
T
eVr
r V
.
pm
2
T
2
L mVr ;
pm z
Lz
eVr
e pm
e
;
.
2mVr
2m L 2m
e
L.
pm L pm
2m
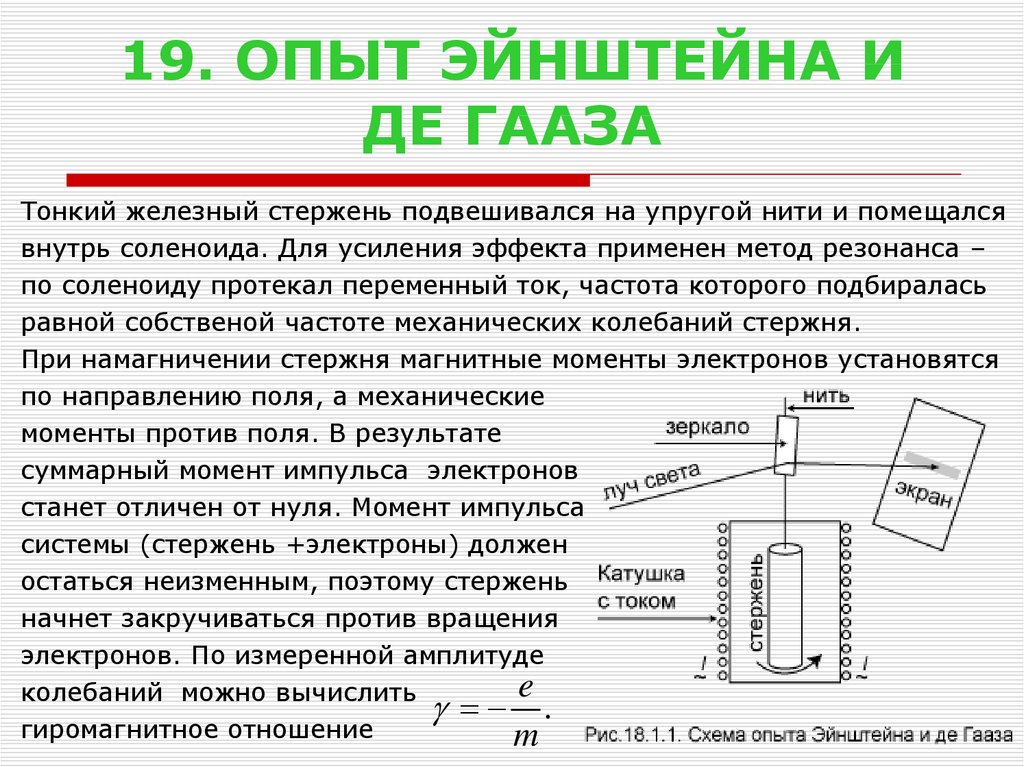
20. 19. ОПЫТ ЭЙНШТЕЙНА И ДЕ ГААЗА
Тонкий железный стержень подвешивался на упругой нити и помещалсявнутрь соленоида. Для усиления эффекта применен метод резонанса –
по соленоиду протекал переменный ток, частота которого подбиралась
равной собственой частоте механических колебаний стержня.
При намагничении стержня магнитные моменты электронов установятся
по направлению поля, а механические
моменты против поля. В результате
суммарный момент импульса электронов
станет отличен от нуля. Момент импульса
системы (стержень +электроны) должен
остаться неизменным, поэтому стержень
начнет закручиваться против вращения
электронов. По измеренной амплитуде
e
колебаний можно вычислить
.
гиромагнитное отношение
m
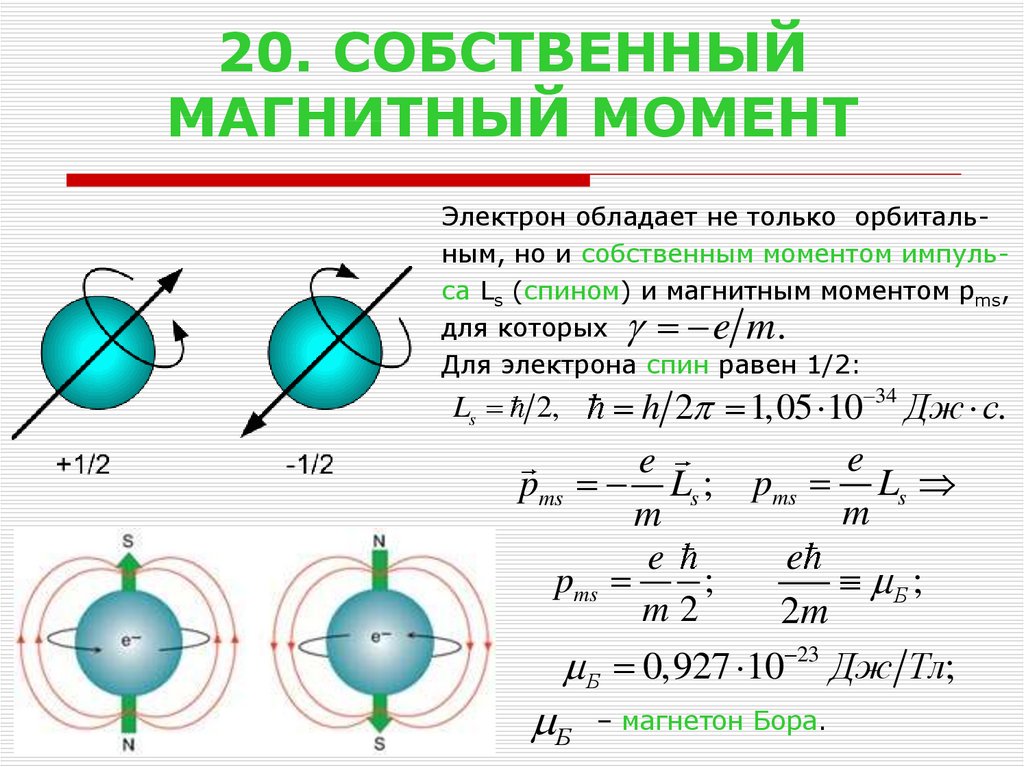
21. 20. СОБСТВЕННЫЙ МАГНИТНЫЙ МОМЕНТ
Электрон обладает не только орбитальным, но и собственным моментом импульса Ls (спином) и магнитным моментом pms,для которых
e m.
Для электрона спин равен 1/2:
Ls
h 2 1,05 10 34 Дж с.
e
e
pms Ls ; pms Ls
m
m
e
e
pms
;
Б ;
m2
2m
2,
Б 0,927 10 23 Дж Тл;
Б
– магнетон Бора.
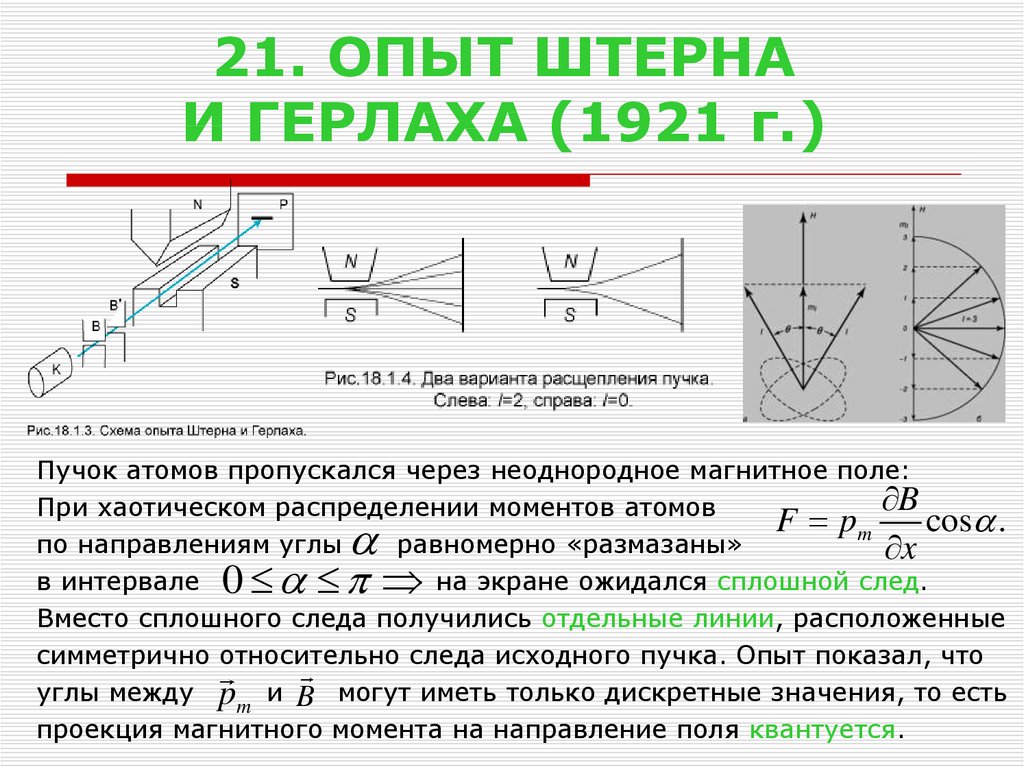
22. 21. ОПЫТ ШТЕРНА И ГЕРЛАХА (1921 г.)
Пучок атомов пропускался через неоднородное магнитное поле:B
При хаотическом распределении моментов атомов
F pm
cos .
по направлениям углы
равномерно «размазаны»
x
в интервале 0
на экране ожидался сплошной след.
Вместо сплошного следа получились отдельные линии, расположенные
симметрично относительно следа исходного пучка. Опыт показал, что
углы между pm и B могут иметь только дискретные значения, то есть
проекция магнитного момента на направление поля квантуется.
23. 22. КЛАССИКИ
Вандер де Гааз1878 – 1960
нидерландский
физик
Отто Штерн
1888 – 1969
немецкий
физик
Вальтер Герлах
1889 – 1979
немецкий
физик
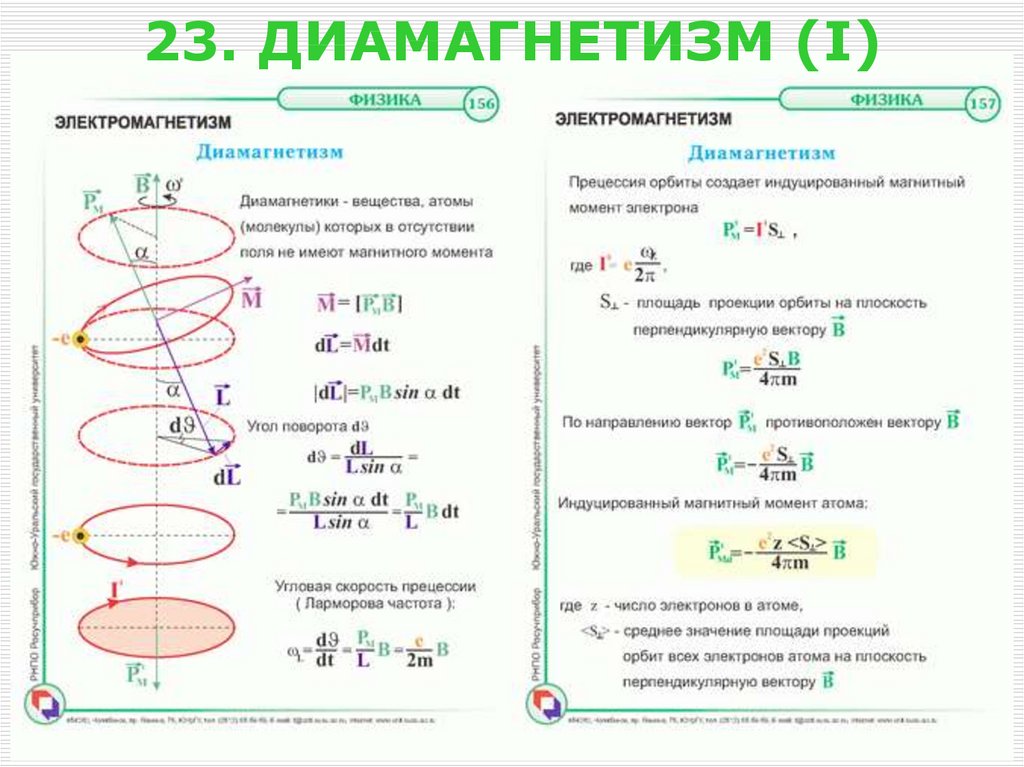
24. 23. ДИАМАГНЕТИЗМ (I)
25. 24. ДИАМАГНЕТИЗМ (II)
e2 z SpMa
B.
4 m
Под действием внешнего поля
происходит прецессия орбит с
одинаковой угловой скоростью.
Прецессия приводит к появлению
индуцированного магнитного
момента атома.
Прецессия орбит возникает у всех
веществ; «чистый» диамагнетизм
проявляют только те вещества, у
которых атомы не обладают магнитным моментом (векторная сумма
орбитальных и спиновых магнитных моментов атома равна нулю).
26. 25. ПАРАМАГНЕТИЗМ
К парамагнетикам относятся вещества, длякоторых орбитальный магнитный момент атома
отличен от нуля, а спиновый равен нулю.
Магнитное поле стремится установить магнитные
моменты атомов вдоль направления индукции,
тепловое движение стремится разупорядочить
ориентацию магнитных моментов.
В результате устанавливается определенная
преимущественная ориентация моментов вдоль
поля, тем большая чем больше величина
индукции магнитного поля, и тем меньшая, чем
выше температура парамагнитного образца.
27. 26. ЗАКОН КЮРИ ДЛЯ ПАРАМАГНЕТИКОВ
Пьер Кюри экспериментально установилзакон, согласно которому магнитная
восприимчивость парамагнитного вещества
обратно пропорционально абсолютной
температуре парамагнетика
C
,
T
где С – постоянная Кюри,
зависящая от рода
вещества.
Пьер Кюри
1859 – 1906
французский физик
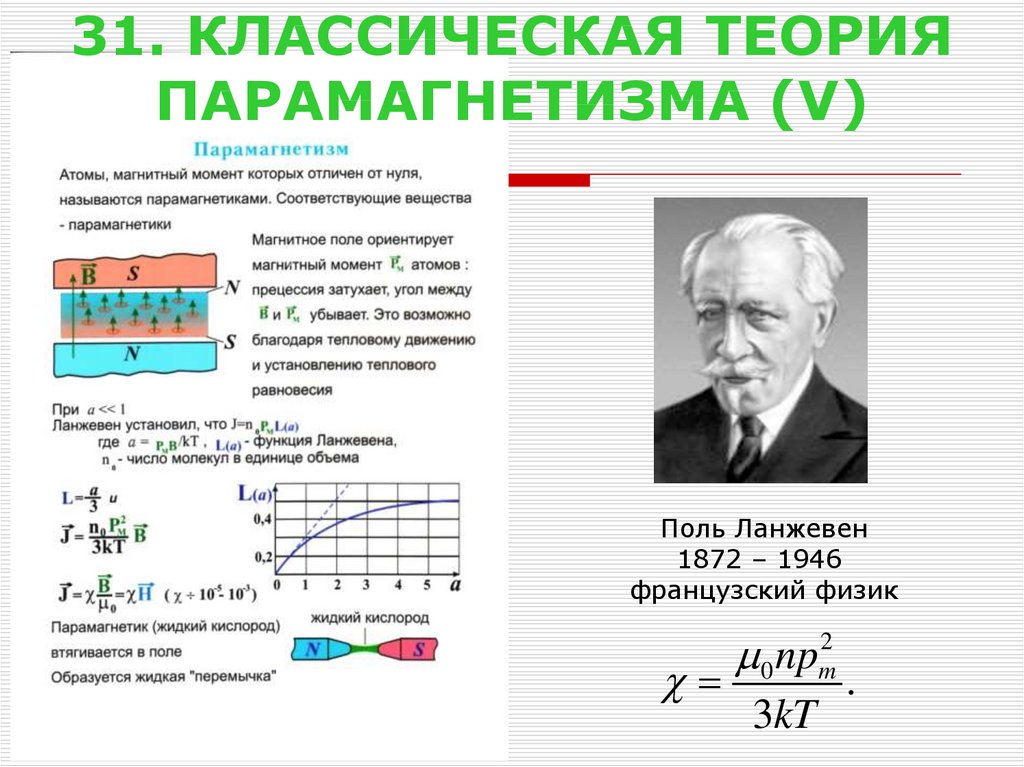
28. 27. КЛАССИЧЕСКАЯ ТЕОРИЯ ПАРАМАГНЕТИЗМА (I)
Теория парамагнетизма была создана П. Ланжевеном в 1905 г.Атом обладает в магнитным поле энергией
W pm B cos .
Равновесное распределение магнитных моментов по направлениям
должно подчиняться распределению Больцмана. Значит вероятность
того, что магнитный момент атома будет образовывать
с направлением вектора B угол, заключенный в
пределах от до d , будет пропорциональна
dw exp W kT dw exp pm B cos kT .
В отсутствии поля все направления магнитных моментов равновероятны,
поэтому вероятность того, что направление момента образует с заданным
направлением угол в пределах от до d , равна
dwB 0
sin d
dS
d
.
; d 2 ; dS 2 r sin rd dwB 0
2
r
4
29. 28. КЛАССИЧЕСКАЯ ТЕОРИЯ ПАРАМАГНЕТИЗМА (II)
При включении магнитного поля в выражениидля вероятности появится сомножитель отражающий распределение Больцмана, то есть
pm B
a
.
kT
Дж Тл; B 1Тл; T 300К
1
dw A exp a cos sin d ;
2
pm
Б 10 23
Для не слишком сильных полей и не очень низких температур
1023 1
3
2,5
10
1,38 10 23 300
a
1
exp a cos 1 a cos
A
dw 1 a cos sin d .
2
Нормировочный множитель A можно найти исходя из того, что сумма
вероятностей всех возможных значений угла должна быть равна 1:
A
1 1 a cos sin d
2
0
2
sin d a cos sin d .
A 0
0
30. 29. КЛАССИЧЕСКАЯ ТЕОРИЯ ПАРАМАГНЕТИЗМА (III)
22
cos
sin d a cos sin d
0 a sin d sin
A
A 0
0
0
sin
2
cos cos0 a
A
2 0
2
2
2
A
A 1
1
dw 1 a cos sin d .
2
В единице объема число атомов, магнитные моменты которых образуют
с направлением поля углы от до d , будет равно
dn ndw
n
dn 1 a cos sin d .
2
Каждый из этих атомов вносит в результирующий магнитный момент
вклад, равный pm cos . Следовательно для магнитного момента
единицы объема (т. е. для намагниченности) получается выражение
J pm cos dn
0
npm
J
cos 1 a cos sin d .
2 0
31. 30. КЛАССИЧЕСКАЯ ТЕОРИЯ ПАРАМАГНЕТИЗМА (IV)
npmJ
cos 1 a cos sin d
2 0
J H
npm
2
J
cos sin d a cos sin d
2 0
0
npm
2
J
sin d sin a cos d cos
2 0
0
npm
J
2
sin 2
cos3 npm
cos3 cos3 0 npm a
a
;
0 a
2
3
3
2 0
3 0
pm B
a
kT
npm2 B
J
;
3kT
B 0 H 0 H
0 npm2
3kT
.
32. 31. КЛАССИЧЕСКАЯ ТЕОРИЯ ПАРАМАГНЕТИЗМА (V)
Поль Ланжевен1872 – 1946
французский физик
0 np
3kT
2
m
.
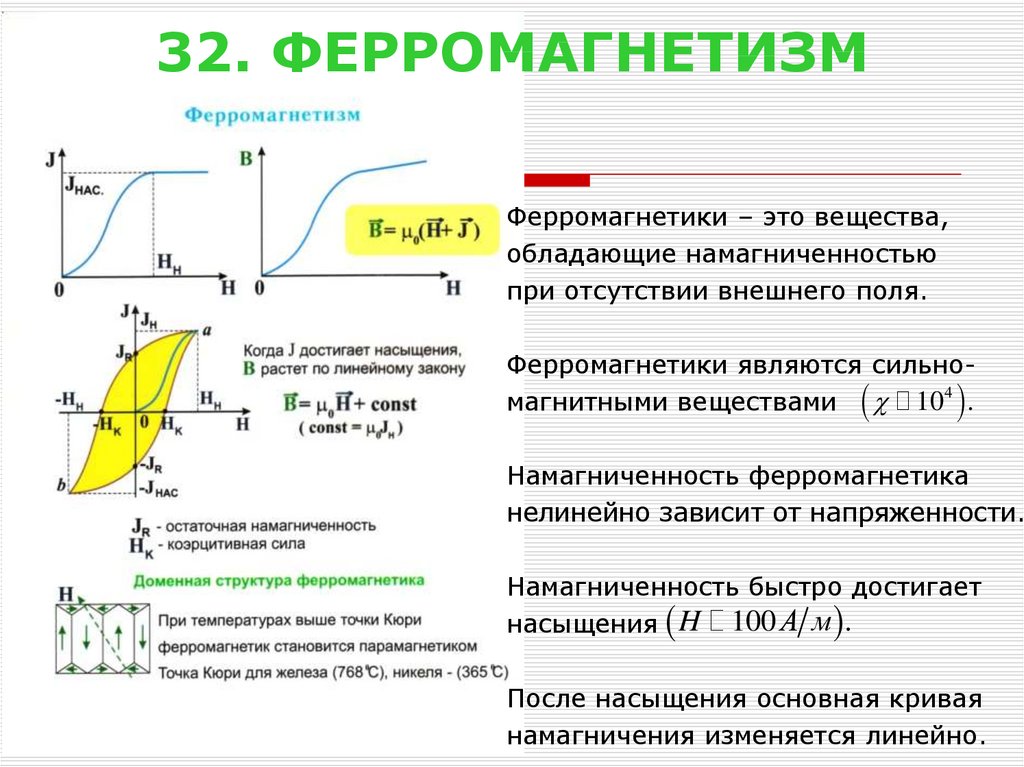
33. 32. ФЕРРОМАГНЕТИЗМ
Ферромагнетики – это вещества,обладающие намагниченностью
при отсутствии внешнего поля.
Ферромагнетики являются сильно4
магнитными веществами 10 .
Намагниченность ферромагнетика
нелинейно зависит от напряженности.
Намагниченность быстро достигает
насыщения H 100 А м .
После насыщения основная кривая
намагничения изменяется линейно.
34. 33. МАГНИТНЫЙ ГИСТЕРЕЗИС
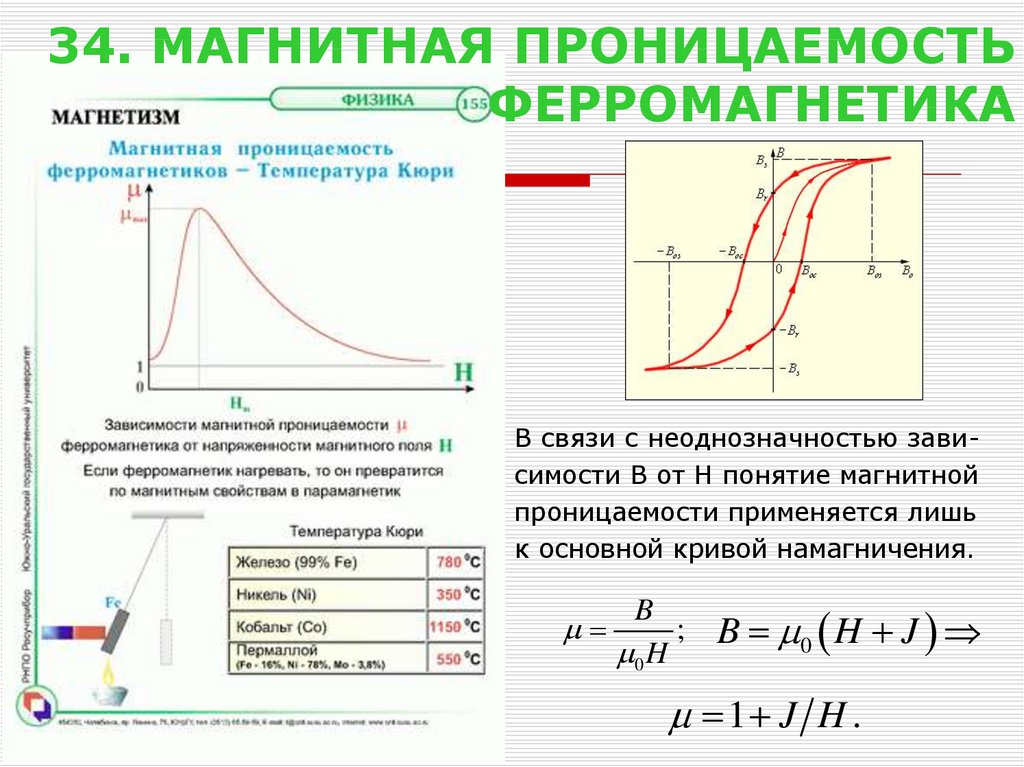
35. 34. МАГНИТНАЯ ПРОНИЦАЕМОСТЬ ФЕРРОМАГНЕТИКА
В связи с неоднозначностью зависимости B от H понятие магнитнойпроницаемости применяется лишь
к основной кривой намагничения.
B
;
0 H
B 0 H J
1 J H .
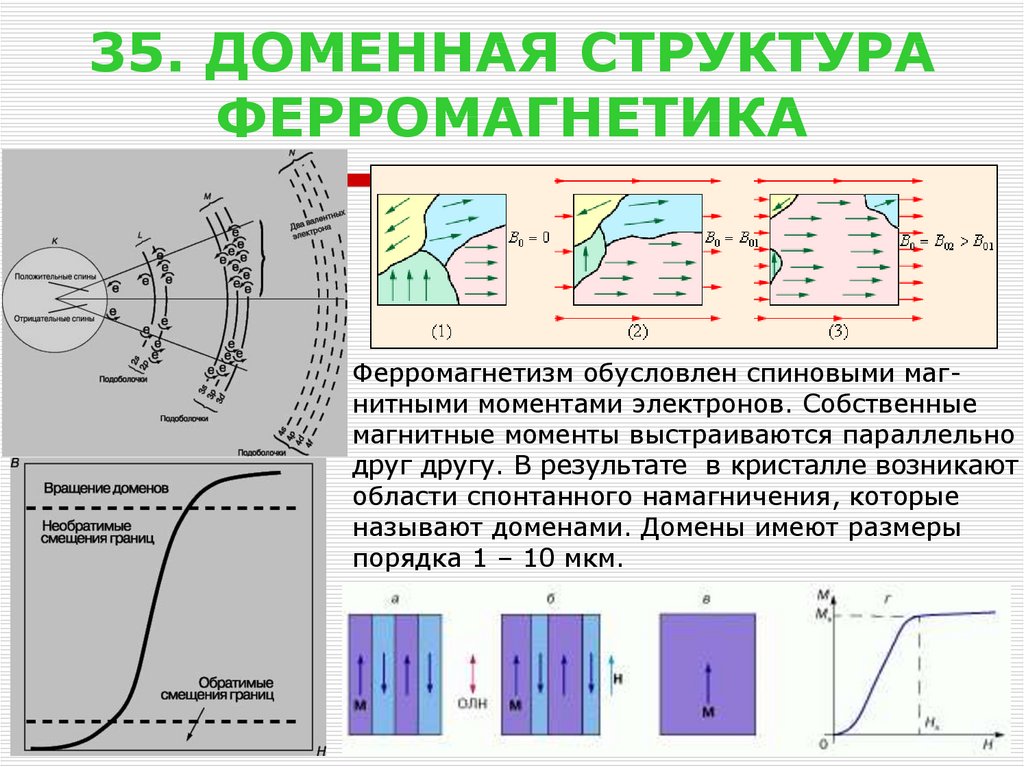
36. 35. ДОМЕННАЯ СТРУКТУРА ФЕРРОМАГНЕТИКА
Ферромагнетизм обусловлен спиновыми магнитными моментами электронов. Собственныемагнитные моменты выстраиваются параллельно
друг другу. В результате в кристалле возникают
области спонтанного намагничения, которые
называют доменами. Домены имеют размеры
порядка 1 – 10 мкм.
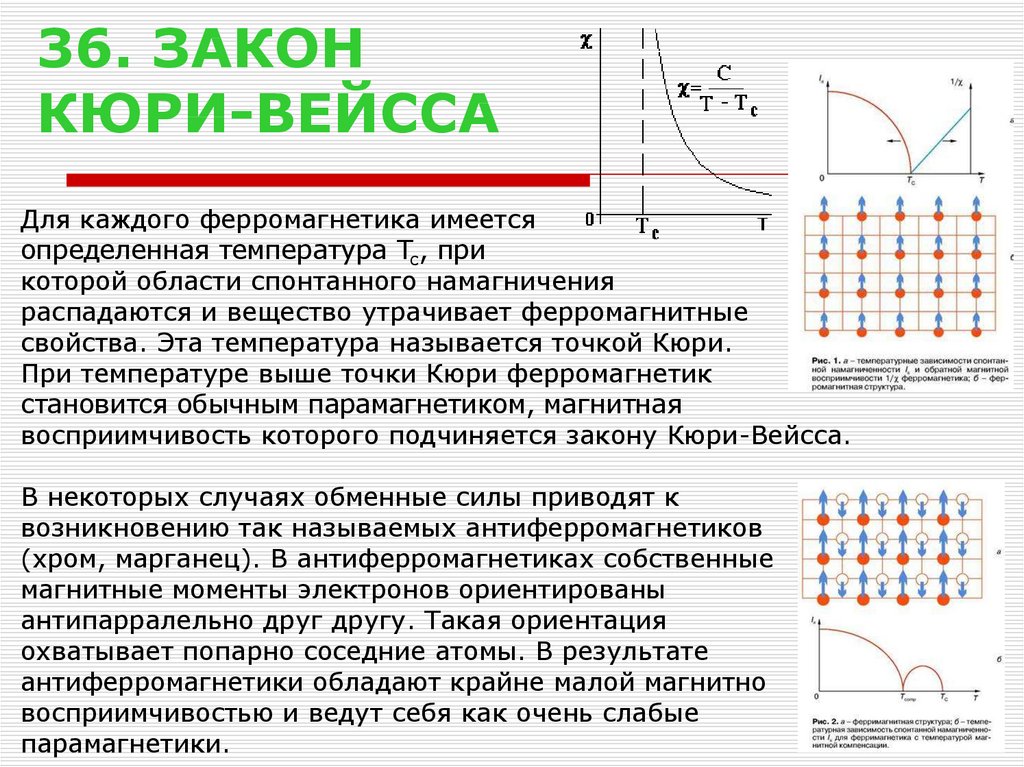
37. 36. ЗАКОН КЮРИ-ВЕЙССА
Для каждого ферромагнетика имеетсяопределенная температура Tc, при
которой области спонтанного намагничения
распадаются и вещество утрачивает ферромагнитные
свойства. Эта температура называется точкой Кюри.
При температуре выше точки Кюри ферромагнетик
становится обычным парамагнетиком, магнитная
восприимчивость которого подчиняется закону Кюри-Вейсса.
В некоторых случаях обменные силы приводят к
возникновению так называемых антиферромагнетиков
(хром, марганец). В антиферромагнетиках собственные
магнитные моменты электронов ориентированы
антипарралельно друг другу. Такая ориентация
охватывает попарно соседние атомы. В результате
антиферромагнетики обладают крайне малой магнитно
восприимчивостью и ведут себя как очень слабые
парамагнетики.


























 Физика
Физика








