Свойства функций. Монотонность

1.

Свойство 1. Монотонность.

2.

y = f(x) – возрастающая функция
y = f(x)

3.

y = f(x) – убывающая функция
y = f(x)

4.

Функция у = f(х) называется монотонной на
множестве Х, если она на этом промежутке или
убывает или возрастает.

5.

Если функция определена и непрерывна в концах
интервала возрастания или убывания (а; b), то эти
точки включаются в промежуток возрастания или
убывания.

6.

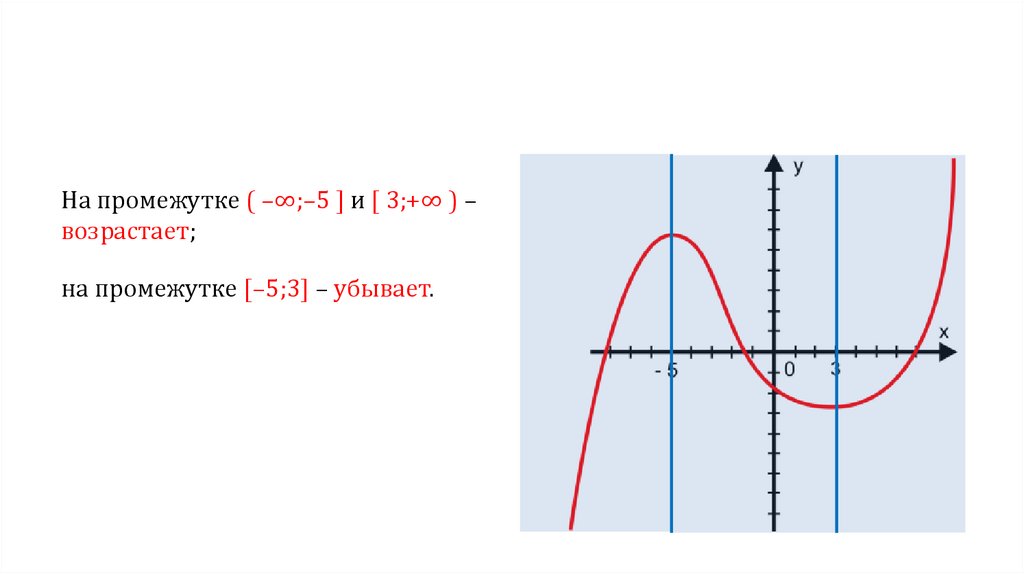
На промежутке ( –∞;–5 ] и [ 3;+∞ ) –
возрастает;
на промежутке [–5;3] – убывает.

7.

Пример. Исследовать функцию на монотонность: у = 6 – 2х.
Решение.
f(х) = 6 – 2х.
х1 < х2 ⟹ –2х1> –2х2;
6 – 2х1 > 6 – 2х2;
f(х1) > f(х2);
Ответ: заданная функция убывает на всей числовой прямой.

8.

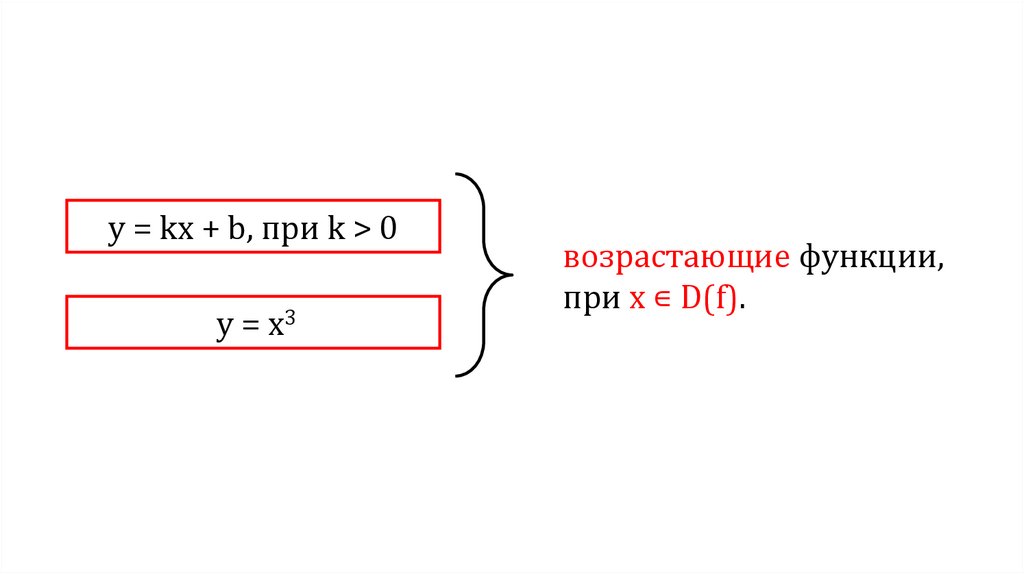
y = kx + b, при k > 0
y = x3
возрастающие функции,
при х ∊ D(f).

9.

Свойство 2. Ограниченность.

10.

Если у = f(х), для любого х ∈ Х, f(х) > m,
где X ∈ D(f), m – некоторое число.
y = f(x)
Функция у = f(х) ограничена снизу.
y=m

11.

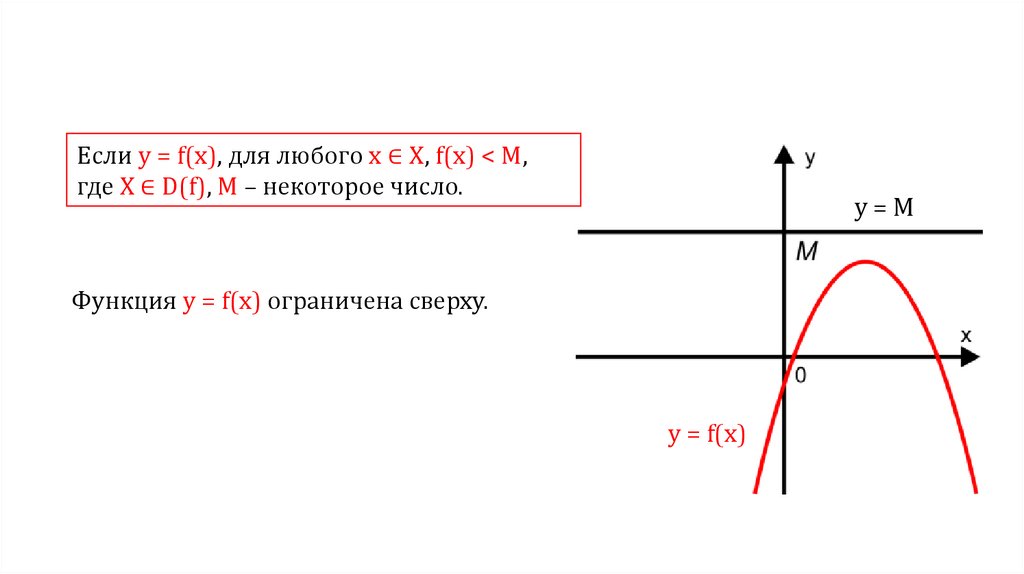
Если у = f(х), для любого х ∈ Х, f(х) < M,
где X ∈ D(f), M – некоторое число.
y=M
Функция у = f(х) ограничена сверху.
y = f(x)

12.

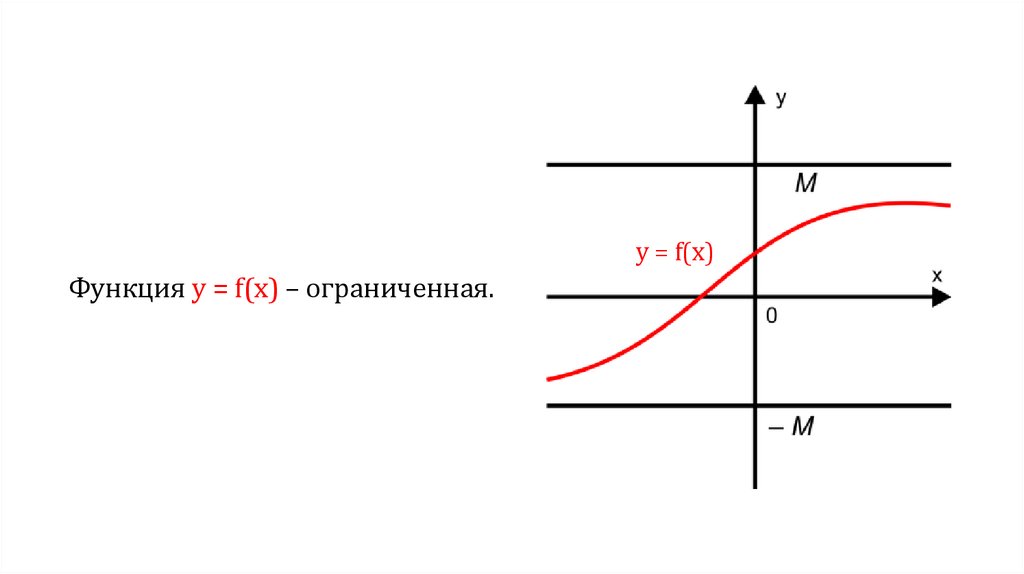
y = f(x)
Функция у = f(х) – ограниченная.

13.

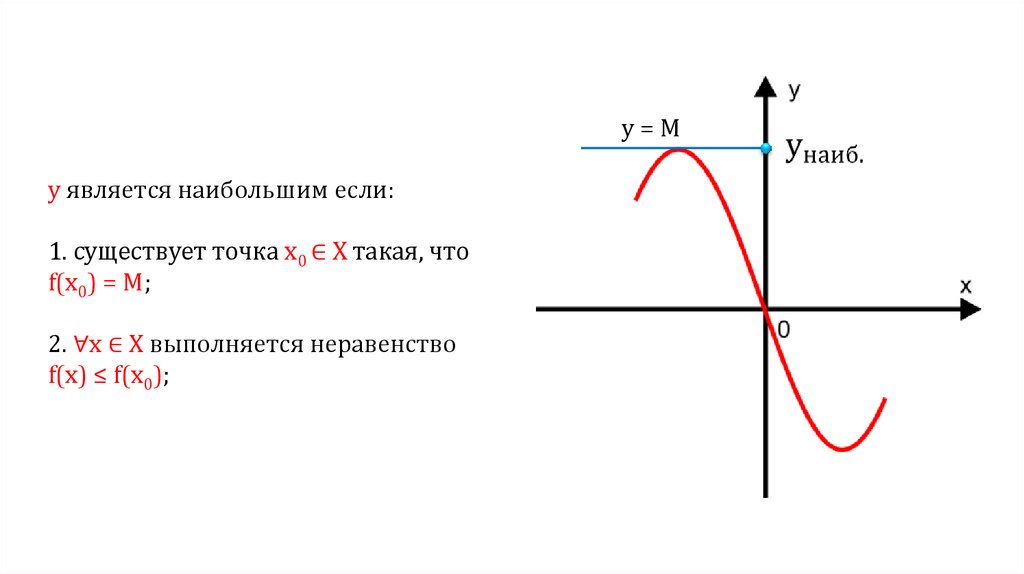
y=M
y является наибольшим если:
1. существует точка х0 ∈ Х такая, что
f(х0) = M;
2. ∀х ∈ Х выполняется неравенство
f(х) ≤ f(х0);

14.

y=M
y=m

15.

Если у функции существует унаим. ,
то она ограничена снизу.
Если унаиб. , то ограничена сверху.

16.

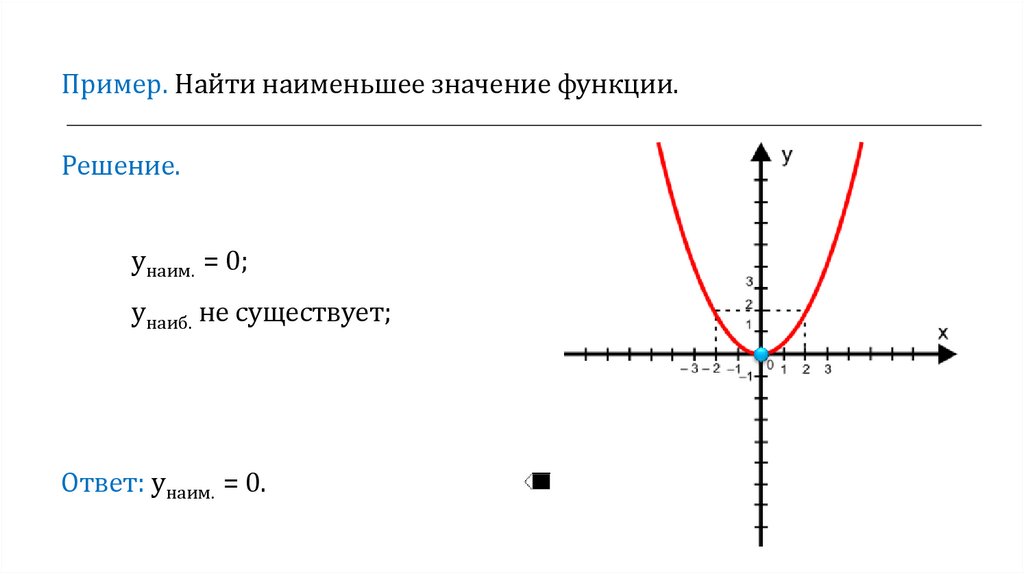
Пример. Найти наименьшее значение функции.
Решение.
унаим. = 0;
унаиб. не существует;
Ответ: унаим. = 0.

17.

Свойство 3. Выпуклость.

18.

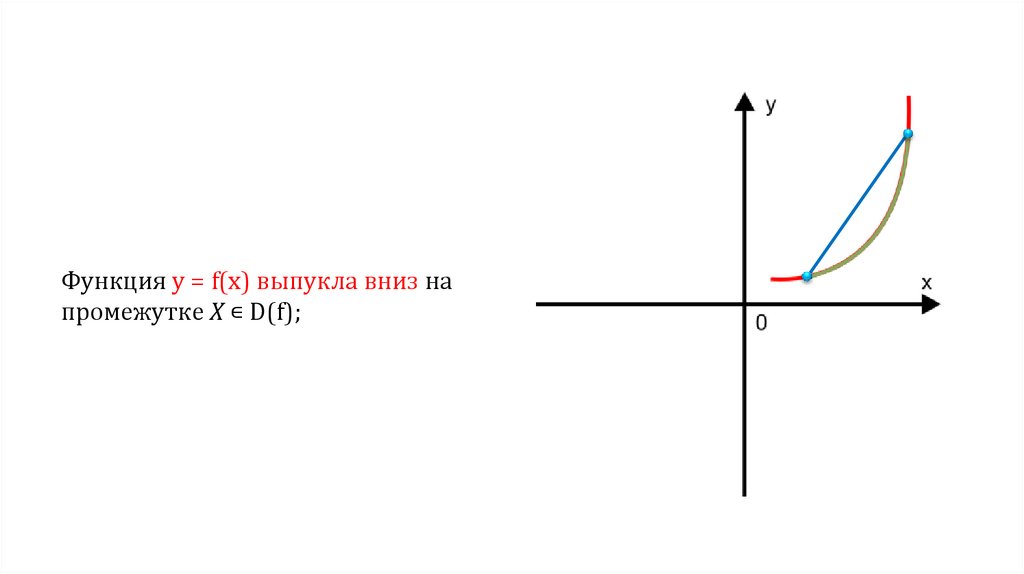
Функция у = f(х) выпукла вниз на
промежутке X ∊ D(f);

19.

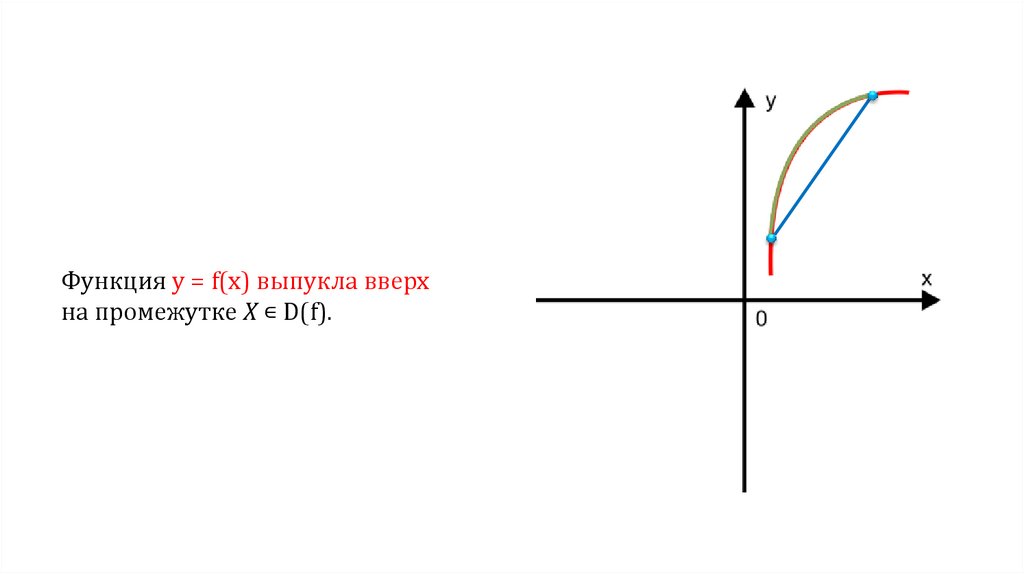
Функция у = f(х) выпукла вверх
на промежутке X ∊ D(f).

20.

Свойство 4. Непрерывность.

21.

Функция называется непрерывной на промежутке,
если она определена на этом промежутке и
непрерывна в каждой точке этого промежутка.

22.

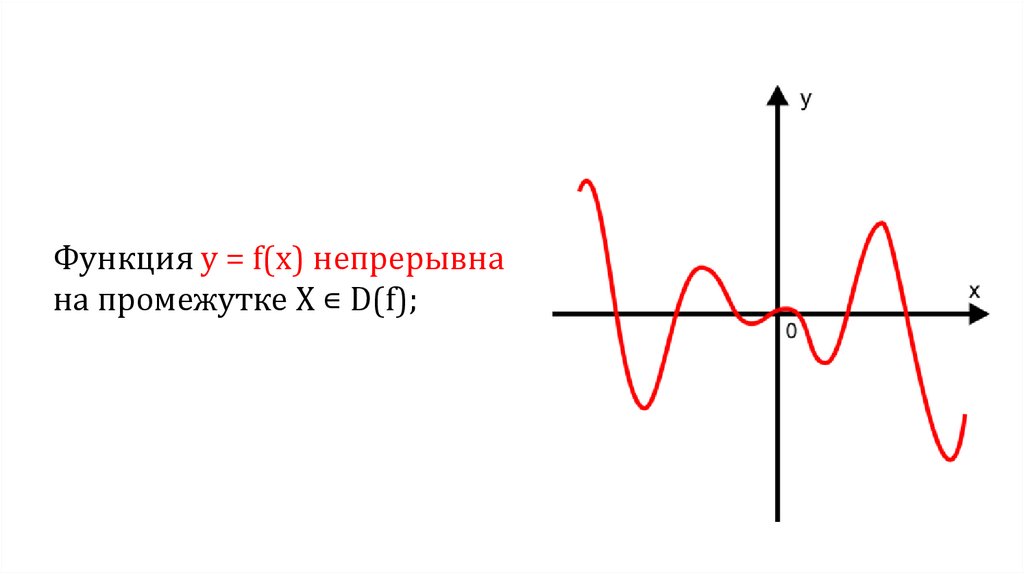
Функция у = f(х) непрерывна
на промежутке X ∊ D(f);

23.

Свойство 5. Четность, нечетность.

24.

Если х ∊ D(f), f(–х)= f(х), то y = f(x) – четная.

25.

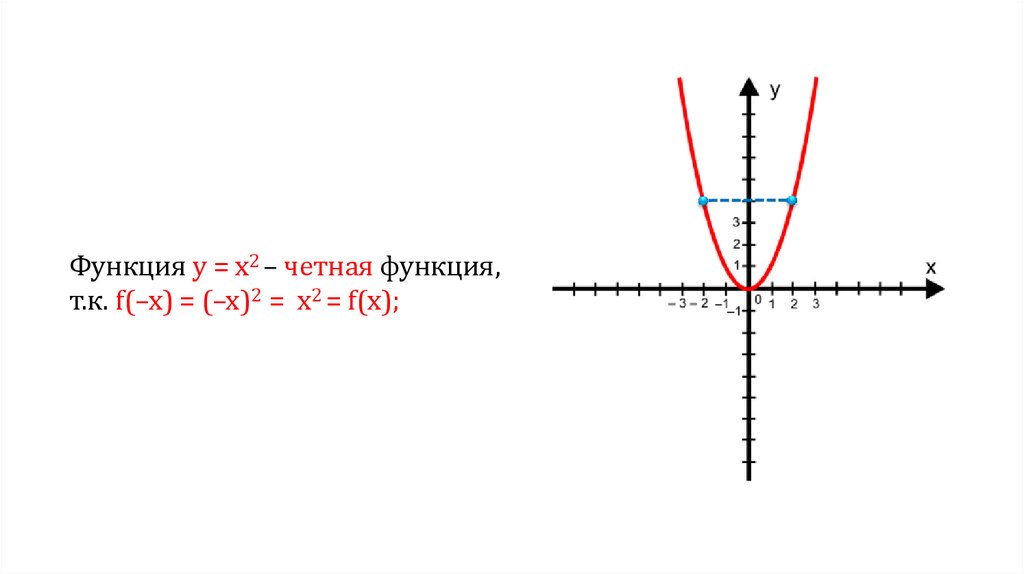
Функция у = х2 – четная функция,
т.к. f(–x) = (–x)2 = x2 = f(x);

26.

Если х ∊ D(f), f(–х)= –f(х), то у = f(x) – нечетная.

27.

Функция у = х3 – нечетная функция,
т.к. f(–x) = (–x)3 = –x3 = – f(x);

28.

Свойство 6. Периодичность.