Способы преобразования чертежа

1.

СПОСОБЫ ПРЕОБРАЗОВАНИЯ
ЧЕРТЕЖА
Горячкина А.Ю.

2.

Преобразование чертежа – приведение геометрических
Фигур в частное положение (параллельное или
проецирующее) относительно плоскостей проекций с
целью обеспечения большей наглядности изображения и
упрощения решения позиционных и метрических задач
a"
B"
A"
A"
C"
A'
C'
B" C"
A'
C'
a"
a'
a'
h0α
B'
f0α
f0α
B'
h0α

3.

Частные положения фигур относительно плоскостей
проекций более удобны для решения геометрических задач:
метрических задач (определение длины, угла, площади) и
позиционных
задач
(определение
положения
геометрических фигур).
Два
пути
решения
задачи
изменения
положения фигуры относительно плоскостей проекций:
1) изменить положение плоскостей
изменяя положения фигуры;
проекций,
не
2) изменить положение фигуры, не меняя положения
плоскостей проекций

4.

Способ замены плоскостей проекций
Условия преобразования:
1). Положение фигуры неизменно;
Рис. 5.3
2). Изменяется положение одной
из двух плоскостей проекций;
3). Новую плоскость проекций располагают
перпендикулярно оставшейся плоскости проекций;
4). Положение новой плоскости проекций может быть
задано или выбрано

5.

Основные задачи,
решаемые заменой одной плоскости проекций
A"
1.
x
zA
B"
π2
π1
zB
Ах
Вх
B'
Преобразовать чертеж прямой
общего положения в чертеж
прямой уровня (рис. 5.5)
3
2
x
x1
1
1
A'
zB
B"'
Новая ось || одной из проекций отрезка
x1 || А'В'
= АВ^π1
zA
Рис. 5.5

6.

2. Преобразовать чертеж прямой уровня в
чертеж проецирующей прямой (рис. 5.6)
A"
x
h"
3
2
x
x1
1
1
B"
z
π2
Новая ось ┴ одноименной
проекции линии уровня
π1
A'
h'
z
B'
Рис. 5.6
π1 π
3
x1
A'"≡ B'"
x1 ^ h'

7.

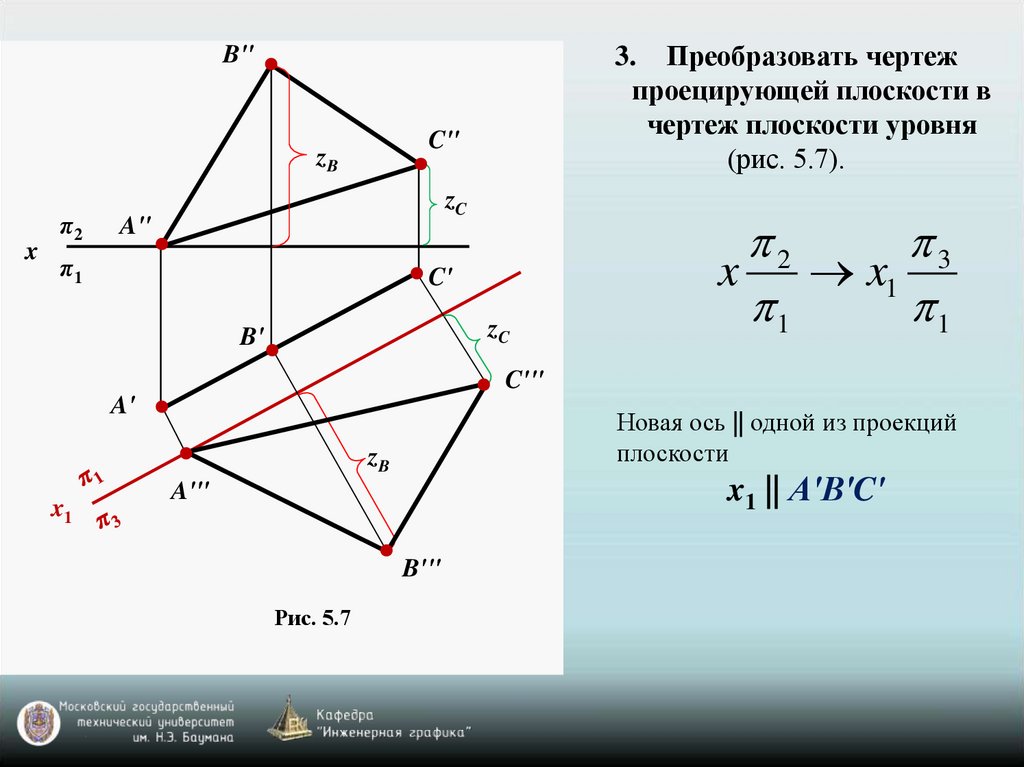
3. Преобразовать чертеж
проецирующей плоскости в
чертеж плоскости уровня
(рис. 5.7).
B"
C"
zB
x
π2
zC
A"
π1
C'
zC
B'
3
2
x
x1
1
1
C'"
A'
Новая ось || одной из проекций
плоскости
zB
x1
x1 || А'В'C'
A'"
B'"
Рис. 5.7

8.

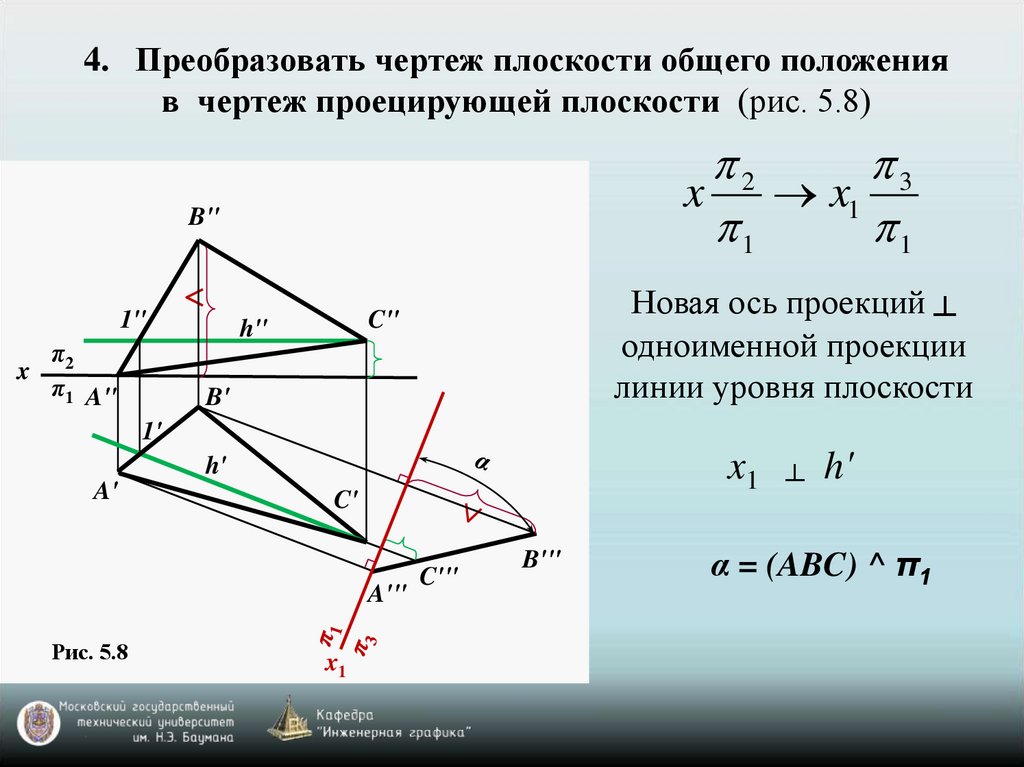
4. Преобразовать чертеж плоскости общего положения
в чертеж проецирующей плоскости (рис. 5.8)
3
2
x
x1
1
1
B"
1"
x
π2
π1 A"
h"
B'
1'
Новая ось проекций ┴
одноименной проекции
линии уровня плоскости
C"
Рис.
x1
h'
A'
C'
A'"
Рис. 5.8
x1
C'"
B'"
┴
h'
α = (ABC) ^ π1

9.

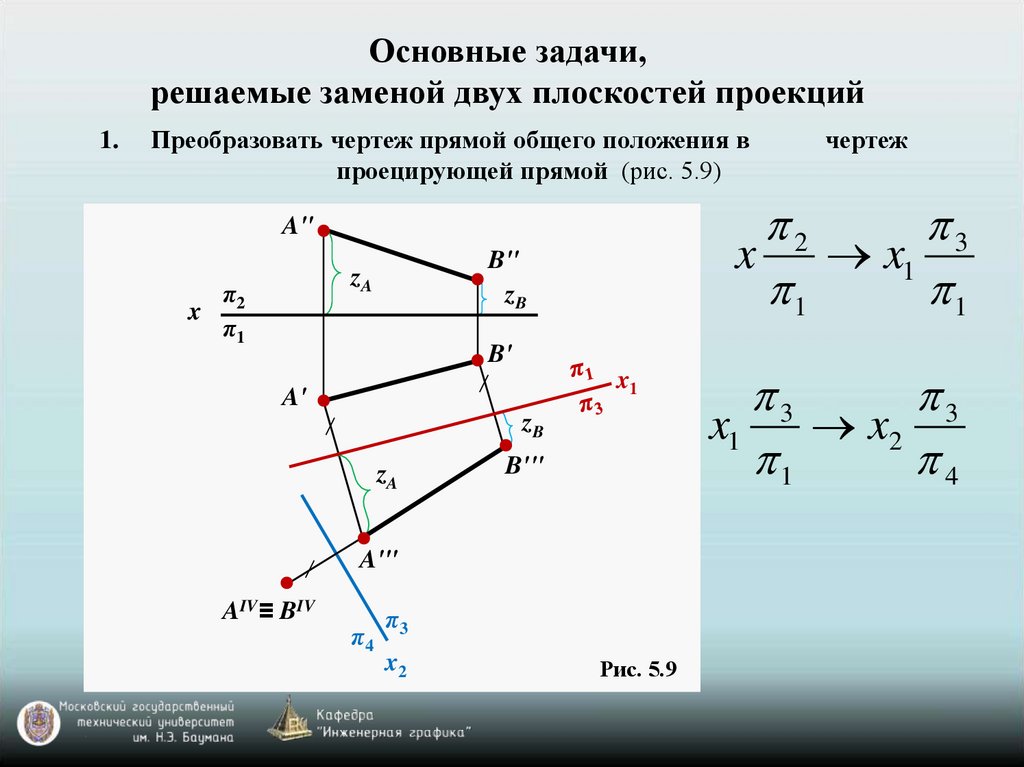
Основные задачи,
решаемые заменой двух плоскостей проекций
1.
Преобразовать чертеж прямой общего положения в
проецирующей прямой (рис. 5.9)
3
2
x
x1
1
1
A"
x
B"
zB
zA
π2
π1
B'
x1
A'
zB
zA
B'"
A'"
AIV≡ BIV
π4
π3
x2
чертеж
Рис. 5.9
3
3
x1
x2
1
4

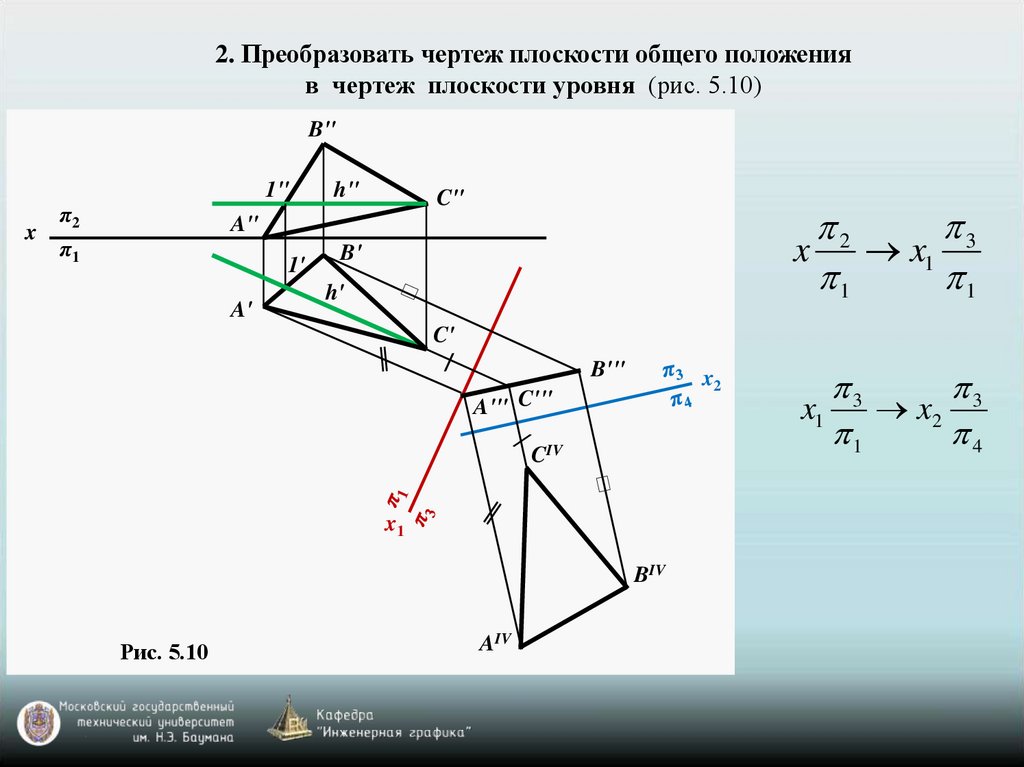
10.

2. Преобразовать чертеж плоскости общего положения
в чертеж плоскости уровня (рис. 5.10)
B"
1"
x
π2
h"
C"
3
2
x
x1
1
1
A"
π1
1'
A'
B'
h'
C'
/
B'"
x2
A'" C'"
x1
CIV
x1
BIV
Рис. 5.10
AIV
3
x2 3
1
4

11.

CПОСОБ ВРАЩЕНИЯ
Суть способа вращения – фигура переводится в частное
положение относительно неизменной системы основных плоскостей
проекций путем вращения вокруг некоторой оси.
Вращение – перемещение точки по окружности в плоскости,
перпендикулярной оси вращения. Пересечение плоскости вращения с
осью вращения – центр вращения. Расстояние от точки до центра
вращения – радиус вращения
Алгоритм построения новой проекции точки A
1.
2.
3.
4.
5.
6.
Задать ось вращения i
Провести плоскость вращения α ┴ i
Найти центр вращения O = α ∩ i
Определить радиус вращения R = |AO|
Задать плоскость совмещения β
«Довернуть» вращаемую точку в положение A1
до совмещения с плоскостью β

12.

СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ
Условия преобразования:
1.
ось
вращения
i
неподвижна
и
перпендикулярна плоскости проекций;
2. все точки фигуры перемещаются по
окружностям,
β
плоскости
которых
перпендикулярны оси i;
3. точки лежащие на оси вращения i
неподвижны
Рис. 5.11

13.

Пример: Повернуть отрезок AB вокруг
проецирующей прямой i
i"
B"
f0α
A1"
A"
O"
α
A2"
m"
x
B'≡ i'≡ O'
h0β
A1'
A2'
A'
Рис. 5.12

14.

СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРЯМОЙ УРОВНЯ
Вращение
геометрической
фигуры
вокруг
линии
уровня
производится с целью ее совмещения с плоскостью уровня.
Применяется этот способ в основном для преобразования плоскости
общего положения в плоскость уровня при решении следующих задач:
1) определение величины плоской фигуры;
2) определение величины плоского угла;
3) построение в заданной плоскости какой-либо фигуры по заданным условиям.
Линия уровня, вокруг которой вращается плоскость общего положения,
должна принадлежать этой плоскости. В этом случае вращение плоскости
сводится к вращению только одной точки, не принадлежащей оси вращения.

15.

СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРЯМОЙ УРОВНЯ
A"
f0β
A1"
R"
O"
f0β
Δz
h"≡ i"
A2"
x
A' A2'
Δz
A0
R'
β
O'
A1'
Рис. 5.13
h0α
Рис. 5.14

16.

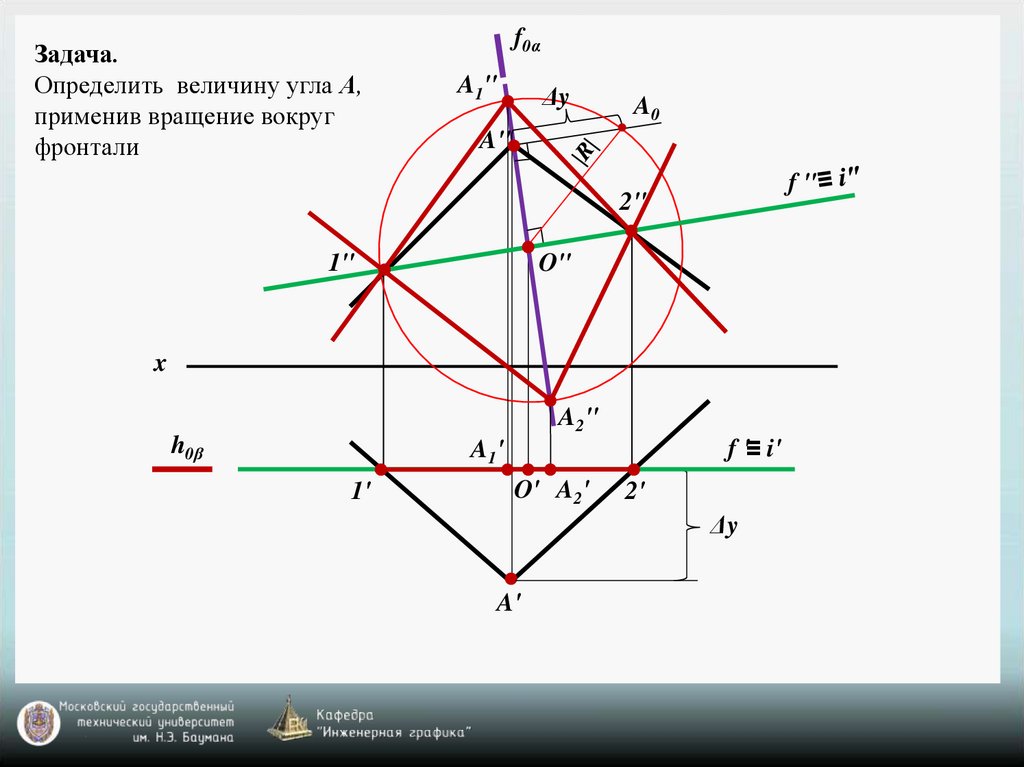
Задача.
Определить величину угла А,
применив вращение вокруг
фронтали
f0α
A1"
Δy
A0
A"
f"
2"
1"
O"
x
A2"
h0β
f '≡ i'
A1'
1'
O' A2'
2'
Δy
A'