Преобразования комплексного чертежа. Способ замены плоскостей проекций. Основные метрические задачи. (Лекция 3)

1.

Омский государственный
университет путей
сообщения
КАФЕДРА: «ИНФОРМАТИКА И
КОМПЬЮТЕРНАЯ ГРАФИКА»
08.10.2021
Лекция 3
1

2.

Лекция 3
Преобразования комплексного
чертежа.
Способ замены плоскостей
проекций.
Основные метрические задачи.
08.10.2021
Лекция 3
2

3.

Содержание
• Способы преобразования комплексного чертежа;
• Четыре основные задачи преобразования чертежа;
• Определение угла наклона плоскости к
плоскостям проекций;
• Линии наибольшего наклона плоскости;
• Решение метрических задач преобразованиями
комплексного чертежа..
08.10.2021
Лекция 3
3

4.

Основные графические задачи
• Все графические задачи условно
делятся на 2 класса.
• 1-й класс – задачи позиционные;
• 2-й класс – задачи метрические.
• Позиционными называются такие
задачи, в которых определяется
взаимное расположение различных
геометрических фигур относительно
друг друга.
08.10.2021
Лекция 3
4

5.

Метрические задачи
• Метрическими (от греческих слов metron –мера,
metreo - мерить)называются задачи, решение
которых связано с нахождением характеристик
геометрических фигур, определяемых
(измеряемых) линейными и угловыми величинами. К
метрическим характеристикам относят длины
участков линий, величины углов, площадей,
объемов и т.п.
• Наиболее сложные задачи, при решении которых
используют как метрические, так и позиционные
свойства геометрических фигур, называют
комплексными.
08.10.2021
Лекция 3
5

6.

08.10.2021
Лекция 3
6

7.

Все метрические задачи сводятся к
двум видам:
• А) задачи на определение расстояния
между двумя точками;
• Б) задачи на нахождение величины угла
между двумя пересекающимися
прямыми.
• Решать такие задачи удобно с помощью
различных способов преобразования
комплексного чертежа.
08.10.2021
Лекция 3
7

8.

Определение расстояния между двумя
точками отрезка прямой и углов наклона
отрезка способом прямоугольного
треугольника
• Натуральная величина отрезка равна
гипотенузе прямоугольного треугольника,
построенного на двух катетах один из
которых проекция отрезка, а второй –
разница координат начала и конца отрезка
в другой плоскости проекций.
08.10.2021
Лекция 3
8

9.

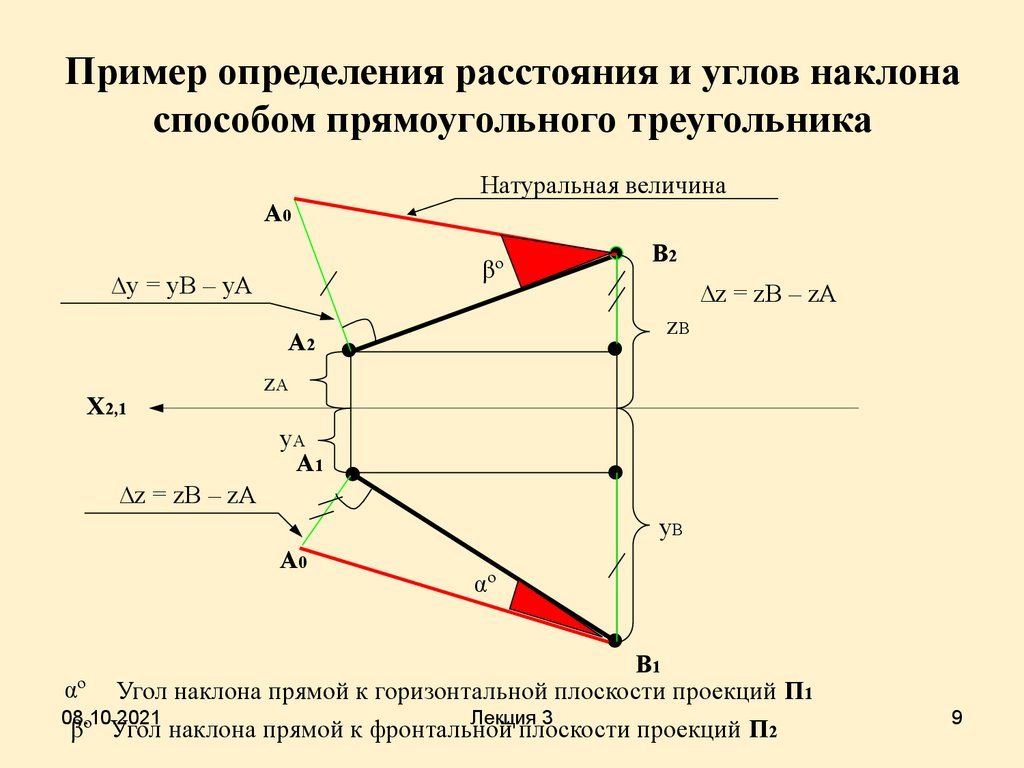
Пример определения расстояния и углов наклона
способом прямоугольного треугольника
A0
Натуральная величина
βº
∆y = yB – yA
∆z = zB – zA
zB
A2
X2,1
B2
zA
yA
A1
∆z = zB – zA
yB
A0
αº
B1
αº Угол наклона прямой к горизонтальной плоскости проекций П1
08.10.2021
Лекция 3
βº Угол наклона прямой к фронтальной
плоскости проекций П2
9

10.

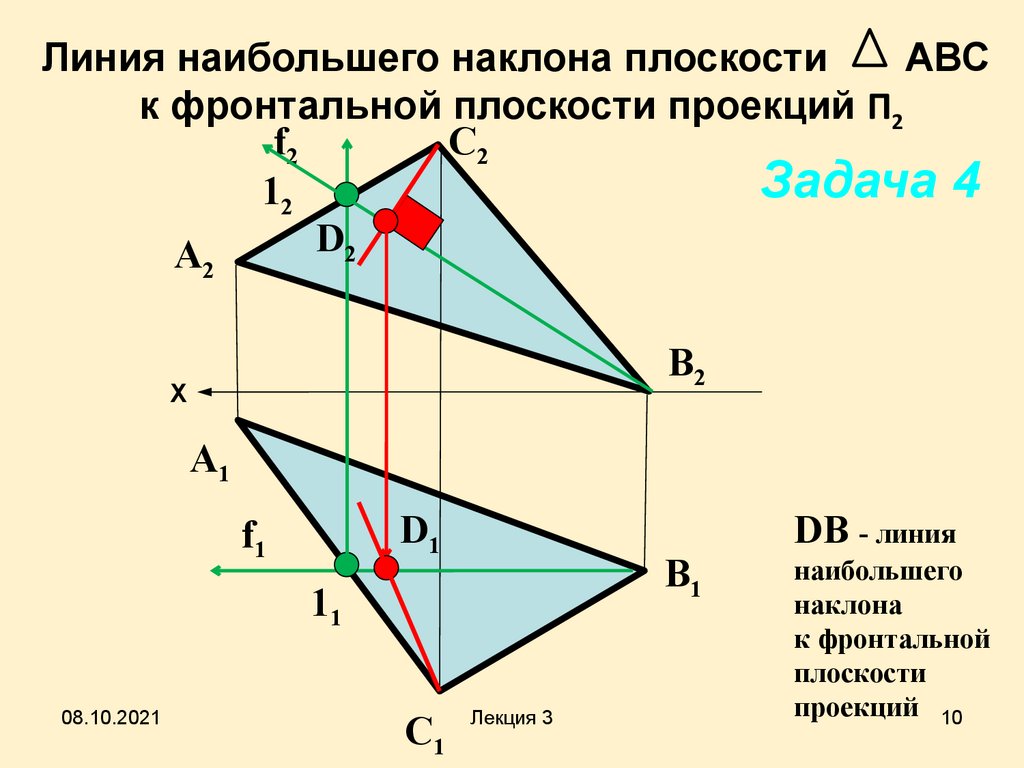
Линия наибольшего наклона плоскости
АВС
к фронтальной плоскости проекций П2
f2
C2
Задача 4
12
D2
A
2
В2
Х
A1
D1
f1
В1
11
08.10.2021
C1
Лекция 3
DВ - линия
наибольшего
наклона
к фронтальной
плоскости
проекций 10

11.

Определить угол наклона плоскости к горизонту
с помощью линий наибольшего наклона
Е2
∆z = zB – zA
B2
A2
С2
F2
B1
Горизонтальная
проекция лнн
перпендикулярна
горизонтальной
проекции горизонтали
h2
D2
Е1
С1
Затем используем
правило треугольника
αº
A1
08.10.2021
F1
Лекция 3 D1
h1
11

12.

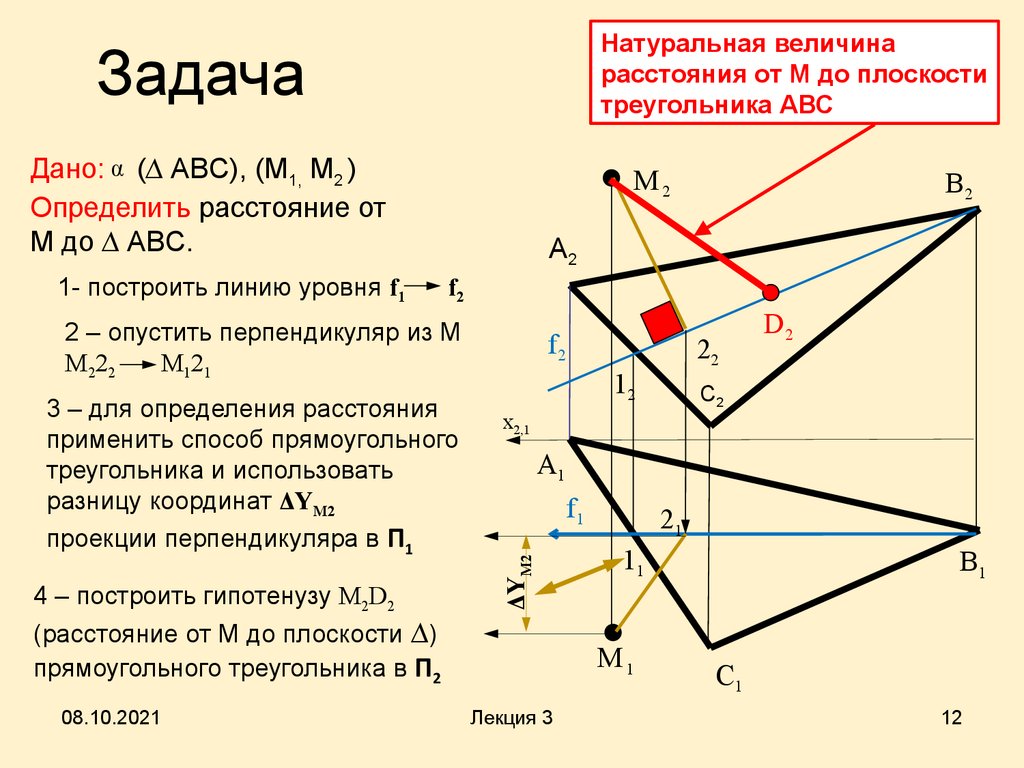
Натуральная величина
расстояния от М до плоскости
треугольника АВС
Задача
Дано: α (∆ ABC), (М1, М2 )
Определить расстояние от
М до ∆ ABC.
1- построить линию уровня f1
М2
A2
f2
2 – опустить перпендикуляр из М
М222
М121
08.10.2021
f2
22
12
D2
C2
x2,1
A1
f1
ΔYM2
3 – для определения расстояния
применить способ прямоугольного
треугольника и использовать
разницу координат ΔYM2
проекции перпендикуляра в Π1
4 – построить гипотенузу М2D2
(расстояние от М до плоскости ∆)
прямоугольного треугольника в Π2
B2
21
11
М1
Лекция 3
B1
C1
12

13.

Пересечение линии с
плоскостью(поверхностью)
• Задача сводится к решению задачи на определение
точки, принадлежащей прямой и поверхности.
• Для решения необходимо:
• 1) через одну из проекций прямой провести
конкурирующую прямую, принадлежащую
поверхности;
• 2) найти ее проекцию во второй плоскости проекций.
• Если эта проекция пересечет проекцию заданной
прямой, значит имеется точка пересечения прямой и
поверхности.
08.10.2021
Лекция 3
13

14.

Способы преобразования
комплексного чертежа
• Исходный чертеж не всегда удобен для
решения позиционных и метрических
задач. В этих случаях чертеж
преобразуют так, чтобы новый
(преобразованный) чертеж позволил
получить нужное решение без сложных
геометрических построений.
08.10.2021
Лекция 3
14

15.

Как вы думаете?
На каком из чертежей уже присутствует натуральная
величина треугольника АВС?
08.10.2021
Лекция 3
15

16.

• Проецируемая фигура
может занимать по
отношению к
плоскостям проекций
• произвольное или
• частное положение.
• В первом случае, как
правило, получаются
проекции неудобные
для решения задач.
• Решение значительно
упрощается, если
фигура оказывается в
частном положении
относительно
плоскости проекций.
08.10.2021
Лекция 3
16

17.

• Наиболее выгодным частным
положением проецируемой фигуры
следует считать:
• 1) положение, перпендикулярное к
плоскости проекций – при решении
позиционных задач;
2) положение, параллельное
плоскости проекций – для решения
метрических задач.
08.10.2021
Лекция 3
17

18.

Метрические задачи
• Метрическими (от греческих слов metron –мера,
metreo - мерить)называются задачи, решение
которых связано с нахождением характеристик
геометрических фигур, определяемых
(измеряемых) линейными и угловыми величинами. К
метрическим характеристикам относят длины
участков линий, величины углов, площадей,
объемов и т.п.
• Наиболее сложные задачи, при решении которых
используют как метрические, так и позиционные
свойства геометрических фигур, называют
комплексными.
08.10.2021
Лекция 3
18

19.

Все метрические задачи сводятся к
двум видам:
• А) задачи на определение расстояния
между двумя точками;
• Б) задачи на нахождение величины угла
между двумя пересекающимися
прямыми.
• Решать такие задачи удобно с помощью
различных способов преобразования
комплексного чертежа.
08.10.2021
Лекция 3
19

20.

Задачи на преобразование комплексного чертежа
1. Преобразование прямой общего
положения в прямую уровня.
2. Преобразование прямой общего положения в
прямую
проецирующую.
3. Преобразование плоскости общего
положения в плоскость
проецирующую.
4. Преобразование плоскости общего
положения в плоскость уровня.
08.10.2021
Лекция 3
20

21.

Основные принципы и последовательность
решения метрических задач
Алгоритмы решения всех метрических
задач опираются на два инварианта
ортогонального проецирования:
1. Теорему (прямую и обратную) о
проецировании прямого угла;
2. Свойство любой плоской фигуры
проецироваться без искажения, в
конгруэнтную фигуру, на ту плоскость
проекций, которая параллельна этой
фигуре.
08.10.2021
Лекция 3
21

22.

• Для решения задач предлагается
следующая последовательность:
• Первый этап. Сосредоточиться и
осмыслить постановку задачи. Что дано?
Что требуется? Какие ставятся условия и
возможно ли их выполнить?
• Второй этап. Поиск связи между
исходными данными и искомыми.
• Третий этап. Реализация (графическая)
плана; здесь необходим контроль
правильности решения и точности
графических операций.
• Завершающий этап. Анализ решения
задачи – при каких условиях и сколько
решений возможно.
08.10.2021
Лекция 3
22

23.

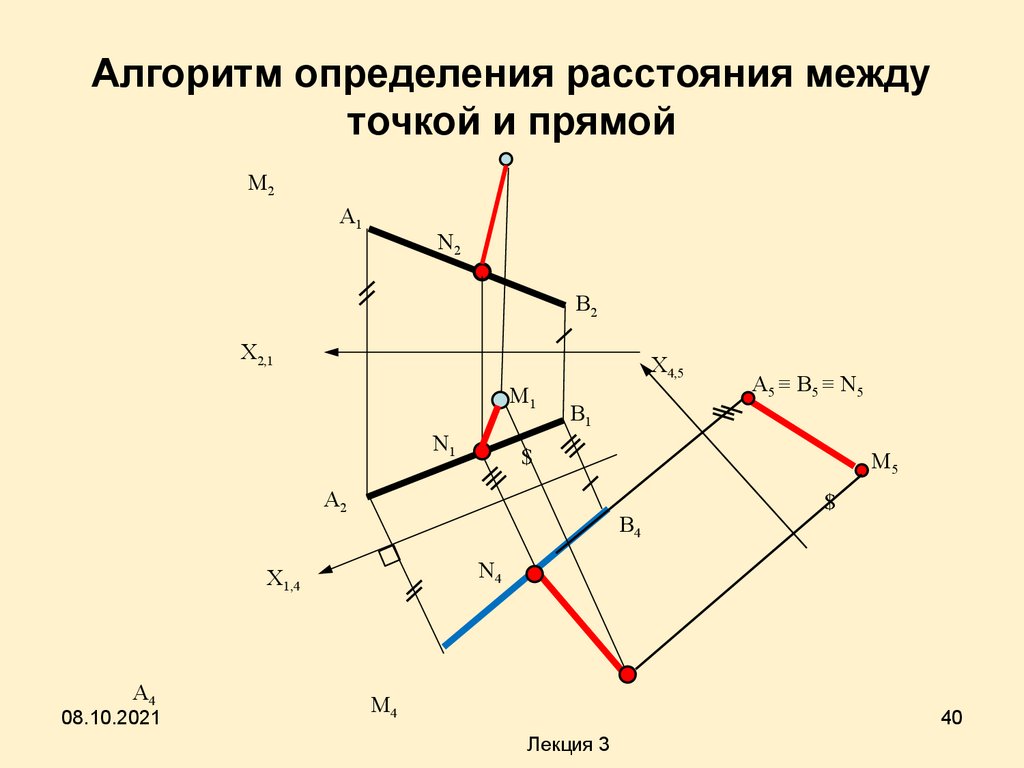
Определение расстояний
• Решение задач на определение
расстояний между точкой и прямой,
двумя параллельными прямыми,
точкой и плоскостью, прямой и
плоскостью, двумя плоскостями,
скрещивающимися прямыми в
конечном счете сводится к
нахождению расстояния между
точками.
08.10.2021
Лекция 3
23

24.

• Решение задачи с
помощью
преобразования
комплексного
чертежа сводится к
переводу отрезка в
положение,
параллельное
какой-либо
плоскости
проекций.
08.10.2021
Лекция 3
24

25.

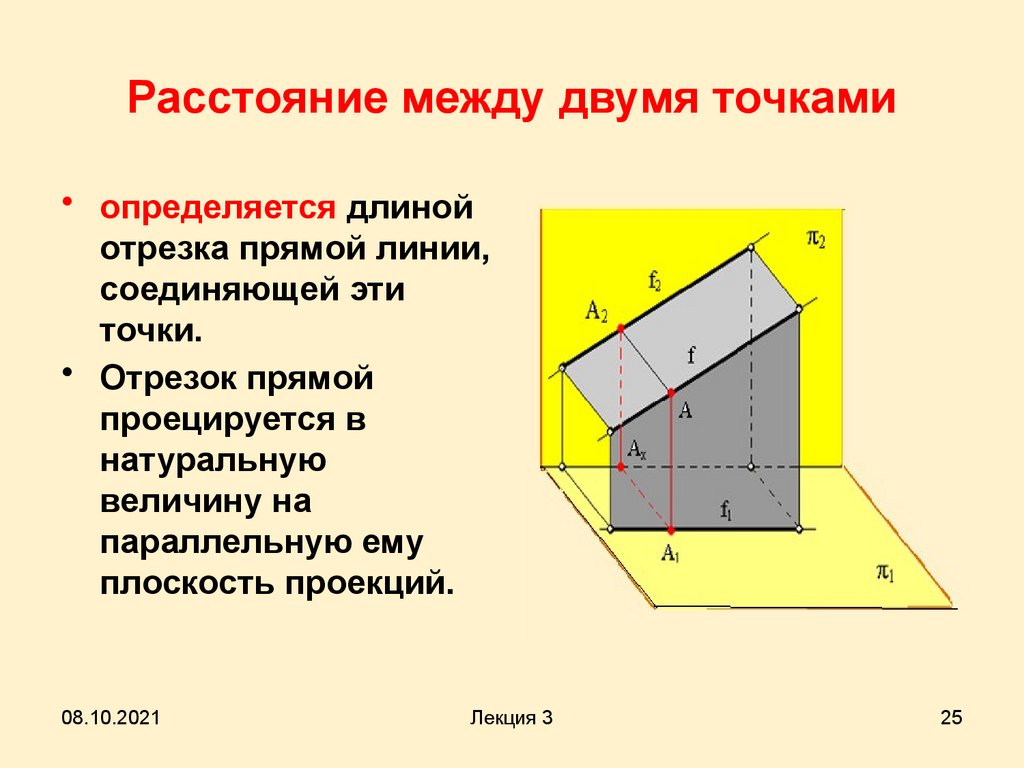
Расстояние между двумя точками
• определяется длиной
отрезка прямой линии,
соединяющей эти
точки.
• Отрезок прямой
проецируется в
натуральную
величину на
параллельную ему
плоскость проекций.
08.10.2021
Лекция 3
25

26.

Пути преобразования
комплексного чертежа
1. Изменение положения объекта
относительно плоскостей
проекций.
2. Изменение положения плоскостей
проекций относительно объекта.
08.10.2021
Лекция 3
26

27.

B2
В2
П4
П2
А2
B
Bx
Х 2,1
Ax
В1
А1
A2
Bx
Ax
В4
X1,4
X2,1
А4
B1
B4
А
A4
П4
A1
X1,4
П1
08.10.2021
Лекция 3
27

28.

Задачи на преобразование
комплексного чертежа
1. Преобразование прямой общего
положения в прямую уровня.
2. Преобразование прямой общего
положения в прямую
проецирующую.
3. Преобразование плоскости общего
положения в плоскость
проецирующую.
4. Преобразование плоскости общего
положения в плоскость уровня.
08.10.2021
Лекция 3
28

29.

Определение расстояния между двумя
точками (Задача 1)
• Для решения задачи необходимо заменить плоскость
проекций П1, или П2 новой плоскостью проекций П4,
параллельной прямой АВ и перпендикулярной к
незаменяемой плоскости проекций. Для того чтобы
прямая АВ в новой системе плоскостей проекций стала,
например, фронталью, нужно заменить фронтальную
плоскость проекций П2 новой плоскостью П4 П1 и
параллельной прямой АВ.
Отрезок [АВ] прямой проецируется на плоскость П4 в
истинную величину, т.е. | А4В4 | = | АB |, - величина угла
наклона прямой АВ к плоскости П1.
08.10.2021
Лекция 3
29

30.

Алгоритм решения первой задачи
• Для решения первой основной задачи на
преобразование комплексного чертежа:
1) провести новую ось проекций х1,4
параллельно А1В1 на произвольном
расстоянии от нее;
• такое положение оси х1,4 обусловливается
тем, что П4 параллельна АВ. В частном
случае, если плоскость П4 проведена
непосредственно через прямую АВ, ось
х1,4 = А1В1;
08.10.2021
Лекция 3
30

31.

Пример решения второй задачи
В2
А2
Х 2,1
Bx
Ax
В1
А1
X1,4
ς
ς
ς
В4
А4
αº
В5 ≡ А5
X4,5
αº- угол наклона прямой к горизонтальной плоскости проекций
08.10.2021
Лекция 3
31

32.

Алгоритм решения второй задачи
• Построения на комплексном чертеже: 1) проводим новую
ось проекций х14 А1В1;
• 2) построим проекции точек А и В на плоскости П4, взяв
координаты точек из плоскости П2.
• 3) Заменим плоскость П1 на новую П5, которая будет П4 и
А4В4. Для этого проводим новую ось проекций х4,5. Так как
расстояния точек А и В до плоскости П4 одинаковы, то
проекции их на плоскости П5 совпадут, А5 ≡ В5.
• Прямая АВ (А5В5) в новой системе плоскостей проекций
заняла проецирующее положение и является
горизонтально проецирующей. Для того чтобы прямую
общего положения преобразовать в проецирующую,
необходимо выполнить две последовательные замены
плоскостей проекций. Вначале прямую следует
преобразовать в линию уровня, а затем линию уровня
преобразовать в проецирующую.
08.10.2021
Лекция 3
32

33.

Алгоритм решения третьей задачи
• Для решения задачи необходимо заменить
плоскость П1 или П2 исходной системы П2/П1
новой плоскостью П4, перпендикулярной
плоскости (АВС). Две плоскости взаимно
перпендикулярны, если одна из них проходит
через прямую, перпендикулярную к другой
плоскости. Следовательно, если какую-либо
прямую, принадлежащую плоскости ,
преобразовать в проецирующую, то плоскость в
новой системе плоскостей проекций станет
проецирующей. Проще всего для этой цели
воспользоваться линией уровня.
08.10.2021
Лекция 3
33

34.

• На чертеже плоскость (АВС)
преобразована во фронтально
проецирующую путем преобразования
горизонтали h(h1,h2), принадлежащей
плоскости , во фронтальнопроецирующую прямую. В новой системе
плоскостей проекций П1/П4 плоскость
является фронтально проецирующей ( 4),
и поэтому ее проекция на П4 вырождается
в прямую линию 4 (С4, А4, В4).
αº - величина угла наклона плоскости к
плоскости П1.
08.10.2021
Лекция 3
34

35.

Алгоритм решения третьей задачи
С2
12
А2
h2
В2
Х 2,1
В1
В4
αº
А1
11
h1
А4
С1
С4
08.10.2021
X1,4 3
Лекция
35

36.

08.10.2021
Лекция 3
36

37.

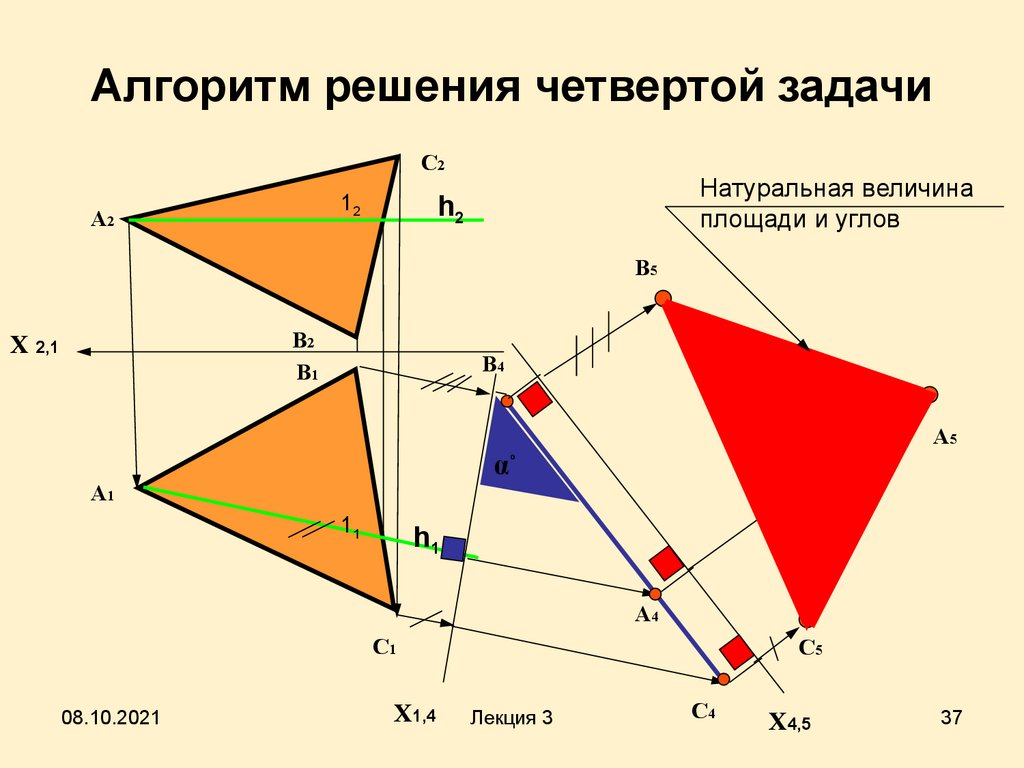
Алгоритм решения четвертой задачи
С2
12
А2
Натуральная величина
площади и углов
h2
В5
В2
В1
Х 2,1
В4
α
А5
º
А1
11
h1
А4
С1
08.10.2021
X1,4
С5
Лекция 3
С4
X4,5
37

38.

08.10.2021
Лекция 3
38

39.

Пример определения расстояния
между плоскостью и точкой
М2
А2
С2
D2
12
h2
В2
Х 2,1
М1
В1
В4
D1
М4
А1
11
h1
D4
А4
С1
С4
08.10.2021
X1,4 3
Лекция
39

40.

Алгоритм определения расстояния между
точкой и прямой
М2
А1
N2
В2
X2,1
X4,5
М1
N1
В1
$
А2
08.10.2021
М5
В4
$
N4
X1,4
А4
А5 ≡ B5 ≡ N5
М4
40
Лекция 3

41.

Пример определения расстояния между
параллельными прямыми
b2
а2
а5
b5
ς
Х 2,1
X4,5
ς
а1
b1
ς
b4
X1,4
08.10.2021
а4
Лекция 3
41

42.

Алгоритм решения четвертой задачи
• Плоскость общего положения
преобразовать в плоскость уровня
заменой только одной плоскости
проекций нельзя, так как плоскость
П4, параллельная ей, не будет
перпендикулярна ни одной из старых
плоскостей проекций и,
следовательно, не образует ни с
одной из них прямоугольной
системы плоскостей проекций.
08.10.2021
Лекция 3
42

43.

• Для того чтобы плоскость общего
положения преобразовать в плоскость
уровня, необходимо выполнить две
последовательные замены плоскостей
проекций.
• Вначале плоскость необходимо
преобразовать в проецирующую, т. е.
решить задачу 3,
• а затем проецирующую плоскость
преобразовать в плоскость уровня.
• На рис. показано преобразование
плоскости ∆(АВС) в горизонтальную
плоскость уровня.
08.10.2021
Лекция 3
2
43

44.

• До свидания.
• Спасибо за внимание.
08.10.2021
Лекция 3
44

45.

Лекцию составил Ведякин Фёдор Филиппович
08.10.2021
Лекция 3
45

46.

Контрольная работа №2
Тема: «Задачи метрические»
08.10.2021
Лекция 3
46

47.

6
8
7
С2
А(х,у,z)
B(x,y,z)
C(x,y,z)
7
D2
β⁰
E2
В2
А2
В5
А1
А4
А1
D1
11
E1
В1
21
D4
Натуральная
величина
11
f1
ЛНН1
В4
С5
В2
22
Δy
h1
Δy
х 2,1
В1
α⁰
f2
А2
х 2,1
А5
ЛНН2
12
12
v
h2
С2
С1
v
С1
E4
С4
х 1,4
х4,5
08.10.2021
Лекция 3
47

48.

08.10.2021
Лекция 3
48