Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов

1.

Носков Владимир Петрович, Киселев Иван Олегович
Использование кватернионов в решении
задачи навигации в трехмерном
пространстве при помощи выделенных
линейных объектов
г. Москва, 2019 г.

2.

Определение и обозначение
Кватернион система гиперкомплексных чисел, образующая векторное
пространство размерностью четыре над полем вещественных чисел. Обычно
обозначаются символом . Предложены Уильямом Гамильтоном в 1843 году.
Стандартное
q = a + bi + cj + dk
a, b, c, d – вещественные числа;
i, j, k – мнимые единицы, такие что i2 = j2 = k2 = ijk = -1, при этом результат попарного
произведения зависит от порядка следования (не является коммутативным):
ij = k, ji = -k
Векторное
Кватернион представляет собой пару (a, u), где u - вектор трехмерного пространства,
а a – скаляр.
2

3.

Операции над кватернионами
Сложение
Вычитание
(a,u) (b, v) (a b,u v)
(a,u) (b, v) (a b,u v)
Перемножение
Сопряжение
(a,u)(b, v) (ab u v,u v av bu)
u v скалярное произведение
u v векторное произведение
НЕ КОММУТАТИВНО!!!
Норма
(a,u)* (a, u)
Обратный кватернион
(a,u) 1
(a,u)*
(a,u)
2
norm( (a,u) ) (a,u) a2 b2 c2 d 2
3

4.

Получение кватерниона
Необходимо совершить вращение на угол вокруг оси, заданной направляющим
единичным вектором v (vx , v y , vz ) .
Это вращение можно задать кватернионом
q [cos( ), v sin( )]
2
2
Вычисление матрицы поворота вокруг произвольной оси в пространстве:
cos vx2 (1 cos )
M (v, ) vx v y (1 cos ) vz sin
v v (1 cos ) v sin
y
x z
vx v y (1 cos ) vz sin
cos v y2 (1 cos )
v y vz (1 cos ) vx sin
vx vz (1 cos ) v y sin
v y vz (1 cos ) vx sin
cos vz2 (1 cos )
4

5.

Применение кватернионов для вращения в
трехмерном пространстве
Кватернионы расширяют концепцию вращения в трехмерном
пространстве до вращения в четырехмерном. Вращение можно
задать единичным кватернионом (norm(q) = 1). Чтобы кватернион
привести к единичному виду, или другими словами нормализовать,
необходимо вычислить его размер norm(q) и все четыре члена
кватерниона разделить на величину полученного размера.
Если вращение задано некоторым кватернионом q
q (a,u),
то вектор v после вращения будет иметь вид v':
v ' qv q 1
В случае, когда последовательно происходит вращение через
несколько кватернионов, итоговый кватернион вращения можно
записать как произведение нескольких:
Q q2 q1
Сначала происходит вращение с помощью кватерниона q1, затем с
помощью кватерниона q2.
5

6.

Преобразование кватернионов в углы Эйлера
Если вам известен кватернион Q=[Q1, Q2, Q3, Q4], с помощью
которого производилось вращение объекта в пространстве, то
вычисление углов Эйлера осуществляется по следующему
алгоритму:
atan 2( 2(Q0Q1 Q2Q3 ),1 2(Q12 Q22 )
asin( 2(Q0Q2 Q3Q1 ))
Тангаж:
2
2
Рысканье: atan 2( 2(Q0Q3 Q1Q2 ),1 2(Q2 Q3 )
Крен:
6

7.

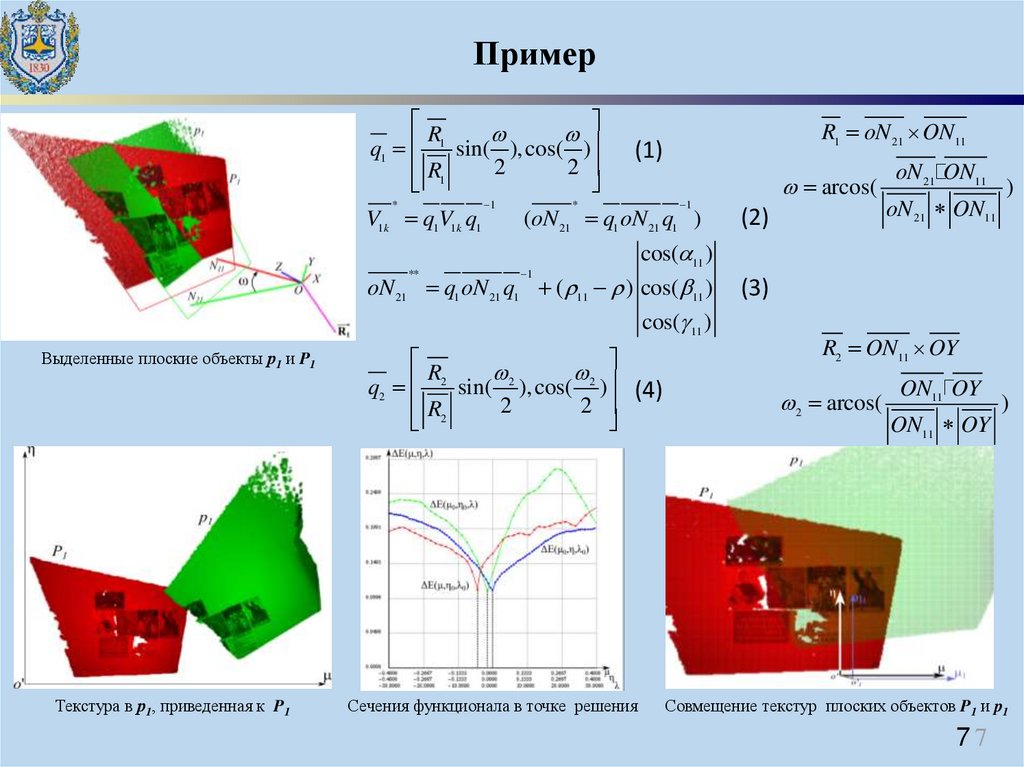
Пример
R
q1 1 sin( ), cos( )
R1
2
2
*
V1k q1V1k q1
**
1
R1 oN 21 ON11
(1)
1
*
(oN 21 q1 oN 21 q1 )
1
cos( 11 )
Текстура в р1, приведенная к P1
R
2
2
2
q2
sin( ), cos( ) (4)
R2
2
2
Сечения функционала в точке решения
(2)
oN 21 ON11
oN 21 ON11
)
cos( 11 )
oN 21 q1 oN 21 q1 ( 11 ) cos( 11 )
Выделенные плоские объекты р1 и P1
arcos(
(3)
R2 ON11 OY
2 arcos(
ON11 OY
ON11 OY
)
Совмещение текстур плоских объектов P1 и p1
77

8.

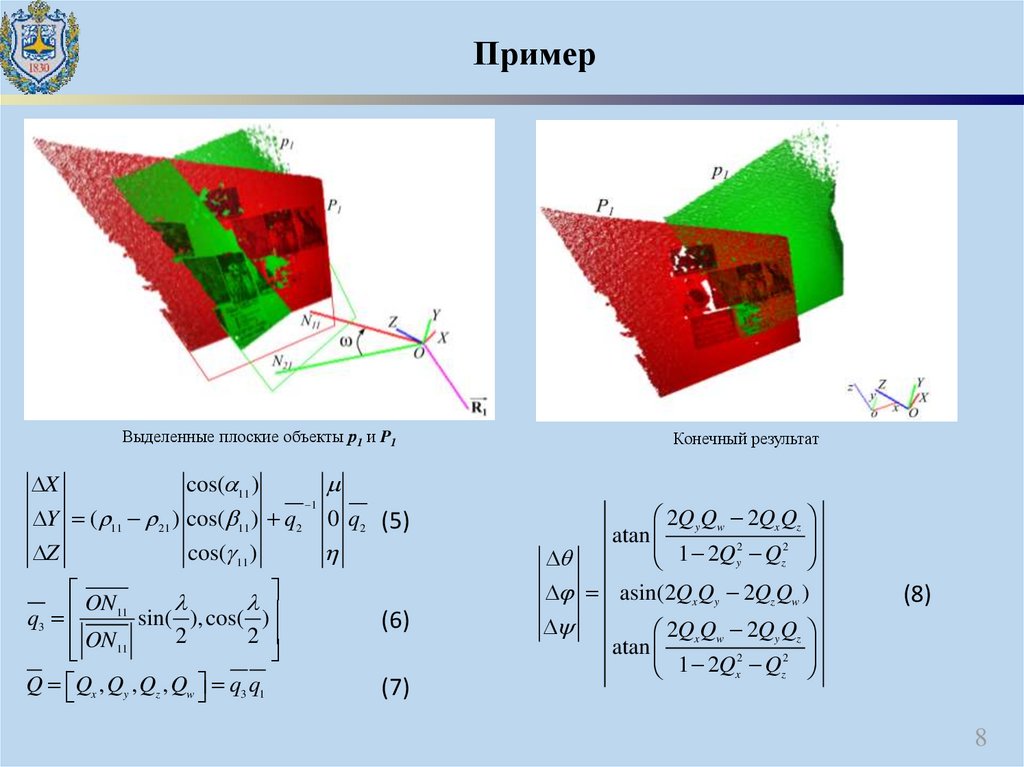
Пример
Выделенные плоские объекты р1 и P1
X
cos( 11 )
Y ( 11 21 ) cos( 11 ) q2
Z
cos( 11 )
ON11
q3
sin( ), cos( )
ON11
2
2
Q Qx , Qy , Qz , Qw q3 q1
Конечный результат
1
0 q2 (5)
(6)
(7)
2Qy Qw 2Qx Qz
atan
2
2
1
2
Q
Q
y
z
asin(2Qx Qy 2Qz Qw )
(8)
2Qx Qw 2Qy Qz
atan
2
2
1
2
Q
Q
x
z
8

9.

Спасибо за внимание !
http://wat.gamedev.ru/articles/quaternions
https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
https://en.wikipedia.org/wiki/Euler_angles
https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D
0%B0_%D0%BF%D0%BE%D0%B2%D0%BE%D1%80%D0%BE%D1%82%D0%B0
9