Корреляция

1.

Корреляция
1

2.

Постановка проблемы
Четыре вопроса:
Вопрос 1. Существует
переменными?
Вопрос 2. Какой тип имеет эта связь?
Вопрос 3. Насколько она сильна?
Вопрос 4. Какой можно сделать прогноз, основываясь на этой связи?
Корреляционный анализ – статистический метод, позволяющий
определить, существует ли зависимость между переменными и на
сколько она сильна.
ли
связь
между
двумя
или
более
2

3.

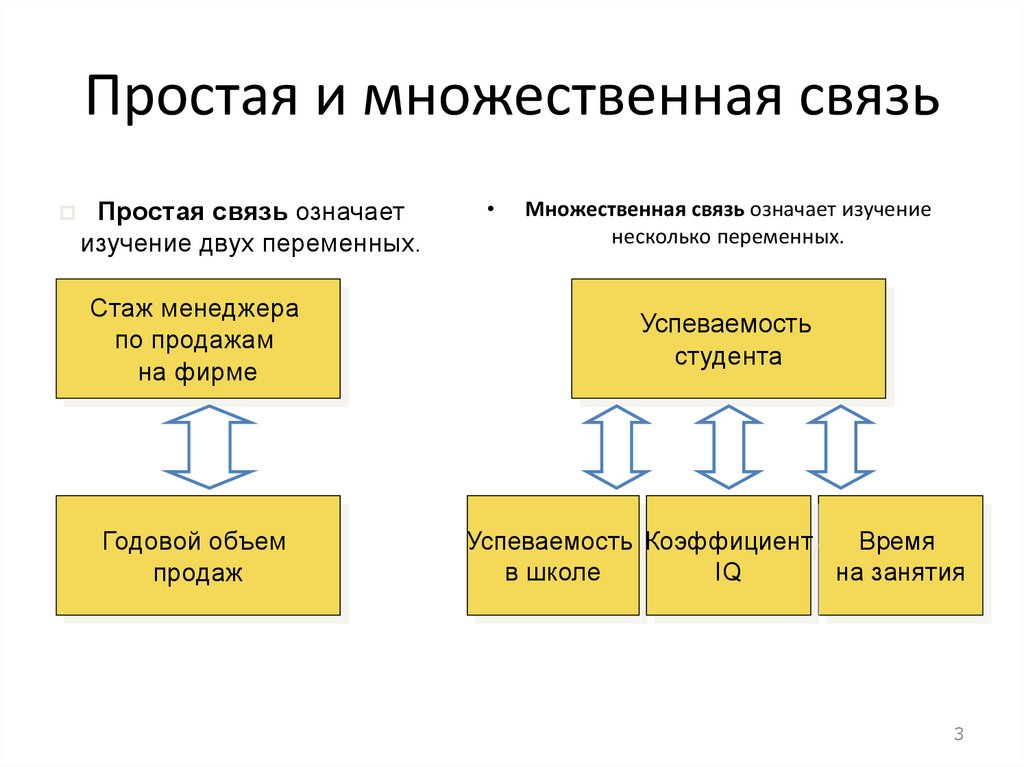
Простая и множественная связь
Простая связь означает
изучение двух переменных.
Стаж менеджера
по продажам
на фирме
Годовой объем
продаж
Множественная связь означает изучение
несколько переменных.
Успеваемость
студента
Успеваемость Коэффициент
Время
в школе
IQ
на занятия
3

4.

Визуальный анализ связи
Рассматриваем две переменные: «продолжительность занятий» студентов перед
экзаменом и «итоговая оценка» (из 100 балов). Пытаемся визуально определить
связь. Правда ли, что чем меньше времени занятий, тем выше оценка?
Студент
Часы
x
Оценка
y
100
80
A
6
82
B
2
63
C
1
57
D
5
88
E
2
68
F
3
75
60
40
20
0
0
1
2
3
4
5
6
7
4

5.

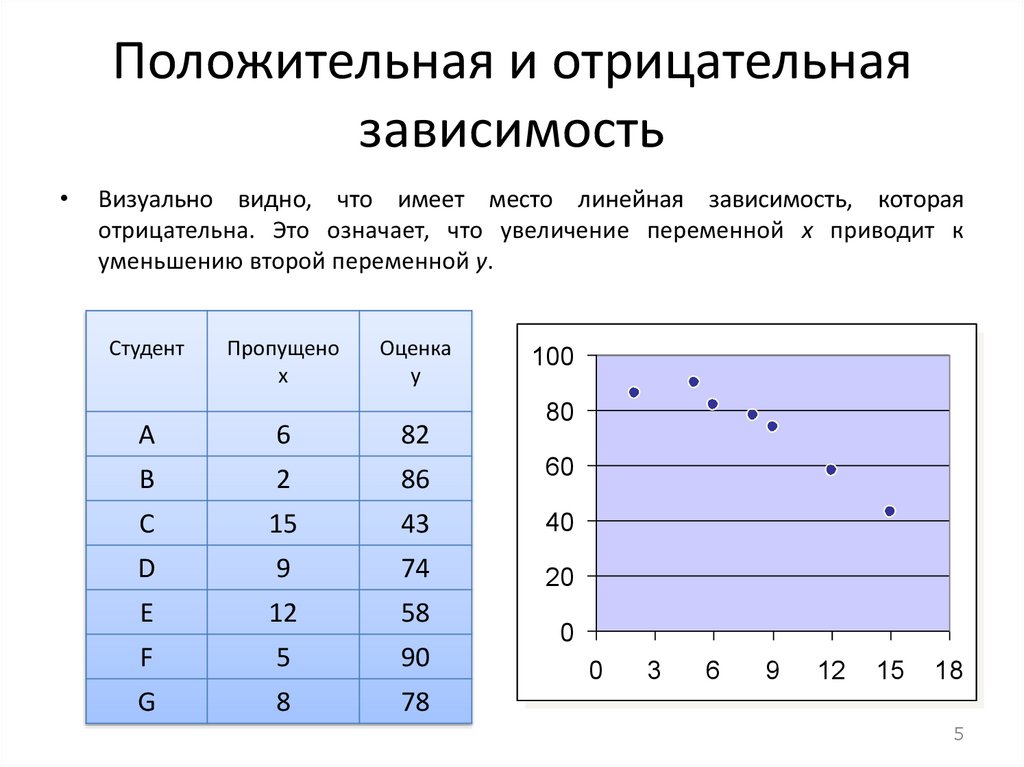
Положительная и отрицательная
зависимость
Визуально видно, что имеет место линейная зависимость, которая
отрицательна. Это означает, что увеличение переменной x приводит к
уменьшению второй переменной y.
Студент
Пропущено
х
Оценка
у
100
80
A
6
82
B
2
86
C
15
43
40
D
9
74
20
E
12
58
F
5
90
G
8
78
60
0
0
3
6
9
12
15
18
5

6.

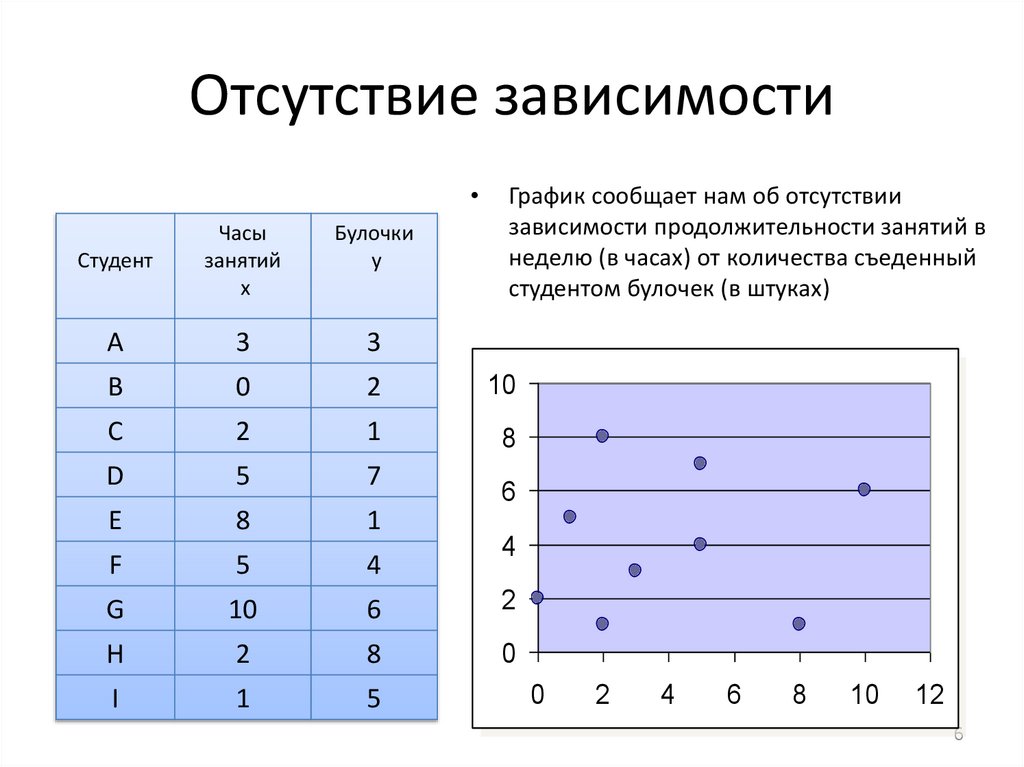
Отсутствие зависимости
График сообщает нам об отсутствии
зависимости продолжительности занятий в
неделю (в часах) от количества съеденный
студентом булочек (в штуках)
Студент
Часы
занятий
х
Булочки
у
A
3
3
B
0
2
10
C
2
1
8
D
5
7
6
E
8
1
F
5
4
G
10
6
2
H
2
8
0
I
1
5
4
0
2
4
6
8
10
12
6

7.

Параметрический критерий
Формула для вычисления r (Пирсона)
Коэффициент корреляции вычисляется по формуле:
r
( x x)( y y )
2
2
( x x) ( y y )
Это, так называемый, коэффициент корреляции Пирсона, равный произведению
моментов. Он назван по имени статистика Карла Пирсона, который первый провел
исследования в этой области.

8.

Коэффициент корреляции
Коэффициент корреляции измеряет силу и направление связи между двумя
переменными.
Если между переменными существует:
сильная положительная связь, то значение r будет близко к +1.
сильная отрицательная связь, то значение r будет близко к –1.
нет линейной связи или она очень слабая, значение r будет близко к 0.
8

9.

Градация силы связи, представленная
шкалой Чертока
Коэффициент корреляции
Характеристика силы связи
|r|<0,1
связь практически отсутствует
0,1<|r|<0,3
слабая связь
0,3<|r|<0,5
умеренная связь
0,5<|r|<0,7
связь средней силы
0,7<|r|<0,9
сильная связь
0,9<|r|<1
очень сильная связь
9

10.

Пять видов связи между
переменными
1. Прямая причинно-следственная связь между переменными (х
определяет у).
2. Обратная причинно-следственная связь между переменными (у
определяет х).
3. Связь между переменными x и y вызвана третьей переменной z.
4. Взаимосвязь между несколькими переменными.
5. Зависимость случайна.
10

11.

Анализ взаимосвязи признаков
параметрические методы
непараметрические методы
• Корреляционный анализ по
Пирсону
• Корреляционный анализ по
Спирмену, Кендаллу, гамма и т.д.

12.

Непараметрические
критерии. Ранговая
корреляция
1. Ранговая корреляция. Коэффициент Спирмена
2. Ранговая корреляция. Коэффициент Кендалла
12

13.

Две порядковые переменные
• Полная связь означает, что если упорядочить объекты по
возрастанию первой переменной, то они окажутся
упорядоченными и по второй.
• В этом случае, для того, чтобы узнать порядок объектов по
второй переменной её можно и не измерять, если известны
все значения первой переменной.
• Пример: если мы знаем оценки всех учеников в классе по
математике, то мы знаем и порядок расположения всех
учеников относительно их отметок по физике!
13

14.

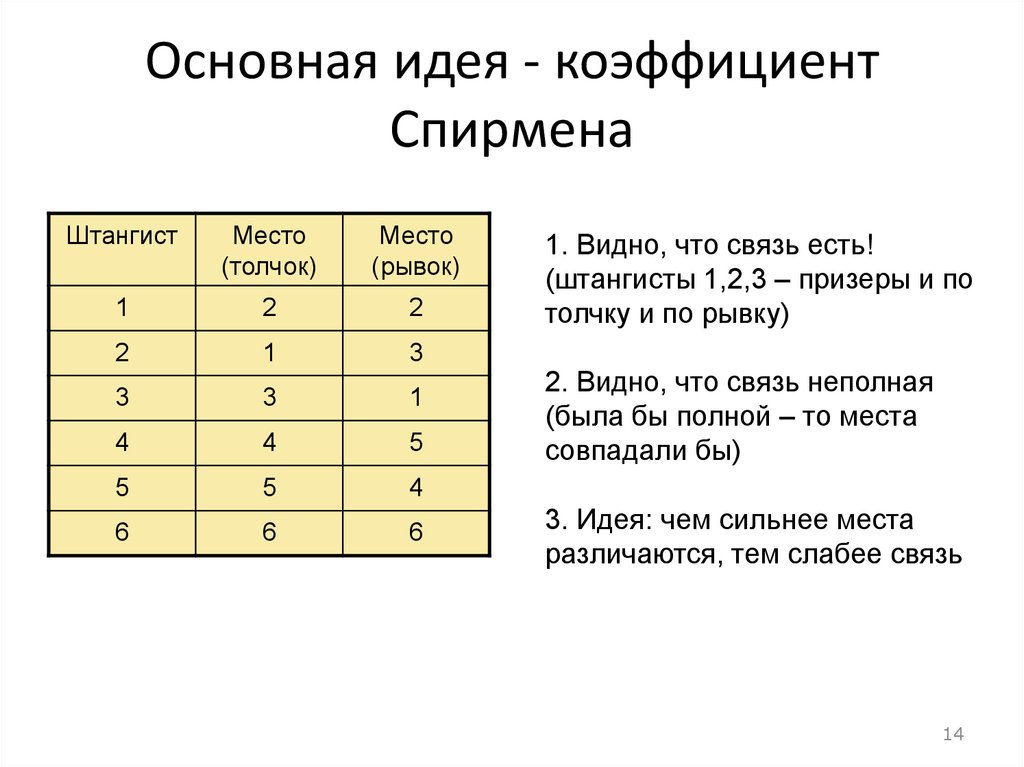
Основная идея - коэффициент
Спирмена
Штангист
Место
(толчок)
Место
(рывок)
1
2
2
2
1
3
3
3
1
4
4
5
5
5
4
6
6
6
1. Видно, что связь есть!
(штангисты 1,2,3 – призеры и по
толчку и по рывку)
2. Видно, что связь неполная
(была бы полной – то места
совпадали бы)
3. Идея: чем сильнее места
различаются, тем слабее связь
14

15.

Полная связь
Штангист
Место
(толчок)
Место
(рывок)
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
Рывок
Толчок
Точки с координатами (место в толчке, место в рывке) лежат
на одной прямой
15

16.

Неполная связь
Штангист
Место
(толчок)
Место
(рывок)
1
2
2
2
1
3
3
3
1
4
4
5
5
5
4
6
6
6
Рывок
Толчок
Точки с координатами (место в толчке, место в рывке) НЕ лежат
на одной прямой, но тенденция есть
16

17.

Коэффициент ранговой корреляции
Спирмена
• Итак, если связь полная, то, хотя пары (xi,yi) не обязательно лежат
на одной прямой, пары (rxi,ryi) лежат на одной прямой.
• То есть коэффициент связи для двух порядковых переменных
вычисляем как коэффициент линейной корреляции для их рангов:
rs 1
6 d
2
i
n(n 2 1)
где
di rank ( xi ) rank ( yi )
Это коэффициент ранговой корреляции Спирмена.
В примере со штангистами мы обошлись без ранжирования, потому
что значения совпадали с их рангами.
17

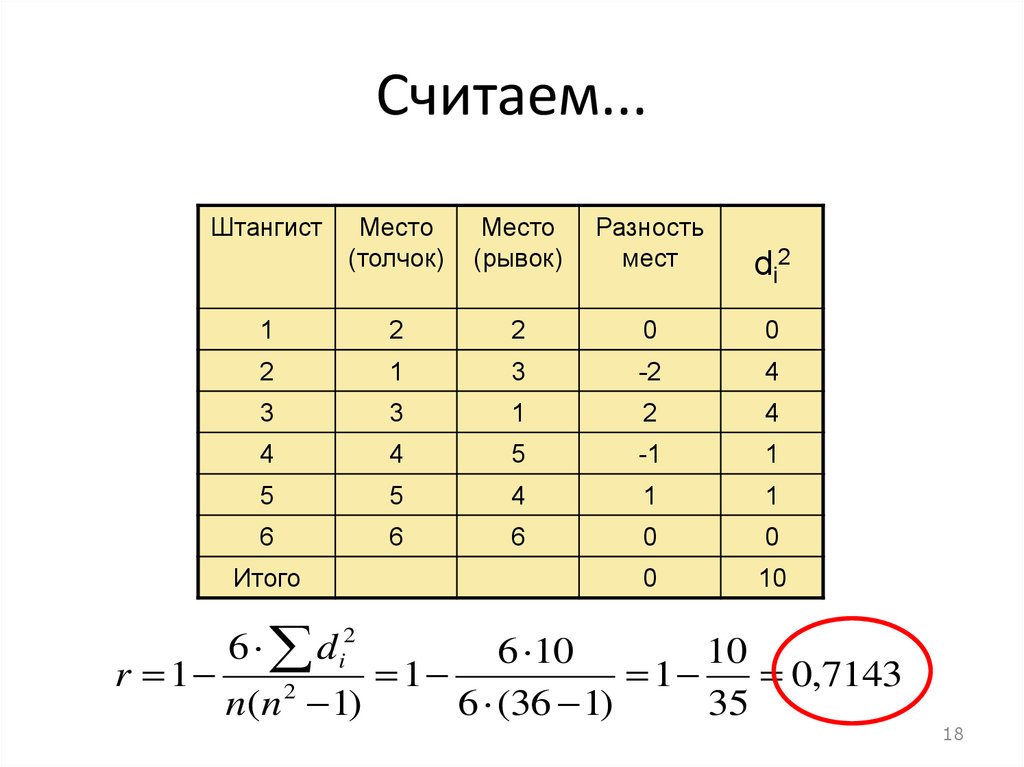
18.

Считаем...
Штангист
Место
(толчок)
Место
(рывок)
Разность
мест
1
2
2
0
0
2
1
3
-2
4
3
3
1
2
4
4
4
5
-1
1
5
5
4
1
1
6
6
6
0
0
0
10
Итого
di2
6 d i2
6 10
10
r 1
1
1
0,7143
2
n(n 1)
6 (36 1)
35
18

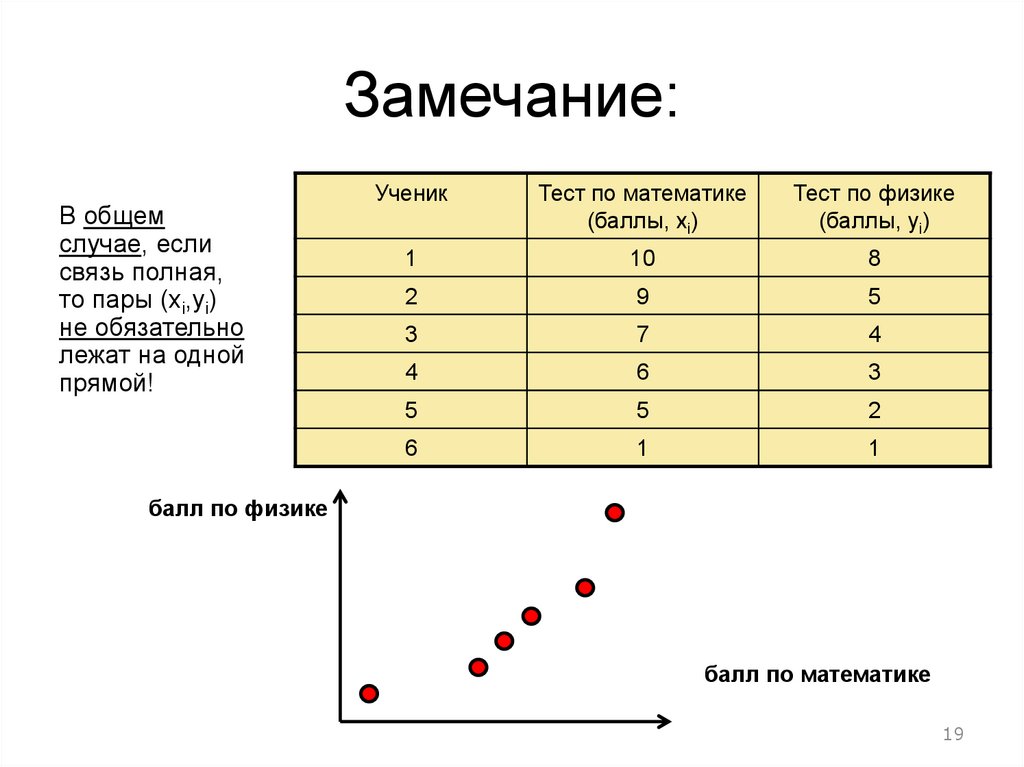
19.

Замечание:
В общем
случае, если
связь полная,
то пары (xi,yi)
не обязательно
лежат на одной
прямой!
Ученик
Тест по математике
(баллы, xi)
Тест по физике
(баллы, yi)
1
10
8
2
9
5
3
7
4
4
6
3
5
5
2
6
1
1
балл по физике
балл по математике
19

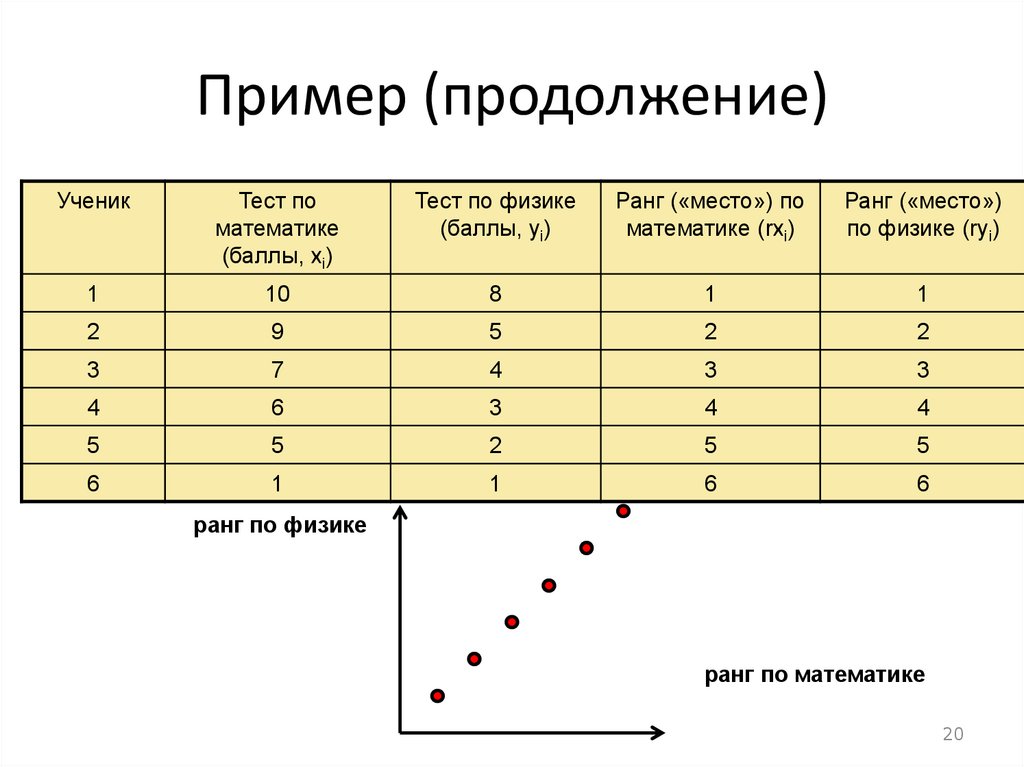
20.

Пример (продолжение)
Ученик
Тест по
математике
(баллы, xi)
Тест по физике
(баллы, yi)
Ранг («место») по
математике (rxi)
Ранг («место»)
по физике (ryi)
1
10
8
1
1
2
9
5
2
2
3
7
4
3
3
4
6
3
4
4
5
5
2
5
5
6
1
1
6
6
ранг по физике
ранг по математике
20

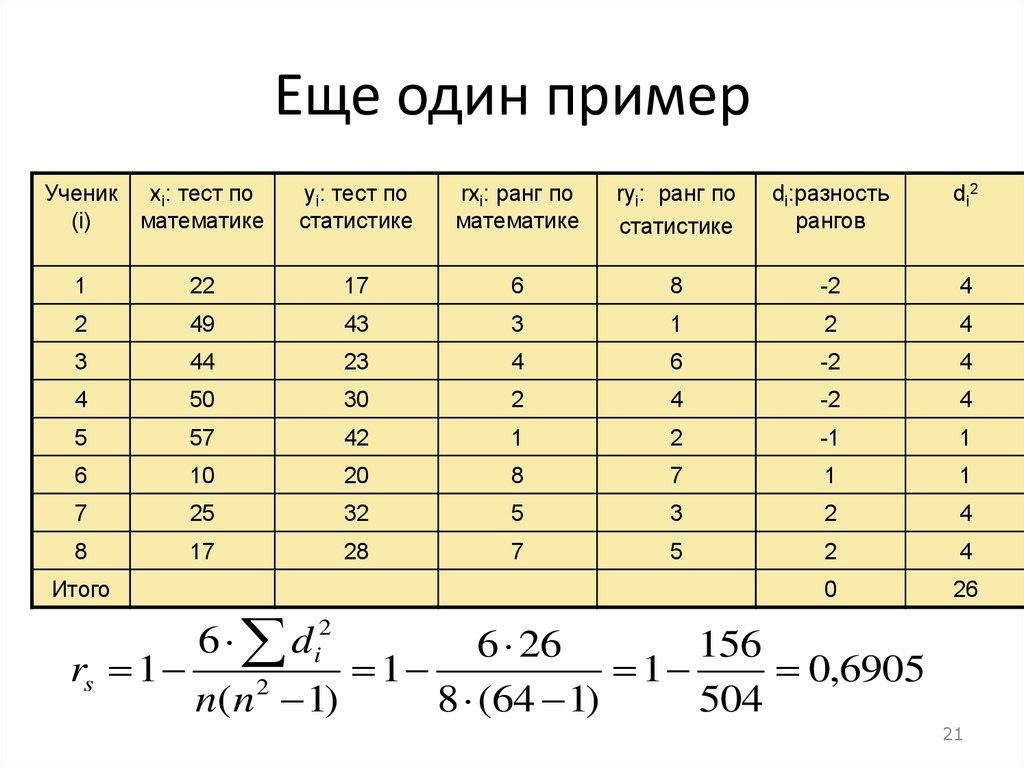
21.

Еще один пример
Ученик xi: тест по
(i)
математике
yi: тест по
статистике
rxi: ранг по
математике
ryi: ранг по
статистике
di:разность
рангов
di 2
1
22
17
6
8
-2
4
2
49
43
3
1
2
4
3
44
23
4
6
-2
4
4
50
30
2
4
-2
4
5
57
42
1
2
-1
1
6
10
20
8
7
1
1
7
25
32
5
3
2
4
8
17
28
7
5
2
4
0
26
Итого
6 d i2
6 26
156
rs 1
1
1
0,6905
2
n(n 1)
8 (64 1)
504
21

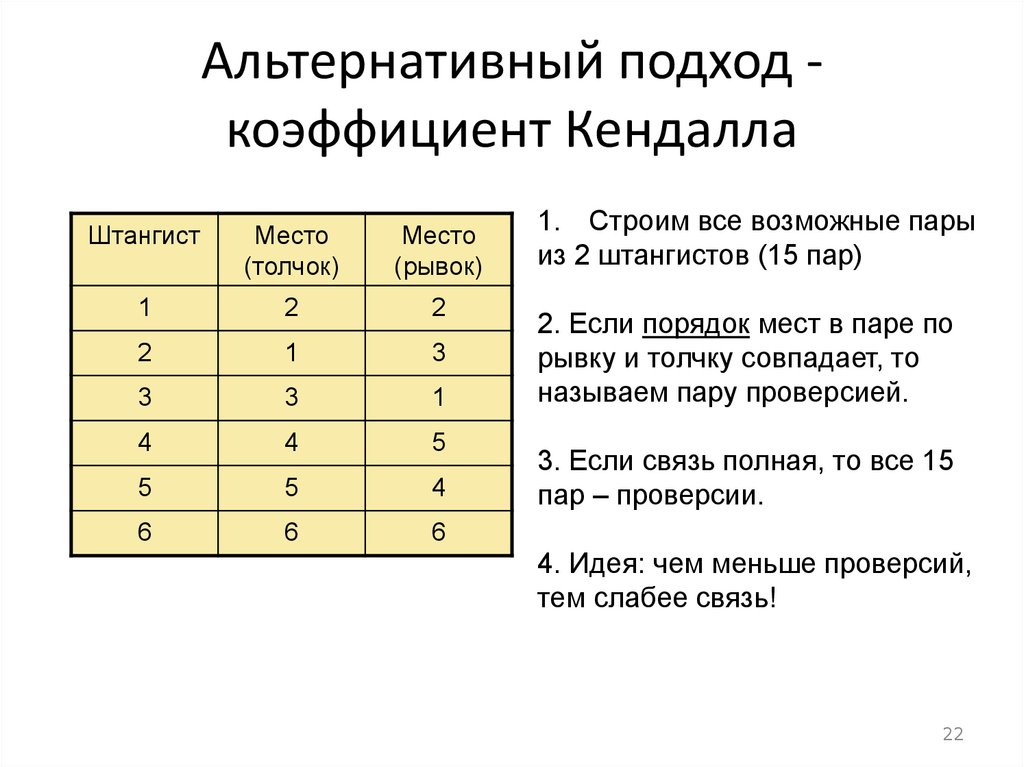
22.

Альтернативный подход коэффициент Кендалла
Штангист
Место
(толчок)
Место
(рывок)
1
2
2
2
1
3
3
3
1
4
4
5
5
5
4
6
6
6
1. Строим все возможные пары
из 2 штангистов (15 пар)
2. Если порядок мест в паре по
рывку и толчку совпадает, то
называем пару проверсией.
3. Если связь полная, то все 15
пар – проверсии.
4. Идея: чем меньше проверсий,
тем слабее связь!
22

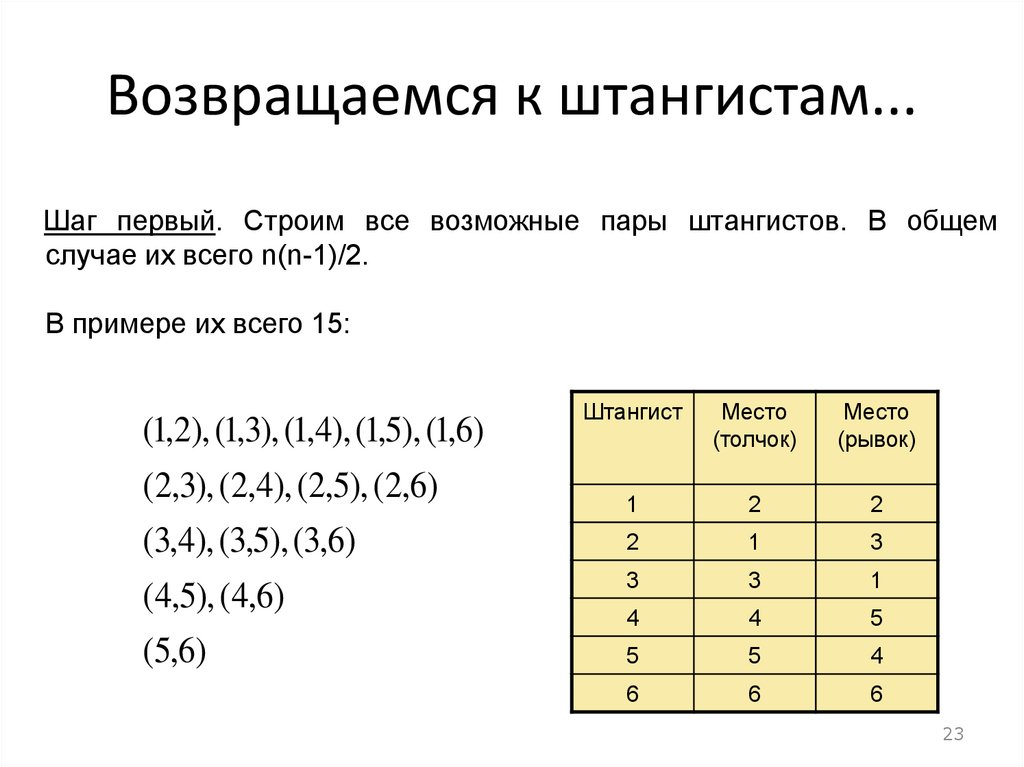
23.

Возвращаемся к штангистам...
Шаг первый. Строим все возможные пары штангистов. В общем
случае их всего n(n-1)/2.
В примере их всего 15:
Штангист
Место
(толчок)
Место
(рывок)
1
2
2
(3,4), (3,5), (3,6)
2
1
3
(4,5), (4,6)
3
3
1
4
4
5
(5,6)
5
5
4
6
6
6
(1,2), (1,3), (1,4), (1,5), (1,6)
(2,3), (2,4), (2,5), (2,6)
23

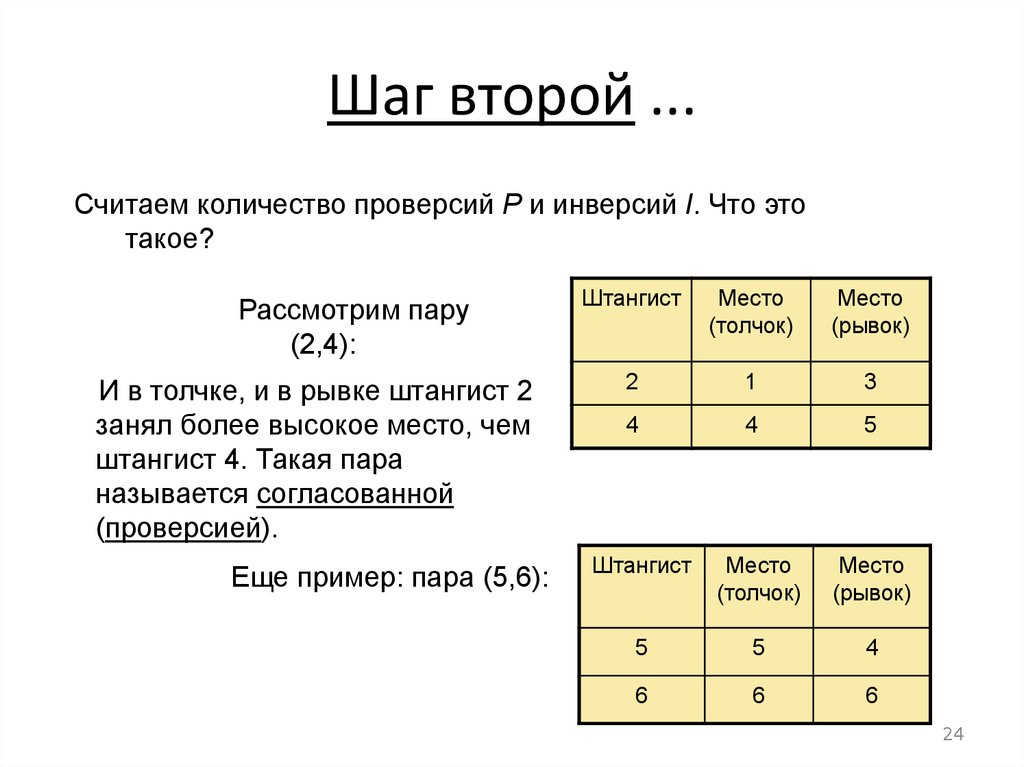
24.

Шаг второй ...
Считаем количество проверсий P и инверсий I. Что это
такое?
Рассмотрим пару
(2,4):
И в толчке, и в рывке штангист 2
занял более высокое место, чем
штангист 4. Такая пара
называется согласованной
(проверсией).
Еще пример: пара (5,6):
Штангист
Место
(толчок)
Место
(рывок)
2
1
3
4
4
5
Штангист
Место
(толчок)
Место
(рывок)
5
5
4
6
6
6
24

25.

Несогласованные пары (инверсии)
Рассмотрим пару (2,3):
Штангист
Место
(толчок)
Место
(рывок)
2
1
3
3
3
1
В толчке штангист 2 занял более высокое место, чем
штангист 3, а в рывке – наоборот. Такая пара называется
несогласованной (инверсией).
Еще пример: пара (4,5):
Штангист
Место
(толчок)
Место
(рывок)
4
4
5
5
5
4
25

26.

Коэффициент Кендалла
Шаг третий.
Находим коэффициент корреляции по формуле
P I
P I
26

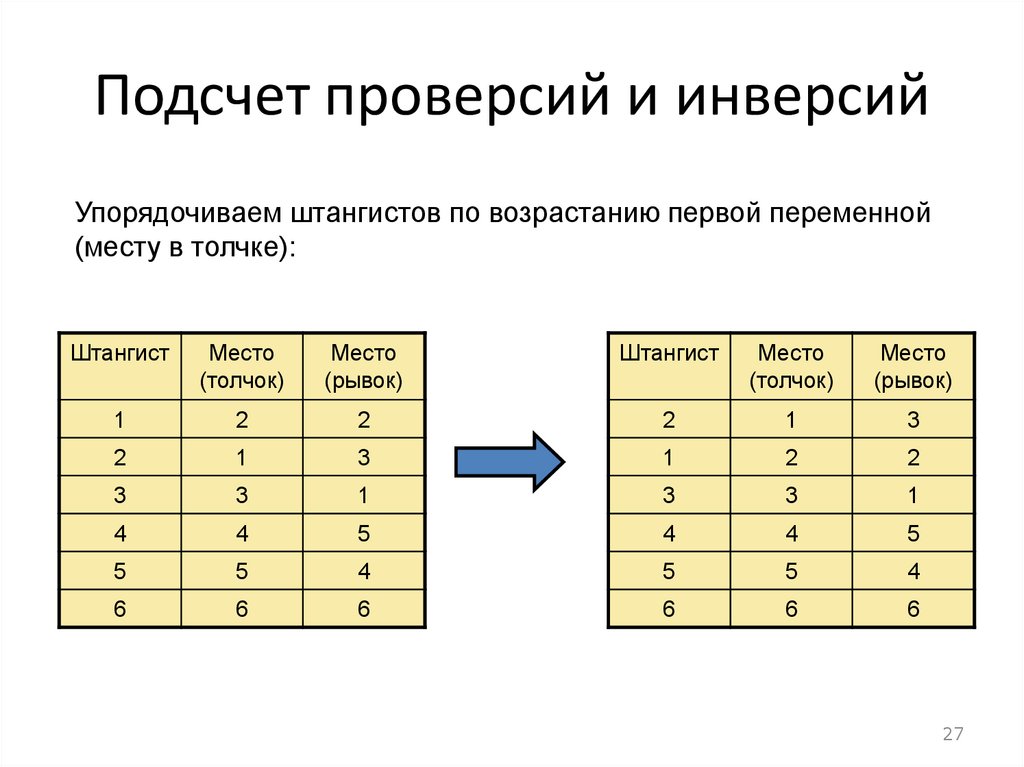
27.

Подсчет проверсий и инверсий
Упорядочиваем штангистов по возрастанию первой переменной
(месту в толчке):
Штангист
Место
(толчок)
Место
(рывок)
Штангист
Место
(толчок)
Место
(рывок)
1
2
2
2
1
3
2
1
3
1
2
2
3
3
1
3
3
1
4
4
5
4
4
5
5
5
4
5
5
4
6
6
6
6
6
6
27

28.

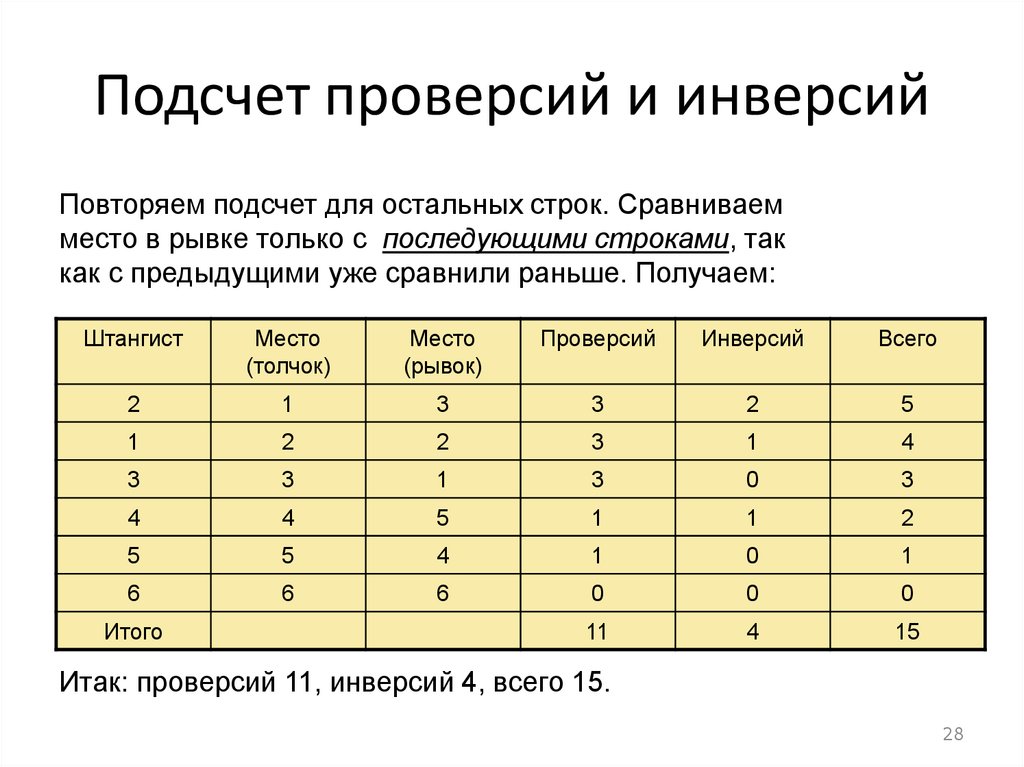
Подсчет проверсий и инверсий
Повторяем подсчет для остальных строк. Сравниваем
место в рывке только с последующими строками, так
как с предыдущими уже сравнили раньше. Получаем:
Штангист
Место
(толчок)
Место
(рывок)
Проверсий
Инверсий
Всего
2
1
3
3
2
5
1
2
2
3
1
4
3
3
1
3
0
3
4
4
5
1
1
2
5
5
4
1
0
1
6
6
6
0
0
0
11
4
15
Итого
Итак: проверсий 11, инверсий 4, всего 15.
28

29.

Считаем коэффициент Кендалла:
P I 11 4 7
0,47
P I 11 4 15
или по альтернативной формуле:
4P
4 11
44
1
1 1 1,47 1 0,47
n(n 1)
6 5
30
29

30.

Итак, ...
Полученный коэффициент нужно проверить на значимость,
которая зависит от вероятности ошибки и объема выборки.
Коэффициент корреляции может быть формально небольшим,
к примеру r=0,17, но если исследование проведено на 500
человек и вероятность ошибки (р) менее 0,05, то мы
признаём значимым даже такой небольшой коэффициент.
С другой стороны, при выборке в 5 человек очень большой
коэффициент мы признаем незначимым, т.к. из-за малого
количества человек мы можем совершить ошибочный вывод
об этой корреляции.
30