Синус, косинус, тангенс, котангенс

1. Синус, косинус, тангенс, котангенс

СИНУС, КОСИНУС,
ТАНГЕНС, КОТАНГЕНС
14.01.2022

2. Планируемые результаты

Познавательные: осознанно владеют логическими
действиями определения понятий.
Регулятивные: умеют осуществлять контроль по
результату и способу действия на уровне
произвольного внимания и вносить необходимые
коррективы.
Коммуникативные: умеют организовывать учебное
сотрудничество и совместную деятельность с
учителем и сверстниками, ясно, точно, грамотно
излагать свои мысли.
Личностные: понимают важность и необходимость
изучения предмета в жизни человека
Планируемые результаты
14.01.2022

3. Мотивация к деятельности

«Первое условие, которое надлежит
выполнять в математике,- это быть
точным, второе- быть ясным и ,
насколько возможно, простым».
Л.Карно(19век Франция)
Мотивация к деятельности
14.01.2022

4.

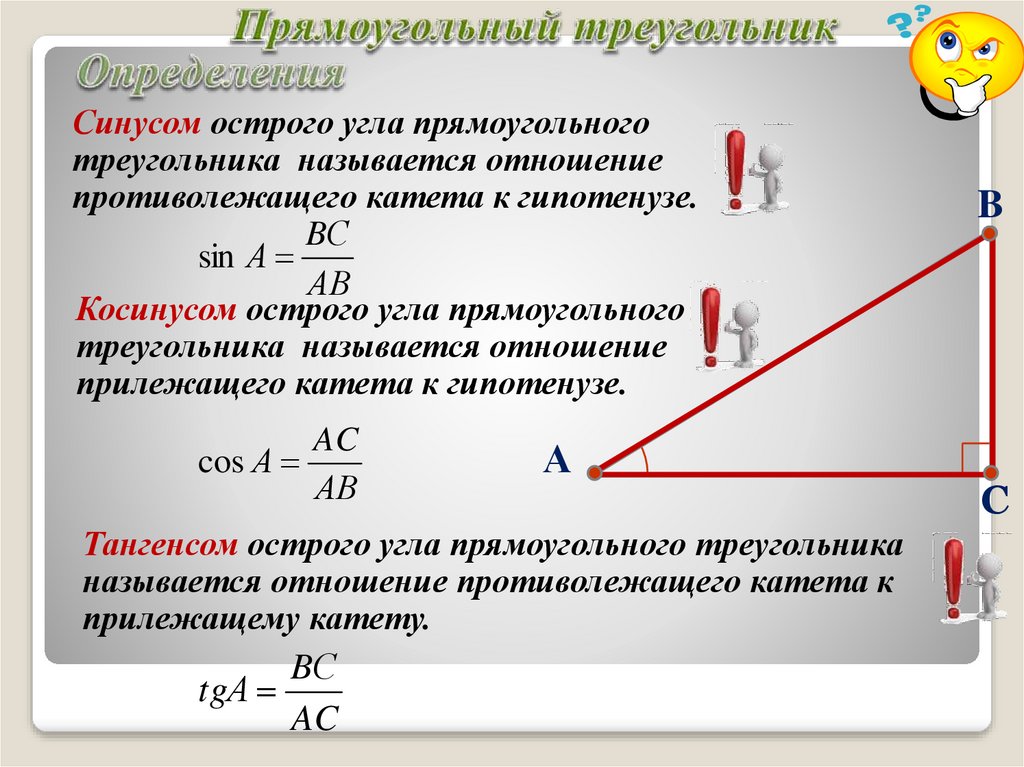
Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе.
BС
sin А
АB
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе.
AC
cos А
АB
А
Тангенсом острого угла прямоугольного треугольника
называется отношение противолежащего катета к
прилежащему катету.
BС
tgА
AC
B
С

5.

300
450
600
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
3
3
1
3
tg

6.

y
1
-1
0
1
x
Единичной полуокружностью называется
полуокружность, расположенная в верхней
полуплоскости, с центром в начале координат,
радиусом равным единице.

7. Определение Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.

y
h
C (0; 1)
M (x; y)
B (-1; 0)
O
y
x
D A(1; 0)
x

8.

∆OMD - прямоугольный
y
h
sin =
C (0; 1)
M (x; y)
MD
OM
sin = y
MD = y
OM = 1
B (-1; 0)
0
x
y
Синус угла – ордината у точки М
cos = OM
OD
D A(1; 0) x
cos = x
OD = x
OM = 1
Косинус угла – абсцисса х точки М
tg =
MD
OD
MD = y = sin
OD = x = cos
tg
sin
cos

9.

y
h
C (0; 1)
M (x; y)
B (-1; 0)
0
x
y
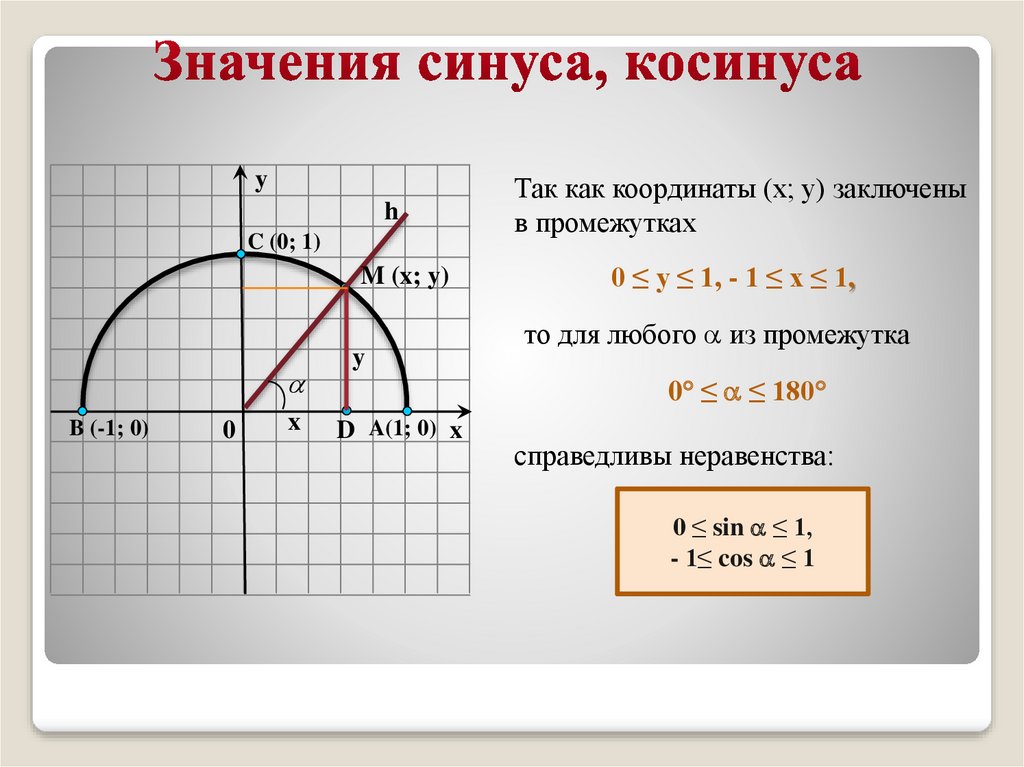
Так как координаты (х; у) заключены
в промежутках
0 ≤ у ≤ 1, - 1 ≤ х ≤ 1,
то для любого из промежутка
0 ≤ ≤ 180
D A(1; 0) x
справедливы неравенства:
0 ≤ sin ≤ 1,
- 1≤ cos ≤ 1

10.

y
h
C (0; 1)
M (x; y)
B (-1; 0)
0
x
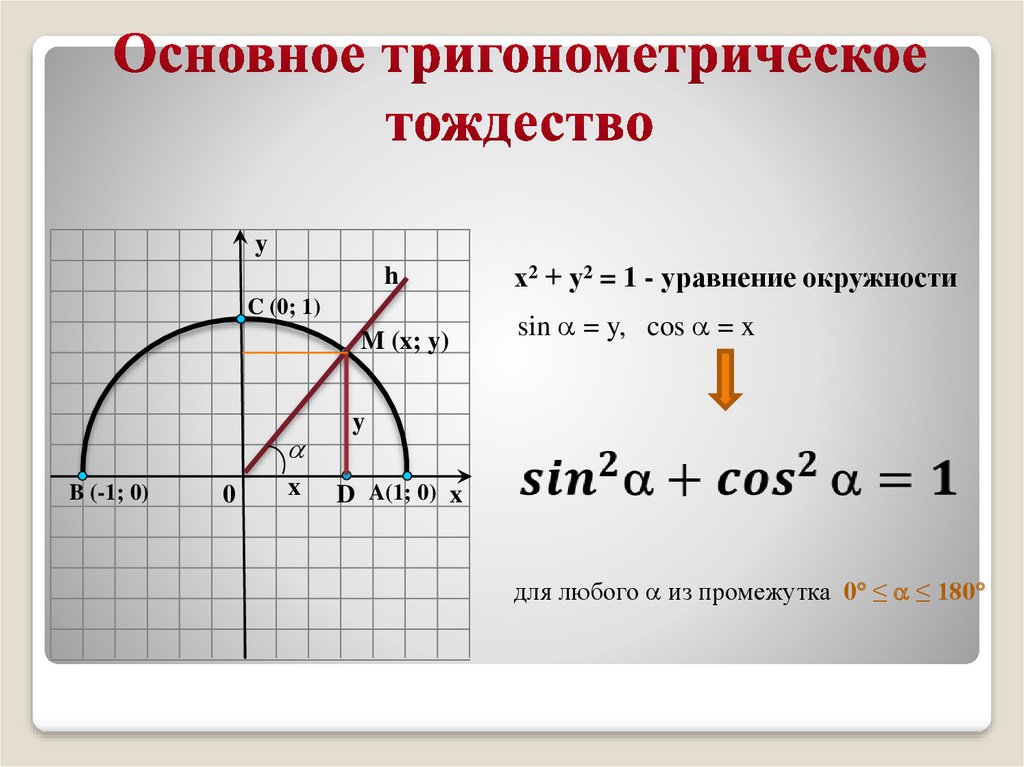
х2 + у2 = 1 - уравнение окружности
sin = y, cos = x
y
D A(1; 0) x
для любого из промежутка 0 ≤ ≤ 180

11.

sin (90 - ) = cos
при 0 ≤ ≤ 90
cos (90 - ) = sin
sin (180 - )= sin
cos (180 - ) = - cos
при 0 ≤ ≤ 180

12.

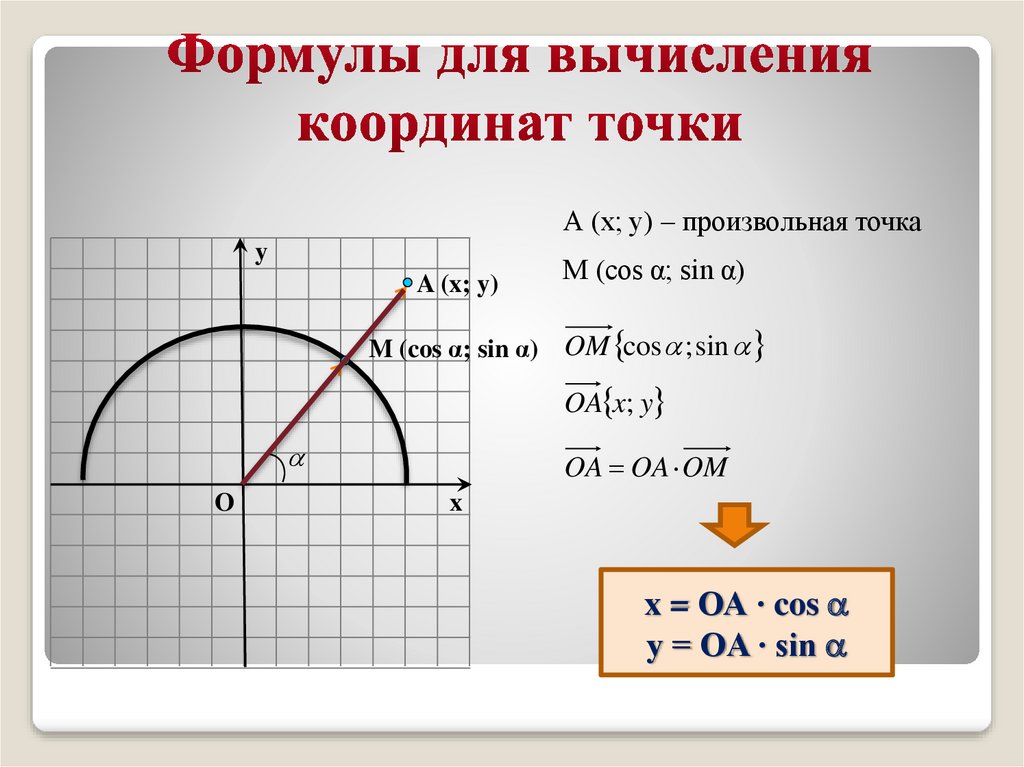
А (x; y) – произвольная точка
y
A (x; y)
М (сos α; sin α)
M (cos α; sin α) OM cos ; sin
OA x; y
O
OA OA OM
x
x = ОА ∙ cos
y = OA ∙ sin

13. Леонард Эйлер

Леонард Эйлер ввел и
само понятие функции и
принятую в наши дни
символику.
Он придал всей
тригонометрии ее
современный вид.

14.

15. Синквейн

Правила написания синквейна:
1 строка - одно слово, обычно существительное или
местоимение, которое обозначает объект или предмет, о котором
пойдет речь.
2 строка - два слова, чаще всего прилагательные или
причастия. Они дают описание признаков и свойств выбранного в
синквейне предмета или объекта.
3 строка - образована тремя глаголами или деепричастиями,
описывающими характерные действия объекта.
4 строка - фраза из четырех слов, выражает личное отношение
автора синквейна к описываемому предмету или объекту.
5 строка - одно слово, характеризующее суть предмета или
объекта.
Синквейн