Простейшие движения твердого тела

1.

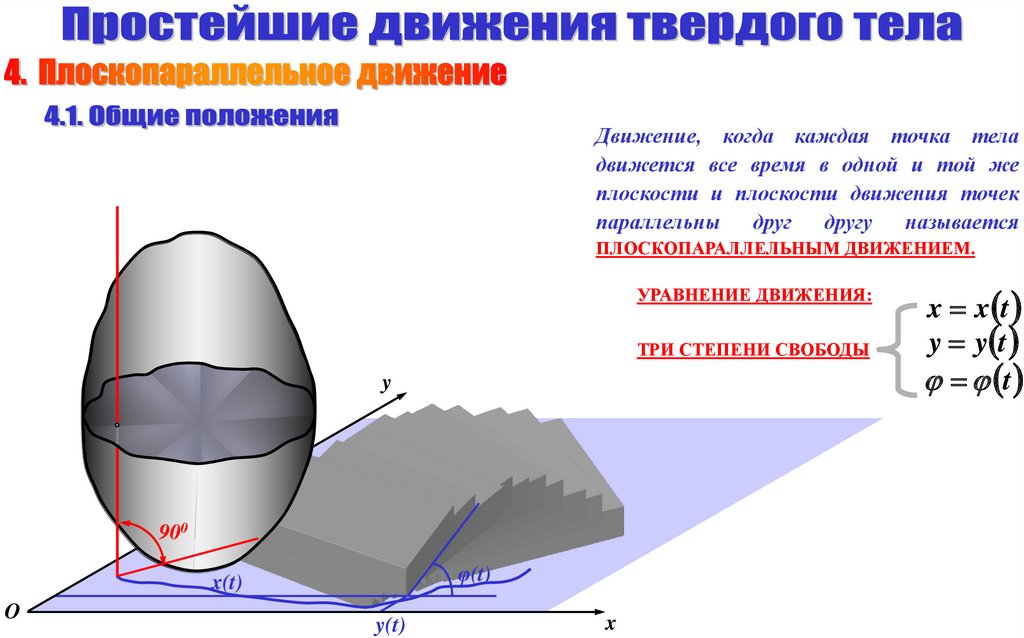
Движение, когда каждая точка тела
движется все время в одной и той же
плоскости и плоскости движения точек
параллельны друг другу называется
ПЛОСКОПАРАЛЛЕЛЬНЫМ ДВИЖЕНИЕМ.
УРАВНЕНИЕ ДВИЖЕНИЯ:
ТРИ СТЕПЕНИ СВОБОДЫ
y
900
φ(t)
x(t)
O
y(t)
x
x x t
y y t
t

2.

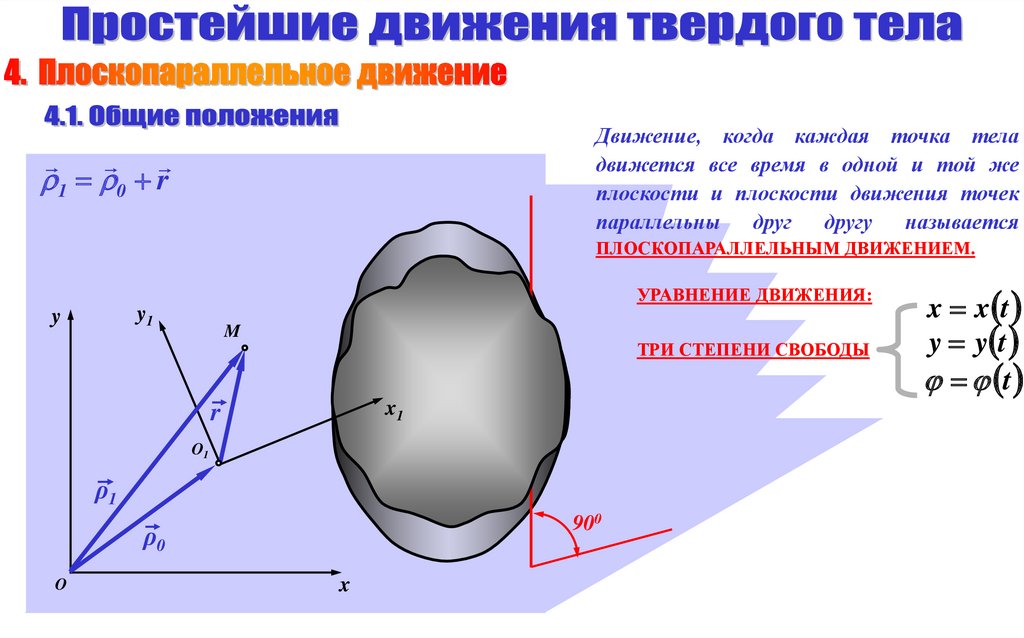
Движение, когда каждая точка тела
движется все время в одной и той же
плоскости и плоскости движения точек
параллельны друг другу называется
1 0 r
ПЛОСКОПАРАЛЛЕЛЬНЫМ ДВИЖЕНИЕМ.
УРАВНЕНИЕ ДВИЖЕНИЯ:
y1
y
M
ТРИ СТЕПЕНИ СВОБОДЫ
x1
r
O1
ρ1
900
ρ0
O
x
x x t
y y t
t

3.

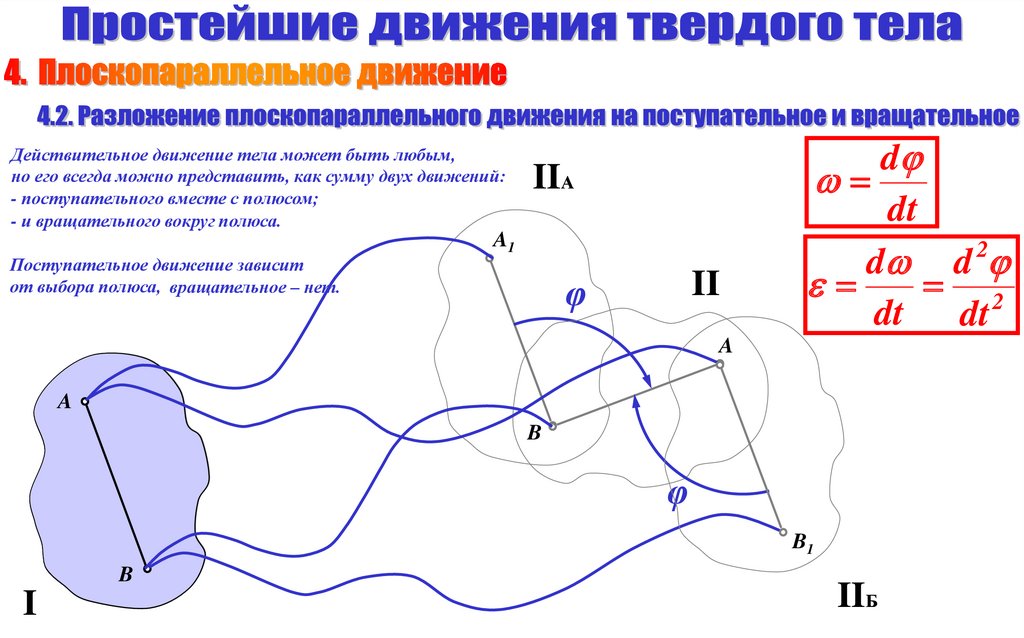
Действительное движение тела может быть любым,
но его всегда можно представить, как сумму двух движений:
- поступательного вместе с полюсом;
- и вращательного вокруг полюса.
Поступательное движение зависит
от выбора полюса, вращательное – нет.
IIА
A1
II
φ
d
dt
2
d d
2
dt
dt
A
A
B
φ
B1
B
I
IIБ

4.

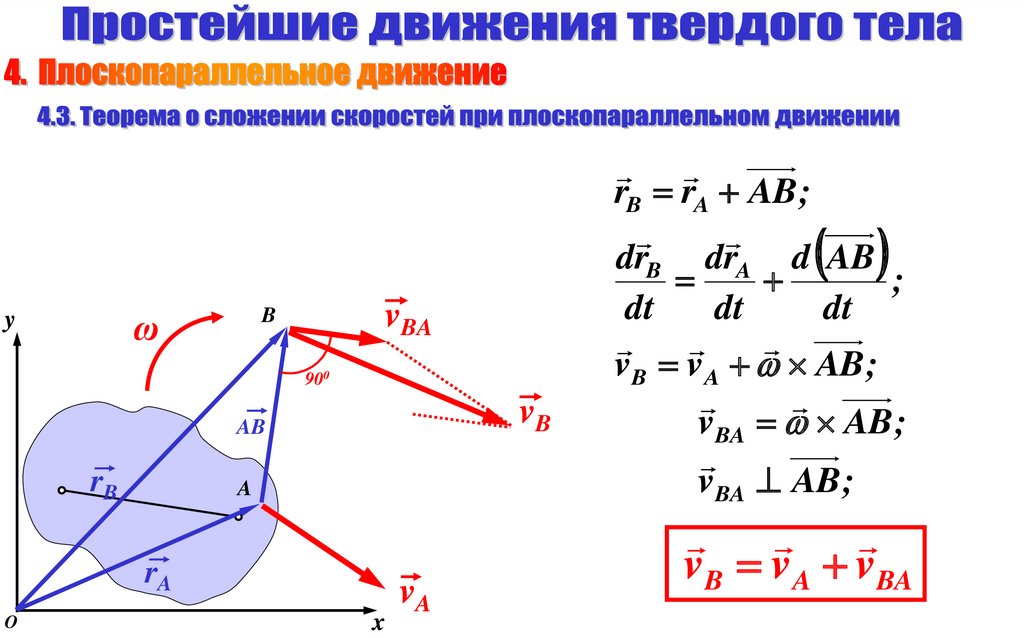
rB rA AB ;
drB drA d AB
;
dt
dt
dt
vB v A AB ;
vBA AB ;
vBA AB ;
vBA
B
ω
y
900
vB
AB
rB
A
rA
O
x
vA
vB v A vBA

5.

vP
vP
vP
vP
vP
vP vO vO vO v
O
vO
vO
vP
vOvP
vO
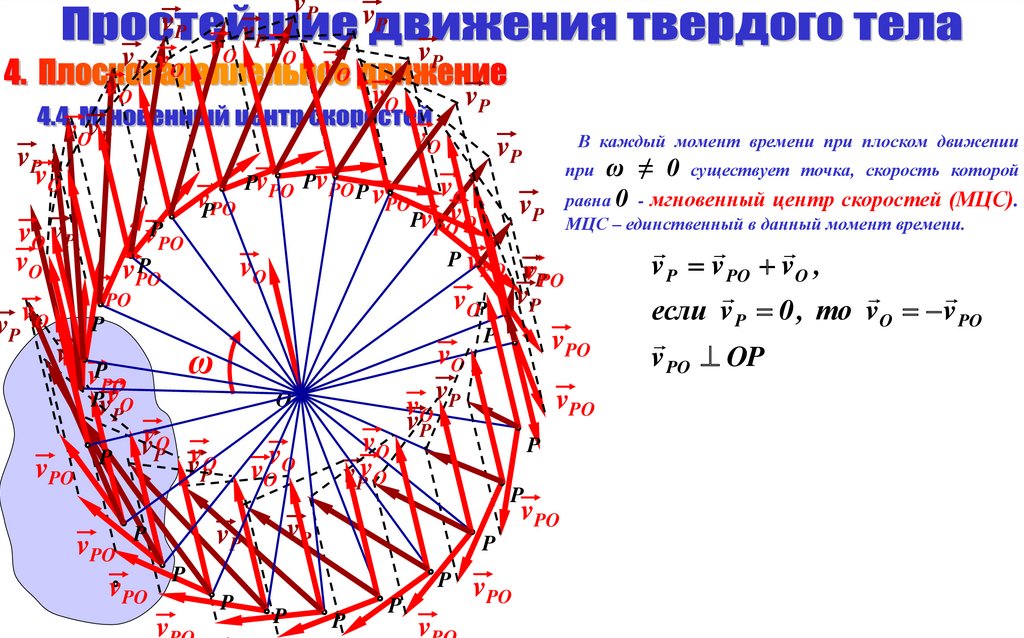
В каждый момент времени при плоском движении
v
P
vP
при ω ≠ 0 существует точка, скорость которой
vO
PvPO PvPO P
vPO vO
равна 0 - мгновенный центр скоростей (МЦС).
vPPO
v
P МЦС – единственный в данный момент времени.
v
P
v
O
PO
vO vP
vPPO
P
vPO vv
vO
P
v P v PO vO ,
vO
vPO
PPO
vPO
v
v
P
OP
если v P 0 , то vO v PO
v
O
P
vP
P
v
PO
vP
vO
v PO OP
ω
P
vPO
vP
O
PvvO
vPO
vO
P
vP
v
O
vO
P
v
P
v
v
P
vPO vO O
vPO
vPvO
P
vPO
vP
P
v
P
P
vPO
P
P v
vPO
PO
P
P
P
P
v
v

6.

В каждый момент времени при плоском движении
ω ≠ 0 существует точка, скорость которой
равна 0 - мгновенный центр скоростей (МЦС).
при
vA
vP
vO
vO
vO
A
vPO
P
ω
900
900
vO
v
O
v
v
O
vO vO O v
B
vP vP v
B P v vvPP
P
P
P
МЦС – единственный в данный момент времени.
v P v PO vO ,
если v P 0 , то vO v PO
v PO OP
v PO vO
.
v PO OP , OP
P
P
P
P P
O
vPO vPO
vPO vPO vvPO vPO
PO
Мгновенный центр скоростей (МЦС) находится в точке
пересечения перпендикуляров, проведенных из точек к их скоростям.
Расстояния от точек до мгновенного центра скоростей прямо
пропорционально отношению скоростей этих точек.
Приняв МЦС за полюс получим:
v A AP ,
v B BP ,
v A AP
vA
v B v BA
,
AP BP AB
v B BP
v A v PA

7.

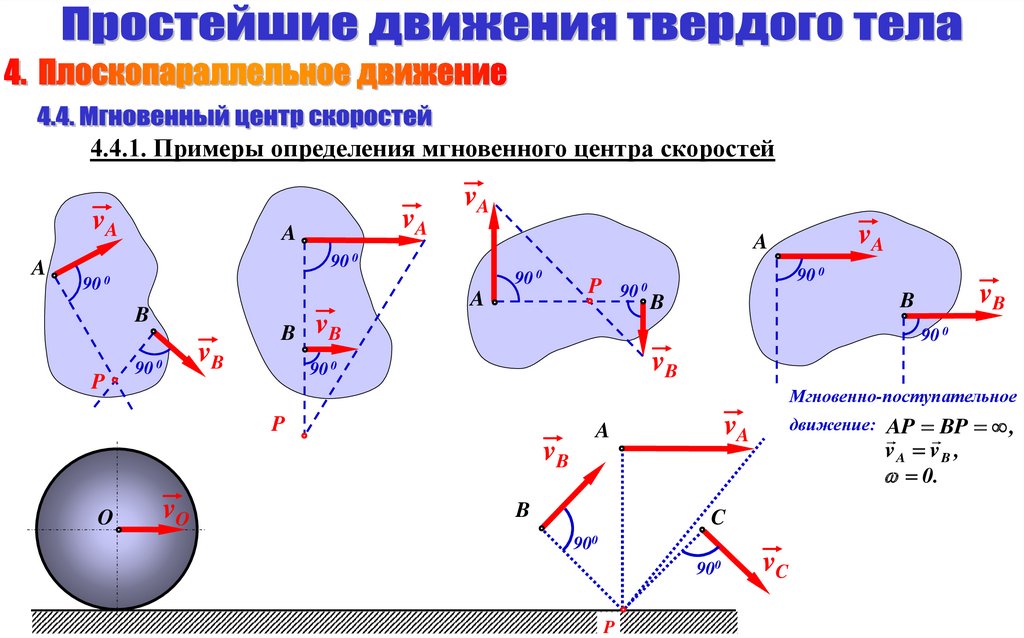
4.4.1. Примеры определения мгновенного центра скоростей
vA
A
vA
A
vA
90 0
90 0
P
90 0
P 90 0
A
B
vB
90 0
B
vB
90 0
vB
B
B
90 0
vB
90 0
Мгновенно-поступательное
P
vB
O
vA
A
vO
B
движение: AP BP ,
vA
A
v A vB ,
0.
C
900
900
P
vC

8.

4.5.1. Пример 1
Прямая AB движется в плоскости рисунка, причем конец ее А все
время находится на полуокружности САD, а сама прямая все время
проходит через неподвижную точку C диаметра CD.
Определить скорость VC точки прямой, совпадающей с точкой
C, в тот момент, когда радиус ОА перпендикулярен CD, если
известно, что скорость точки А в этот момент равна 4 м/с.
x
B
1-й способ:
Решение:
VCA
Применение теоремы о сложении скоростей
VC
900
O
C
D
VC VA VCA ; VCA AC ;
прx VC прx VA прx VCA ;
VC VA cos 45 0 ;
0
450
VA
VAx = VAcos450
A
VC VA cos 45 4 0.707 2.83 м / с .
0
Ответ:
VC 2.83 м / с

9.

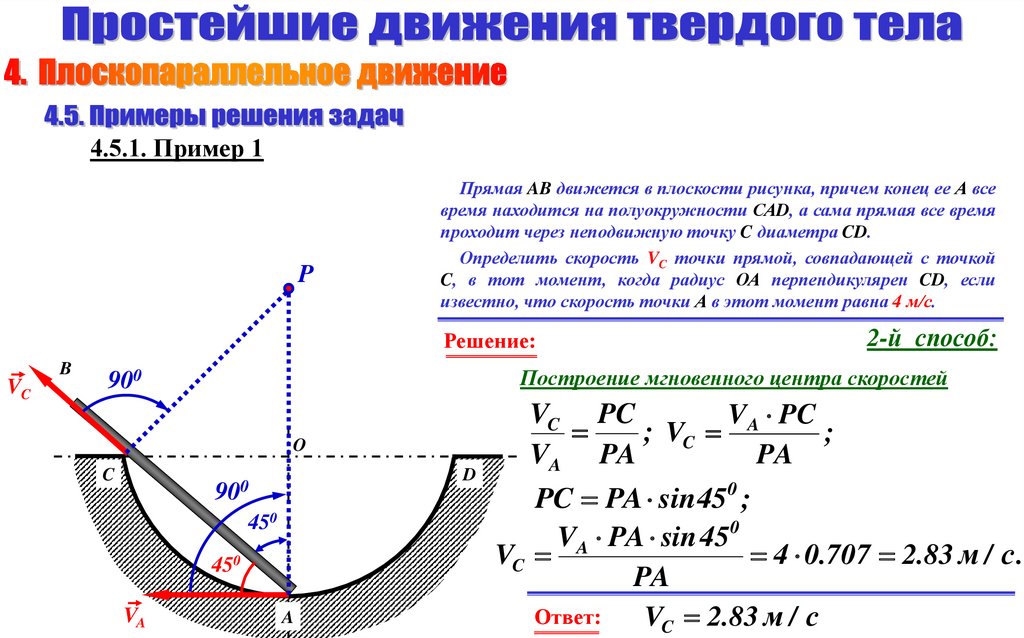
4.5.1. Пример 1
P
Прямая AB движется в плоскости рисунка, причем конец ее А все
время находится на полуокружности САD, а сама прямая все время
проходит через неподвижную точку C диаметра CD.
Определить скорость VC точки прямой, совпадающей с точкой
C, в тот момент, когда радиус ОА перпендикулярен CD, если
известно, что скорость точки А в этот момент равна 4 м/с.
Решение:
B
VC
Построение мгновенного центра скоростей
900
O
C
D
900
450
450
VA
2-й способ:
A
VC PC
VA PC
; VC
;
PA
VA PA
PC PA sin 450 ;
0
VA PA sin 45
VC
4 0.707 2.83 м / с .
PA
Ответ:
VC 2.83 м / с

10.

4.5.1. Пример 1
Прямая AB движется в плоскости рисунка, причем конец ее А все
время находится на полуокружности САD, а сама прямая все время
проходит через неподвижную точку C диаметра CD.
Определить скорость VC точки прямой, совпадающей с точкой
C, в тот момент, когда радиус ОА перпендикулярен CD, если
известно, что скорость точки А в этот момент равна 4 м/с.
3-й способ:
Решение:
B
Применение теоремы о равных проекциях
VC
прAB VC прAB VA ;
O
C
VC VA cos 450 ;
D
450
VA
VAB = VAcos450
A
VC 4 0.707 2.83 м / с .
Ответ:
VC 2.83 м / с

11.

4.5.2. Пример 2
Колесо катится без скольжения по горизонтальной поверхности. Скорость центра колеса равна V0 =
10 м/с, радиус колеса R = 0.5 м. Определить угловую скорость колеса ω и скорости точек А, B, C в
положении, указанном на чертеже.
Решение: Мгновенный центр скоростей колеса находится в точке касания с поверхностью качения.
VO VA VB VC
; AP 2 AO ; BP CP OP 2 OP 2 OP 2 R 2 ;
OP AP BP CP
VO AP
VA
2VO 20 м / с ;
OP
A
VO BP
v
B
VB VC
2VO 14.1 м / с ;
vA
OP
B
vO
C
VO O
Ответ:
20 рад / с
900
R
vC VA 20 м / с ;
900
P
VB VC 14.1 м / с ;
20 рад / с ;

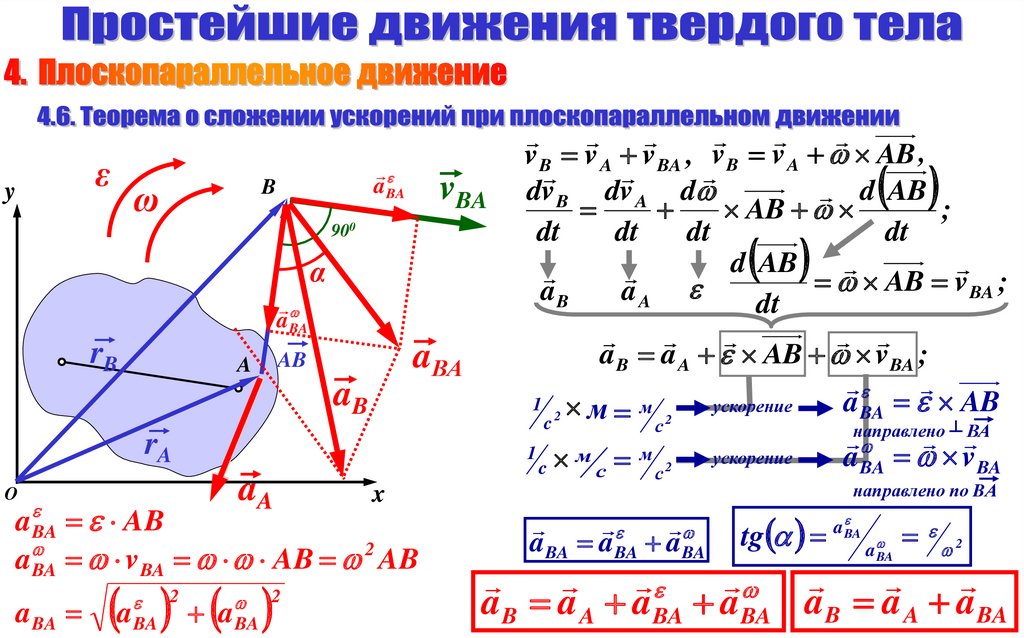
12.

ε
y
a BA
B
ω
vBA
α
a BA
aВА
AB
A
aB
rA
aA
O
a BA
a a
BA
BA
2
направлено по BА
x
a BA
AB
2
a BA v BA AB AB
2
900
rB
v B v A v BA , v B v A AB ,
dv B dv A d
d AB
AB
;
dt
dt
dt
dt
d AB
AB v BA ;
aB
aA
dt
a B a A AB v BA ;
1 м
a BA AB
ускорение
м
AB
2
2
c
с
направлено ┴ ВА
1 v
м м 2
ускорение
a BA v BA
c
BA
с
с
a BA a BA a BA
tg
a BA
a BA
2
a B a A a BA a BA a B a A a BA

13.

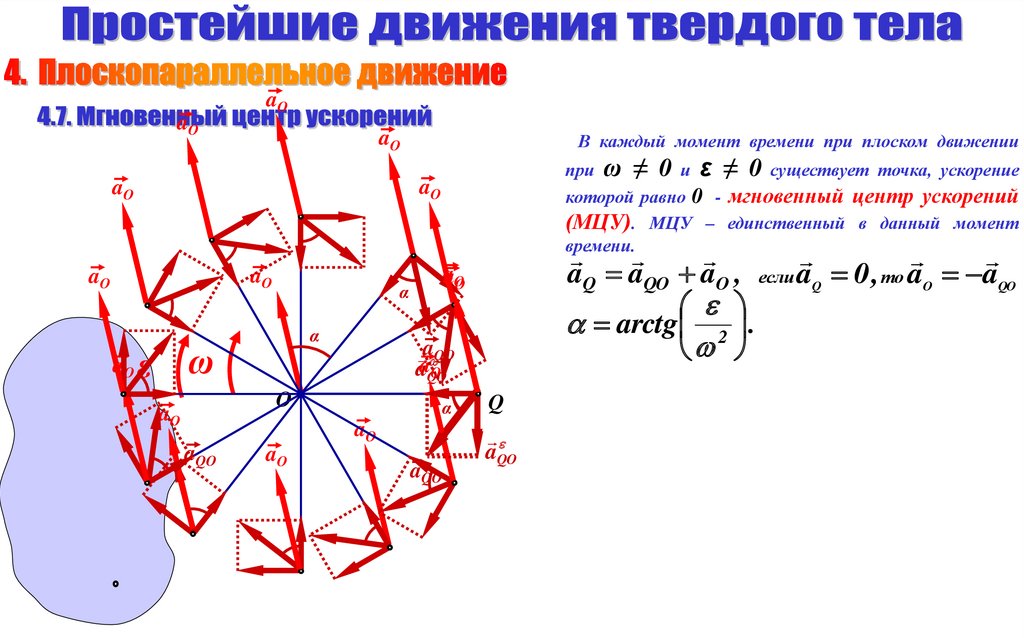
aO
aO
aO
при ω ≠ 0 и ε ≠ 0 существует точка, ускорение
которой равно 0 - мгновенный центр ускорений
(МЦУ). МЦУ – единственный в данный момент
времени.
aO
aO
aO
aO
aO
В каждый момент времени при плоском движении
ω
ε
aa QO
aQO
O
O
aO
aOO
α
α
α
aO
aQO
aO
aQ aQO aO , если aQ 0 , то aO aQO
arctg 2 .
aQO
Q
aQO

14.

aO
aO
В каждый момент времени при плоском движении
aO
при ω ≠ 0 и ε ≠ 0 существует точка, ускорение
которой равно 0 - мгновенный центр ускорений
(МЦУ). МЦУ – единственный в данный момент
времени.
aO
aO
ε
ω
Q
Q
aQO
aQO
α aQO
Q
aQO α
aO
aQO
Q
aQO α a
QO
a QQO
aQO
aQO α aQO
α
aQO
α
α
aQO
a
QO
a
a
A
aB
QO
B
O
α
A
Расстояния от точек до мгновенного центра
ускорений прямо пропорционально отношению
ускорений этих точек.
Мгновенный
центр
ускорений
находится в точке пересечения линий,
проведенных из точек к их ускорениям
по углом α.
aQ aQO aO , если aQ 0 , то aO aQO
arctg 2 .
2
2
aO aQO aQO aQO
QO
2
QO QO
2 2
OQ
aO
2 4
2
4 ,
.
a A a AQ a A AQ ; a A AQ
; tg 2 .
a a a BQ 2 4 ; a B BQ
2
B
BQ
B
4

15.

4.8.1. Пример 1
VB
VB
B
B
B
B V
VBB
B
V
VBB VBB
B VB
BB
V
V
B
V
BB
B
VBBBB
V
VBBBBB
VB
VB
V
B
V
B
V
VBB
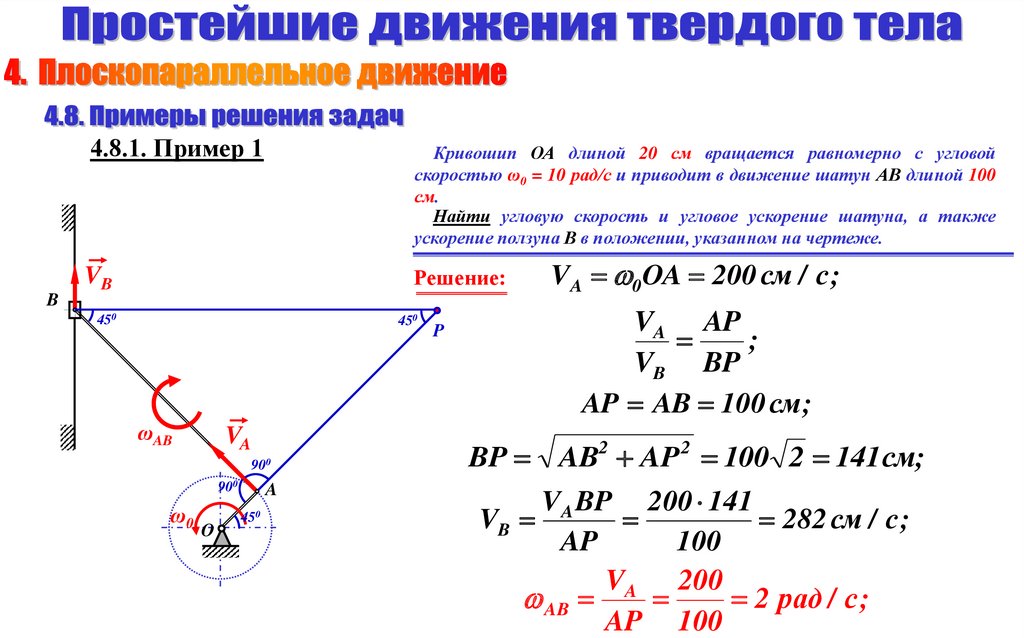
Кривошип ОА длиной 20 см вращается равномерно с угловой
скоростью ω0 = 10 рад/с и приводит в движение шатун АВ длиной 100
см.
Найти угловую скорость и угловое ускорение шатуна, а также
ускорение ползуна В в положении, указанном на чертеже.
Решение:
VVAA
VAVAV
A
VA
A
A A VA
A
A 90 AA
VA
A VA
VA A
A ω0
45 A VA
A V
O
A
A
VA
A V
A
A
A
VA A
A
VA A A A A A VVA
VAVA
VAVV A
V
AA
0
0
A

16.

4.8.1. Пример 1
Кривошип ОА длиной 20 см вращается равномерно с угловой
скоростью ω0 = 10 рад/с и приводит в движение шатун АВ длиной 100
см.
Найти угловую скорость и угловое ускорение шатуна, а также
ускорение ползуна В в положении, указанном на чертеже.
Решение:
VB
B
450
450
ωAB
VA
ω0
O
A
450
VA AP
;
VB BP
AP AB 100 см ;
BP AB AP 100 2 141см;
VA BP 200 141
VB
282 см / с ;
AP
100
VA 200
AB
2 рад / с ;
AP 100
2
900
900
P
VA 0OA 200 см / с ;
2

17.

4.8.1. Пример 1
aBA
y
n
Решение: aA aA aA ; a A 0 OA ;
aA 0 ;
0 d 0 dt 0 , т .к . 0 const ;
n
2
aAn 02 OA 2000 см / с 2 ;
aA aA 2000 см / с ;
aBA
B
aB
Кривошип ОА длиной 20 см вращается равномерно с угловой
скоростью ω0 = 10 рад/с и приводит в движение шатун АВ длиной 100
см.
Найти угловую скорость и угловое ускорение шатуна, а также
ускорение ползуна В в положении, указанном на чертеже.
aBA
aB aA aBA aBA ;
ωAB
900
ω0
O
450
n
aA aA
x
aBA
AB AB ;
aB cos 45 aBA ;
aB 400 0.707 565.7 cм / с ;
0
aB sin 45 aA aBA ; aBA
aA aB sin 450 1600 cм / с 2 ;
2
AB aBA AB 1600 / 100 16 рад / с .
0
A
2
a BA AB
AB 4 100 400 см / с 2 ;
Ответ:
2
AB 2 рад / с ; aB 565.7 cм / с ; AB 16 рад / с .
2
2

18.

4.8.2. Пример 2
VB
B
B
B
B
Решение:
BB
B
B
B
B
A
VA
A
A
VA 0OA a 0 ;
0
30
A
VA AP
;
VB BP
A
ω0
A
O1
O
A
A
A
A
A
A
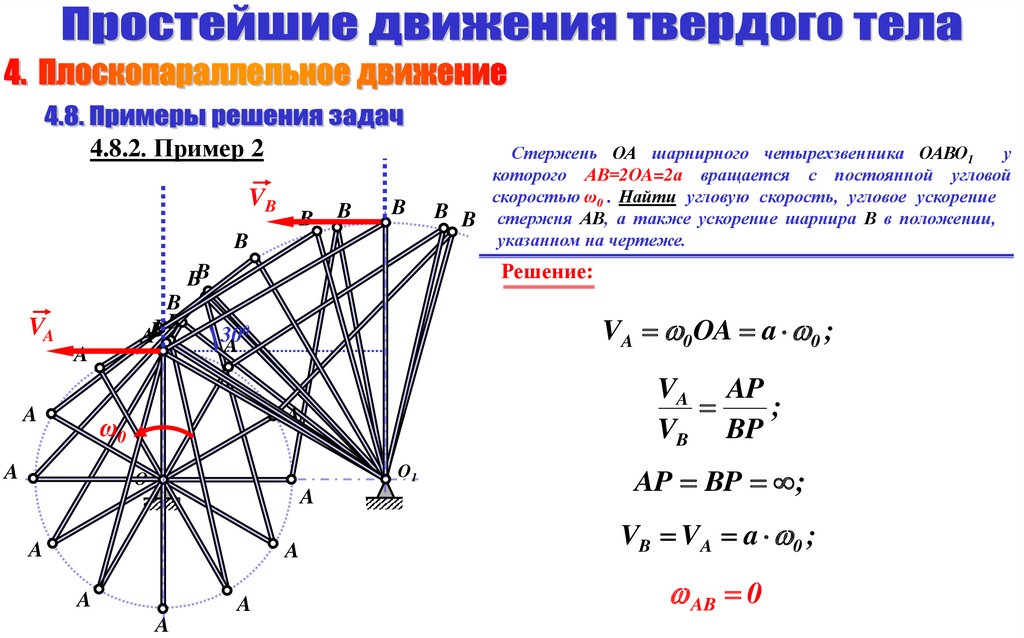
Стержень ОА шарнирного четырехзвенника ОАВО1
у
которого АВ=2ОA=2а вращается с постоянной угловой
скоростью ω0 . Найти угловую скорость, угловое ускорение
B B стержня АВ, а также ускорение шарнира В в положении,
указанном на чертеже.
AP BP ;
VB VA a 0 ;
AB 0

19.

4.8.2. Пример 2
B
300
Стержень ОА шарнирного четырехзвенника ОАВО1
у
которого АВ=2ОA=2а вращается с постоянной угловой
скоростью ω0 . Найти угловую скорость, угловое ускорение
стержня АВ, а также ускорение шарнира В в положении,
указанном на чертеже.
Решение:
A
ω0
O
300
n
aA aA
n
aA aA aA ;
a A 0 OA ;
O1
0 d 0 dt 0 , т .к . 0 const ;
aA 0 ;
aAn 02 OA 02 a ;
aA
n
aA
a;
2
0

20.

aBA
4.8.2. Пример 2
aB
300
y
B
900
x
600
n
aB
A
300
600
ω0
O
aB
n
aA aA
O1
aB
2
0a
Ответ:
Стержень ОА шарнирного четырехзвенника ОАВО1
у
которого АВ=2ОA=2а вращается с постоянной угловой
скоростью ω0 . Найти угловую скорость, угловое ускорение
стержня АВ, а также ускорение шарнира В в положении,
указанном на чертеже.
Решение:
aB aA aBA aBA ;
n
aB aB aB ;
n
aB aB aA aBA aBA ;
2
a BA AB
AB 0 ;
aBA
AB AB ;
aBn VB2 O1 B 02 a 2 ;
a B O1 B O1 B ;
a cos 60 aB cos 30 aA cos 60 ;
a sin 600 a B sin 300 aA sin 600 aBA
;
n
B
n
B
3
; aB
6
0
0
0
3
3
2
2 3
; aBA 0 a ; AB 0
;
3
3
6
3
3
2
2
AB 0 ; aB 0 a
; AB 0
;
3
6
n 2
aB
2
aB
2
0a