Похожие презентации:
Плоское движение твердого тела
1.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
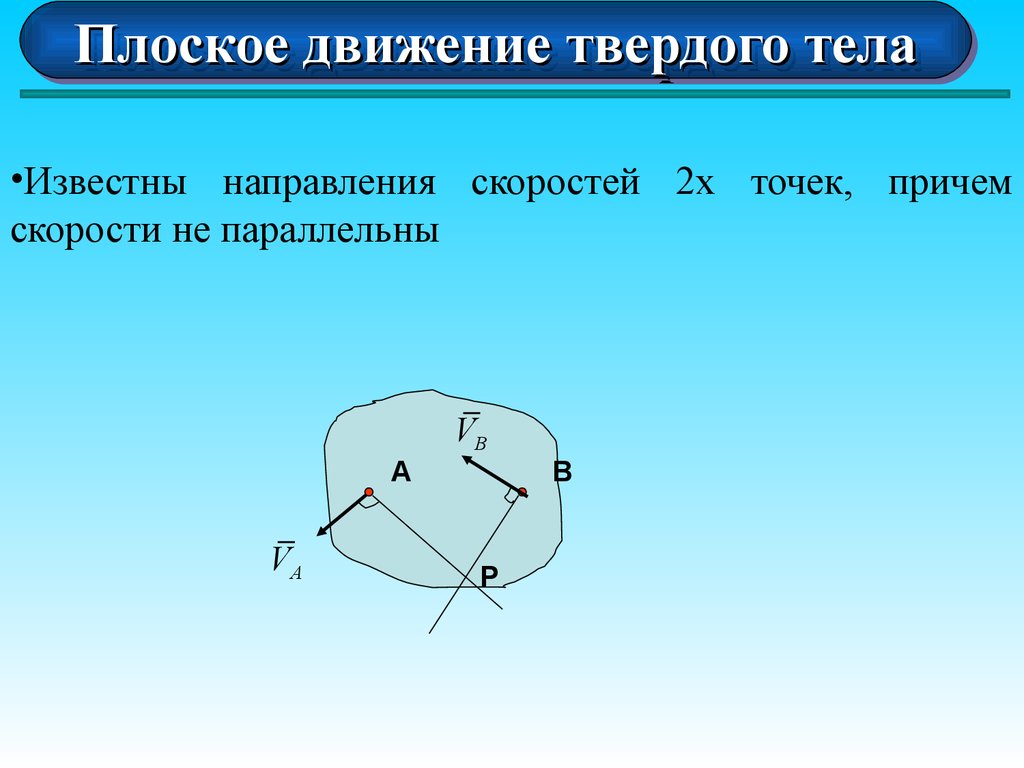
•Известны направления скоростей 2х точек, причем
скорости не параллельны
VB
А
VA
В
Р
2.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
•Скорости двух точек тела параллельны, не равны между
собой и перпендикулярны прямой, соединяющей эти
точки
BP = x
VA
VA
VB
=
= w.
AB + x x
VB
А
В
х
Р
3.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
VA
BP = x
VA
VB
=
= w.
AB - x x
х
AB-x
А
В
Р
VB
4.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
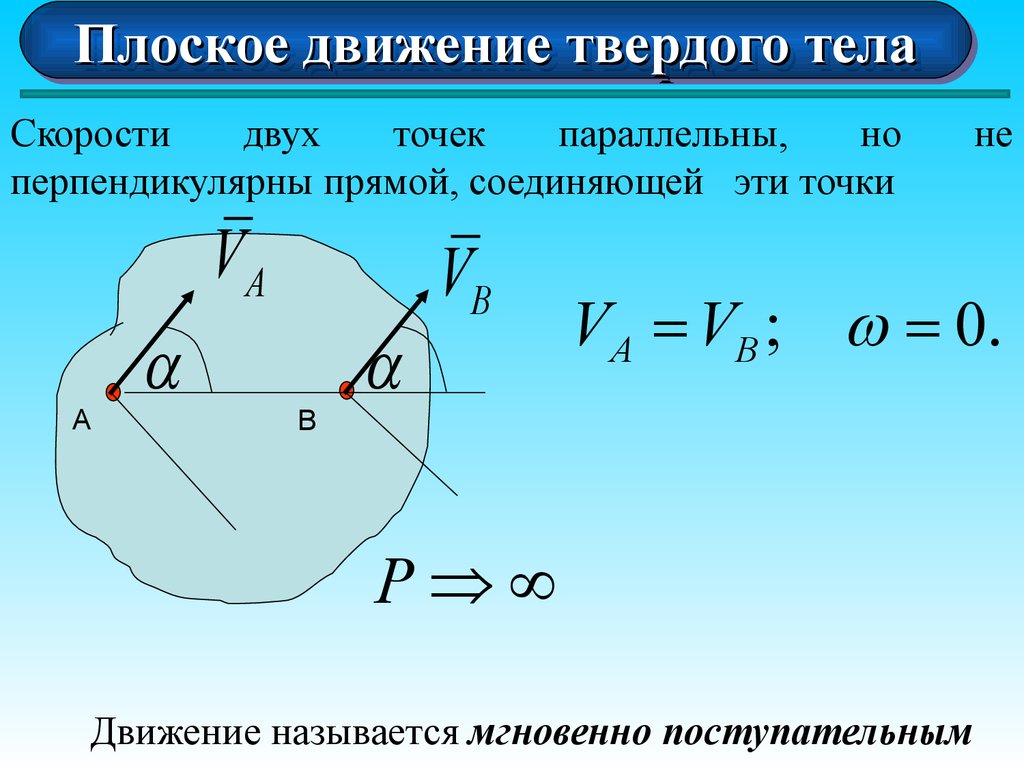
Скорости двух точек параллельны и равны
перпендикулярны прямой, соединяющей эти точки
VA = VB
VA
VB
А
PÞ¥
В
w = 0.
Движение называется мгновенно поступательным
и
5.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
Скорости
двух
точек
параллельны,
но
перпендикулярны прямой, соединяющей эти точки
VA
А
a
В
a
VB
не
VA = VB ; w = 0.
PÞ¥
Движение называется мгновенно поступательным
6.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
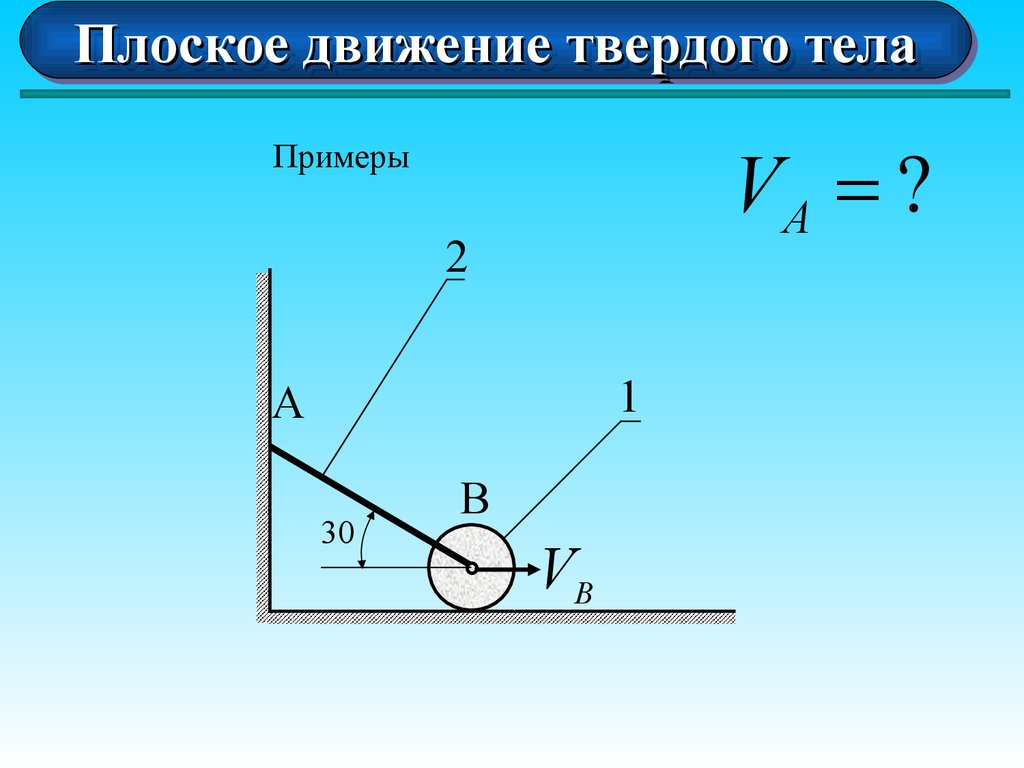
VA = ?
Примеры
2
1
А
30
В
VB
7.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
VA
VB
=
AP2 BP2
А
VA
P2
В
VB
VA
VB
=
AB cos30 AB sin 30
VA × 2 VB × 2
=
1
3
VA = 3 VB
8.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
Vc=?
R
r
w1
С
9.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
VA=w×r
VA
VB
Vc
VB
VA
Р
VB=w×R
10.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
Дано:
w0 = const ;
OA = 2r ;
R3 = r ;
AB = 4r.
Качение без скольжения
w2 = ?; w3 = ?;
A
VC = ?;VB = ?;
2
1
3
w0
O
30o
B
C
11.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
VA
A
w0
VC
O
30o
B
VB
C
w3
P
VA = w0 × OA = 2rw0 ; w2 = 0.
VB = VA
w3 = VB / BP = 2w0 ; VC = w3 × PC = 2w0 r 2.
12.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
Ускорения точек плоской фигуры
a
w
O
e
t
AO
a
aO
a A = aO + a
A
n
AO
a
t
AO
t
AO
^ OA; a
+a ;
n
AO
n
AO
POA;
t
AO
= e × OA;
n
2
a AO = w × OA.
a
Ускорение любой точки А геометрически складывается
из ускорения полюса
О
и осестремительного и
вращательного ускорений во вращении тела вокруг
полюса
13.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
Дано :
Пример
450
А
1
О
ОА = 40 см
w1
2
3
АВ = 80 см
В
рад
w1 = 2
с
e1 = 0
Найти :
аВ ; e 2
14.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
VA
45
А
1
О
w1
2
0
VB
В
3
VA=w×OA=2×40=80 см/c
15.
ПлоскоеПлоское движение
движение твердого
твердого тела
тела
w2 e 2
a
450
А
n
A
О
w1
a
aB
n
BA
t
BA
a
В
16.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
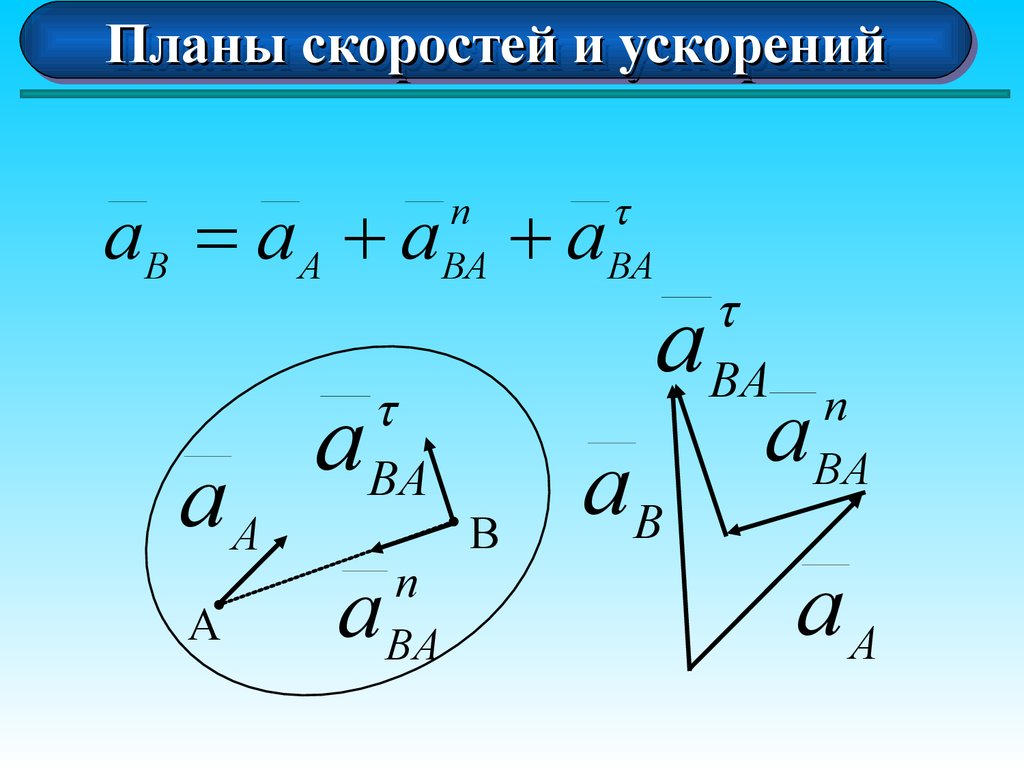
Планом
скоростей
(ускорений)
называется
диаграмма, на которой от некоторого центра (полюса)
отложены векторы скоростей (ускорений) точек тела
VB = VA + VBA
VBA
А
VA
В
VB
VA
VBA
17.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
aB = a A + a + a
n
BA
aA
А
a
t
BA
a
n
BA
В
t
BA
a
aB
t
BA
a
n
BA
aA
18.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
Свойства планов скоростей и ускорений
1. Векторы выходящие из полюса плана скоростей
(ускорений) изображают в масштабе векторы
абсолютных скоростей (ускорений) соответствующих
точек
2. Отрезки, соединяющие концы векторов, выходящих из
полюса,
изображают
в
масштабе
векторы
относительных
скоростей
(ускорений)
соответствующих точек
3. Сходственные фигуры звеньев на плане механизма и
плане скоростей (ускорений) – подобны
Примечание (правило обхода букв): направление обхода
букв сходственных фигур на плане механизма и плане
скоростей (ускорений)- одинаково
19.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
Определить
B
1
А
w1
VB, VC, VE,
aB, aC, aE,
2
w2, w3
D
E
3
C
e2 , e3
20.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
VB = w1 × l AB
Задаем масштаб плана скоростей
B
1
А
w1
VB
Длина вектора скорости точки В:
2
D
E
3
pv
VB
pvb =
mV
VB
C
b
21.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
ìïVC = VB + VCB ;
í
ïîVC = VD + VCD ;
B
1
А
w1
VB
E
VCD
^ BC c
^ DC
C
VCD ^ DC
2
D
VCB 3
VCB ^ BC
VCD = VC
VCB
pv
VB
b
22.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
^ BC c
B
VB
1
А
w1
D
VCBw
3
VCD
C
pv
VCB
VB
b
2
w2
^ DC
VCD = VC
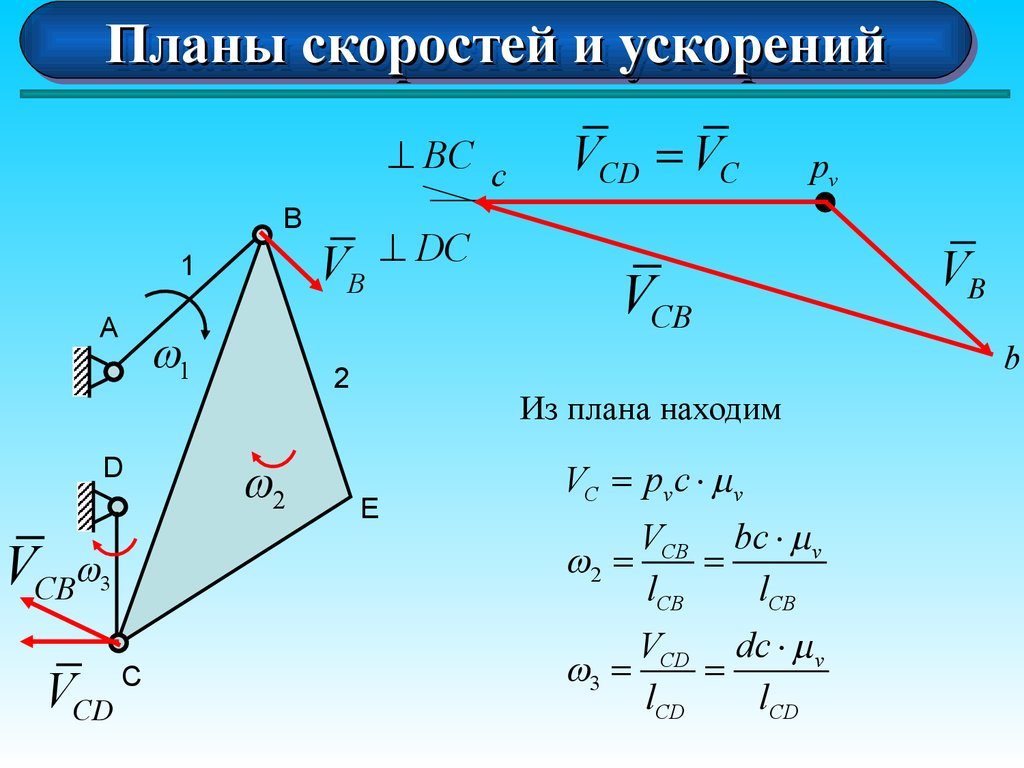
Из плана находим
E
VC = pv c × mv
VCB bc × mv
w2 =
=
lCB
lCB
VCD dc × mv
w3 =
=
lCD
lCD
23.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
Скорость точки Е найдем по правилу подобия
DBCE : Dbce
BE be
bc × BE
=
=> be =
BC bc
BC
CE ce
bc × CE
=
=> ce =
BC bc
BC
B
1
А
w1
VB
2
D
E
VCB 3
VCD
^ BC c
VCD = VC
^ DC
VCB
C
VE = pv e × mv
VE
e
pv
VB
b
24.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
aB = aBn = w12 × l AB
aB
Задаем масштаб плана ускорений
B
1
А
w1
Длина вектора ускорения точки В:
2
aB
pab =
ma
D
E
aB
3
C
b
pa,a,d
25.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
ìïaC = aB + a + a ; a PBC , a ^ BC
í
n
t
n
t
a
=
a
+
a
+
a
;
a
P
DC
,
a
ïî C
D
CD
CD
CD
CD ^ DC
n
a
n
aCB
= w22 × lBC => bn1 = CB
ma
n
CB
n
aCD
= w32 × lDC
t
CB
a
= e 2 × lBC
t
aCD
= e 3 × lDC
t
CB
n
CB
n
aCD
=> dn2 =
ma
t
CB
26.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
^ BC
aB
1
А
w1
a a
t
CB
t
CD
a
D
C
a
t
CB
a
n2
aÑ
a
2
Из плана находим
aC = pa c × m a
t
aCB
n1c × m a
e2 =
=
lCB
lCB
t
aCD
n2c × ma
e3 =
=
lCD
lCD
n
CD
a
n1
n
CB
E
n
CB
c
^ DC
e2
e3
n
CD
B
t
aCD
b
pa,a,d
aB
27.
ПланыПланы скоростей
скоростей ии ускорений
ускорений
^ BC
aB
B
t
aCD
c
^ DC
aÑ
1
А
w1
n
CD
a a
t
CB
t
CD
a
D
C
t
CB
a
aE
2
n
CB
a
e
e2
e3
n2
n
CD
a
n1
pa,a,d
aB
b
E
n
CB
a
Ускорение точки Е найдем по правилу подобия
DBCE : Dbce
aE = pa e × ma






















 Физика
Физика








