Похожие презентации:
Введение в математический анализ
1. Введение в математический анализ
Модуль 32. Понятие функции. Способы задания функций
• Пусть X – некоторое множестводействительных чисел.
3.
• Определение. Если каждомуэлементу x из множества X по
некоторому закону f ставится в
соответствие вполне
определённое действительное
число y, то говорят, что y есть
функция переменной величины
x и пишут y = f(x).
4.
• Множество X называетсяобластью определения
функции f(x) и обозначается D(f
). Множество всех значений y
функции y = f (x), когда x
пробегает всю область
определения, называется
областью изменения или
областью значений функции и
обозначается E(f ).
5.
• Например, для функции y = sin xобласть определения D(f ) = R,
область значений E(f ) = [–1; 1].
6.
• Различают следующие способызадания функции: табличный,
графический, аналитический (с
помощью формул).
7.
• Под графиком функциипонимают множество точек
плоскости, абсциссы которых
есть значения независимой
переменной, а ординаты равны
соответствующим значениям
функции. График фукции есть
некоторая линия на плоскости.
Например, уравнение y = x2
задает функцию, графиком
которой является парабола.
8.
• К основным элементарнымфункциям относятся:
• y = xa (при постоянном a ∊ R) –
степенная функция;
x
• y = a (при постоянном a ∊ R,
a > 0, a ≠ 1) – показательная
функция;
• y = loga x (при постоянном a ∊ R,
a > 0, a ≠ 1) – логарифмическая
функция;
9.
y = sin x, y = cos x, y = tg x,
y = ctg x – тригонометрические
функции;
y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x –
обратные тригонометрические
функции.
10.
• Функция, заданнаяпоследовательной цепью
нескольких функций (y = f(u), где
u = φ(x)), называется сложной
функцией. Например, функция
y = lg3(2x) сложная, и она может
быть представлена следующей
цепью основных элементарных
3
x
функций: y = z , z = lg u, u = 2 .
11.
• Функции, образованные изосновных элементарных
функций посредством конечного
числа алгебраических операций
и взятия функции от функции,
называются элементарными.
12.
• Все остальные функцииназываются неэлементарными.
Примером неэлементарной
функции может служить
функция вида
y 1 x x x ... x ...
2
3
n
13.
• Функция, определяемаяуравнениями y (t ),
x (t ),
в которых зависимость между y
и x устанавливается
посредством третьей
переменной t, называется
заданной параметрически, при
этом t – параметр.
14.
• Например, уравненияy 2t 1, x t 2
определяют линейную функцию
y 2(x 2) 1 2x 5
15. Предел числовой последовательности. Предел функции
16.
• Определение. Число Aназывается пределом
последовательности
a1, a2, …,an,…, если для любого
положительного числа ε
существует такой номер
N = N(ε), что при всех n > N
выполняется неравенство .
an A
17.
• Если последовательность a1, a2,…an,… имеет своим пределом
число A, то это записывается
следующим образом:
lim a n A
n
• или
an A npu n
18.
• Определение. Число Аназывается пределом функции
y = f(x) при x → a (в точке x = a),
если для каждого числа ε > 0
найдется такое число
δ = δ(ε) > 0, что при 0 <|x – a| < δ
выполняется неравенство
|f(x) – A| < ε.
19.
• Обозначают этот факт так:lim f ( x) A
x a
20.
• Если число A являетсяпределом функции y = f(x) при
x → a, то на графике это
иллюстрируется следующим
образом.
21.
• Так как из неравенства 0 <|x – a| < δследует неравенство |f(x) – A| < ε, то
это значит, что для всех x,
отстоящих от a не далее чем на δ,
точка M графика функции y = f(x)
лежит внутри полосы шириной 2ε,
ограниченной прямыми y = A – ε и
y = A + ε. Очевидно, что с
уменьшением ε величина δ также
уменьшается.
22.
23.
• Число A называется пределомфункции y = f(x) при x → ±∞,
если для любого ε > 0
существует число M > 0, что при
всех |x| > M выполняется
неравенство |f(x) – A| < ε.
24.
• Функция y = f(x) называетсяограниченной в области D,
если существует постоянное
число M > 0, что для всех x ∊ D
выполняется неравенство
|f(x)| < M.
25.
• Например, функция2
y
2
1 x
ограничена для всех x ∊ R, так
как в этой области |f(x)| ≤ 2.
26. Бесконечно малые и бесконечно большие функции
27.
• Определение. Функция α(x)называется бесконечно малой
при x → a, если lim ( x) 0
x a
• Функция β(x) называется
бесконечно большой при x → a,
если lim ( x)
x a
28.
• Например, функция y = sin xявляется бесконечно малой при
1
y
2
x → 0, а функция
x 1 есть
бесконечно малая при x → ±∞,
так как их пределы равны нулю.
Функция y = tg x является
бесконечно малой при x → 0 и
бесконечно большой при
x → π/2.
29.
• Теорема. Если функция α(x) –бесконечно малая при x → a, то
1
( x)
— бесконечно большая
функция при x → a
1
0
30.
• Если функция β(x) – бесконечнобольшая при x → a, то
1
( x) – бесконечно малая
функция при x → a 1
0
31.
• Справедливы следующиеутверждения:
• Сумма конечного числа
бесконечно малых функций есть
бесконечно малая функция.
32.
• Произведение ограниченнойфункции на бесконечно малую
есть бесконечно малая функция.
• Произведение конечного числа
бесконечно малых функций есть
бесконечно малая функция.
33. Теоремы о пределах
• Если пределы lim u ( x) и lim v( x)x a
x a
существуют и конечны, то
34.
1) limx a
cu( x) c lim u( x)
x a
где с = const;
2)
lim (u ( x) v( x))
x a
lim u ( x) lim v( x)
x a
x a
35.
3)lim (u ( x) v( x))
x a
lim u ( x) lim v( x)
x a
4)
x a
lim u ( x)
u ( x ) x a
lim
lim v( x)
x a v ( x )
x a
где lim v( x) 0
x a
36. Замечательные пределы
• Первый замечательный предел:sin x
lim
1
x 0 x
37.
• Второй замечательный предел:x
1
lim 1 lim 1 x
x
x
x
1
x
e
где e — иррациональное число,
e ≈ 2,718281828 — одна из
фундаментальных величин в
математике.
38.
• Функция y = ex = exp(x)называется экспонентой;
y = loge x = ln x называется
натуральным логарифмом.
39.
• Пример. Вычислить2
lim
x 2
x 3x 3
2
x x 3
40.
• Решение.Так как2
2
lim ( x x 3) lim x lim x 3 3 0
x 2
x 2
x 2
то применима теорема о
пределе частного. Значит,
2
x 3x 3
2
lim ( x 3x 3)
1
lim
2
x 2 x 2 x 3
lim ( x x 3) 3
x 2
x 2
41.
• Пример. Вычислить3
lim
x
2
2 x 3x 1
3
x 4x 2
42.
• Решение. Так как при x → ∞числитель и знаменатель дроби,
стоящей под знаком предела,
стремятся к бесконечности, то
имеем неопределенность вида
43.
• Для раскрытия такихнеопределенностей делят
числитель и знаменатель дроби
на старшую степень x. После
деления на x3 получаем:
44.
3 12 3
3
2
2 x 3x 1
x
x
lim 3
lim
x x 4 x 2
x
4 2
1 2 3
x
x
2 0 0
2
1 0 0
45.
• Пример. Вычислить2
lim
x 3
x x 12
2
x 9
46.
• Решение. Так какlim ( x x 12) 0,
2
x 3
lim ( x 9) 0
2
x 3
то имеем неопределённость
вида
0
0
47.
• Так как,x x 12 ( x 3)( x 4);
2
x 9 ( x 3)( x 3)
2
• то
x x 12
( x 3)( x 4)
lim
lim
2
x 3
x 3 ( x 3)( x 3)
x 9
x 4 7
lim
x 3 x 3
6
2
48.
• Пример. Вычислитьlim
x 2
x 7 3
2
x 3x 2
49.
• Решение. Имеемнеопределенность вида
Умножим числитель и
знаменатель дроби на
выражение ( x 7 3 ), а
также разложим знаменатель на
линейные множители:
0
0
50.
x 7 3 0lim 2
x 2 x 3x 2
0
x 7 3 x 7 3
lim
x 2 x 1 x 2
x 7 3
51.
x 7 9lim
x 2 x 1 x 2
x 7 3
x 2
lim
x 2 x 1 x 2
x 7 3
lim
x 2
x 1
1
1
x 7 3 6
52.
• Пример. Вычислитьsin 7 x
lim
x 0 tg 3 x
53.
• Решение. Для раскрытия0
неопределённости
0
воспользуемся первым
замечательным пределом.
Считая, что x ≠ 0, проведём
очевидные преобразования:
54.
sin 7 xlim
x 0 tg 3 x
sin 7 x
sin 7 x
7x
7
7
x
7
x
lim
lim
cos 3 x
x 0
x 0 sin 3 x
sin 3 x
3x
3
cos 3x 3x
3x
sin 7 x
lim
7 x 0 7 x
7 1
7
lim cos 3x 1
sin 3x x 0
3
3 1
3
lim
x 0 3x
55.
• Пример. Вычислить2
lim 1
x
x
x
56.
• Решение. Для раскрытия∞
неопределённости 1
воспользуемся вторым
замечательным пределом:
57.
2lim 1
x
x
x
x
2 2
lim 1
x
x
2
e
2
поскольку
x
2 2
lim 1
x
x
y
1
lim 1 e
x
y
y
2
58. Сравнение бесконечно малых функций
• Для сравнения двух бесконечномалых функций α(x) и β(x) в
точке x = a находят предел
( x)
отношения
lim
x a
( x)
A
59.
• Если A ≠ 0 и A ≠ ∞, то функцииα(x) и β(x) называются
бесконечно малыми одного
порядка.
• Если A = 0, то α(x) называется
бесконечно малой высшего
порядка по сравнению с β(x).
Записывается это так:
α(x) = o(β(x)).
60.
• Если A = 1, то бесконечно малыефункции α(x) и β(x) называют
эквивалентными и обозначают
α(x) ~ β(x). Например, sin x ~ x
при x → 0, так как
sin x
lim
1
x 0 x
61.
• Основные эквивалентностипри x → 0:
• sin kx ~ kx,
tg kx ~ kx,
• arcsin kx ~ kx,
arctg kx ~ kx,
• ln (1+kx) ~ kx,
ekx – 1 ~ kx.
62.
• При вычислении пределовиспользуют следующую
теорему.
• Теорема. Предел отношения
двух бесконечно малых функций
в некоторой точке равен
пределу отношения
эквивалентных им бесконечно
малых функций в той же точке.
63.
• Пример. Вычислить1 cos 5 x
lim
x 0 x sin 3 x
64.
• Решение. Воспользуемсяэквивалентными бесконечно
малыми функциями. Так как при
x→0
5x
1 cos 5 x 2 sin
2
2
2
x
5x
~ 2 25
2
2
• и sin 3x ~ 3x, то
2
~
65.
1 cos 5 x 0lim
x 0 x sin 3 x
0
2
x
25
25
2
lim
x 0 x 3 x
6
66. Сравнение бесконечно малых функций
• Для сравнения двух бесконечномалых функций α(x) и β(x) в
точке x = a находят предел
отношения
( x)
lim
x a
( x)
A
67.
• Если A ≠ 0 и A ≠ ∞, то функцииα(x) и β(x) называются
бесконечно малыми одного
порядка.
• Если A = 0, то α(x) называется
бесконечно малой высшего
порядка по сравнению с β(x).
Записывается это так:
α(x) = o(β(x)).
68.
• Если A = 1, то бесконечно малыефункции α(x) и β(x) называют
эквивалентными и обозначают
α(x) ~ β(x). Например, sin x ~ x
при x → 0, так как
sin x
lim
1
x 0 x
69.
• Основные эквивалентностипри x → 0:
• sin kx ~ kx,
tg kx ~ kx,
• arcsin kx ~ kx,
arctg kx ~ kx,
• ln (1+kx) ~ kx,
ekx – 1 ~ kx.
70.
• При вычислении пределовиспользуют следующую
теорему.
• Теорема. Предел отношения
двух бесконечно малых функций
в некоторой точке равен
пределу отношения
эквивалентных им бесконечно
малых функций в той же точке.
71.
• Пример. Вычислить1 cos 5 x
lim
x 0 x sin 3 x
72.
• Решение. Воспользуемсяэквивалентными бесконечно
малыми функциями. Так как при
x→0
2
2
5
x
5x
x
1 cos 5x 2 sin
~2
25
2
2
2
2
и sin 3x ~ 3x, то
73.
1 cos 5 x 0lim
x 0 x sin 3 x
0
2
x
25
25
2
lim
x 0 x 3 x
6
74. Непрерывность функции
• Определение. Функция y = f(x)называется непрерывной в
точке x = x0, если предел
функции в точке x0 существует и
lim f ( x) f ( x0 )
x x0
75.
• Односторонними называютсяпределы:
левосторонний предел в точке a:
lim f ( x) lim
x a
x a
x a 0
f ( x) f (a 0)
правосторонний предел в точке
a: f ( x) lim f ( x) f (a 0)
lim
x a
x a
x a 0
76.
• Определение. Функция y = f(x)называется непрерывной в
точке x = x0, если существуют
односторонние пределы в точке
x0 и
lim
x x0 0
f ( x)
lim
x x0 0
f ( x) f ( x 0 )
77.
• Если односторонние пределыконечны, но нарушается хотя бы
одно из равенств
lim
x x0 0
f ( x)
lim
x x0 0
f ( x) f ( x 0 )
то x0 называется точкой
разрыва 1-го рода.
78.
• Если хотя бы один из этиходносторонних пределов не
существует или равен
бесконечности, то x0 называется
точкой разрыва второго рода.
79.
• Например, функцияnpu x 1,
1,
y
x 1
1, npu x 1
x 1
имеет в точке x = 1 разрыв 1-го
рода
80.
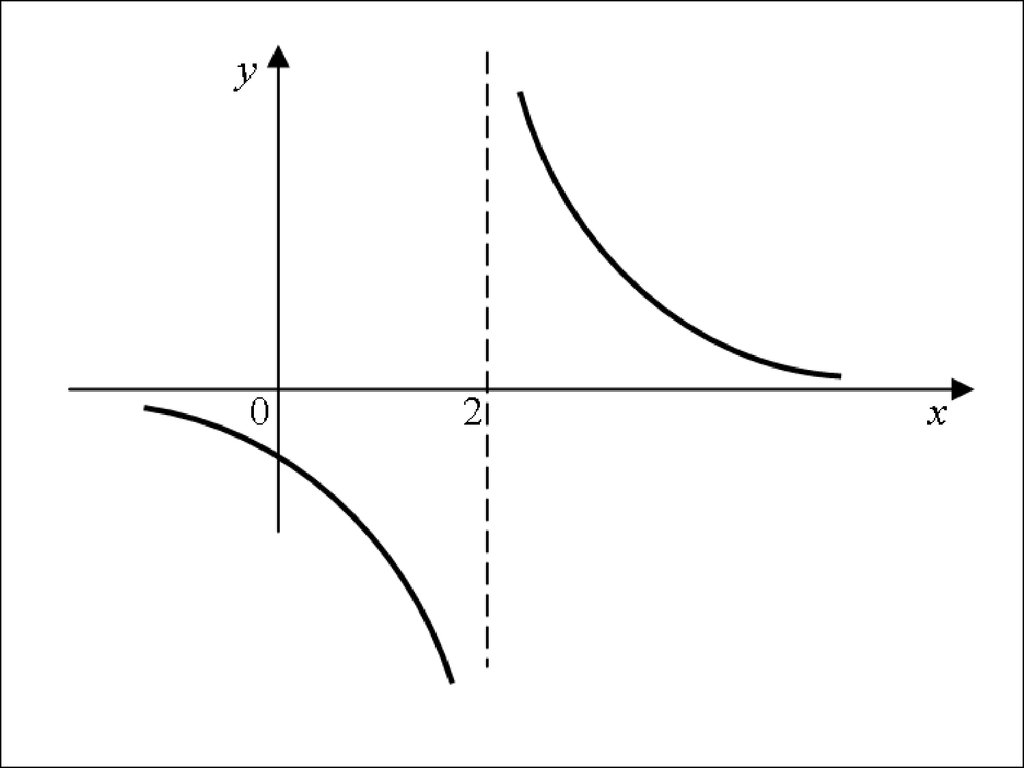
81.
• Функция1
y
x 2
имеет в точке x = 2 разрыв
второго рода
82.
83.
• Если функция непрерывна вовсех точках отрезка [a; b], то она
называется непрерывной на
этом отрезке.
84.
• Из определения непрерывностифункции и теорем о пределах
следуют теоремы:
• I. Если функции f(x) и g(x)
непрерывны в точке x0, то в этой
точке непрерывны функции
f (x) g(x)
f (x) g(x)
f ( x)
g ( x)
( g ( x0 ) 0)
85.
• II. Сложная функция,составленная из непрерывных
функций, непрерывна в
соответствующей точке.
• III. Всякая элементарная
функция непрерывна в каждой
точке своей области
определения.


































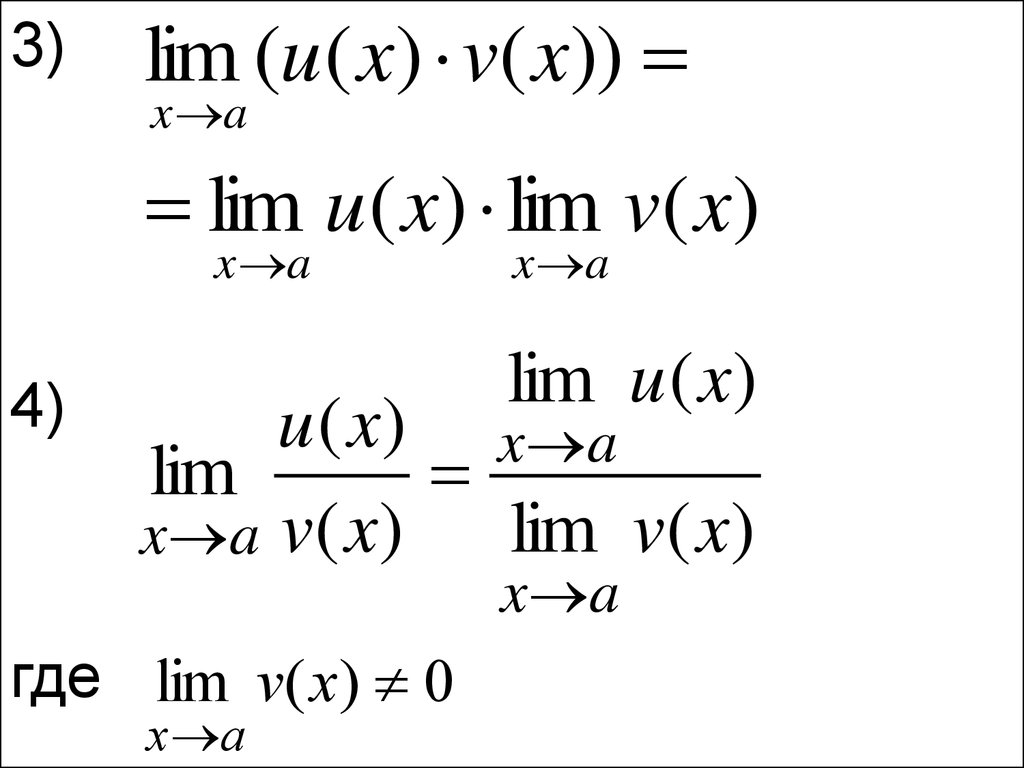








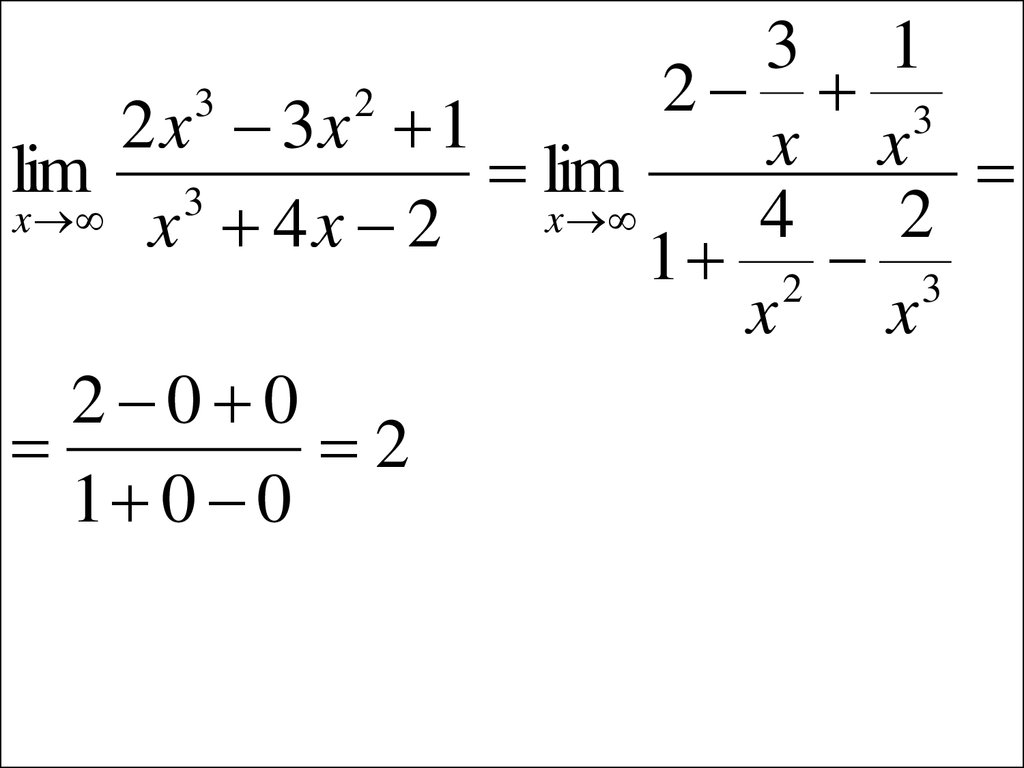












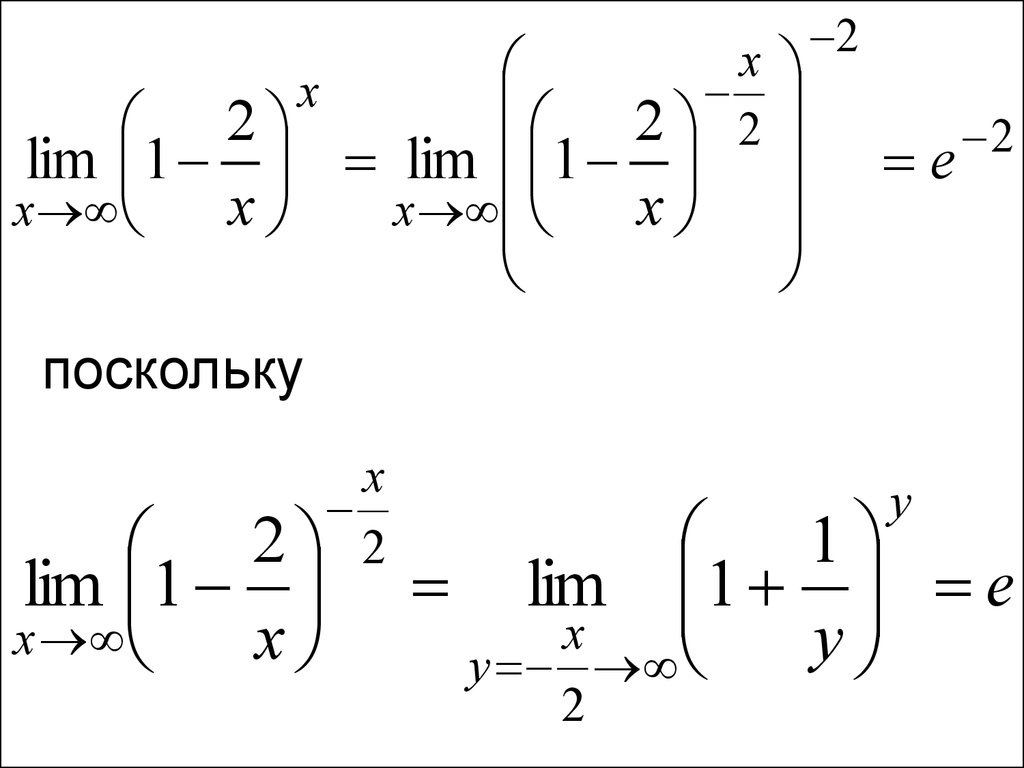










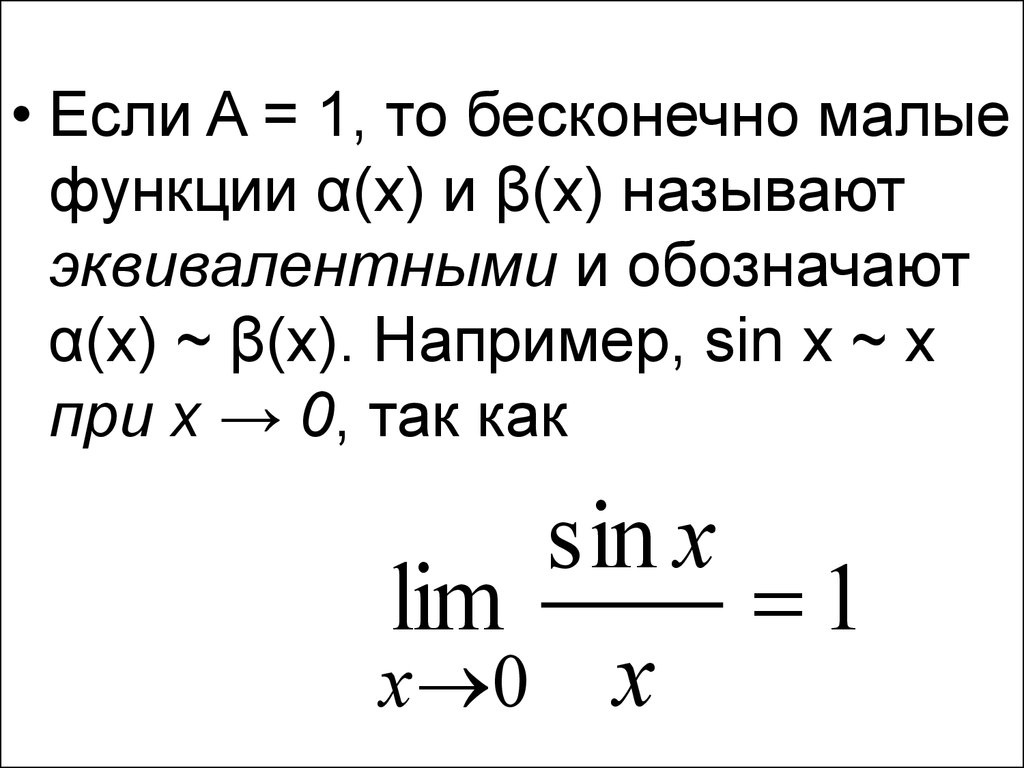


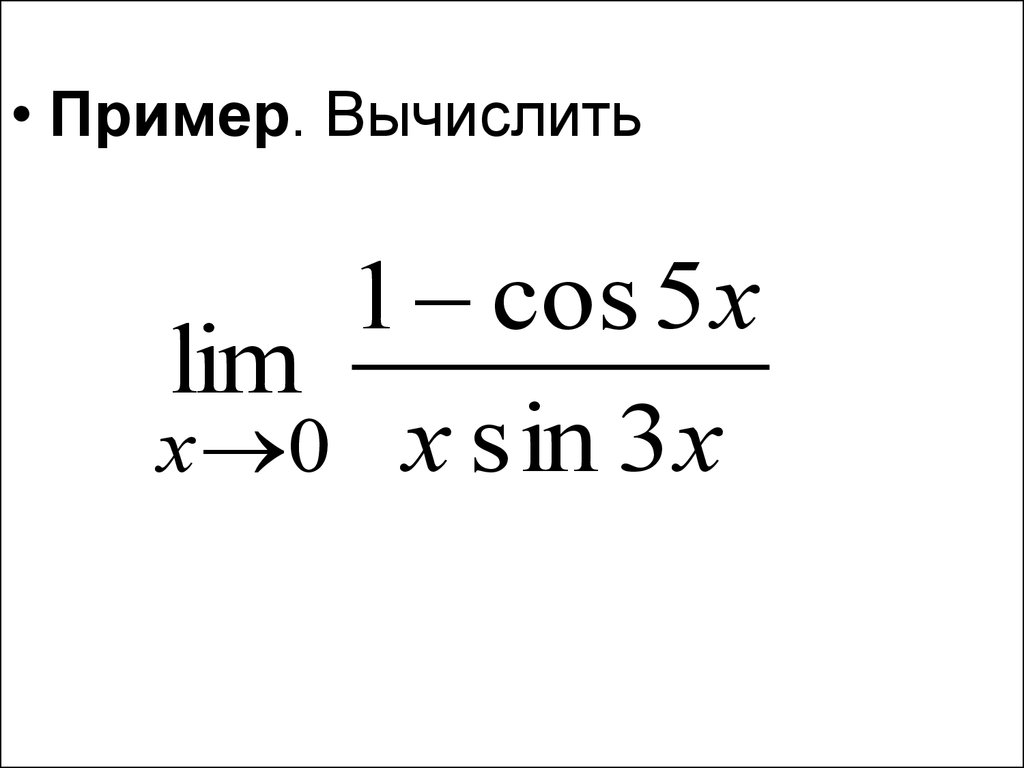













 Математика
Математика








